概率论
超级简要的知识点复习,针对面试的简单问题
基本概念¶
- 互斥事件 \(a\cap b=\phi\)
- 对立事件 \(a\cap b=\phi,a\cup b=S\)
- 乘法定理 (基于条件概率):\(P(A_{1}A_{2}\ldots A_{n})=P(A_{1})P(A_{2}|A_{1})\ldots P(A_{n-1}|A_{1}A_{2}\ldots A_{n-2})\) \(P(A_{n}|A_{1}A_{2}\ldots A_{n-1})\)
随机变量及其分布律¶
- 分布函数 \(F(x)=P\{ X\leq x \}\)
- 具有单调性,规范性(负无穷为 0 正无穷为 1),右连续性
- 对于连续分布有 \(F\left(x\right)=\int_{-\infty}^{x}f\left(t\right)dt\) 其中 \(f\) 为概率密度函数
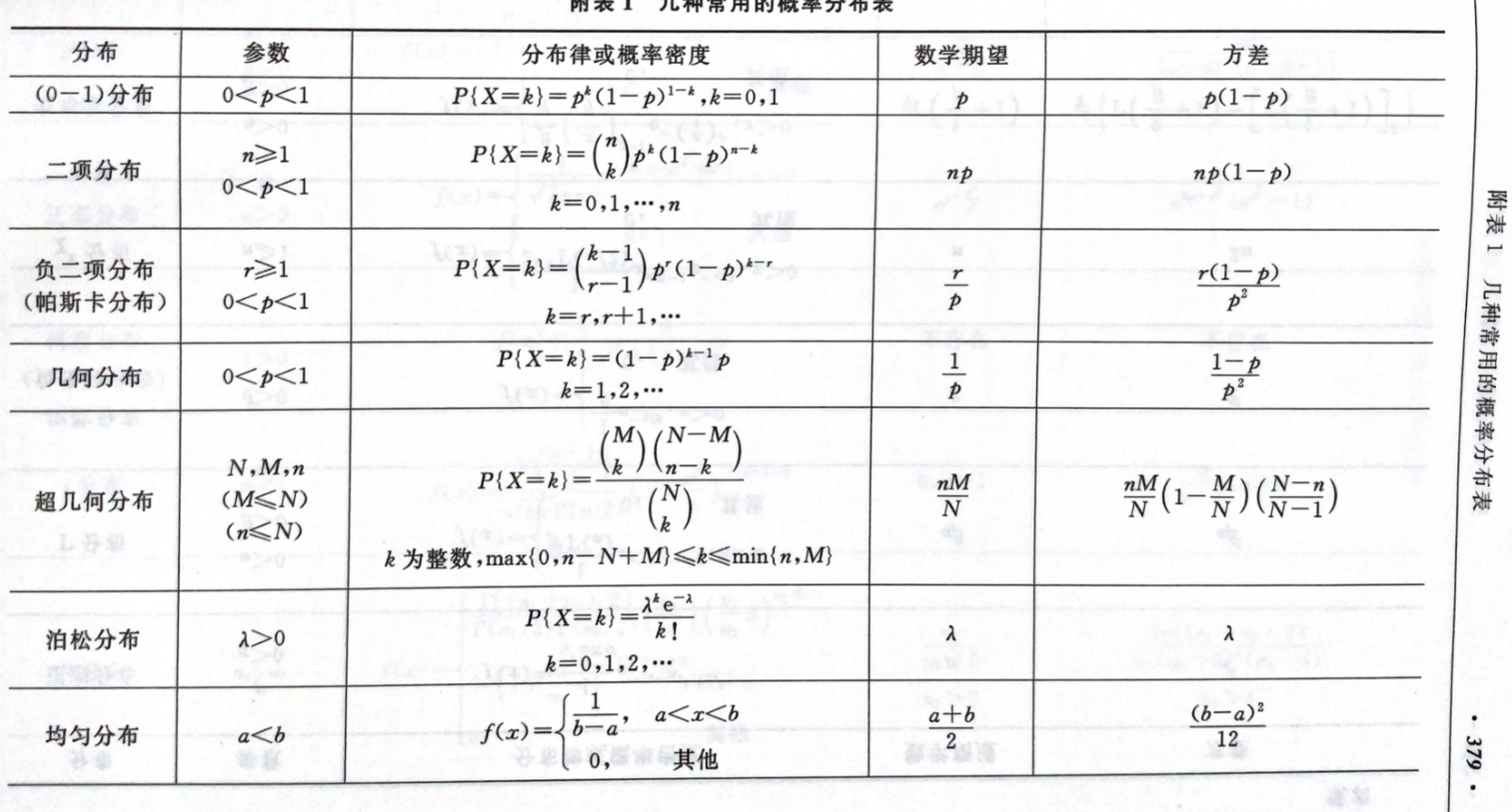
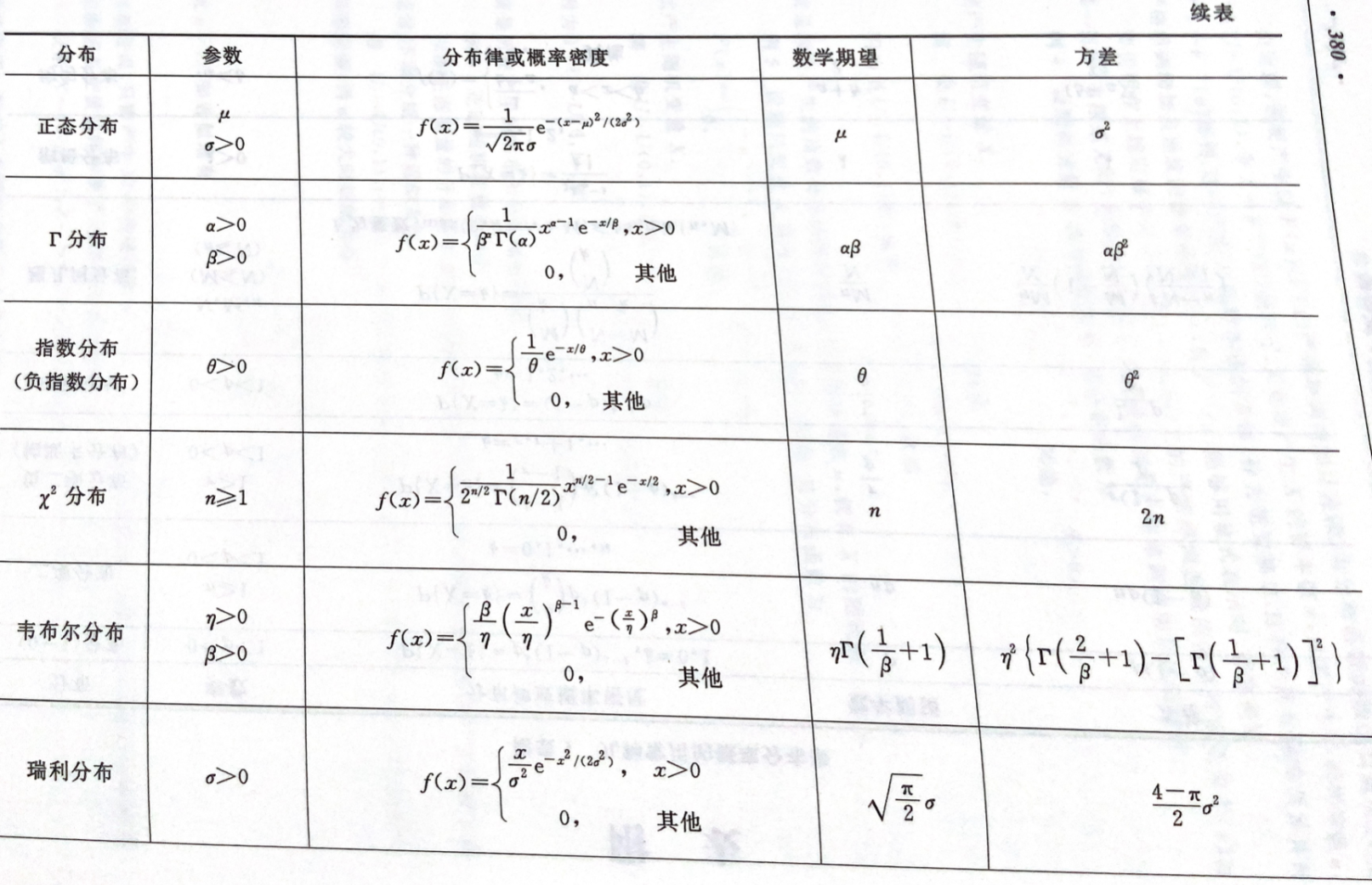
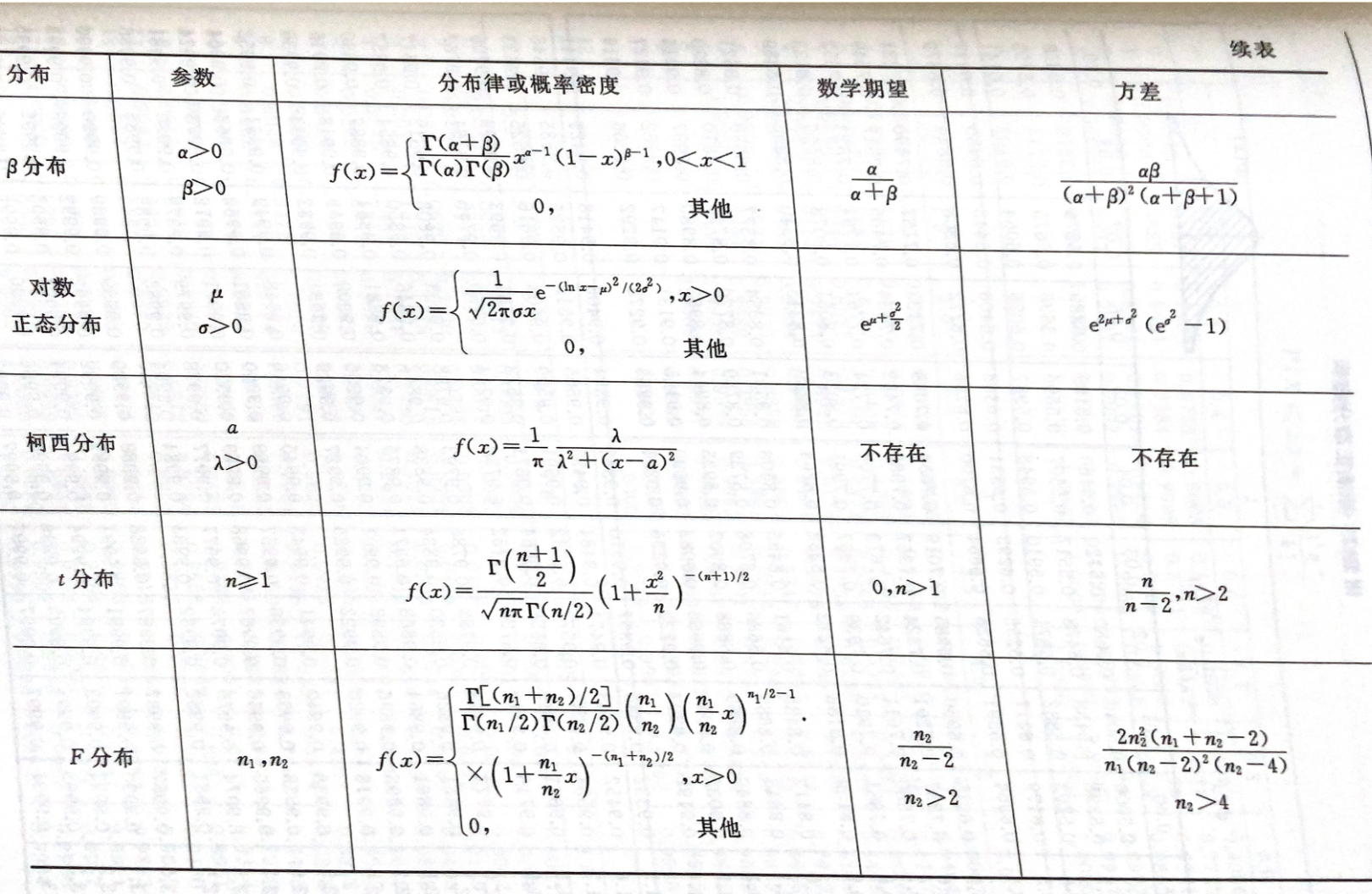
常见离散分布¶
- 二项分布:\(P\{x=k\}=C_{n}^{k}p^{k}q^{n-k}(k=0\cdots n)记 X\sim b (n, p)\)
- \(n\) 较大 \(p\) 较小时可以近似为泊松分布
- 负二项分布(实验 k 次时结果第 r 次出现):\(P\left\{x=k\right\}=C_{k-1}^{r-1}p^{r}\left(1-p\right)^{k-r}\)
- 几何分布:\(p\{ x=k \}=q^{k-1}p\)
- 超几何分布:\(P\{x=k\}=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}}\)
常见连续分布¶
- 均匀分布
- 指数分布:具有无记忆性
- 正态分布:\(X\sim N(\mu,\delta^{2})\)
- 其中 \(\delta\) 越小,图形越陡峭
- 若 \(P\{ x>Z_\alpha \}=\alpha\) 则 \(Z_{\alpha}\) 为标准正态分布上的 \(\alpha\) 分位点
联合分布¶
- 联合分布: \(F(x,y)=P\{X\leq x\}\cap\{Y\leq y\}=P\{x\leq x,Y\leq y\}\)
- 边缘分布:
- \(F_X(x)=F(x,+\infty)=\int_{-\infty}^x\left[\int_{-\infty}^{+\infty}f(u,y)dy\right]du\)
- \(F_Y(y)=F(+\infty,y)=\int_{-\infty}^y\left[\int_{-\infty}^{+\infty}f(x,v)\:dx\right]\:dv\)
- 有联合分布可以唯一确定边缘分布,反之不成立 (具有独立性时成立 \(f(x,y)=f_{X}(x)f_{Y}(y)\))
- 条件分布的分布函数
- \(F_{X|Y}(x|y)=\int_{-\infty}^x\frac{f(u,y)}{f_Y(y)}du\)
- \(F_{Y|X}(y|x)=\int_{-\infty}^y\frac{f(x,v)}{f_X(x)}dv\)
期望与方差¶
- 期望 \(E(x)=\int_{-\infty}^{+\infty}xf(x)dx\)
- 如果 \(E(x)=\int_{-\infty}^{+\infty}|xf(x)|dx\) 收敛则存在数学期望
- 条件期望:\(E[x|Y=y]=\int_{-\infty}^{+\infty}xf_{X|Y}(x|y)dx\)
- 方差 \(D(x)=\int_{-\infty}^{+\infty}[x-E(x)]^{2}f(x)dx\)
- 条件方差:\(D(X|Y)=E[(x-E(x|Y))^2|Y]\)
- 切比雪夫不等式:给出均值和方差估计分布 \(P\{|x-\mu|\geq\epsilon\}\leq\frac{\delta^{2}}{\epsilon^{2}}\)
- 协方差 \(Cov(X,Y)=E(XY)-E(X)E(Y)\)
- \(D(X\pm Y)=D(X)+D(Y)\pm 2Cov(X,Y)\)
- 相关系数 \(p_{xy}=\frac{Cov(X,Y)}{\sqrt{D(Y)D(Y)}}\)
- 有 \(\leq 1\)
- 若等于 1 则 XY 线性相关
- 若等于 0 则 XY 不相关(不是说独立)
特征函数¶
- 特征函数完全刻画了随机变量的分布,可以通过它唯一确定随机变量的概率分布。并且具有良好的数学性质,便于研究。
- \(\varphi_X(t)=\mathbb{E}[e^{itX}]=\int_{-\infty}^{+\infty}e^{itx}f_X(x)dx\)
- 可以通过特征函数得到期望及方差 \(f^{(k)}(0)=i^kE(i^k)\)
大数定律与中心极限定理¶
- 大数定律
- 定义:大数定律说明了在进行大量独立同分布的随机试验时,样本均值将趋近于总体均值。换句话说,随着样本数量的增加,观测值的平均值会越来越接近期望值。
- 意义:大数定律保证了长期来看,随机现象的平均结果是稳定的。例如,投掷足够多次硬币,正反面的比例将趋近于50%。
- 中心极限定理
- 定义:中心极限定理表明,对于一组独立同分布的随机变量,其和或均值在样本数量趋近于无穷大时,其分布将趋近于正态分布,无论这些随机变量的原始分布是什么。
- 意义:中心极限定理解释了为什么正态分布在自然和社会科学中如此普遍存在,即使单个现象不是正态分布,但它们的累加结果却趋近于正态分布。这使得正态分布成为许多统计分析方法的基础。