离散数学

时间紧迫，以概念为主，附加简单例子。限于之前笔记形式，图片质量较低

逻辑与推理

命题逻辑

• 命题：
  • 是一个陈诉事实的句子
  • 要么为真要么为假
• 使用小写字母（命题变元）代表命题，取值范围为 \(\{T,E\}\)
• 命题表达式：命题表达式由命题变元和运算符组成

• 运算符

  • 非 \(\neg\)
  • 合取 \(\wedge\)
  • 析取 \(\vee\)
  • 蕴含 \(p\to q\)：p=1 q=0 是为 false，其他时候为 true
  • 双蕴含 \(p\leftrightarrow q\)：“当仅当“，具有相同值时为 true（也称 pq 逻辑等价）
  • 优先级：\(\neg, \wedge,\vee,\to,\leftrightarrow\)

• 将自然语言翻译为命题表达式（例子）

  • 
  • 

• 特殊的命题表达式

  • 永真式
  • 矛盾式
  • 可能式

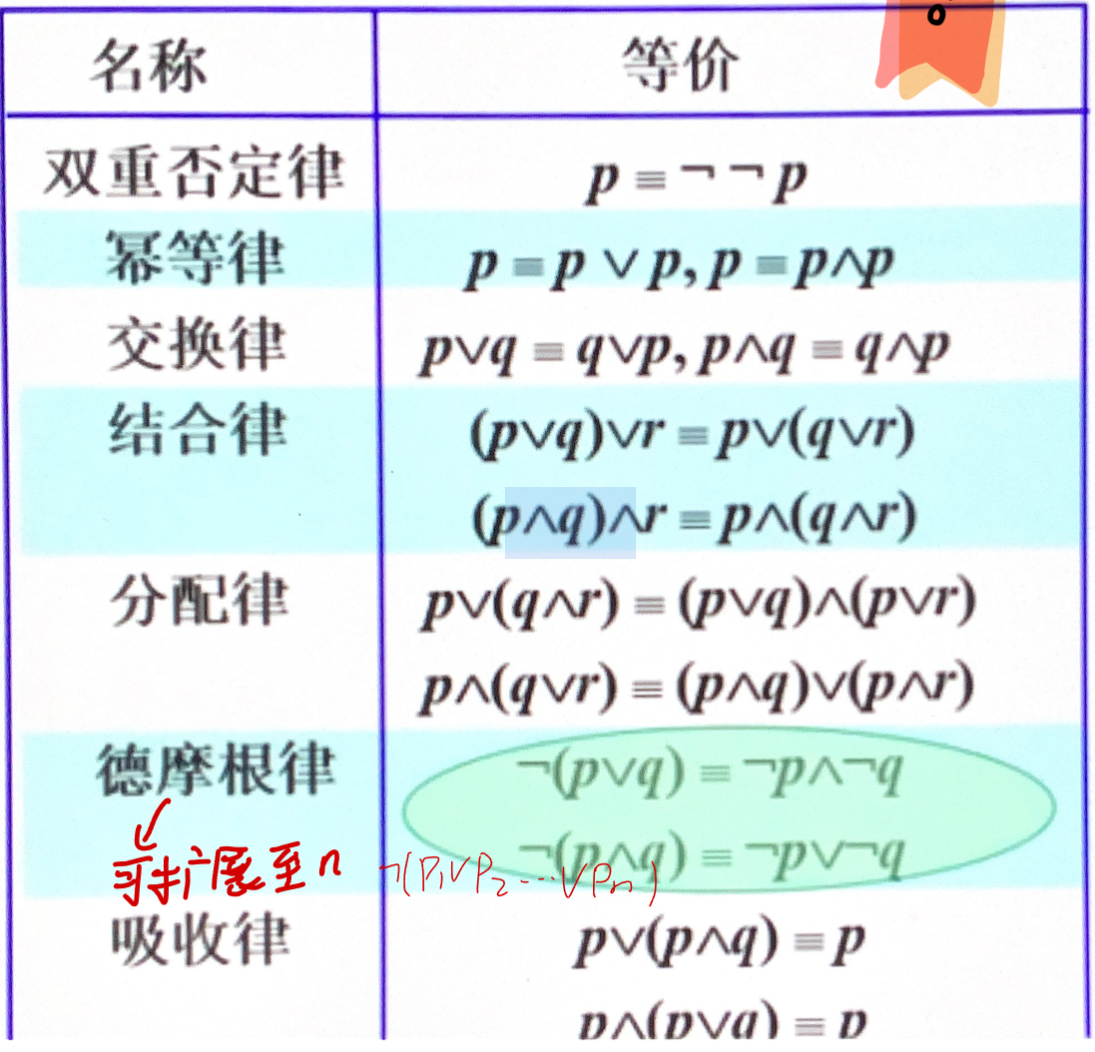
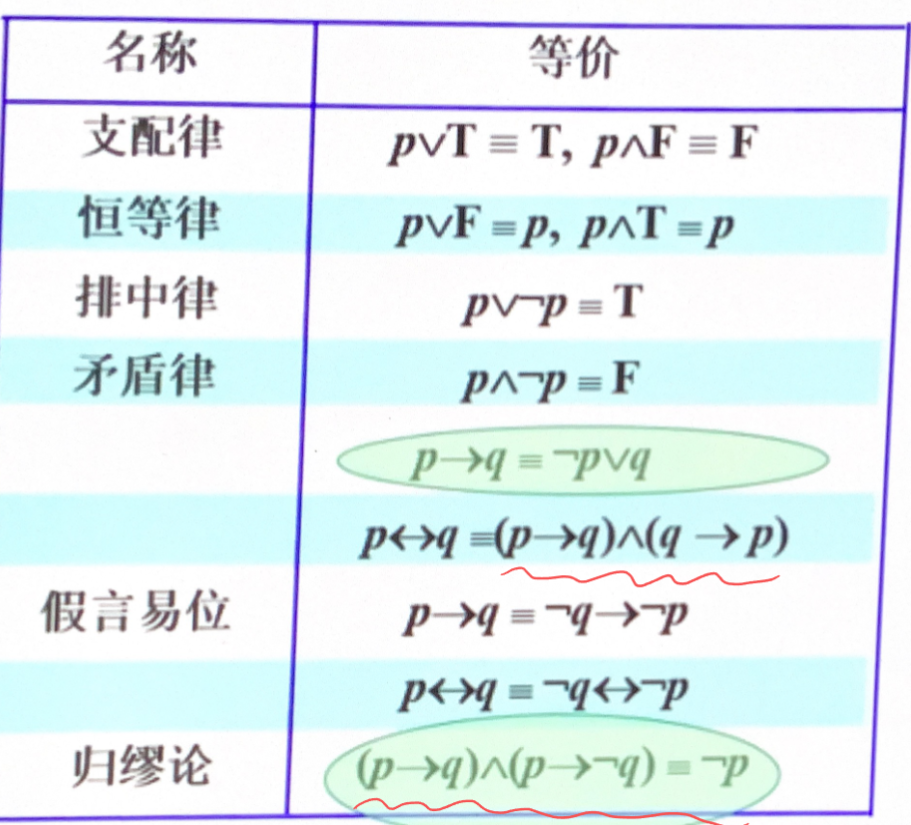
• 逻辑等价

  • 
  • 
  • 

• 合取范式 CNF

  • 可以用于判断满足性，求解假指派
• 析取范式 DNF
  • 可以用于求解真指派
• 直接化简表达式较麻烦，可以用真值表求解范式
  • 合取取成假的，即出现一个这种取值就为 false
  • 析取取成真的，出现一个这种取值就为 true
• 主范式：每个括号内都出现所有命题变元，并按照自然顺序进行排序
• 使用真值表求解的例子
  • \(A\vee(B\wedge C)\)
  • CNF：\((A\lor B\lor C)\land(A\lor B\lor\lnot C)\land(A\lor\lnot B\lor C)\)
  • DNF：\(A \lor (\neg A \land B \land C)\)

A	B	C	B ∧ C	A ∨ (B ∧ C)
F	F	F	F	F
F	F	T	F	F
F	T	F	F	F
F	T	T	T	T
T	F	F	F	T
T	F	T	F	T
T	T	F	F	T
T	T	T	T	T

• 命题推理

逻辑关系	表达式	结果
假言推理	p, p→q	q
取拒式	¬q, p→q	¬p
假言三段论	p→q, q→r	p→r
析取三段论	¬p, p∨q	q
附加律	p	p∨q
化简律	p∧q	p
合取律	p, q	p∧q
消解律	p∨q, ¬p∨r	q∨r
-
#### 谓词逻辑
- 允许使用量词来表达某些属性或关系适用于一些或所有可能的对象。谓词逻辑比命题逻辑表达能力更强，因为它能详细描述事物之间的关系以及事物的属性。
- 全称量词：\(\forall\)
- 存在量词：\(\exists\)
- 谓词：
- 一元谓词 ：\(P (x)\)
- 二元谓词：\(P(x,y)\)
- 约束变元：受到量词约束；自由变元：不受到两次约束
- 
- 量词公式
- \(\forall x\forall y=\forall y\forall x\)
- \(\exists x\exists y=\exists y \exists x\)
- 对于混合 \(\forall \exists\) 的情况不能随意调换顺序
- 

• 等价式
  • \(\neg\forall xp(x)\equiv\exists x\neg p(x)\) \(\neg\exists xp(x)\equiv\forall x\neg p(x)\)
  • \(\begin{aligned}\forall x(P(x)\wedge Q(x))\equiv(\forall x P(x))\wedge(\forall xQ(x))\\\exists x(P(x)\vee Q(x))\equiv(\exists xP(x))\vee(\exists xQ(x))\end{aligned}\)
  • \(\begin{aligned}(\forall xP(x))\vee(\forall xQ(x))\to\forall x(P(x)\vee Q(x))\\\exists x(P(x)\wedge Q(x))\to(\exists xP(x))\wedge(\exists xQ(x))\end{aligned}\)
  • \(\begin{aligned}\forall x(P(x)\vee R)\equiv(\forall xP(x))\vee R\\\exists x(P(x)\wedge R)\equiv(\exists xP(x))\wedge R\end{aligned}\)
  • \(\begin{aligned}\forall x({R}\rightarrow p(x))\equiv{R}\rightarrow\forall xP(x)\quad\exists x({R}\rightarrow{P}(x))\equiv{R}\rightarrow\exists xP(x)\\\forall x(P(x)\rightarrow{R})\equiv(\exists xP(x))\rightarrow{R}\quad\exists x({P}(x)\rightarrow{R})=(\forall xP(x))\rightarrow{R}\end{aligned}\)

• 前束范式：将 \(\forall \exists\) 放在表达式最前面

  • 

• 自然演绎规则

  • 全称例示 \(\forall p(x)\to p(c)\)
  • 全称生成 \(p(c)对任意 c\to\forall xp(x)\)
  • 存在例示 \(\exists xp(x)\to p(c)对于某个c\)
  • 存在生成 \(p(c)对某个 c\to \exists xp(x)\)

• 

• 谓词逻辑具有：不可判定性和推理复杂性

  • 不存在一个通用的算法能够判定任意给定的逻辑陈述是否是可证的
  • 在谓词逻辑中，推理任务通常是非常复杂的，它们可以是NP-难的

证明方法

• 定理：能被证明为真的陈述
  • 证明：表明陈述为真的有效论证
  • 定理证明中可以使用的陈述：定理前提、术语定义、公理、已经证明的定理
• 直接证明
  • 
• 反证法 \(\neg q \to\neg p\) 推导出 \(p\to q\)（是归谬法的特例，通常用于证明命题的真实性）
  • 
  • 广义反证法：\(p_{1}\wedge\dots\wedge p_{n}\to q\equiv\neg q\wedge p_{1}\dots\to F\)
• 归谬法：通过假设某个命题为真，然后从这个假设出发逻辑推导，直至推出一个矛盾或荒谬的结论，从而证明这个命题实际上是假的
  • 
• 等价性证明
  • 
• 分类讨论
• 存在性证明
  • 构造性证明（构造说明给出具体示例）
  • 非构造性性证明（说明存在，但是不给出具体实例）
• 唯一性证明
  • \(\begin{aligned}&\exists x\left(P(x)\wedge\forall y\left(y\neq x\rightarrow\neg P(y)\right.\right)\\&\exists x\left.P(x)\wedge\forall y\right.\forall z\left(P(y)\wedge P(z)\rightarrow y=z\right)\end{aligned}\)
• 寻找反例
  • 找出一个反例进行否定

数学归纳法与良序原理

• 数学归纳法的基本过程

  • 基础步骤：证明 \(P(0)\)
  • 归纳步骤： 归纳假设 \(P(k)\) 证明 \(P(k+1)\)

• 强数学归纳法

  • 归纳步骤改为假设 \(P(0)\dots P(k)\) 成立，证明 \(P(k+1)\) 成立

• 良序原理：自然数 \(N\) 的任何非空子集 \(S\) 均有最小元素\(\exists a\in S(\forall b\in S(a\neq b\to a<b))\)

  • 数学归纳法实际上是基于自然数集的良序性质。由于自然数集是良序的，我们可以确定序列的起点，并且可以保证每个数都有一个后继数，即 𝑘 之后有 𝑘+1。这就提供了数学归纳法中从 𝑘 到 𝑘+1 这一步骤的逻辑基础。（并且保证证明是完全的不会有遗漏）

• 结构归纳法

  • 结构归纳法不局限于自然数，适用于任何可以递归定义的结构，适用于逻辑表达式、树、图等数据结构
  • 基础步骤：证明对于初始元素来说命题成立
  • 递归步骤：针对生产新元素的规则，若相关元素满足命题，则新元素也满足命题

• 程序的正确性

  • Hoare 三元组 \(\{ P \}S\{ Q \}\)：\(S\) 是一段程序，\(PQ\) 是程序中变量的断言，分为前置断言和后置断言
  • 如果 \(S\) 执行之前 \(P\) 成立，那么就有 \(S\) 运行完之后 \(Q\) 成立
  • 这就满足了部分正确性，完全正确性还要求程序能在有限步内终止

数学

数论

数及运算

• 皮亚诺公理
  • 零是自然数
  • 每个自然数都有一个自然数后继
  • 零不是任何自然数的后继
  • 不同自然数有不同的后继
  • 若由自然数组成的某个集合含有零，并且每当该集合含有某个自然数时便也同时含有这个自然数的后继，那么该集合定义所有自然数
• 自然数的集合表示：\(0\) 表示 \(\phi\)；\(S(x)=x\cup \{ x \}\) \(\begin{aligned}1&=S(0)=S(\emptyset)=\emptyset\cup\{\emptyset\}=\{\emptyset\}=\{0\}\\2&=S(1)=S(\{0\})=\{0\}\cup\{\{0\}\}=\{0,\{0\}\}=\{0,1\}\\3&=S(2)=S(\{0,1\})=\{0,1\}\cup\{\{0,1\}\}=\{0,1,\{0,1\}\}=\{0,1,2\}\end{aligned}\)
• 加法定义：\(m+0=m\)，\(m+S(n)=S(n+m)\)
• 乘法定义：\(m\times{0}=0\)，\(m\times S(n)=S(m\times n)\)
• 减法不封闭：将自然数扩展至整数
• 除法扩展至实数

数论初步

• 整除：\(b=ac\) 称 \(a\) 整除 \(b\) 记作 \((a|b)\)
  • \(a\mid b\) 则 \(a\mid bc\)
  • \(a\mid b\) 且 \(b\mid c\) 则 \(a\mid c\)
  • \(a\mid b\) 且 \(a\mid c\) 则 \(a\mid(mb+nc)\)
• 带余除法
  • \(a\) 为整数，\(d\) 为正整数，则存在唯一的整数 \(0\leq r<d\) 满足 \(a=dq+r\)，记 \(q=a\ div\ d\)，\(r=a\ mod\ d\)
  • 同余：\(a,b\in Z;m\in Z^+\) 若 \(m|(b-a)\) (即 \(a=b+km\))则称 \(a\) 与 \(b\) 模 \(m\) 同余，记为 \(a\equiv b(mod\ m)\) ，同余具有传递性和对称性

• 同余算术：在模 \(m\) 同余的情况下将算术范围限制在 \(Z_{m}=\{ 0,\dots,m-1 \}\)

  • 模 \(m\) 加：\(a+_{m}b=(a+b)mod\ m\)
  • 模 \(m\) 乘：\(a·_{m}b=(a·b)mod\ m\)
  • 

• 对于 \(a_{1}\equiv b_{1}(mod\ n)\) 和 \(a_{2}\equiv b_{2}(mod\ n)\)

  • 支持加减乘除以及幂运算（即任意整系数多项式）
  • \(p(a)\equiv p(b)(mod\ n)\)
    • 应用 \(32^{68}mod\ 31\to 1\dots 1mod\ 31\)
    • （因为 \(32\equiv 1(mod/ 31)\)）
  • 但注意 \(k^a!\equiv k^b(mod\ n)\)
  • 若 \(d\mid m\) 则 \(a\equiv b(mod\ m)\to a\equiv b(mod\ d)\)
  • \(a\equiv b(mod\ m)\iff da\equiv db(mod\ dm)\)
  • \(c,m\) 互素 \(a\equiv b(mod\ m)\iff ca\equiv cb(mod\ m)\)

• 算术基本定理：每个大于 1 的正整数都可以唯一的写为一个素数或若干素数的乘积，其中素数因子以非递减出现 \(n=p_{1}^{\alpha_{1}}\dots p_{k}^{\alpha_{}k}\)

  • 最大公约数（能整除两个整数的最大正整数）：\(gcd(a,b)=min\{ d\in N^+\mid d\mid a,d\mid b \}\)；另一种表述：若 \(a=p_{1}^{\alpha_{1}}\dots p_{k}^{\alpha_{k}}\)，\(b=p_{1}^{\beta_{1}}\dots p_{k}^{\beta_{k}}\) 有 \(gcd(a,b)=p_{1}^{\gamma_{1}\dots p_{k}^{\gamma_{k}}},\gamma_{i}=min(\alpha_{i},\beta_{i})\)
  • 最小公倍数就是换成 \(max\)
• 辗转相除法求最大公约数
  • 利用 \(a\) 除 \(b\) 余 \(c\)，有 \(gcd(a,b)=gcd(b,c)\)
  • 

• 裴蜀定理：\(gcd(a,b)\) 一定是 \(a\) 和 \(b\) 的线性组合，即 \(\forall a,b\in Z^+(\exists s,t\in Z(gcd(a,b)=sa+tb))\)

  • 即 \(ax+by=c\) (即 \(ax\equiv c(mod\ b)\))有整数解当仅当 \(gcd(a,b)\mid c\)

• 同余方程： \(ax\equiv b(mod\ m)\) 称为线性同余方程

• 中国剩余定理：求解线性同余方程组

  • \(\left\{\begin{matrix}x\equiv a_1\pmod{m_1}\\x\equiv a_2\pmod{m_2}\\\vdots\\x\equiv a_n\pmod{m_n}\end{matrix}\right.\)
  • 假设 \(m_{1}\dots m_{n}\) 两两互素，则一元线性同余方程组在模 \(M\) 下有唯一解 (\(M=\prod_{{i=1}}^nm_{i}\))
  • 令 \(M_{i}=\frac{M}{m_{i}}\)，\(t_{i}=M_{i}^{-1}\)（模 \(m_{i}\) 下的逆 \(t_{i}M_{i}\equiv 1(mod\ m_{i})\)）
  • 方程组的解为 \(x=a_{1}t_{1}M_{1}\dots+a_{n}t_{n}M_{N}+kN\)
  • 

• 费马小定理：设正整数 \(a\) 不是素数 \(p\) 的倍数 (\(gcd(a,p)=1\))有 \(a^p\equiv a(mod\ p)\) 即 \(a^{p-1}\equiv 1(mod\ p)\)

  • 如 \(5^{116}\equiv 1(mod\ 59)\)
  • 费马小定理实际上是欧拉定理的特例
• 欧拉定理
  • 若 \(a\) 与 \(n\) 互素，则 \(a^{\varphi(n)}\equiv 1(mod\ n)\)
  • \(\varphi(n)\) 称为欧拉函数，为不大于 \(n\) 且与 \(n\) 互质的正整数的个数，即 \(\varphi(n)=\mid \{ k\mid{1}\leq k\leq n,gcd(k,n)=1 \}\mid,n\in N^+\)
  • 欧拉函数的计算 \(\varphi(n)=\prod_{i=1}^kp_{i}^{\alpha_{i}}\left( 1-\frac{1}{p_{i}} \right)\)
  • 如 \(\varphi(12)=12\left( 1-\frac{1}{2} \right)\left( 1-\frac{1}{3} \right)=4\)
  • \(\varphi(p)=p-1\)（p 是素数）(费马小定理)
  • 若\(m\)与\(n\)互素，则\(\varphi(mn)=\varphi(m)\varphi(n)\)

组合数学

基本公式

• 乘法原则：做一件事有多个步骤，第一步 n 种，第二部 m 中，则完成需要 \(m\times n\) 种
• 加法原则：一件事有两种做法，第一种做法有 \(n\) 种，第二种有 \(m\) 种，则总共有 \(m+n\) 种方法
• 排列：\(P(n,r)=\frac{n!}{(n-r)!}\) (\(P(n,n)\) 是一个集合上的双射)，从 n 个元素有序取出 r 个
• 组合：\(C(n,r)=\frac{P(n,r)}{P(r,r)}=\frac{n!}{r!(n-r)!}\)
  • \(C(n,r)=C(n,n-r)\)
  • \(C(n,k)=C(n-1,k-1)+C(n-1,k)\) 即 \(\sum^n_{j=r}C(j,r)=C(n+1,r+1)\)
  • \(kC(n,k)=nC(n-1,k-1)\)

• 二项式系数

  • \((x+y)^n=\sum^n_{j=0}C(n,j)x^{n-j}y^j\)
  • \(\sum^n_{k=0}(-1)^kC(n,k)=0\)，\(\sum^n_{k=0}2^kC(n,k)=3^n\)；分别对应 \((1-1)^k(2+1)^k\)
  • 扩展到多项式 \((x_{1}\dots x_{m})^n=\sum_{k_{1}+\dots+k_{m}=n}C(n,k_{1}\dots k_{m})\prod_{t=1}^mx_{t}^{k_{t}}\) ；其中 \(C(n,k_{1}\dots k_{m})={\frac{n!}{k_{1}!\dots k_{m}!}}\)

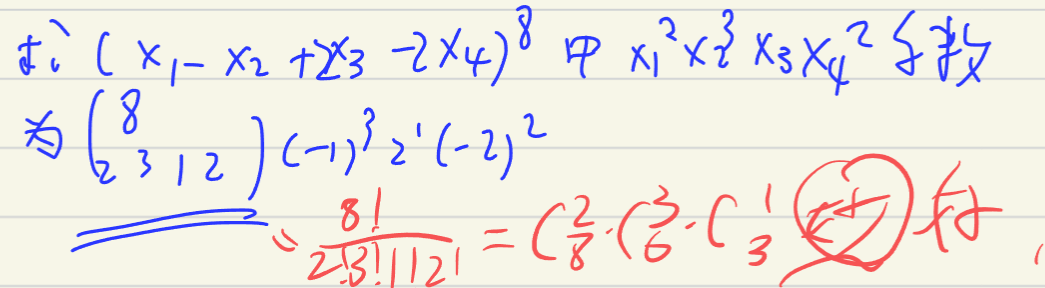
• 范德蒙恒等式

  • \(C(m+n,r)=\sum^r_{k=0}C(m,r-k)C(n,k)\)
  • \(C(2n,n)=\sum_{k=0}^n C(n,k)^2\)

计数原理

• 容斥原理：
  • \(\bigcup_{i=1}^nA_i=S_1-S_2+S_3-...+(-1)^{k+1}S_k+...+(-1)^{n-1}S_n\) 其中 \(S_k=\sum_{1\leq i_1\leq i_2\leq..\leq i_k\leq n}\lvert A_{i_1}\cap A_{i_2}\cap...\cap A_{i_k}\mid\quad k=1,2,...,n\)
• 错位排列：有 \(n\) 个普通的数，重新排列使得所有数都不在原先的位置，有多少方案
  • 称满足 \(i_{k}=k\) 的排列为性质 \(A_{k}\) ，那么错位排列个数有 \(N(\overline {A_{1}}\dots \overline{A_{n}})=n!-S_{1}+S_{2}\dots\) 其中 \(\sum_{1\leq i_1\leq i_2\ldots\leq i_k\leq n}\lvert A_{i_1}\cap A_{i_2}\cap...\cap A_{i_k}\rvert\) 有 \(S_{k}=\binom{n}{k}(n-k)!=\frac{n!}{k!}\)
  • 这样 \(P=\begin{aligned}n!\sum_{k=0}^n\frac{(-1)^k}{k!}\end{aligned}\to \frac{n!}{e}\)
  • \(D_{1}=0,D_{2}=1,D_{3}=2\dots\) 存在递推 \(D_{n}=(n-1)(D_{n-1}+D_{n-2})\)
  • 假设第一个元素 a 放在 b 位置上，b 有两种选择：放在 a（\(D_{n-2}\)）；不放在 a（此时每个元素有一个位置不能放，就是 \(D_{n-1}\)）
• 鸽笼原理
  • 将 n 只鸽子放到 m 个笼子中，若 \(m<n\) 则至少有一个笼子要装 \(2\) 个或更多鸽子（即 \(\mid A\mid>\mid B\mid\) 则不存在 \(A\to B\) 的单射）
  • 推广：\(n\) 只鸽子置于 \(m\) 个笼子，至少有一个有至少 \(\left\lfloor \frac{n-1}{m} \right\rfloor+1\) 只鸽子
• 拉姆齐数
  • \(R(k,l)=n\) 表示最小的 \(n\) 使得必有 \(k\) 个人相识或 \(l\) 个人互不相识
  • \(R(3,3)=6\)
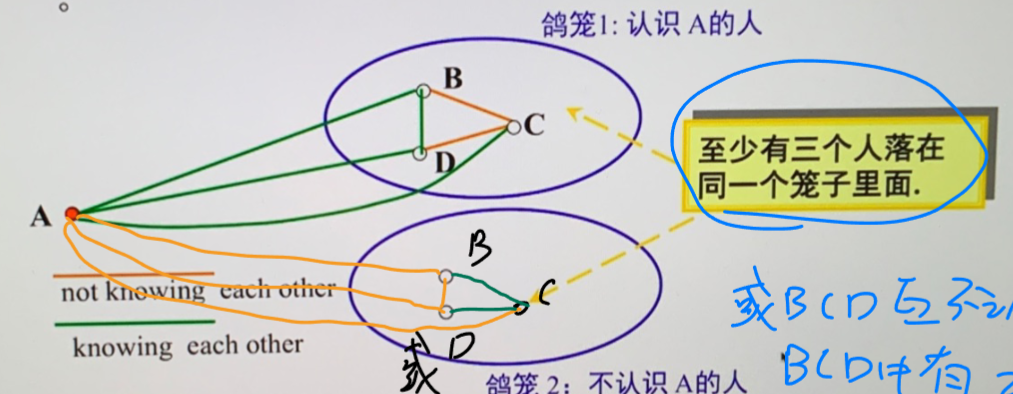
  • 依据是否认识 A 进行划分，其中一组至少有 3 个人，（以认识 A 为例）这三个人只要两个互相认识，那么就闭合得到三个人互相认识，如果全不认识，那就得到 3 个人互相不认识

典型排列/组合

• 圆排列：从 \(n\) 个不同元素中，取 \(r\) 个不重复的元素排成一个圆圈 \(\frac{P(n,r)}{r}\)
• 隔板法：将一组相同物品分配到不同的容器，并且可以处理容器可以/不可以为空的情况
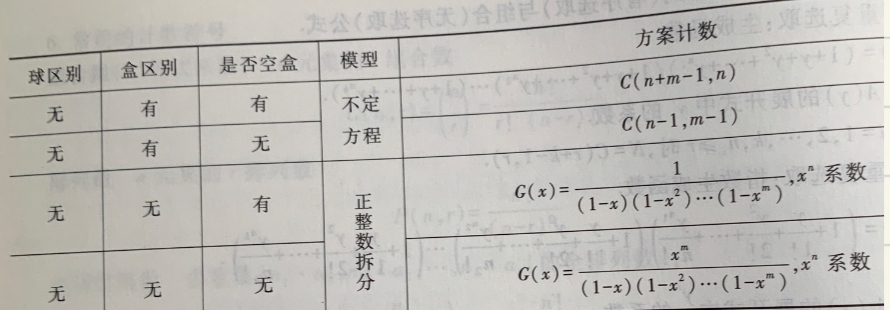
  • 假设不可以为空，有 k 个桶，n 个物品，分配方式数目有 \(C(n+k-1,k-1)\)
  • 应用：三种水果（足够多），选 4 个有多少方案：\(C(6,2)\) 即 4 个物品 3个桶

• 有重复元素的排列：\(n\) 个元素，\(m_{i}\) 是第 \(i\) 个重复项的重复次数，这 \(n\) 个元素的排列结果有 \(\frac{P(n,n)}{\prod m_{i}!}\)

• 第二类斯特林数 \(S(n,k)\) 记 \(\left\{\begin{matrix}n\\k\end{matrix}\right\}\)

  • 将 n 个不同元素的集合划分为 k 个非空子集
  • \(S(n+1,k)=kS(n,k)+S(n,k-1)\) 前一项表示新元素和原先某一组一起，后一项表示自己一组
  • 斯特林数没有简单的通项公式，难以求解

概率论

• 试验：从一组可能的结果中得到一个结果的过程
• 样本空间：所有可能的结果的集合，表示随机试验可能出现的所有结果

• 概率分析的基本步骤：选定样本空间，定义相关事件，确定结果概率，计算事件概率

• 古典概率：实验结果数目有限；等可能性；互斥性；可加性

• 频率主义概率：试验次数无穷多时得到结果概率

• 概率空间：基于集合论的概率定义

  • 样本空间 \(S\) 中的一个元素 \(w\) 称为一个结果
  • 在 \(Pr: S\to R\) 的函数满足 \(\forall_{w\in S}Pr[w]\geq 0,\sum_{w\in S}Pr[w]=1\) 则为一个样本空间 \(S\) 上的概率函数：描述随机变量取值的概率分布的函数
  • \(S\) 的一个子集 \(E\) 称为一个事件（部分结果的集合）\(Pr[E]=\sum_{w\in E}Pr[w]\)

• 均匀分布：指每个结果的概率相同，为 \(\frac{1}{\mid S\mid}\)，可以通过计数计算概率

• 条件概率：给定 \(F\) 条件下 \(E\) 的概率 \(Pr[E\mid F]={\frac{Pr[E\cap F]}{Pr[F]}}\)

• 贝叶斯定理：\(Pr[F\mid E]=\frac{Pr[E\mid F]Pr[F]}{Pr[E\mid F]Pr[F]+Pr[E\mid\overline F]Pr[\overline F]}\)

  • 
  • 

• 事件独立性：EF 为相互独立当仅当 \(Pr[E\cap F]=Pr[E]\cdot Pr[F]\)

• 随机变量：将样本空间中的每个结果映射到实数的函数 (便于进一步计算期望等统计信息) \(X: S\to R\)
  • 
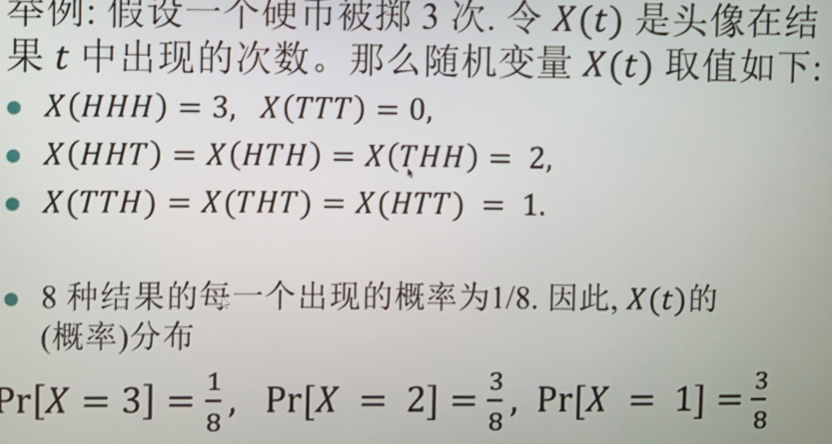
  • 随机变量的分布：\((r,Pr[X=r])\) 其中 \(r\in X(S)\)，\(Pr[X=r]\) 为 \(X\) 取值 \(r\) 的概率
  • 期望：\(Ex[x]=\sum_{w\in S}X(w)Pr[w]\)，记 \(X\) 在 \(w\) 的偏差为 \(X(w)-Ex[X]\)

• 条件期望：一个随机变量在条件下的结果的取值的概率加权平均

  • \(Ex[R\mid A]=\sum r·Pr[R=r\mid A]\)
  • 全期望公式：\(A_{1}A_2\dots\) 为 \(S\) 的一个划分，则 \(Ex[R]=\sum_{i}Ex[R\mid A_{i}]Pr[A_{i}]\)
  • 
  • 

• 期望的性质

  • 线性（可加性）：\(E[X+Y]=E[X]+E[Y]\)，\(E[ax+b]=aE[x]+b\)
  • 对于独立事件还有：\(E[XY]=E[X][Y]\)
  • 
  • 

• 方差：\(Var[X]=Ex[(X-Ex[X])^2]\)

  • 使用期望计算 \(Var[X]=E[X^2]-E[X]^2\)
  • 标准差 \(\sigma_{X}=\sqrt{ Var[X] }\)
  • 对于独立随机变量有 \(Var[X+Y]=Var[X]+Var[Y]\)
  • 

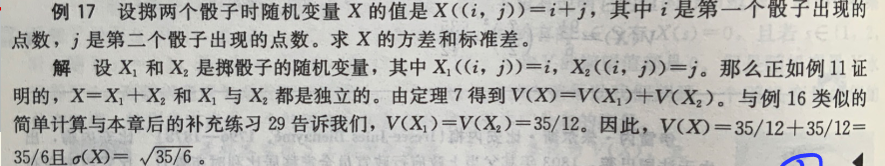
关系代数

集合

• 集合是一组无序、确定的（要么属于，要么不属于）相互区分的对象，这些对象成为集合的元素
• 集合相等 \(A=B\iff\forall x(x\in A\leftrightarrow x\in B)\)
  • 子集 \(\subseteq\) 有 \(\forall (x\in A\to x\in B)\)
  • 真子集 \(\subset\) (\(A\neq B\))
• 有限集合：若集合 S 有 n 个不同元素，且 n 为自然数，那么就称 S 为有限集合，基数为 \(\mid S\mid =n\)
  • 否则为无限集合
• 空集 \(\phi\)
  • 是所有集合的子集
  • 空集是唯一的
  • 注意 \(\{ \phi \}\) 不是不是空集
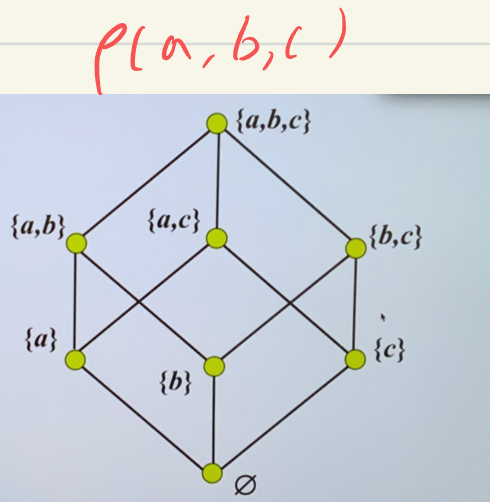
• 幂集：
  • 对于集合 \(S\)，幂集为 \(S\) 的所有子集的集合\(\rho(S)=\{ x\mid x\subseteq S \}\)
  • \(\rho(\{a,b\})=\{\phi,\{ a \},\{ b \},\{ a,b \}\}\)
  • 若 \(\rho(A)\subseteq\rho(B)\) 则 \(A\subseteq B\)
  • 若集合的基数为 \(n\) 则 \(\mid\rho\mid=2^n\)
  • \(x\in P(A)\iff x\subseteq A\)
• 归纳集 \(\phi\in A\)，\(\forall a(a\in A\to S(a)\in A)\)

集合运算

• 差集 \(A-B\to a\in A\wedge a\notin B\)
• 对称差 \(A\oplus B=(A-B)\cup(B-A)=(A\cup B)-(A\cap B)\)
• 广义并：集合 A 的所有元素的并为 \(\cup A=\{ x\mid\exists y(y\in A\wedge x\in y) \}\)
• 广义交：集合 A 的所有元素的交为 \(\cap A\{ x\mid\forall y(y\in A\to x\in y) \}\)
• 

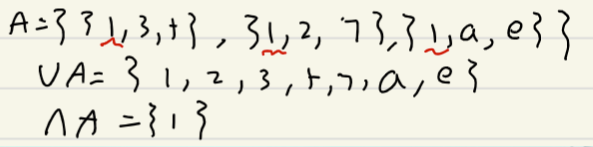
集合的基数

• 等势：如果存在集合 A 到 B 的双射，称集合 A 与 B 等势，记为 \(A\approx B\)（元素间一一对应，有 \(\mid A\mid=\mid B\mid\)）
• 若存在 \(n(n\in N)\)（自然数集合子集） 与 \(S\) 等势，则称 \(S\) 为有限集，否则称为无限集
  • 可数集即存在集合到 N 的一个单射
  • 与自然数集 N 等势的集合称为可数无限集
  • 有限集都是可数集，都可以与一个 \(n\) 等势
• \(S\) 是无限集 iff 存在 S 的真子集 S' 使得 S 与 S‘等势、
• 整数集与自然数集等势
• 可数个可数集的并集仍然是可数集
  • 
• \((0,1)\) 不可数
  • 
  • 无法数清（总是能构造一个没数到的情况）

• 不是所有无限集都等势

  • 等势的无限集：\((0,1)\to R\)；直线上点 \(\to\) 平面内点；
  • 康托尔定理：任何集合与其幂集不等势 \(A\neq\rho(A)\)
  • 证明思路与上面 \((0,1)\) 不可数类似，构造出于与每一行都不一样的集合，说明不是双射

• 优势关系：

  • 如果存在从 A 到 B 的单射，称 B 优势于 A，记为 \(\mid A\mid\leq\mid B\mid\) 或 \(A\preceq·B\)
  • 若 AB 不等势，则记为真优势 \(\mid A\mid<\mid B\mid\) 或 \(A\prec B\)
  • 对于任何集合 A 都有 A 的幂集真优势于 A
  • 实数集真优势于自然数集
• 使用优势关系说明等势 \(\mid A\mid\leq\mid B\mid,\mid B\mid\leq\mid A\mid\to\mid A\mid=\mid B\mid\)，即找到正反两个单射就可以说明等射（这往往比直接找双射更为简单）
  • 实数集与幂集等势
• 连续统假说
  • 自然数集合基数记为 \(\aleph_{0}\)，其幂集（或实数集）记为 \(\aleph_{1}(=2^{\aleph_{0}})\) (连续统基数 \(c\))
  • \(\aleph_{2}\) 平面上的曲线的基数
  • 连续统假说就是说：不存在 \(A\) 使得 \(\aleph_{i}<\mid A\mid<\aleph_{i+1}\)

关系与函数

• 有序对 \((a,b)\) 是集合 \(\{ \{ a \},\{ a,b \} \}\) 的缩写
  • \((x,y)==(u,v)\iff x=u\&\&y=v\)
• 笛卡尔积
  • 对于集合 \(A,B\) 有 \(A\times B=\{ (a,b), a\in A,b\in B\}\)
  • 若均为有限集合则 \(\mid A\times B\mid=\mid A\mid\times\mid B\mid\)
  • \(A\times B=B\times A\iff[(A=\phi)\vee(B=\phi)\vee(A=B)]\)
  • 支持分配率 $$\begin{aligned}&A\times(B\cup C)=(A\times B)\cup(A\times C)\&A\times(B\cap C)=(A\times B)\cap(A\times C)\&(B\cup C)\times A=(B\times A)\cup(C\times A)\&(B\cap C)\times A=(B\times A)\cap(C\times A)\end{aligned} $$

• 二元关系：两类对象建立联系

  • 若 \(A,B\) 是集合，则从 \(A\) 到 \(B\) 的关系是 \(A\times B\) 的一个子集(二元关系是笛卡尔积的一个子集)
  • 全域关系：\(\{ (x,y)\mid x,y\in A \}\)
  • 恒等关系：\(\{ (x,x)\mid x\in A \}\)
  • 控关系：\(\phi\subseteq A\times A\)
  • 对于 \((a,b)\in R\) 记为 \(aRb\)
  • \((a,b)\notin R\) 记为 \(\neg aRb\)

• 关系 R 的重要集合，设 \(R\subseteq A\times B\)

  • \(R\) 的定义域：\(Dom(R)=\{ x\mid(\exists y\in B)(x,y)\in R \}\)
  • \(R\) 的值域：\(DRan(R)=\{ y\mid(\exists x\in B)(x,y)\in R \}\)
  • \(R\) 的域：\(Fld(R)=Dom(R)\cup Ran(R)\)
  • 关系的逆 \(R\subseteq A\times B\) 即 \(R^{-1}=\{(x,y)|(y,x)\in R\}\)

• 关系矩阵可以用来表示二元关系，\(m_{ij}\) 就表示存不存在 \((i,j)\)

• 复合关系：\(S \subseteq A\times B\)，\(R\subseteq B\times C\) ，复合为 \(R\circ S=\{(x,y)|(\exists t\in B)((x,t)\in S\wedge(t,y)\in R)\}\)

  • 
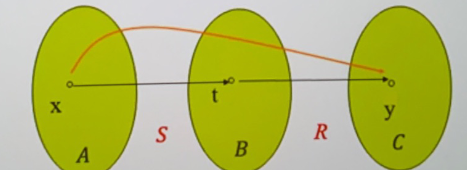
  • 要注意的是，复合关系从右向左 \(xStRy\)
  • \(R_1\circ(R_2\circ R_3)=(R_1\circ R_2)\circ R_3\)
  • \((R\circ S)^{-1}=S^{-1}\circ R^{-1}\)
  • 
  • 对应到矩阵上就是右边的关系矩阵乘左边的关系矩阵

• 关系的幂

  • 对于 \(R\subseteq A\times A\)，关系 \(R\) 的 \(n\) 次幂定义为 \(R^0=I_{A},R^{n+1}=R\circ R^n\)
  • 通过关系矩阵计算较为方便
  • \({R^m\circ R^n=R^{m+n}}，({R}^m)^n={R}^{mn}\)
  • 若 \(R^S=R^{S+T}\) 则 \(\forall k\geq S,R^k=R^{k+T}\) 以及 \(R^k=R^{k+nT}\)
  • 由鸽笼原理还能得到 \(\mid A\mid=n\) 则 \(R^{s}=R^{t}\wedge0\leq s<t\leq2^{n^{2}}\)

• 函数（映射） \(f: A\to B如R=\{ (x,f(x))\mid x\in A \}\)

  • 函数是一种特殊的二元关系，对集合 \(A\) 中的每一个元素，存在唯一一个 \(B\) 中的元素与之对应
  • 函数具有决定性，同一输入总是对应同一输出
  • \(A\) 为定义域，\(B\) 为伴域
  • 存在 \(\mid B\mid^{\mid A\mid}\) 种函数
  • 对于 \(f(a)=b\) 称 \(b\) 为 \(a\) 的像；\(a\) 为 \(b\) 的反像；\(b\) 的集合构成 \(f\) 的值域，是伴域的一个子集
  • 
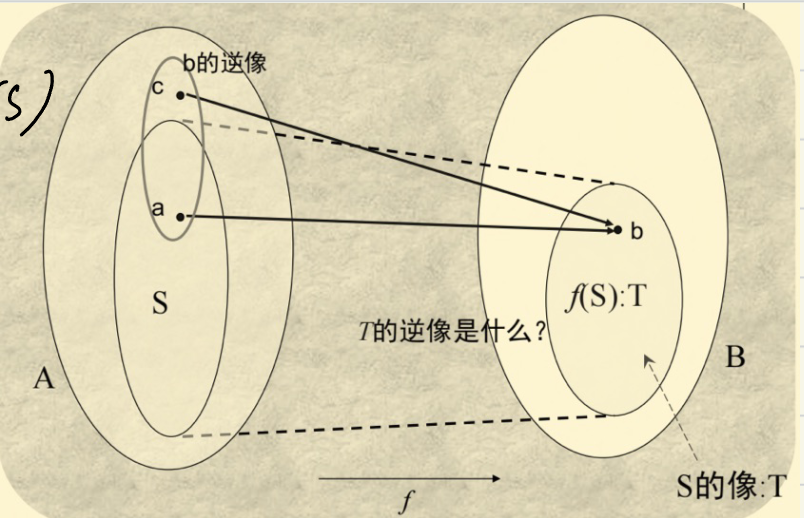
  • \(X,Y\) 为 \(A\) 的子集
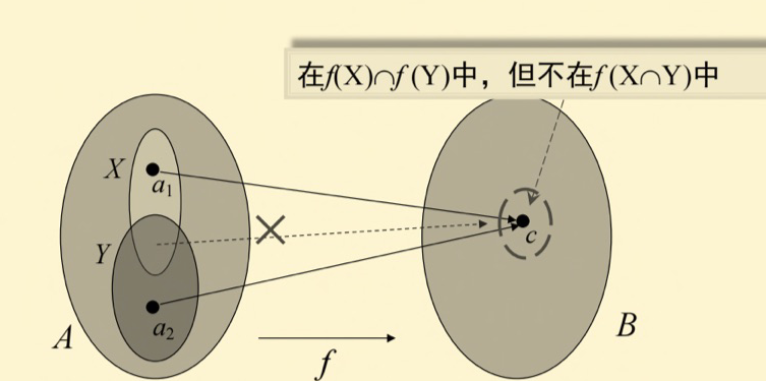
  • 并集的像：\(f(X\cup Y)=f(X)\cup f(Y)\)
  • 交集的像：\(f(X\cap Y)\subseteq f(X)\cap f(Y)\)
    • 

• 函数的分类

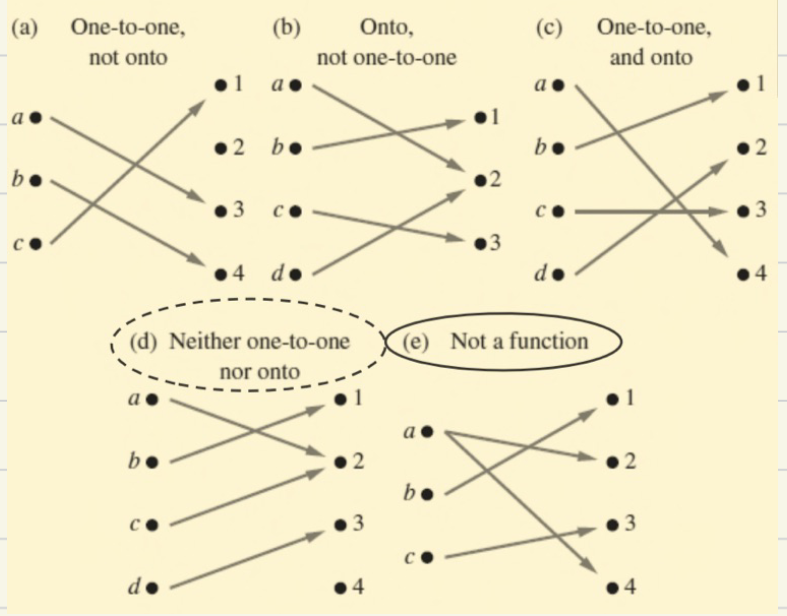
  • 单射：一对一的，\(\forall x_{1}x_{2}\in A,如果f(x_{1})=f(x_{2})则x_{1}=x_{2}\)
  • 满射：映上的，\(\forall y\in B\exists x\in A使得f(x)=y\)
  • 双射：一一对应的，满射+单射（或者双向单射）
  • 

• 函数的比较与运算

  • \(f=g\iff dom(f)=dom(g) \forall x(x\in dom(f)\to f(x)=g(x))\)
  • \((f_1+f_{2})(x)=f_{1}(x)+f_{2}(x)\)
  • \((f_{1}f_{2})(x)=f_{1}(x)f_{2}(x)\)

• 反函数：仅有双射函数才存在反函数 \(f(a)=b,f^{-1}(b)=a\)

• 复合函数 \((fog)(a)=f(g(a))\)，\(g\) 的值域为 \(f\) 定义域的子集

  • 满足结合率到那时不满足交换律
  • \(fog\) 是满射：\(f\) 一定是满射，但是 \(g\) 不一定是
  • \(fog\) 是单射，\(g\) 一定是单射，但是 \(f\) 不一定是
  • 满射的复合是满射
  • 单射的复合是单射
  • 双射的复合是双射

• 序列：

  • 一个序列是从 Z 的一个子集到集合 S 的一个函数，用 \(a_{n}\) 表示 n 的像，称为序列的项
  • 主要限制了离散整数定义域（有点类似一个数组）

关系的性质

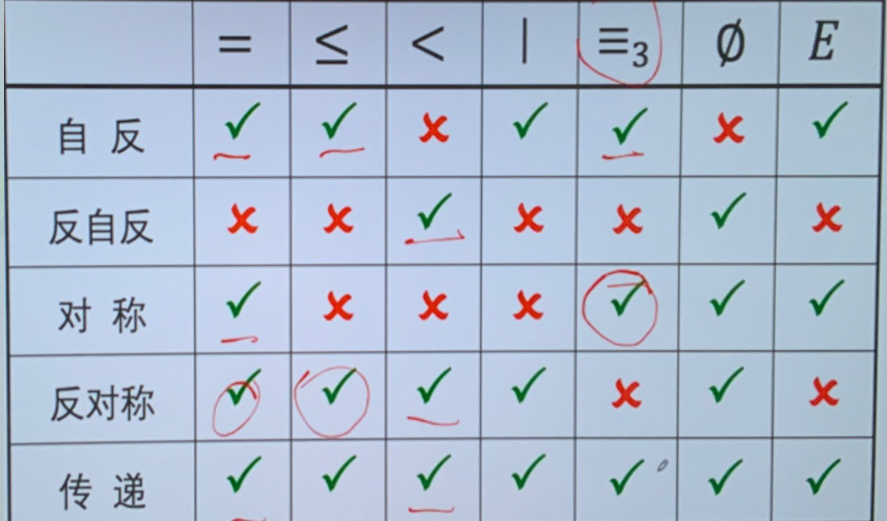
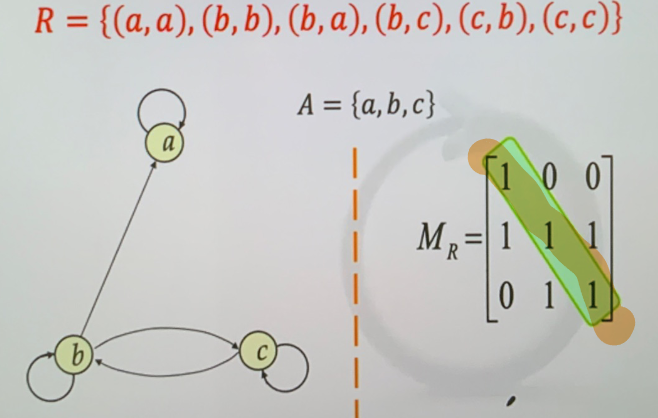
自反性 - 自反 \((\forall x\in A)(xRx)\) - 反自反 \((\forall x\in A)(\neg xRx)\) - 非自反：既不是自反也不是反自反 - - 自反的充要条件 \(I_{A}\subseteq R\)，反自反充要条件 \(R\cap I_{A}=\phi\) - 关系矩阵对角线为全 1 -

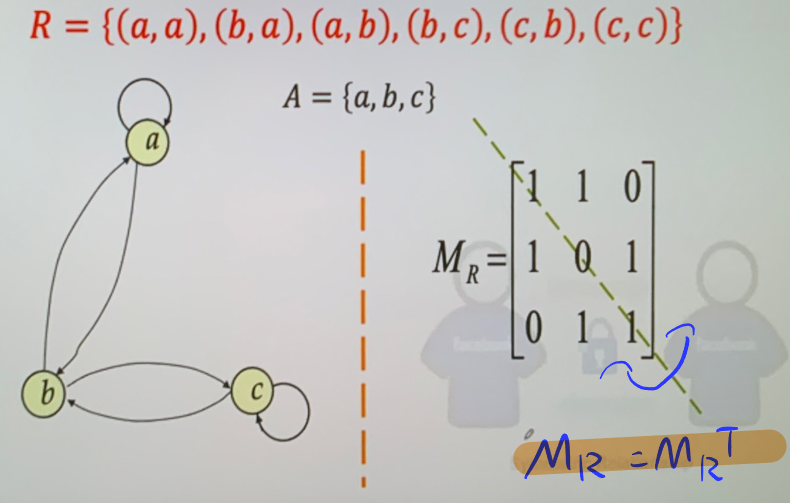
对称性 - 对称 \((\forall x,y\in A)(xRy\to yRx)\) - 反对称 \((\forall x,y\in A)(xRyRx\rightarrow x=y)\) 即只允许 \((x,x)\) 这种对称 - 如果不存在 \(xRyRx\) 也是反对称的！ - 强反对称 \((\forall x,y\in A)(xRy\rightarrow\neg yRx)\)，不允许一切对称 - - \(\phi\) 属于上面全部三种对称 - 对称关系的充要条件 \(R=R^{-1}\) - 反对称充要条件 \(R\cap R^{-}\subseteq I_{A}\) - 对称的关系矩阵有 \(M_{R}=M_{R}^T\) -

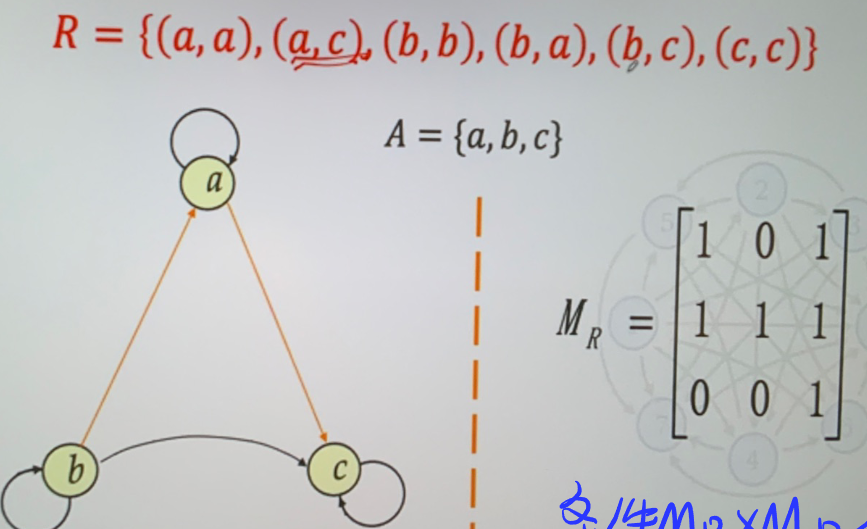
传递性 - 传递是指 \(\left(\forall x,y,z\in A\right)\left(xRyRz\rightarrow xRz\right)\) - - 传递的充要条件 \(R^n\subseteq R\) - 关系矩阵有 \(M_{R}\times M_{R}\leq M_{R}\) -

• 

等价关系

• 同时满足自反、对称、传递的为等价关系，记 \(x\sim y\)
• 等价类：
  • 对于 \(R\) 为 \(A\) 上的等价关系，\(a\) 关于 \(R\) 的等价类为 \([a]_{R}=\{ b\in A\mid aRb \}\)，称 \(a\) 为这个等价类的代表元素（等价类中每个元素都可以作为代表元素）
  • 比如对于模 n 同余关系，有 \([x]=\{ y\mid x\equiv y(mod\ n) \}=\{ x+kn\mid k\in Z \}\)
  • \(\(\begin{aligned}&(1)\:(\forall x\in A)(x\in[x])\\&(2)\:(\forall x,\:y\in A)(x\sim y\mapsto[x]=[y])\\&(3)\:(\forall x,\:y\in A)(\neg(x\sim y)\hookrightarrow[x]\cap[y]=\emptyset)\\&(4)\:(\forall x,\:y\in A)([x]=[y]\:\text{与 }[x]\cap[y]=\emptyset\text{恰具其一}\\&(5)\:\cup\{[x]\mid x\in A\}=A\end{aligned}\)\)

• 商集：以关系 \(R\) 的所有等价类作为元素的集合称为 A 关于 \(R\) 的商集 \(A/R=\{ [x]_{R}\mid x\in A \}\)

  • 
  • 非空集合的每一商集对应 \(A\) 的唯一划分（因此有几种等价关系就有几种划分），划分中的元素称为划分块（\(\cap\) 为 \(\phi\)；\(\cup\) 为 \(A\)）

• 闭包：\(R\) 的 \(P\) 性质的闭包，存在 \(S\subseteq A\times A\)

  • \(R\subseteq S\)
  • \(S\) 具有性质 \(P\)
  • \(\forall T(R\subseteq T\wedge T有性质P\to S \subseteq T)\)（表示闭包是最小的，符合性质的关系）
  • \(S\) 就是 \(R\) 的 \(P\) 闭包（存在且唯一）
• 构造方式
  • 自反闭包：\(r(R)=R\cup I_{A}\)
  • 对称闭包：\(s(R)=R\cup R^{-1}\)
  • 传递闭包：\(t(R)=\cup \{ R^n\mid 1\leq i\leq\mid A\mid \}\)
• 对应到矩阵运算
  • \(M_{r(R)}=M_{R}\vee M_{I_{A}}=M_{R}\vee I_{A}\)
  • \(M_{S(R)}=M_{R}\vee M_{R}^{T}\)
  • \(M_{t(R)}=M_{R}\lor M_{R}^{[2]}\lor\cdots\lor M_{R}^{[n]}\)
• 闭包运算
  • 
• 传递闭包 Warshall 算法
  • 迭代的使用 \(W_{i-1}\) 计算 \(W_{i}\)
  • \(W_{0}=M_{R}\)
  • \(W_k[i,j]=1\iff W_{k-1}[i,j]或 W_{k-1}[i,k]=1\ and\ W_{k-1}[k,j]=1\)
  • \(W_{n}\) 就是结果
• 使用 \(R^{(i)}\) 表示使用前 \(i\) 个点作为中间结点
  • \(R_{ij}^{(k)}=R_{ij}^{(k-1)}\vee(R_{ik}^{(k-1)}\wedge R_{kj}^{(k-1)})\)
  • 

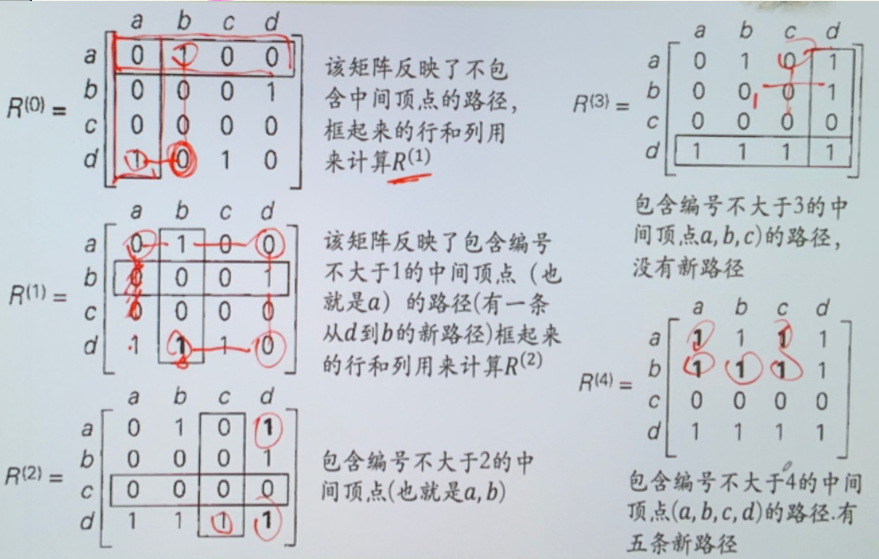
偏序集

• 偏序：自反、反对称、传递关系称为偏序关系，记作 \(a\preceq b\)（这种偏序也称为自反偏序、非严格偏序）
  • 严格偏序、反自反偏序：将自反更换为反自反
• 偏序集：集合 \(A\) 及其上的偏序关系 \(\preceq\) 一道称为偏序集，记作 \((A,\preceq)\)
  • 偏序集是他的覆盖关系的传递自反闭包
• 可比：对于 \(A\) 中的元素，有 \(x\preceq y\) 或者 \(y\preceq x\) 则称 \(x\) 与 \(y\) 可比
  • 不可比的情况：\((\{ 1,2,4,6,8 \},\mid)\) 中的 \(4,6\) 就是不可比的
• 全序：若 \(A\) 中任何两个元素都是可比，称 \(R\) 为 \(A\) 上的全序关系
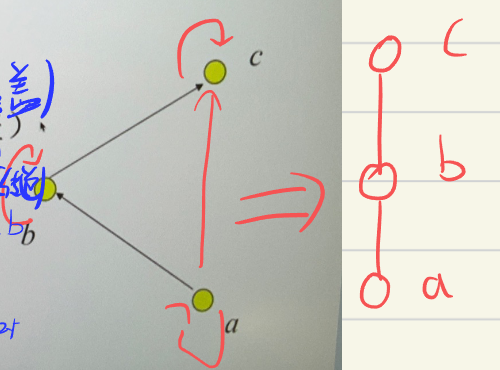
• 覆盖：\(y\) 覆盖 \(x\) 当仅当 \(x\prec y\) 并且不存在 \(z\in A\) 使得 \(x\prec z\prec y\)
• 良序：\(A\) 的任意非空子集都有最小元素，则称为良序
  • 良序必为全序
  • 良序上支持数学归纳法
  • 全序不一定是良序（如 \(A\) 为无穷集合 \((R,\leq)\)）
  • 良基：存在极小元

哈斯图

• 利用特定性质简化图的表示

  • 利用自反性质省略圈
  • 利用反对称省略箭头
  • 利用传递性省略部分连线（覆盖）
  • 
  • 

• 特殊元素 (\(x\)，\((A,\preceq)\))

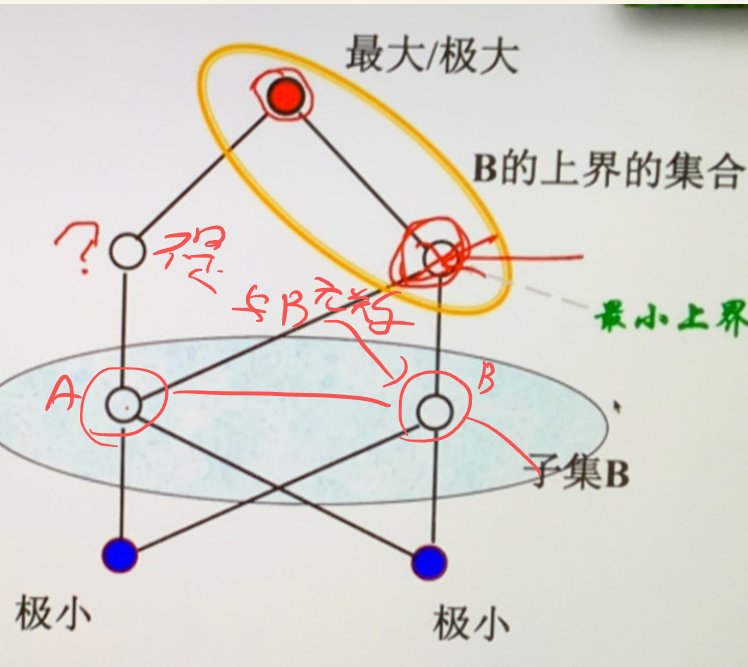
  • 极大元素：没有更大元素了 \(\forall y\in A\) 若 \(x\preceq y\)，那么 \(x=y\)
    • 
  • 极小元素：没有更小元素了 \(\forall y\in A\) 若 \(y\preceq x\)，那么 \(x=y\)
  • 最大元素：比所有元素都大 \(\forall y\in A\) 有 \(y\preceq x\)
    • 最大最小是不一定存在的，但是由穷集合一定有极大极小元
    • 
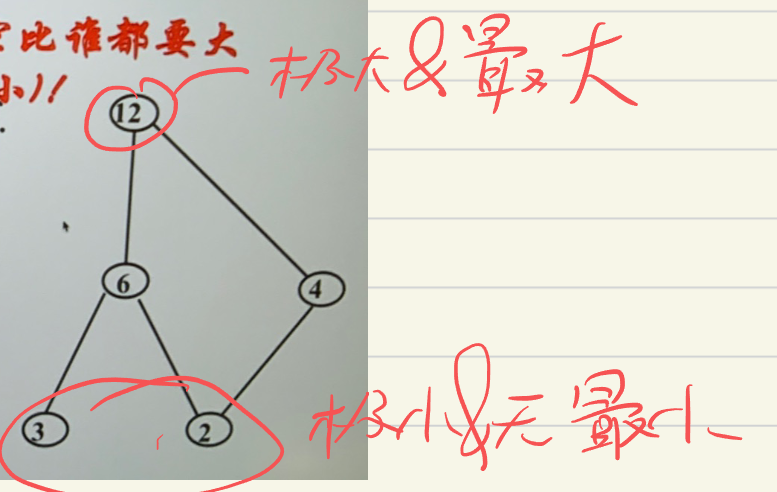
  • 最小元素：比所有元素都小 \(\forall y\in A\) 有 \(x\preceq y\)
  • 上界：对于偏序集的子集 \(B\) 若存在 \(y\in A\) 对 \(\forall x\in B\) 有 \(x\preceq y\) 则 \(y\) 是 \(B\) 的上界
  • 最小上界（上确界）：如果上界构成的偏序集有最小元，则该最小元为 \(B\) 的最小上界（上确界）
    • 不一定存在，若存在则唯一
    • 

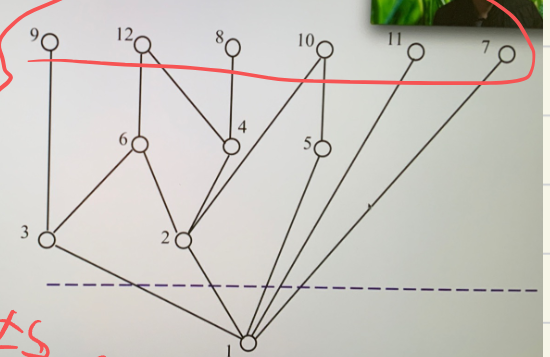
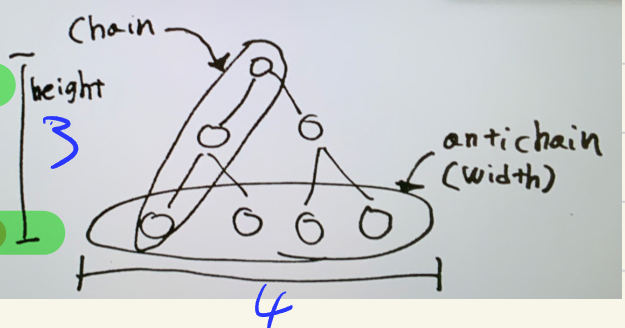
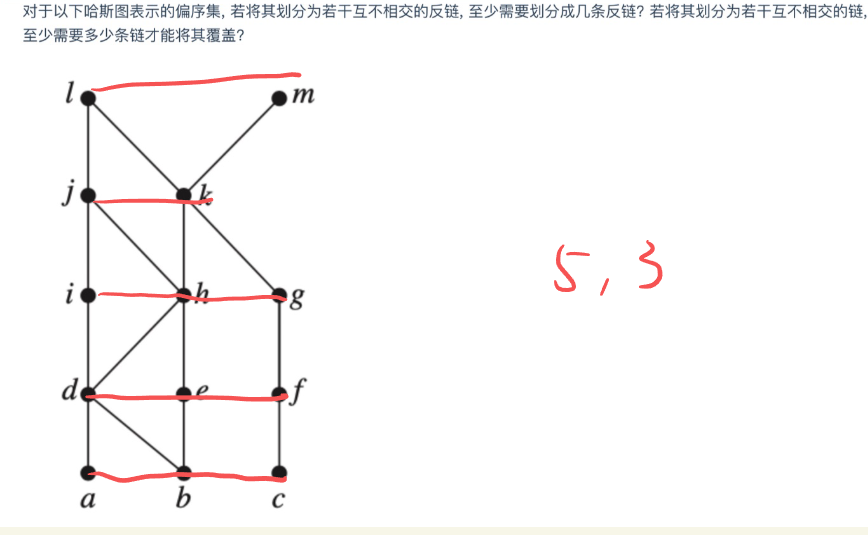
链与反链

• 链：\(C\) 为偏序集的一个子集，如果 \(C\) 中任何两个元素均可比，则 \(C\) 构成一个链
  • 如果不是任何其他链的子链，则称为极大化链（即 \(C\) 之外不存在一个元素与 \(C\) 中所有元素都可比）
• 反链：\(C\) 中任何两个元素均不可比，那么构成一个反链
  • 同样如果 \(C\) 不是其他反链的子链，那么就是极大化的（\(C\) 外没有一个元素与 \(C\) 中每一个元素都不可比）
• 高度：有限偏序集中最长的链的节点个数

• 宽度：最大反链的元素个数

  • 

• 偏序集的划分

  • 若高度为 \(t\) 则可以划分为 \(t\) 个反链
  • 要么一条长度至少为 \(t\) 的链，一条长度至少为 \(\frac{\mid A\mid}{t}\) 的反链
  • 链覆盖：一组互不相交的链，包含了偏序集中的所有元素
  • 宽度为 \(w\) 的偏序集可以划分成 \(w\) 个链，即覆盖的最小链数等于最长反链的长度
  • 

格

• 偏序格：\((L,\preceq)\) 为偏序集

  • 对于 \(\forall x,y\in L\) 均存在最小上界 \(lub\{ x,y \}\) 记为 \(x\vee y\)
  • 对于 \(\forall x,y\in L\) 均存在最大下界 \(glb\{ x,y \}\) 记为 \(x\wedge y\)
  • 格上支持两种二元运算 \(\vee\wedge\)
    • 支持结合律，交换律，幂等律，吸收律 (\(a\wedge(a\vee b)=a,\:a\vee(a\wedge b){=}a\))
  • 则称 \(L\) 关于 \(\preceq\) 构成一个格
  • 
  • 

• 性质

  • \(a\leq c,b\leq c\Rightarrow a\lor b\leq c\)
  • \(c\leq a,c\leq b\Rightarrow c\leq a\wedge b\)
  • \(a\leq c,b\leq d\Rightarrow a\lor b\leq c\lor d,a\land b\leq c\land d\)
  • \(a\leq b\iff a\wedge b=a\iff a\vee b=b\)
• 对偶命题
  • 如果命题对一切格为真，那么对偶命题也对一切格为真
  • \(P*\) 对偶命题是将 \(P\) 中的 \(\leq\geq\vee\wedge\) 分别替换为 \(\geq\leq\wedge\vee\)

代数格

• 代数格是满足结合律、交换律、吸收率（针对 \(\vee\wedge\) 操作）
  • 代数格与偏序格是等价的（代数格是从满足运算性质的角度出发定义；偏序集则是从偏序关系，上下界的角度出发定义的）

• 子格

  • 对于非空集合 \(S\subseteq L\)，若 \(S\) 关于 \(\vee \wedge\) 仍然构成格，则称 \((S,\vee,\wedge)\) 构成 \(L\) 的子格（即任意两点的上确界和下确界均在子集中）
  • 

• 假设有两个格 \((L_1,\wedge_{1},\vee_{1})\) 和 \((L_{2},\wedge_{2},\vee_{2})\)

• 格同态
  • 存在 \(f: L_{1}\to L_{2}\) 使得对 \(\forall a,b\in L_{1}\) 有 \(\begin{aligned}f\left(a\wedge_{1}b\right)=f\left(a\right)\wedge_{2}f\left(b\right)\\f\left(a\vee_{1}b\right)=f\left(a\right)\vee_{2}f\left(b\right)\end{aligned}\)
  • 称 \(f\) 为从 \(L_{1}到\) \(L_{2}\) 的同态映射，即格同态
  • 格同态不改变偏序关系 \(\forall x,y\in L_{1}(x\leq_{1}y\to f(x)\leq_{2}f(y))\)
    • 逆命题不一定成立

• 格同构

  • 若同态映射 \(f\) 为一个双射，则称为格同构
  • \(格同构 \iff \forall x,y\in L_{1}\left(x\leq_{1}y\Leftrightarrow f\left(x\right)\leq_{2}f\left(y\right)\right)\)
  • 

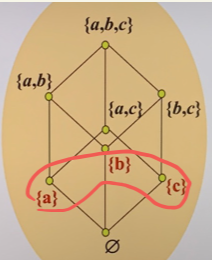
• 典型的格

  • 链、钻石格（M3）、五角格（N5）
  • 
  • 钻石格和五角格均不具有分配性 (如 bcd)

• 分配格，对于 \(\forall a,b,c\in L\) 有

  • \(\begin{aligned}a\wedge(b\vee c)&=(a\wedge b)\vee(a\wedge c)\\a\vee(b\wedge c)&=(a\vee b)\wedge(a\vee c)\end{aligned}\)
  • 要注意对于所有的格都有 \(\begin{aligned}a\wedge(b\vee c)&\leq(a\wedge b)\vee(a\wedge c)\\a\vee(b\wedge c)&\geq(a\vee b)\wedge(a\vee c)\end{aligned}\)
• 分配格的判定定理
  • 当仅当不含有与 \(M_3,N_5\) 同构的子格(注意区分子图和子格)
  • 当仅当 \(\left(a\wedge b=a\wedge c\right)\wedge\left(a\vee b=a\vee c\right)\rightarrow b=c\)
• 有界格
  • 若存在 \(b\in L\) 使得 \(\forall x\in L\) 有 \(b\leq x\) 则 \(b\) 为 \(L\) 的全下界，也记为 \(0\)
  • 相反地 \(t\in L\) 使得 \(\forall x \in L\) 有 \(x\leq t\) 则称 \(t\) 为全上界, 也记为 \(1\)
  • 若存在格中存在全上界或全下界则一定唯一，有界限格也可以记为 \((L,\wedge,\vee,0,1)\)，有介格的对偶命题还需要对 \(0,1\) 进行调换
  • 对于 \(0,1\) 有界格也满足同一律及支配律
  • 有限格都是有界格，求法：\(\frac{a_1\wedge a_2\wedge\cdots\wedge a_n\text{是L的全下界}}{ a _ 1 \vee a _ 2 \vee \cdots \vee a _ n\text{是}L\text{的全上界}}\)
• 补元（有界格才有补元）
  • \(a\in L\) 的补元 \(b\) 为 \(a\wedge b=0,a\vee b=1\) (0,1 就是一组补元)
  • 
  • 有界分配格的补元存在且唯一
• 有补格
  • 对于有界格，如果所有元素均存在补元，则称其为有补格
  • \(M_{3}N_{5}\) 就都是有补格

布尔代数

• 布尔代数是一种分配有补格，具有封闭性质的代数系统
• 三种运算 \(\sim\)，\(\vee(+)\)，\(\wedge(·)\)
• 同态
  • \(\begin{aligned}f(x\wedge y)&=f(x)\cap f(y),\\f(x\vee y)&=f(x)\cup f(y),\\f(x^{\prime})&=\sim f(x),\\f(0)&=\theta,f(1)=I\end{aligned}\)
  • 若 \(f\) 为一个满射，则称为满同态
• 同构
  • 如果同态 \(f\) 是一个双射，那么称为同构，记 \(B\cong P\)
• \(B=(\{0,1\},+,\cdot,^{-},0,1)\) 为布尔代数
  • \(B^{n}=\{(x_{1},\ldots,x_{n})|x_{i}\in{B},i=1,\ldots,n\}\)构成布尔代数
  • 幂集也构成了一个布尔代数
• 原子：\(a\neq 0\) 对 \(\forall x\in L\) 有 \(0<x\leq a\to x=a\)
  • 对于原子 \(a\neq b\) 有 \(a\wedge b=0\)
  • 
• 有限布尔代数表现代理
  • 对于任意有限布尔代数 \(B\) 同构与 \(B\) 中所有原子构成的集合 \(A\) 的幂集 \(\rho(A)\)
  • \((B,\wedge,\vee,-,\mathbf{0},\mathbf{1})\cong(P(A),\cap,\cup,\tilde{\mathbf{0}},A)\)
  • 推论：任何有限布尔代数的基数均为 \(2^n\)，所有等势的布尔代数均同构
  • 
• 布尔函数
  • \(B^n\to B\) 的函数（即 n 格输入一个输出的逻辑电路）
  • 举止范围为 \(B\) 的变元称为布尔变元
  • 布尔和：\((f+g)(x_{1}\dots x_{n})=f(x_{1}\dots x_{n})+g(x_{1}\dots x_{n})\)
  • 布尔积：\((\mathrm{f·g})(x_1,\ldots,x_n)=\mathrm{f}(x_1,\ldots,x_n)\cdotp\mathrm{g}(x_1,\ldots,x_n)\)
  • 补函数：\(\overline{f}(x_1,\ldots,x_n)=\overline{f(x_1,\ldots,x_n)}\)
  • n 元布尔函数全体也构成了一个布尔代数
• 卡诺图化简
• 相邻元素只有一项不同
• 

代数系统

• 函数 \(A^n\to B\) 称为从 \(A\) 到 \(B\) 的的 \(n\) 元运算
  • 若 \(B\subseteq A\) 则称则称运算在集合 \(A\) 上封闭
• 在有限集合上 \(m\) 元运算的个数是确定

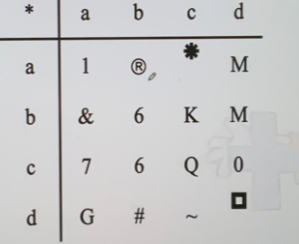
• 运算表

  • 用于定义有限集合（元素较少）上的一元或二元运算
  • 

• 代数系统：

  • 给定一个非空集合，以及 1 个或若干个运算，并且运算对上述集合封闭
  • 如 \(<Z,+>\)
• 结合性：保持次序不变的前提下可以按照任何的顺序进行计算
• 分配性：运算 \(·\) 对 \(*\) 满足分配性即 \(\forall x,y,z\in A,x\circ(y*z)=(x\circ y)*(x\circ z)\)

• 交换性：可以重新排列先后次序

• 单位元：\(\forall x\in S,e\circ x=x\circ e=x\) 则称 \(e\) 为单位元，简记 \(1\)

  • 左单位元 \(e_L\circ x=x\)
  • 右单位元 \(x\circ e_{R}=x\)
  • 左右单位元不一定存在，如果存在则一定唯一
  • 如果一个代数系统同时有做单位元和右单位元，那么相等且唯一（即为单位元）
• 子代数：子集、运算封闭，具有相同的代数常数（单位元，零元）
• 逆元
  • 只有存在单位元的代数系统才有逆元
  • 左逆元 \(a^{-1}_{L}\circ a=1\)
  • 右逆元 \(a\circ a^{-1}_{R}=1\)
  • 逆元 \(a^{-1}\circ a=a\circ a^{-1}=1\)，两个元素互为逆元
  • 当代数系统具有结合性时：
    • 既有左逆又有右逆，则二者必相等且唯一
    • 如果每个元素都有左逆，那么左逆即右逆且逆元唯一
• 零元
  • \(\forall x\in S,t\circ x=x\circ t=t\)

• 

• 同构映射：代数系统 \(<S_{1},\circ>\) 和 \(<S_{2},*>\) 同构 \(S_{1}\cong S_{2}\) 当仅当 \(\forall x,y\in S_1,f({x}\circ y)=f(x)*f(y)\)，其中双射函数 \(f\) 称为同构映射

  • 同构关系是一种等价关系
  • 只有两个代系统集合等大才可能同构
• 同态映射：\(S_{1}\sim S_{2}\)
  • 不要求双射，如果是满射称为满同态
  • 
• 

群论

• 半群 (Semigroup)：代数系统（运算封闭）+结合性
• 幺半群（monoid）：半群+单位元
• 群：幺半群+逆元
  • 即：代数系统+结合性+单位元+逆元（群论公理）
  • 
• 根据集合是否有穷还划分为有限集和无限集
• 如果还满足交换律则称为交换群（abelian 群）
• 群的性质
  • 群是满足消去律的（由于有逆元）\(ac=ab\iff c=b\)
  • \(ax=b\) 及 \(ya=b\) 均有唯一解

• 群的阶数

  • 三阶群唯一
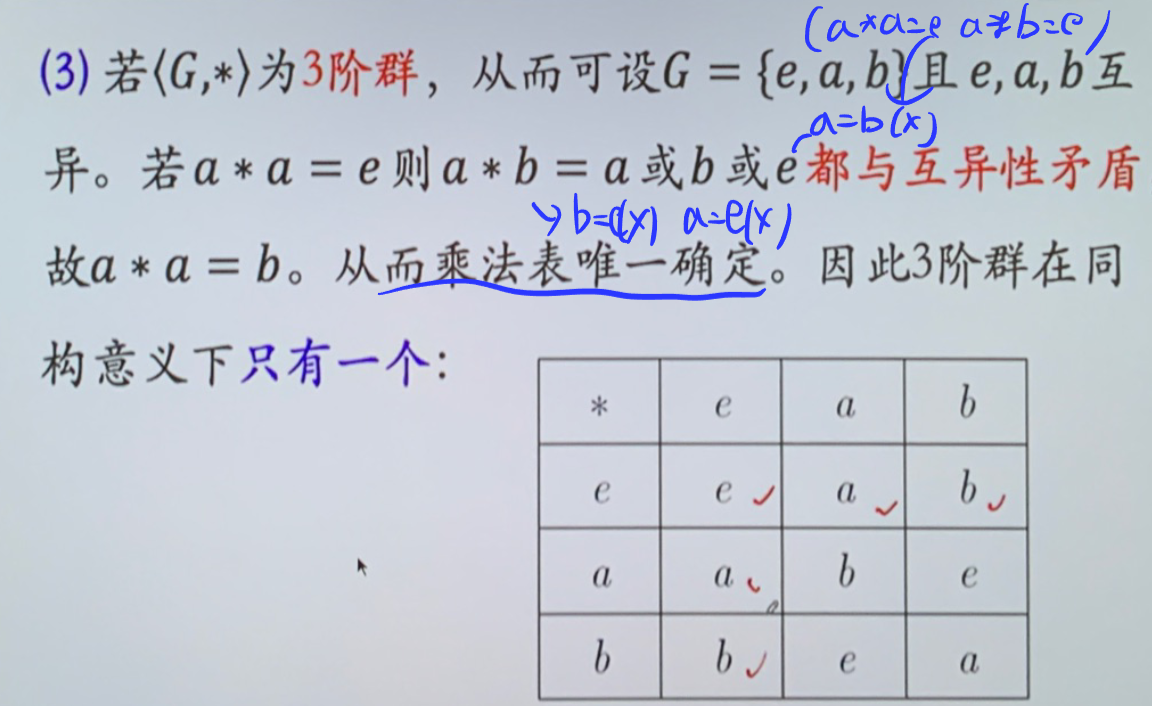
  • 四阶群只有两种 \(Klein\) 四元群和 \(<Z_4,\oplus_4>\) ，并且均为交换群
  • 1-5 阶均为阿贝尔群

• 子群

  • 子集
  • 运算封闭
  • 单位元封闭（还在集合中）
  • 逆元封闭
  • 记为 \(<H,*>\leq<G,*>\)
• 平凡子群：两个特殊的子群，\(\langle\{e\},*\rangle,\langle G,*\rangle\) 单位元和自身

• 子群的判定

  • 
  • 对于有限子群（非空有穷子集），进一步简化为 \(\forall a,b\in H,ab\in H\)
    • 一定存在 \(a^{-1}\)，因为根据鸽笼原理一定有 \(a^i=a^j\)

• 元素的阶

  • \(a^n\)： \(n<0\) 时 \(a^n=(a^{-n})^{-1}\)
  • 若 \(\exists n\in N^+,a^n=e\) 则称阶有穷为 \(\mid a\mid=min\{ n>0\mid a^n=e \}\)，否则称阶无穷 \(\mid a\mid=\infty\)
  • \(\begin{aligned}&(1)\:\text{对}k\in\mathbb{Z}^+,\:a^k=e\Leftrightarrow\mid a\mid\mid k\\&(2)\:|a|=|a^{-1}|\\&(3)\:|ab|=|ba|\\&(4)\:|b^{-1}ab|=|a|\end{aligned}\)
  • 阶大于 2 的元素一定有偶数个
  • 如果只有 1,2 阶元，则是阿贝尔群

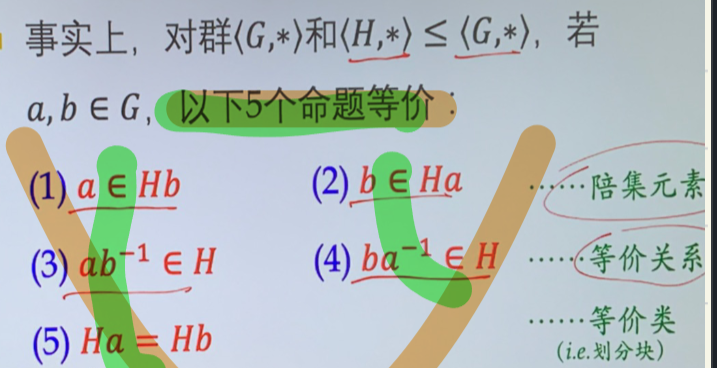
陪集

• 陪集：子群将群分解为培集
  • 对于 \(<H,*>\leq<G,*>,a\in G\)，令 \(H{a}=\{ha|h\in H\},\:aH=\{ah|h\in H\}\) 称为右/左陪集，H 在 G 中陪集的个数，称为 \(H\) 在 \(G\) 中的指数 \([G:H]\)
  • 
  • 右陪集关系（等价关系）：\((\forall a,b\in G)aRb\Leftrightarrow ab^{-1}\in H\)，\(R\) 是 \(G\) 上的等价关系，\([a]_{R}=Ha\)
    • 
  • 相似的左陪集关系：\(\left(\forall a,b\in G\right)a\boldsymbol{R}^{\prime}b\Leftrightarrow b^{-1}a\in H\)
• 陪集与划分
  • \(\begin{aligned}&(1)He=H\\\\&(2)(\forall a\in G)(a\in Ha)\text{ 从而 U}\{Ha|a\in G\}=G\\\\&(3)(\forall a,b\in G)(Ha=Hb\lor Ha\cap Hb=\emptyset)\\\\&(4)\left\{Ha|a\in G\right\}\text{为}G\text{之划分}\end{aligned}\)
• 陪集的势
  • \(\text{设}\langle H,*\rangle\leq\langle G,*\rangle,\quad a\in G,\quad\text{则}H\approx Ha\approx aH\)
• Lagrange 定理：若 \(<G,*>\) 为有限群：\(|G|=|H|\cdot[G:H]\)
  • 子群的阶数是原先群的阶数的因子
  • 元素的阶数也是原先群的阶数的因子（元素的阶数决定生成子群 \(<a>\) 的元素数目）
  • 若群的阶数为质数，则 \((\exists a\in G)(\langle a\rangle=G)\)
  • 

循环群

• 若 \((\exists a\in G)(G=<a>)\) 则 \(<G,*>\) 为循环群
  • 其中 \(<a>=\{ a^n\mid n\in Z \}\)，则 \(a\) 称为 \(G\) 的生成元
  • 充要条件为 \(\exists a\in G,\mid a\mid=\mid G\mid\)
• 有限循环群：若生成元的阶为 \(n\) 则为 \(n\) 阶有限循环群 \(G=\{ a^0,a^1\dots a^{n-1}\}\)
  • 
  • 若 \(\mid a\mid=n\) 则对不大于 \(n\) 的正整数 \(r\) 也有，\(G=<a^r>\iff gcd(n,r)=1\)，也就是说 \(n\) 阶循环群的生成元的数目刚好等于不大于 \(n\) 并且与 \(n\) 互质的正整数数目 (欧拉函数 \(\phi(n)\))
  • 对于有限群均有 \(<G,*>\cong <Z_{n},\oplus_{n}>\)

• 无限循环群：\(a\) 为无限阶元 \(G=a^0,a^{\pm 1}\dots\)

  • 若 \(a\) 是无限循环群的生成元，则 \(a^{-1}\) 也是，并且无限循环群有且仅有这两个生成元
  • 对于所有无限群均有 \(<G,*>\cong <Z,+>\)
  • 

• 循环群的子群

  • 循环群的子群为循环群
  • 无限循环群的子群除 \(\{ e \}\) 之外都是无限循环群
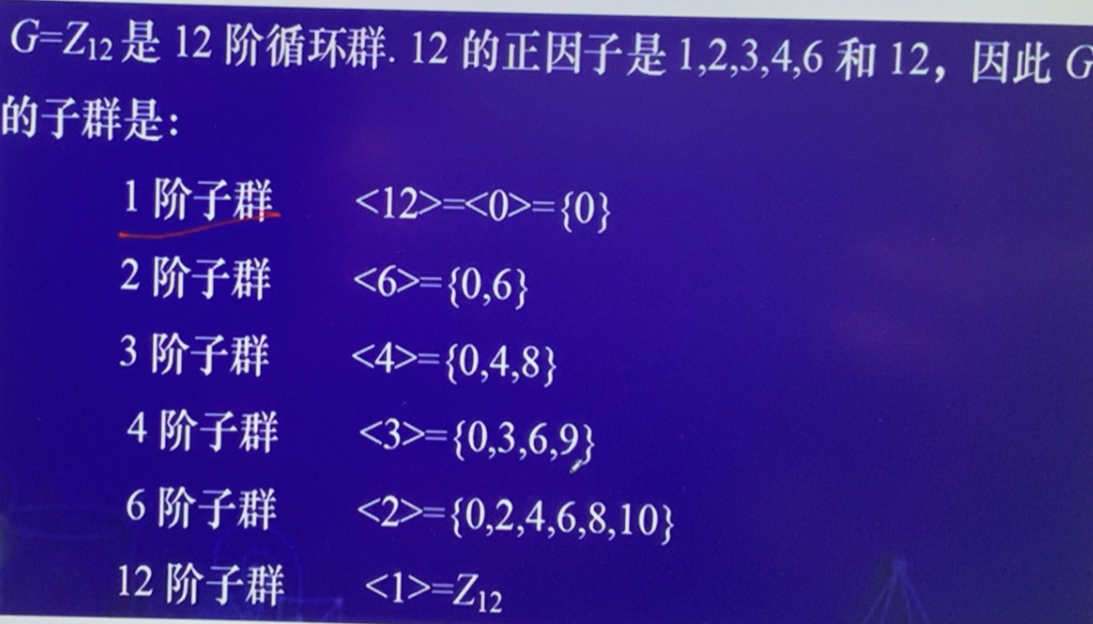
  • 对 \(n\) 的每一个因子 \(d\)，循环群中都恰有一个 \(d\) 阶子群
  • 

• \(\text{设}f\text{为从群}\langle G,*\rangle\text{到群}\langle H,0\rangle\text{的同态}\)

  • \(f(e_G)=e_H\) 同构下可以保证唯一
  • \(f\left(a^{-1}\right)=\left(f\left(a\right)\right)^{-1},\forall a\in G\)
• 群同构的证明过程：
  • 构建 \(\forall x,y\in G_{1},\:f(x\circ y)=f(x)*f(y)\)
  • 证明双射
• 循环群都是阿贝尔群

图论

图的定义和表示

• 图 \(G\) 是一个三元组 \(G=(V,E,\varphi)\)
  • 分别表示顶点集合、边集 （\(V\bigcap E=\phi\)）、边对应的端点集
  • 简单图：\(\forall e\in E,|\varphi(e)|=2\) 并且 \(e_{1}\neq e_{2}\to \varphi(e_{1})\neq \varphi(e_{2})\) 即不含自环和多重边
  • 伪图正相反
• 有向图的底图：把每一条有向边替换为无向边（简单有向图的底图不一定是简单无向图）
• 使用 \(d_{G}^+\) 和 \(d_{G}^-\) 表示入度和出度，注意自环会共享两个边

• 平凡图：只有一个点没有边的图

• 弱连通有向图：底图为连通无向图

• 强连通有向图：对任意 ab 有 \(a\to b,b\to a\)

• 握手定理：因为 \(\sum d=2m\)，因此无向图中奇数点的个数一定是偶数个

• 子图
  • \(G=<V,E>,G'=<V',E'>\) 若 \(V'\subseteq V,E'\subseteq E\) 则称 \(G'\) 为 \(G\) 的子图（若边/点不完全相同，则为真子图）
  • 导出子图：保留了原图中选定顶点之间的所有连接关系（即子图中两点有边当今当原图中两点之间有边）

特殊简单图

• 完全图 \(K_n\)：简单图中任意两点都相连，即每个顶点为 \(n-1\) 度
• 圈图 \(C_{n}\)
  • 
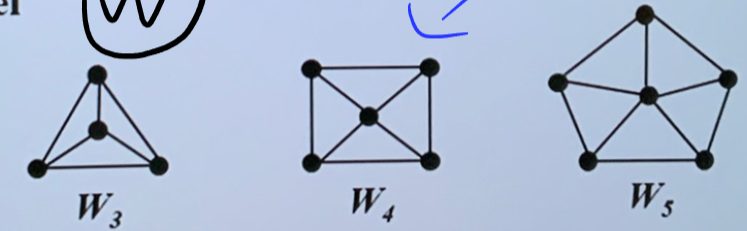
• 轮图 \(W_{n}\)
  • 
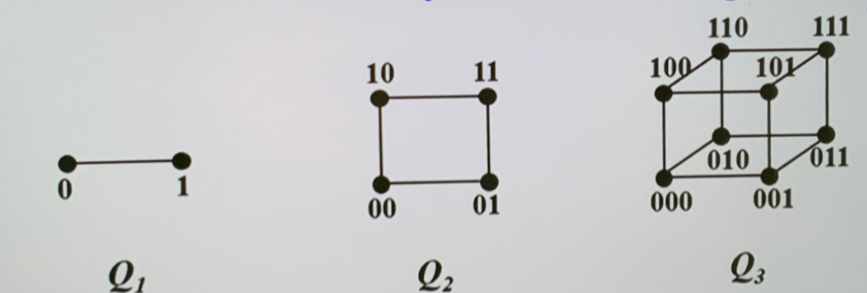
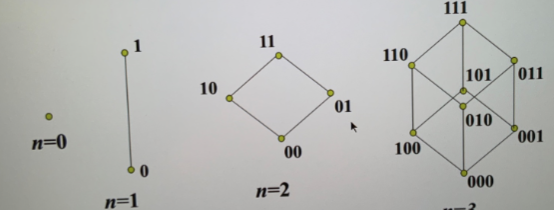
• 立方体图 \(Q_{n}\)
  • 
• 正则图：各点度相同

图的表示与同构

• 邻接矩阵、邻接表

• 关联矩阵：是点与边的关联关系（邻接矩阵是点与点）

  • 设有 n 个点 m 条边，就有一个 \(n\times m\) 阶矩阵，\(m_{ij}=1\iff e_{i}关联v_{i}\)
  • 适用于无向图，不能表示边的方向
  • 

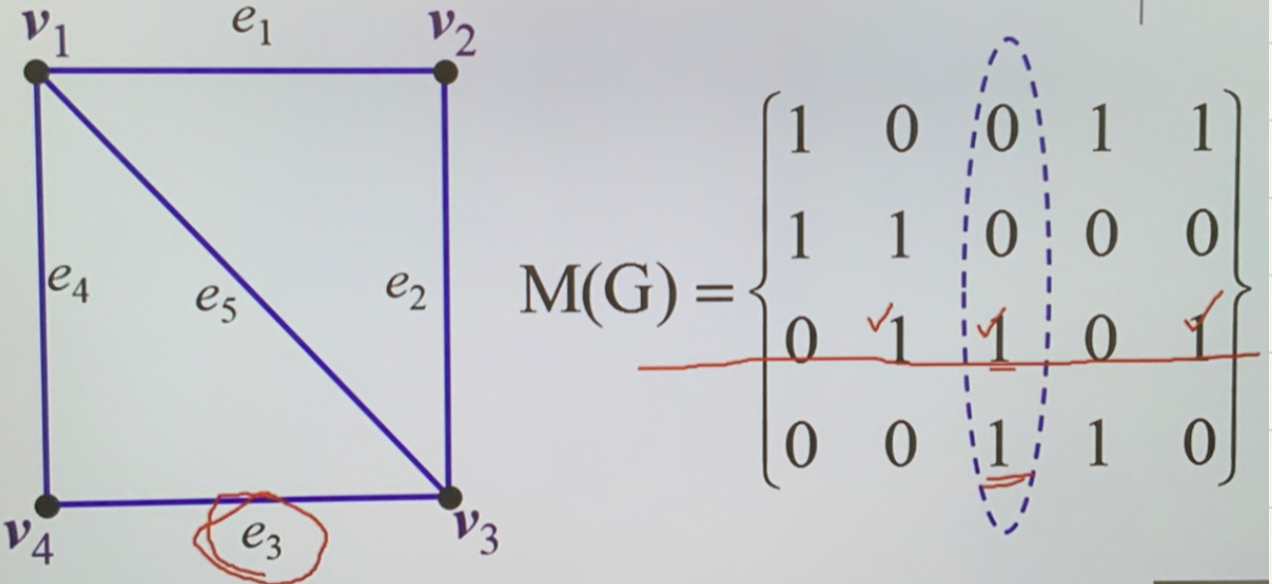
• 邻接矩阵的运算

  • 行中的 1 的个数表示出度；列中的 1 的个数表示入度
  • 逆图的邻接矩阵就是原图的邻接矩阵的转置
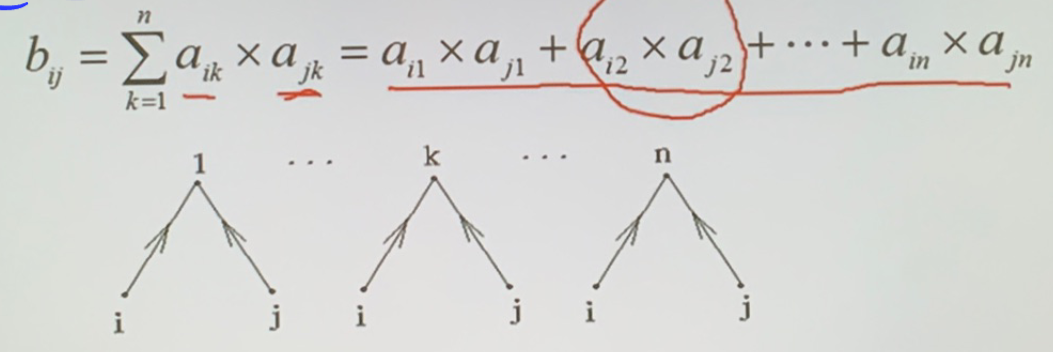
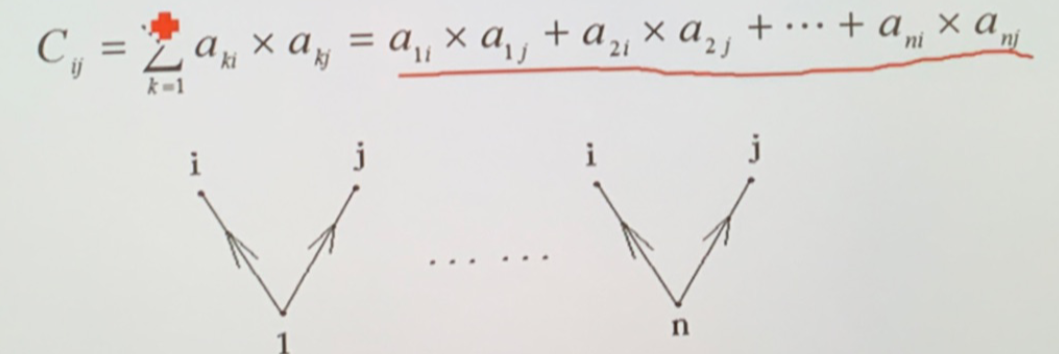
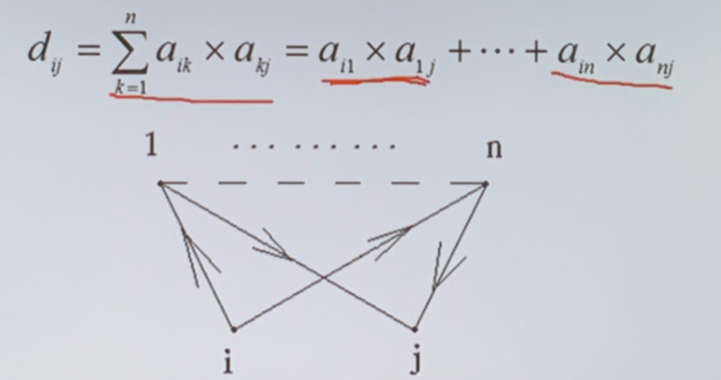
  • \(A\times A^T\)，\(b_{ij}\) 表示顶点 \(i\) 和顶点 \(j\) 均有边指向的那些顶点的个数
    • 
  • \(A^T\times A\)，\(b_{ij}\) 表示同时有边指向顶点 \(i\) 和 \(j\) 的顶点个数
    • 
  • \(A\times A\)，\(b_{ij}\) 表示 \(i\) 和 \(j\) 之间具有的长度为 \(2\) 的通路的数目
    • 

• 应用：

  • 

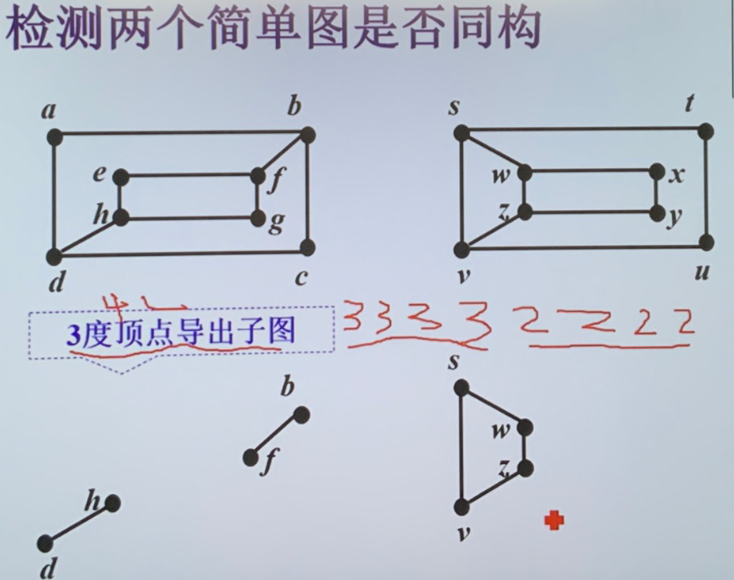
• 图的同构

  • \(\mathbf{G}_{1}=(\mathbf{V}_{1},\mathbf{E}_{1},\mathbf{\varphi}_{1})\text{和}\mathbf{G}_{2}=(\mathbf{V}_{2},\mathbf{E}_{2},\mathbf{\varphi}_{2})\)
  • 若存在双射 \(f{:}V_{1}{\to}V_{2},g{:}E_{1}{\to}E_{2}\) 使得 \(\forall e{\in}{E}_1,\varphi_1(e){=}\{u,v\}\iff g(e){\in}\mathbb{E}_2,\varphi_2(g(e)){=}\{f(u),f(v)\}\)
  • 
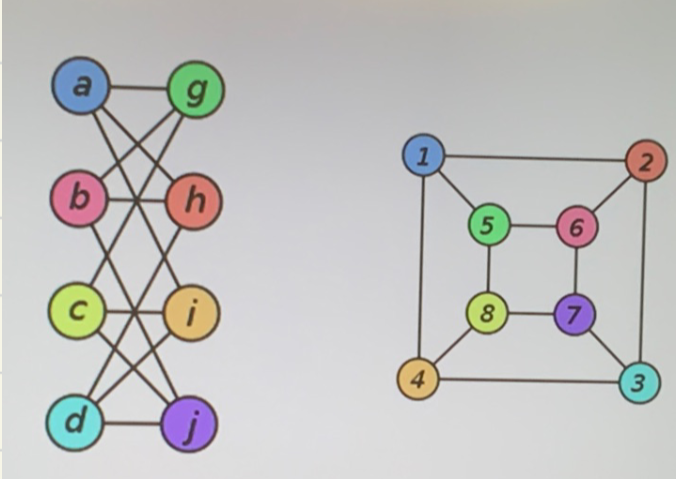
• 检测图是否同构：
  • 考察图的不变量：如长度为 \(k\) 的回路的存在性
  • 若 \(G\) 和 \(H\) 同构，则 \(G\) 的 \(k\) 度点导出子图与 \(H\) 的 \(k\) 度点导出子图同构
  • 

图的运算

• 
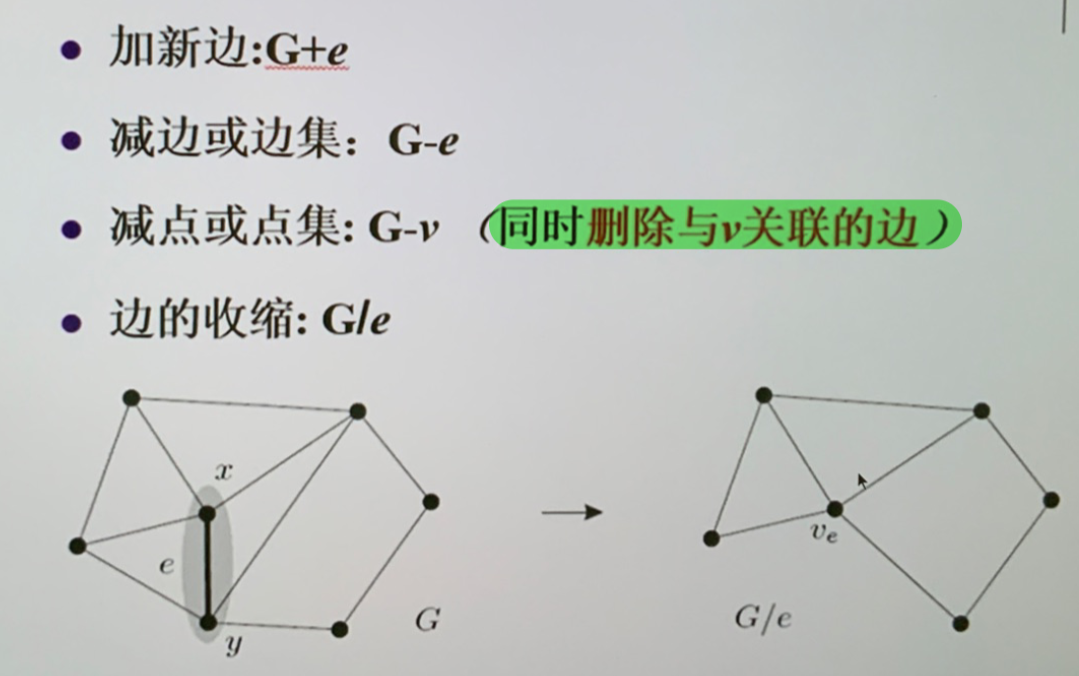
• \(G\bigcup G'\)：以 \(V(G)\bigcup V(G')\) 作为点集，\(E(G)\bigcup E(G')\) 作为边集
• \(G*G'\)：对于不想交的无向图，以 \(V(G)\bigcup V(G')\) 作为点集，以 \(E (G)\cup E (G^{\prime})\cup\{\{x, y\}|x\in V (G), y\in V (G^{\prime})\}\) 为边集, 如 \(K_{2}*K_{3}=K_{5}\)
• \(\overline G\) 补图：\(G({V},[{V}]^2\setminus{E})\)

连通图

• 通路：从 \(v_{0}\) 到 \(v_{n}\) 的长度为 \(n\) 的通路（\(n\) 条边 \(e_{1}\dots e_{n}\) 的序列）

  • 不区分多重边时可以直接用顶点的序列表示
  • 回路：起点与终点相同（长度大于 0）
  • 简单通路：边不重复；
  • 初级通路（路径）：点不重复（边更不重复）

• 对于无向图，如果图中任意两点之间都有通路（这是一个等价关系），那么称无向图 \(G\) 为连通的

• 连通分支：极大连通子图，每个无向图是若干个不相交的连通分支的并

  • \(p(G)\) 表示 \(G\) 的连通分支的数目
  • 删除一个点之后，连通分量数目可能不变，减少（-1）, 增加（可能增加多个）
  • 删除一条边后有 \(p(G)\leq p(G-e)\leq p(G)+1\)

• 割点：对于 \(v\in V_{G}\)，若 \(p(G-v)>p(G)\) 则称 \(v\) 为割点，三个等价命题：

  • \(v\) 是割点
  • 存在 \(V-\{v\}\) 的划分 \(\{ V_{1},V_{2} \}\) 对于 \(\forall u\in V_{1},w\in V_{2}\)， \(uw\) -通路均包含 \(v\)
  • 存在顶点 \(u,v\) 使得任意 \(uw\) 通路都包含 \(v\)
• 割边：\(p(G-e)>p(G)\) 则称 \(e\) 是 \(G\) 中的割边，四个等价命题
  • \(e\) 是割边
  • \(e\) 是割边当仅当 \(e\) 不在 \(G\) 的任一简单回路上
  • 存在 \(V-\{v\}\) 的划分 \(\{ V_{1},V_{2} \}\) 对于 \(\forall u\in V_{1},w\in V_{2}\)， \(uw\) -通路均包含 \(e\)
  • 存在顶点 \(u,v\) 使得任意 \(uw\) 通路都包含 \(e\)
• 点连通图：
  • 使非平凡连通图 \(G\) 成为不连通图或者平凡图需要删除的最少（不是说删除了这么多就不连通了）定点数称为点连通度，记为 \(\kappa(G)\)
  • 不连通图的连通度为 0，\(\kappa (K_{n})=n-1\)
  • 若 \(\kappa (G)\geq k\) 则称 \(G\) 是 \(k\) 连通图（删除少于 \(k\) 个点仍然连同）

• 边连通图：与点联通图的定义类似，记为 \(\lambda(G)\)

• 连通度的上限

  • 对于非平凡简单图有 \(\kappa(G)\leq\lambda(G)\leq\delta (G)\)（最小顶点度）
  • 
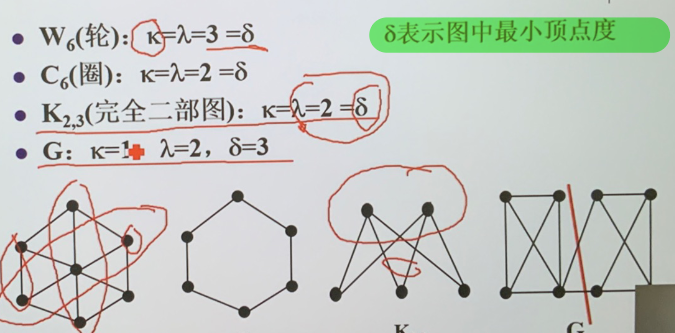
• 设 \(G\) 为简单图 \(\mid G\mid=n\geq 3\) 且 \(\delta_{G}\geq n-2\) 则 \(\kappa(G)=\delta_{G}\)
• 图 \(G\) 是 \(k\) 连通图，当仅当 \(G\) 中任意两点至少被 \(k\) 条除端点外顶点不想交的路径路径所连接
• 图 \(G\) 是 \(k\) 边连通图，当仅当 \(G\) 中任意两点被至少 \(k\) 条边不相交的路径所连接
• 一个图是 2 连通的 \(\iff\) 是一个回路互是在一个已有的 2 连通图上一次增加路径（连接两个点）
  • 

欧拉图

• 包含图中每一条边的简单通路为欧拉通路（简单回路为欧拉回路）
  • 若一个图中有欧拉回路，则称为欧拉图，如果只有欧拉通路没有欧拉回路，那么称 G 为半欧拉图
• 连通图为欧拉图，当仅当所有顶点的度均为偶数
  • 与命题“图中所有边包含在若干个相互没有公共边的简单回路中”等价
• 连通图为半欧拉图，当仅当恰有两个奇度点（必须以这两个点为简单通路的起始点）

• 有向欧拉图：有向图中含所有边的有向简单回路称为有向欧拉回路，对应的图为有向欧拉图

  • 

• 构造欧拉回路 Fleury 算法（输入欧拉图，输出一个欧拉回路）

  • 任取 \(v_{0}\in V_{G}\) 令 \(P_{0}=v_{0}\)
  • 设 \(P_{i}=v_{0}e_{1}v_{1}\dots e_{i}v_{i}\) 按照下列规则从剩下的点中选择 \(e_{i+1}\)
  • 要求 \(e_{i}\) 与 \(v_{i}\) 关联，除非别无选择，否则不应该选择割边（删除这条边之后剩下的边应该在同一个连通分量）

• 随机欧拉图：从 \(v\) 开始，每次从当前点关联的边种随机选一条边，均可以构造欧拉回路，\(G\) 为以 \(v\) 为始点的随机欧拉图

  • 
  • \(G\) 为欧拉图当仅当 \(G\) 中任一回路都包含 \(v\)

哈密顿图

• 哈密顿通路 (哈密顿图)：包含所有顶点，通路上各顶点不重复
• 哈密顿回路：起点重终点相同（与环同构）

• 若有点的度为 1 则没有哈密顿回路，并且不能存在割点；对于每一个顶点只会使用其两条边；n 个顶点的哈密顿回路有 n 调边

• 必要条件：对于任意 \(S\subseteq V\) 有 \(P(G-S)\leq\mid S\mid\)

• 充分条件（Ore 定理）：对于无向简单图 \(\mid G\mid=n\geq 3\)，若任意不相邻的顶点对都满足 \(d(u)+d(v)\geq n\) 则有哈密顿回路（或者是 \(\delta(G)\geq \frac{n}{2}\)）

  • G 的闭合图，\(C(G)\) 连接 \(G\) 中不相邻并且度之和不小于 \(\mid G\mid\) 的点对，直到没有哦，\(G是哈密顿\iff C(G)是哈密顿\)
  • \(d(u)+d(v)\geq n-1\) 则说明有哈密顿通路(哈密顿图)

• 竞赛图：底图为完全图的简单有向图

  • 
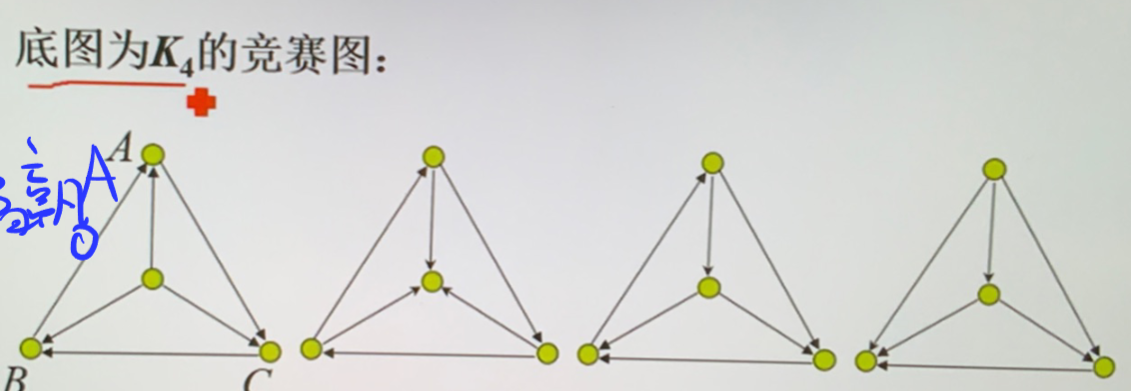
  • 可以看做 \(n\) 个选手循环赛的结果
  • 竞赛图一定有哈密顿通路
  • 
  • 

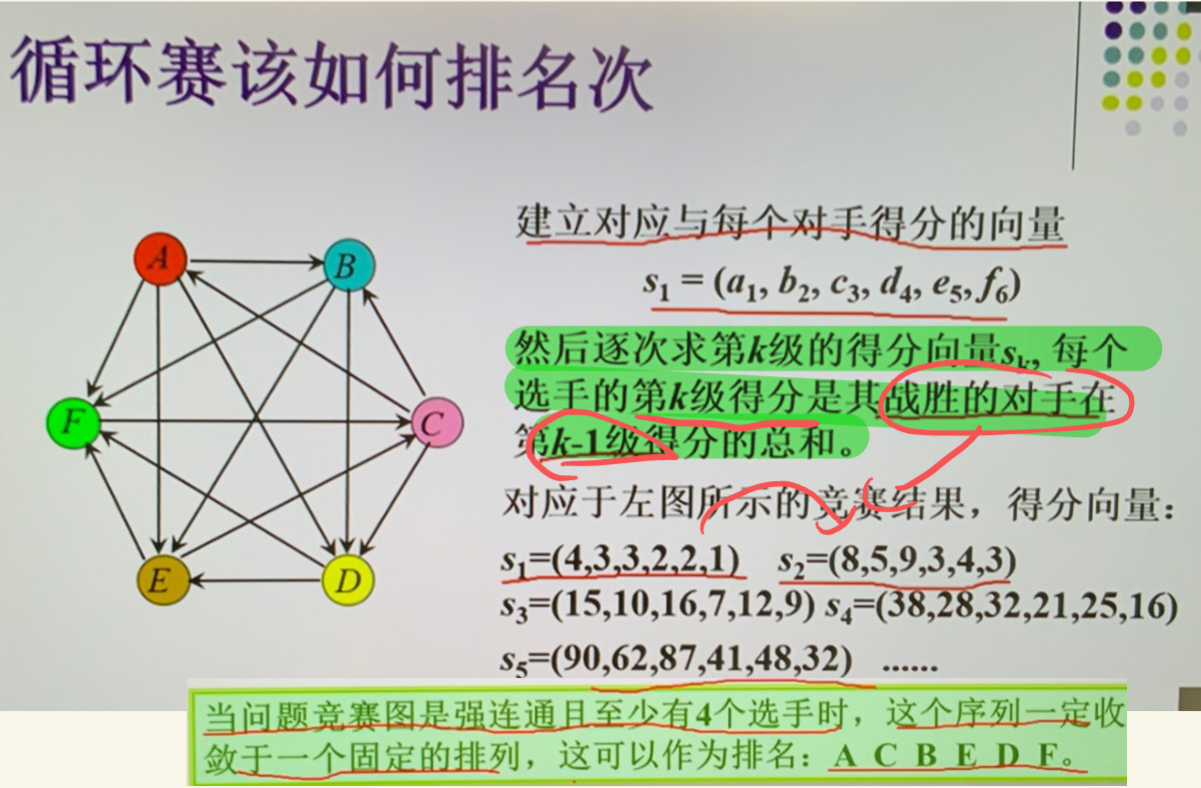
• *旅行商问题

  • 找最短哈密顿回路（找哈密顿回路本身就是 NPC）
  • 对于完全图，有 \(\frac{(n-1)!}{2}条\) 是一个 NPC 问题
  • 近似算法：总是选择最近的点

二部图

• 二部图
  • 顶点集划分为两个集合, 边端点位于不同类别
  • 完全二部图 \(K_{n,m}\)：来自不同类别的两个顶点之间均有边
  • 

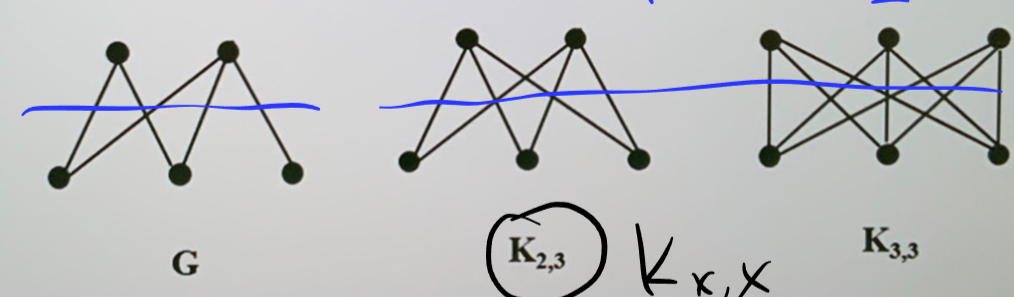
• \(G\) 为二部图当仅当不含奇圈

• 匹配：\(E^*\subseteq E\) 为 \(G\) 的匹配，其中 \((\forall e_{1},e_{2}\in E^*)\) 均有 \(e_{1},e_{2}\) 不相邻

• 极大匹配：再加一条边就是非匹配了
• 匹配数：图 \(G\) 的匹配数为 \(\beta_{1}(G)=max\{ \mid E^*\mid\mid E^*为G的匹配 \}\)
• 最大匹配：即 \(\mid E^*\mid=\beta_{1(G)}\)
• \(v_{i}\) 与 \(v_{j}\) 被 \(M\) 匹配：\((v_{i},v_{j})\in M\)
• \(v\) 为 \(M\) 饱和点：有 \(M\) 中边与 \(v\) 关联（非饱和点正好相反）
• 完美匹配：\(G\) 中无 \(M\) 非饱和点
• 交错路径：\(M\) 与 \(E-M\) 中交替取边构成的 \(G\) 中路径

• 可增广路：起点和终点都是非饱和点的交错路径

  • 增广路：将可增广路的匹配边变为非匹配边，非匹配边变为匹配边，得到的新路径为增广路
  • 最大匹配 \(\iff\) 不含可增广路

• 对于二部图中两个点集 \(V_{1},V_{2}(\mid V_{1}\mid<\mid V_{2}\mid)\) 若 \(V_{1}\) 中全部为饱和点，则为完备匹配（当 \(\mid V_{1}\mid=\mid V_{2}\mid\) 时为完美匹配）

  • 完备匹配一定是极大匹配
  • Hall 定理：对于上述二部图有完备匹配当仅当 \(V_{1}\) 中任意 \(k\) 个点至少与 \(V_2\) 中任意 \(k\) 个顶点相邻
  • 推论：二部 k-正则（k 一定偶数）图总是有完美匹配；\(V_{1}\) 中每个顶点至少关联 \(t\) 条边，若 \(V_{2}\) 中每个顶点至多关联 \(t\) 条边，则存在完备匹配

树

• 不含回路的连通简单图为树，是边最少的连通图（每条边都是割边），边最多的无回路图 （加一条边产生唯一回路）
• 树中任意两点之间存在唯一路径

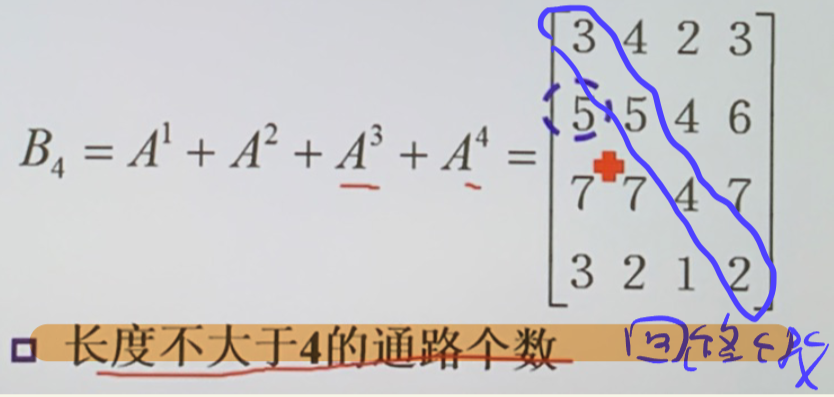
• \(n=\left|V(T)\right|,\:m=\left|E(T)\right|\) 有 \(m=n-1\) (因此连通图有 \(m\geq n-1\))

  • 树等价与：不含回路并且 \(m=n-1\)；连通并且 \(m=n-1\)

• 生成子图：保留点，减少边

  • 若生成子图为树，则为生成树，无向图有生成树当仅当连通
  • 图有唯一的生成树当仅当自身就是树

• 生成树的个数

  • 对于完全图 \(n^{n-2}\)
  • 对于完全二部图 \(p^{q-1}q^{p-1}\)

• 有向树：底图为有向图

• 根树

  • 有向树，恰有一个入度为 0 的顶点（根），其他节点入度都为 1，
  • 存在从根到其他点的唯一通路

• m 元树：每个内点至多 m 个子女（m 叉）

  • \(m^{h-1}<l\leq m^{h}\)
• 完全 m 元树：每个内点恰好 m 个子女（m 叉正则）
  • \(n-1=m\times i\) 入度等于出度，因此 \(\frac{{n-1}}{m}\) 个内点 \(n-\frac{{n-1}}{m}\) 个叶节点
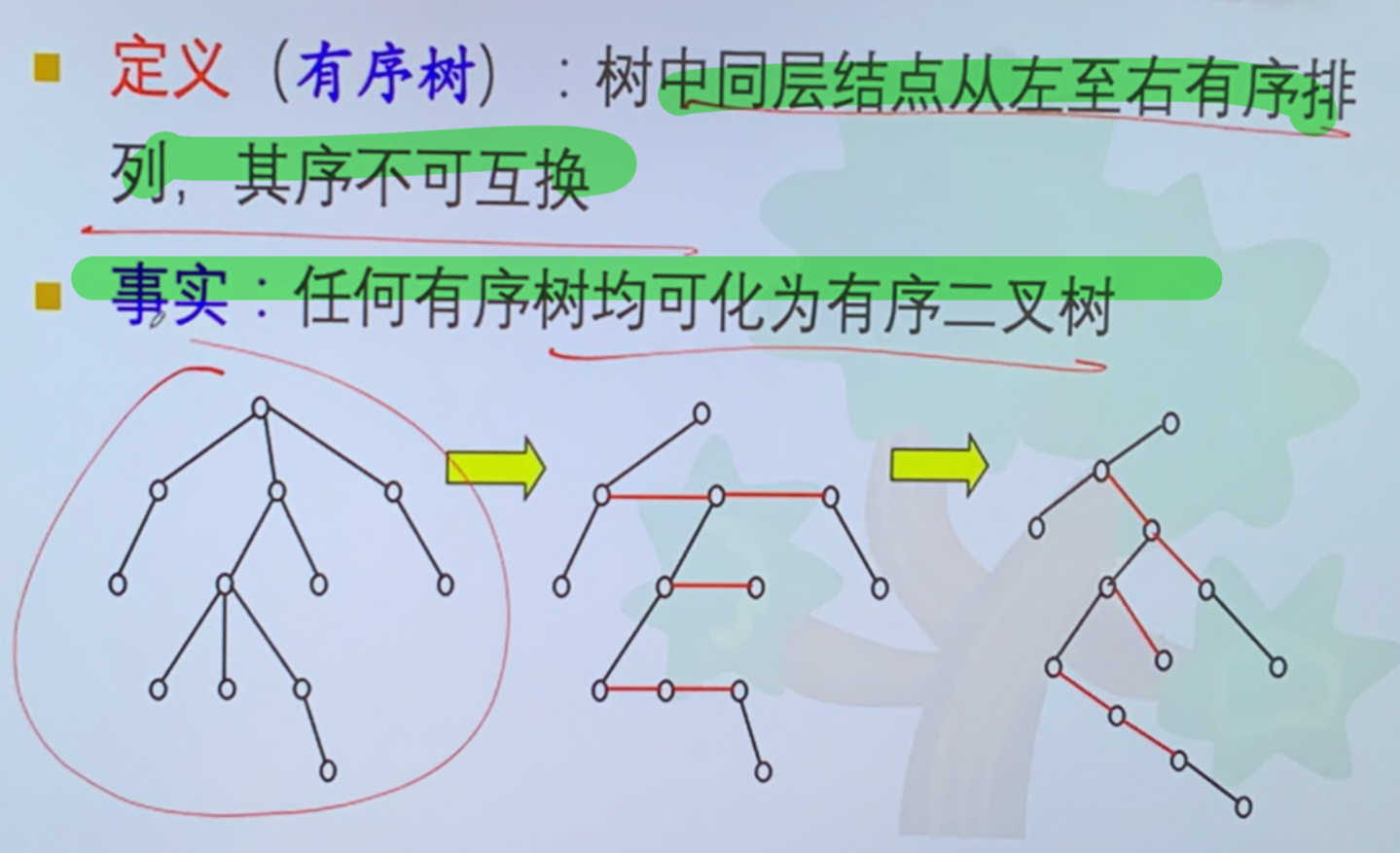
• 平衡：树叶都在 h、h-1
• 有序：同层顶点固定次序

-