P2
实验内容¶
实验一 :3-8译码器¶
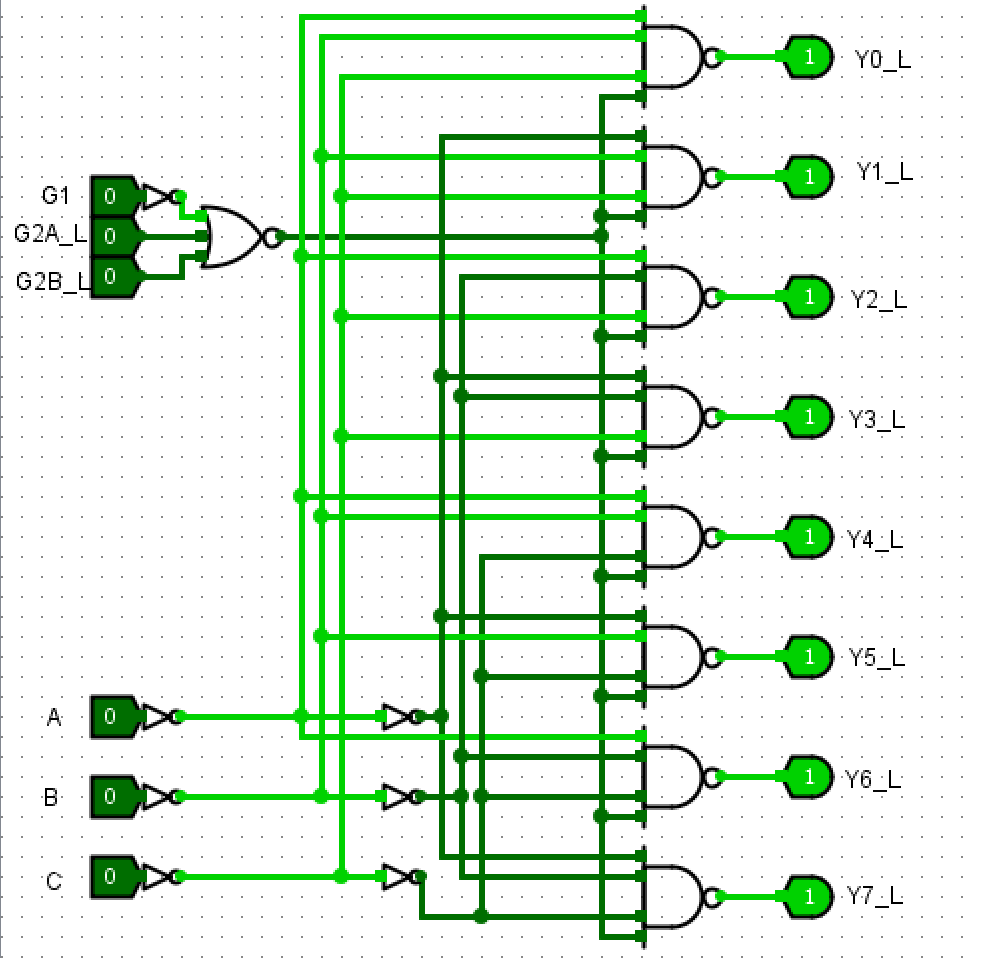
- 设计一个由反相逻辑门电路构成的 3-8 译码器,并对电路进行仿真测试,以验证电路的功能。
整体方案设计¶
输入输出引脚¶
- G1、G2A_L、G2B_L:三个控制位
- ABC:三位二进制输出
- Y0_L~Y7_L:8位译码后的二进制输出
电路图¶
仿真测试¶
| G1 | G2A_L | G2B_L | C | B | A | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 1 | X | X | X | X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| X | X | 1 | X | X | X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | X | X | X | X | X | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
实验二 :8-3编码器¶
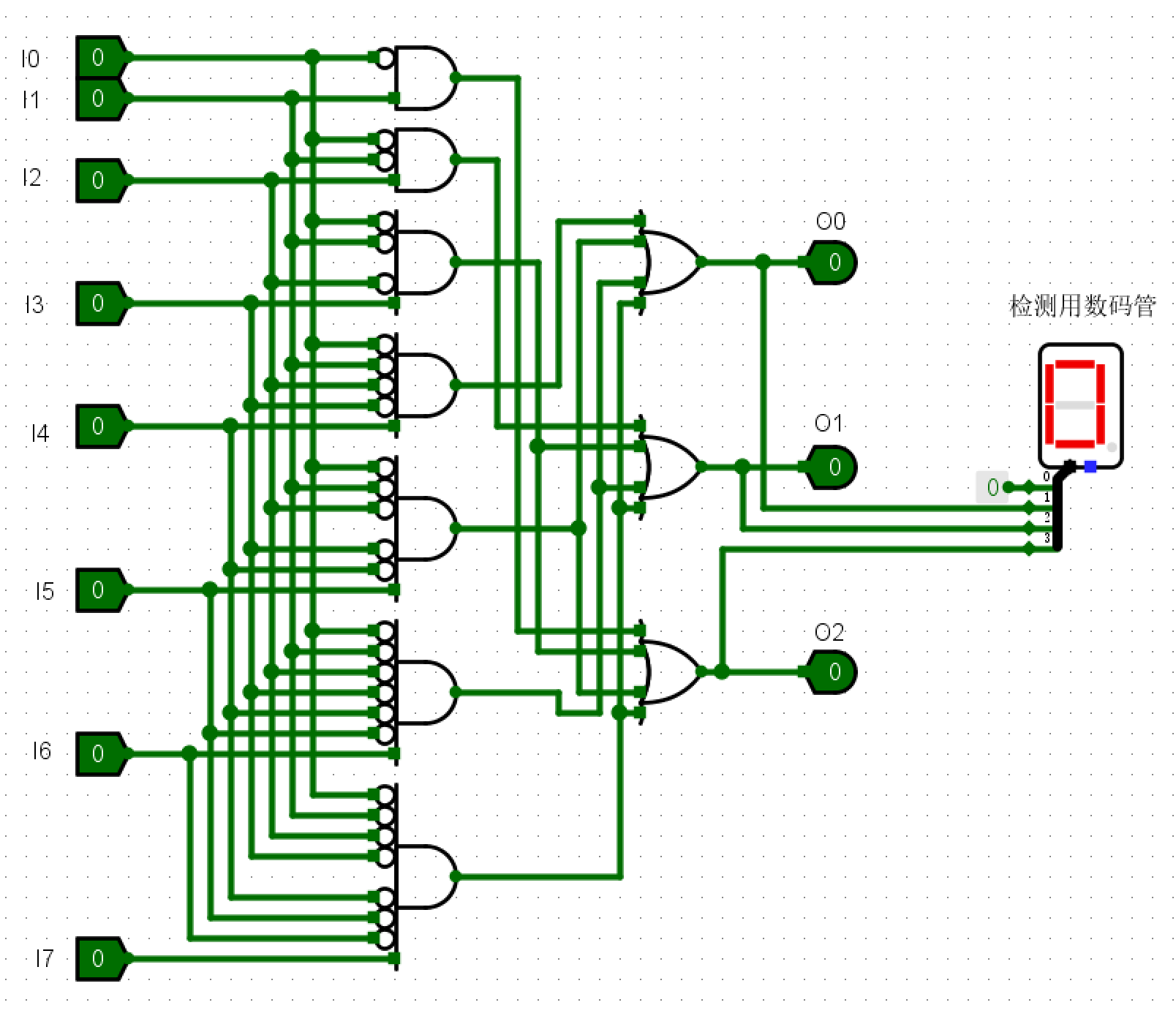
- 设计一个由逻辑门电路构成的 8-3 优先级编码器,并将编码器输出连接到一个十六进制数码管,通过数码管的输出显示来验证和测试电路。
整体方案设计¶
输入输出引脚¶
- I0~I7:8位输入
- O0~O2:3为编码结果输出
- 数码管:显示输出
电路图¶
仿真测试¶
| I0 | I1 | I2 | I3 | I4 | I5 | I6 | I7 | O2 | O1 | O0 | Hex |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | x | x | x | x | x | x | x | 0 | 0 | 0 | 0 |
| 0 | 1 | x | x | x | x | x | x | 1 | 0 | 0 | 8 |
| 0 | 0 | 1 | x | x | x | x | x | 0 | 1 | 0 | 4 |
| 0 | 0 | 0 | 1 | x | x | x | x | 1 | 1 | 0 | C |
| 0 | 0 | 0 | 0 | 1 | x | x | x | 0 | 0 | 1 | 2 |
| 0 | 0 | 0 | 0 | 0 | 1 | x | x | 1 | 0 | 1 | A |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | 0 | 1 | 1 | 6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | E |
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
实验三 :加减法器¶
- 设计一个支持4位数加减法的器件
整体方案设计¶
输入输出引脚¶
- X:被加(减)数
- Y:加(减)数
- Cin:模式选择
- Cout:进位
电路图¶
- 全加器
-
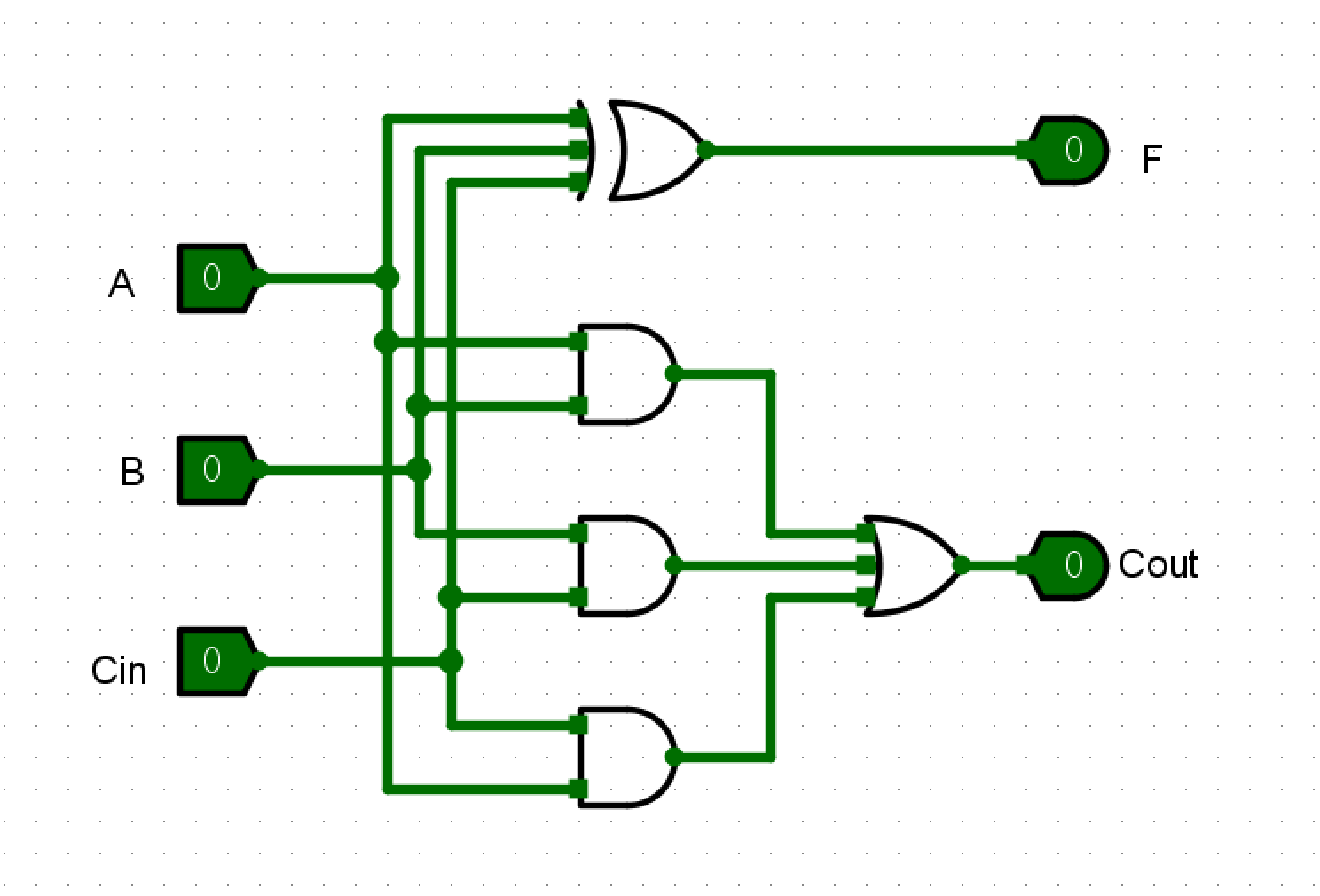
-
使用全加器实现加减法器
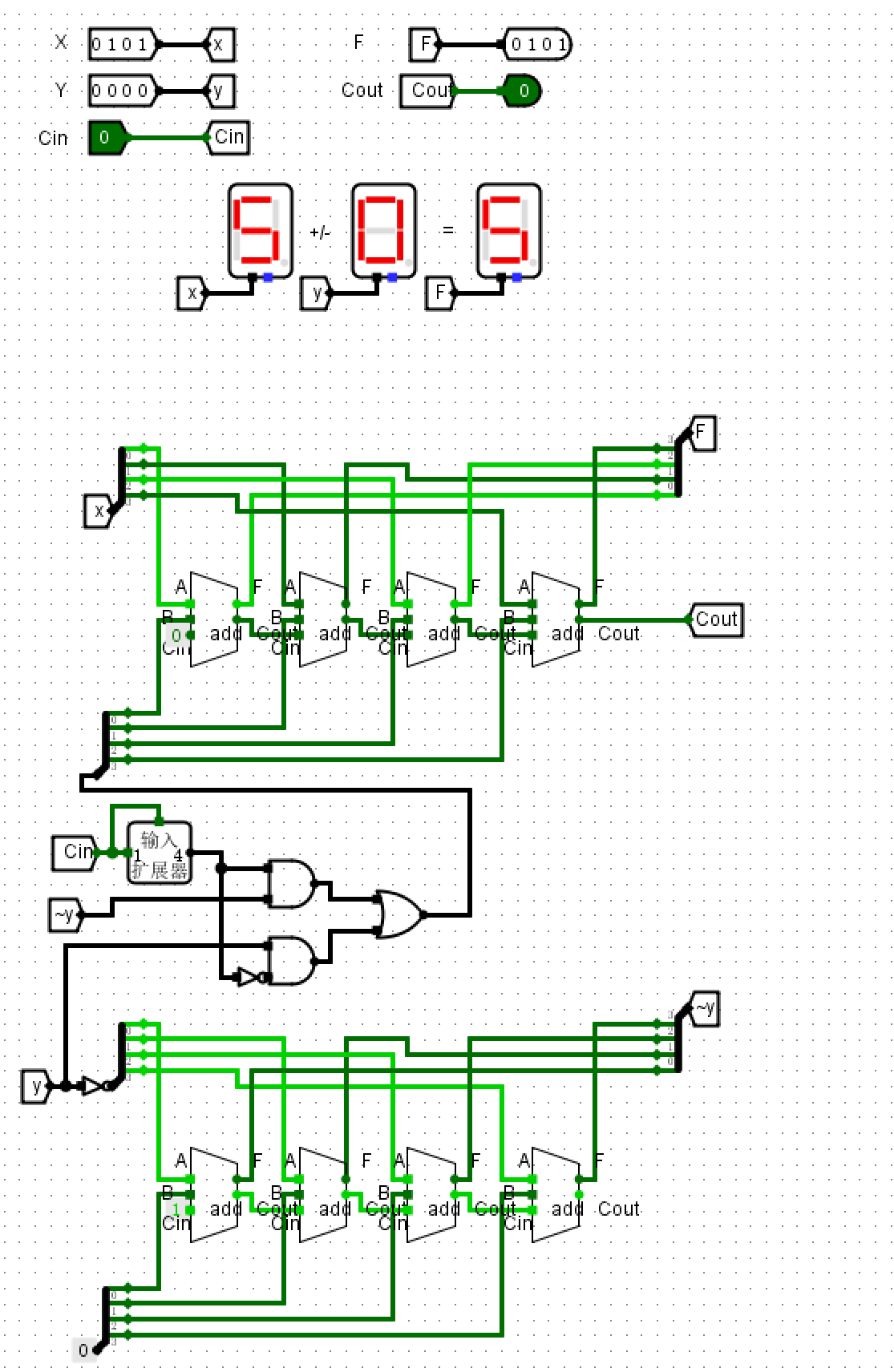
- 原理图
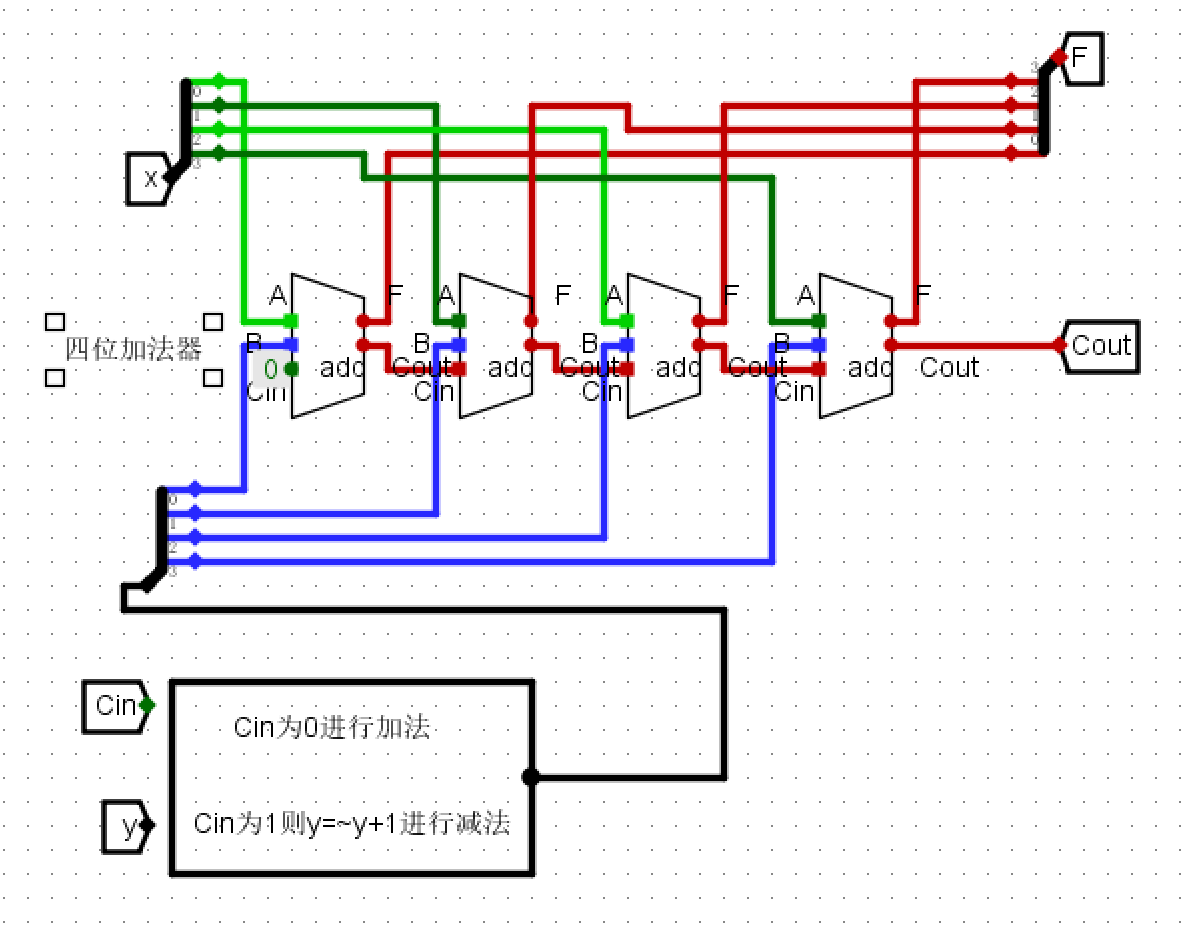
仿真测试¶
- 输入\(x=4 \ y=5\)得到\(F=9 \ Cout=0\)
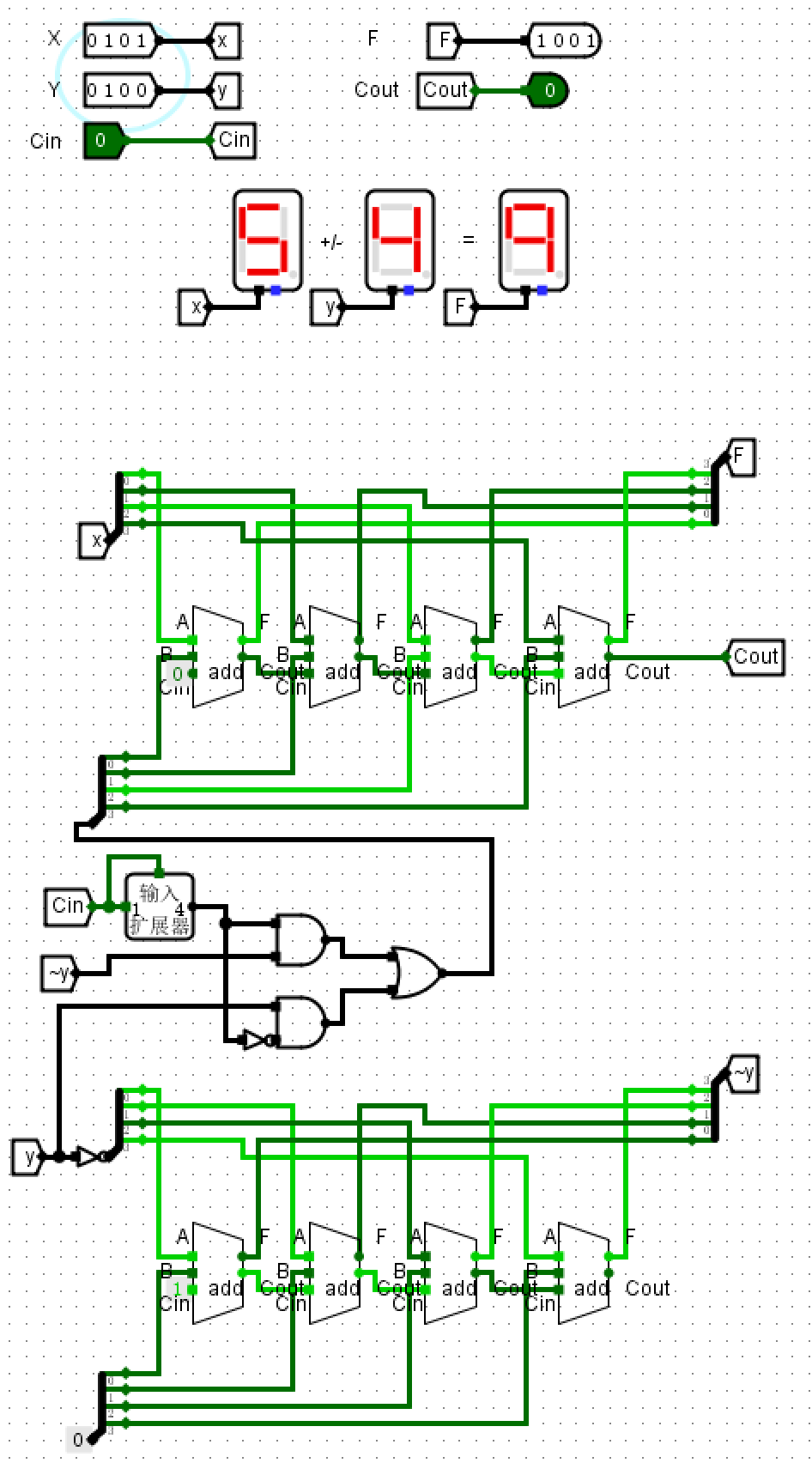
- 输入\(x=2 \ y=4 \ Cin=1\)得到\(F=E \ Cout=0\)
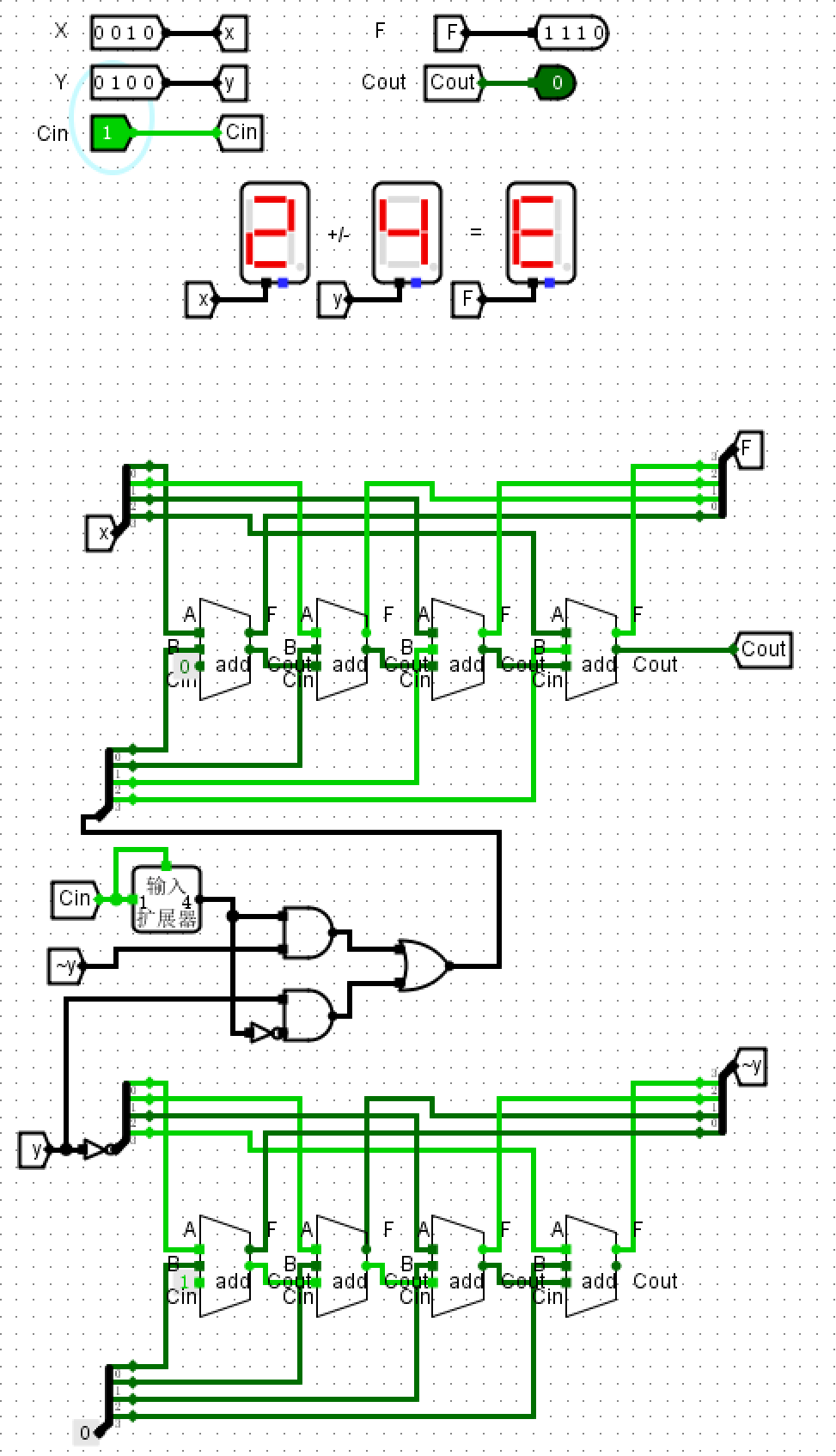
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
实验四 :海明码校验¶
- 设计一个支持7位海明码校验及自动纠错的元器件
整体方案设计¶
输入输出引脚¶
- Input:输入的7位
- Output:校验结果
- Ok、Error:是否出错的判定
电路图¶
- 4位奇校验码计算
-
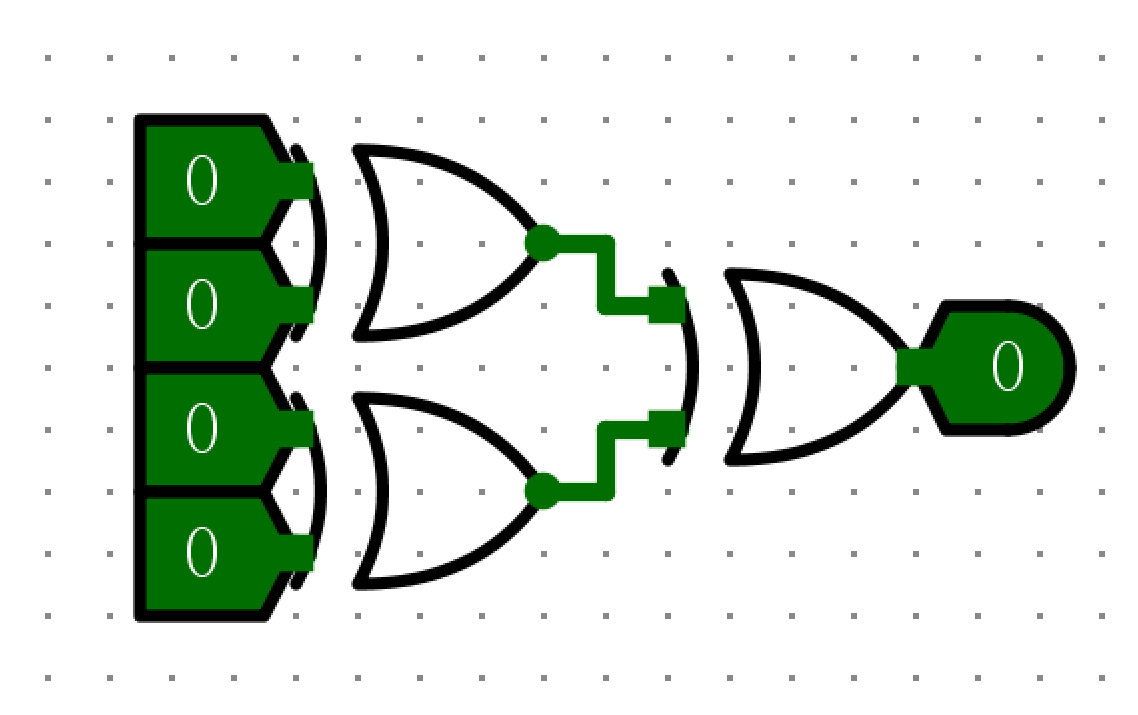
-
使用全加器实现加减法器
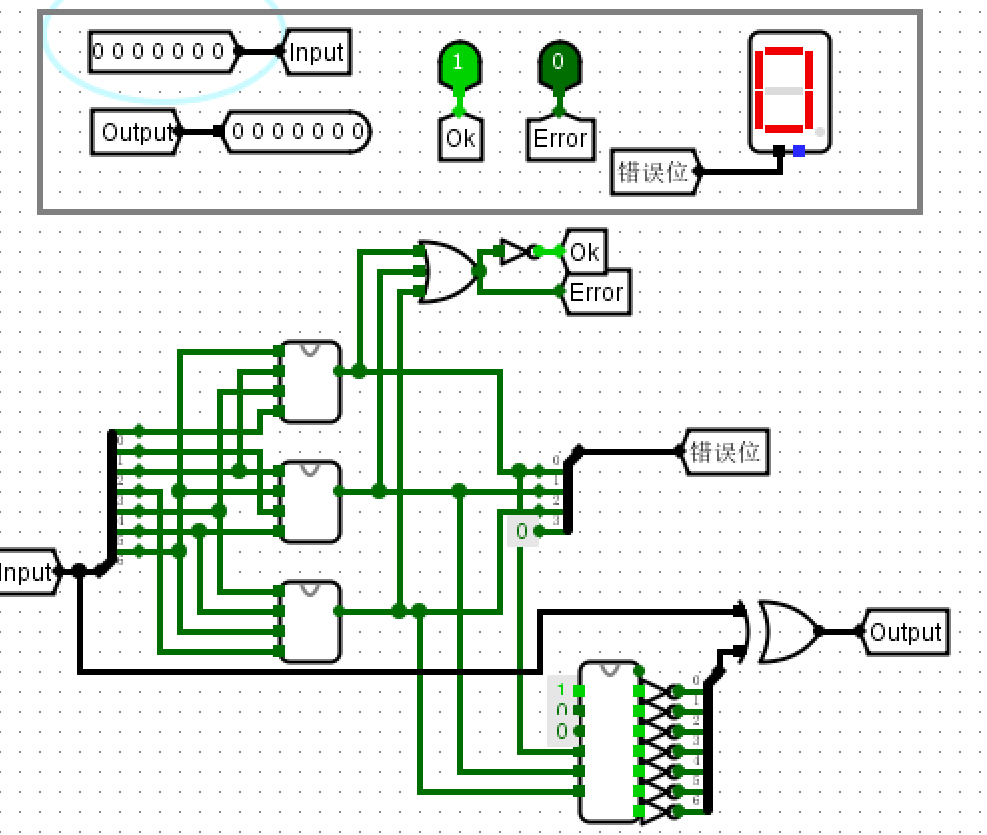
- 原理图
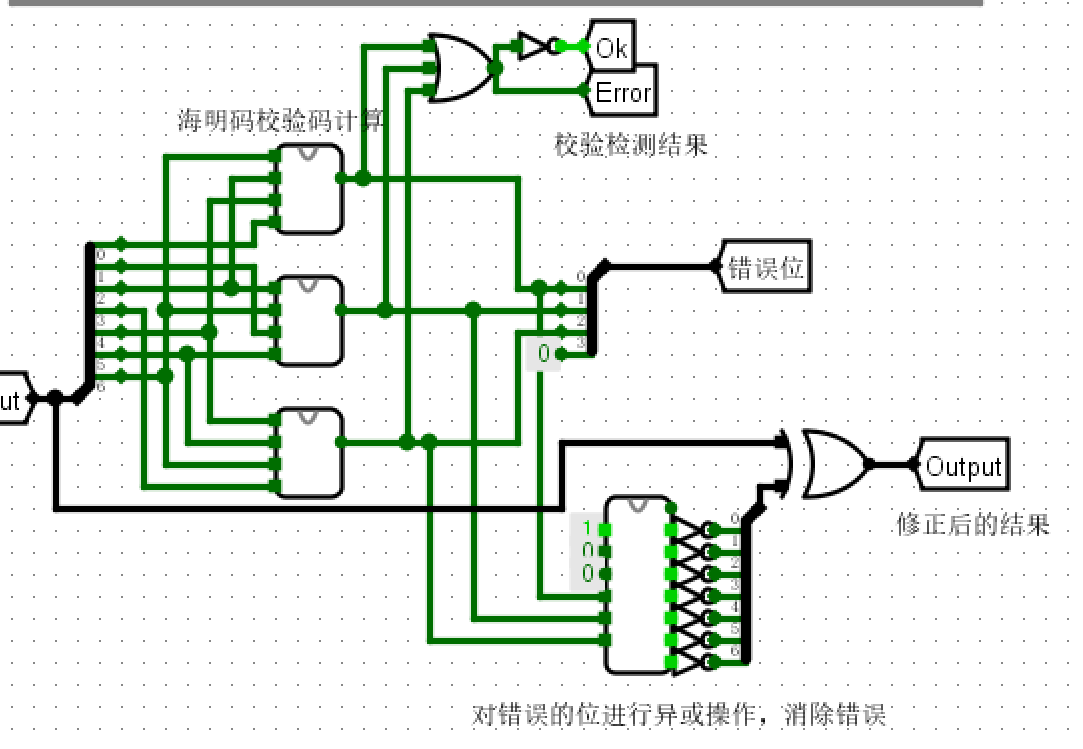
仿真测试¶
- 输入\(1000001\)对照发现是\(M_3\)出错
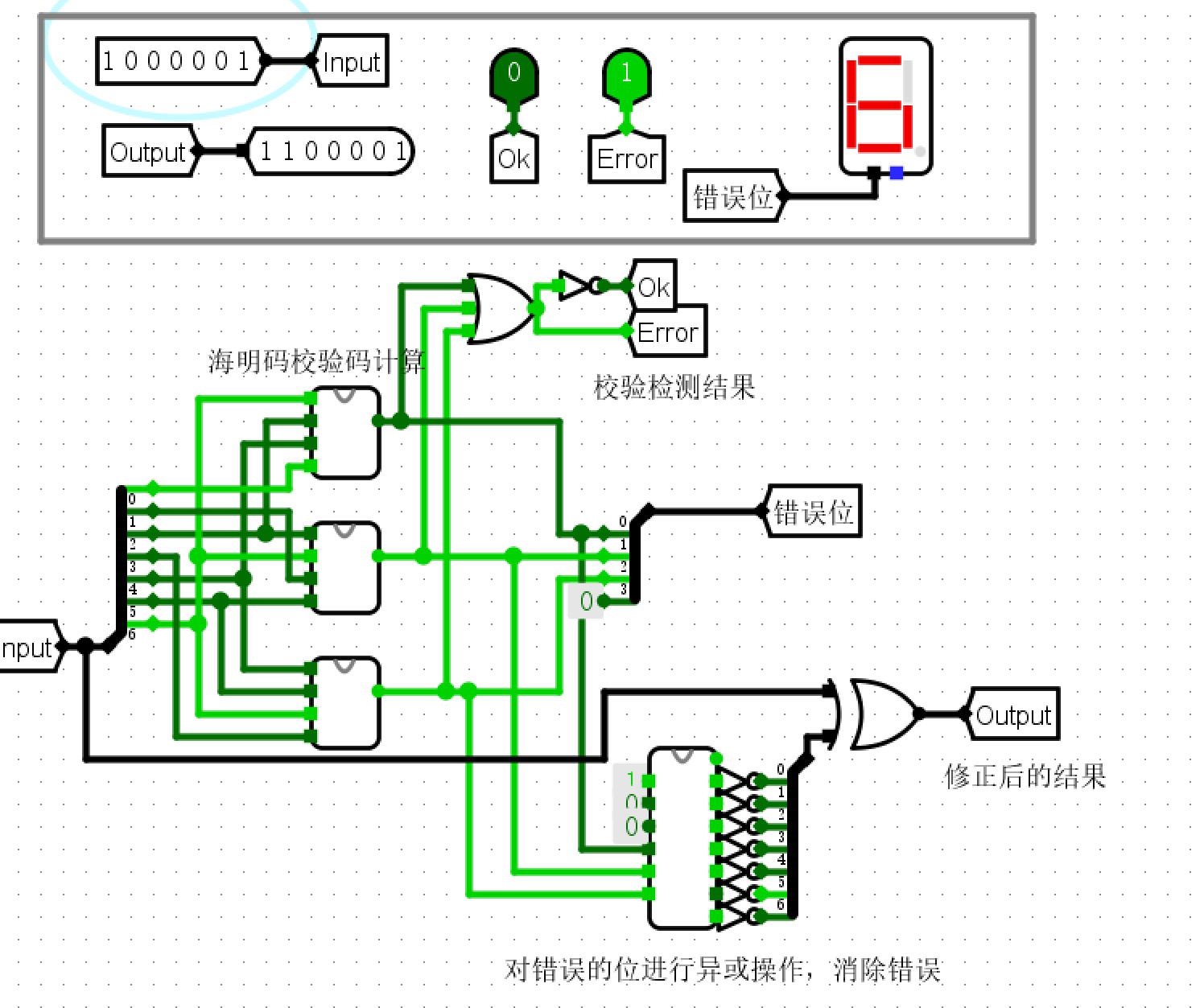
- 输入\(1100001\)没有发生错误
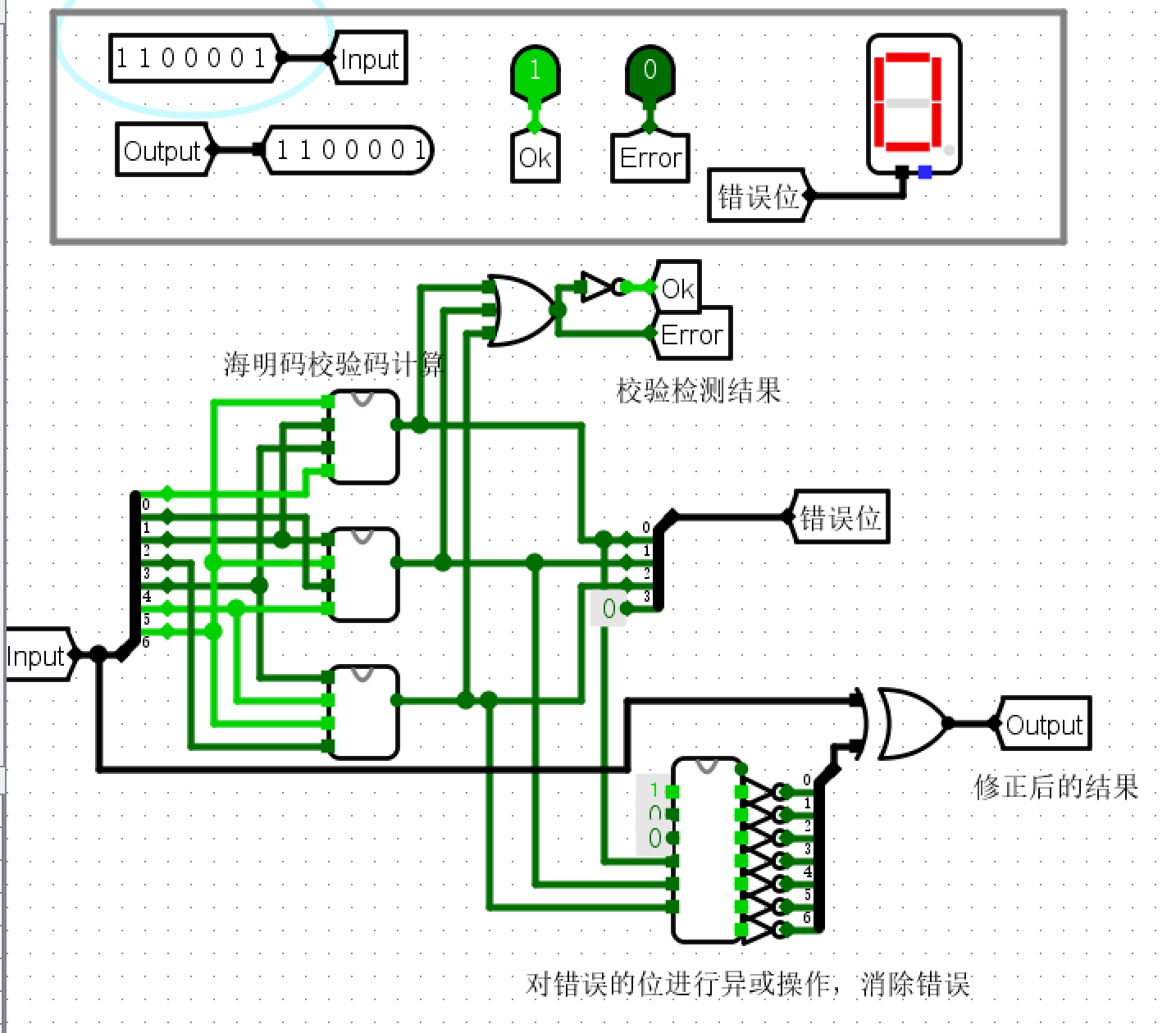
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
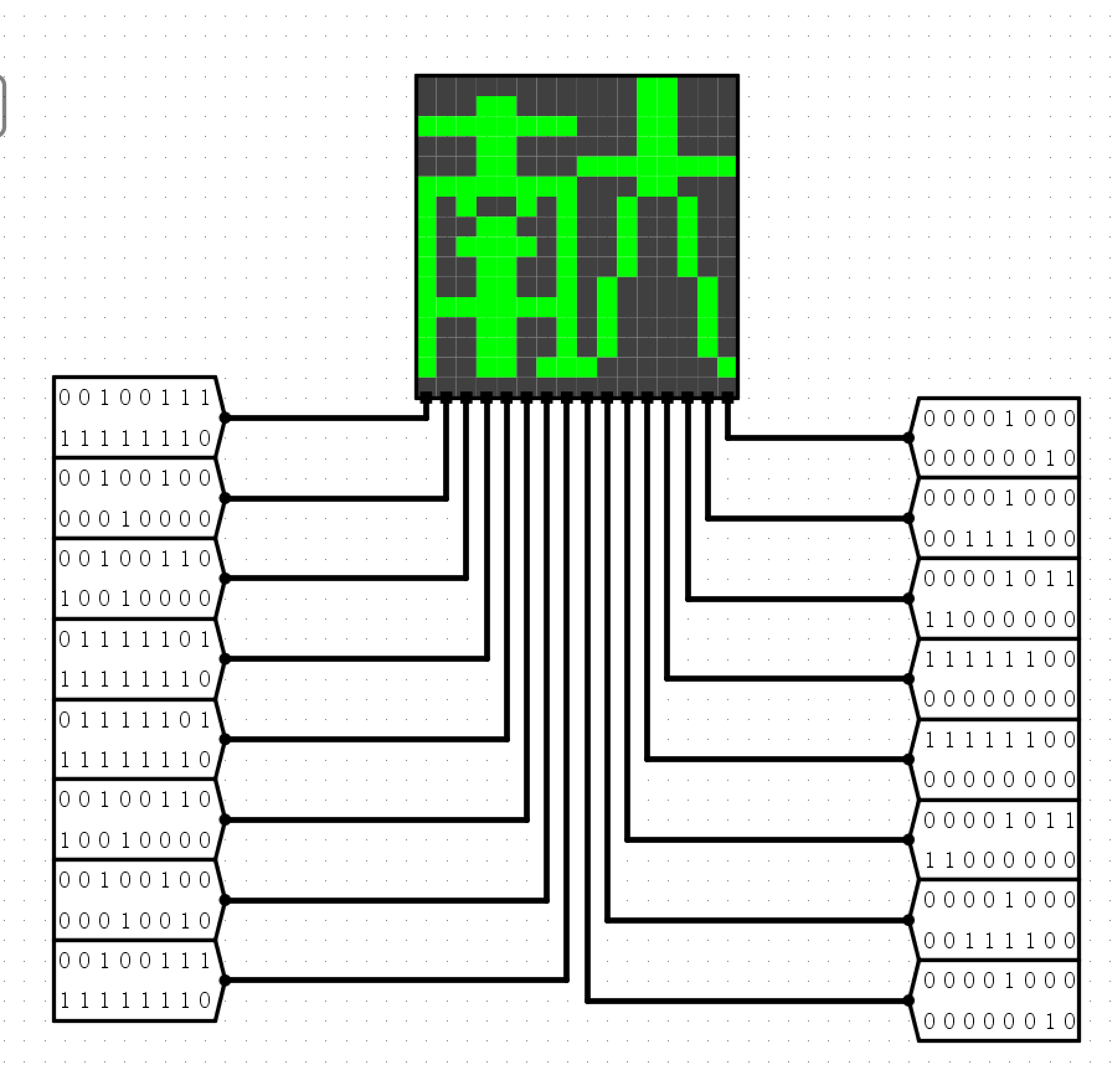
实验五 :桶形移位器¶
- 设计一个支持8位数左右移的元器件
整体方案设计¶
输入输出引脚¶
- Input:Din输入的8位数字
- Dout:移位后的结果
- left/right:移动方向设置
- math/logic:两种移动方式选择
- shamt:移动位数
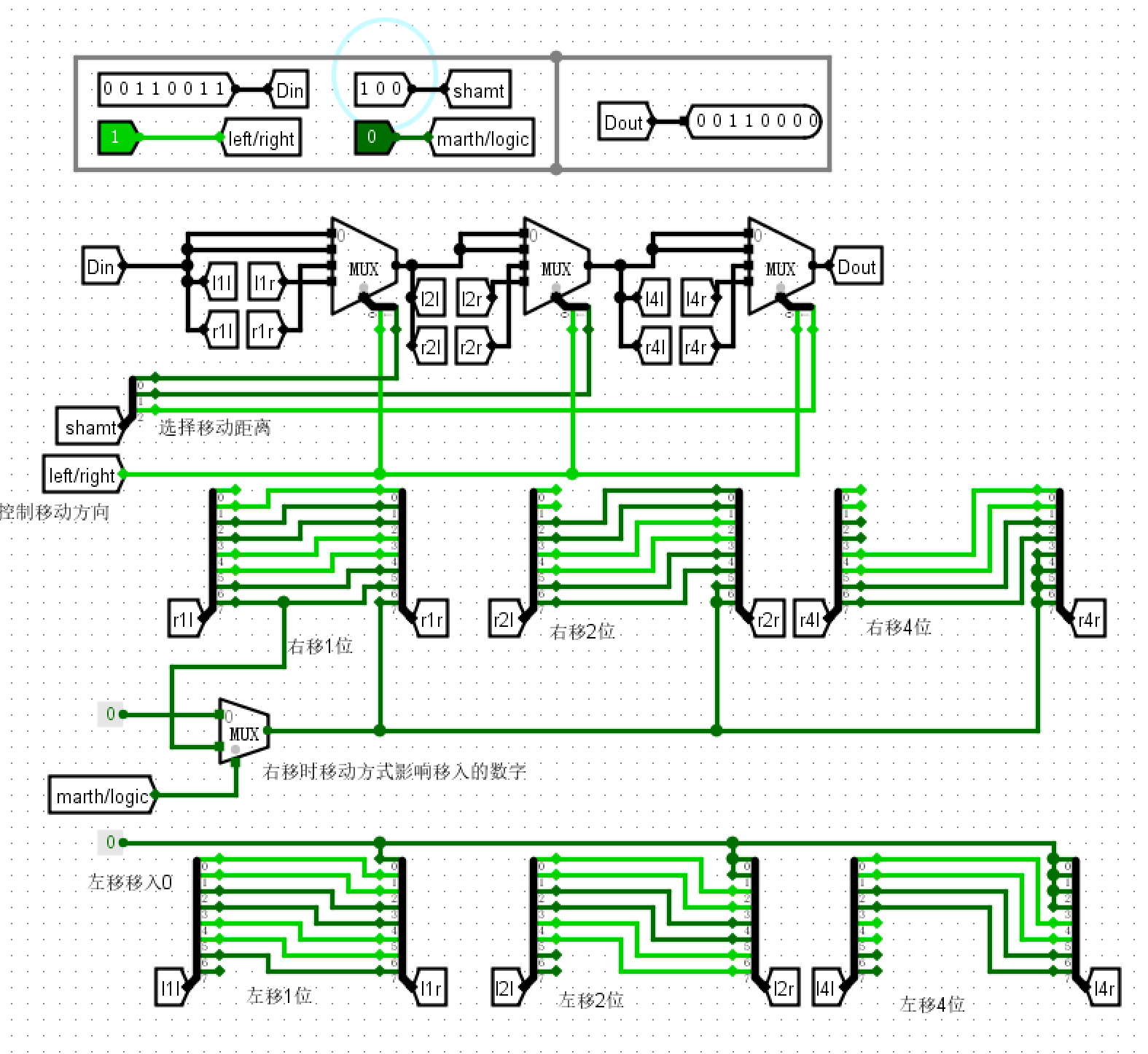
电路图¶
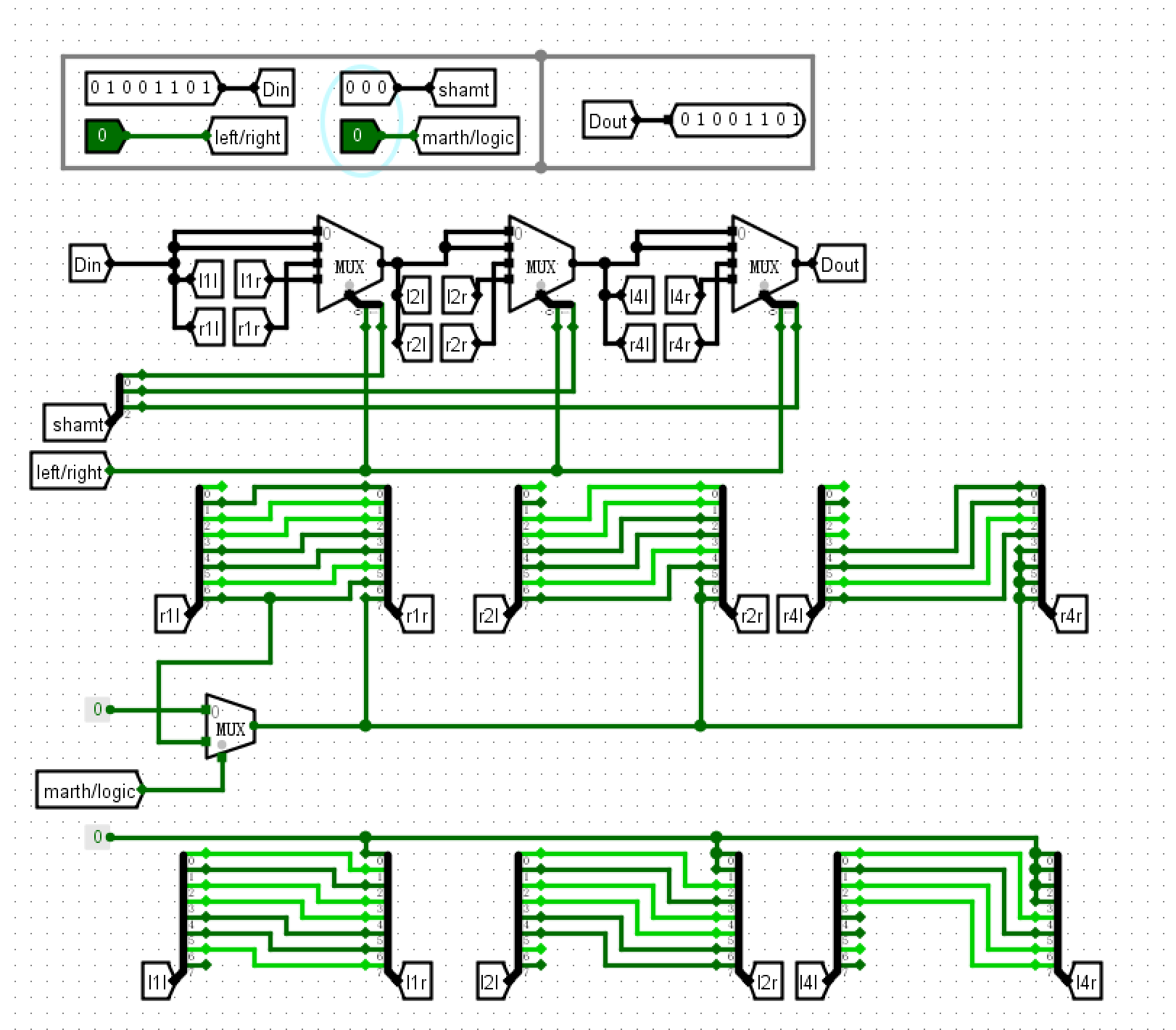
- 原理图
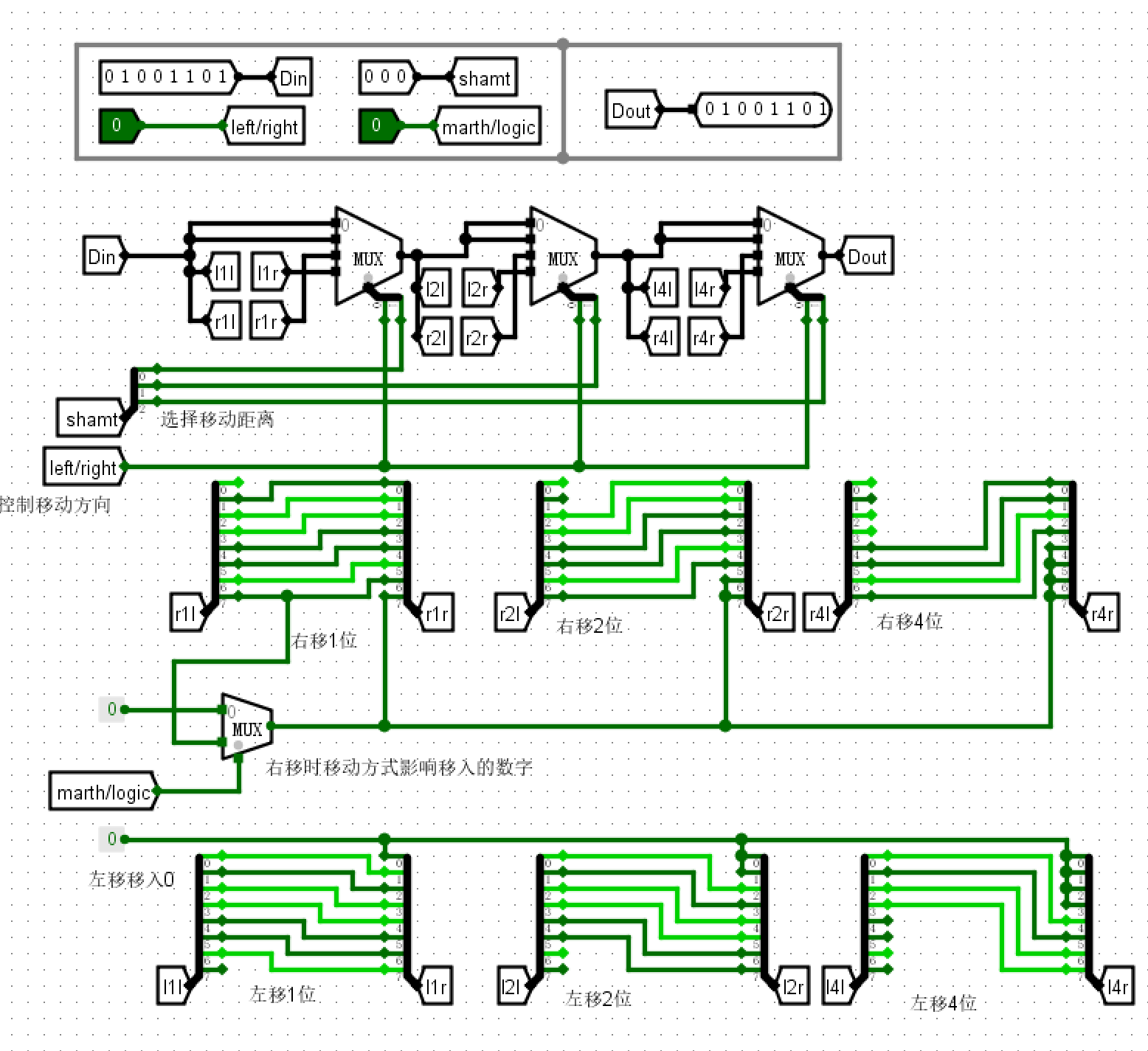
仿真测试¶
- 输入\(10000000\)数学右移\(2\)位,得到\(11100000\)
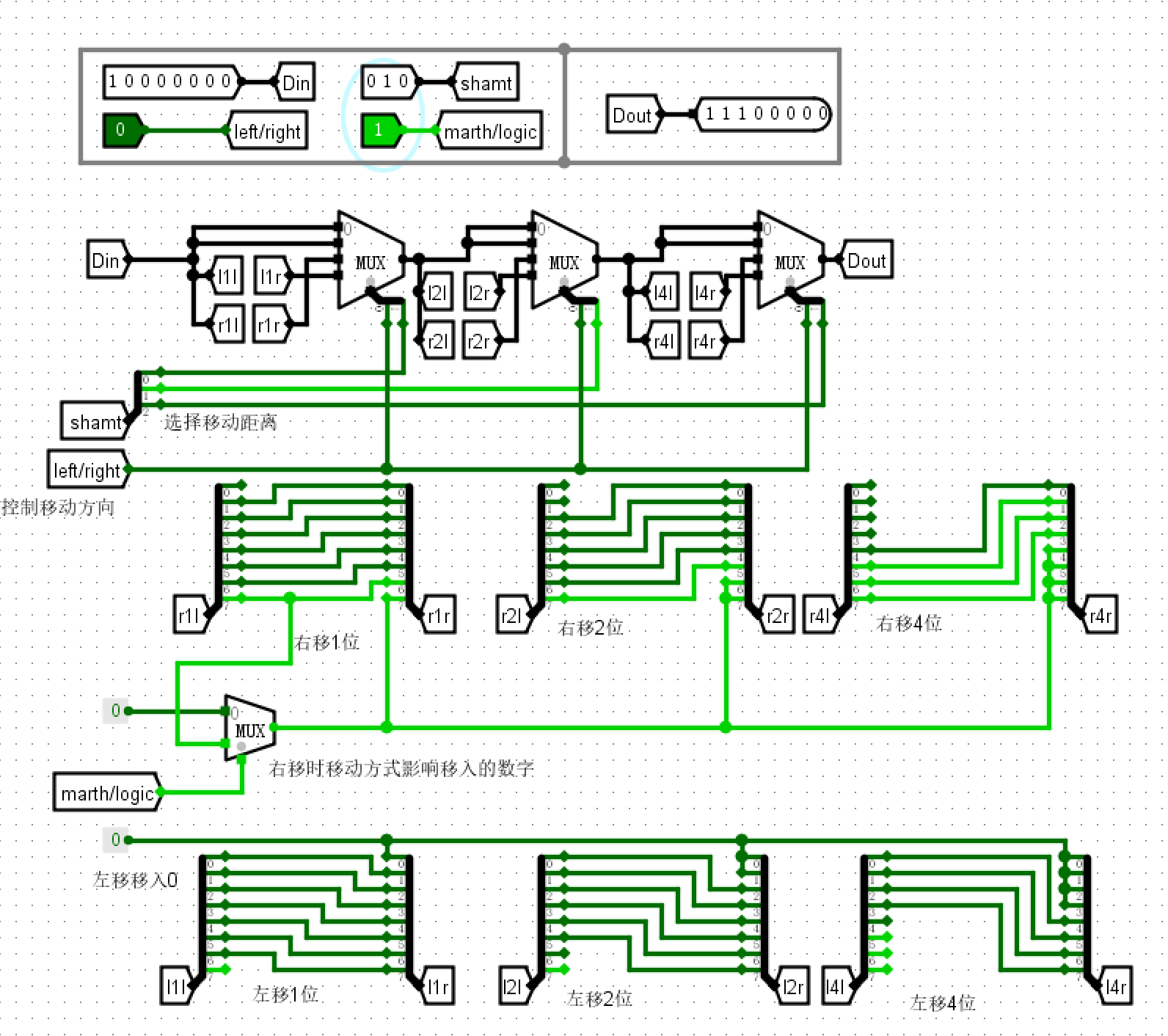
- 输入\(00110011\)逻辑左移\(4\)位得到\(00110000\)
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
思考题¶
1修改加法器,增添标志位¶
- 修改电路图增加关于标志位的计算
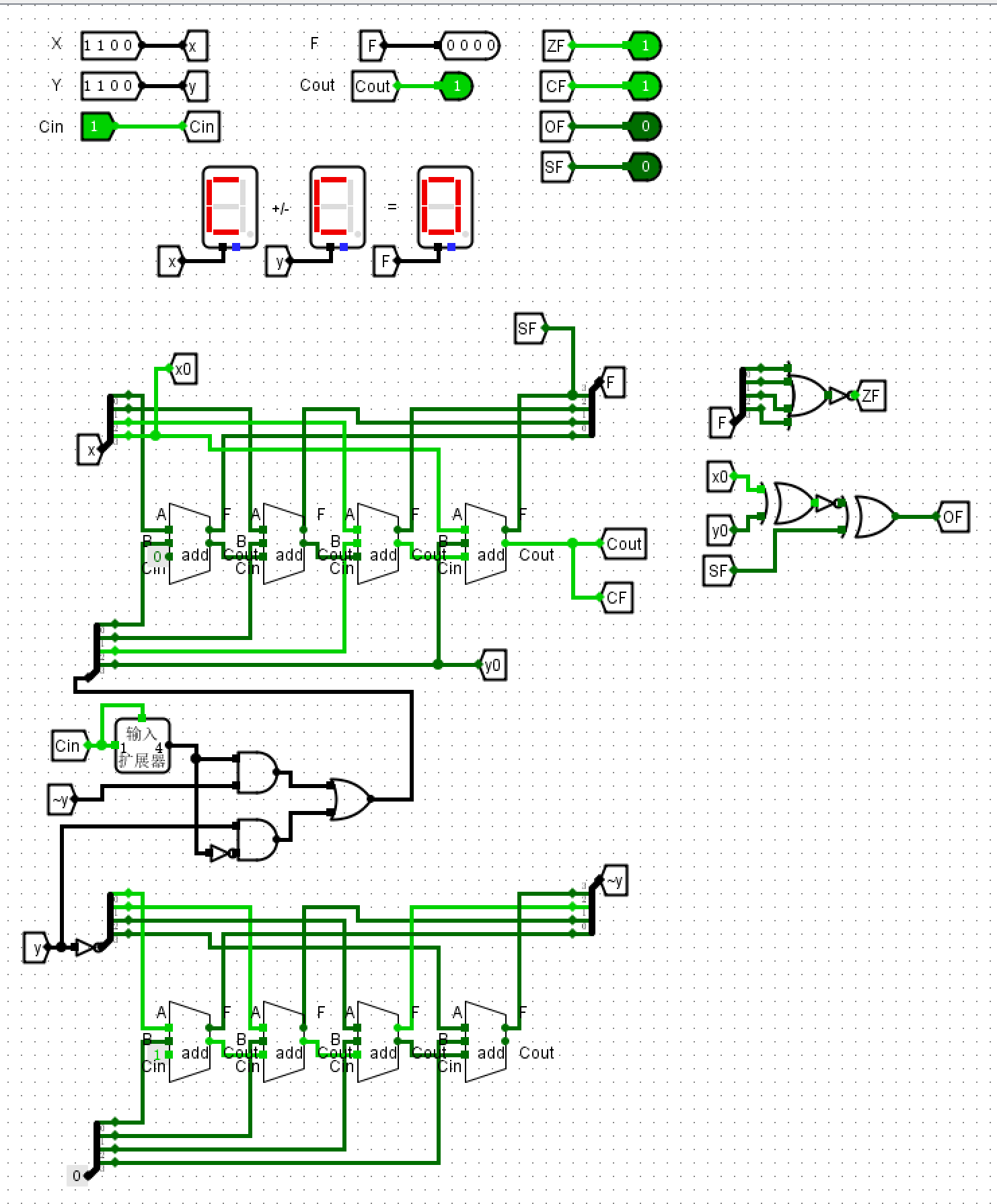
- SF:直接取F最高位
- ZF:判断F是否每一位都是0
- CF:判断首位相加是否有进位,如果是减法要再取反
- OF:发生溢出只可能是两个加数的符号相同(减法看作加法处理),并且与结果番号
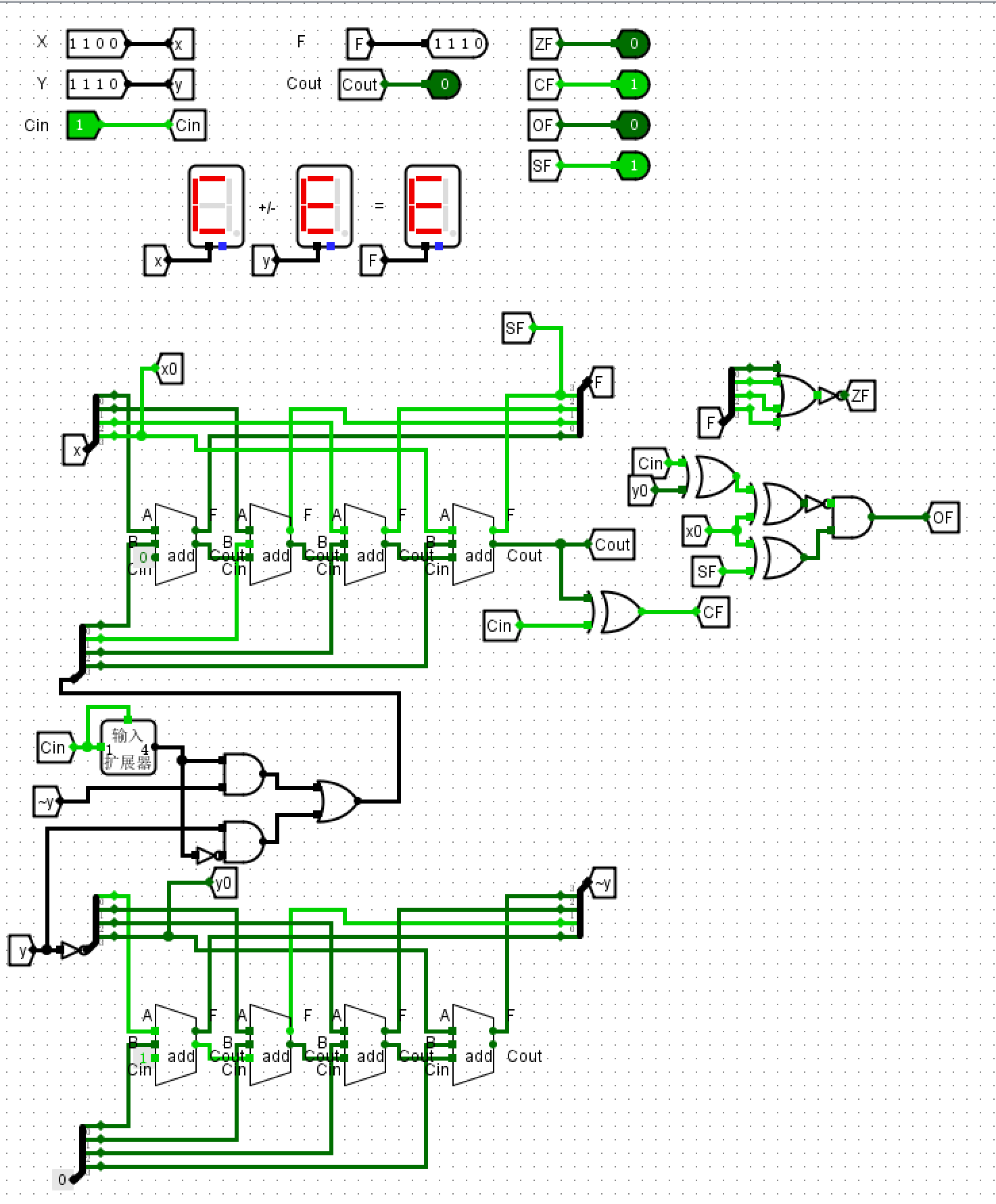
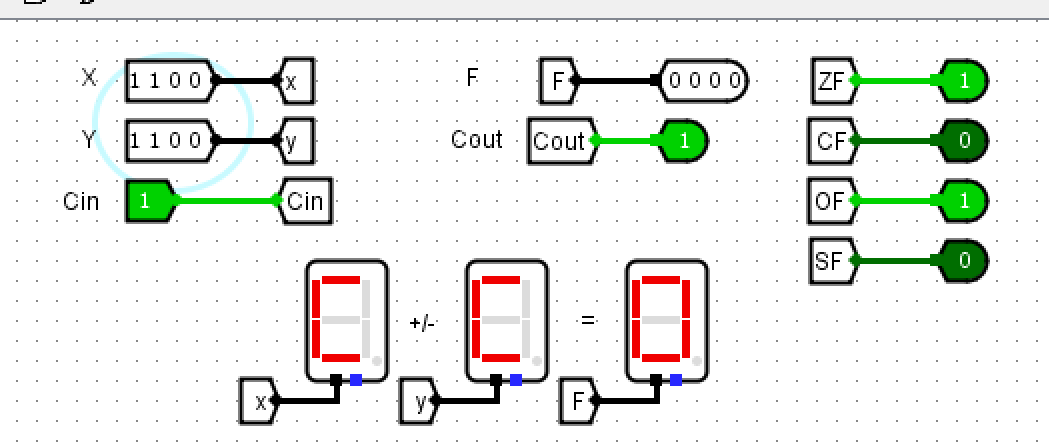
- 测试
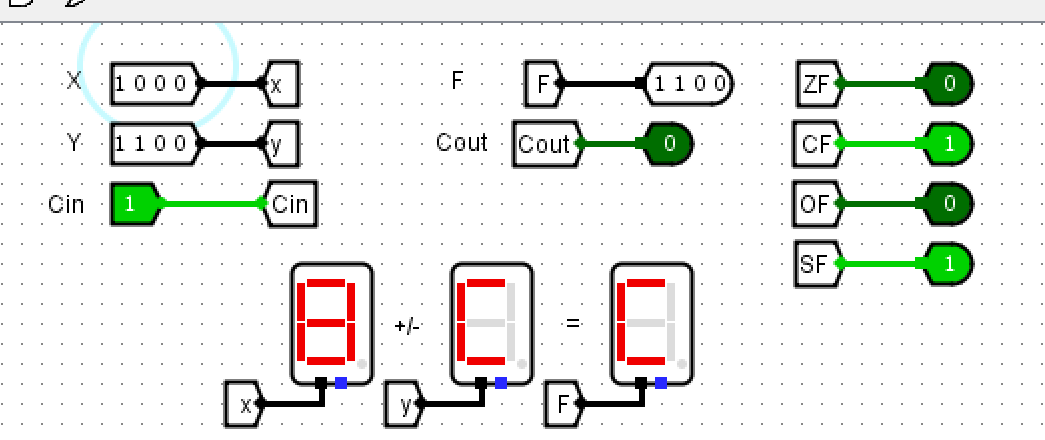
- 测试\(1100+1100\),得到\(CF=1\)(进位),\(SF=1\)(符号位为1),\(OF=0\)(未发生进位),\(ZF=0\)(结果不为0)
2使用标志位判别比较¶
无符号整数¶
- 如果 ZF=1:A和B相等
- 如果 ZF=0 且 CF=1:A小于B
- 如果 ZF=0 且 CF=0:A大于B

有符号整数¶
- 如果 ZF=1:A和B相等
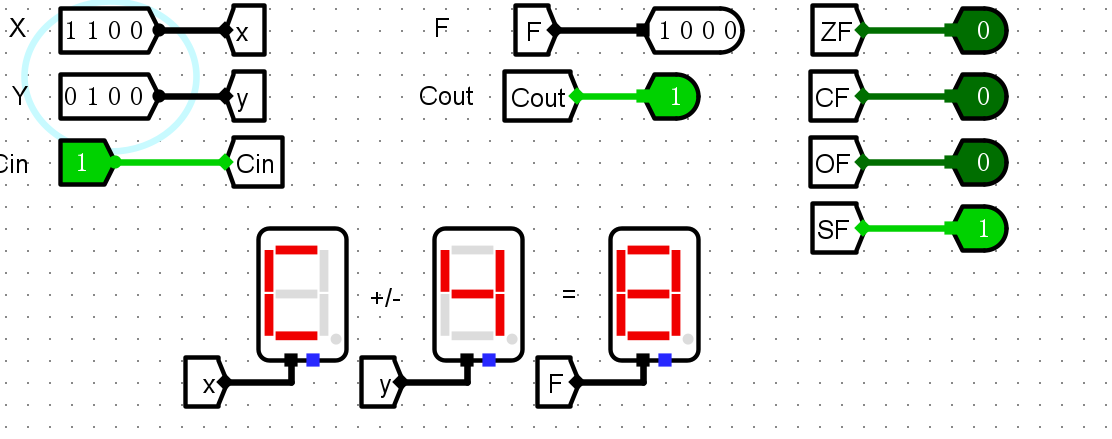
- 如果 ZF=0 且 SF=0 且 OF=0 或 SF=1 且 OF=1:A大于B
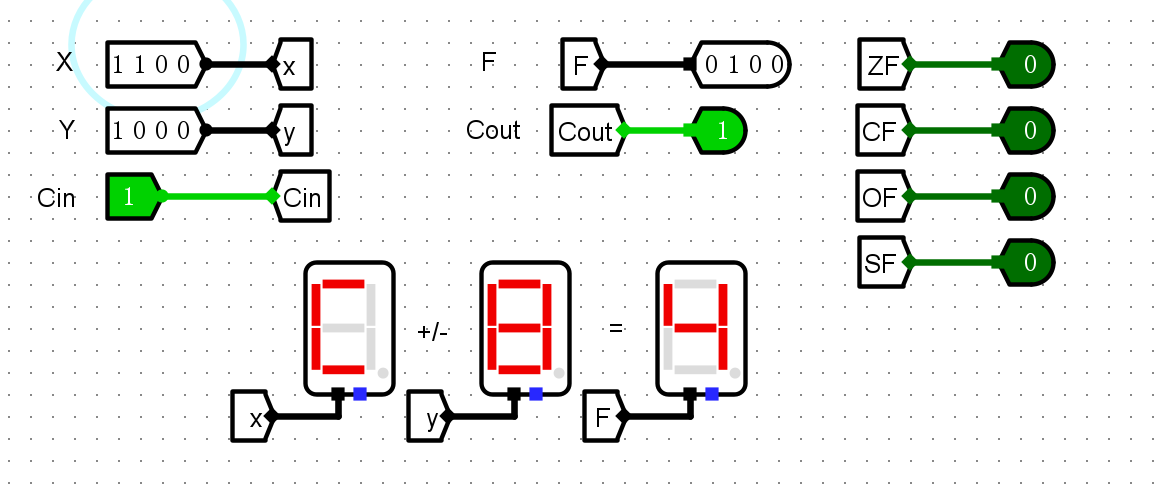
- 如果 ZF=0 且 SF=0 且 OF=1 或 SF=1 且 OF=0:A小于B
3扩展32位桶移位器¶
-
将32位划分为4块,分别对应4个8位移位器
-
不能直接使用8位桶移位器实现32位桶移位器,因为在移位时会造成数据丢失,如果想要使用8位桶移位器实现32位桶移位器,则必须为8位桶移位器添加移出数据的记录和输出,并且还需要在不同块进行数据传递(相邻快要移入移出数据)。
- 由此可以使用8为移位器实现32位移位器移动1-7位
- 对于8、16位移动,直接把块当成一个单位,对块进行交换即可
具体实现¶
- 改造的8位移位器:不再区分math/logic而是接受一个8位数据作为移入数据
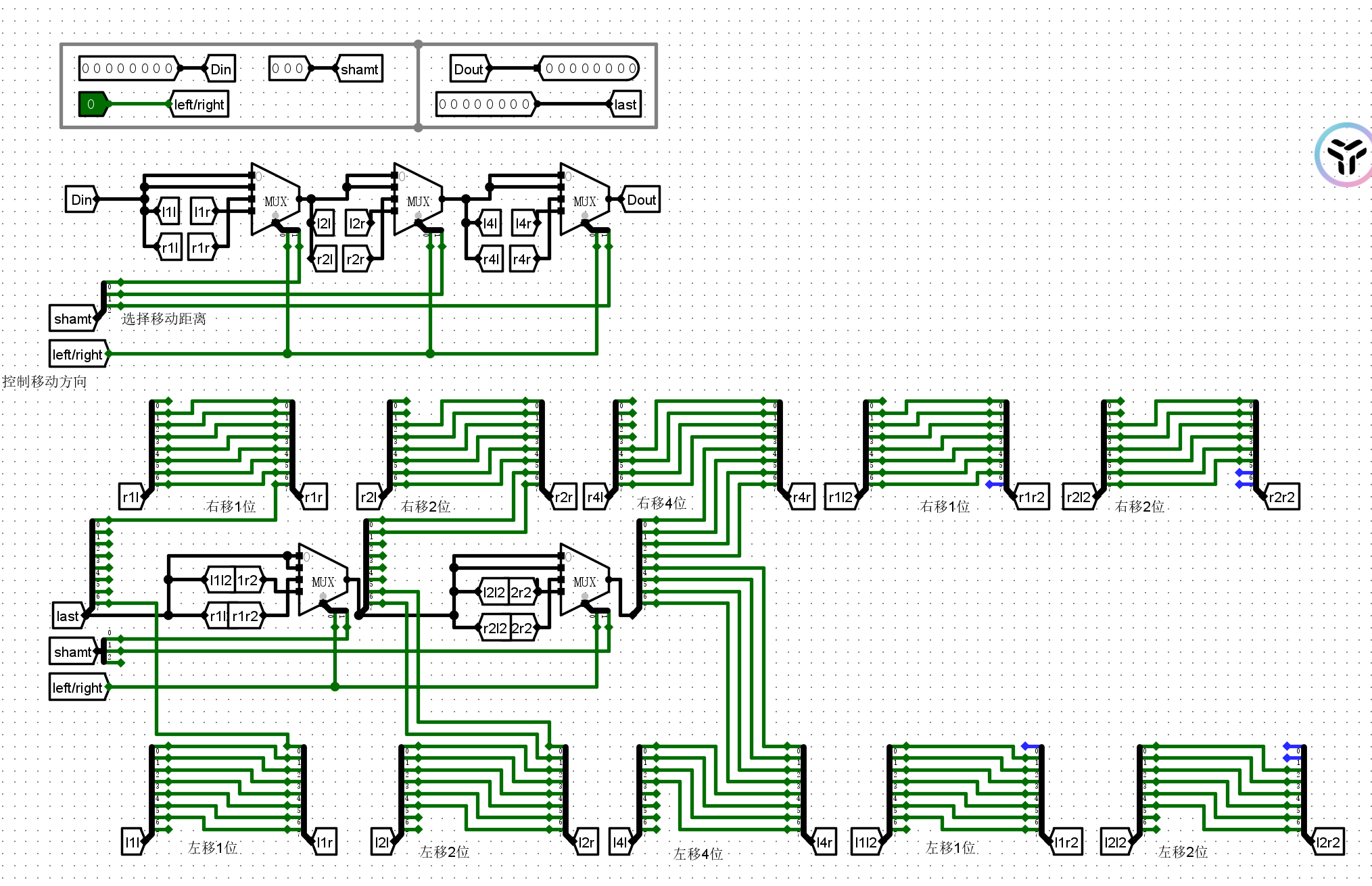
- 即使用last补上空位而不是原先的0/1
- 实现32位桶移位器
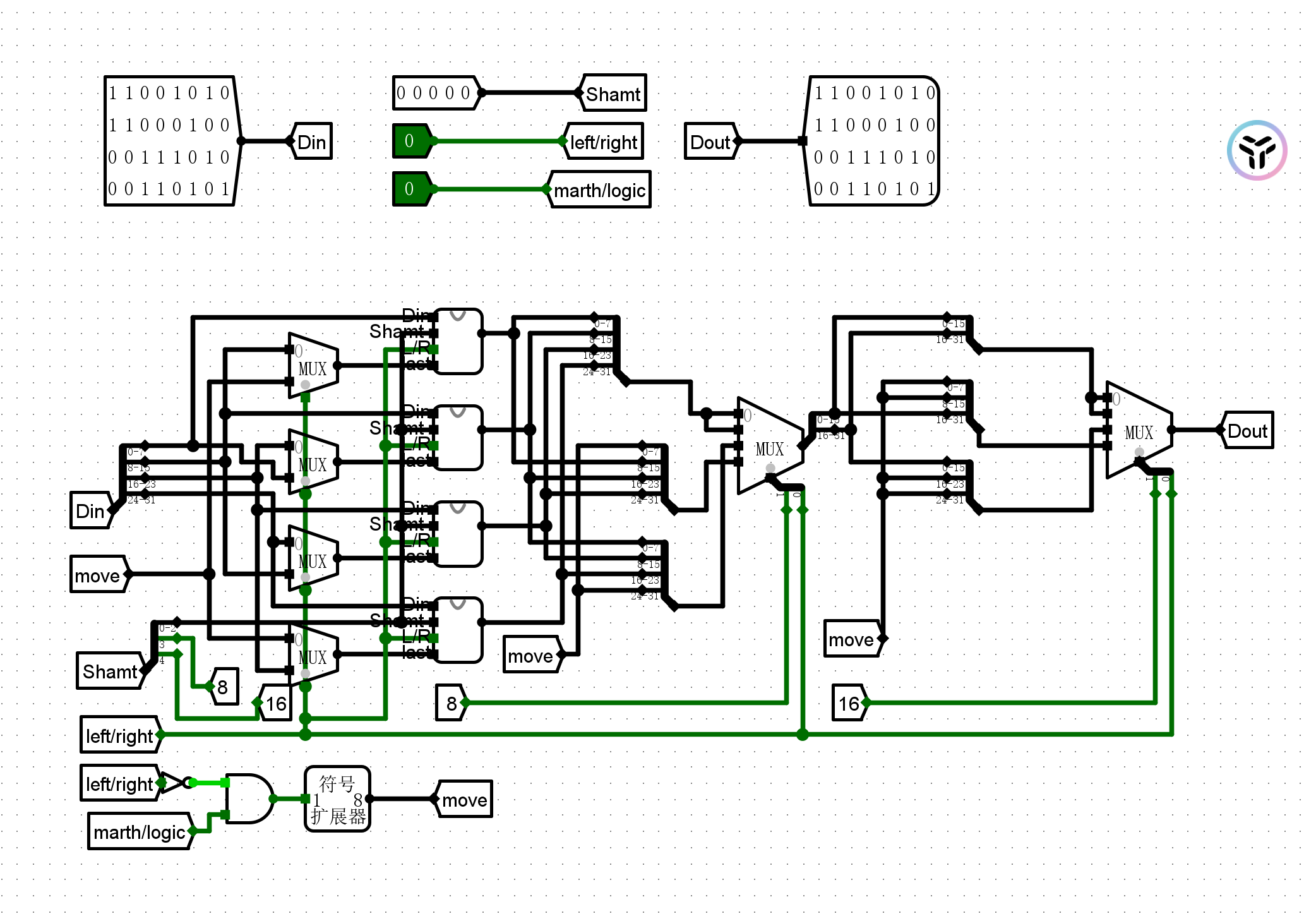
- 对于8位以下移动使用8位桶移位器完场,根据left/right决定每个桶移位器的last输入(边界为全0/1由移动方向和math/logic决定,存储在move中)
- 对于8位和16位直接分块交换实现