P4
实验内容¶
实验一 :4 位先行进位加法器 CLA¶
- 实现4 位快速加法器 CLA
整体方案设计¶
输入输出引脚¶
- 1位全加器
- AB操作数
- Cin进位输入
- F计算结果
- G进位生成
-
P进位传递
-
4位CLA加法器
- x,y四位输入
- Cin进位输入
- z计算结果
- Cout进位输出
- Gg进位生成
- Pg进位传递
电路图¶
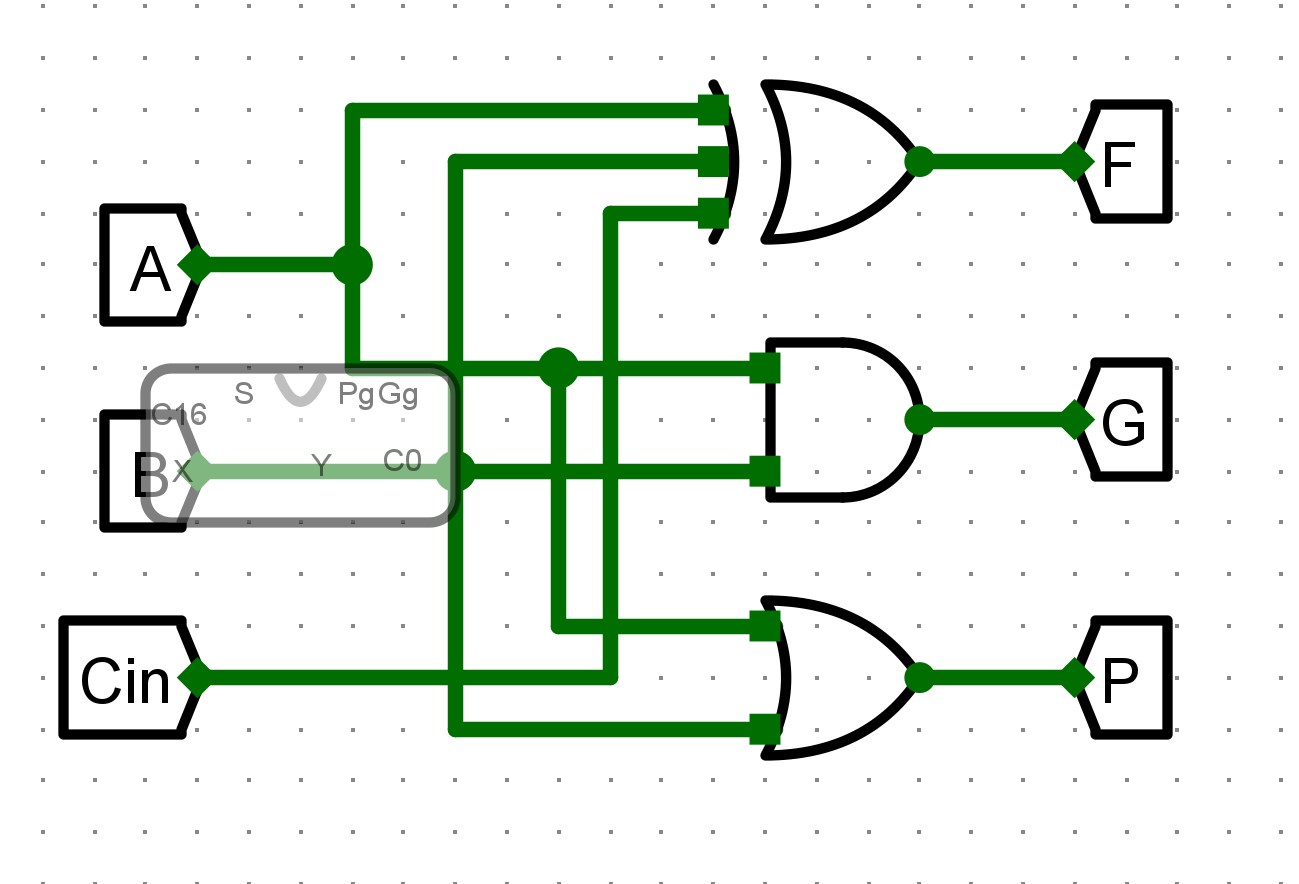
- 1位全加器
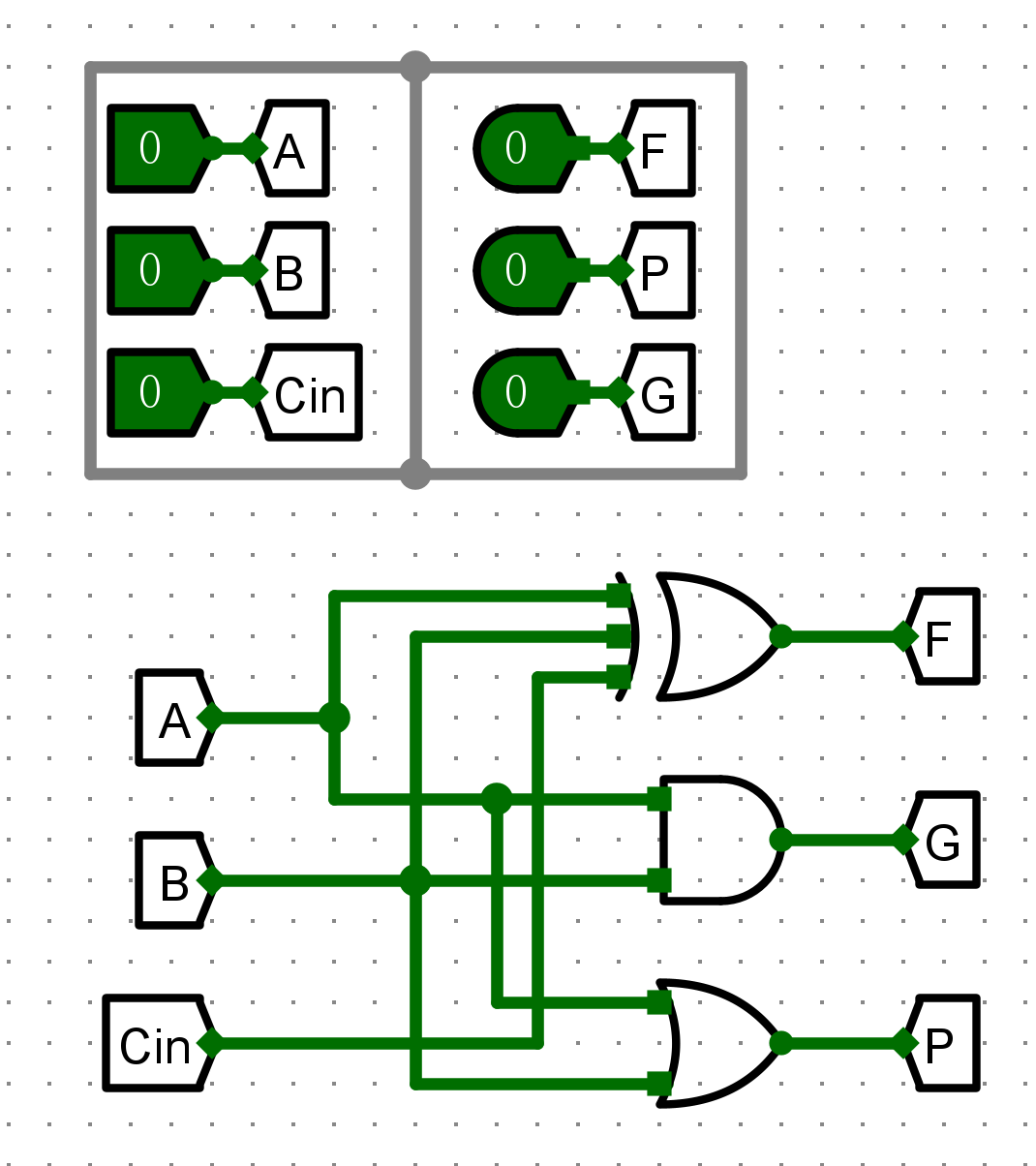
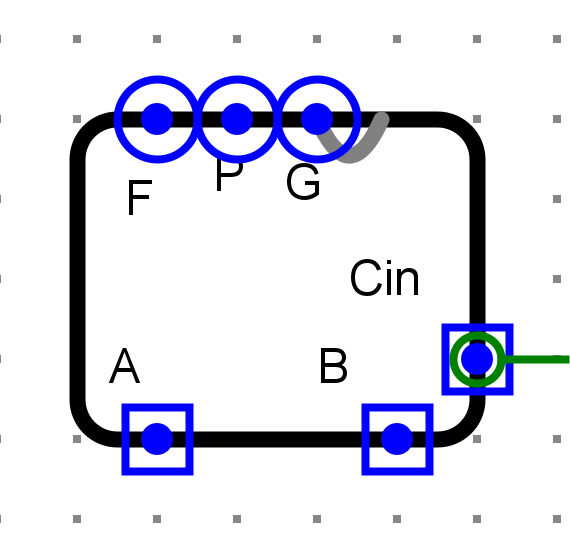
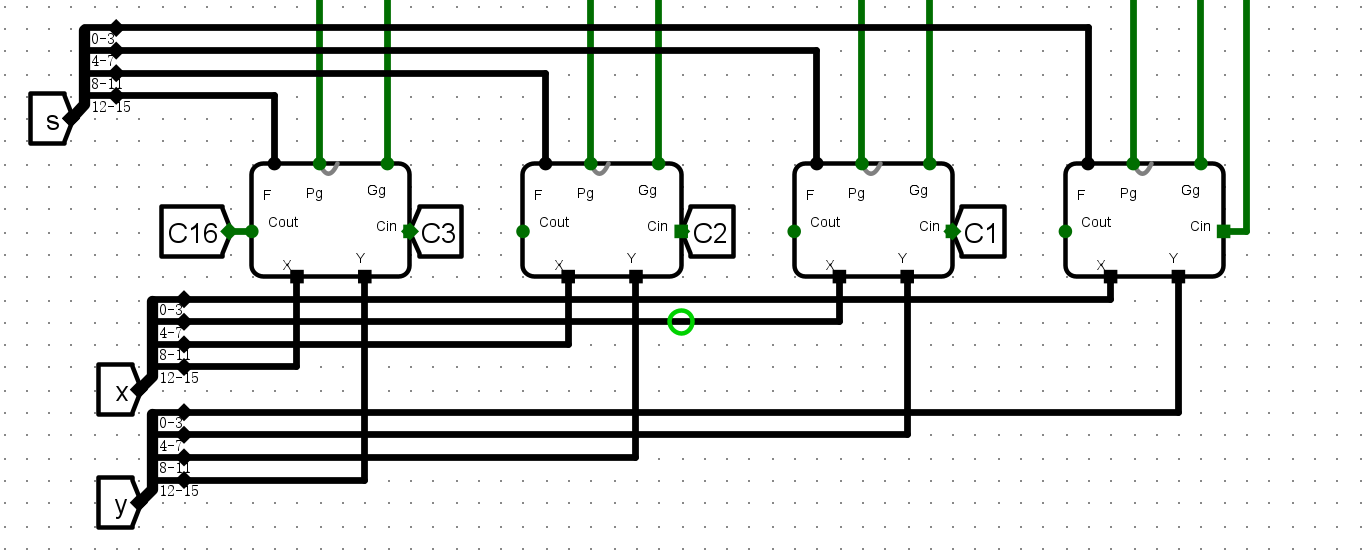
- 4位CLA进位器
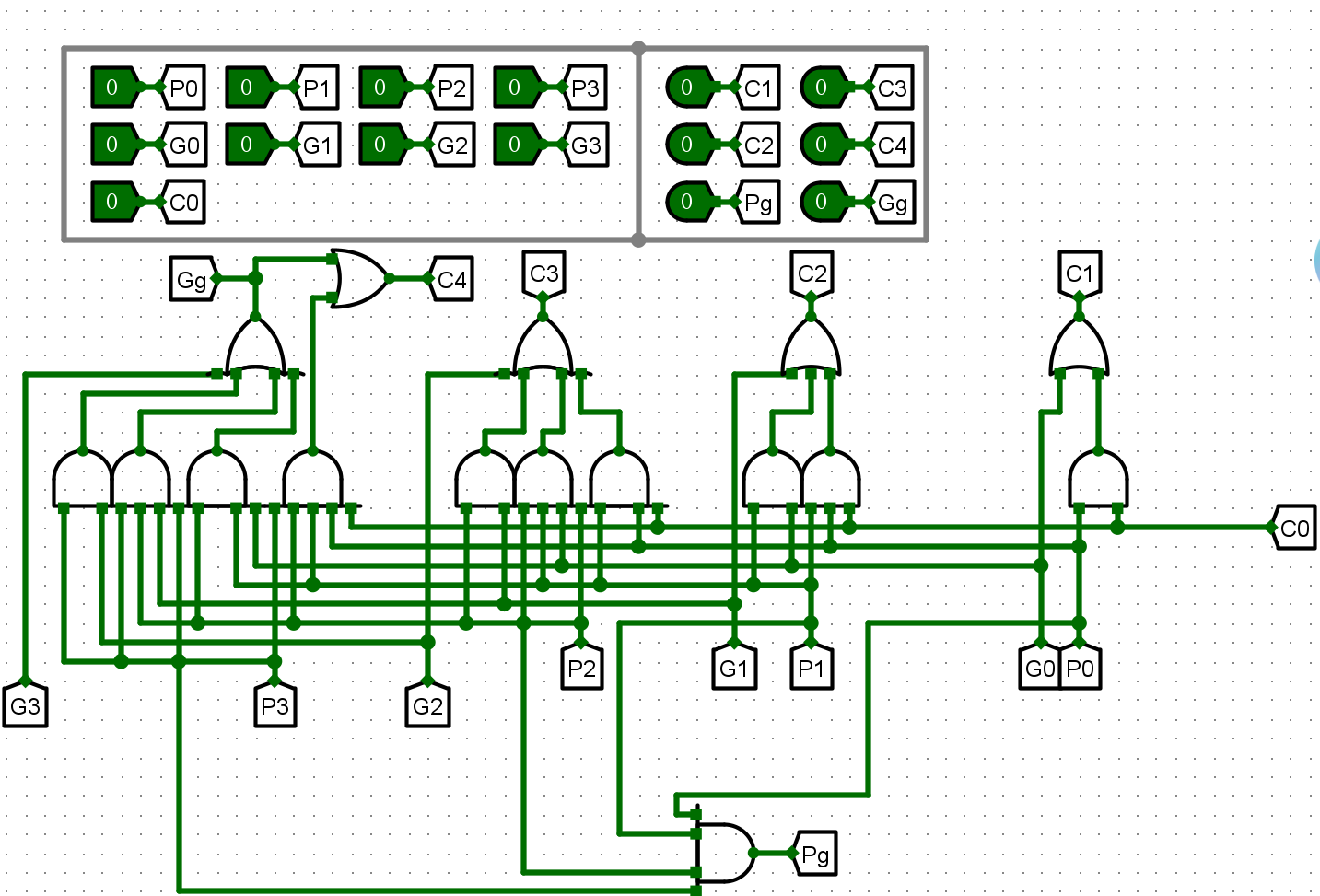
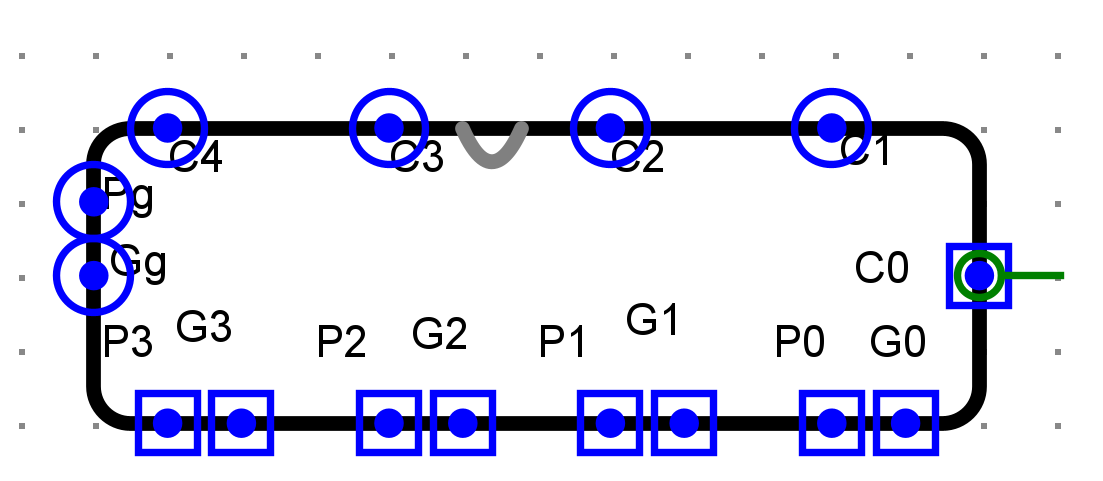
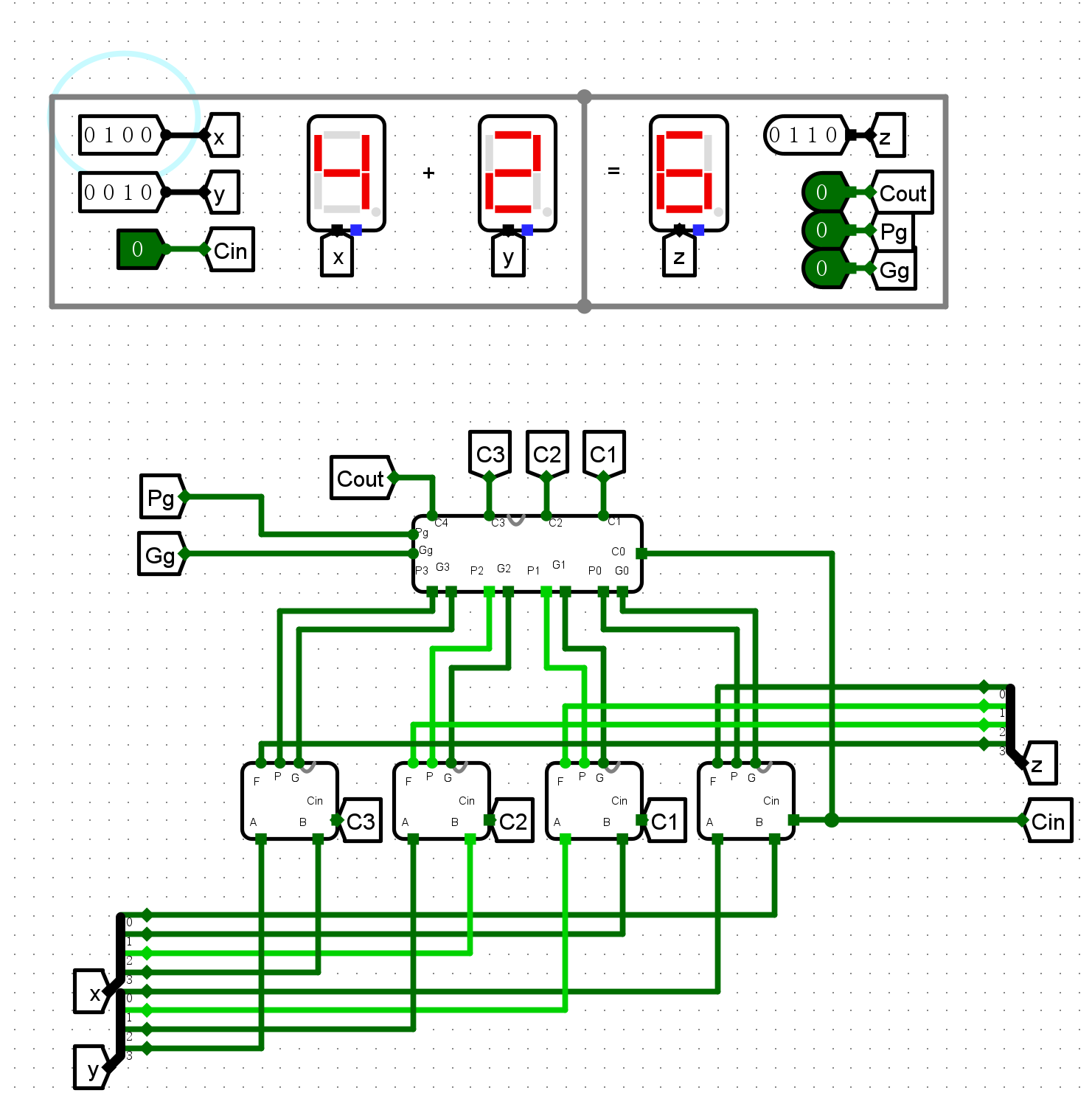
- 4位CLA加法器
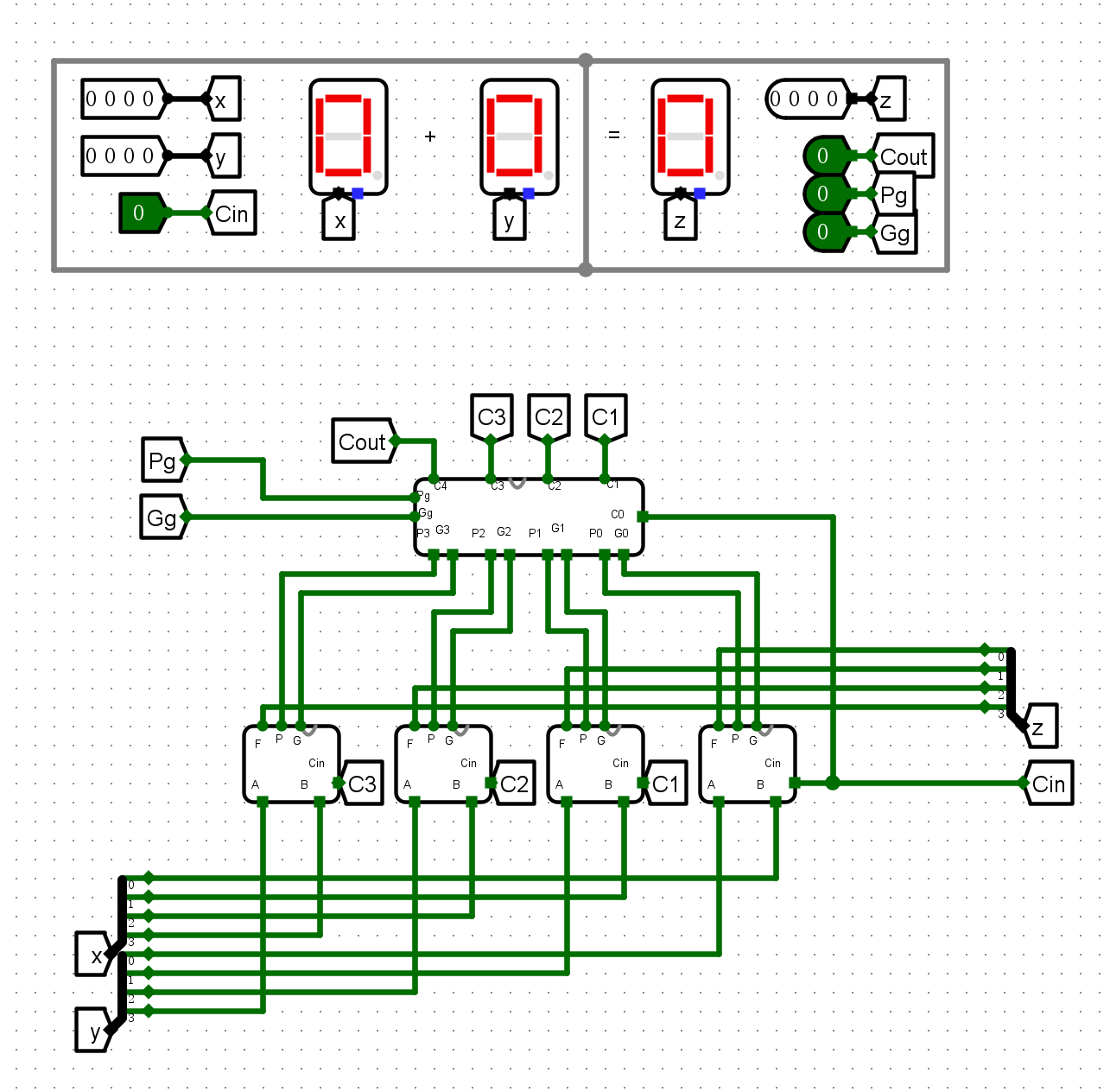
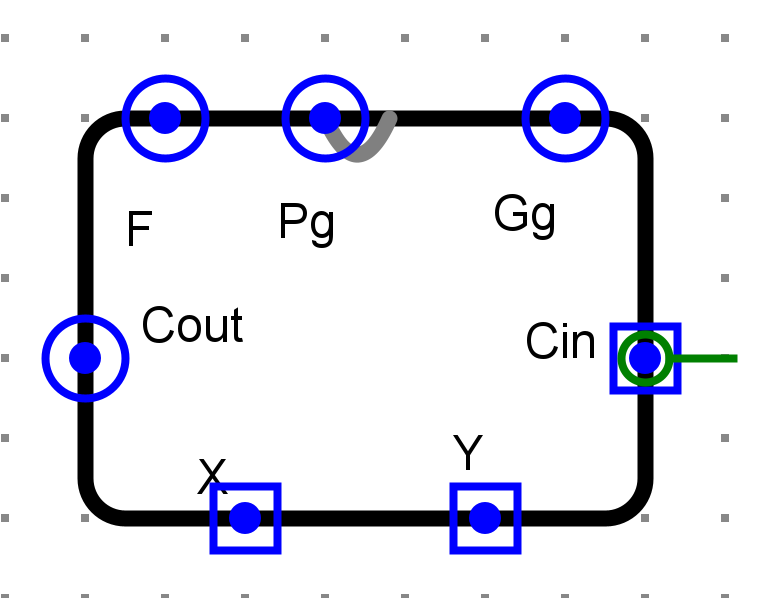
仿真测试¶
- 1位全加器
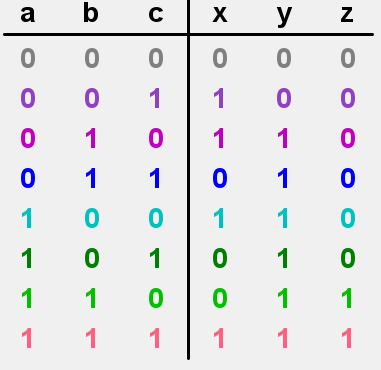
-
经测试电路可以实现功能
-
4位CLA进位器
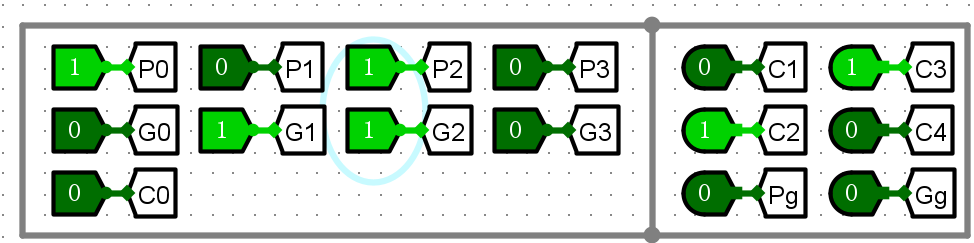
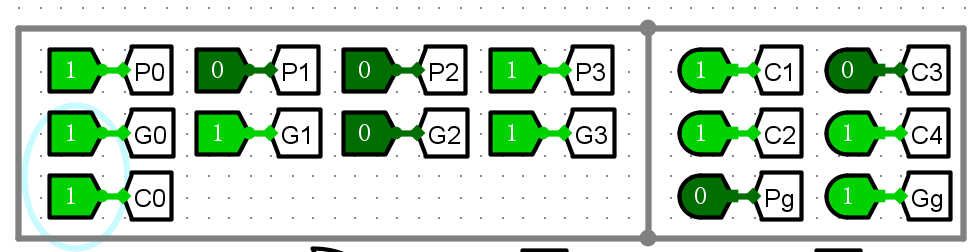
-
经过几组测试与CLA加算公式比对,电路可以实现功能
-
4位CLA加法器
-
普通加法测试
-
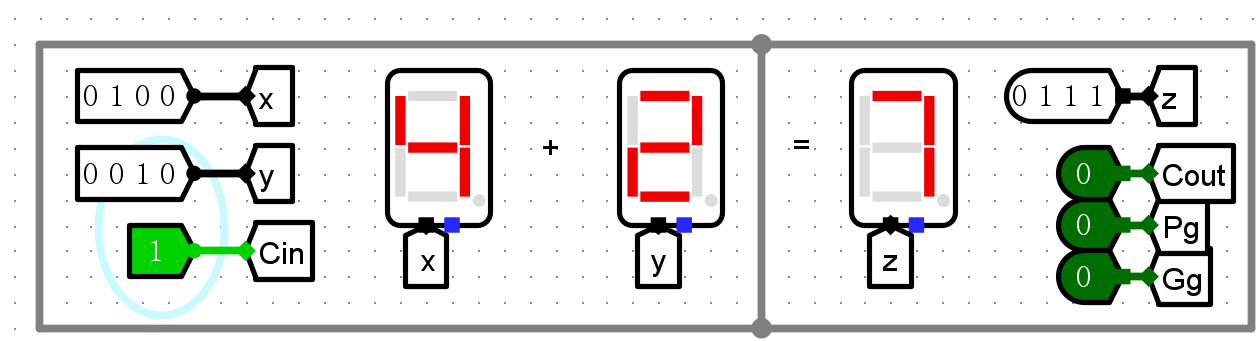
Cin测试
-
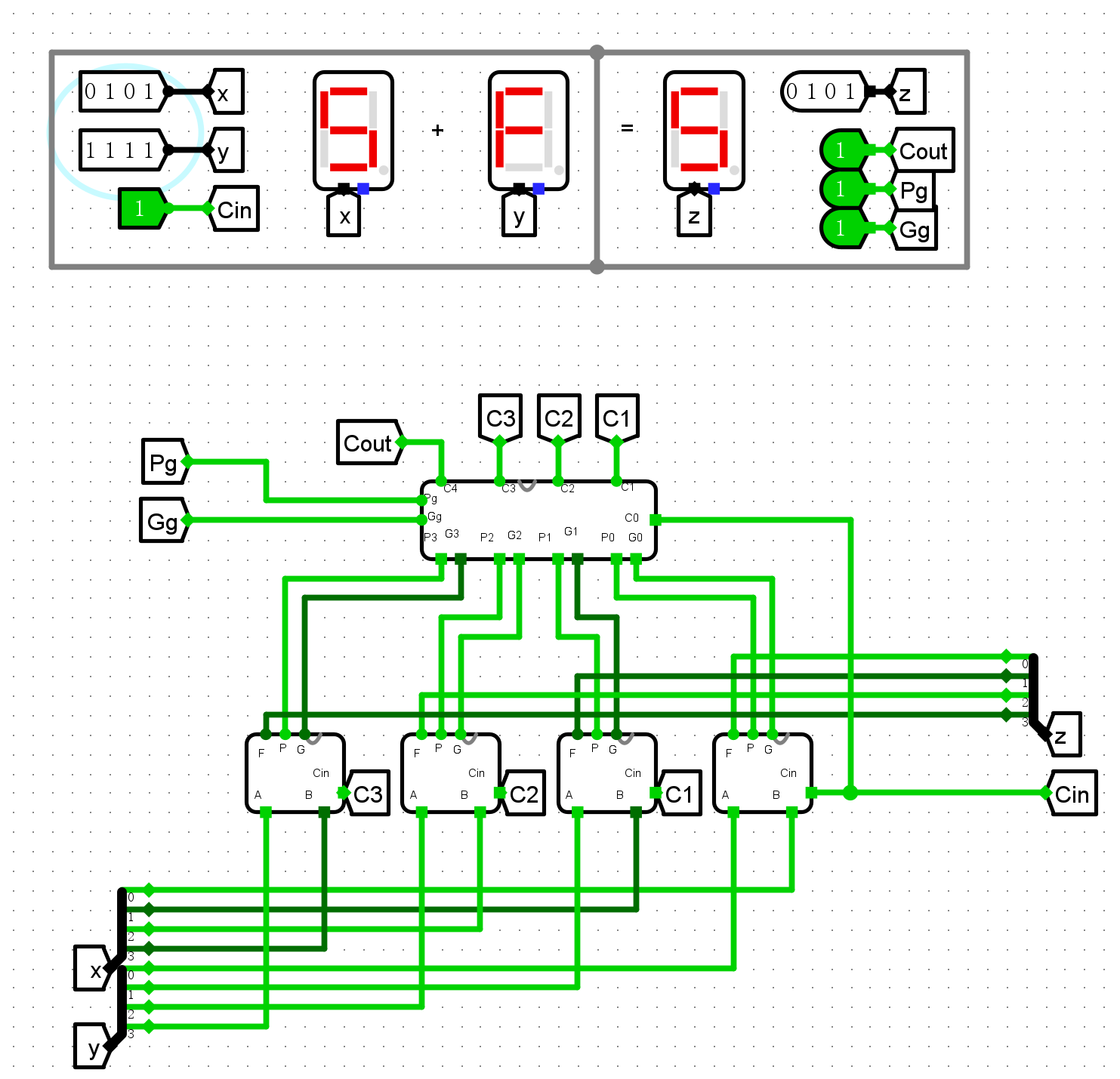
输出标志测试
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
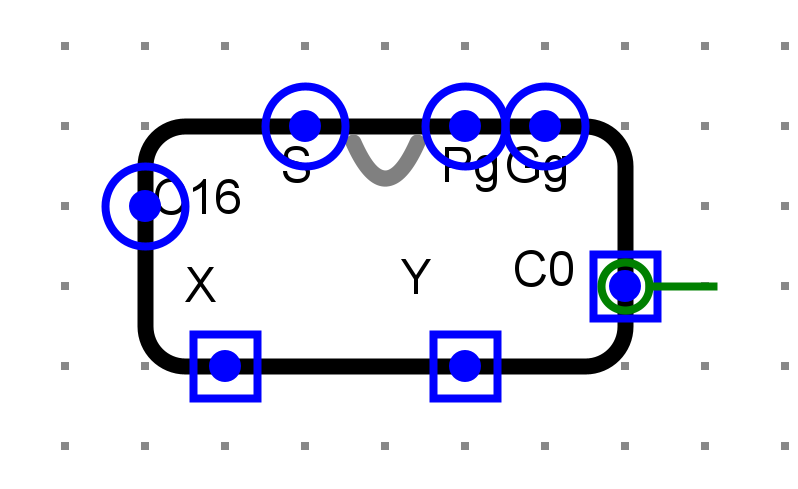
实验二 :16 位两级先行进位加法器实验¶
- 使用4个并行的4 位快速加法器 CLA 实现16为CLA加法器
整体方案设计¶
输入输出引脚¶
- X,Y两个16位输入
- C0进位输入
- s计算结果
- C16进位输出
- PgGg用于CLA的标志位
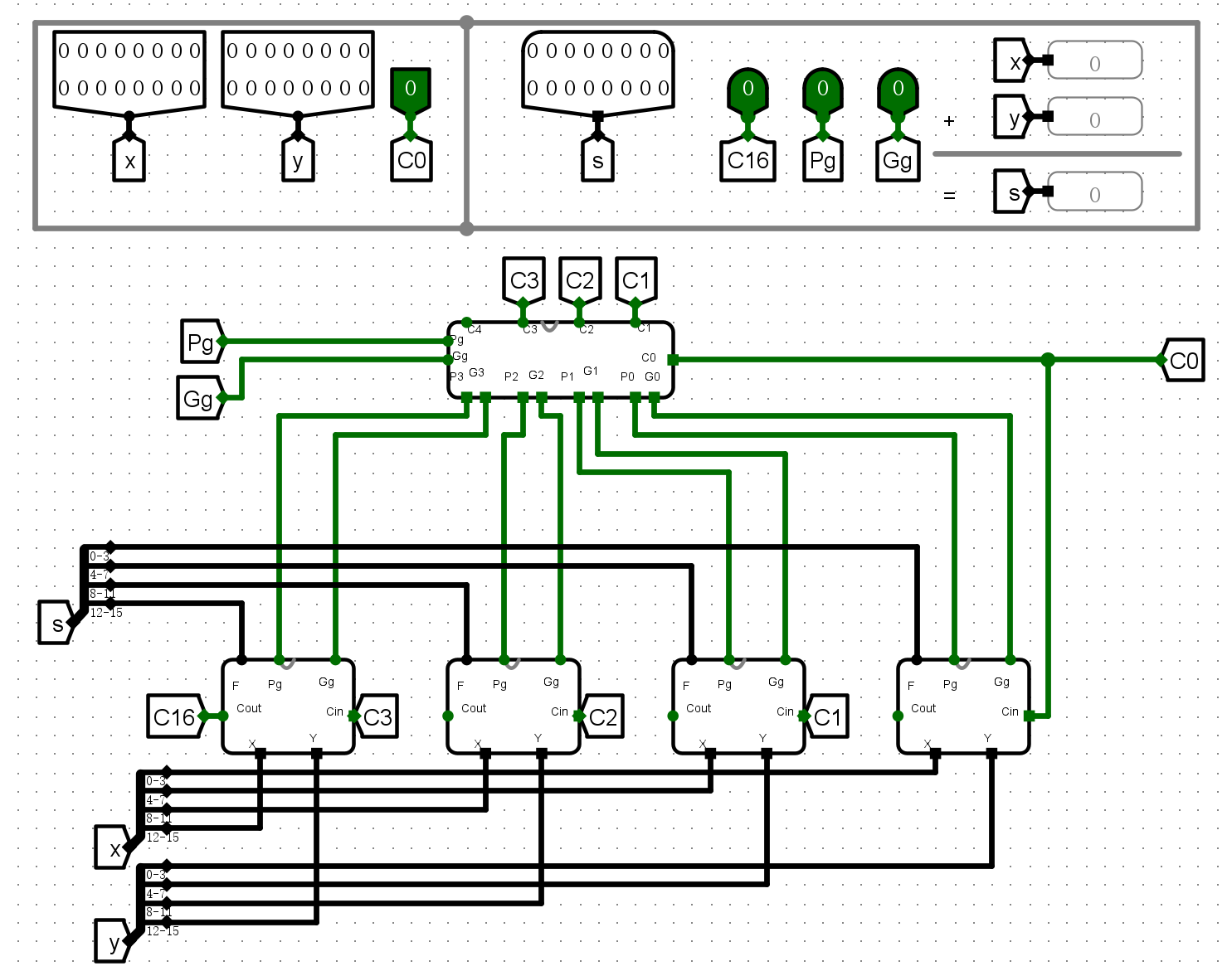
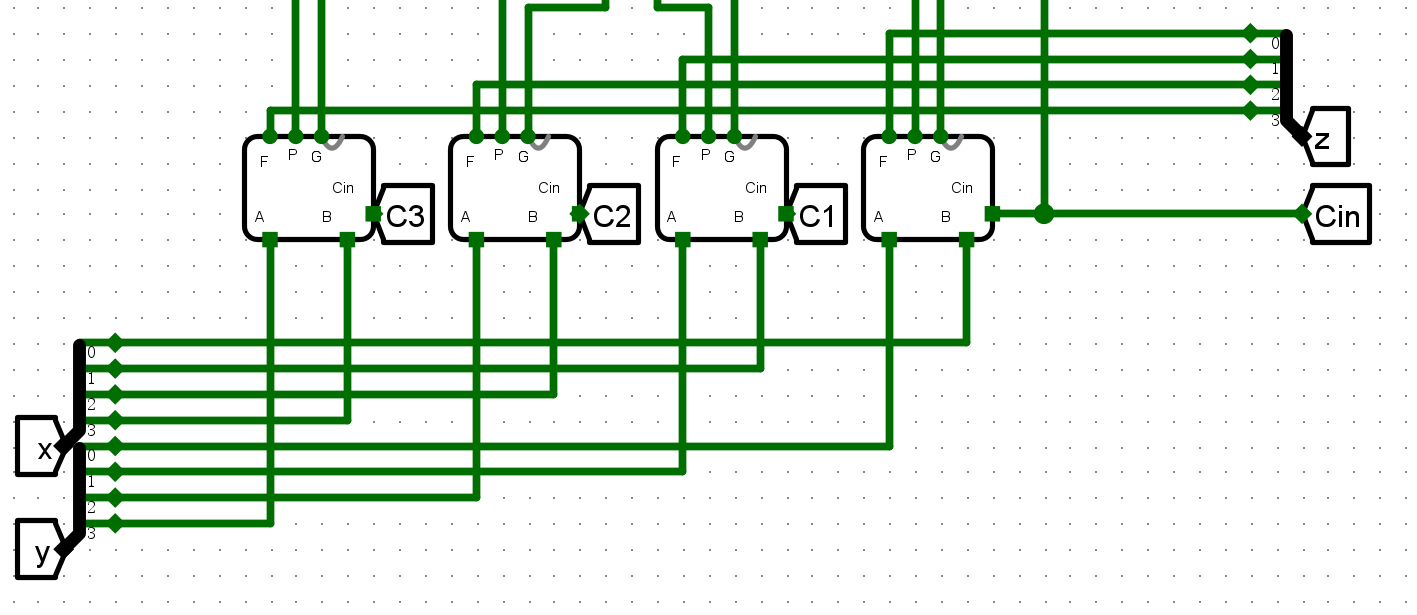
电路图¶
仿真测试¶
- 普通加法
-
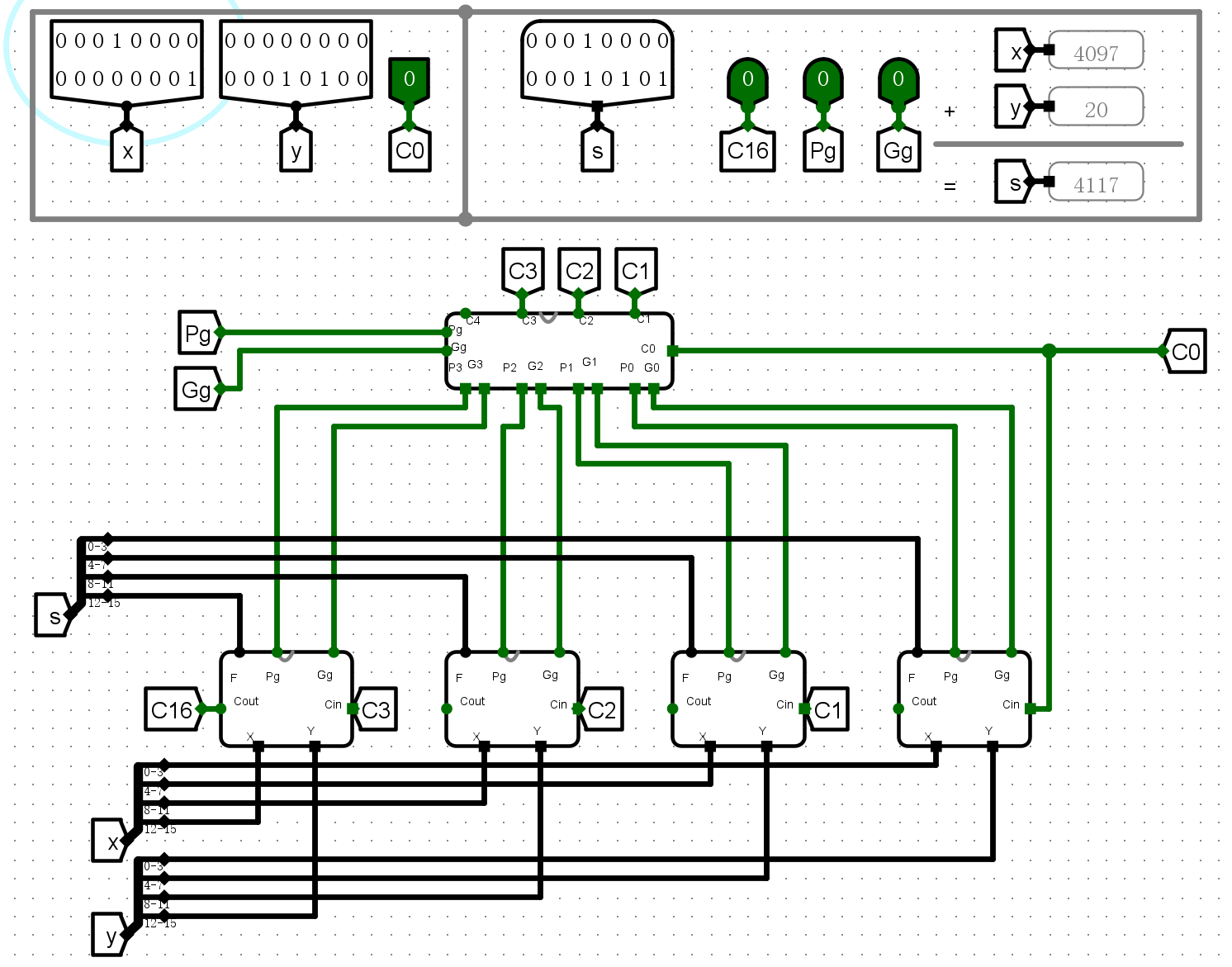
-
C0测试
-

-
C16输出测试

错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
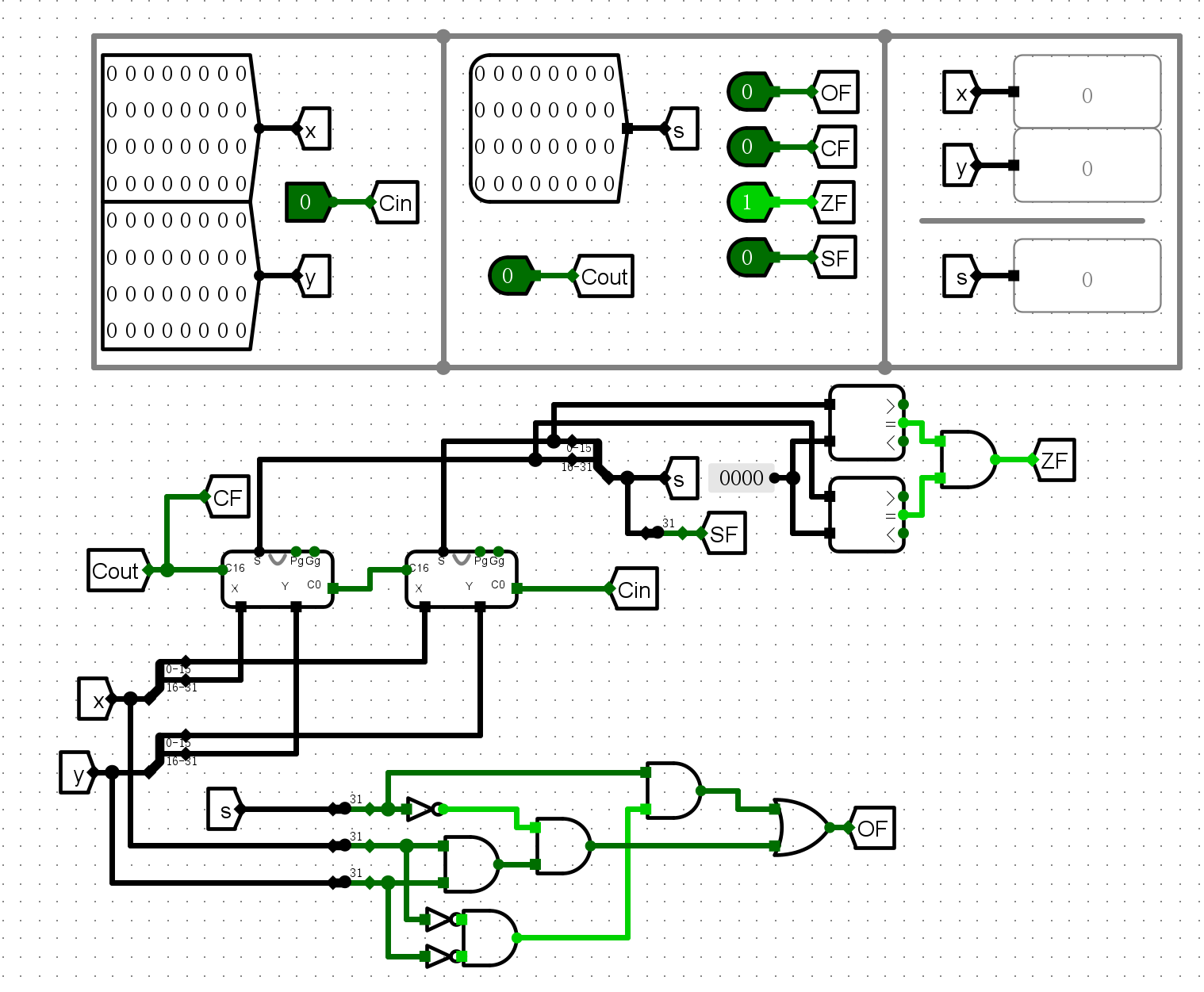
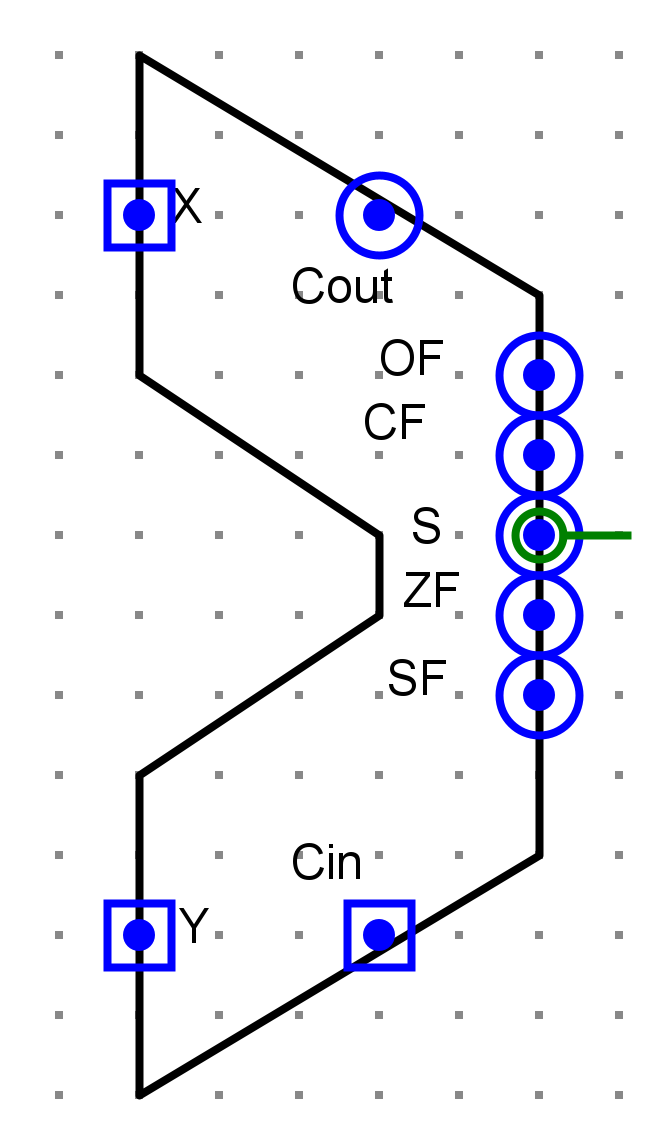
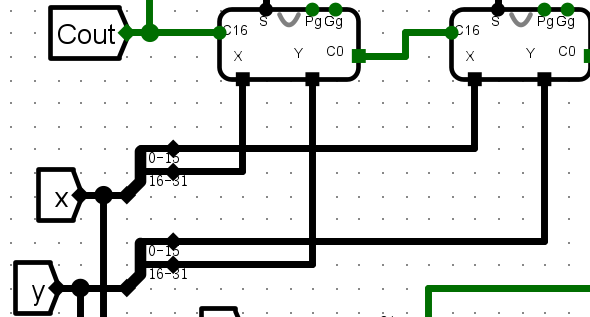
实验三 :32 位加法器构建实验¶
- 串行两个16位CLA加法器,得到32位加法器,并添加4个标志位
整体方案设计¶
输入输出引脚¶
- x,y32位输入
- Cin进位输入
- Cout进位输出
- s32位计算结果
- OF溢出标志位
- CF进位标志位
- SF符号标志位
- ZF零标志位
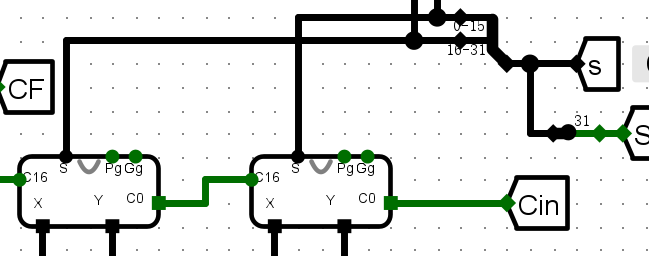
电路图¶
仿真测试¶
- 加法测试
-
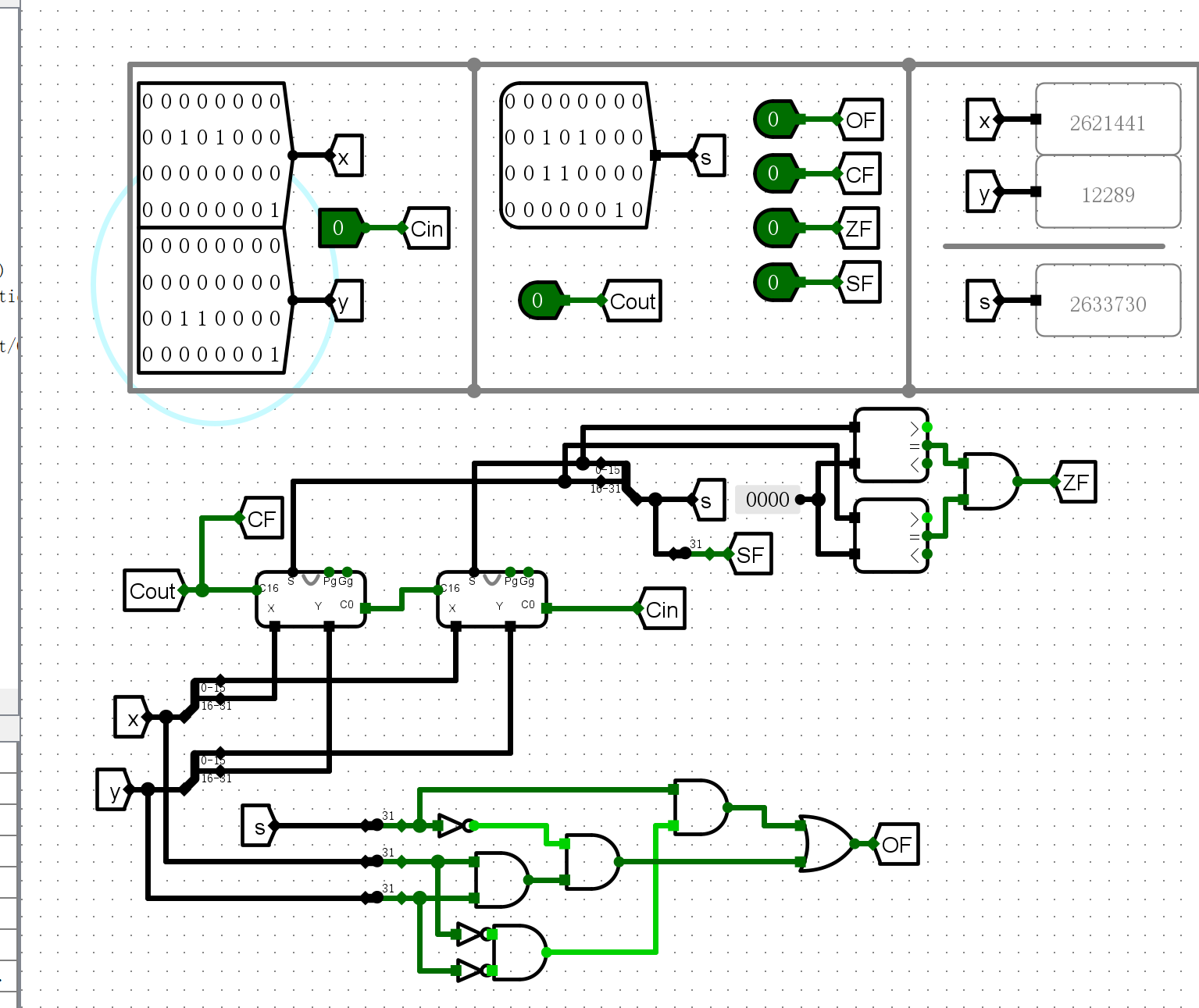
-
ZF
-
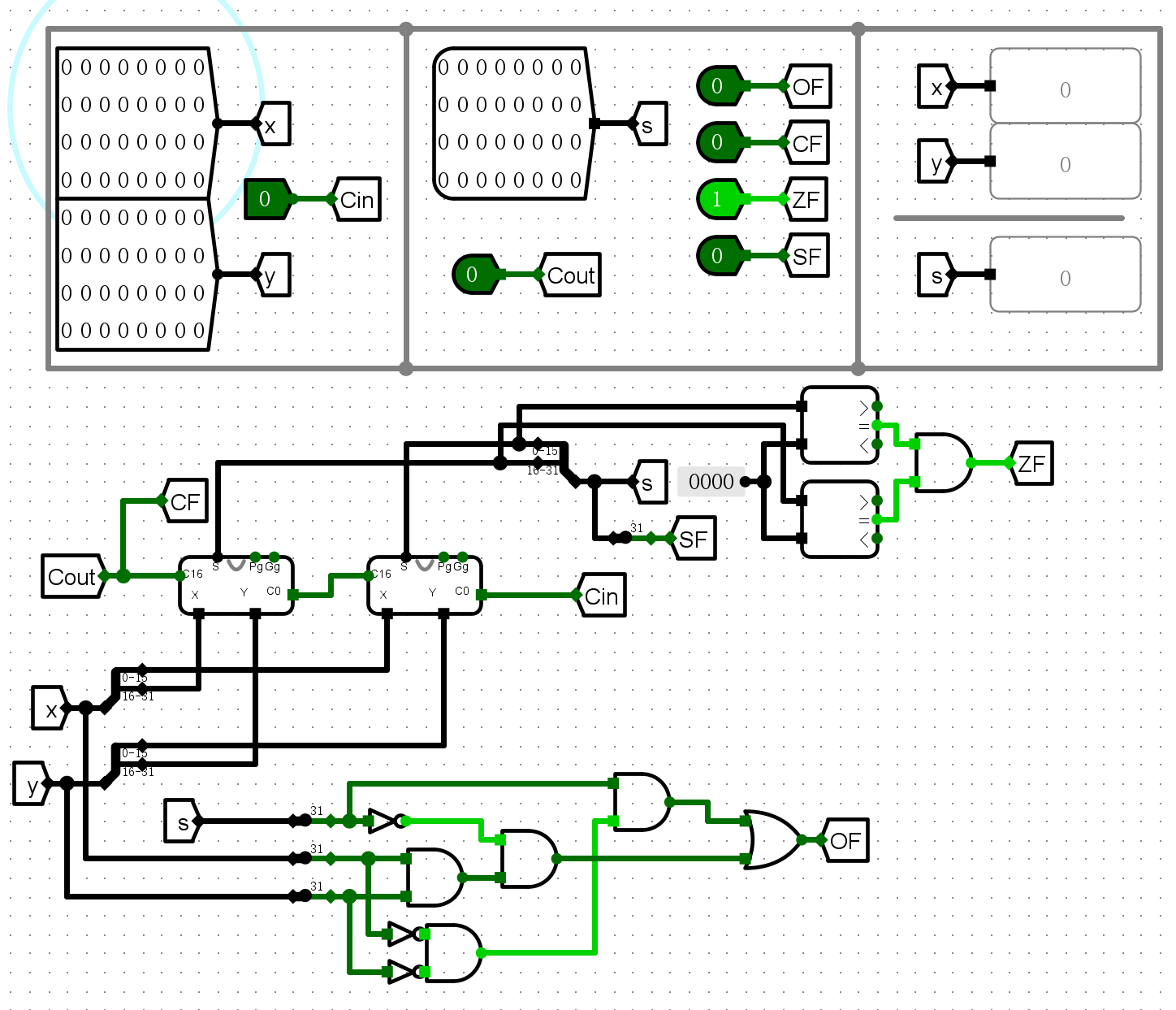
-
SF
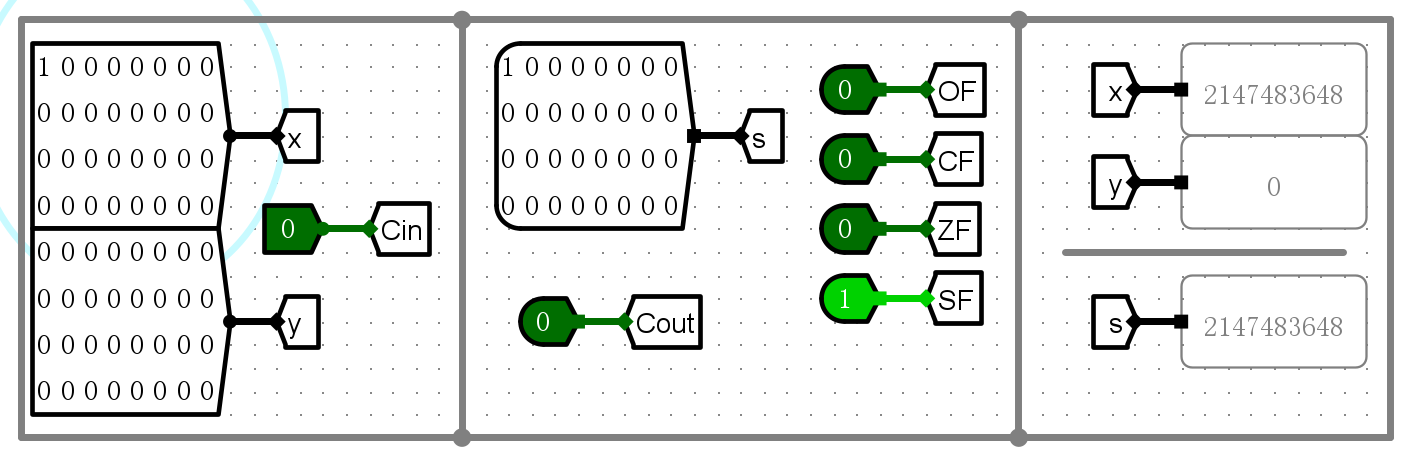
-
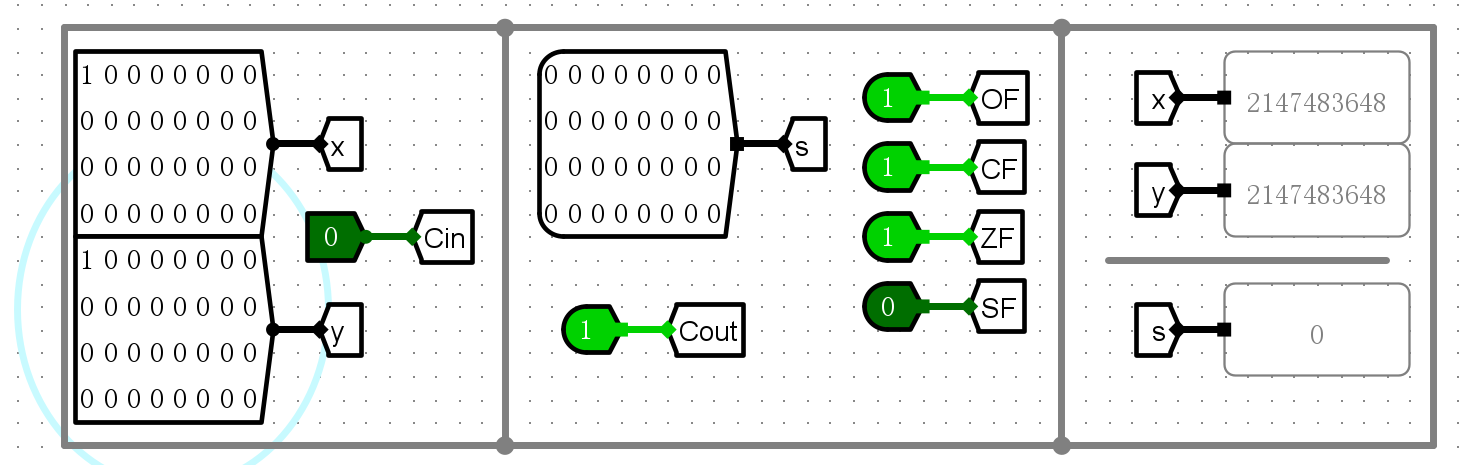
-
CF
-
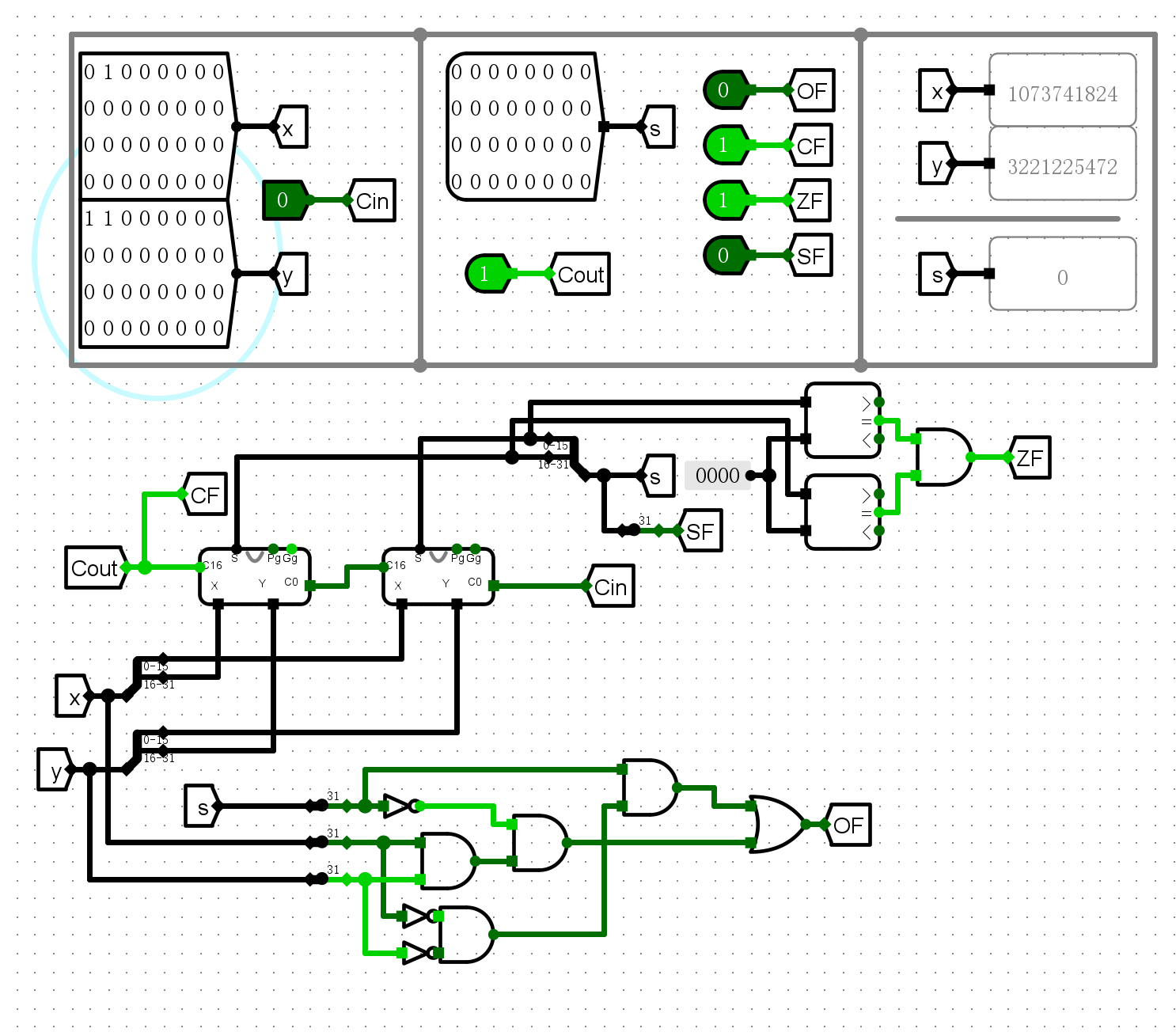
-
OF
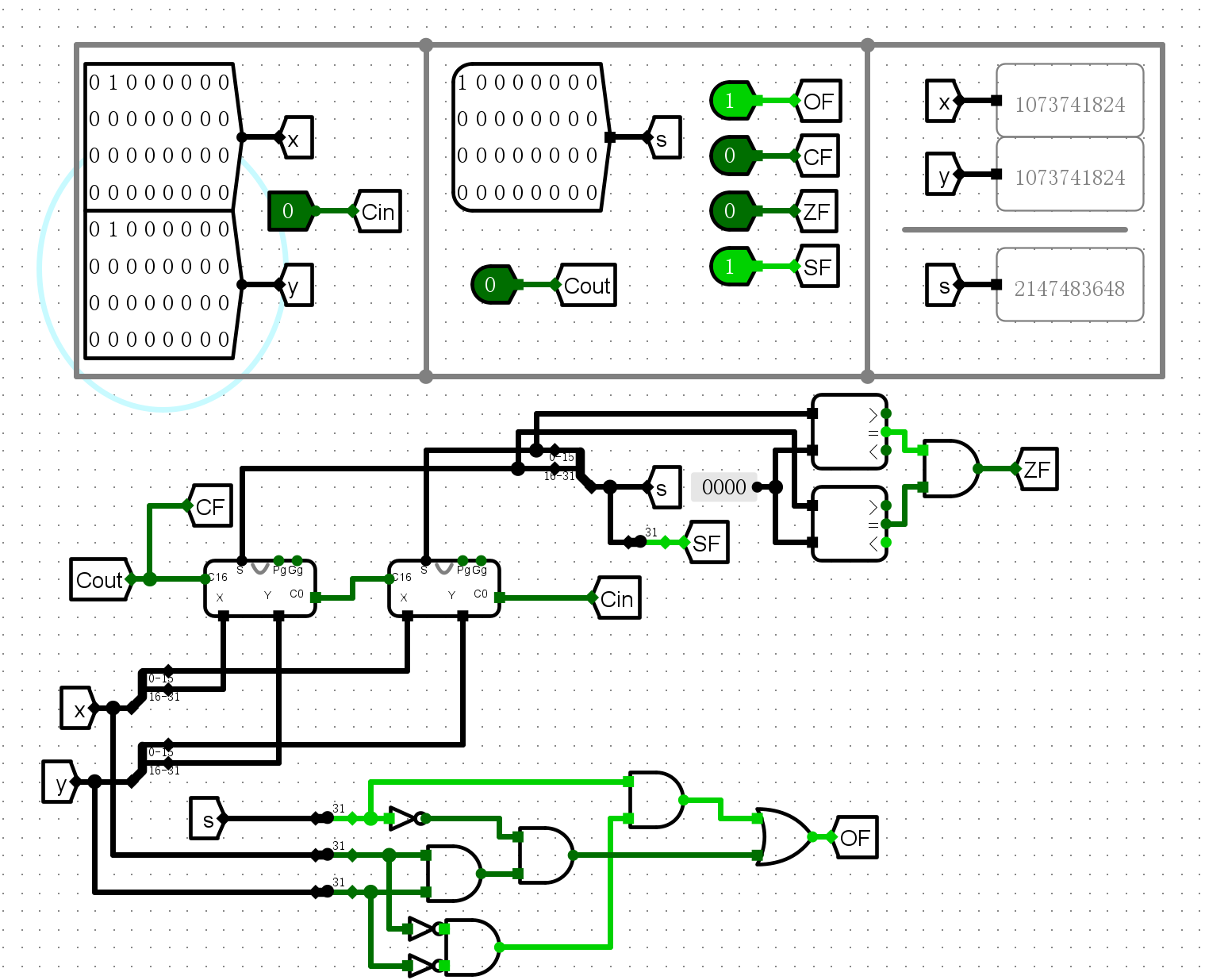
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
实验四 :ALU 设计实验¶
- 实际具有多种计算功能的32位ALU运算器
整体方案设计¶
输入输出引脚¶
- 操作解码器
- ALUctr操作码
- SUBctr减法标志
- SIGctr有符号数标志
- LRctr移动方向标志
- ALctr移动类型标志
-
OPctr操作选择标志
-
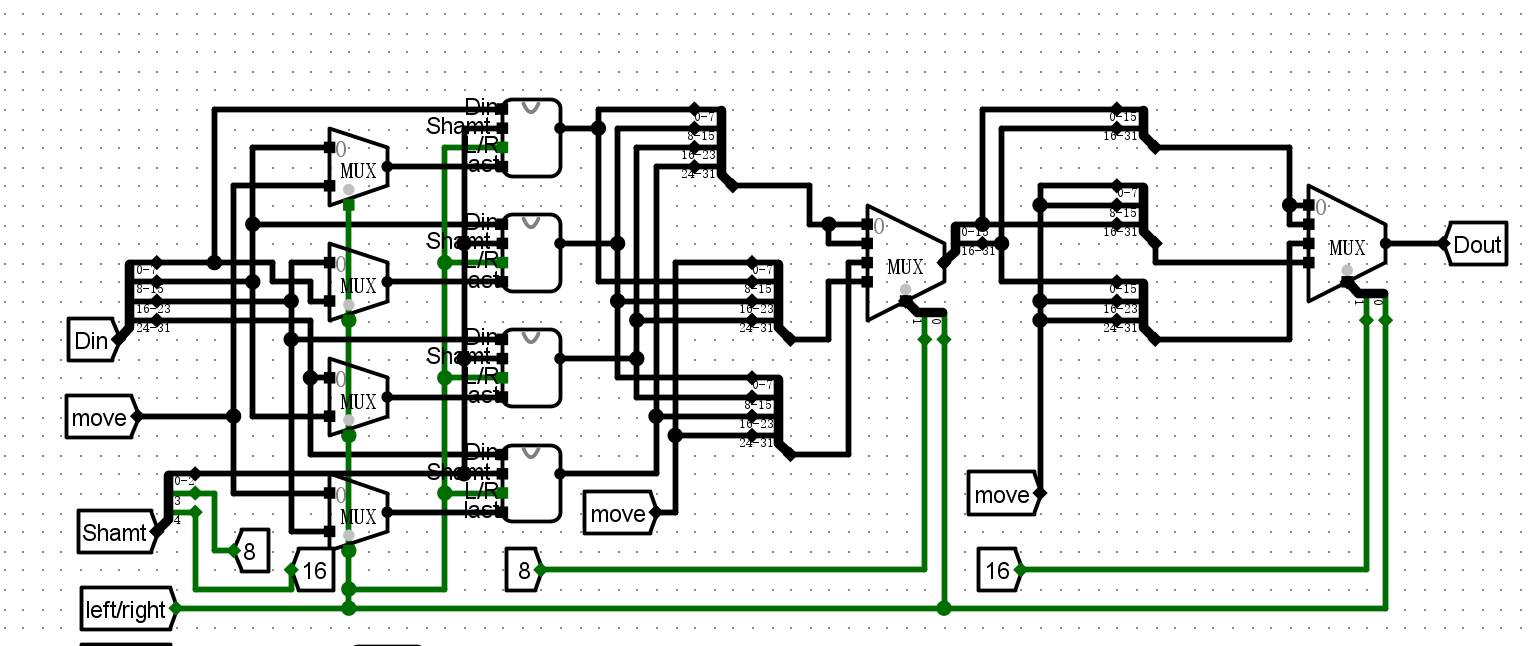
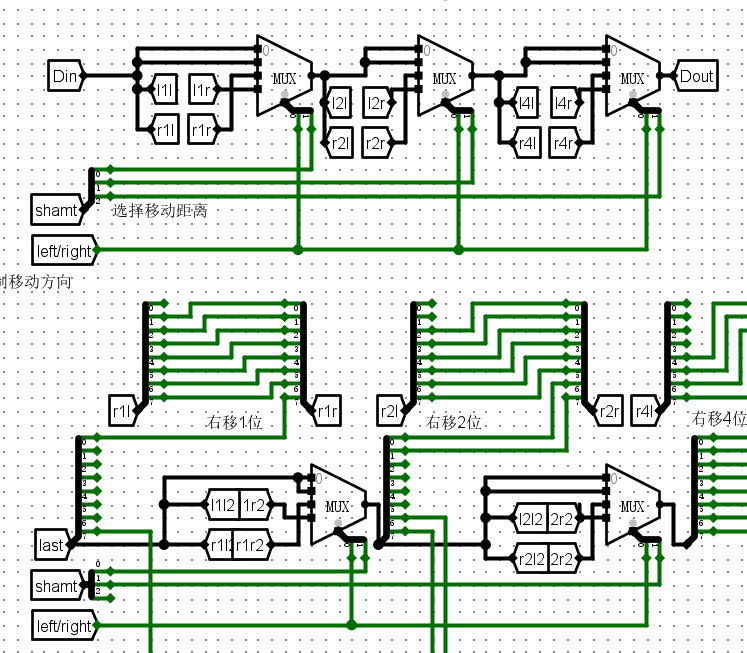
桶形移位器(直接使用了lab2中思考题的32位桶型移位器)
- Din32位输入
- Dout移动结果
- Shamt偏移量
- L/R移动方向标志位
-
A/L移动类型标志位
-
ALU
- A,B32位两个操作数
- Result计算结果
- Zero输出结果的零标志位
- ALUctr操作码
电路图¶
- 操作解码器
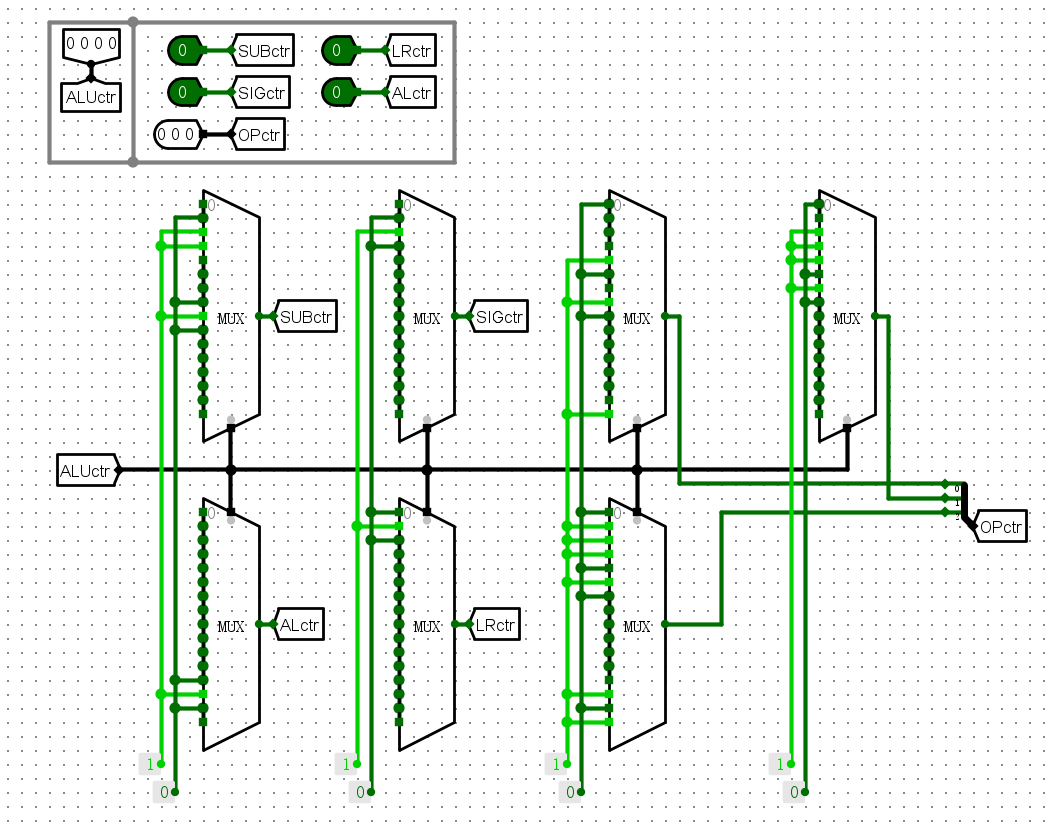
-
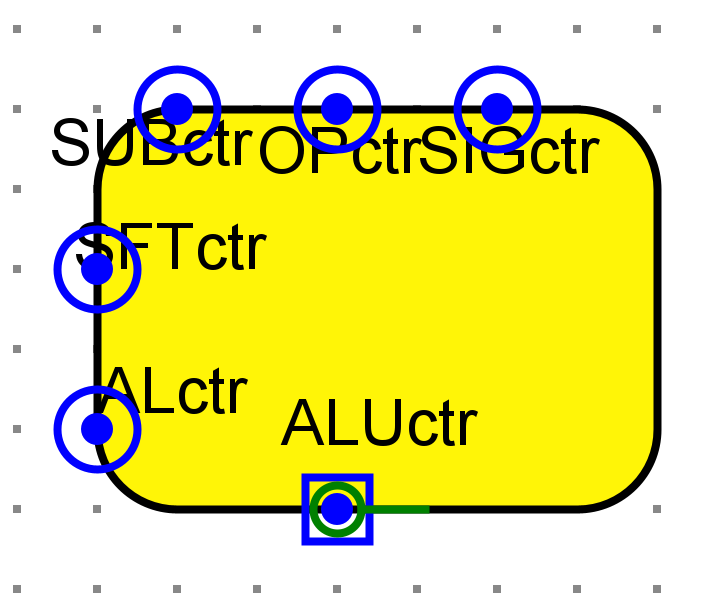
-
桶形移位器
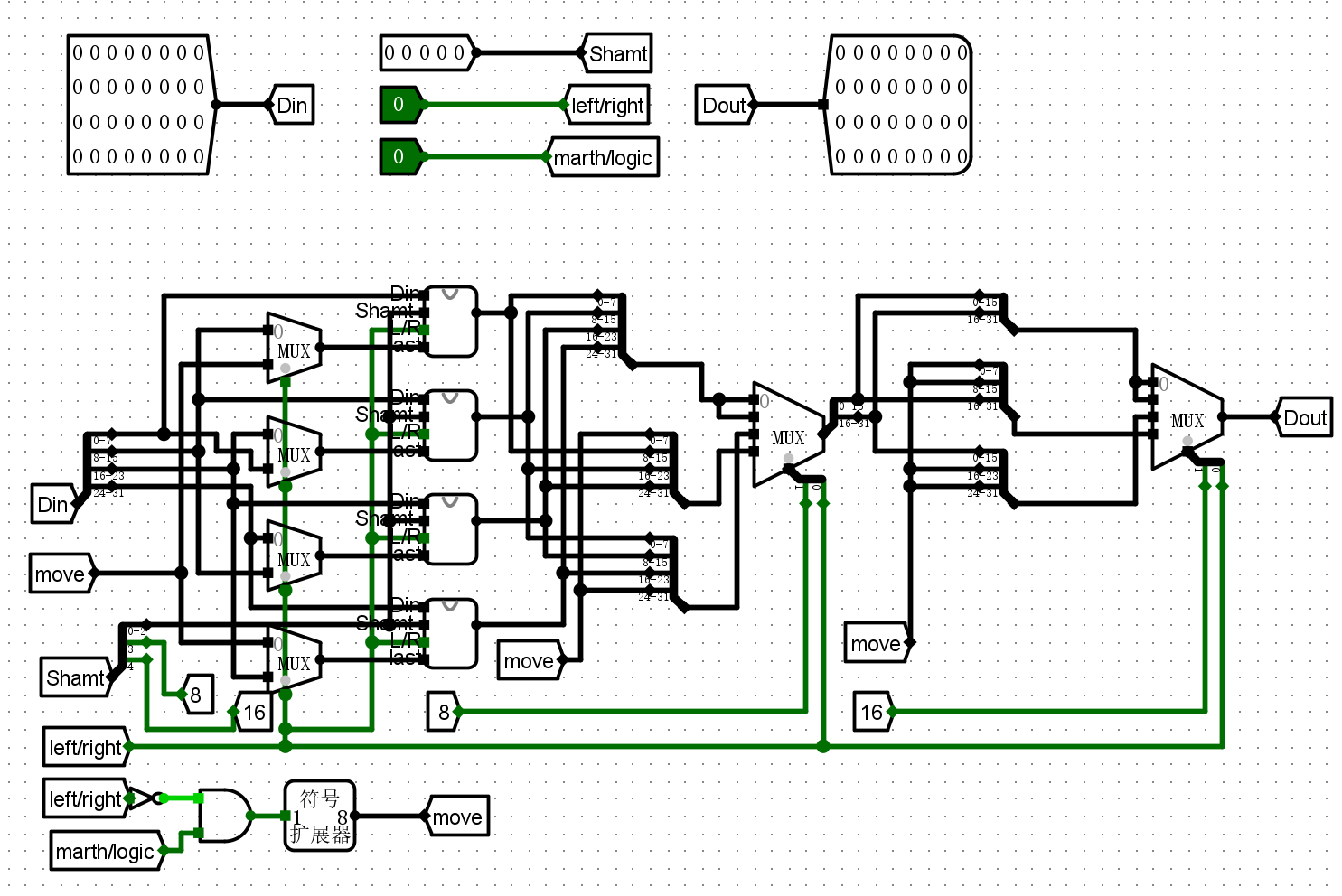
-
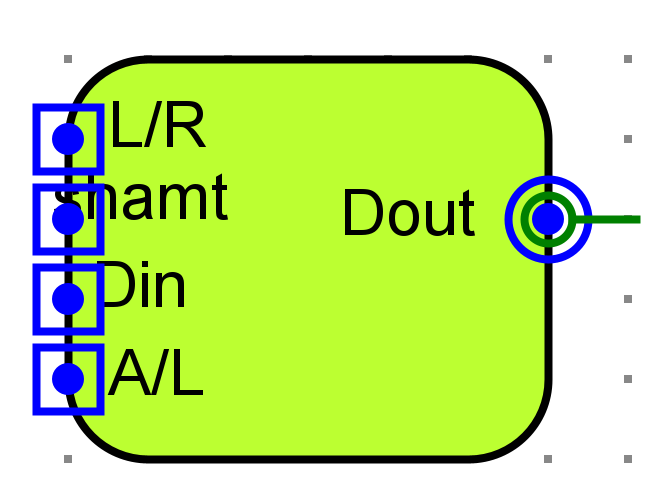
-
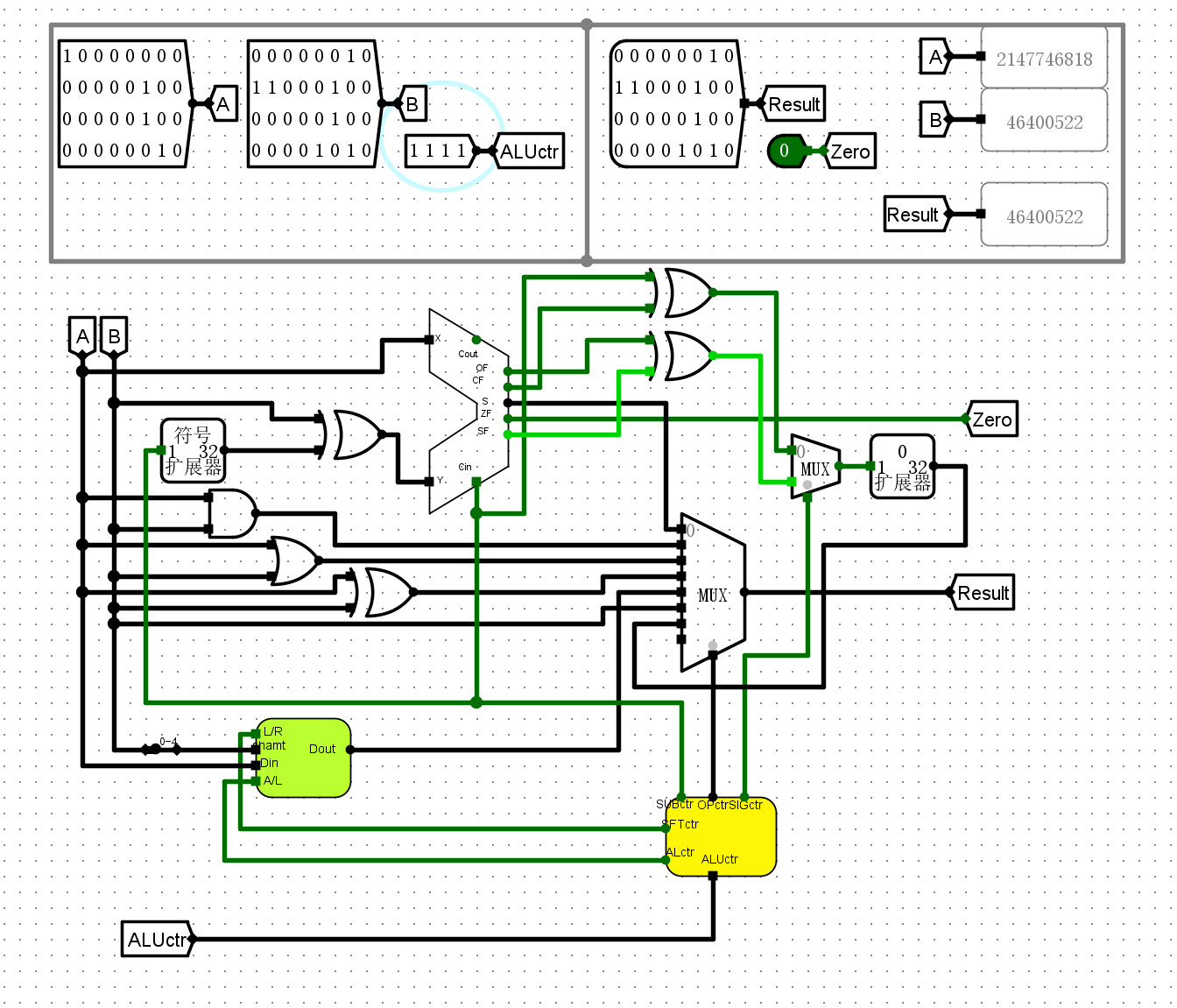
ALU
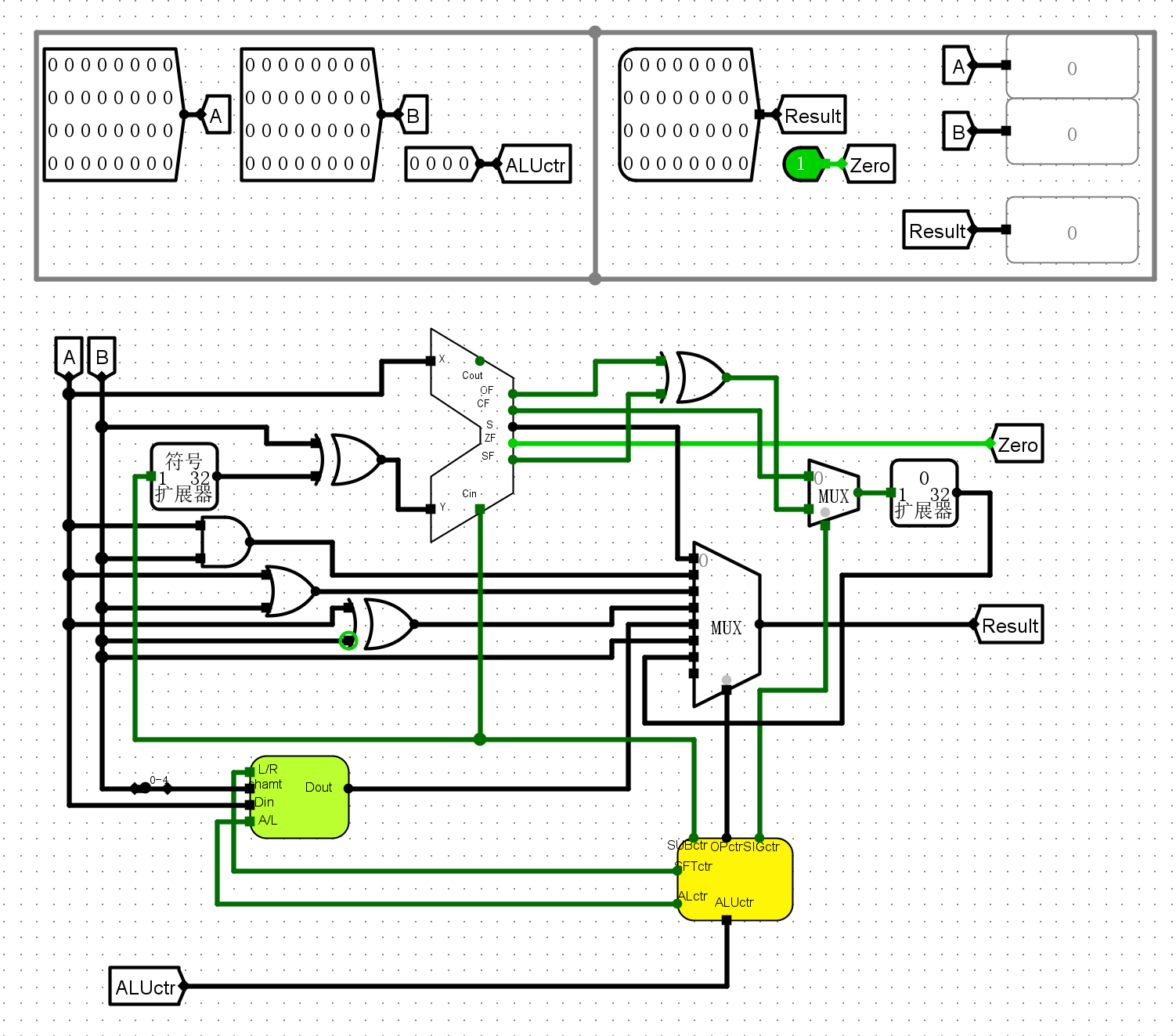
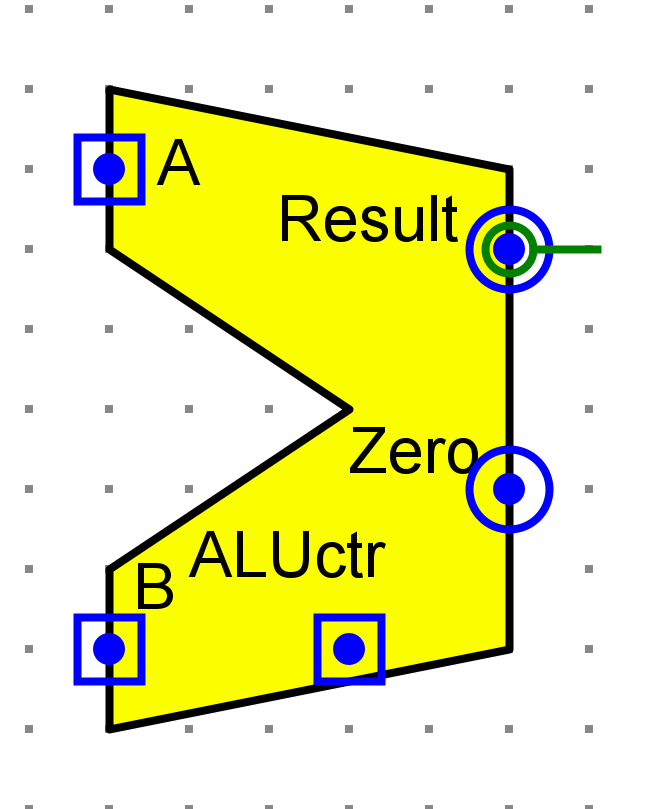
仿真测试¶
- 针对不同操作逐个进行运算
- 0000无符号数加法
-
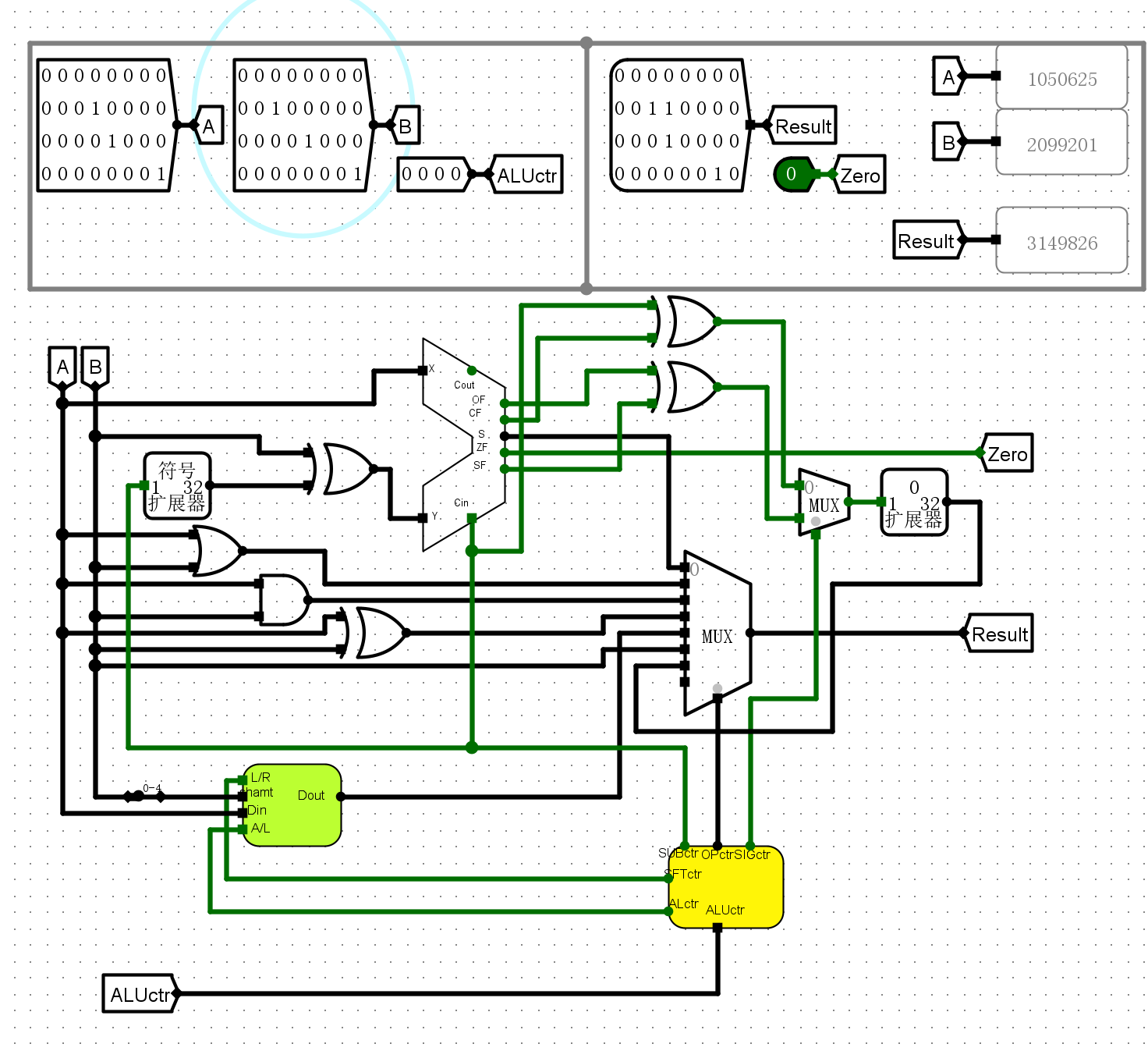
-
0001逻辑左移
-
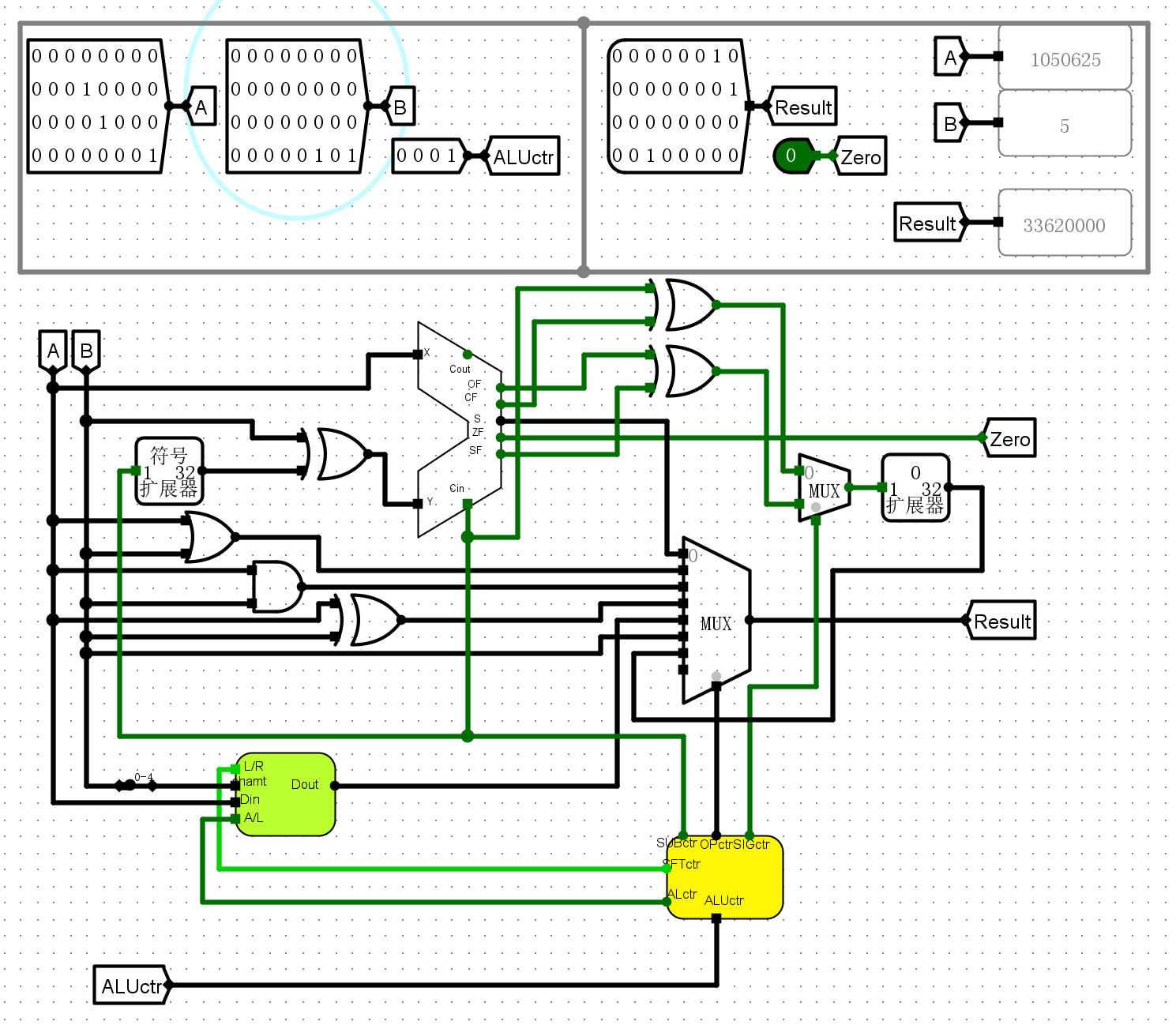
-
0010带符号数比较
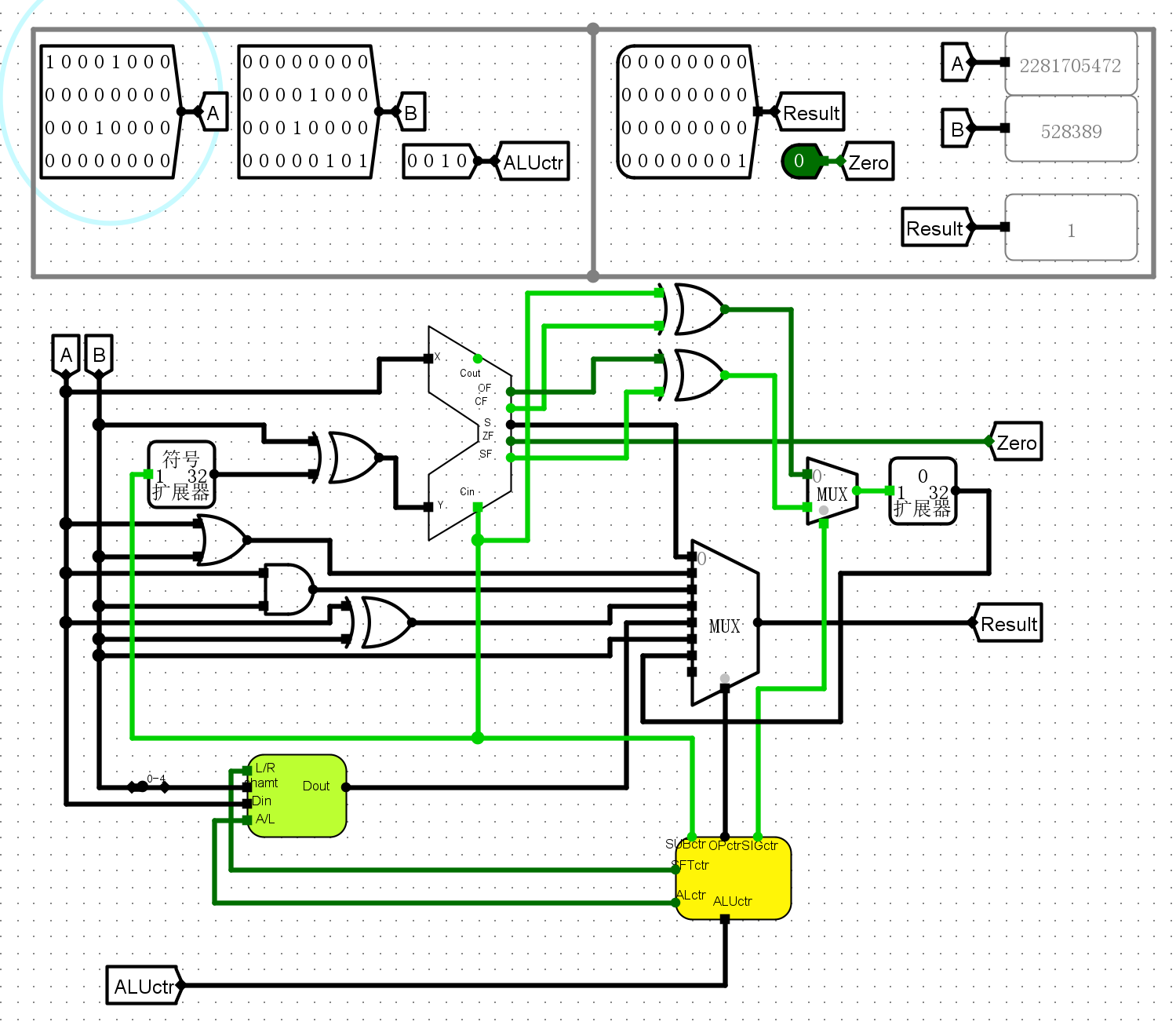
-
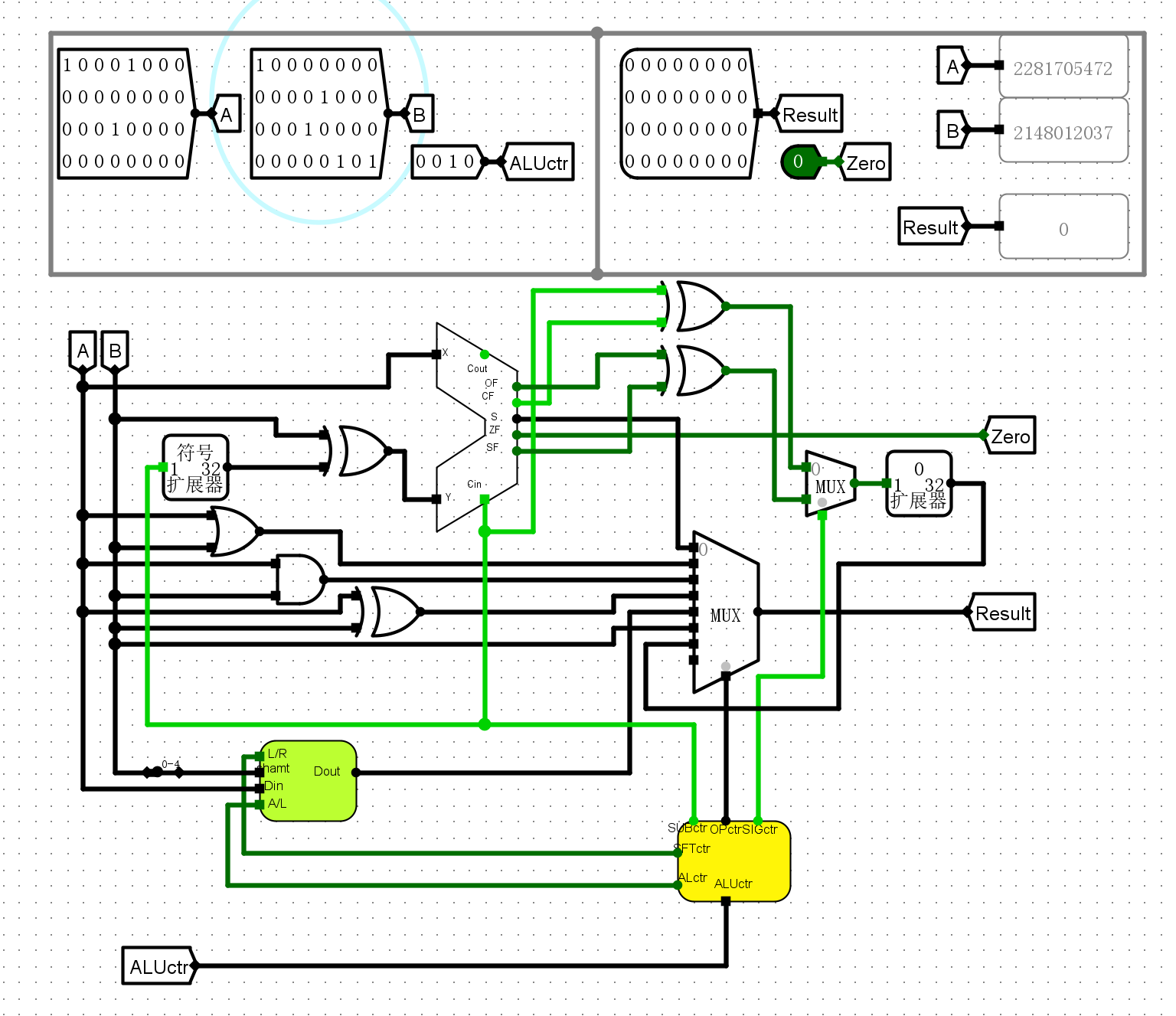
-
0010无符号数比较
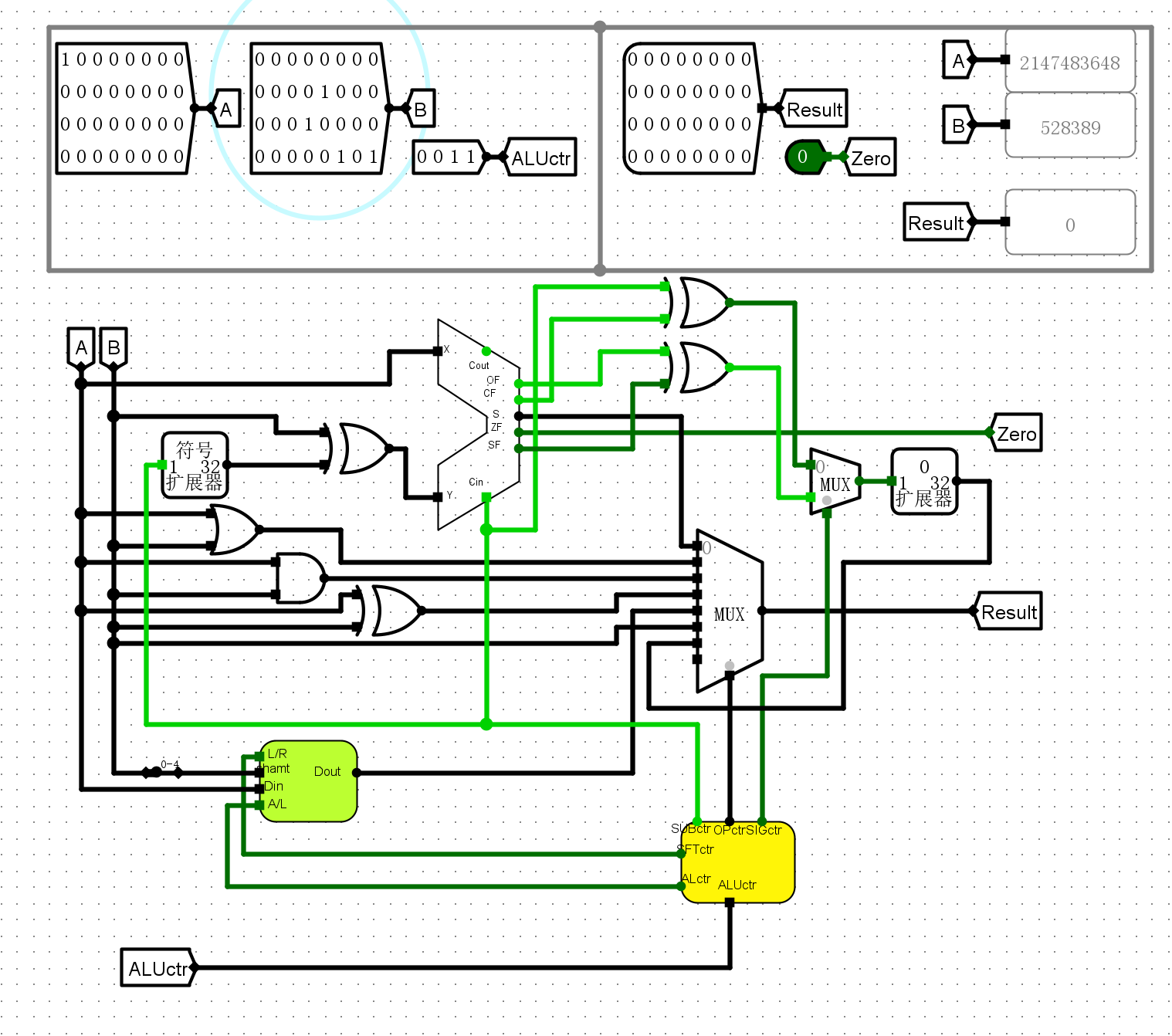
-
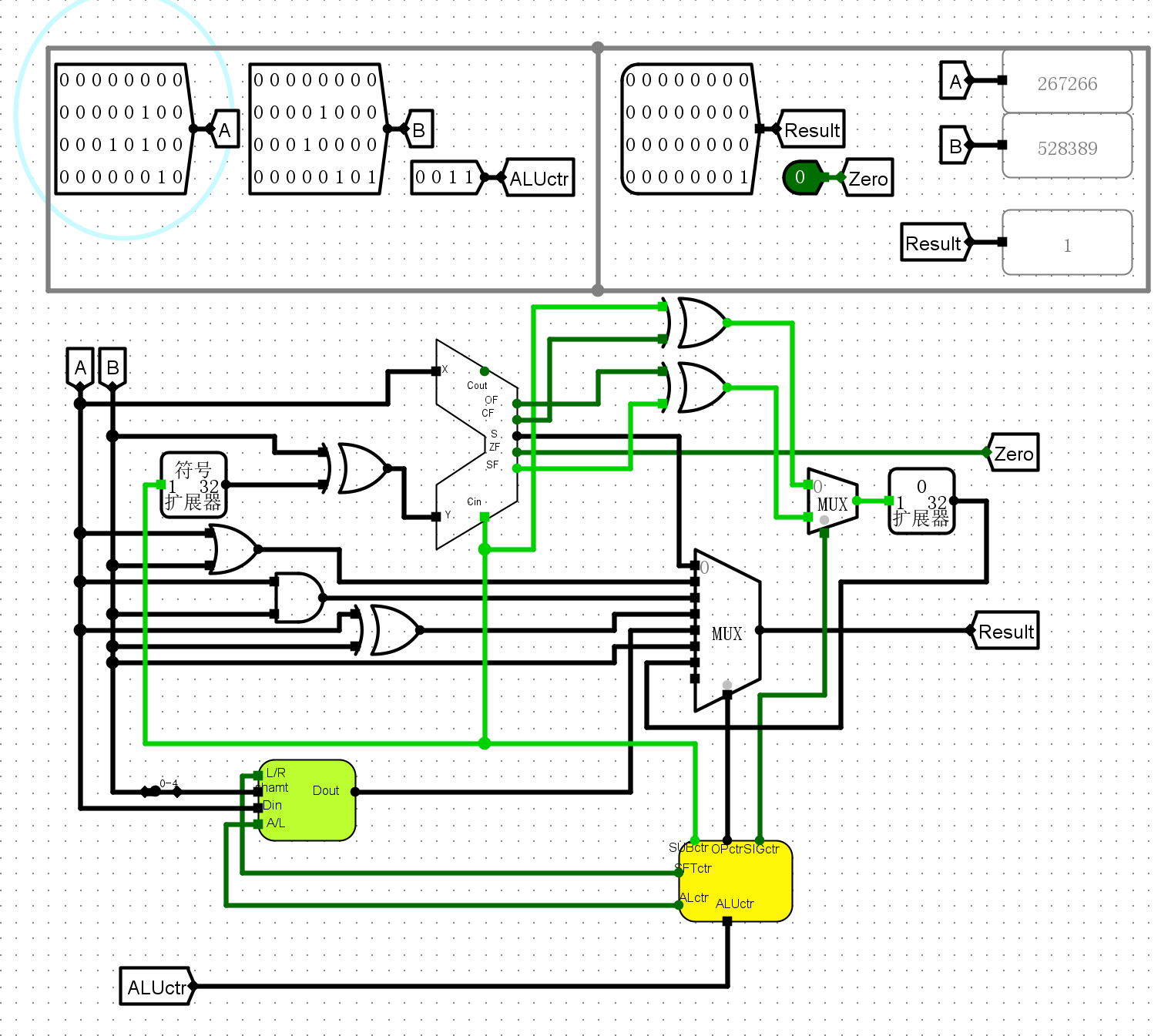
-
0100异或
-
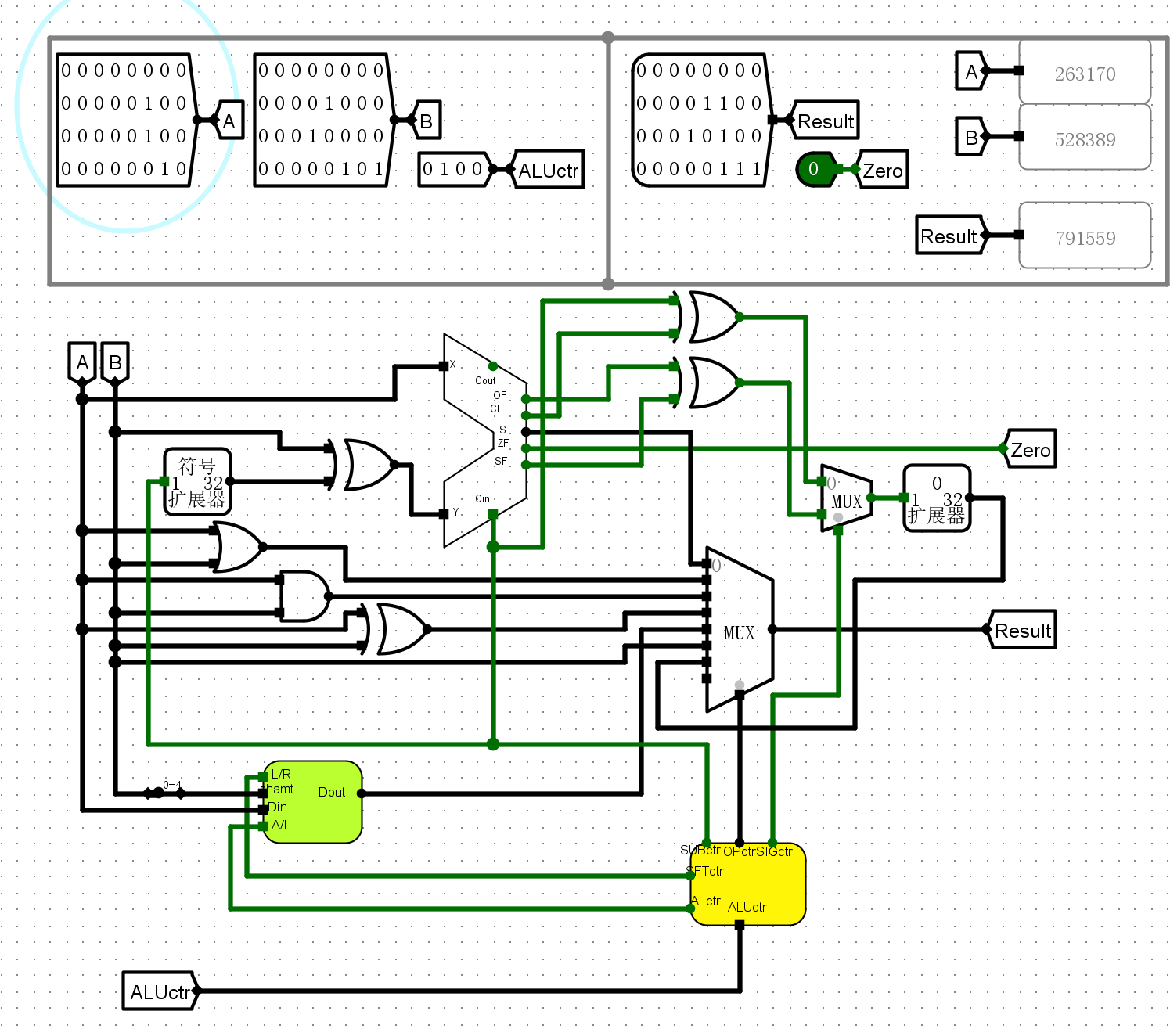
-
0101逻辑右移
-
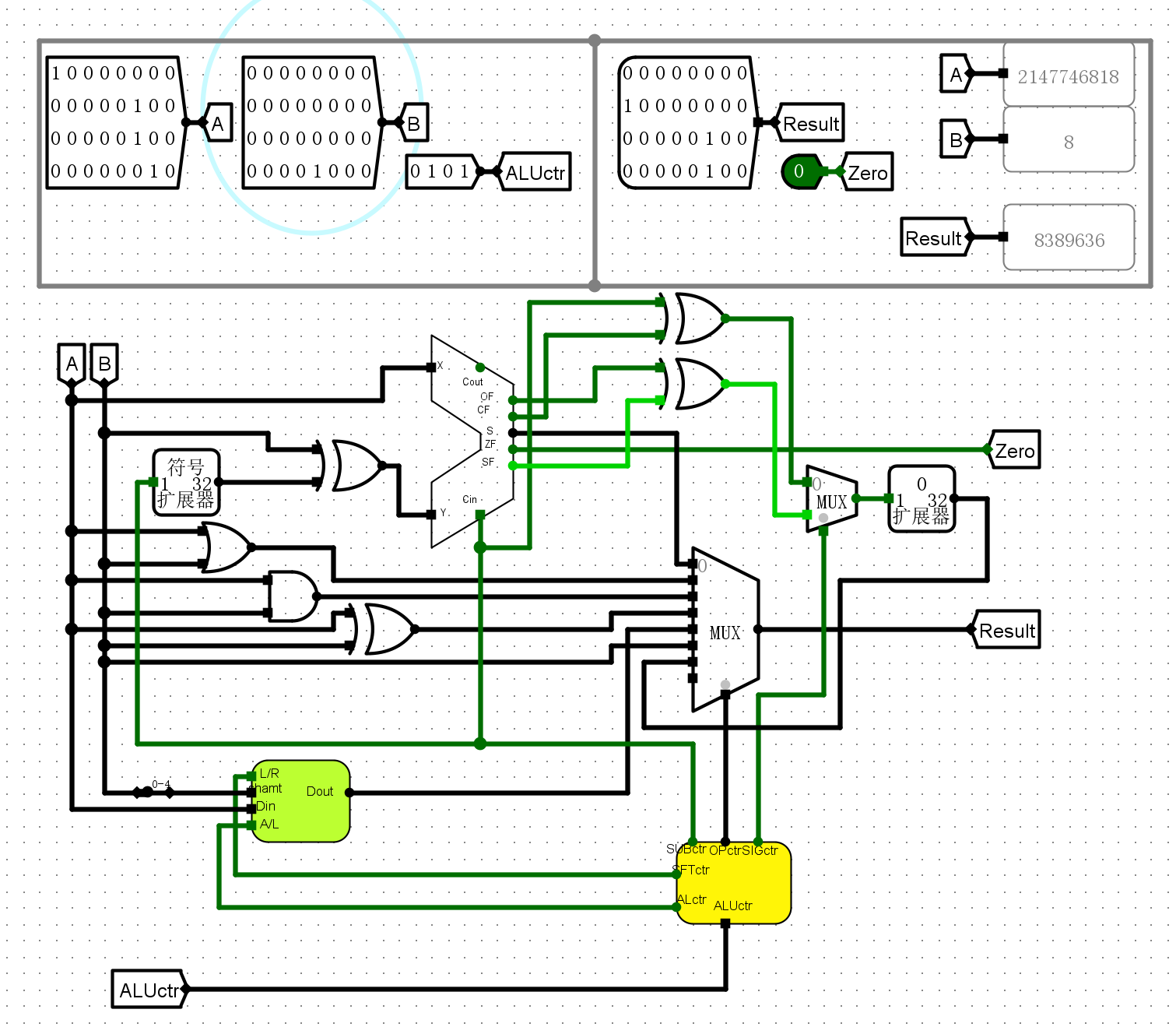
-
0110或运算
-
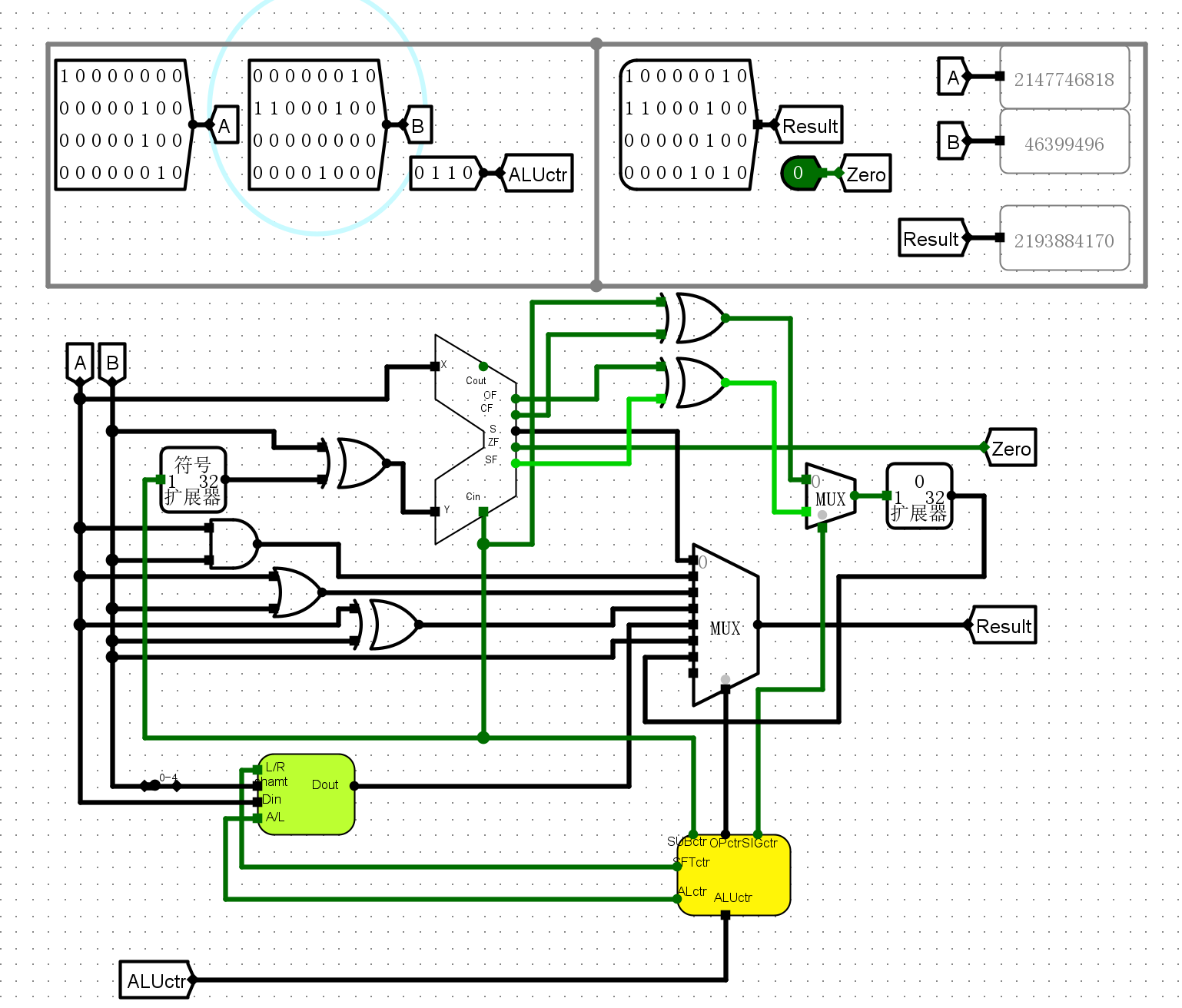
-
0111与运算
-
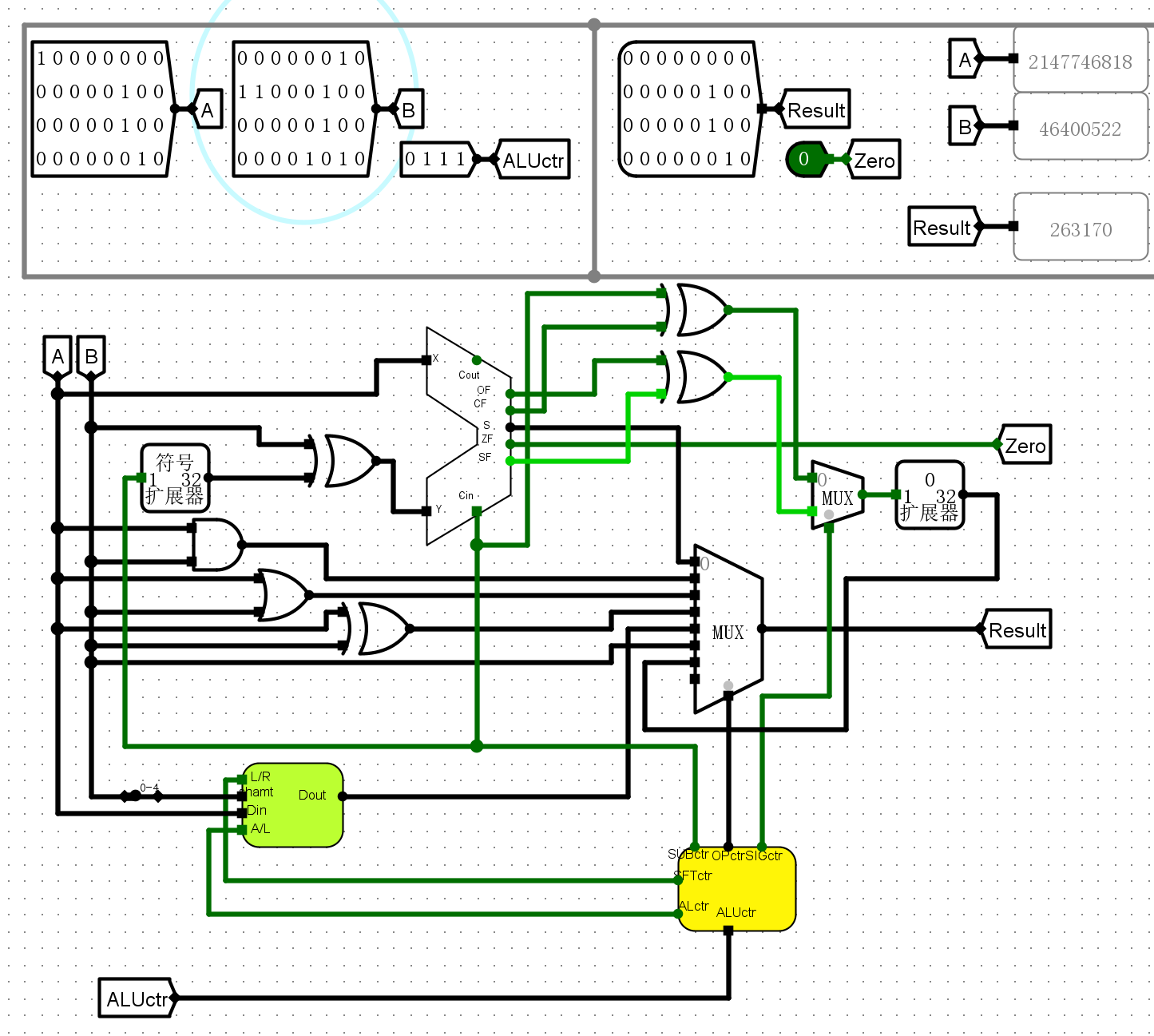
-
1000无符号数减法
-
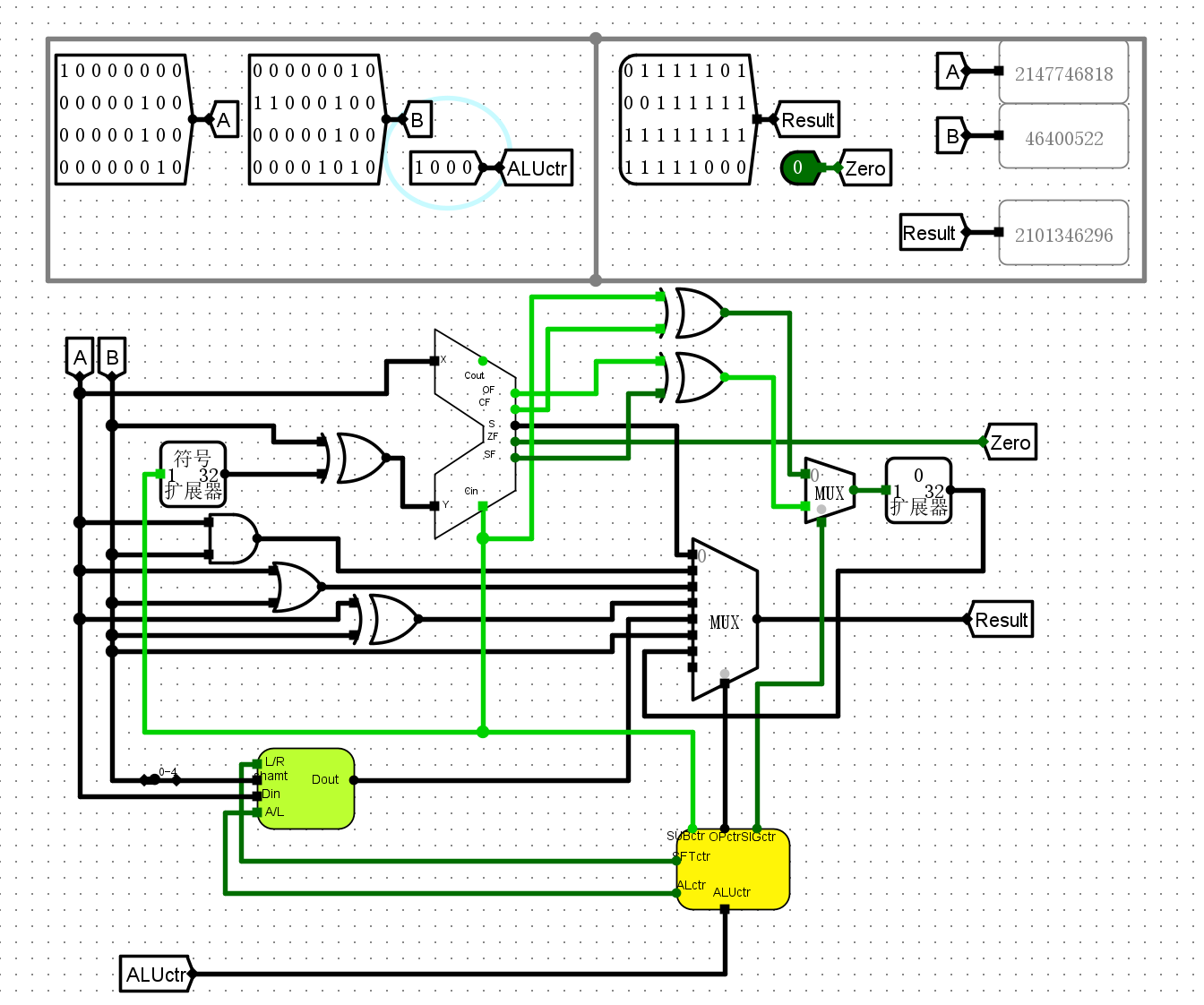
-
1101算数右移
-
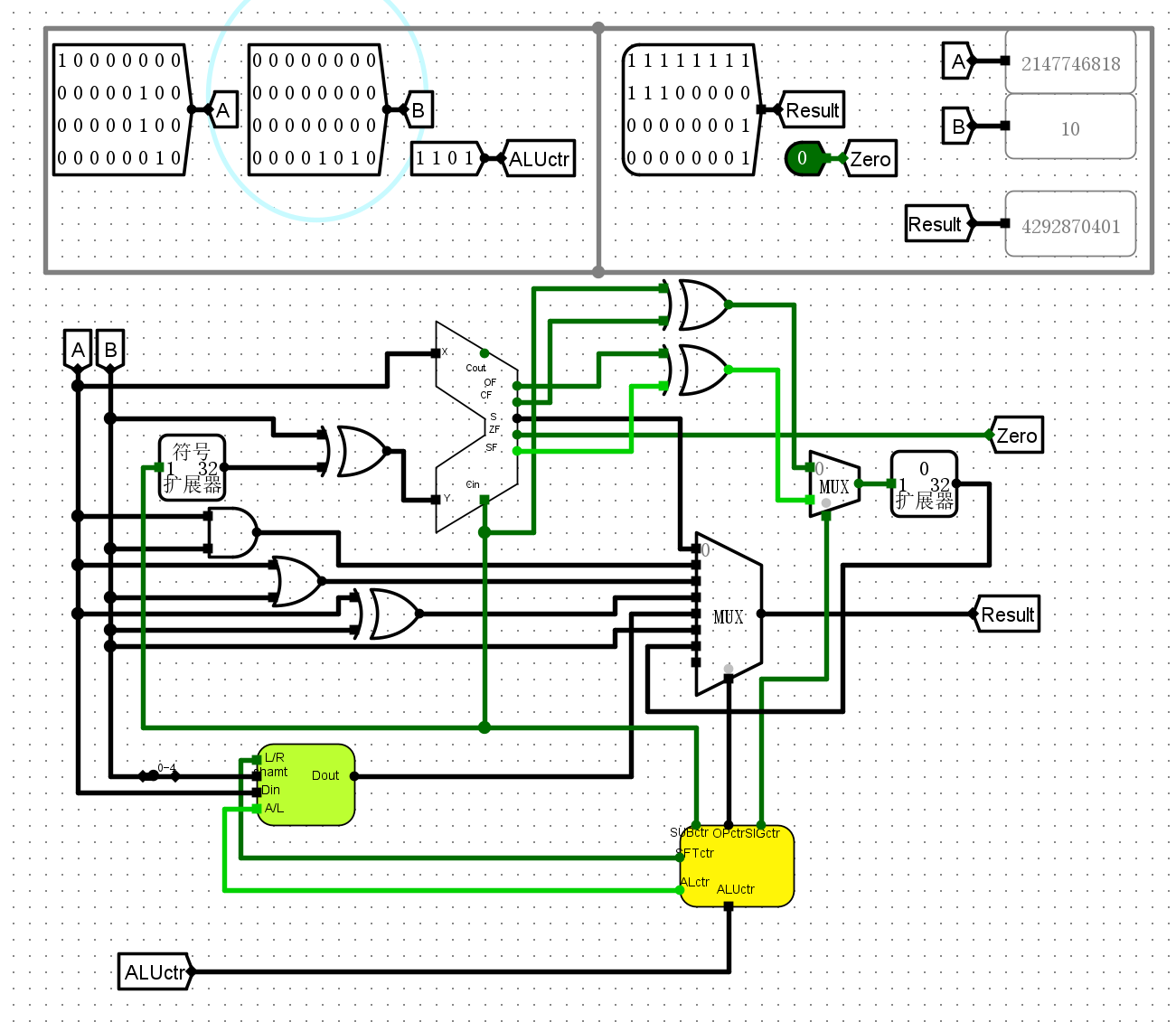
-
1111取操作数B
错误现象及分析¶
- 在完成实验的过程中,没有遇到任何错误。
思考题¶
利用设计的 ALU,举例说明如何实现一个 32 位整数和一个常量的乘法运算¶
- 使用左移和加法操作实现乘法运算
- 假设有一个32位整数x,不妨设常数为6(110),那么可以如下计算
- x<<2+x<<1=x*5,即实现了乘法
- 也就是说,将结果初始化为0,从低位检查常数,如果第i为1,难么就将结果加上被乘数左移i位得到的值。
说说除了先行进位加法器以外还有哪些高速并行多位二进制数加法算法,至少简要说明一种算法的实现流程¶
- 超前进位加法器
- 首先,将整个加法器的位宽分成多个较小的块。
- 在每个块内部,使用一系列全加器进行基本的二进制加法。每个全加器负责计算一个位的和以及产生一个进位。
- 对于每个块,设计一个进位生成器。这个进位生成器用来检测当块的进位输入为1时,这个进位是否会传递到块的最后。基本上,进位生成器会产生一个信号,指示块内所有位的进位传递情况。
- 跳过逻辑:
- 在每个块的输出端,加入一个跳过逻辑。如果进位生成器表示进位会穿过整个块,则跳过逻辑会将该块的进位输入直接传递到下一个块的进位输入端,这样就跳过了块内的所有进位计算。
- 如果进位生成器表示进位不会穿过整个块,则跳过逻辑会等待该块内的所有进位计算完成。
- 通过跳过逻辑,进位可以快速传递到需要它的块。这减少了进位在加法器中传播的时间,从而加快了整个加法操作的速度。
- 最后,每个块的和输出和最终的进位输出组合起来,形成整个加法器的结果。
- 条件和加法器
- 将加数分成若干块,每块包含若干个位。
- 对于每个块,同时计算两个条件和:一个假设该块的进位输入为0,另一个假设为1。
- 进位查找:
- 同时计算每个块可能产生的进位。
- 计算每个块的进位产生和进位传递信号。
- 递归结构:
- 使用递归结构来确定每个块的实际进位输入。
- 第一个块的进位输入来自于加法器的进位输入。对于后续的每个块,其进位输入取决于前一个块的进位输出。
- 对于每个块,一旦确定了实际的进位输入,就从两个条件和中选择正确的和。
- 合并所有块的条件和来形成最终的加法结果。
- 除此之外还有:管线化加法器、并行级联加法器等加速方法
简要分析加法运算、比较运算和移位运算三种运算中操作数在 ALU 中经过的逻辑门级数¶
-
加法运算
-
首先在进入加法器之前,B先经过了一个异或门,比A多了一级逻辑门
- 在32位加法器中,操作数没有经过逻辑门直接进入了16位CLA加法器
- 在16位加法器中,又4个并行的4位并行加法器,操作数直接进入,没有经过别的逻辑门
- 在4位加法器中,操作数直接进入全加器,没有经过其他的逻辑门
- 在全加器中,操作数经过了一级逻辑门
- 回到32位加法器中,离开16位加法器后直接进入结果s,没有再经过其他逻辑门
- 回到ALU,在输出之前又经过8路多路选择器,大致经过4级逻辑门
-
总计:A:5;B:6;
-
比较运算
-
比较运算实际上就是进行了一次加法,对结果的符号位进行分析
-
-
这次的结果是由CF、OF、SF决定的,而不是加法的运算结果s
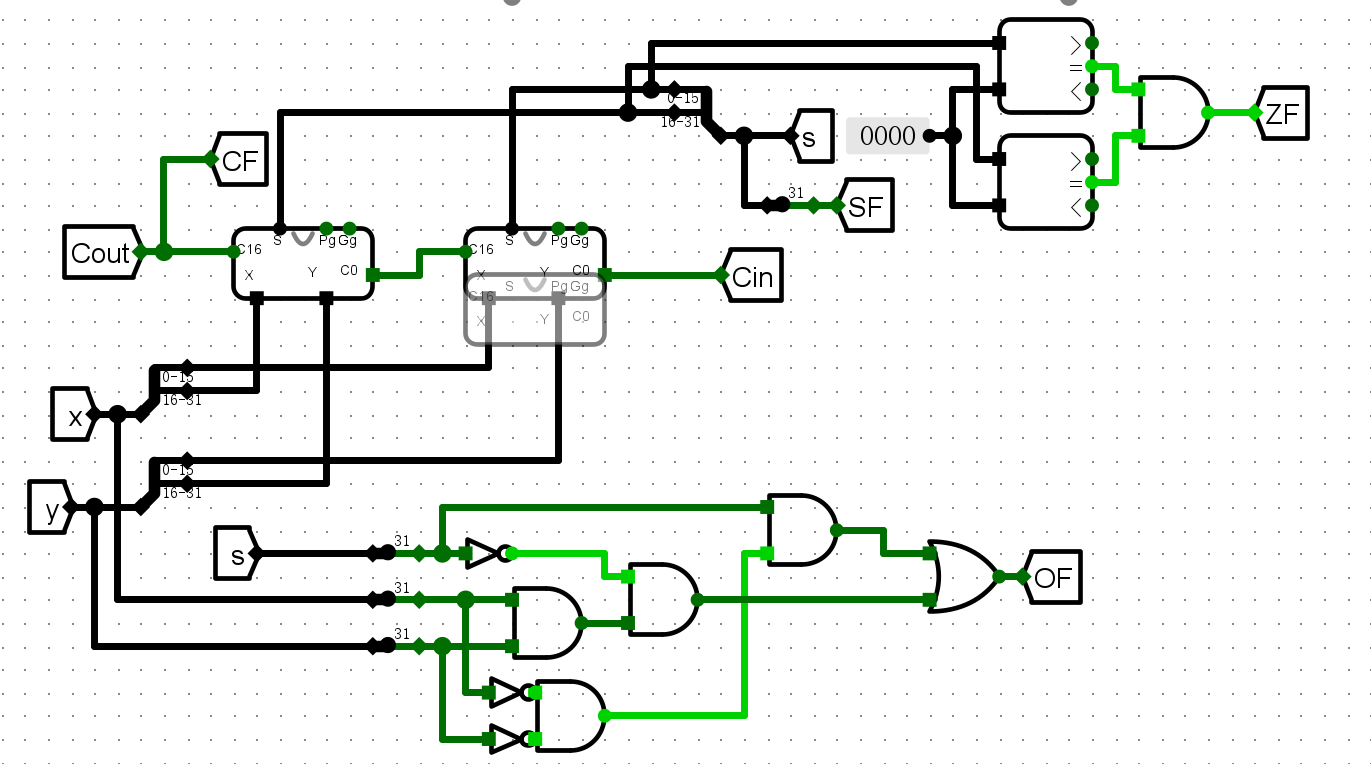
- 在32位加法器中,得到OF需要经过最多4级逻辑门;得到SF需要经过1级;得到CF需要在CLA-4中进入进位计算器额外经过3级逻辑门,即总共需要至多4级逻辑门
- 位得到结果,还需要经过异或门和两级多路选择器,大致2道逻辑门
-
因此操作数至多经过1+4+3+4=12道逻辑门
-
移位运算
-
操作数直接进入了移位器
- 在32位移位器中,出去8位移位器,至多会经过2+3+3=8道逻辑门
- 在8位移位器中,至多会经过9道逻辑门
- 也因此操作数至多经过1+8+9+4=22道逻辑门