数字逻辑电路基础

概述

• 数字逻辑电路可以看成有若干输入和输出的黑盒，输入和输出之后1、0两种状态
• 分为组合逻辑电路和时序逻辑电路
• 组合逻辑电路的输出值仅依赖于输入
• 时序逻辑电路还依赖电路的状态（电路中存在存储部件或反馈结构）
• 
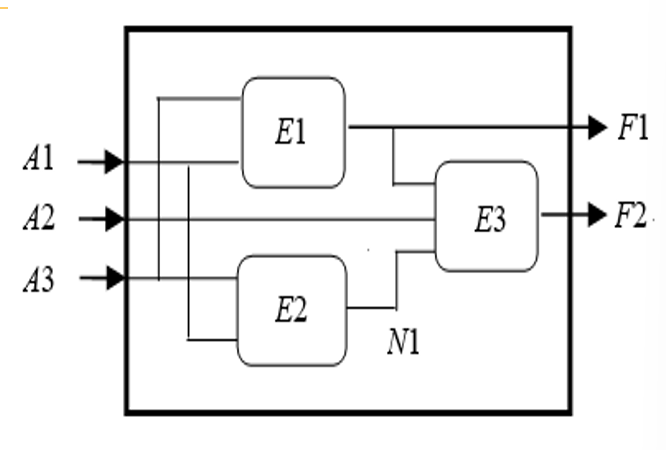
• 每个元器件又可以看作一个数字逻辑电路
• 节点分为输入节点、输出节点、内部节点

逻辑元件

逻辑门

• 逻辑门电路是最基础的数字电路，具有允许或禁止信号传输的功能，也称为门电路。有一/多个输入，一个输出，输入输出都是0/1
• 输入输出的关系可以使用真值表/逻辑表达式来描述
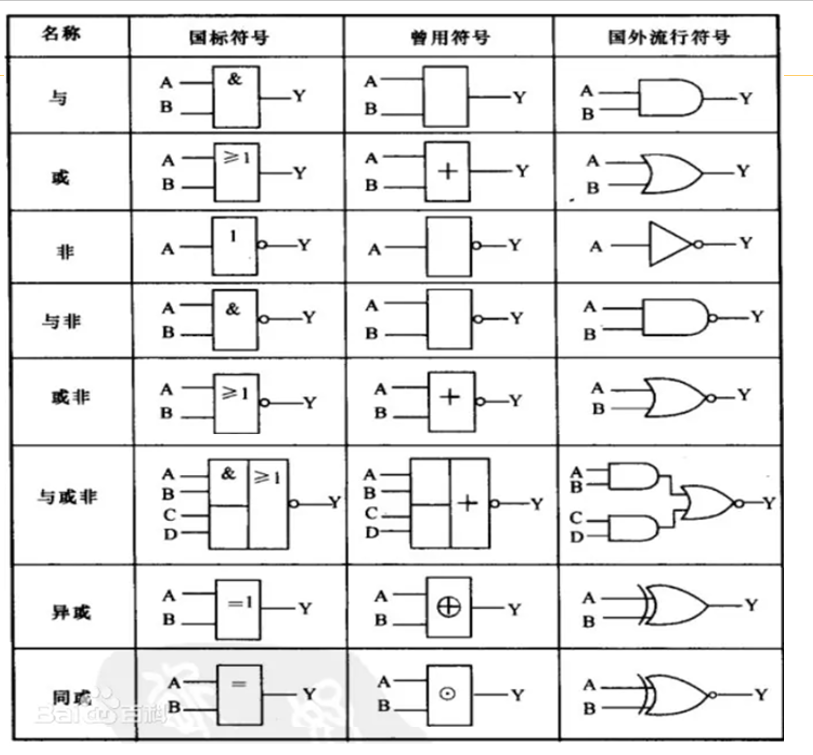
• 基本逻辑门：
• 与门and、或门or、非门not
  • 
• 与非门nand、或非门nor
  • 
• 异或门xor、同或门nxor
  • 
• *

数字抽象

• 将物理量的实际值映射为两个子集，通常使用高电平H、低电平L进行映射

• 低电平和高电平指的都是一个电压范围

• 
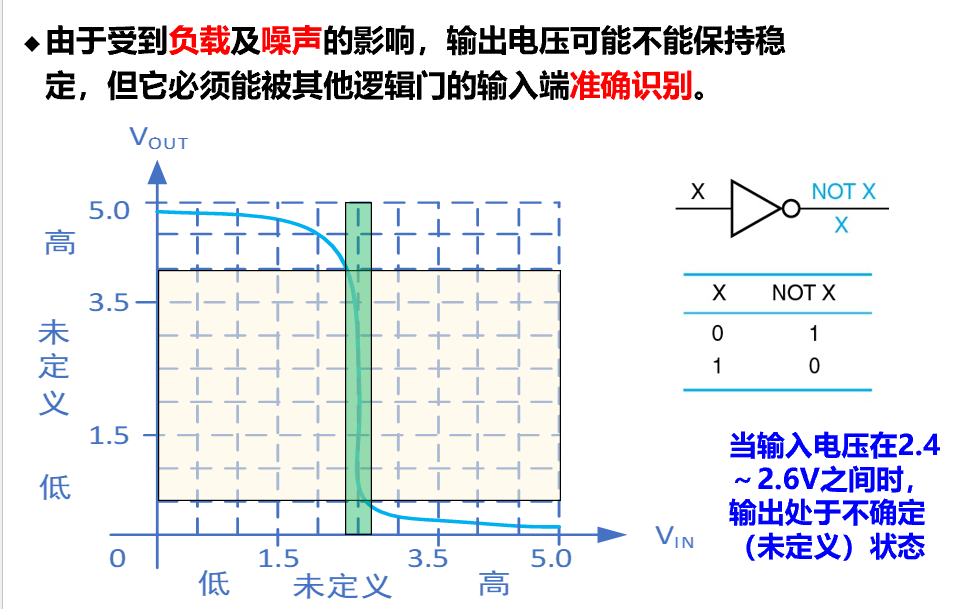
• 输入电压主要由晶体管的关阈值电压决定，而输出电压则主要由晶体管导通时的电阻决定
• 
• 需要在 vih、hoh 之间/vil、vol 之间才能获得较为稳定定的正确输出
• 输入的范围大、容错好，输出的范围小、较为精确
• 
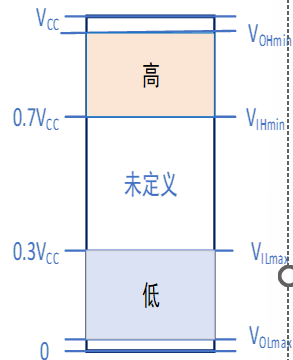
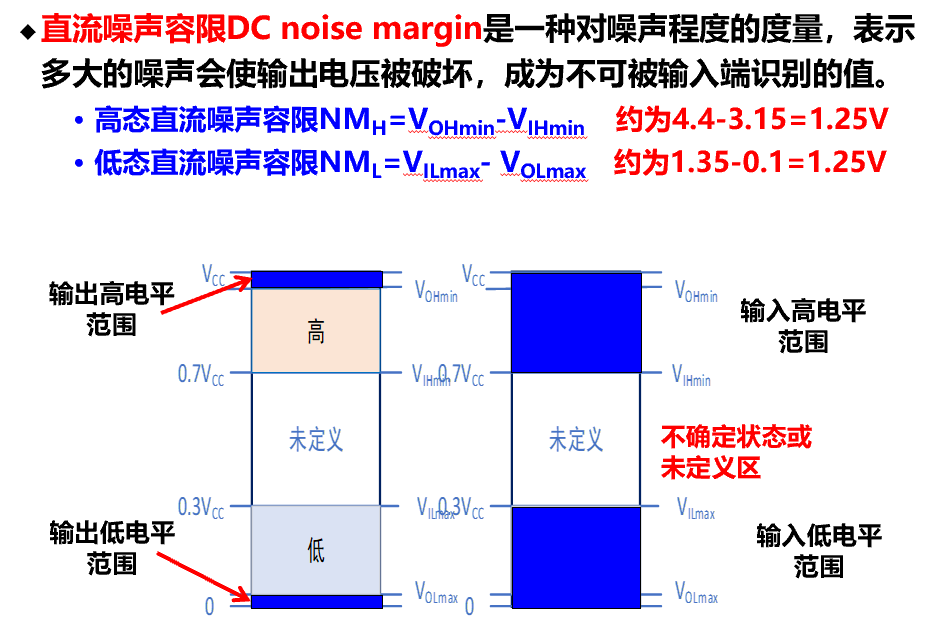
• VCC/VDD 称为电源电压，典型值为 5.0 V±10%；GND 称为地线，0V
• 

CMOS晶体管

难点

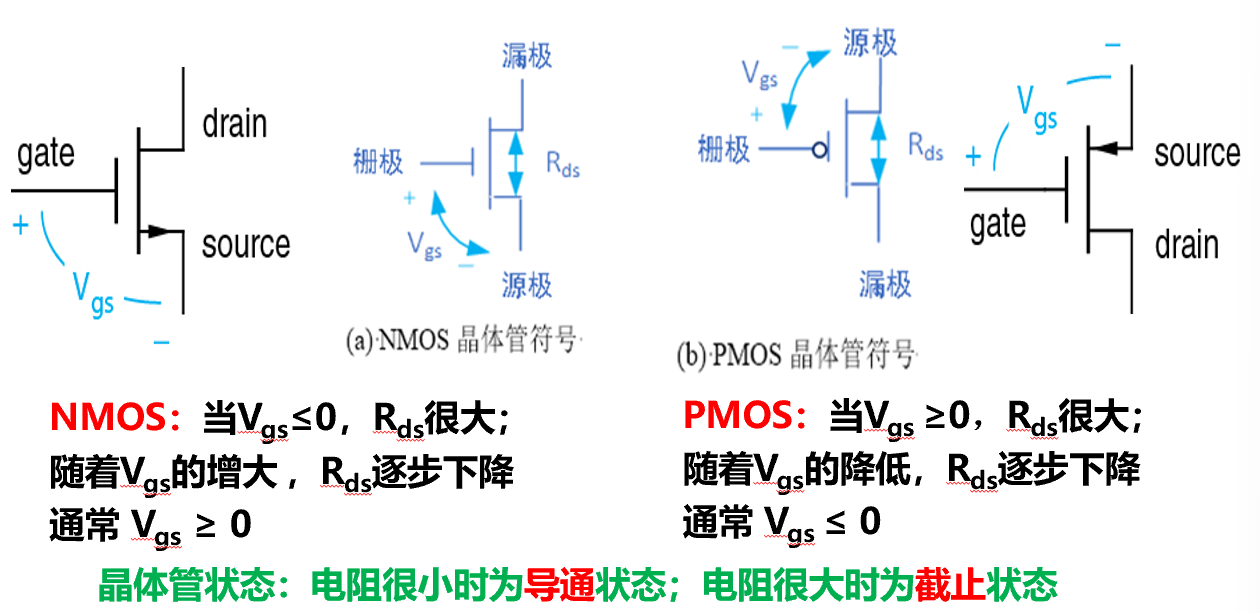
• MOS晶体管可被模型化为一种3端子压控电阻导体，将电压加到一个端子，来控制其他两个端子间的电阻。
• 
• 栅极和源级之间的电压差 \(V_{gs}\) 控制源极和漏极间电阻 \(R_{ds}\)
• 

• NMOS:栅极高电平导通；PMOS:栅极低电平导通

• CMOS 晶体管

• 使用一对NMOS和PMOS
• 
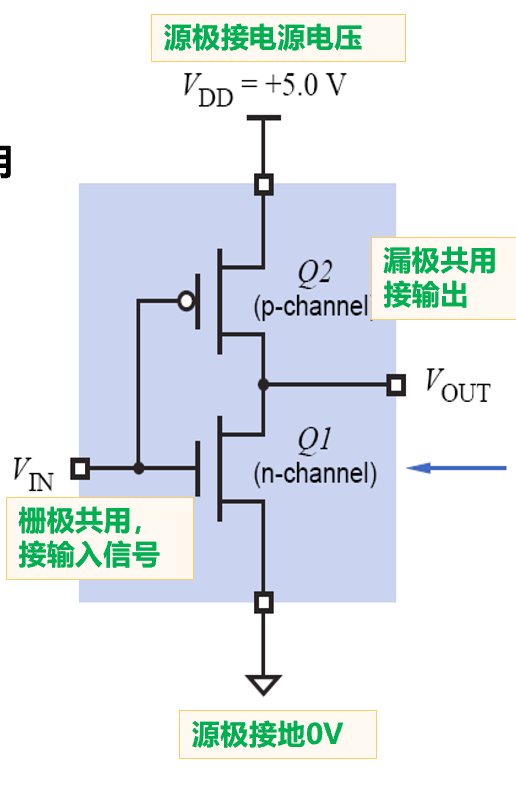
• 通过栅极输入电压改变漏极的输出电压

• NMOS源级接GND、PMOS源级接电源

• 非门

• 

• 

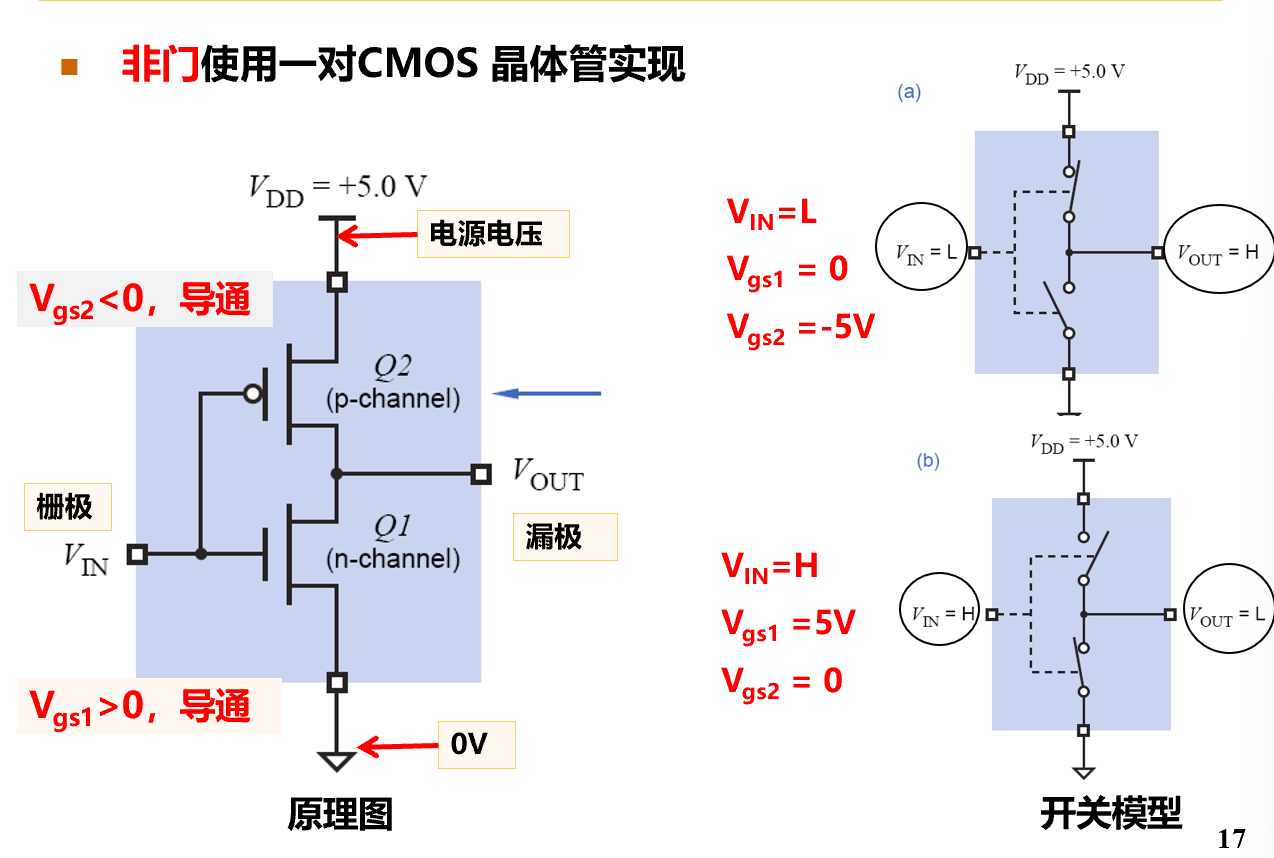
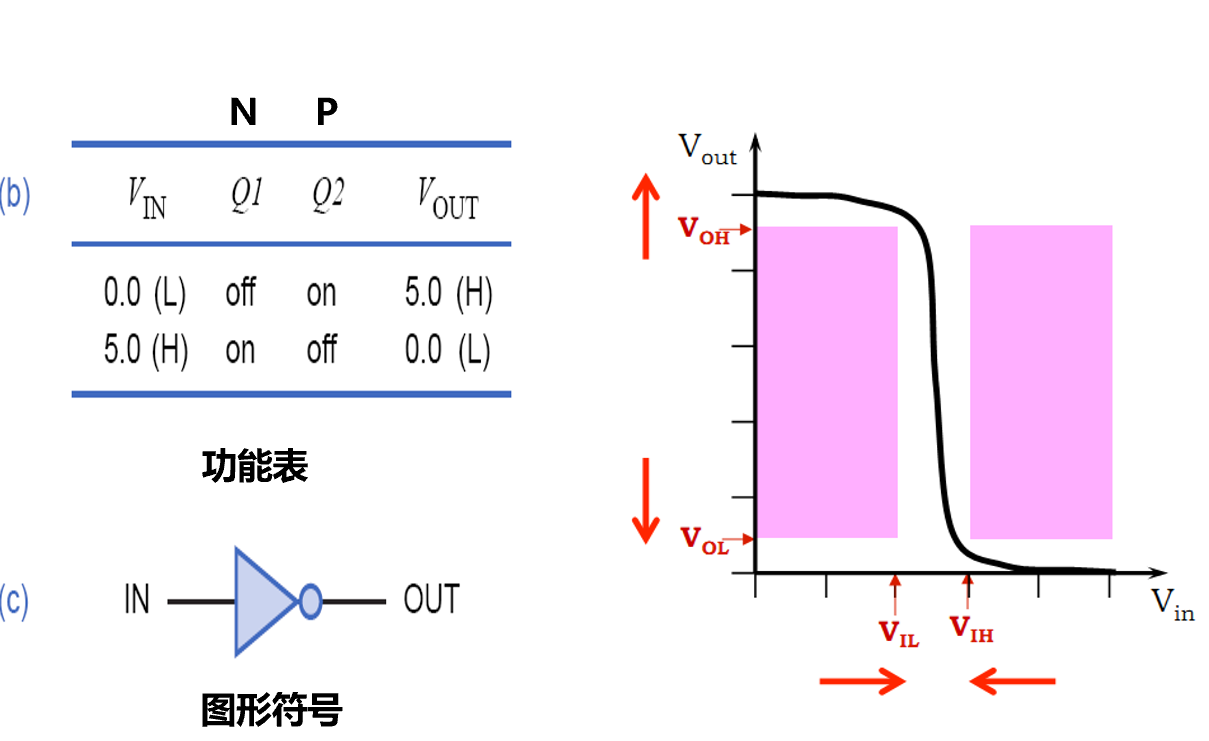
  • b称作功能表，表示晶体管开关以及输出状态

• 与非门

• 
• 
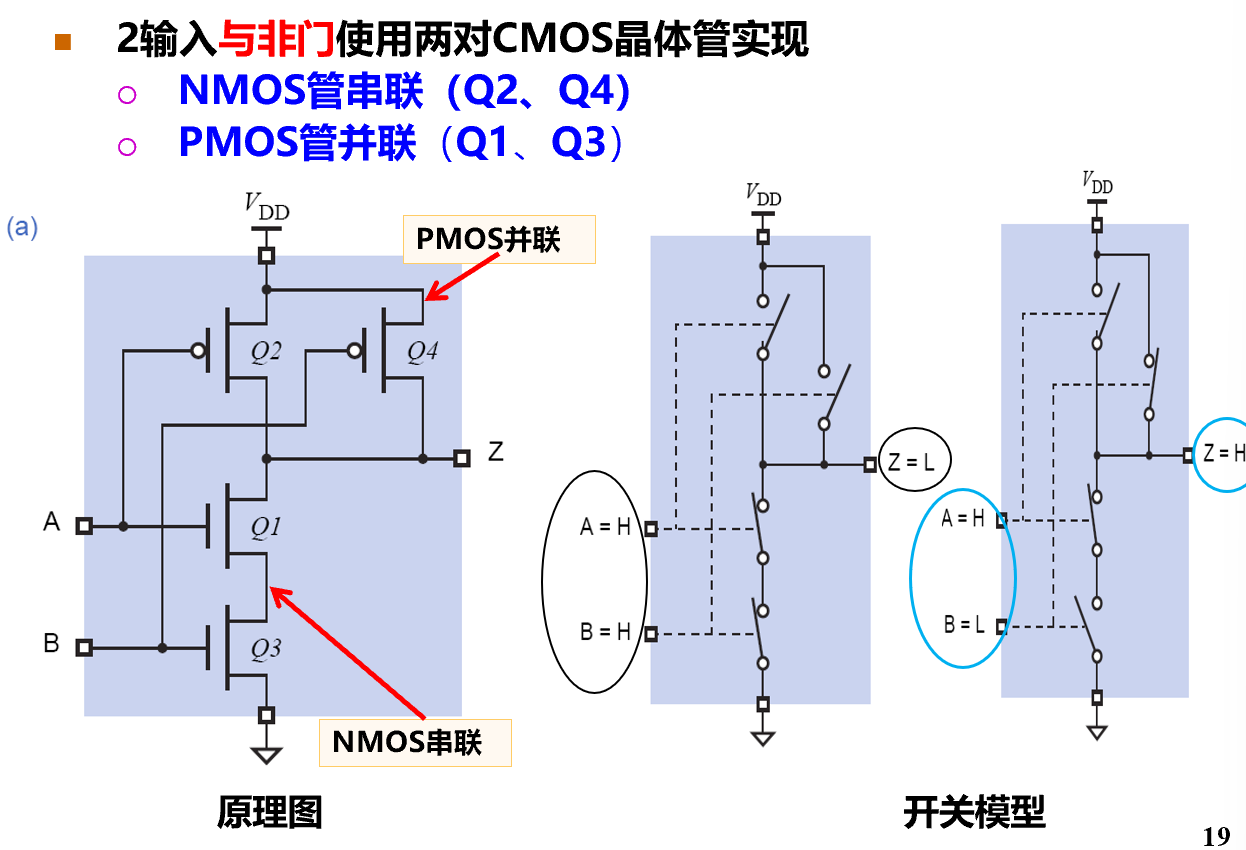
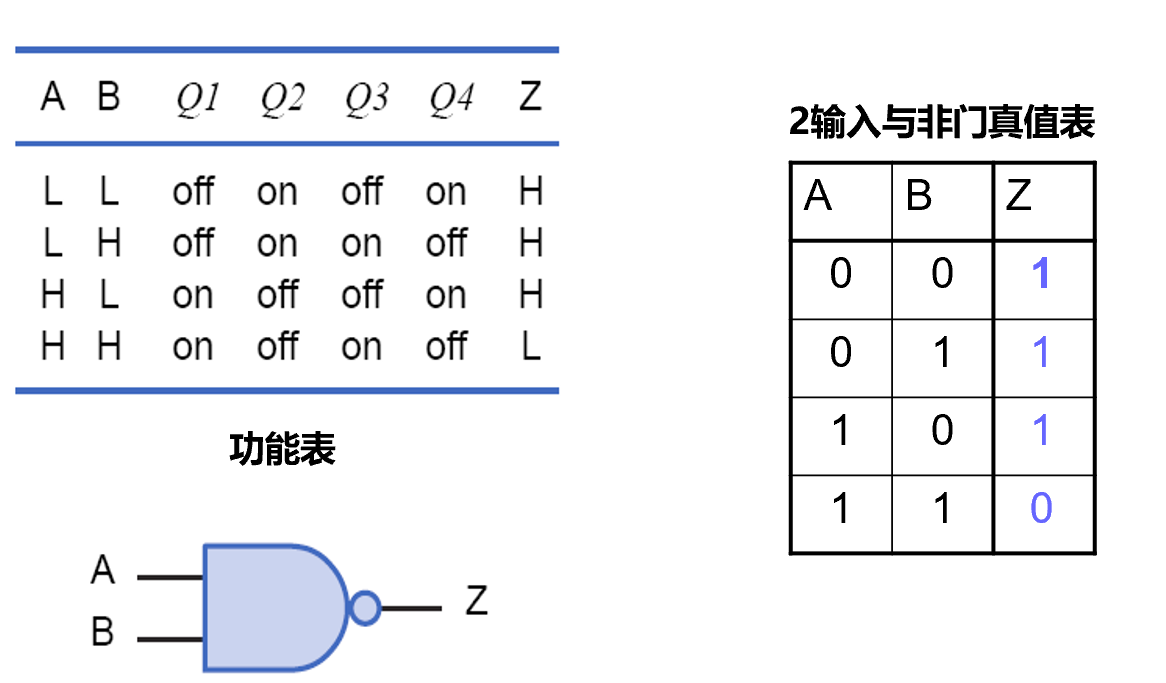
• 或非门
• 
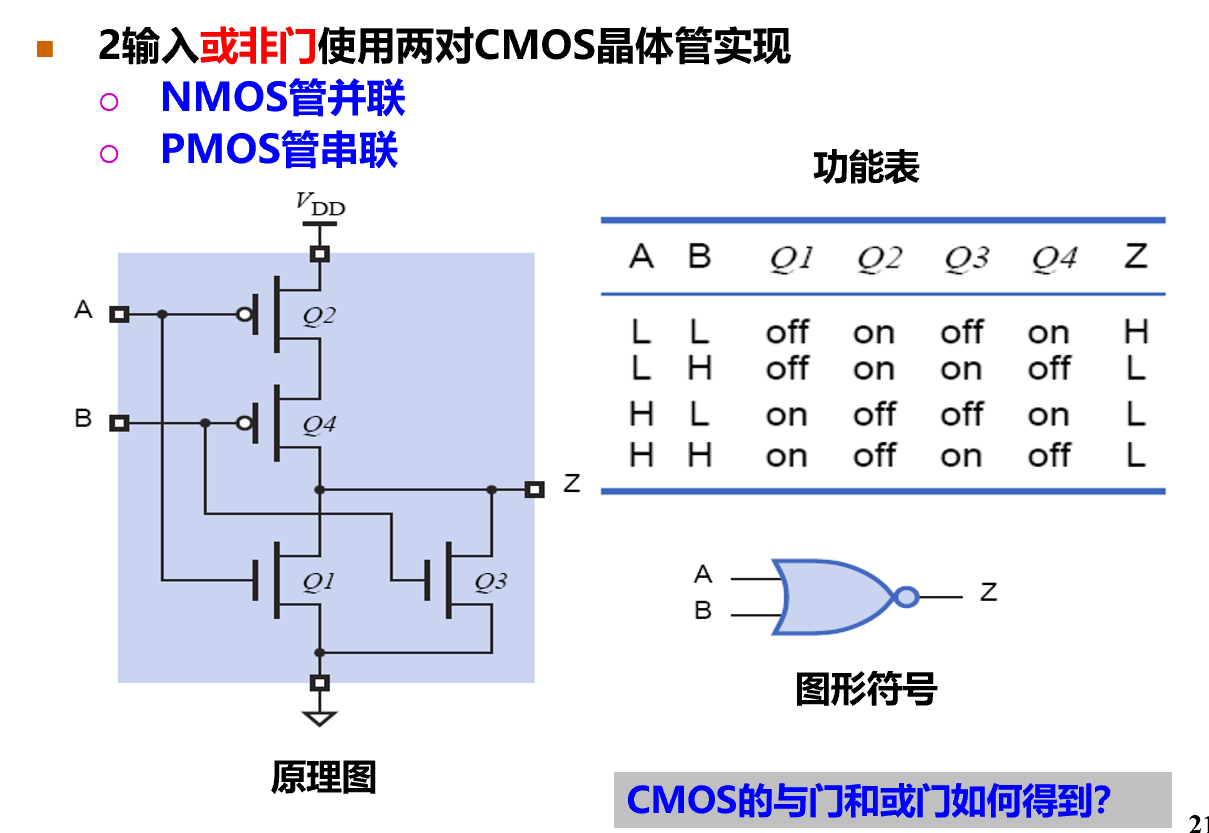
• 与、或需要额外加一个非
• 推广（k输入）
• 
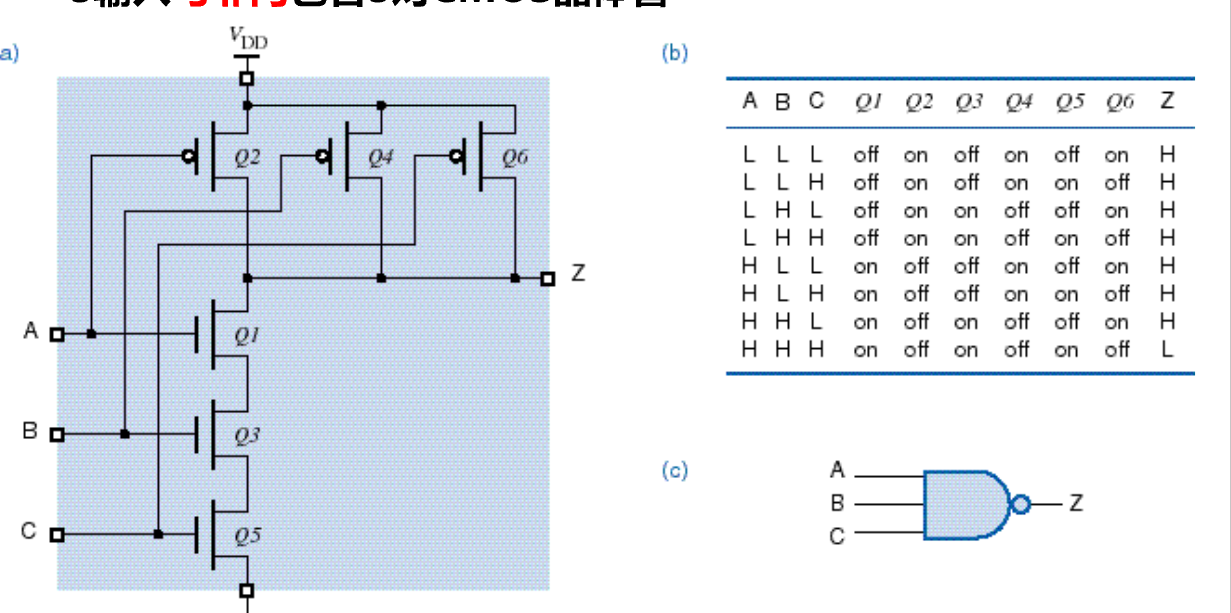
• 级联，受物理限制，不能对一个器件无限增大，一般输入端数目小于等于5，不超过8，输入较多的门电路可以使用输入较少的门电路级联
• 
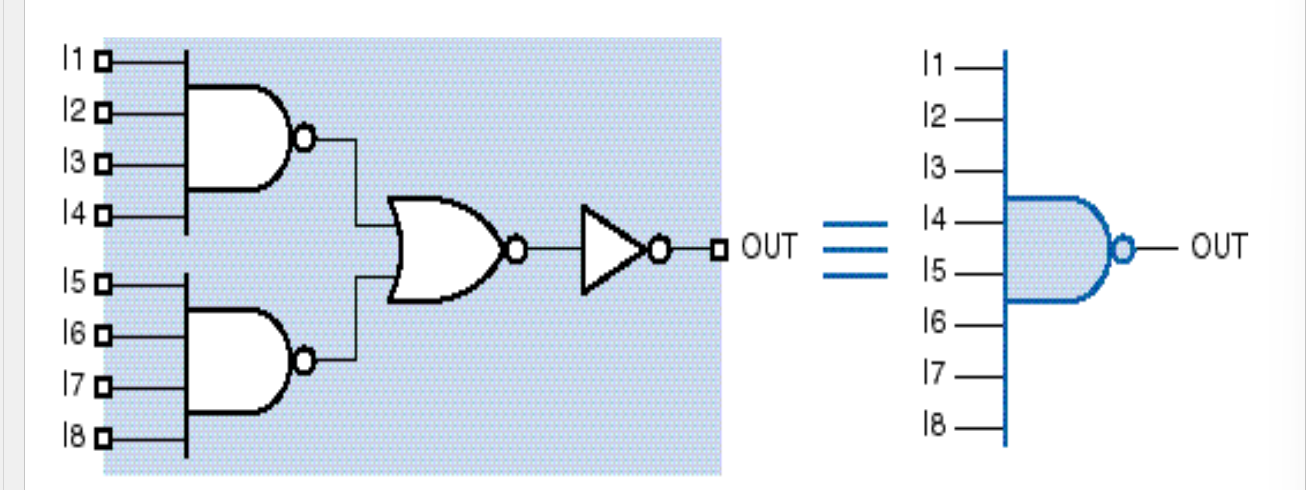
• 级联实现与门

• 

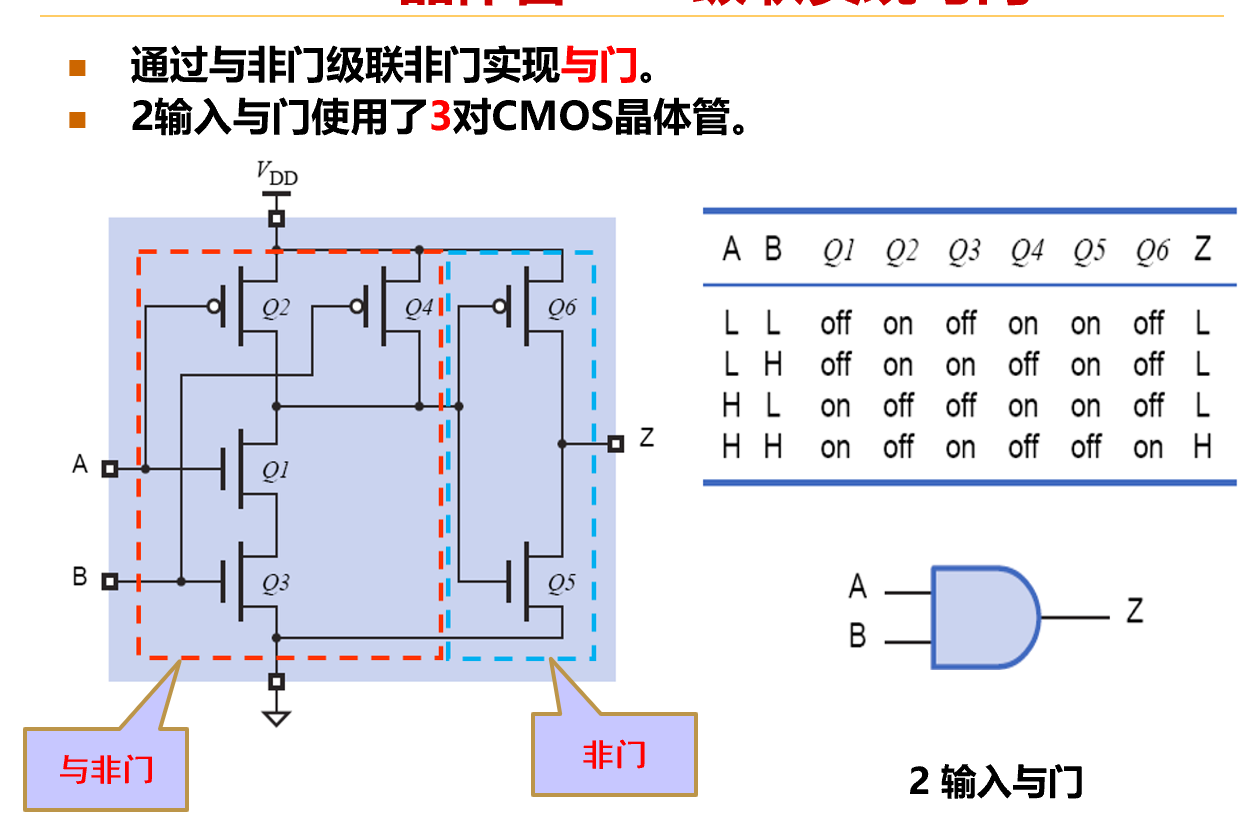
• 缓冲器

• 将一个弱信号转化为具有相同逻辑的强信号（连续两个非门）

• 

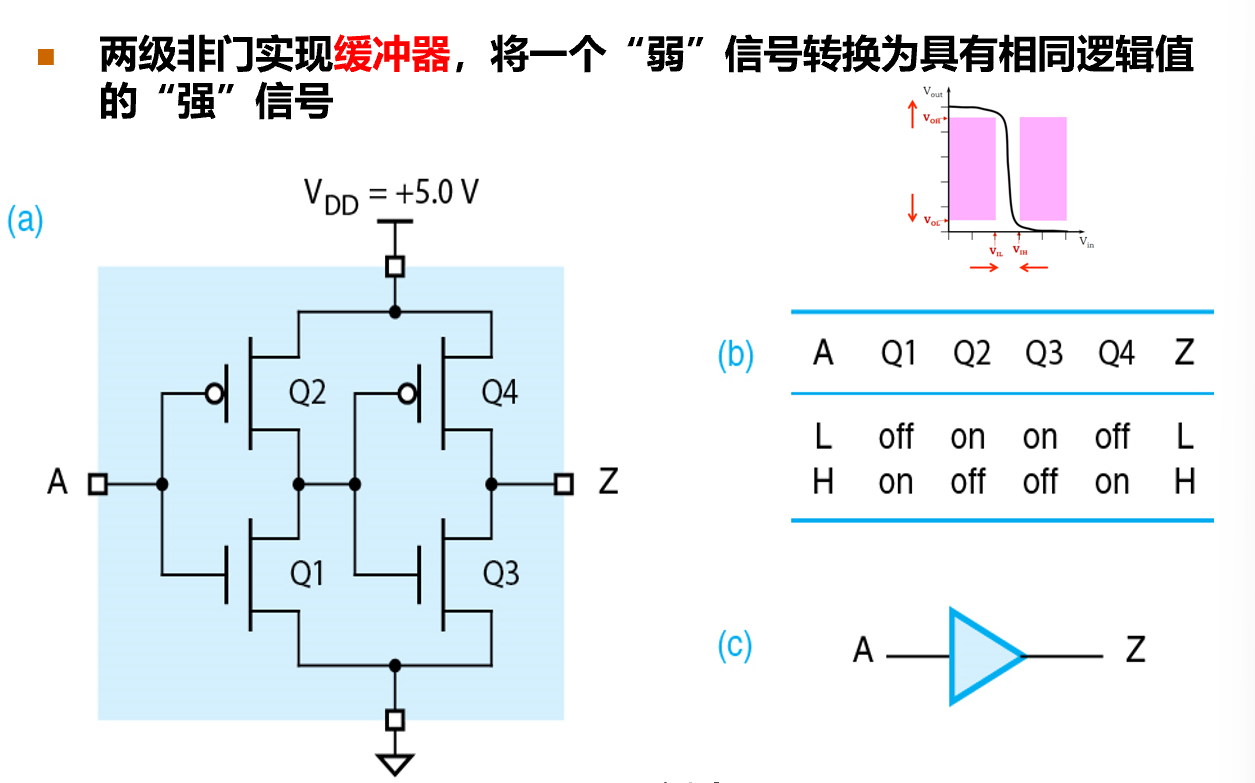
• 传输们

• 用于控制精体管的导通与截止，即逻辑开关，EN 为高态，则导通，否则不导通
• 
• 之所以使用一对cmos，是为了实现双向传输

电路电气特征

^e23c4e

• 转换时间：输入信号/输出信号从一种状态转换到另一种状态所需要的时间
• 上升时间：低态到高态
• 下降时间：高态到低态
• 
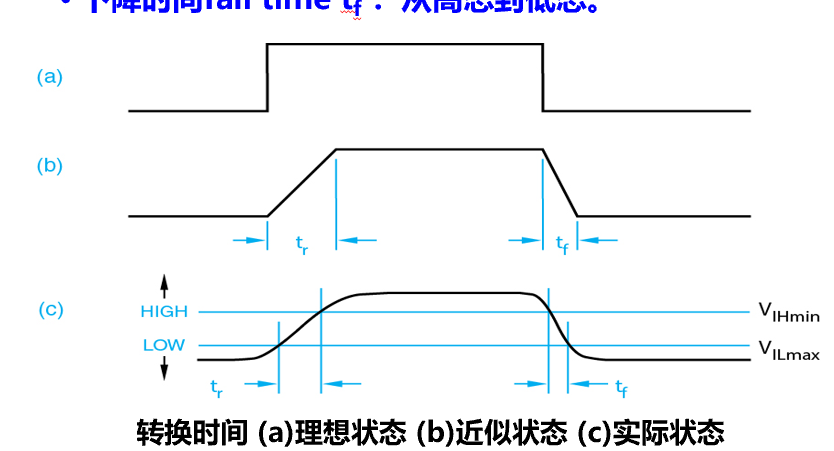
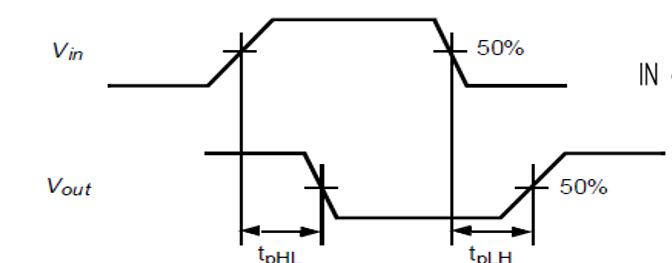
• 传播延迟：从输入信号变化到引起输出信号变化所需的时间
• \(t_{pHL}\)：输入变化引起相应输出从高到低变化的时间
• \(t_{pLH}\)：输入变化引起相应输出从低到高变化的时间
• 

• 信号通路：是指一个特定输入信号到逻辑元件的特定输出信号所经历的电器通路

• 数字电路在输出信号不变时的功率称为静态功率，常忽略

• 输出信号高低状态转换时的功率损耗称为动态功耗（主要）

布尔代数

逻辑运算

• 

• 

• 对偶定律：

• 对于原式 Y，将 · 和 + 以及 0 和 1 互换，得到对偶式 \(Y^D\)
• 若两个逻辑表达式相等，则它们的对偶式也相等
• 注意要操持运算次序不变（这可能需要添加括号）
  • 
• 
• 
• 
• 

逻辑函数

• 反映输入变量和输出变量之间逻辑关系的表达式\(F(x_1,\dots,x_n)\)
• 每个输入组合都有一个确定的输出值，n 个变量有 \(2^{2^n}\) 种不同的逻辑函数
  • 
  • 这样理解：有 n 个变量则一共有 \(2^n\) 种组合，每个组合可选 2 种输出，固 \(2^{2^{n}}\)
  • 如 2 个变量有 16 种，3 个变量有 256 种

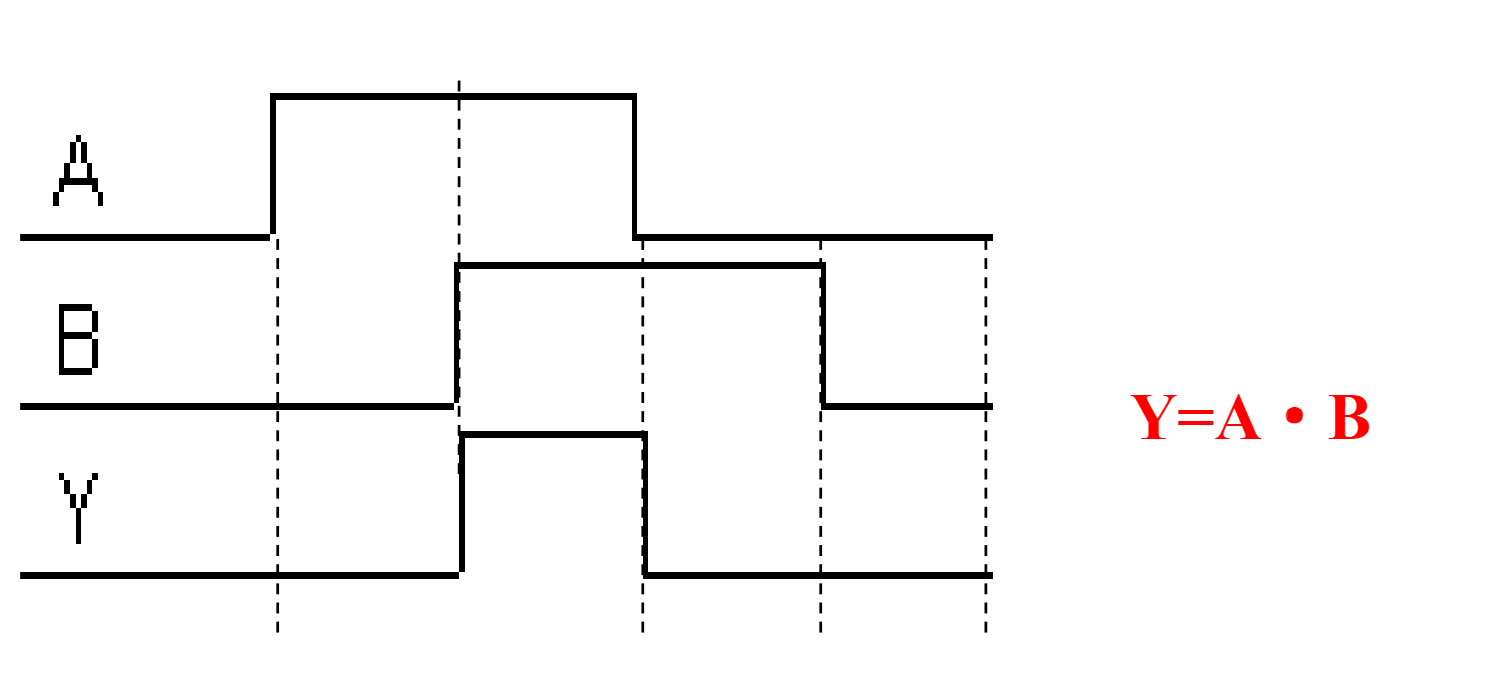
真值表与波形图

• n个变量的真值表有\(2^n\)行，通常按输入的字典序排列
• 波形图描绘输出对输入变化的响应，横轴表示时间，纵向表示逻辑值的大小，完整波形图要列出所有的输入组合和对应的输出
• 

标准范式表示

• 与-或 表达式（积之和）\(x·y+y·z\)
• 或-与 表达式 （和之积）\((x+y)·(y+z)\)
• 标准乘积和：每个逻辑变量出现且仅出现一次的乘积项，有\(2^n\)个
• 标准求和项同理
• 
• 标准乘积项也称为最小项，每个最小项对应真值表中一个输入组合，赋值该输入组合后，最小项的运算结果为1。记 \(m_{i}\)
• 标准求和项也称为最大项，每个最大项对应真值表中一个输入组合，赋值该输入组合后，最大项的运算结果为0。记 \(M_{i}\)
• i 是输入值使结果特殊的二进制 (作为最大/小项的编号)
• 有多项时可以记作 \(\sum m(0,6,7) \prod M(1,2,3)\)，称为标准和/最小项列表；标准积/最大项列表
• 两个列表之间可方便转换，只需对相应的编号集合求补即可
  • 
• 

逻辑函数的化简与变换

*代数法

• 利用布尔代数的公理、定理、定律等，消去逻辑表达式式中多余的乘积项或多余的因子，进行化简。

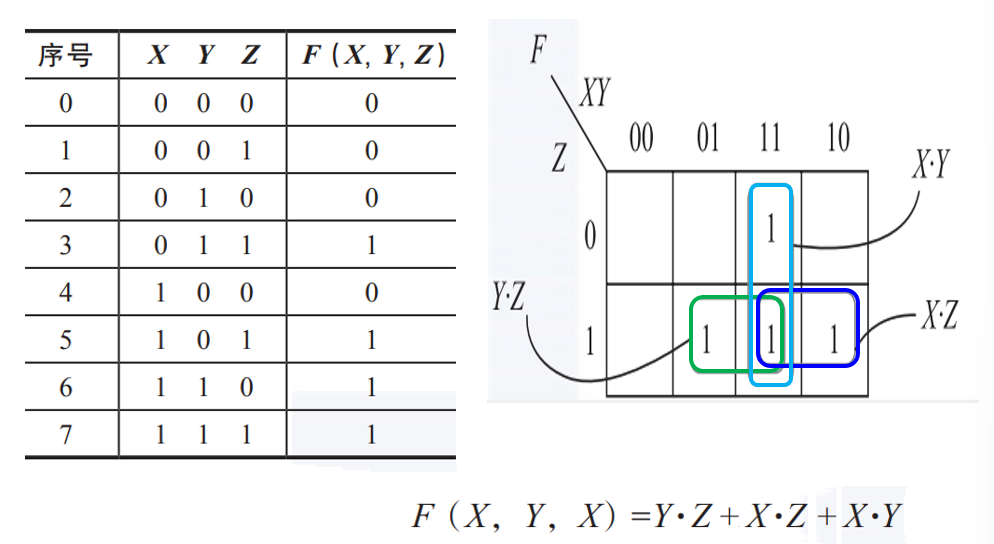
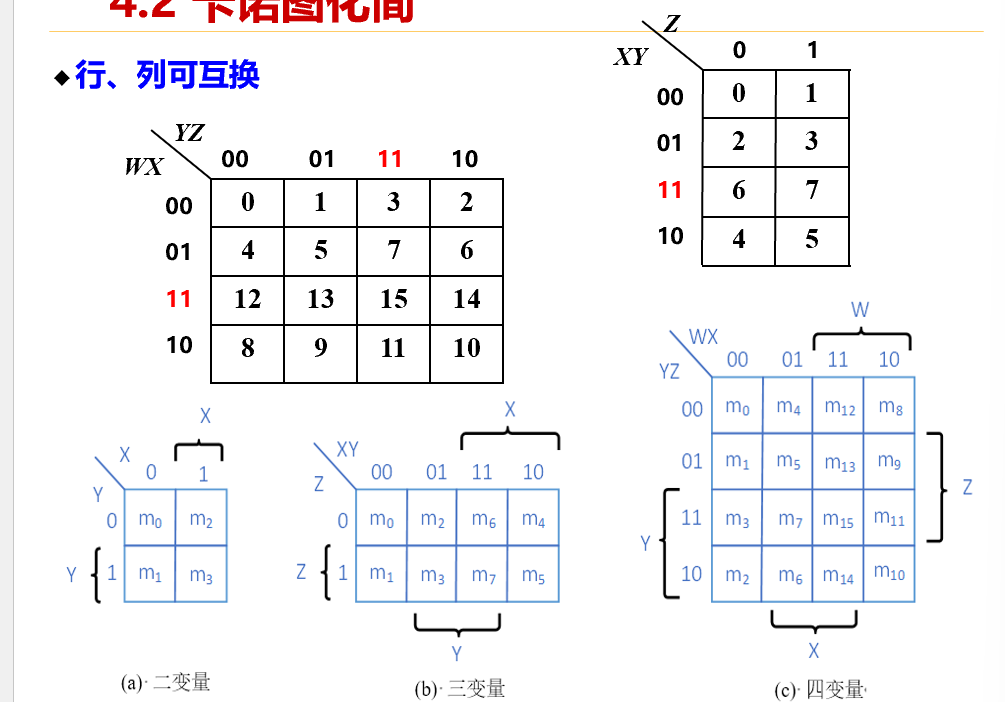
卡诺图法

• 真值表的图形化表示，把能化简的最小项通过相邻项合并的可视化方式标识出来。
• 行和列使用格雷码n ^ (n >> 1)即相邻项只有一位不同，由此相邻的格子之间有逻辑相邻性
• 行列可以互换
• 格子中为输入组合的输出（行二进制+列二进制的拼接）（横纵坐标项表示输入）
• 

难点

卡诺图化简

• 以结果为积之和为例：（由于积和可以转换，因此通常直接转化为积之和再处理）

• 向图中填入输入组合对应的真值表的输出值（0/1）

• 
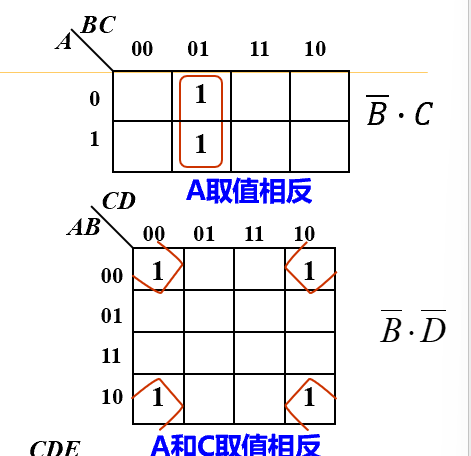
• 若两个单元（左右、上下、收尾）相邻为1（这两项有且仅有一个变量取值相反），可以消去具有不同值的那个变量，如\(x·y+x·\overline{y}=x\)
• 相邻\(2^i\)个单元可以合并为一个乘积项，消去i个变量，保留不发生变化的
  • 
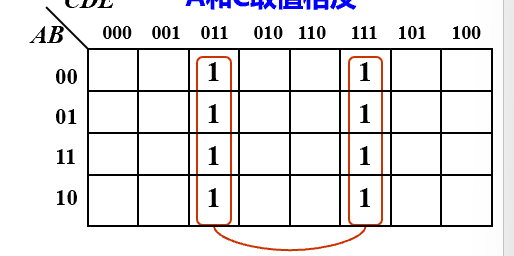
  • 八连：abc，结果DE

• 若有多组1，则相加，每一圈对应一个积，加起来就是结果

  • 

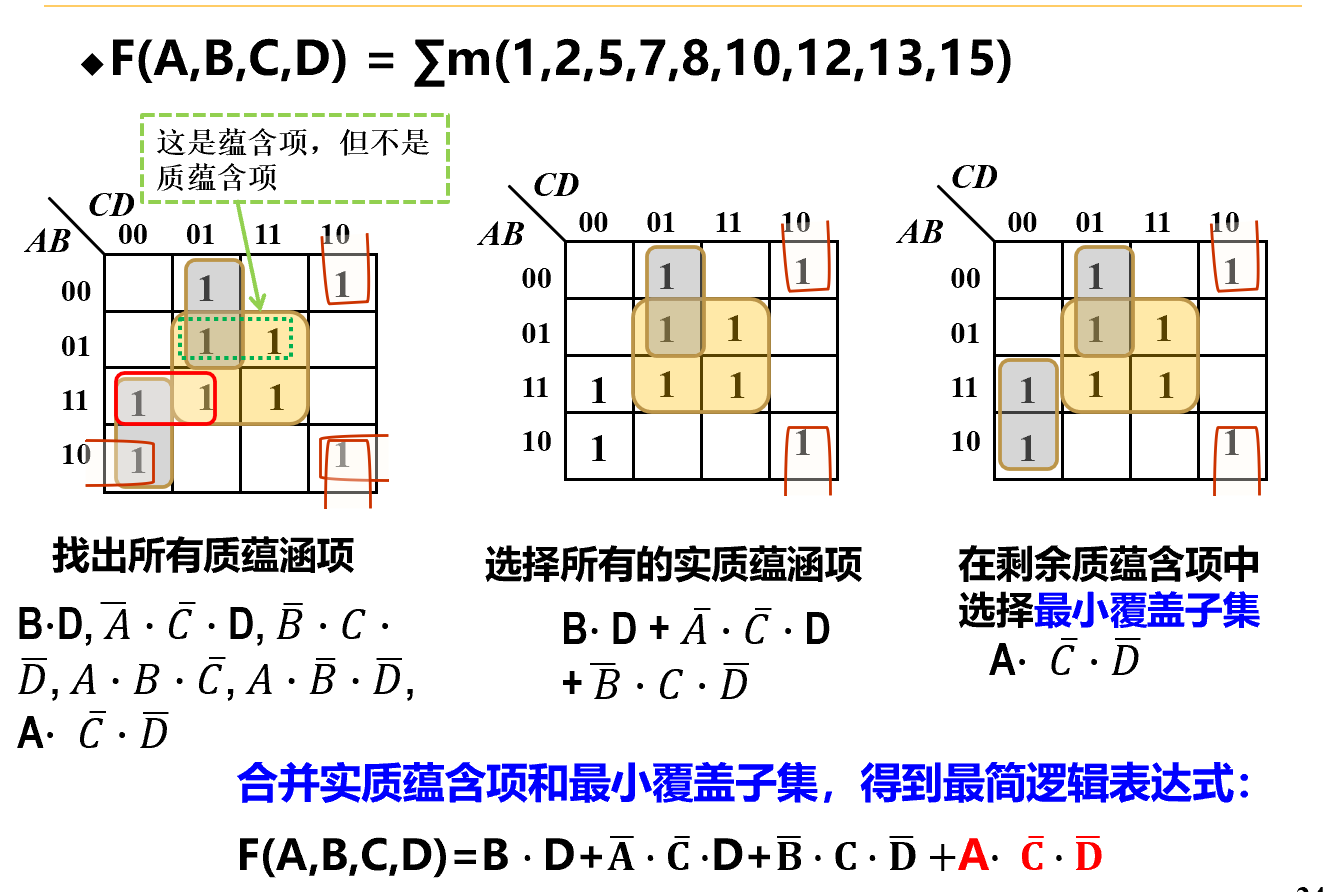
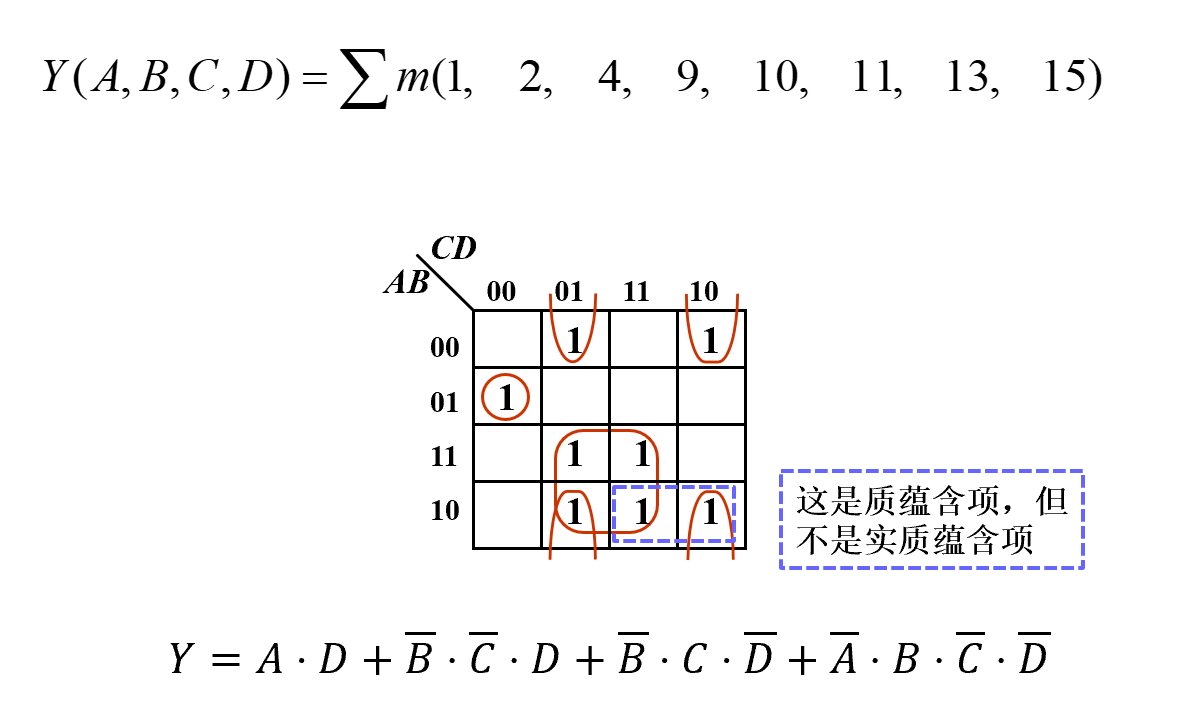
• 蕴涵项是一个乘积项，覆盖了逻辑函数的1个或多个最小项。

• 
• 质蕴涵项：不能被逻辑函数的其它蕴涵项所覆盖的蕴涵项。
• 
• 实质蕴涵项：覆盖的最小项中至少有一个最小项是没有被其他质蕴涵项所覆盖的质蕴涵项。
• 

• 质蕴涵项覆盖的最小项越多（即卡诺圈越大）越可能是实质蕴涵项

  • 即使是重叠的圈也要选择尽可能大的，这样变量数较少

• 若逻辑函数的所有最小项都被一组质蕴涵项所覆盖，则该组质蕴涵项称为函数的一个覆盖，它一定包含所有的实质蕴涵项。

• 
• 最小覆盖：包含质蕴涵项数最少，并且质蕴涵项中的变量总数也是最少。

• 最小覆盖对应的逻辑表达式称为：最简逻辑表达式

• 

• 

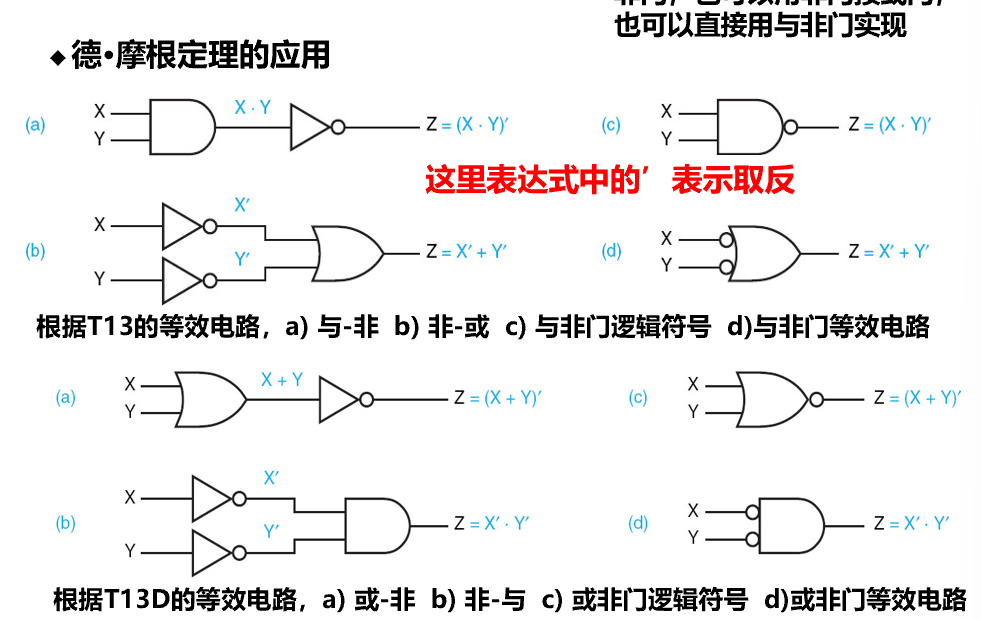
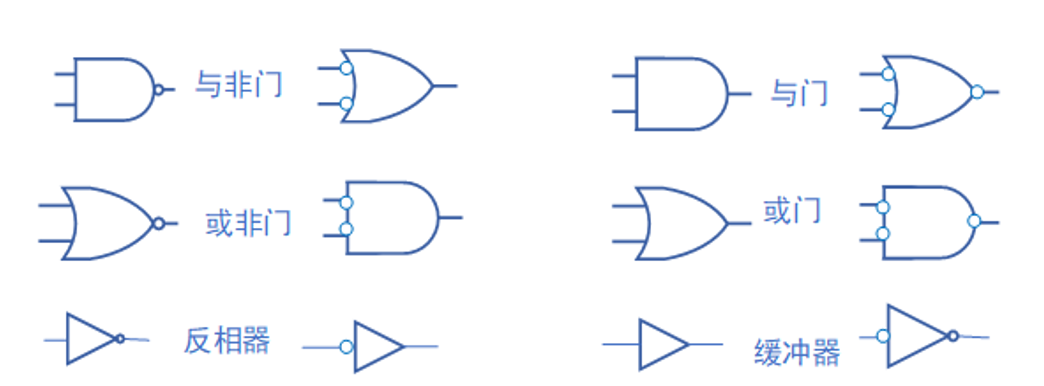
等效逻辑符号表示

• 

• 在数字电路中，与非门和或非门通常比与门和或门的执行速度快。

• 将“与-或”表达式整体两次取反，然后运用德摩根定律转换下层的取反运算，就可以得到“与非-与非”表达式
• 
• 
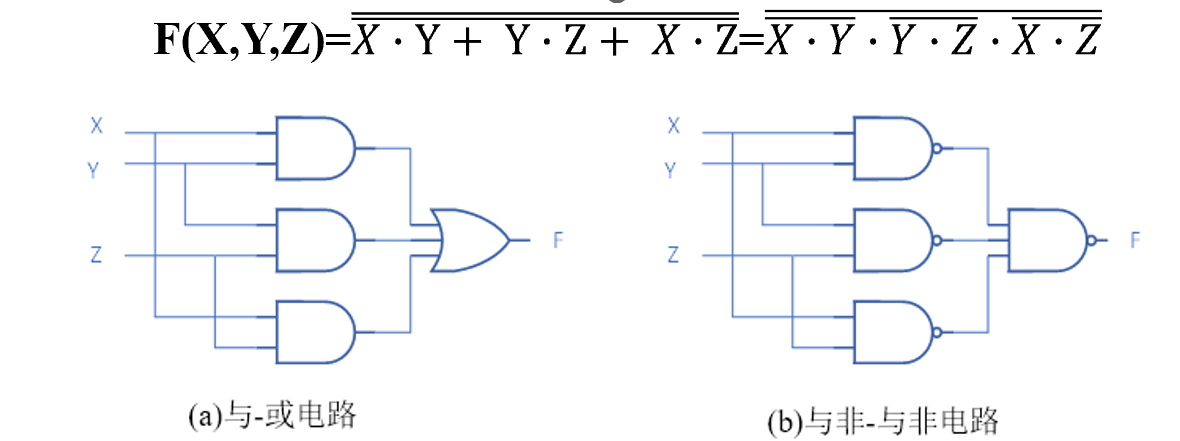
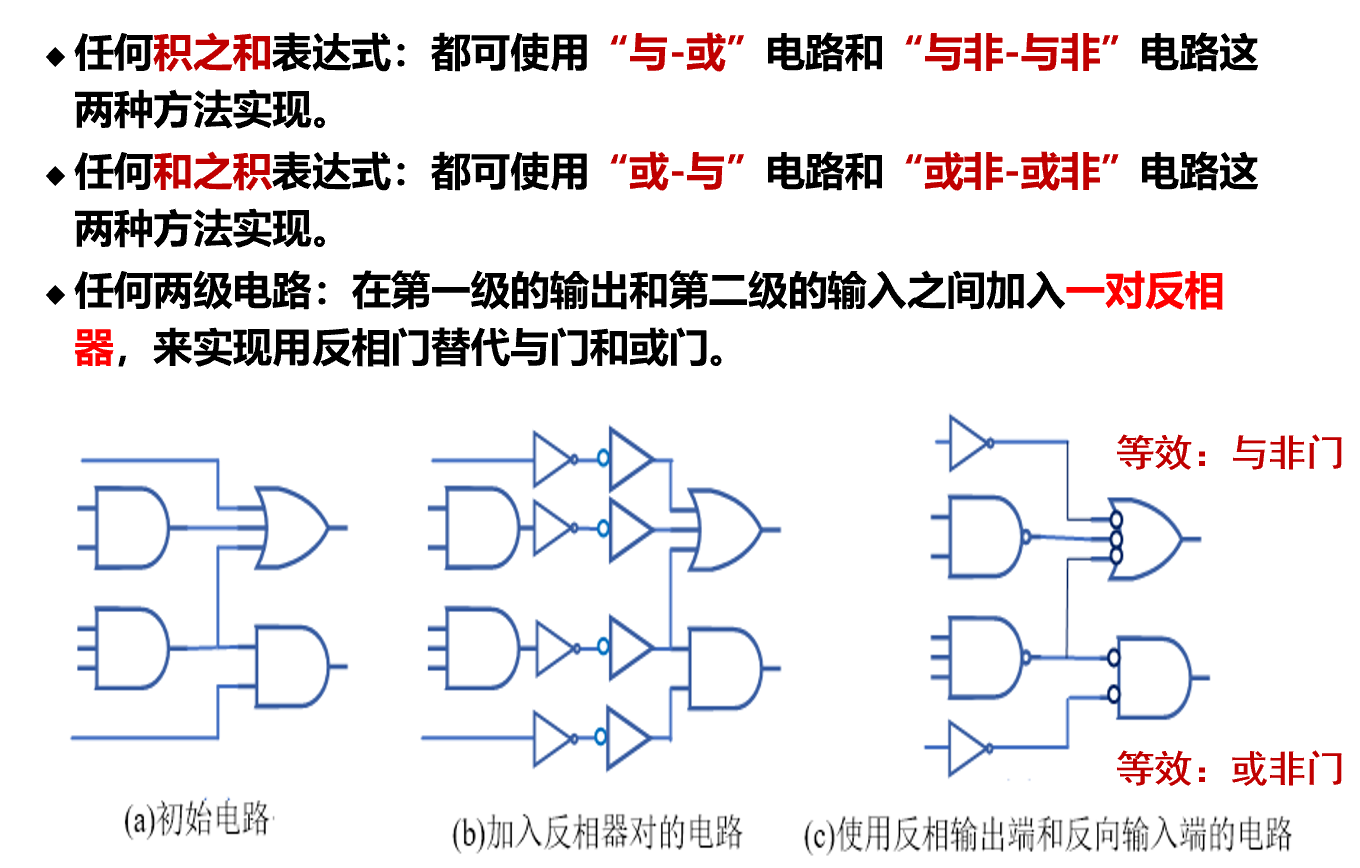
• 第一级直接头部加非，第二集尾部加非等价于头部加非并转化类型，导致前后变成相同类型