定点数运算：
算术运算：
- 带符号整数：取负/符号扩展/加减乘除/算术移位
- 无符号整数：0扩展/加减乘除
逻辑运算：
- 与或非
- 逻辑左右移
浮点数运算：
加减乘除
所有运算都可以由ALU或加法器+移位器+多路选择器+控制逻辑实现

基本运算部件¶

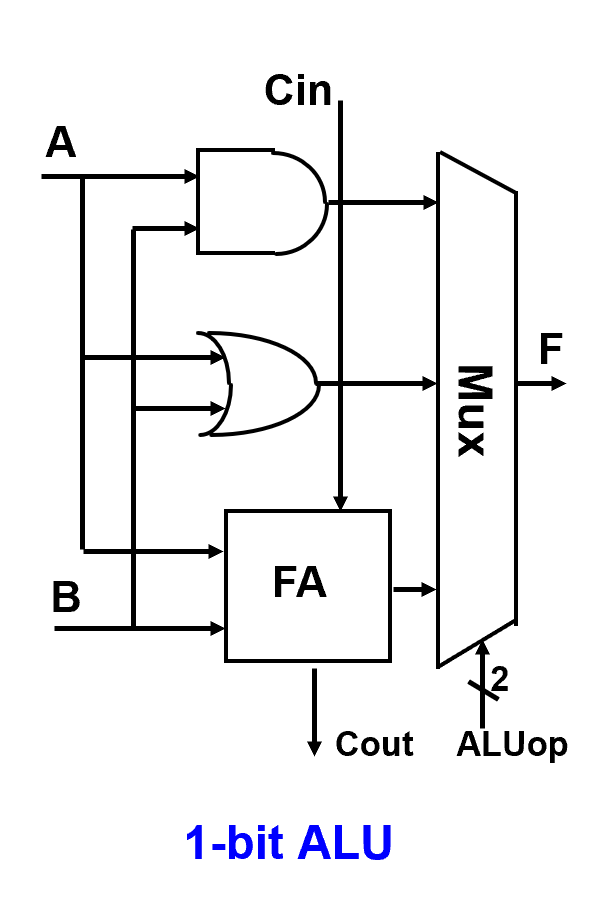
算数逻辑部件ALU¶

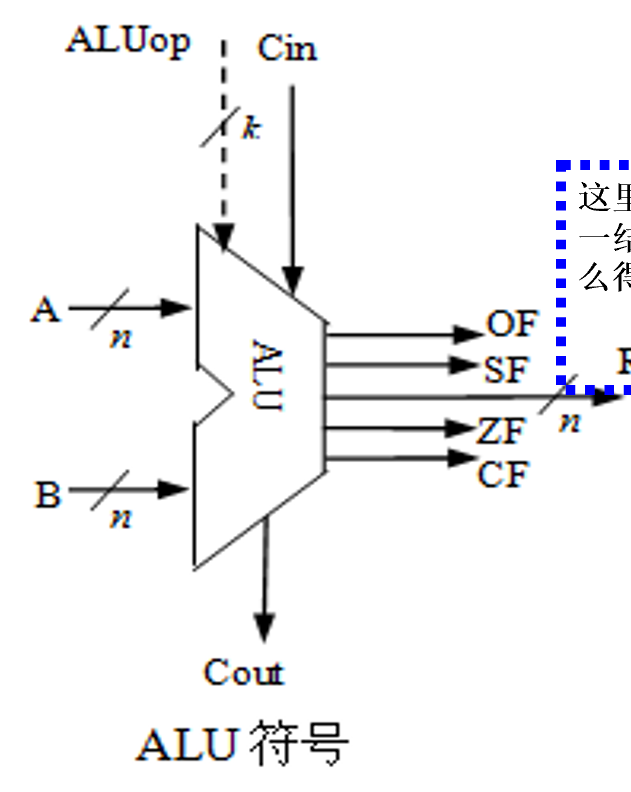
操作控制端ALUop决定ALU进行操作的种类数目（\(2^k\)）

串行进位加法器¶

从低位开始进行串行计算
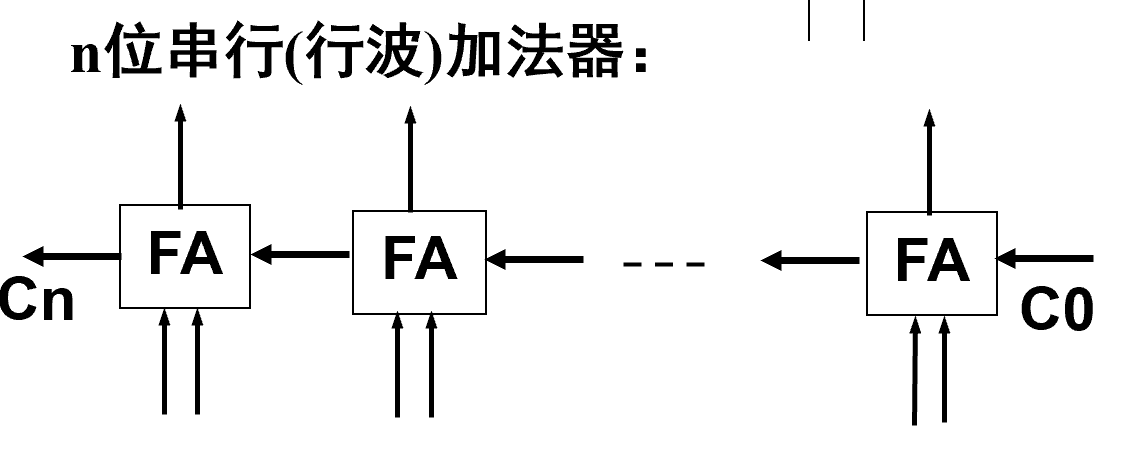
从 \(C_0\) 到 \(C_n\) 会产生约 \(2n\) 级门延迟
延迟大，速度慢

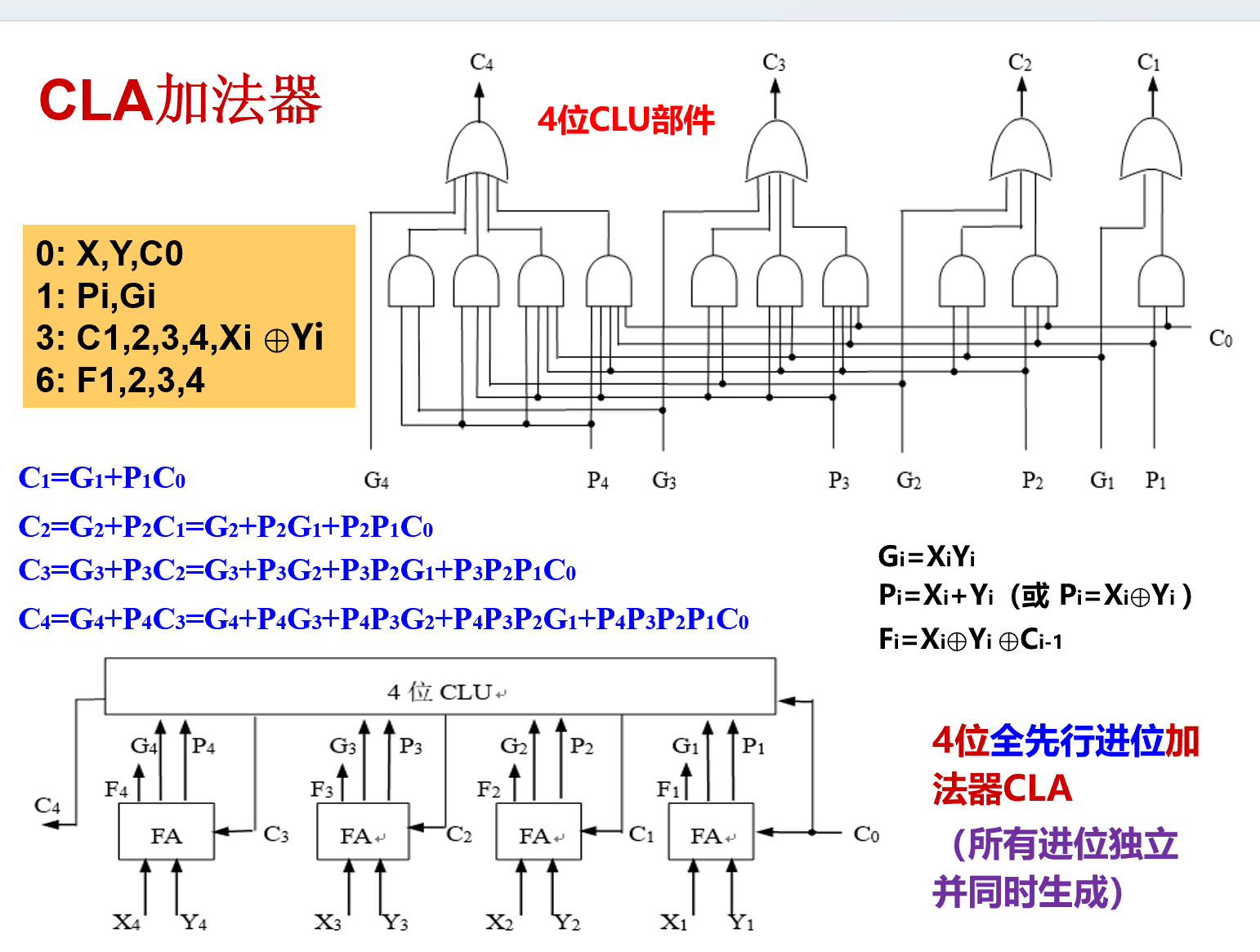
并行进位加法器CLA¶

采用先行进位的方式，减少电路延迟
辅助函数
进位生成函数\(G_i=A_iB_i\)
- 两个数都是1，则该位产生进位
进位传递函数 \(P_i=A_i+B_i\)
- 两个数至少有一个 1，则该位有一个进位要传递
全加逻辑方程：\(\displaylines{F_i=A_i\bigoplus B_i\bigoplus C_{i-1} \\ C_i=G_i+P_iC_{i-1}(i=1,\dots,n)}\)
进位条件：产生进位/上一位产生进位并且本位可以传递进位
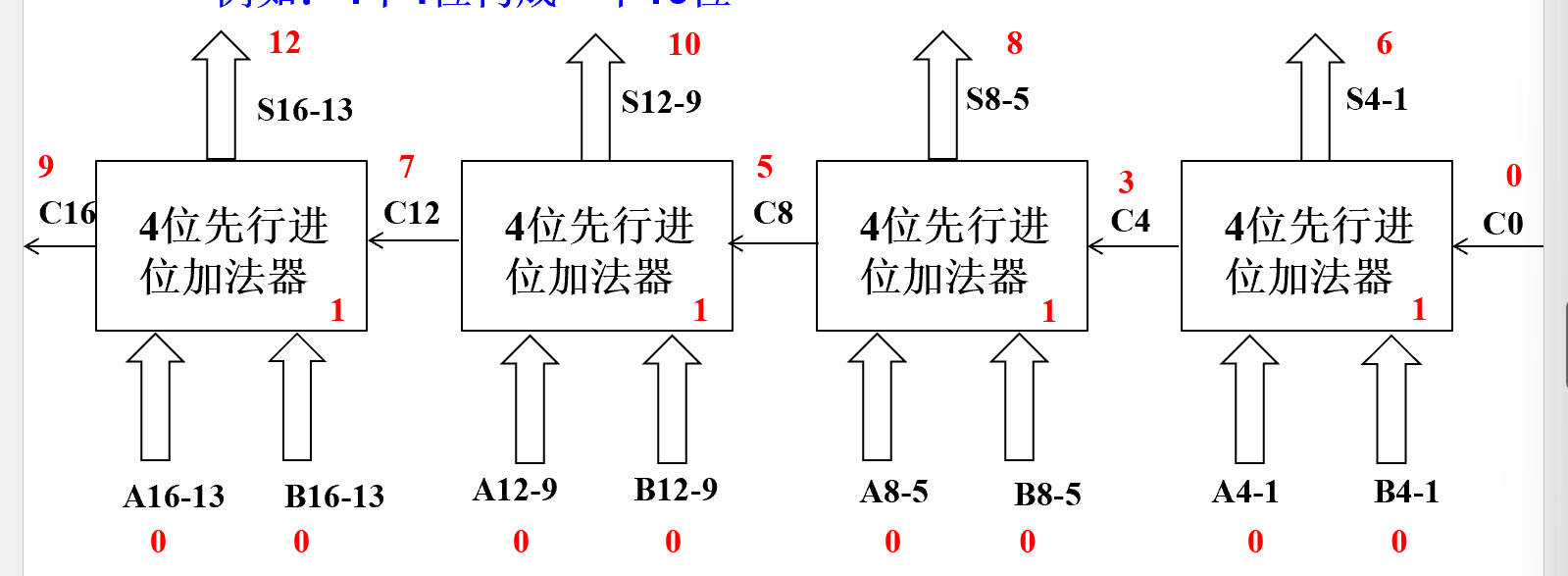
位数较多时逻辑方程很长，成本高。可以使用分组，组内并行组间串行

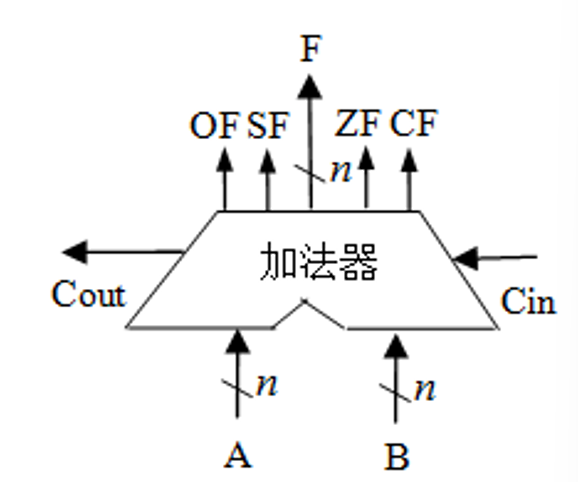
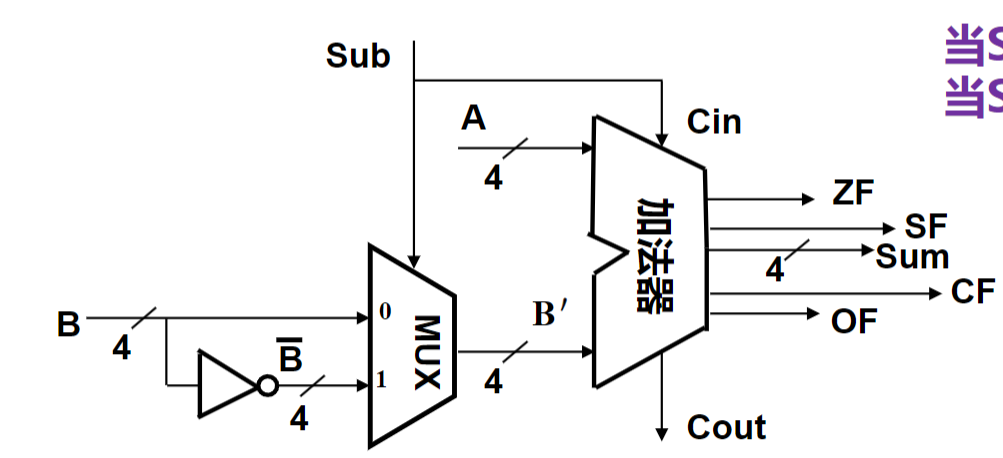
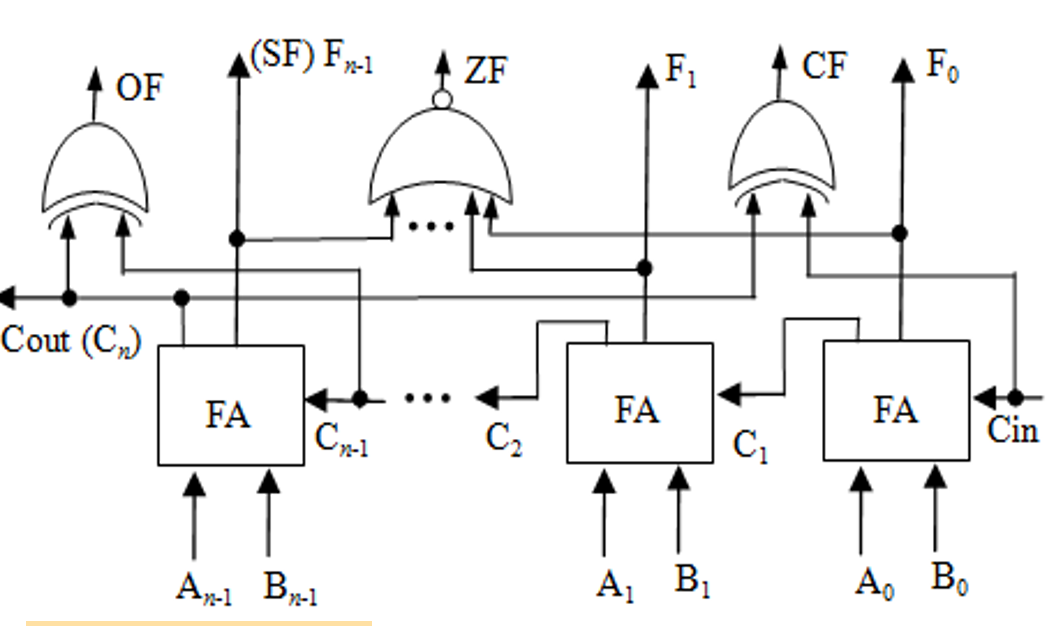
n位带标志加法器¶

难点¶

标志位
（有符号）溢出标志位\(OF=C_n\bigoplus C_{n-1}\)
符号标志\(SF=F_{n-1}\)
零标志位\(ZF=1 \ iff \ F=0\)
（无符号）进位、借位标志\(CF=Cout\bigoplus Cin\)
- \(Cin=sub=1\)（这里这个 1 的作用就是减法时的"各位取反，末位加一"）

定点数运算¶

加减运算¶

补码运算规律
\[ \displaylines{ [X]_补=2^n+X \ (-2^n<=X<2^n,mod \ 2^n) \\ [-X]_补=\overline{[X]_补}+1\\ [X+Y]_补=[X]_补+[Y]_补(mod \ 2^n)\\ [X-Y]_补=[X]_补+[-Y]_补(mod \ 2^n)\\ } \]
有无符号的差别仅限于使用标志位解释结果的方式不同
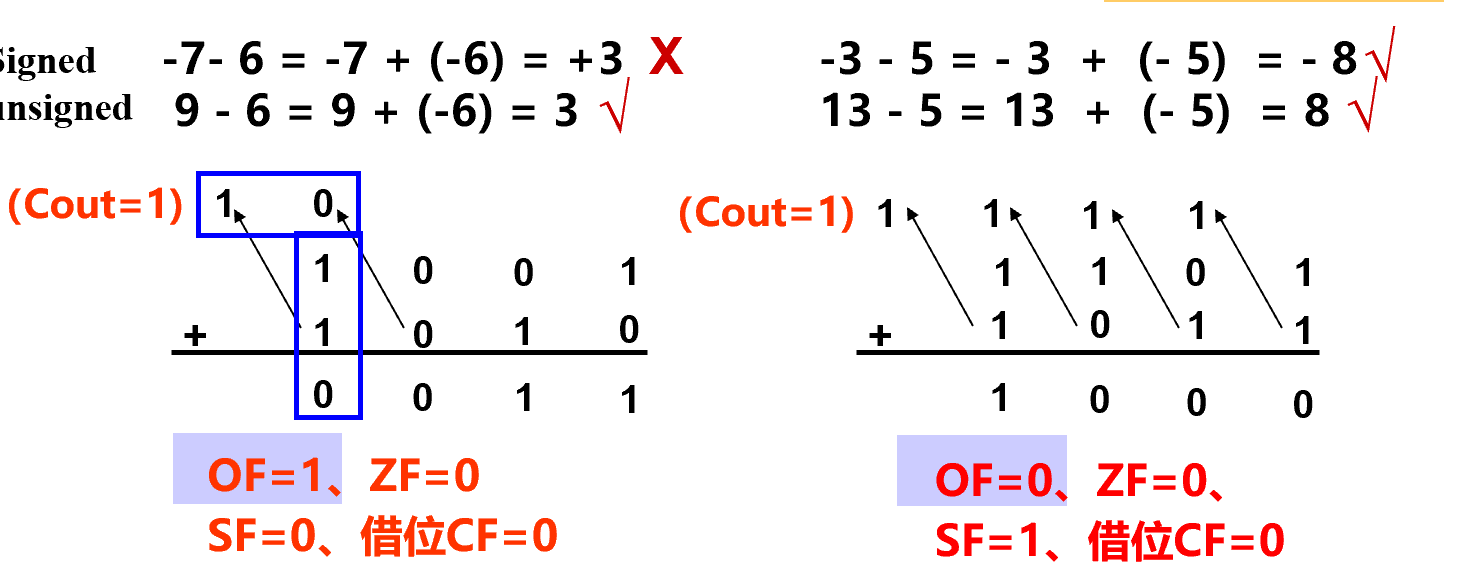
有符号做减法 \(OF=SF\) 表示大于
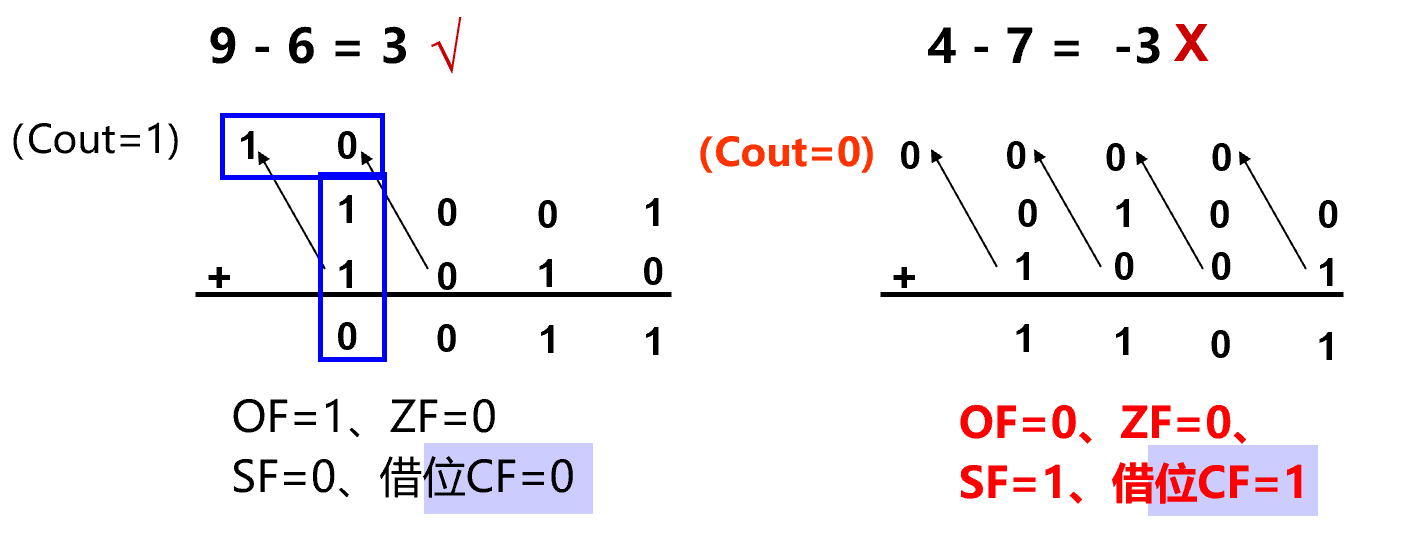
无符号溢出判断：CF=1（减法时代表差为负数，即产生了借位）（加法时Cin=0，所以CF=1代表产生了进位，也就是加法溢出了）
无符号 \(CF=0\) 表示大于
溢出分类
减法
加法

乘法运算¶

使用加法+移位实现
由于源码运算只用于浮点数尾数计算，因此约定数据：
\([X]_原=x_0.x_1...x_n \ \ [Y]_原=y_0.y_1...y_n\)
数值部分的下标从1开始

无符号乘法¶

假定 \([X]_{原}=x_0.x_{1}\dots x_{n} \ \ \ y_{原}=y_{0}.y_{1}\dots y_{n}\)
\(P_i=2^{-1}(Xy_i+P_{i-1})\)
即相加+右移
硬件实现
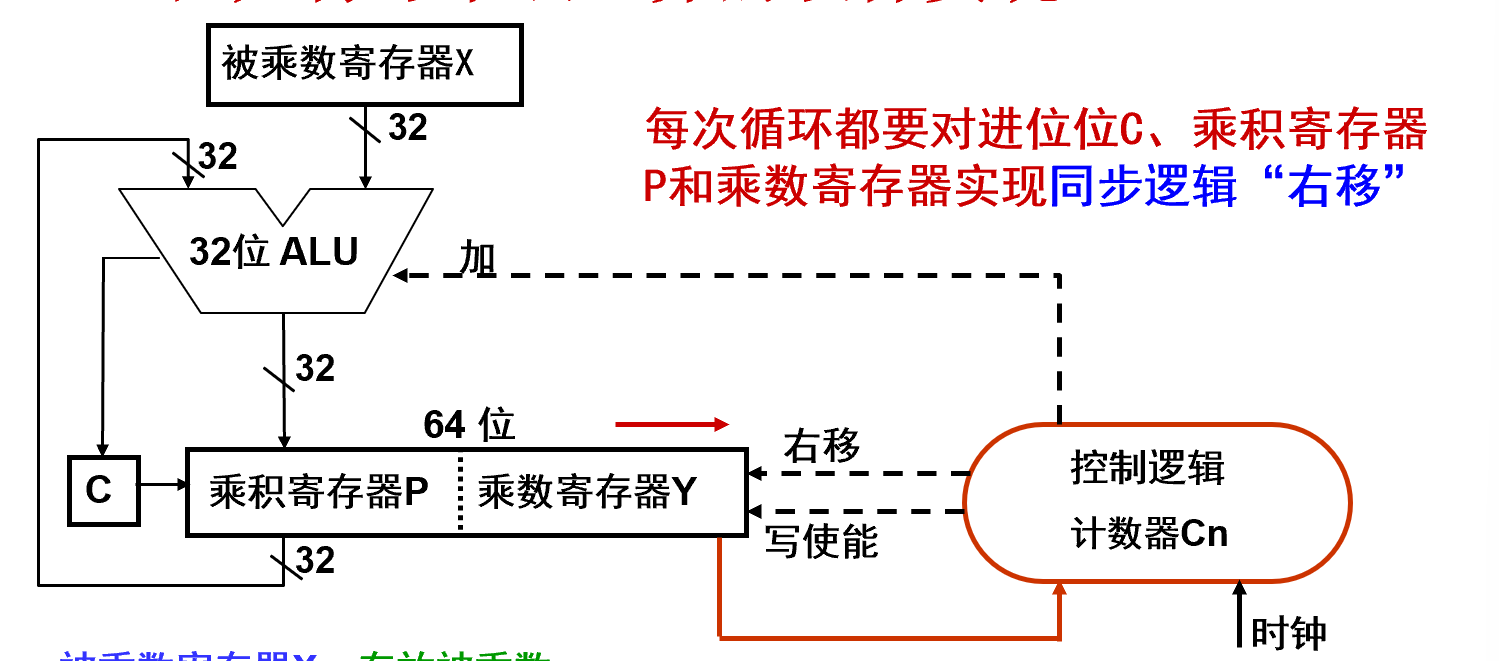
被乘数寄存器X：存放被乘数
乘积寄存器P：开始置初始部分积P0 = 0；结束时，存放的是64位乘积的高32位
乘数寄存器Y：开始时置乘数；结束时，存放的是64位乘积的低32位
进位触发器C：保存加法器的进位信号（进位信号在右移时要移入）
循环次数计数器Cn：存放循环次数。初值32，每循环一次，Cn减1，Cn=0时结束
ALU：乘法核心部件。在控制逻辑控制下，对P和X的内容“加”，在“写使能”控制下运算结果被送回P，进位位在C中

难点¶

有符号乘法¶

原码乘法¶

用于浮点数尾数乘运算，符号与数值分开处理
一位乘法：每次只取乘数的一位判断，需 n 次循环，速度慢。
两位乘法：每次取乘数两位判断，只需 n/2次循环，快一倍。
原码两位乘法
使用T触发器向下一级传递信息，告知是否在下一级+x，因为+x，+2x很方便，但是+3x很慢
由于x有加有减，使用补码算术右移。
使用三位符号位，因为若用模4补码（2位），中间涉及+2X会导致P和Y同时右移2位时，得到的P3是负数，就错了。（1位就更不行，2x直接溢出）
- 如00 111+111*2=00 111 + 01 110= 10 101，再右移变成了负数！
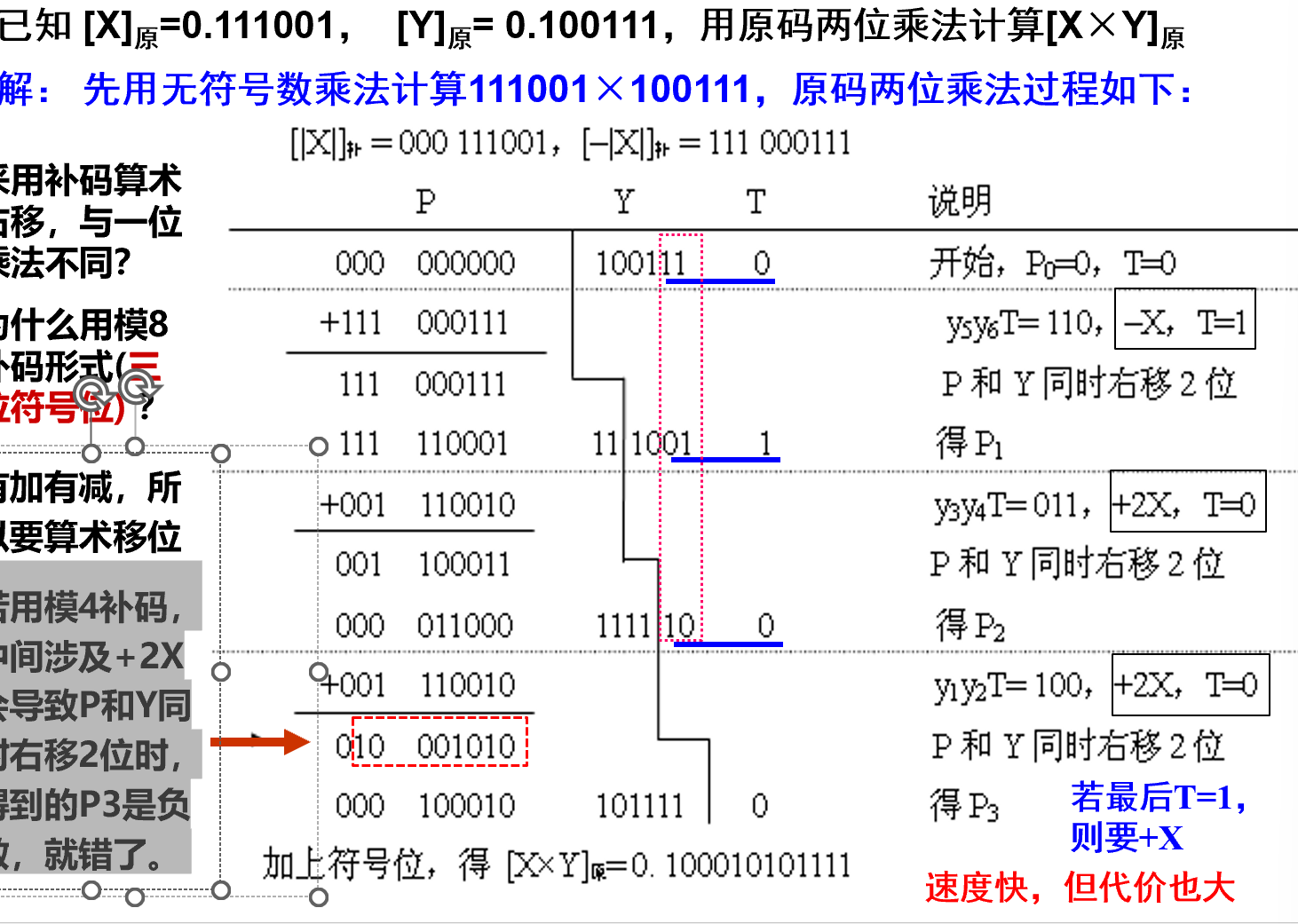
- 使用3(符号位)+len(x/y)*2+1(T)

补码乘法（booth）¶

用于带符号整数的乘法运算，因为\([x*y]_补!=[x]_补*[y]_补\)
补码的部分积公式\([P_i]_补=[2^{-1}([P_{i-1}]_补+(y_{i-1}-y_i)\cdot x)]\)
下标从低位到高位递增，\(y_{-1}=0\)

- 先把xy都转化为整数计算，最后看是否需要转化为负数，即对符号位单独考虑 - 注意移位使用算数右移 - 每一位可以分为：+-x以及右移两个过程 - 不用使用类似原码乘法的C位缓存进位

补码两位乘法

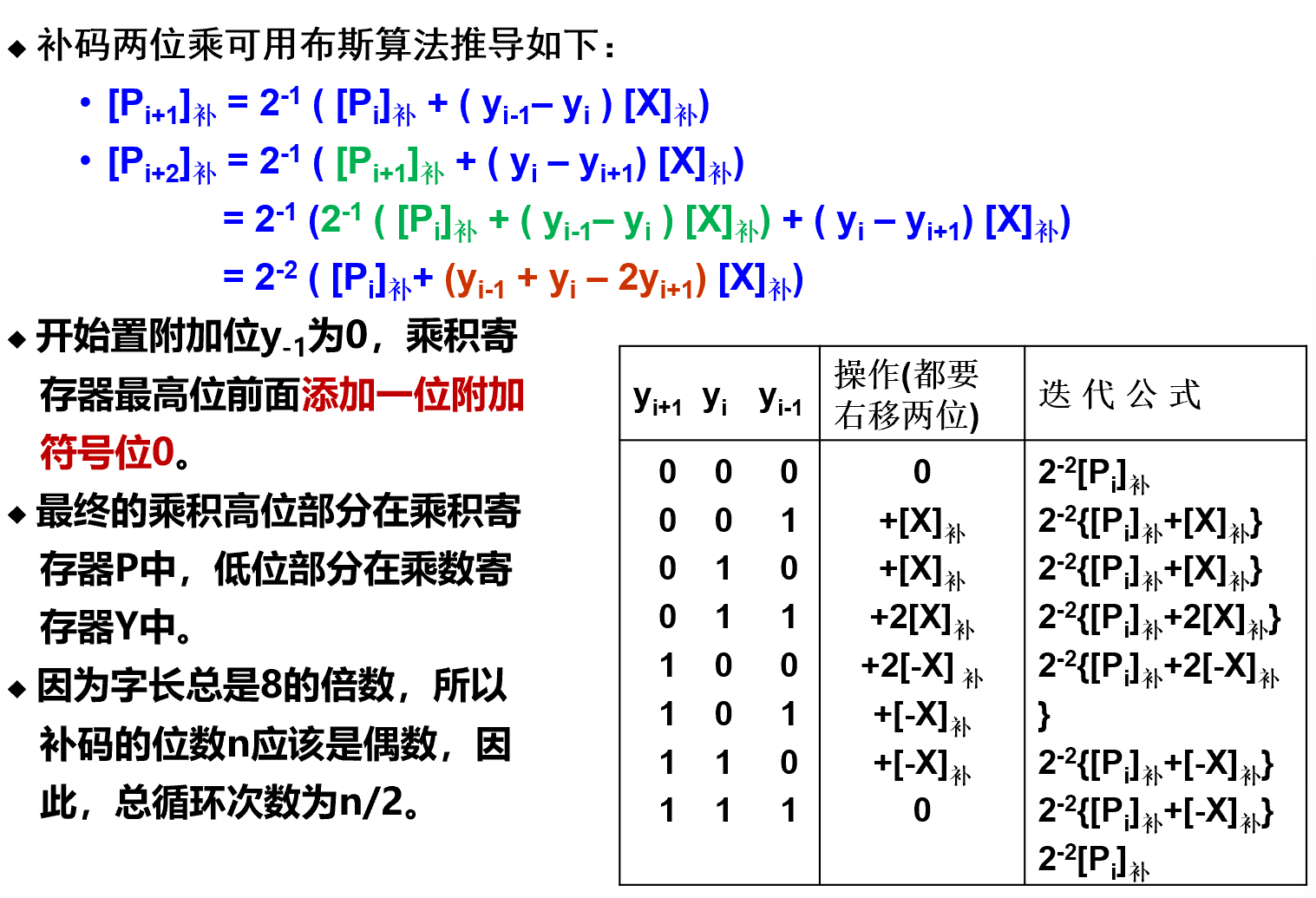
补充¶

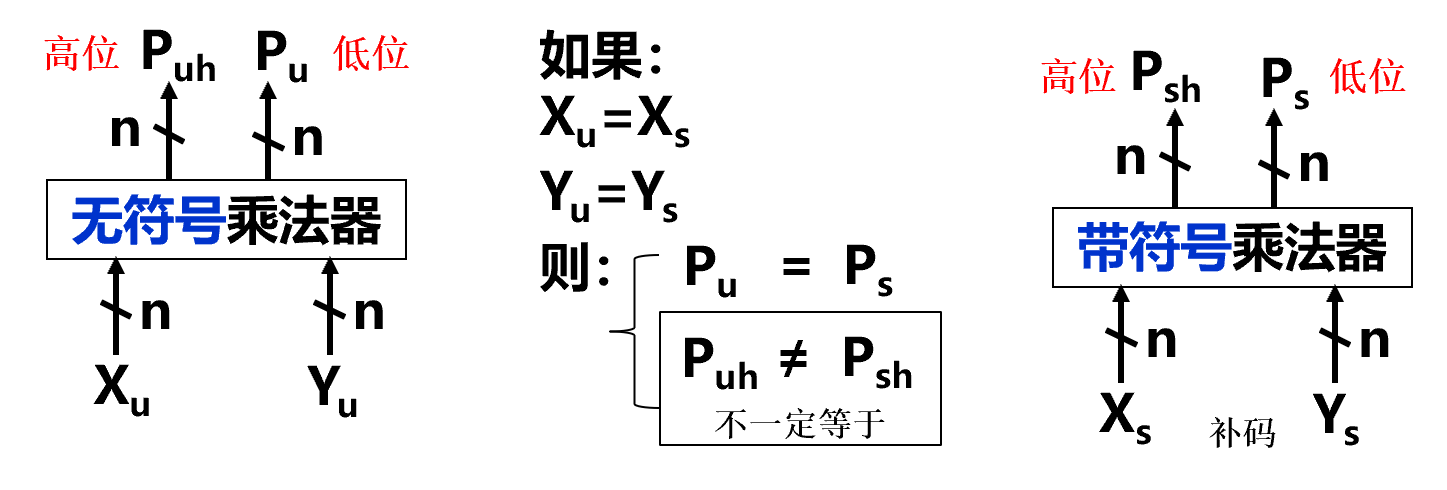
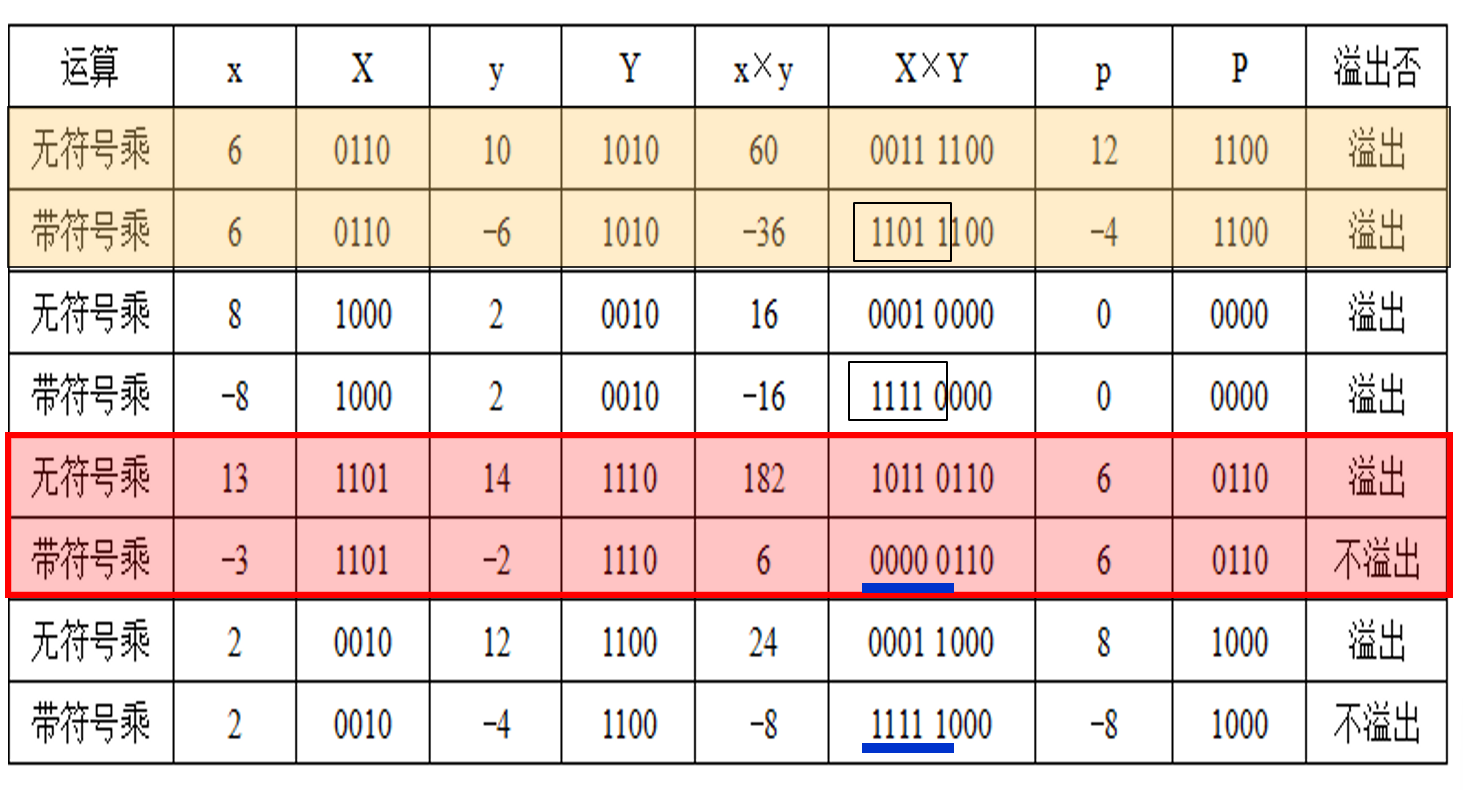
乘法结果的位数是乘数和被乘数的二倍，对于无符号乘法和有符号乘法低位是完全一致的。可以使用高位判断是否（从低位到高位）溢出
仅保留低位时使用高位判断是否发生溢出
无符号：全0则不溢出
有符号：高位全部等于低位最高位

*除法运算¶

无符号除法¶

进行除法前的判断：由软件/硬件进行
被除数=0，除数!=0或被除数的绝对值小于除数的绝对值则商为0
被除数!=0，除数=0则发生除数为0异常
被除数=0，除数=0则返回NaN
被除数和除数均！=0才进一步进行除法运算
通过被除数（中间余数）减除数得到每一位商（够减为1）
基本操作为减法（加法实现）和移位，与乘法用同一套硬件
定点无符号数相除前要在被除数的高位添加n个0，定点小数则在低位添加
即被除数被扩展到2n位
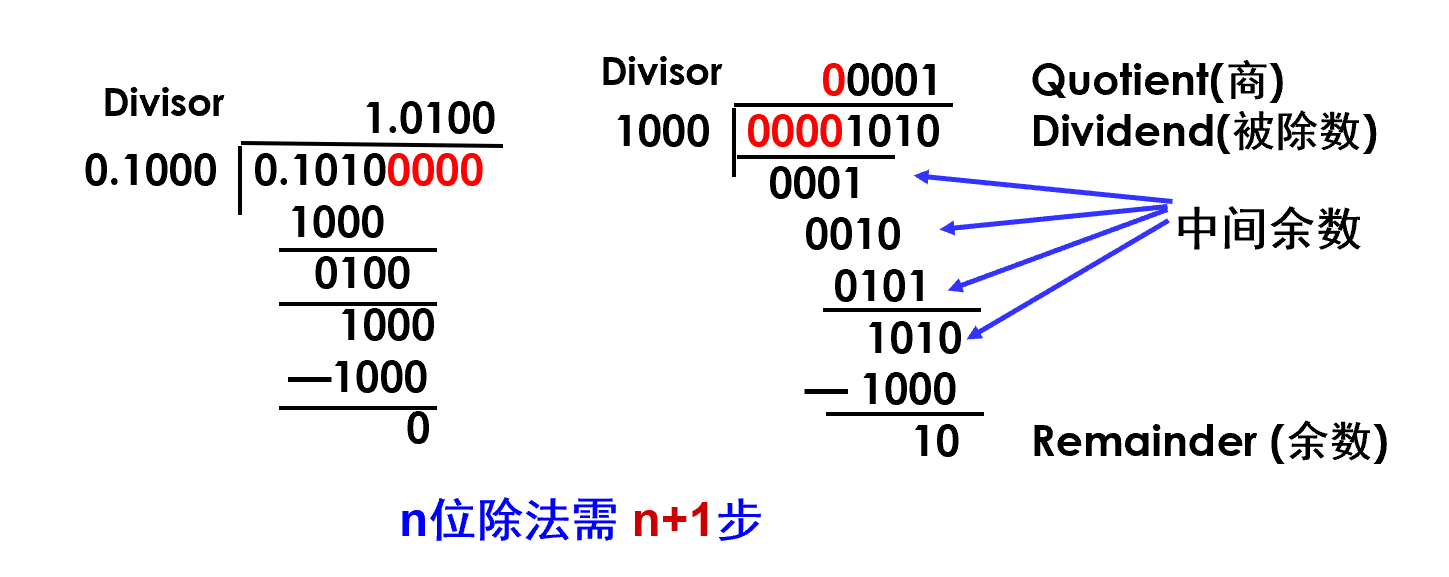
若第一次试商(第n+1位)商为1，则说明结果不能使用n位无符号整数表示，即会发生溢出
\(1111 \ 1111/1111=1 \ 0001\)
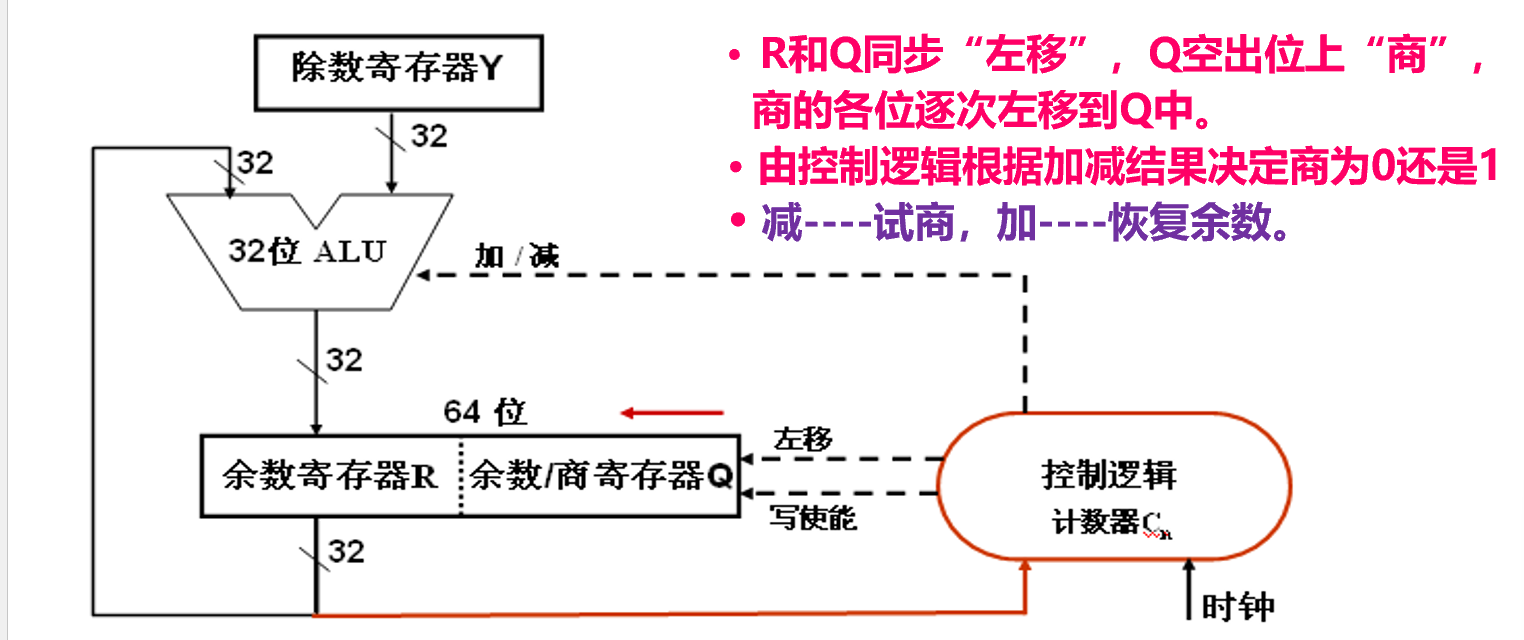
除数寄存器Y：存放除数。
余数寄存器R：初始时高位部分为高32位被除数；结束时是余数。
余数/商寄存器Q：初始时为低32位被除数；结束时是32位商。
循环次数计数器Cn：存放循环次数。初值是32（不包括第一次试商），每循环（移位）一次，Cn减1，当Cn=0时，除法运算结束。
ALU：除法核心部件。在控制逻辑控制下，对于寄存器R和Y的内容进行“加/减”运算，在“写使能”控制下运算结果被送回寄存器R。
- 加减是因为需要“试减”，即比大小，看能不能直接间减
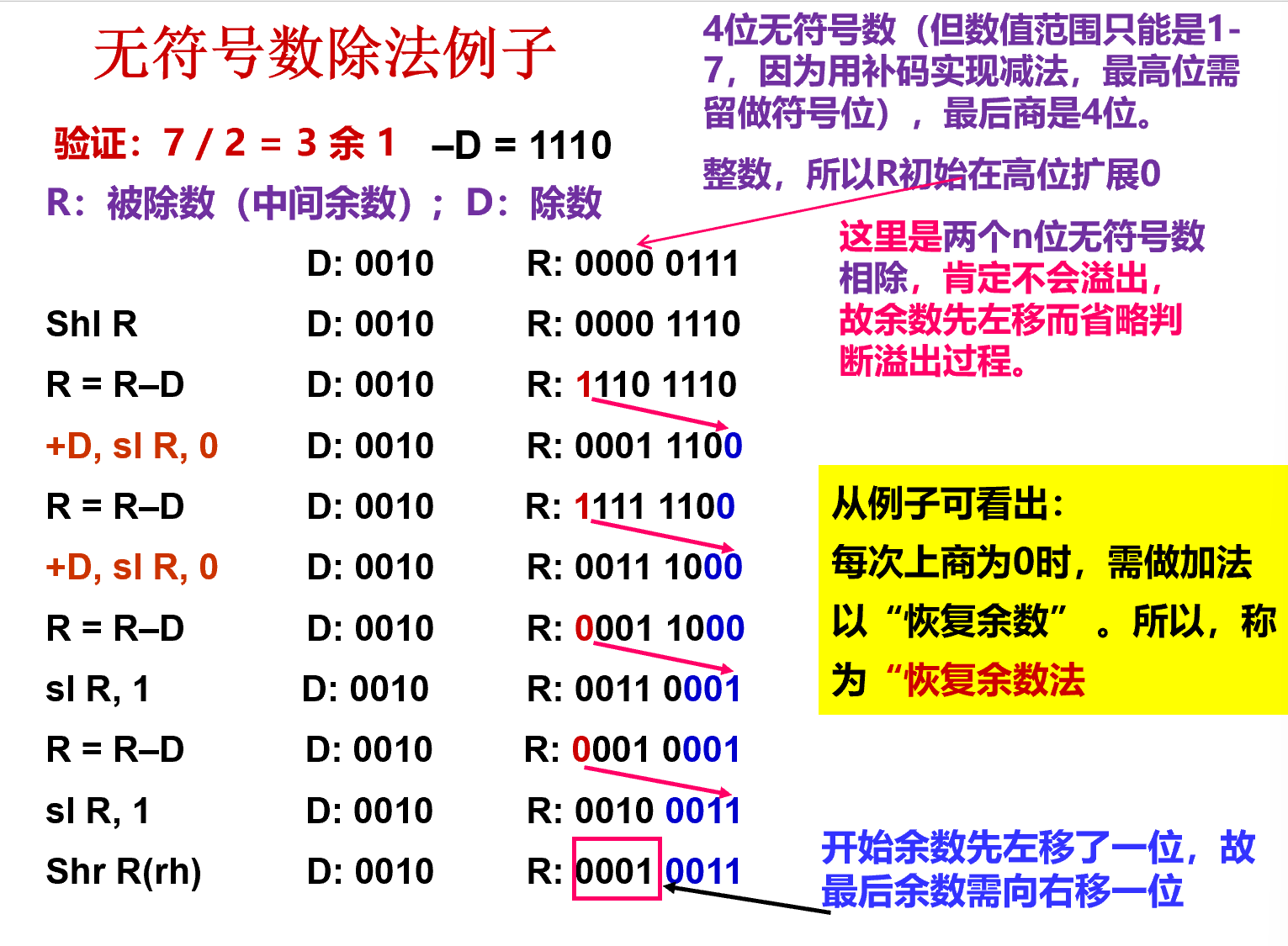
恢复余数法的试除后如果最高位为1则说明要恢复（变为负数了，不该减！），即下一步加回来（现恢复再左移），为0则表示可以减，如果可以除则下次左移移入1，否则移入0。
实际上，商有n+1位，但是在高位中的那一位应该是0（否则会发生溢出）,即第一位不用于结果，只用于判断是否发生溢出
余数是高位部分的前n-1位，因此最终还要右移一次
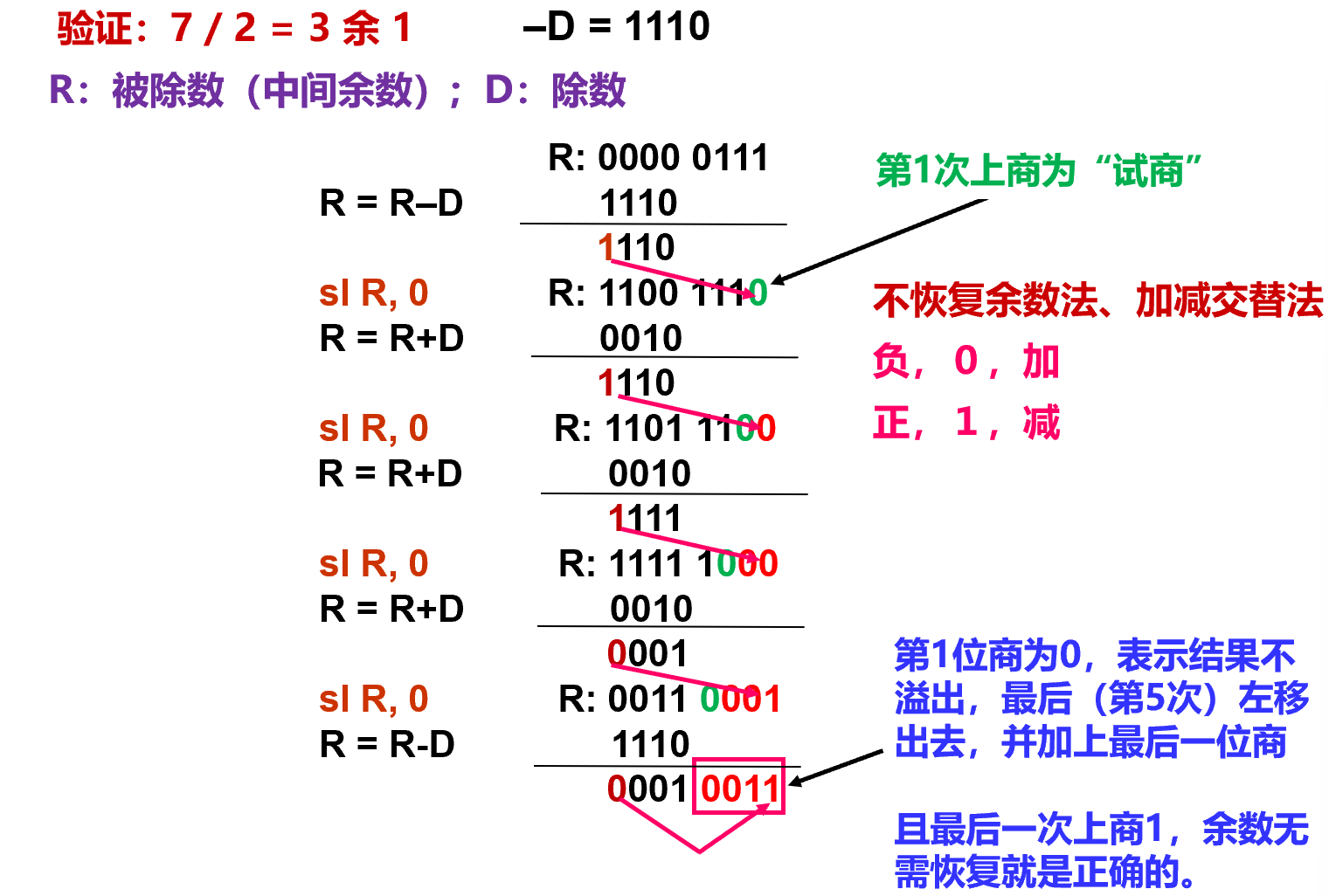
加减交替法（不恢复余数除法）
\(R_i=2R_{i-1}-D\)为第i次中间余数（D为除数）
下一次的加减是由上一次决定的，负（1开头）上0下次加是联动的
注意：最后一次上商为“0”的话，需要“纠余”处理，即把试商时被减掉的除数加回去，恢复真正的余数。（为1则不需要）
- 要注意的是，在左移之前的基础上加
- 如5/2可以得到11110001，此时还要进行最后一次计算
- 易知为11100010，因为最后一位加了0，所以进行纠正，因该加上0010（2），即1111+0010=0001（不是用0111）

有符号除法¶

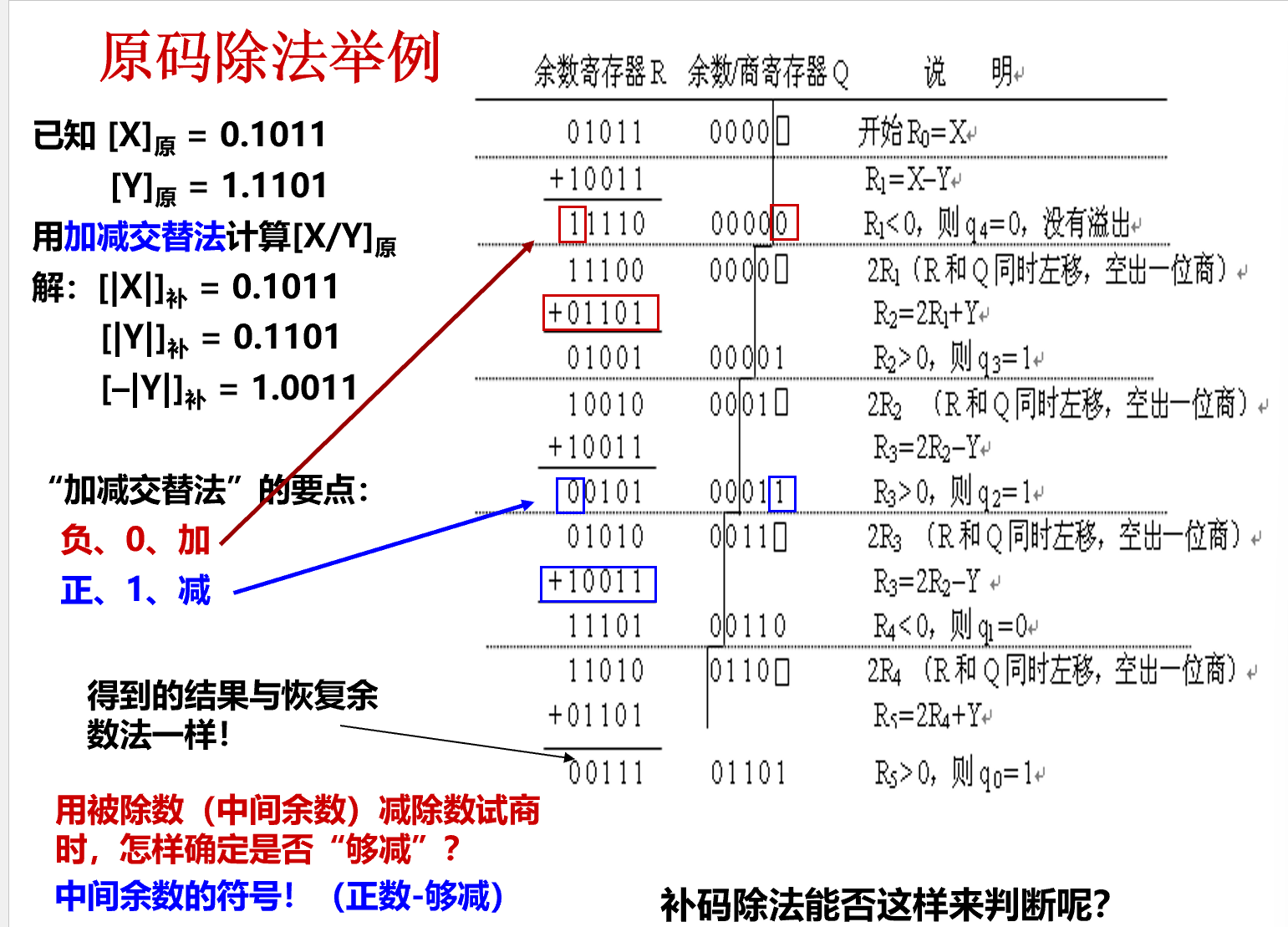
原码除法¶

商的符号和值分开处理
数值由无符号除法求出
符号由被除数和除数是否同号判断
余数的符号同被除数的符号
使用恢复余数法实现
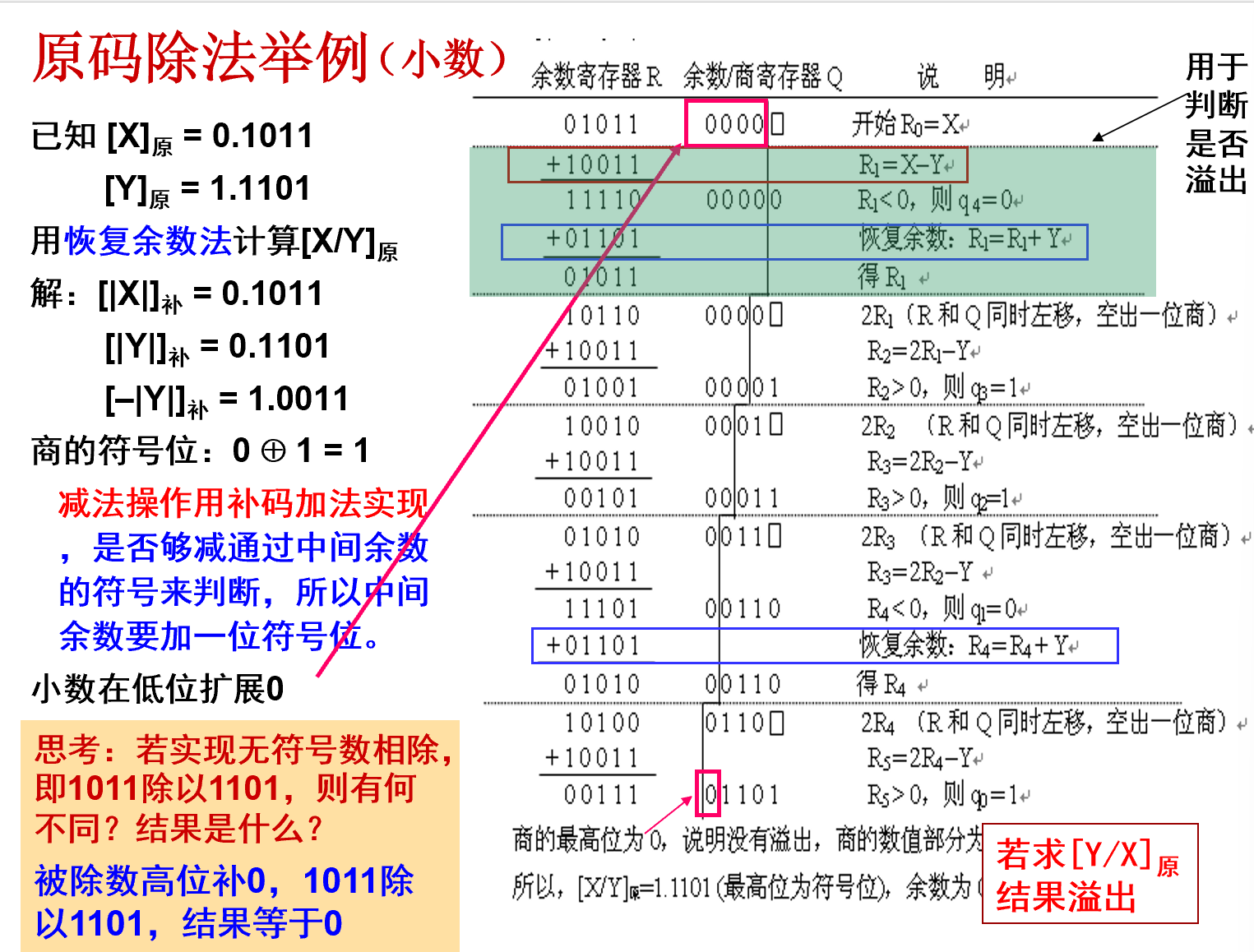
因为一开始余商寄存器就设为5位（最右边留了空位给第一次试商结果），所以后面只需要左移四次（填入四位后面的试商结果），就能够获得五位的商了，而且最后一次减法算出了余数，这个余数也没有再被移动了。
前面几个例子，一开始余商寄存器的后半部分是只有4位的，所以需要左移5次才能空出5个位置给5次试商结果。
使用交替加减法实现

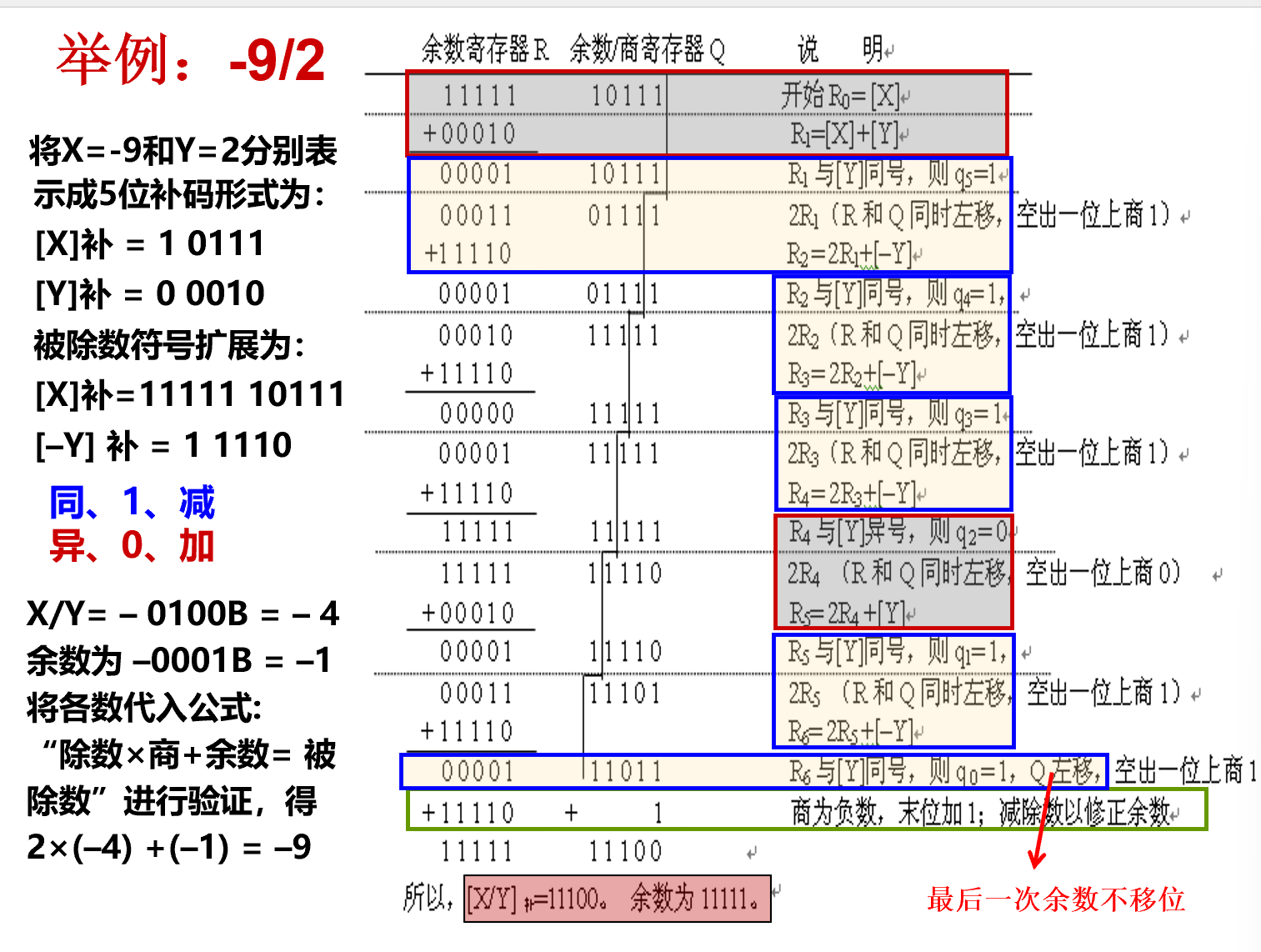
补码除法k*¶

方法1：同原码除法一样，先转换为正数，先用无符号数除法，然后修正商和余数。
方法2：直接用补码除法，符号和数值一起进行运算，商符直接在运算中产生。
被除数可能需要符号扩展，被除数的长度应该是除数的二倍
也使用加减交替法（不恢复余数法）
补码除法判断是否“够减”的规则
当被除数（或当前余数）与除数同号时，做减法，得到新余数
当被除数（或当前余数）与除数异号时，做加法，得到新余数
若新余数的符号与当前余数符号一致表示够减（即不变号），否则为不够减；
、

快速除法¶

除以\(2^k\)：
无符号整数：逻辑右移，高位补0，低位丢弃
无符号整数：逻辑右移，高位补0，低位丢弃
除以\(2^k\)时整数除法的近似处理
不能整除时，采用朝零舍入，即截断方式
无符号数、带符号正整数（地板）：移出的低位直接丢弃
带符号负整数（天板）：加偏移量(2k-1)，然后再右移k 位，低位截断（这里K 是右移位数）

补充¶

变量与常数之间的除运算
只使用右移、加法位运算实现x/32
问题：不能通过比较判断x是否需要纠偏

    int div32(int x)
    {  /* 根据x的符号得到偏移量b */
        int b=(x>>31) & 0x1F;
        return (x+b)>>5;
    }

定点运算部件
所有运算都可以通过加和移位实现
以一个或多个ALU为核心，加上移位器、存放中间临时结果的寄存器组，在相应控制逻辑的控制下，通过多路选择器和实现数据传送的总线等，即可以实现各种运算——也就是构成了一个运算数据通路。