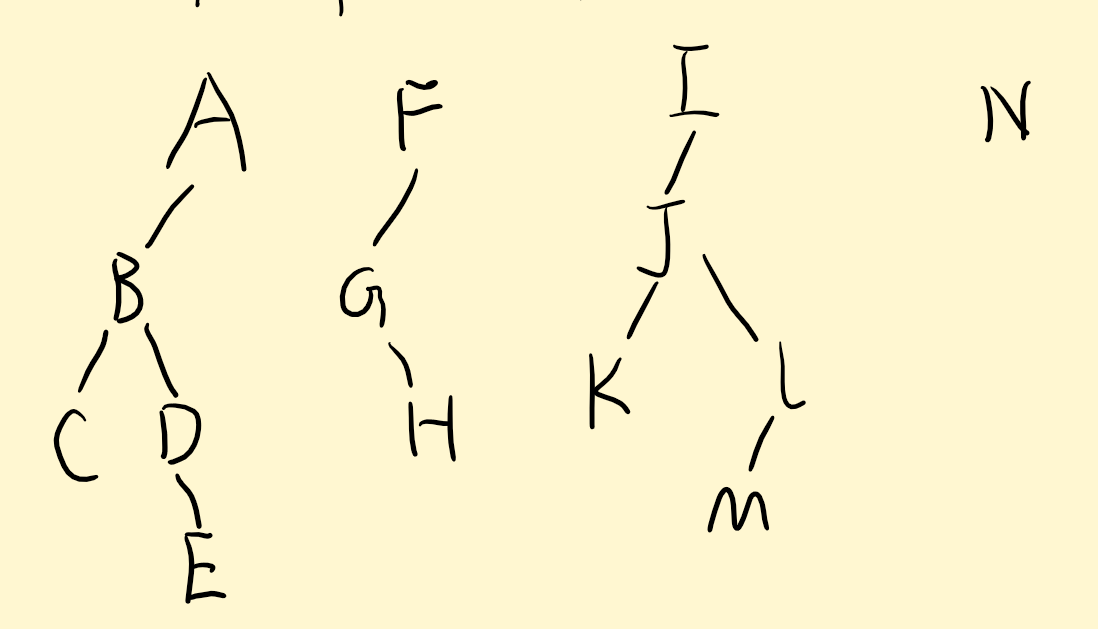P4

211275022

田昊东

5.9

（1）

• 若树的深度为k，此时结点数目最少
• \(2^{k-1}+m-1\)
• 若树的深度为k+1，并且第k层的每个非叶结点都有两个子女，此时结点数目最多
• \(2^k-1+(2^{k-1}-m)*2=2^{k+1}-2m-1\)

（2）

• 深度计算公式为\(\lceil\log_2(n+1)\rceil\)
• 深度范围\([\lceil\log_2(2^{k-1}+m-1)\rceil,\lceil\log_2(2^{k+1}-2m-1)\rceil]\)
• 故可能的取值为\(k,k+1\)

5.16

（3）

• 绘制为堆
• 
• 有多处不满足最小堆的性质，如根节点为103大于左右子结点
• 调整为最小堆
• [06,12,20,23,30,38,42,52,56,55,97,103]
• 

（4）

• 绘制为堆
• 
• 有多处不满足最小堆的性质，如节点2为56大于左右子结点
• 调整为最小堆
• [05,23,20,35,28,38,29,61,56,76,40,100]
• 

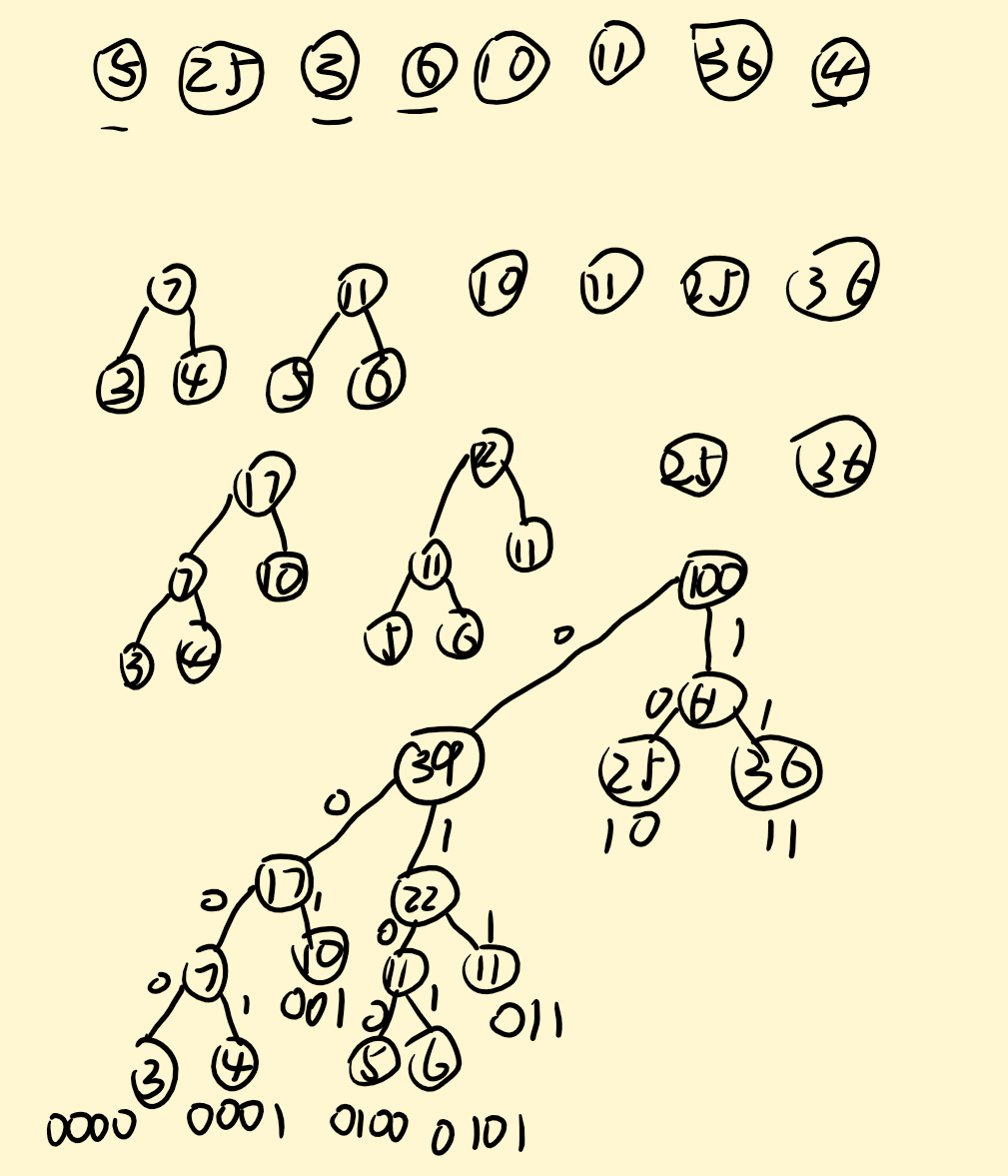
5.20

• 

• 字母	编码
  c1	0100
  c2	10
  c3	0000
  c4	0101
  c5	001
  c6	011
  c7	11
  c8	0001

• 总码数为：\((3+4+5+6)*4+(10+11)*3+(25+36)*2=257\)

4

（1）

• 

（2）

• 绘制二叉树T
• 

leftChild	ltag	data	rtag	rightChild
B	0	A	0	F
C	0	B	0	D
null	1	C	1	B
B	1	D	0	E
D	1	E	1	A
G	0	F	0	I
A	1	G	0	H
G	1	H	1	F
J	0	I	0	N
K	0	J	0	L
F	1	K	1	J
M	0	L	1	I
J	1	M	1	L
I	1	N	1	null

（5）

• 由构造过程看，每次合并两个结点就会新增加一个节点，因此结点数目为\(n+n-1=2n-1\)
• 最好的情况下构成一个满二叉树，深度为\(\log_2n+1\)
• 最差情况下构成一条类似链的形状，除第一层外每层两个结点，深度为\(n\)
• 故范围为\([log_2n+1,n]\)

（6）

• 001->e
• 011->f
• 101->d
• 100->a
• 101->d
• 0001->g
• 100->a
• 11->b
• 001->e
• 即结果为：efdadgabe