Skip to content

P6

1

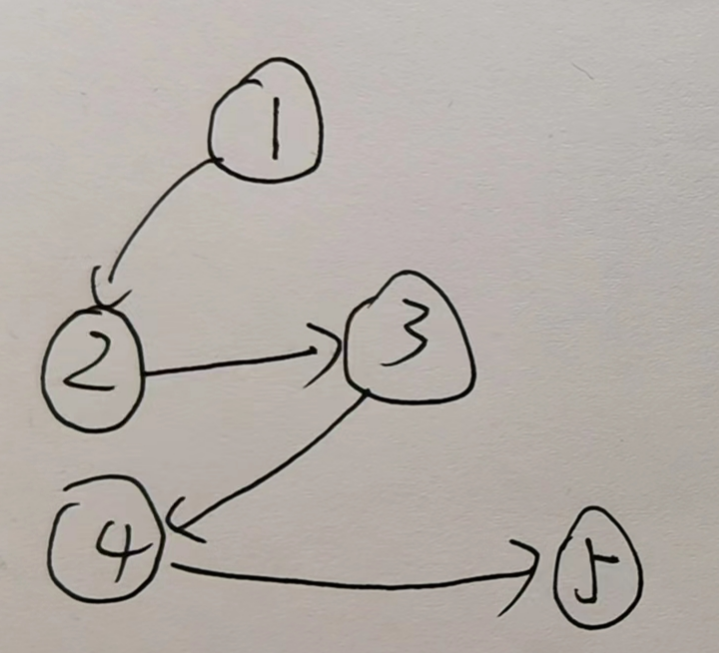
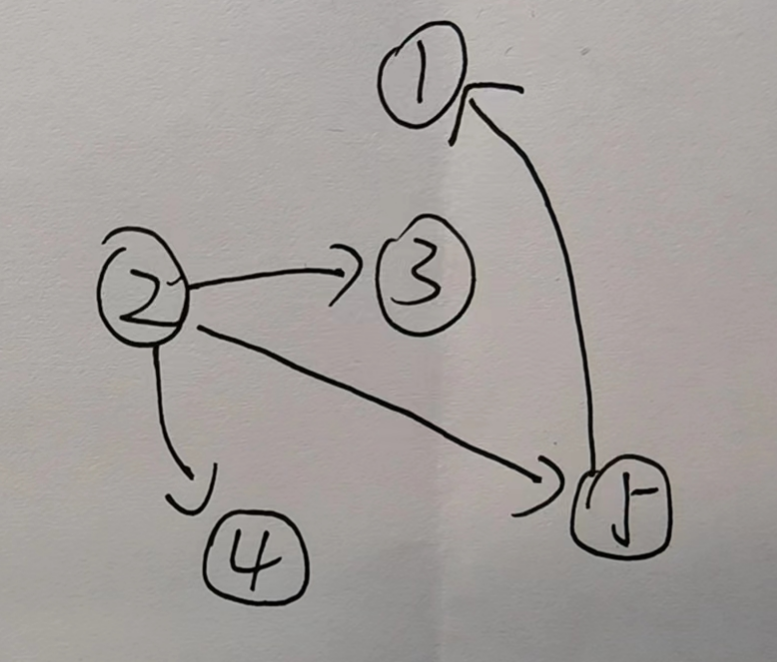
  • 不是强连通的，强连通分量：A，B，C，D，E，F是六个独立的强连通分量，没有任意两个点可以相互到达。

  • 简单路径：AB,AD,ADB,ABC,ADBC,ABE,ADE,ABSF,ABCFE,ADBCF,ADBCFE, BC,BCF,BE,BCFE,CF,CFE,DB,DBC,DBCF,DBCFE,DE,DBE,FE；有向环:没有有向环；

  • 入度 出度
    A 0 2
    B 2 2
    C 1 1
    D 1 2
    E 3 0
    F 1 1

  • 邻接矩阵

  • A B C D E F
    A 0 1 0 1 0 0
    B 0 0 1 0 1 0
    C 0 0 0 0 0 1
    D 0 1 0 0 1 0
    E 0 0 0 0 0 0
    F 0 0 0 0 1 0

  • 邻接表

  • A B D
    B C E
    C F
    D B E
    E
    F E

  • 逆邻接表

  • A
    B D
    C B
    D A
    E B D F
    F C
10

  • image-20231209222408671

  • image-20231209222417002

11
  • 边权重各不相同的图的最小生成树是唯一的
  • kruskal由于要对边进行排序，此外并查集操作的时间复杂度为\(O(1)\),因此总的复杂度为\(O(E*log(E))\)
  • 对于使用数组实现的Prime算法的时间复杂度为\(O(V^2+E)\)
  • 因此Prim算法适用于边稠密的图，Kruskal算法适合于边稀疏的情况
17

  • 从1到6的最长路径为13256，边权和为15+4+19+5=43,因此最早可能在43结束

  • 活动 e l
    12 0 17
    13 0 0
    32 15 15
    24 19 27
    25 19 19
    35 15 27
    46 29 37
    56 38 38

  • 比较e和l可以发现关键活动为：13,32,25,56