- 有向图的顶点的度等于入度与出度之和
图的存储¶
-
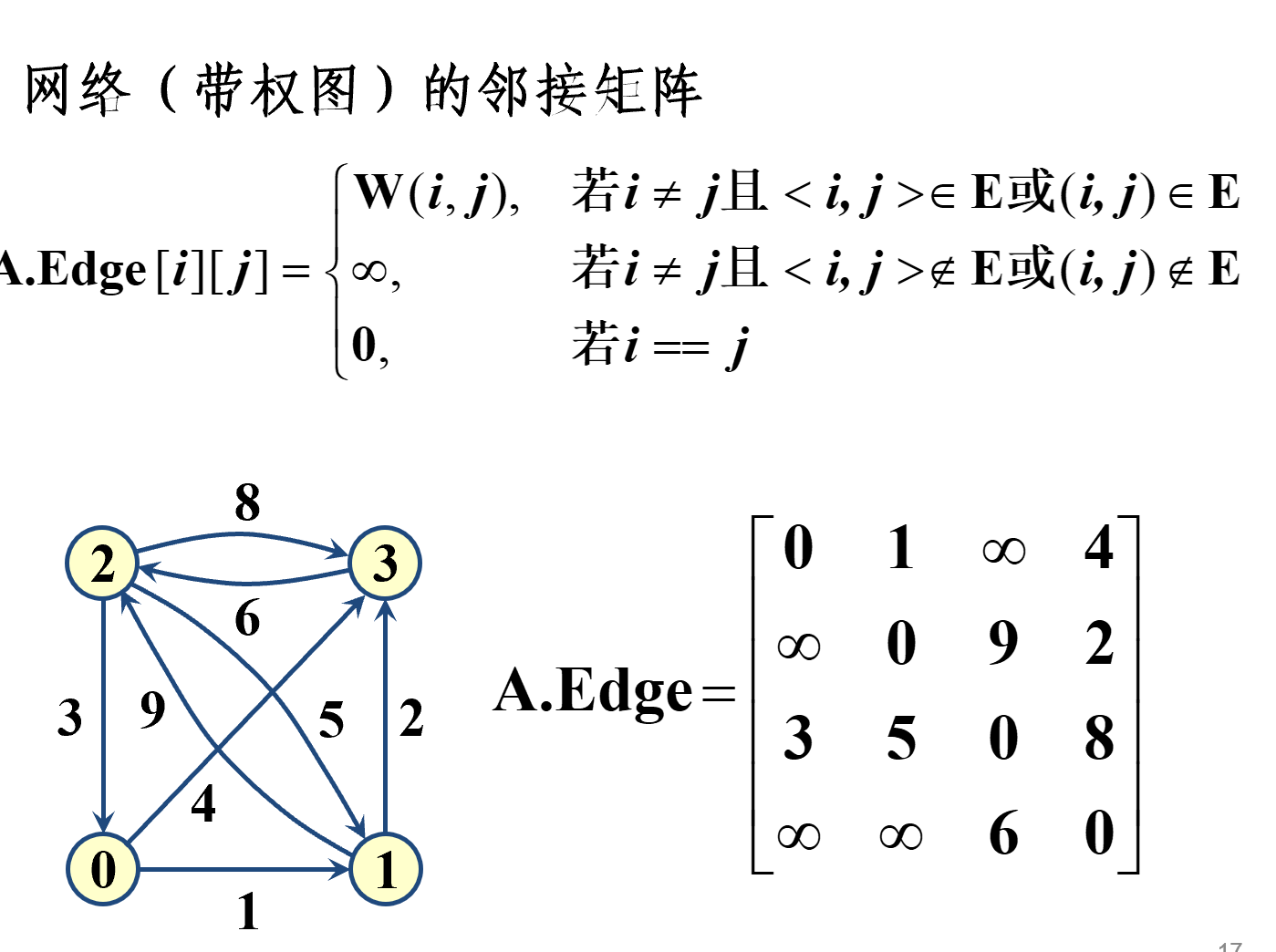
邻接矩阵
-
邻接表
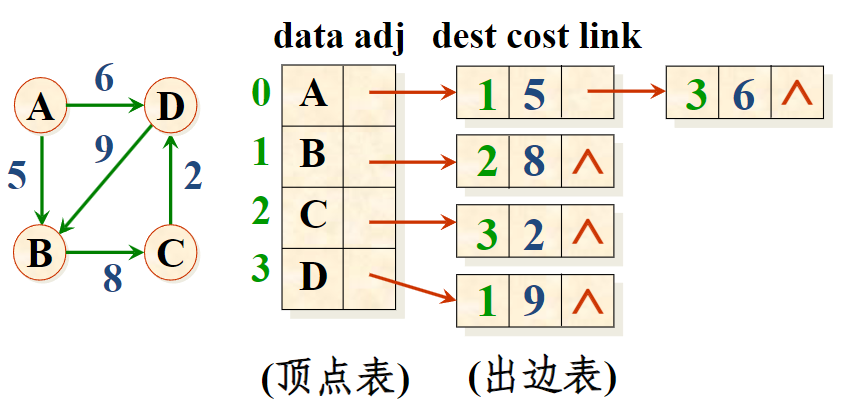
- 为了更方便的查询,表示有向图时可以加一个逆邻接表(入边表)
难点¶
邻接多重表¶
- 无向图的邻接表表示中,每条边被存储了两遍,既浪费了空间,又造成为边做标记等有关边的处理的不方便
-
在邻接多重表中, 每一条边只有一个边结点。为有关边的处理提供了方便。
-
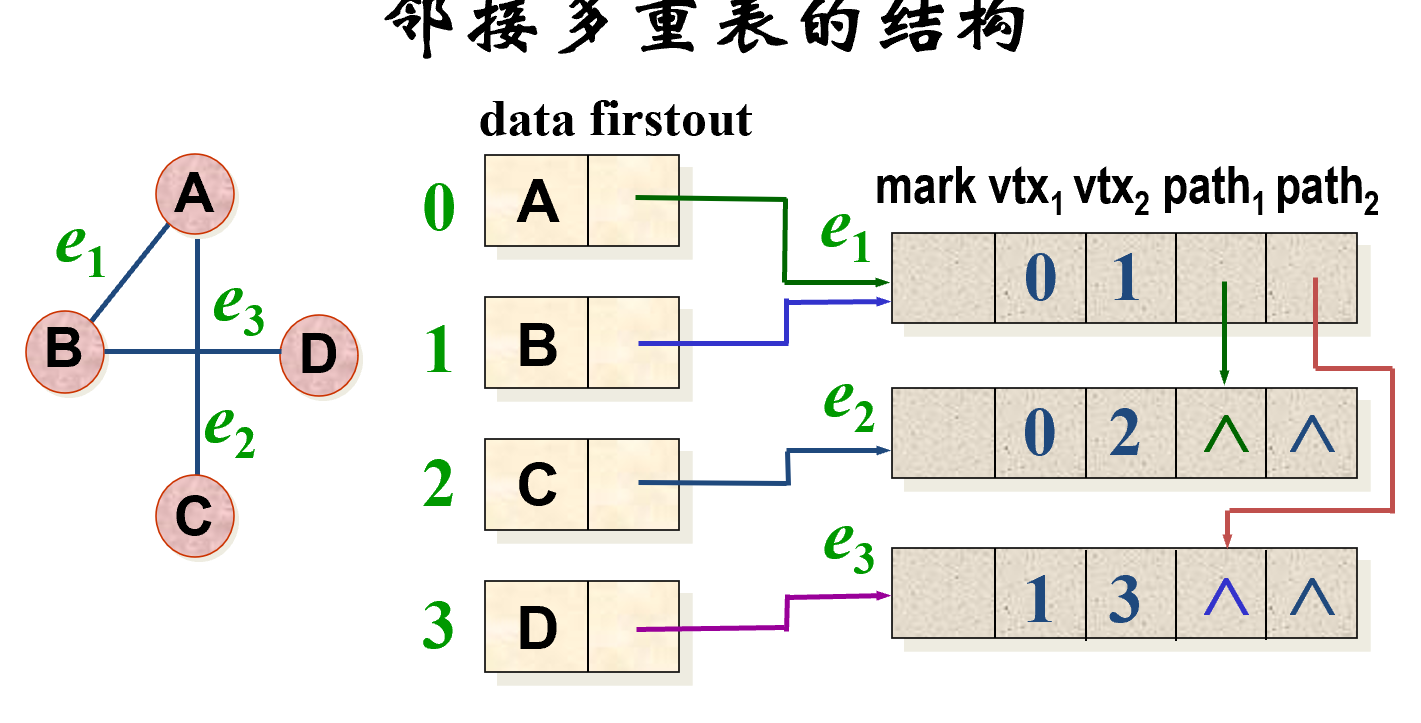
无向图
- 边结构

- vertex 1 和 vertex 2 是该边两顶点位置。path 1 域是链接指针, 指向下一条依附顶点 vertex 1 的边;path 2 是指向下一条依附顶点 vertex 2 的边链接指针。
- 点结构

- data 存放与该顶点相关的信息,firstout 是指向依附于该顶点的第一条边的指针。
-
-
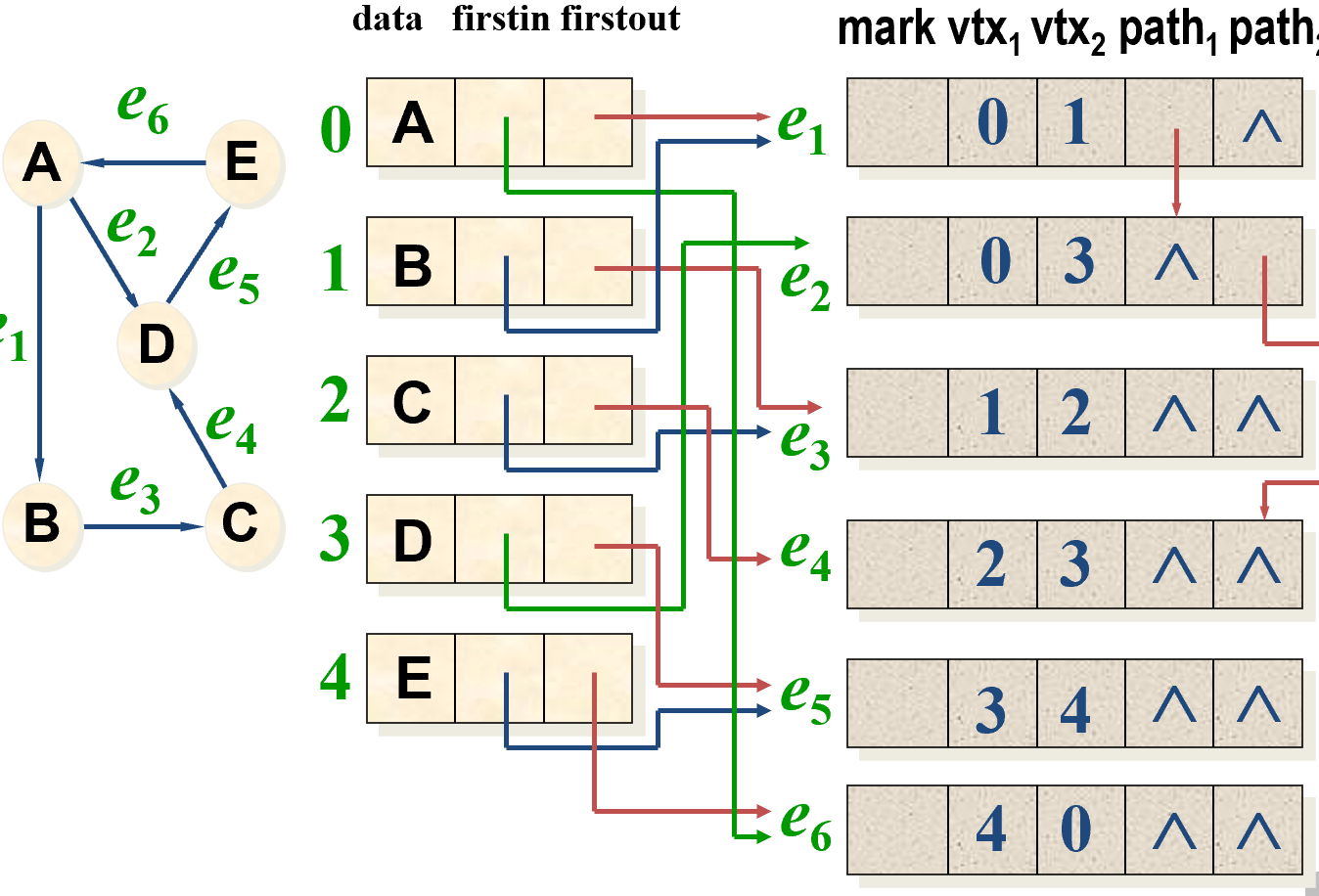
有向图
- 用有向图的邻接多重表可以结合邻接表和逆邻接表
- 点结构

- 数据成员 data 存放与该顶点相关的信息,指针 firstout 指向以该顶点为始顶点的出边表的第一条边, firstin 指向以该顶点为终顶点的入边表的第一条边。
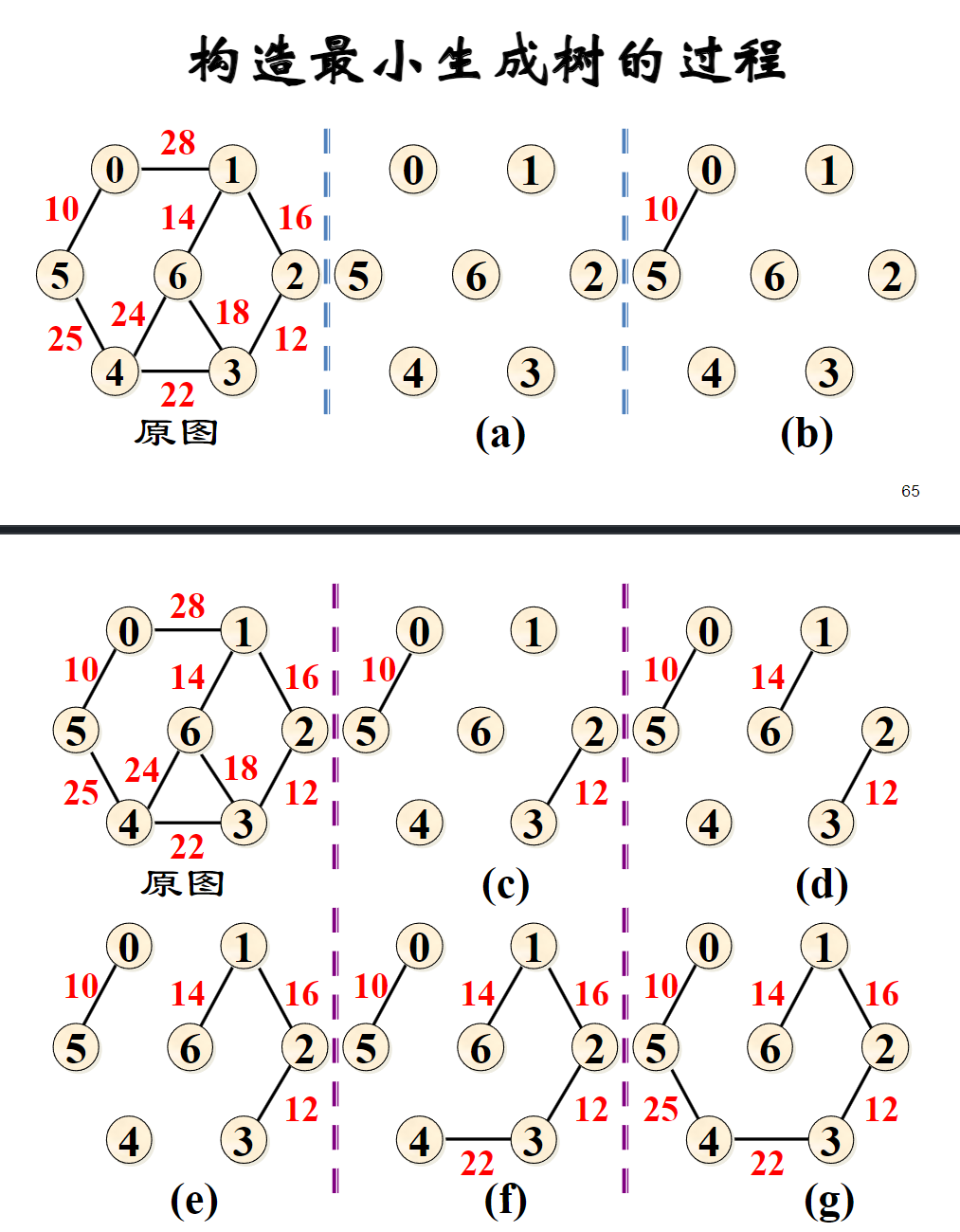
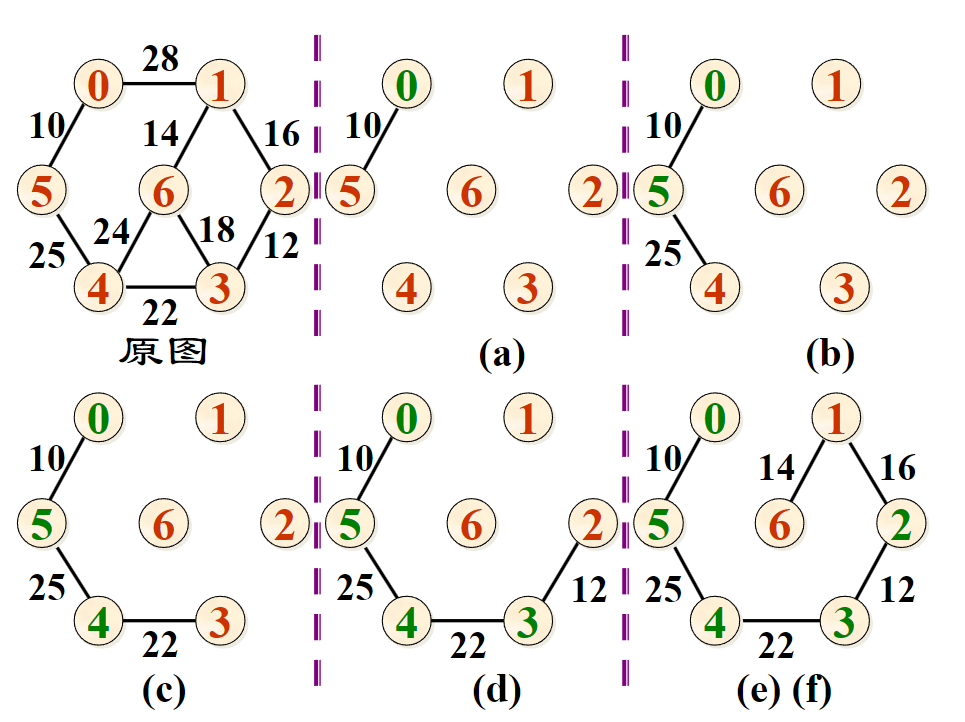
最小生成树¶
-
克鲁斯卡尔(Kruskal):并查集+堆
-
普里姆 (Prim):每次选已经确定的点相邻最近的点加入
最短路径¶
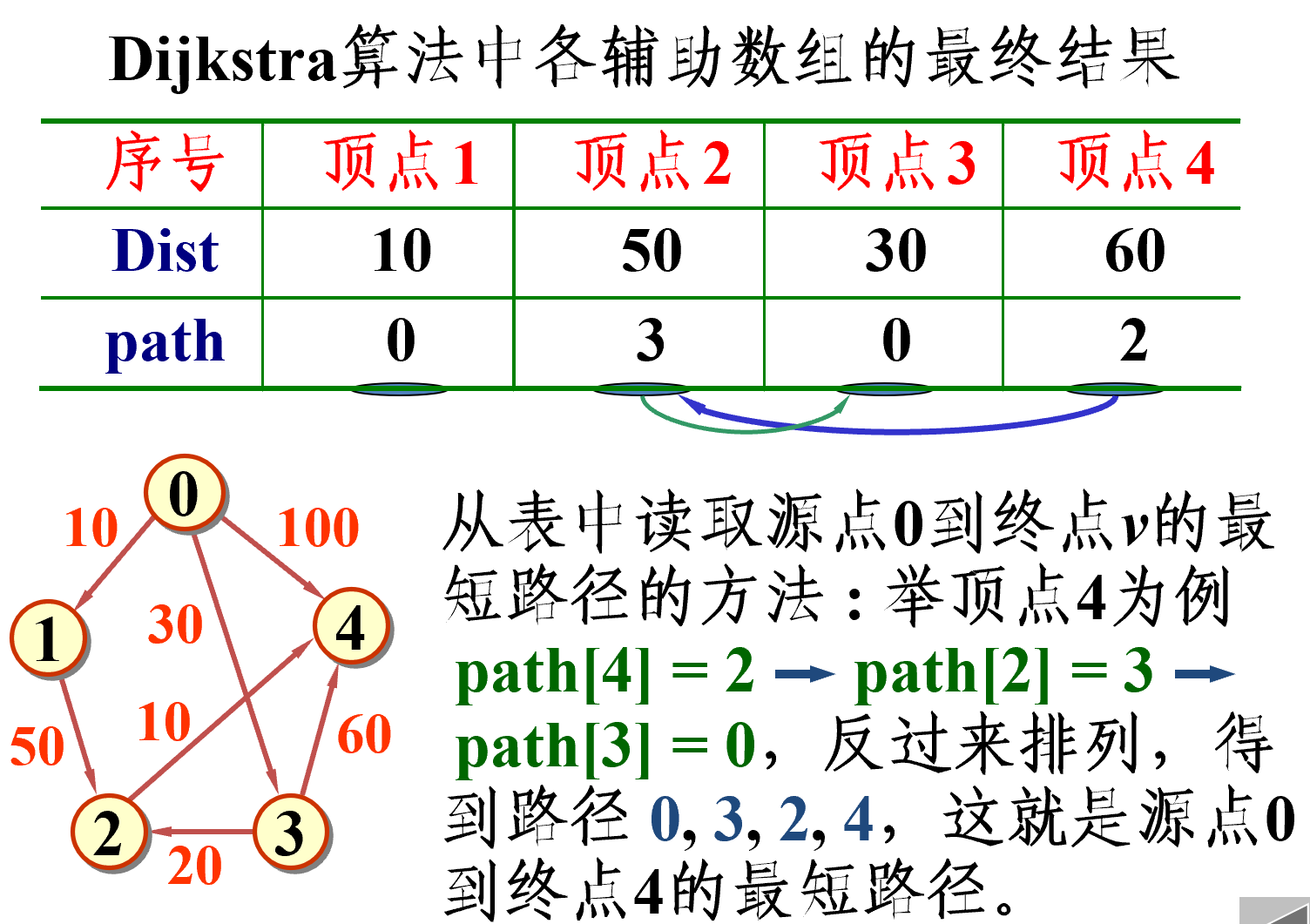
- Dijkstra
-
-
Floyd
template <class T, class E> void Floyd (Graph<T, E>& G, E a[][], int path[][]) { //a[i][j]是顶点i和j之间的最短路径长度。path[i][j] //是相应路径上顶点j的前一顶点的顶点号。 for (i = 0; i < n; i++)//矩阵a与path初始化 for (j = 0; j < n; j++) { a[i][j] = G.getWeight (i, j); if (i != j && a[i][j] < maxValue) path[i][j] = i; else path[i][j] = 0; } for (k = 0; k < n; k++)//针对每一个k, 产生a(k)及path(k) for (i = 0; i < n; i++) for (j = 0; j < n; j++) if (a[i][k] + a[k][j] < a[i][j]) { a[i][j] = a[i][k] + a[k][j]; path[i][j] = path[k][j]; //缩短路径长度, 绕过 k 到 j } }; -
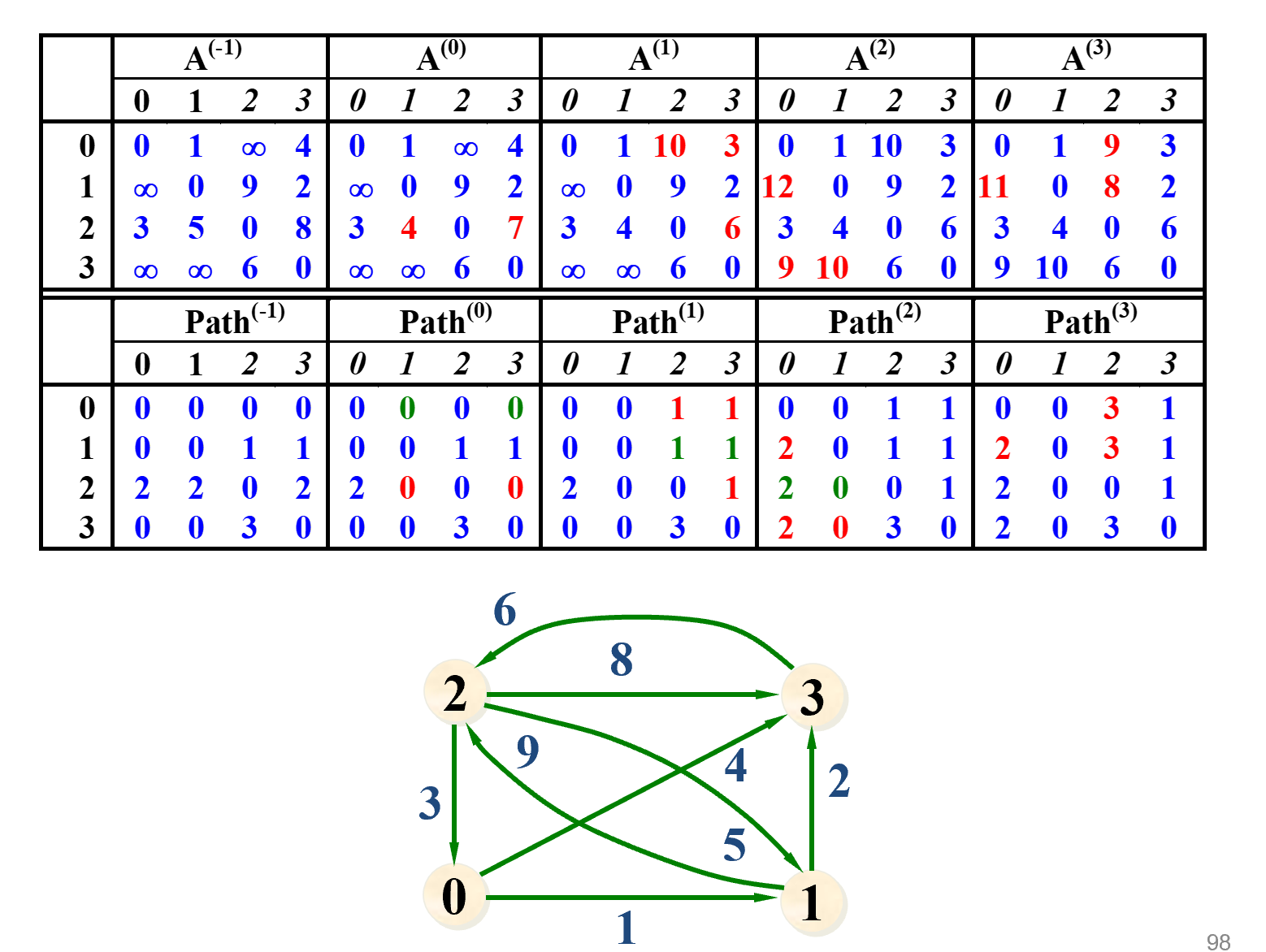
难点¶
活动网络¶
AOV网络¶
- 对给定的AOV网络,必须先判断它是否存在有向环,如果出现了有向环,则意味着某项活动应以自己作为先决条件。
-
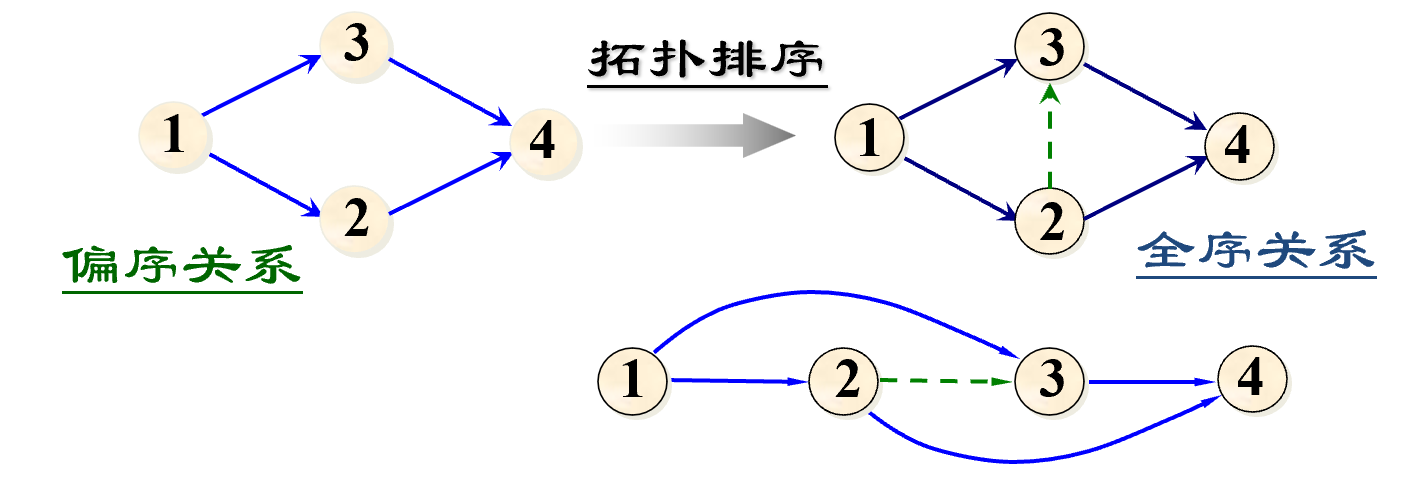
-
拓扑排序
- bfs(逐渐删去度为0的点)
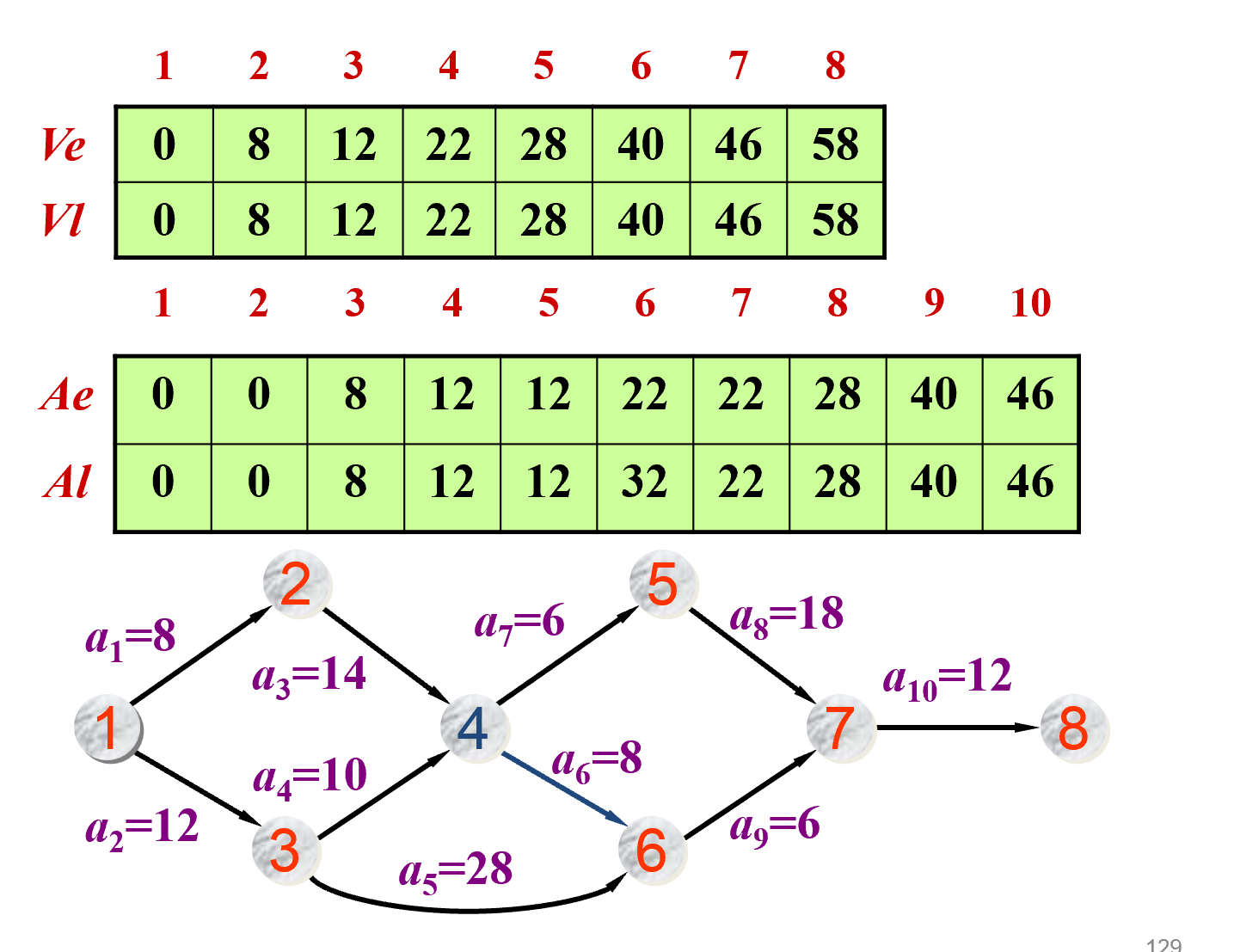
AOE网络¶
- 在无有向环的带权有向图中, 用有向边表示一个工程中的活动 , 用边上权值表示活动持续时间 , 用顶点表示事件 , 则这样的有向图叫做用边表示活动的网络
-
表示完成全部任务需要的最少时间
-
整个工程只有一个开始点和一个完成点,开始点(即入度为零的顶点)称为源点,结束点(即出度为零的顶点)称为汇点。
- 完成整个工程所需的时间取决于从源点到汇点的最长路径长度,这条路径长度最长的路径就叫做关键路径
-
关键路径上的所有活动都是关键活动
-

-

-
先求解Ve、Vl
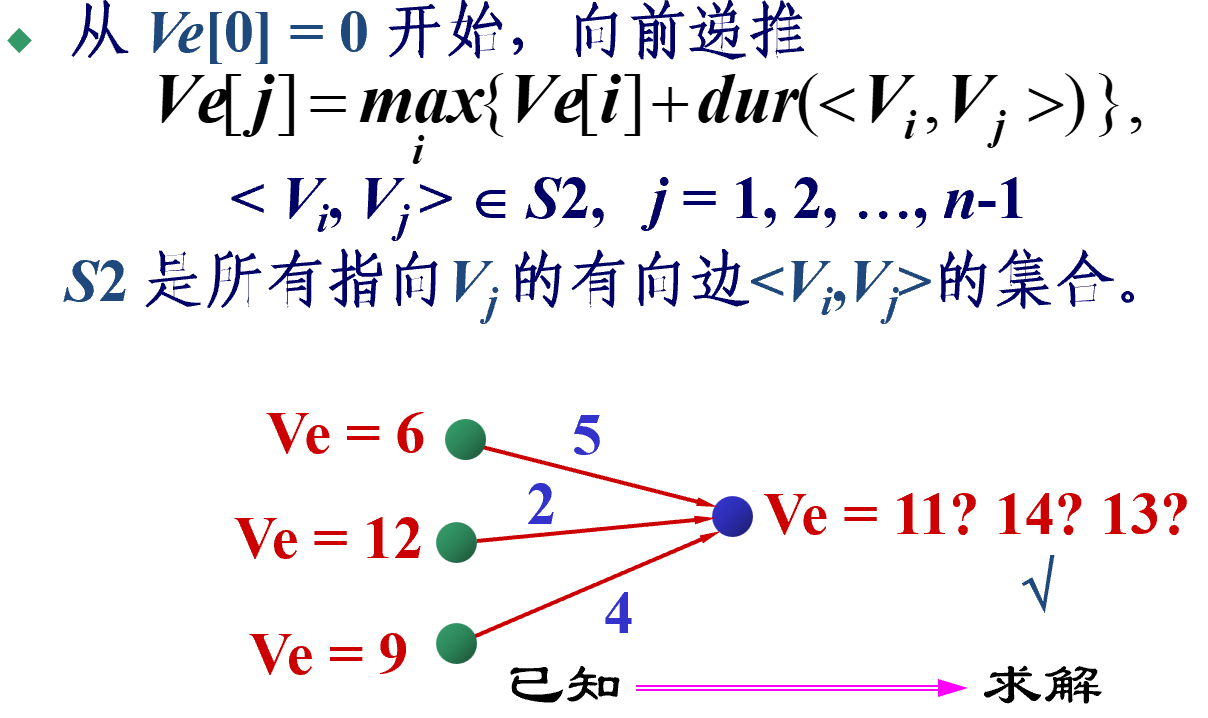
-

-
计算Ae、Al