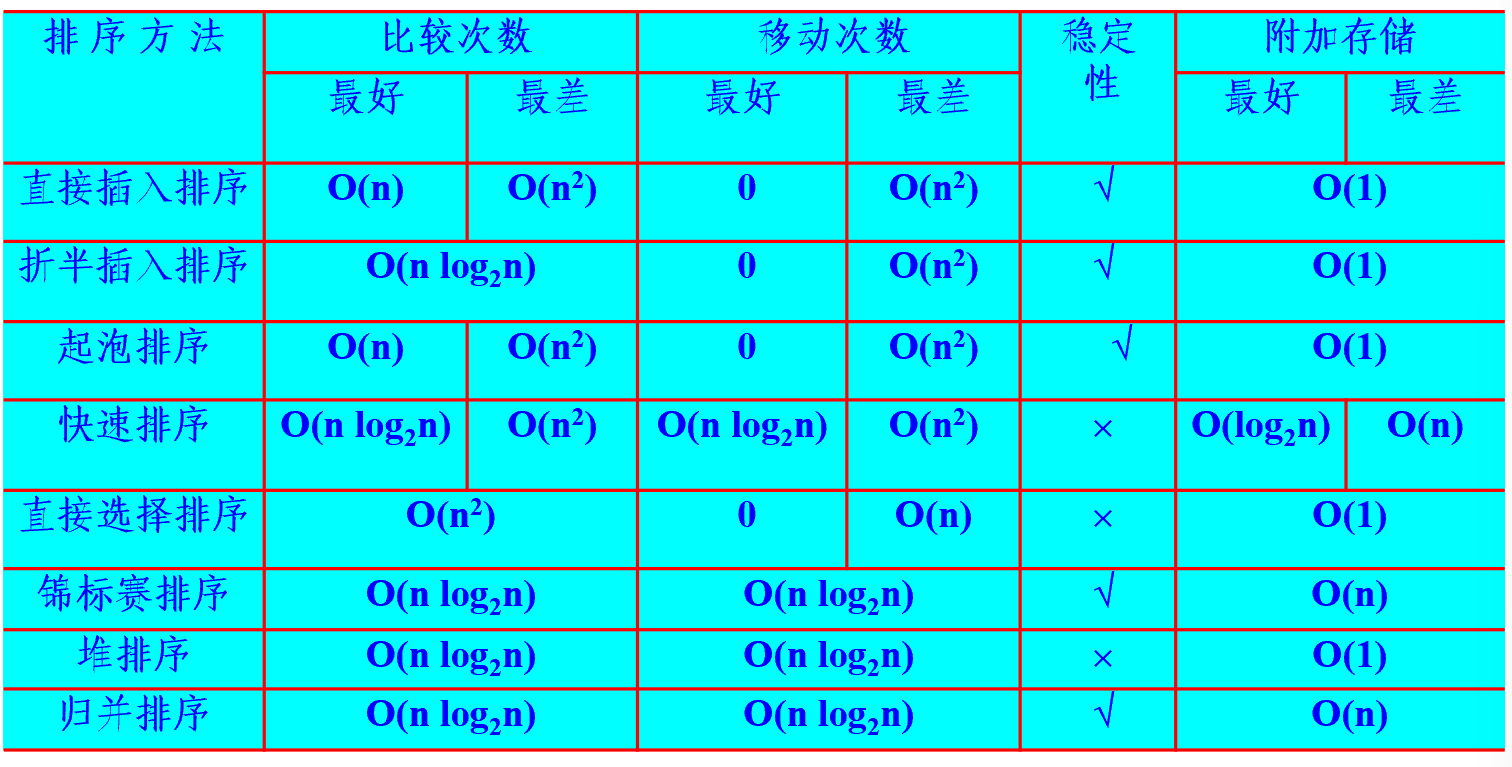
排序

• 内排序与外排序: 内排序是指在排序期间数据元素全部存放在内存的排序；外排序是指在排序期间全部元素个数太多，不能同时存放在内存，必须根据排序过程的要求，不断在内、外存之间移动的排序。

• 排序的复杂度：排序码的比较次数和元素移动次数

• 不稳定排序：希尔排序，快速排序，直接选择排序，堆排序

插入排序

• 每步将一个待排序的元素，按其排序码大小，插入到前面已经排好序的一组元素的适当位置上, 直到元素全部插入为止。

直接插入排序

• 即传统的插入排序，从后向前比较插入，不能放就交换位置，即将元素向后移动

• 

  for (i = left+1; i <= right; i++)
      if (L[i] < L[i-1]) {
          temp = L[i];  j = i-1;  
          do {
              L[j+1] = L[j];  j--;
          } while (j >= left && temp < L[j]);
          L[j+1] = temp;  
      }
  }
  

• 事件复杂度分析

• 最好情况下如元素已经排好序，则比较次数为 n-1 移动次数为0
• 最坏情况下逆序，比较和移动均为 \(n^2/2\)
• 平均为 \(O(n^2)\)
• 稳定排序

折半插入排序

• 在查找位置时使用折半查找而不是从后向前逐一比对

  int i, low, high, middle, k;
  for (i = left+1; i <= right; i++) {
      temp = L[i];  low = left;  high = i-1; 
      while (low <= high) {   //折半搜索寻找插入位置
          middle = (low+high)/2;  //取中点
          if (temp < L[middle])     //插入值小于中点值
              high = middle-1;      //向左缩小区间
          else low = middle+1;      //否则, 向右缩小区间
      }
      for (k = i-1; k >= low; k--) L[k+1] = L[k];
      //成块移动,空出插入位置
      L[low] = temp;       //插入
  }
  

• 平均比较次数

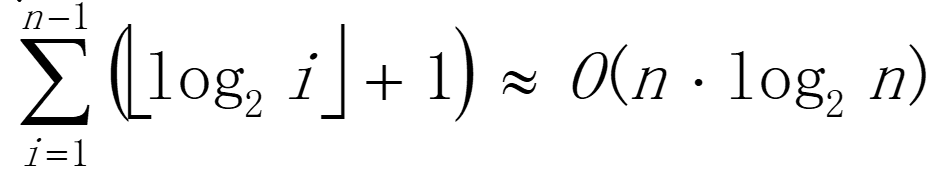
• 折半插入排序的元素移动次数与直接插入排序都依赖于元素的初始排列，但折半插入的比较次数较少并且与元素的初始排列无关（只改进了比较过程，移动和直接插入一致）。
• 当 n 较大时，总排序码比较次数比直接插入排序的最坏情况要好得多，但比其最好情况要差。
• 稳定的排序方法

希尔排序

• 取一个整数 gap < n 作为间隔，将全部元素分为 gap 个子序列，所有距离为 gap 的元素放在同一个子序列中，在每一个子序列中分别施行直接插入排序。然后缩小间隔 gap, 例如取 gap = gap/2，重复上述的子序列划分和排序工作。直到最后取 gap == 1，将所有元素放在同一个序列中排序为止。

• 开始时 gap 的值较大，子序列中的元素较少，排序速度较快; 随着排序进展，gap 值逐渐变小, 子序列中元素个数逐渐变多，由于前面工作的基础，大多数元素已基本有序，所以排序速度仍然很快。

• 示例

• 

void ShellSort (dataList<T>& L, 
                const int left, const int right) {
    int i, j, gap = right-left+1;       //增量的初始值
    Element<T> temp;
    do {
        gap = gap/3+1;          //求下一增量值
        for (i = left+gap; i <= right; i++)
            if (L[i] < L[i-gap]) {      //逆序
                temp = L[i];  j = i-gap;
                do {
                    L[j+gap] = L[j];  j = j-gap;
                } while (j >= left && temp < L[j]);
                L[j+gap] = temp;    //将vector[i]回送
            }
    } while (gap > 1);
};

- 复杂度约为 \(n^{1.25}\) - 不稳定排序

快速排序

• 不稳定的排序方法（partition 引起, 对于等于 mid 的值会被放在一边，破坏了与 mid 的顺序关系）
• 对于 n 较大的平均情况而言, 快速排序是“快速”的, 但是当 n 很小时, 这种排序方法往往比其它简单排序方法还要慢。

交换排序

冒泡排序

while (pass <= right && exchange) {
    exchange = 0;               //标志为0假定未交换
    for (int j = right;  j >= pass;  j--)      
        if (L[j-1] > L[j]) {    //逆序
            Swap (L[j-1], L[j]);    //交换
            exchange = 1;           //标志置为1,有交换
        }
    pass++;
}

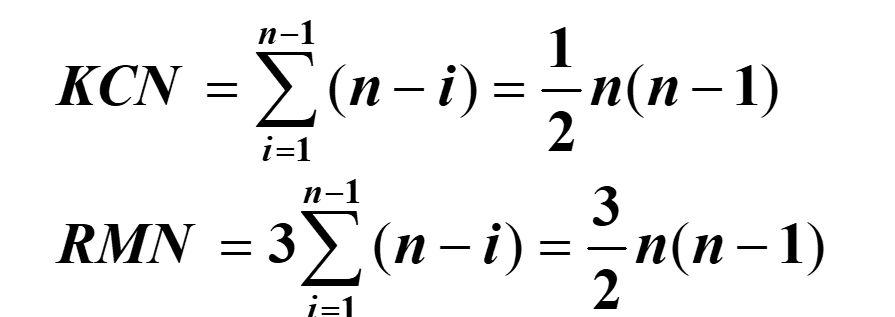- 在元素的初始排列已经按排序码从小到大排好序时，此算法只执行一趟起泡，做 n-1 次排序码比较，不移动元素。这是最好的情形。 - 最坏的情形是算法执行 n-1 趟起泡, 第 i 趟 (1≤ in) 做 n-i 次排序码比较, 执行 n-i 次元素交换。 - - tip: 一次交换相当于进行三次移动 - 稳定的排序

选择排序

• 基本思想是: 每一趟 (例如第 i 趟, i = 0, 1, …, n-2) 在后面 n-i 个待排序元素中选出排序码最小的元素，作为有序元素序列的第 i 个元素。待到第 n-2 趟作完，待排序元素只剩下 1 个, 就不用再选了。

直接选择排序

• 

  void SelectSort (dataList<T>& L, 
            const int left, const int right) {
      for (int i = left; i < right; i++) {
          int k = i;    //在L[i]到L[right]之间找最小排序码元素
          for (int j = i+1;  j <= right;  j++) 
              if (L[j] < L[k]) k = j;
          if (k != i) Swap (L[i], L[k]);  //交换 
      }
  };
  

• 比较次数固定为 \(\frac{n(n-1)}2\)

• 当这组元素初始状态是按其排序码从小到大有序的时候, 元素的移动次数达到最少 RMN = 0，最坏情况是每一趟都要进行交换，总的元素移动次数为 RMN = 3 (n-1)。
• 不稳定的排序方法 (交换过程引起，可能破坏相同元素的顺序)

锦标赛排序

• 
• 每次两两比较的结果是把排序码小者作为优胜者上升到双亲结点，所以称这种比赛树为胜者树。
• 示例
  • 
• 第一次为构建树，之后只需要对树进行更新即可
• 
• 与堆相比存储空间的利用率较低，仅在叶子节点存储元素
  • 需要使用 2n-1 个节点存储 n 个元素
• 稳定的排序方法

堆排序

template <class T>
    siftDown (dataList<T>& L, const int start, const int m){
    //私有函数: 从结点start开始到m自上向下比较, 
    //如果子女的值大于双亲的值, 则相互交换, 将一
    //个集合局部调整为最大堆。
    int i = start;  int j = 2*i+1;   //j是i的左子女
    Element<T> temp = L[i];  //暂存子树根结点
    while (j <= m) {             //逐层比较
        if (j < m && L[j] < L[j+1]) j++;
        //让j指向两子女中的大者
        if (temp >= L[j]) break;     //temp排序码大,不调整
        else {              //否则子女中的大者上移
            L[i] = L[j];
            i = j;  j = 2*j+1;          //i下降到子女位置
        }
    }
    L[i] = temp;            //temp放到合适位置
};
template <class T>
    void HeapSort (dataList<T>& L) {
    //对表L.Vector[0]到L.Vector[n-1]进行排序, 使得表
    //中各个元素按其排序码非递减有序
    int i, n = L.length();
    for (i = (n-2)/2; i >= 0; i--)  //建堆
        siftDown (L, i, n-1);   
    for (i = n-1; i >= 0; i--) {        //修堆
        L.Swap(0, i);  siftDown (L, 0, i-1);
    }
};
//一个支持更加完整操作的堆
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int heap[2005],heapSize=0;
void fixHeap(int root){
    int left = 2 * root, right = 2 * root + 1;
    if(left<=heapSize){
        int small;
        if(left==heapSize) small = left;
        else if(heap[left]>heap[right]) small = right;
        else small = left;
        if(heap[root]>heap[small]){
            swap(heap[root],heap[small]);
            fixHeap(small);
        }
    }
}
void insertHeap(int val){
    heap[++heapSize] = val;
    int cur = heapSize;
    while(cur>1){
        int parent = cur/2;
        if(heap[parent]>heap[cur]){
            swap(heap[parent],heap[cur]);
            cur = parent;
        }
        else break;
    }
}
void deleteHeap(){
    heap[1] = heap[heapSize--];
    fixHeap(1);
}
int main()
{
    int n,res=0;
    cin>>n;
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        insertHeap(t);
    }
    while(heapSize>1){
        int a = heap[1];
        deleteHeap();
        int b = heap[1];
        deleteHeap();
        res+=a+b;
        insertHeap(a+b);
    }
    cout<<res;
    return 0;
}

• 
• 示例
• 
• 
• 堆排序是一个不稳定的排序方法（每次将堆顶移动到尾部的交换引起）。

归并排序

• 
• 
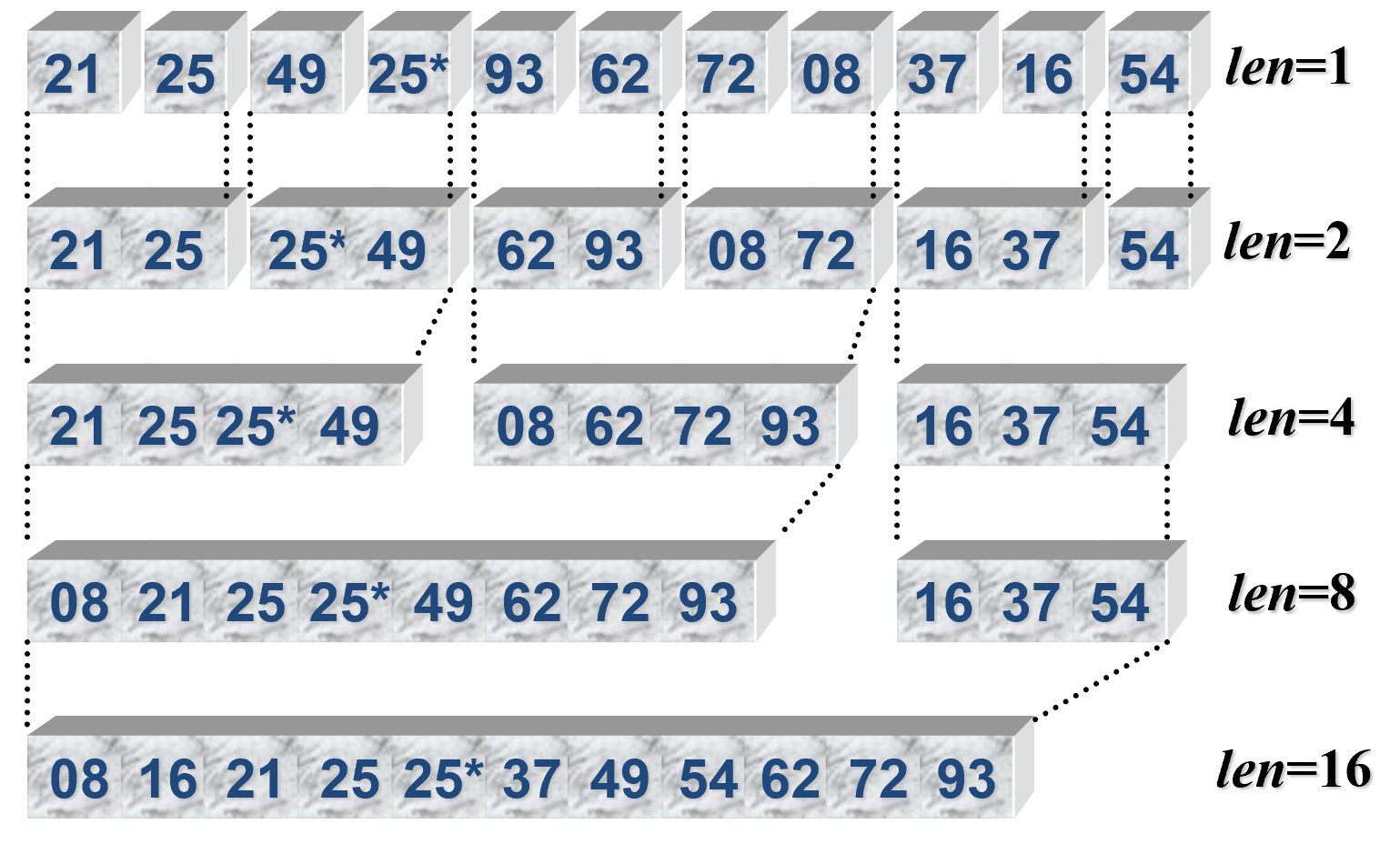
• 归并排序是一个稳定的排序方法。