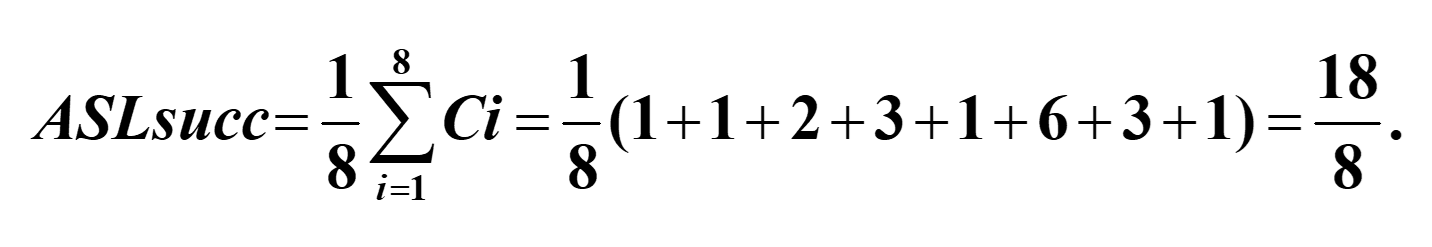静态环境，搜索结构在插入和删除等操作的前后不发生改变。（静态搜索表）
动态环境，为保持较高的搜索效率, 搜索结构在执行插入和删除等操作的前后将自动进行调整，结构可能发生变化。（动态搜索表）
无论搜索成功还是失败都要返回一些信息，比如是啊比了也要报告位置，插入操作可能依赖于这个位置（比如二叉搜索树）

集合¶

集合是成员的一个集群，集合中的成员可以是原子（单元素），也可以是集合；集合的成员必须互不相同，并具有相同的数据类型。
集合的成员一般是无序的，但是在存储时通常有一定规则，为了便于合并查找等操作。
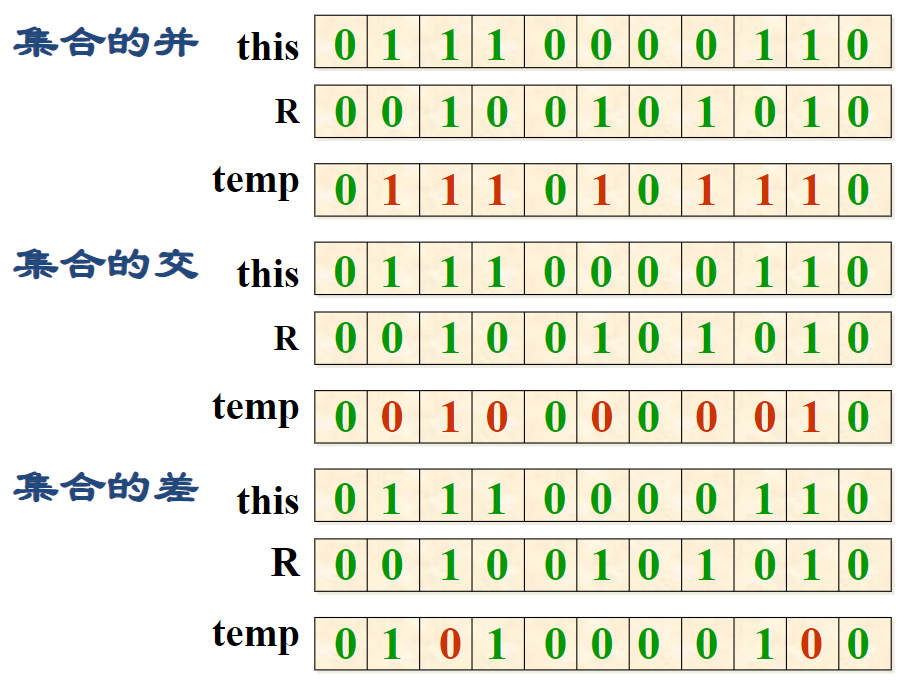
用位向量表示集合：用 01 表示元素是否在集合中（状态压缩）
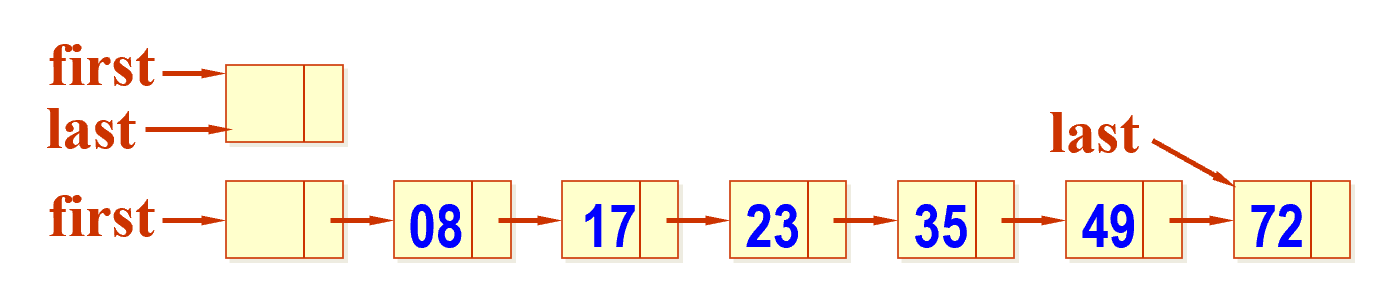
使用有序链表表示：链表中的每个节点表示集合中的一个元素

并查集¶

等价关系：自反性、对称性、传递性
根据等价关系划分集合得到等价类
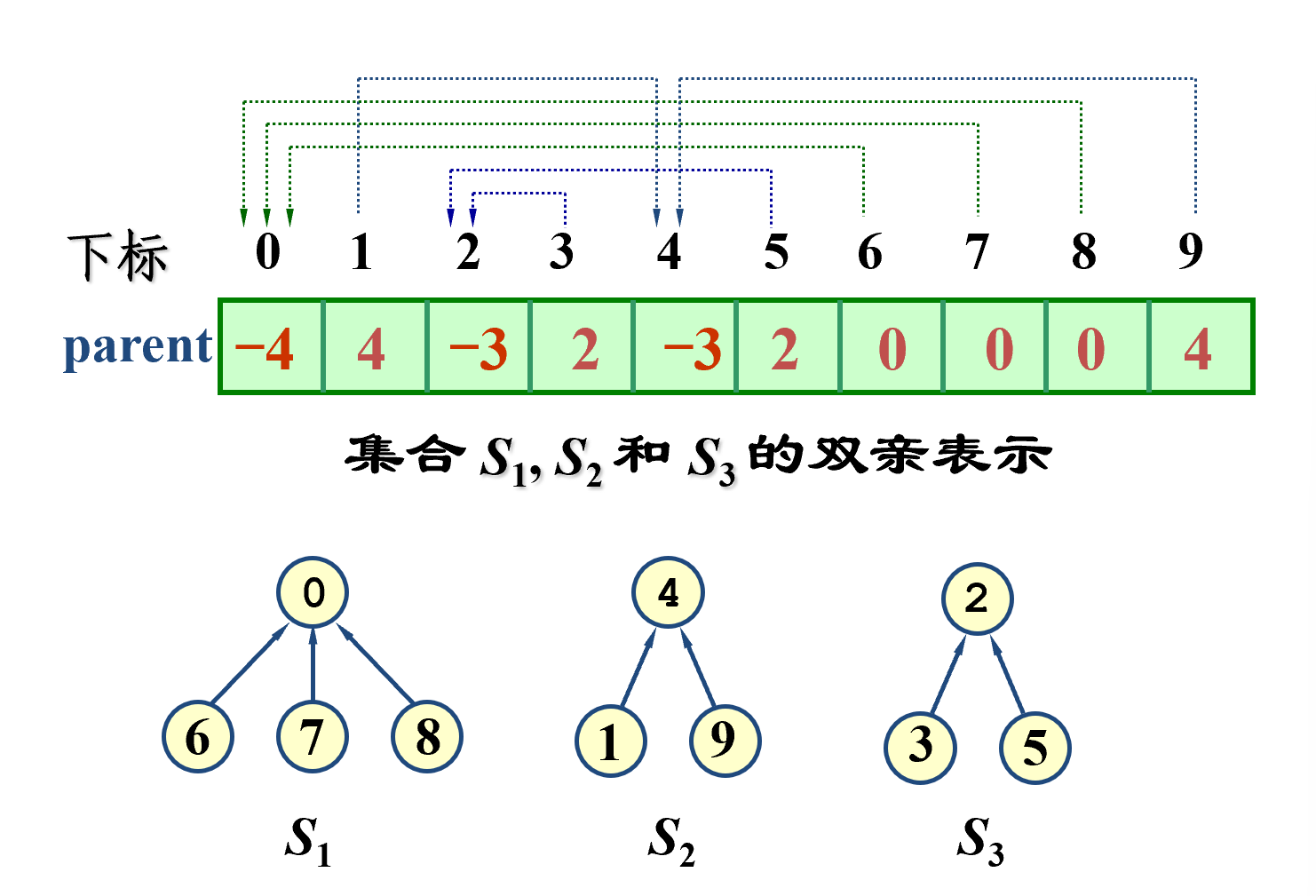
并查集使用树的双亲表示，根节点为 \(-k\) 表示集合中的元素个数（初始时都初始化为-1）
支持：合并、查询、构造
、
图论#并查集

字典¶

字典的顺序表示¶

字典保存在线性序列中，关键码从左到右依次增大，可以使用有序顺序表或有序链表
衡量一个搜索算法的时间效率的标准是：在搜索过程中关键码平均比较次数，也称为平均搜索长度 ASL。搜索第 \(i\) 个元素的概率为 \(p_i\) ，搜索到时所需的比较次数为 \(c_i\) ，搜索成功的平均搜索长度 \(ASL_{succ}=\sum_{i=1}^{n}p_i\cdot{c_i}\)
在有序顺序表中成功查找的平均比较次数为 \(\frac1n\frac{(n+1)n}2=\frac{n+1}2\)
- 搜索不成功时不需一直比较到表尾，只要发现下一个元素的值比给定值大，就可断定搜索不成功
使用判定树描述顺序查找
搜索成功时停在内结点，搜索失败时停在外结点
判定树是一种扩充二叉树。内结点代表顺序表中已有的元素，外结点代表失败结点，它表示在两个相邻已有元素值之间的值。
\(ASL_{unsucc}=\frac1{n+1}(\sum^n_{i=1}i+n)\)
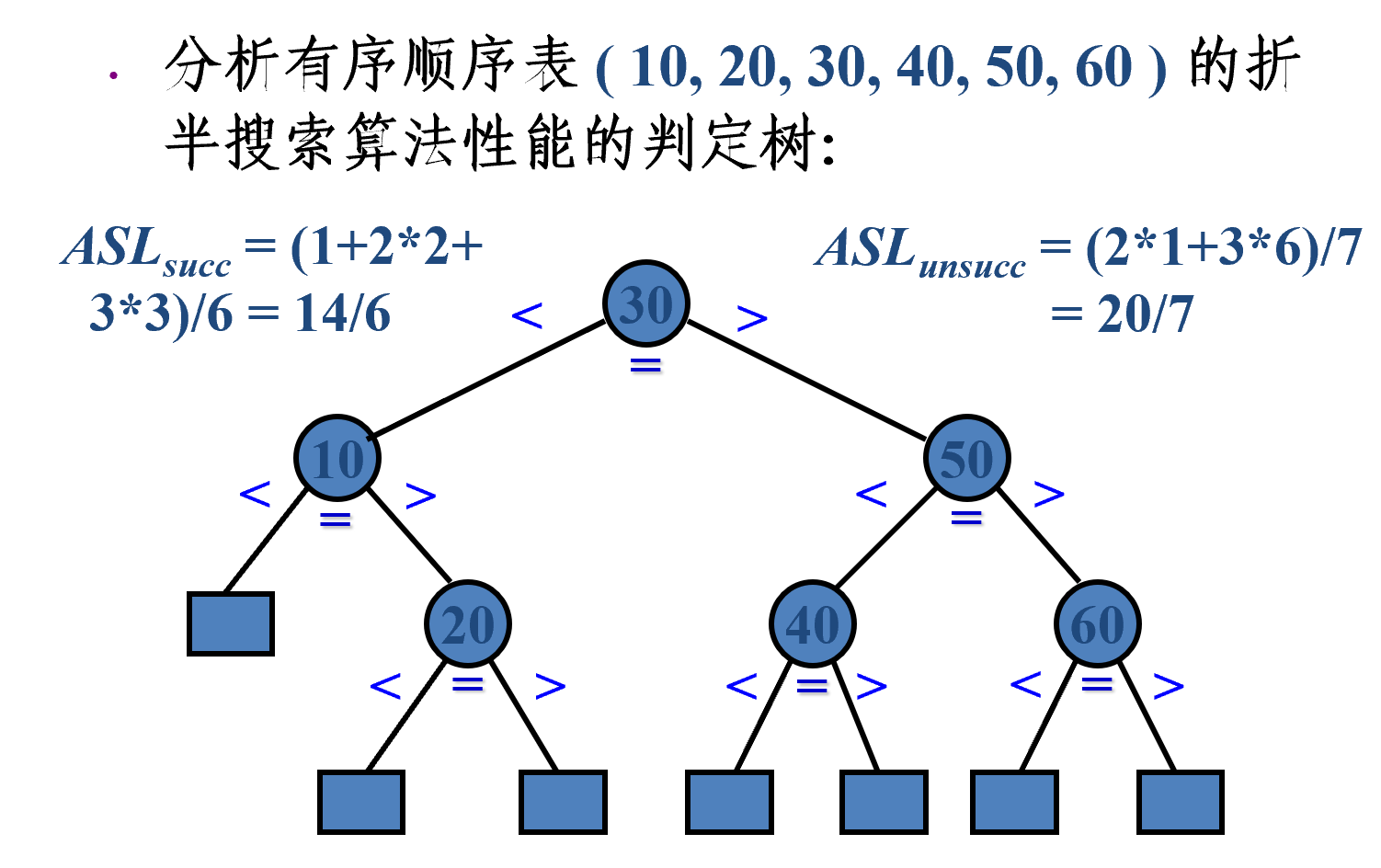
使用判定树描述折半查找

散列表¶

不经过比较，一次直接从字典中得到搜索元素
在元素存储位置与其关键码之间建立一个确定的对应函数关系 Hash ()，使得每个关键码与唯一的存储位置相对应 Address ＝ Hash(key)
在插入时依此函数计算存储位置并按此位置存放。在搜索时对元素的关键码进行同样的计算，把求得的函数值当做元素存储位置，然后按此位置搜索。这就是散列方法

散列函数¶

要求
散列函数应是简单的，能在较短的时间内计算出结果。
散列函数的定义域必须包括需要存储的全部关键码
散列函数计算出来的地址应能均匀分布在整个地址空间中
直接定址法
取关键码的线性函数值为散列地址 \(Hash(key)=a*key+b\)
这类散列函数是一对一的映射，一般不会产生冲突。但它要求散列地址空间的大小与关键码集合的大小相同。（本质上就是一个数组了，占用空间太大）
数字分析法
设有 n 个 d 位数, 每一位可能有 r 种不同的符号。这 r 种不同符号在各位上出现的频率不一定相同。根据散列表的大小, 选取其中各种符号分布均匀的若干位作为散列地址。
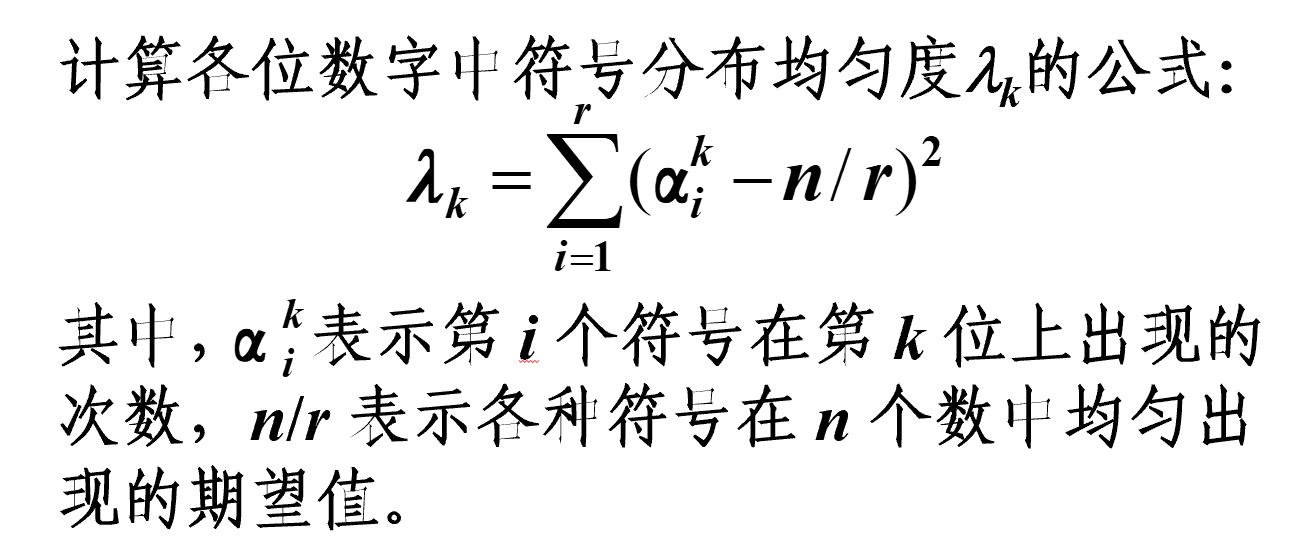
- 选取 \(\lambda_k\) 小的位
- 应该取关键码的 456 位作为散列地址
数字分析法仅适用于事先明确知道表中所有关键码每一位数值的分布情况
除留余数法
设散列表中允许地址数为 m，取一个不大于 m，但最接近于或等于 m 的质数 p 作为除数 \(hash(key)=key\%p \ p<=m\)
可按计算出的地址存放记录。注意, 使用散列函数计算出的地址范围是 0 到 22，而 23、24 这几个地址实际上不能用散列函数计算出来，只能在处理冲突时达到这些地址。
平方取中法
首先计算构成关键码的标识符的内码的平方, 然后按照散列表的大小取中间的若干位作为散列地址。
因为内码平方数的中间几位一般是由标识符所有字符决定, 所以对不同的标识符计算出的散列地址大多不相同。
一般取散列地址为8 的某次幂。例如, 若散列地址总数取为 \(m=8^r\)，则对内码的平方数取中间的 r 位。
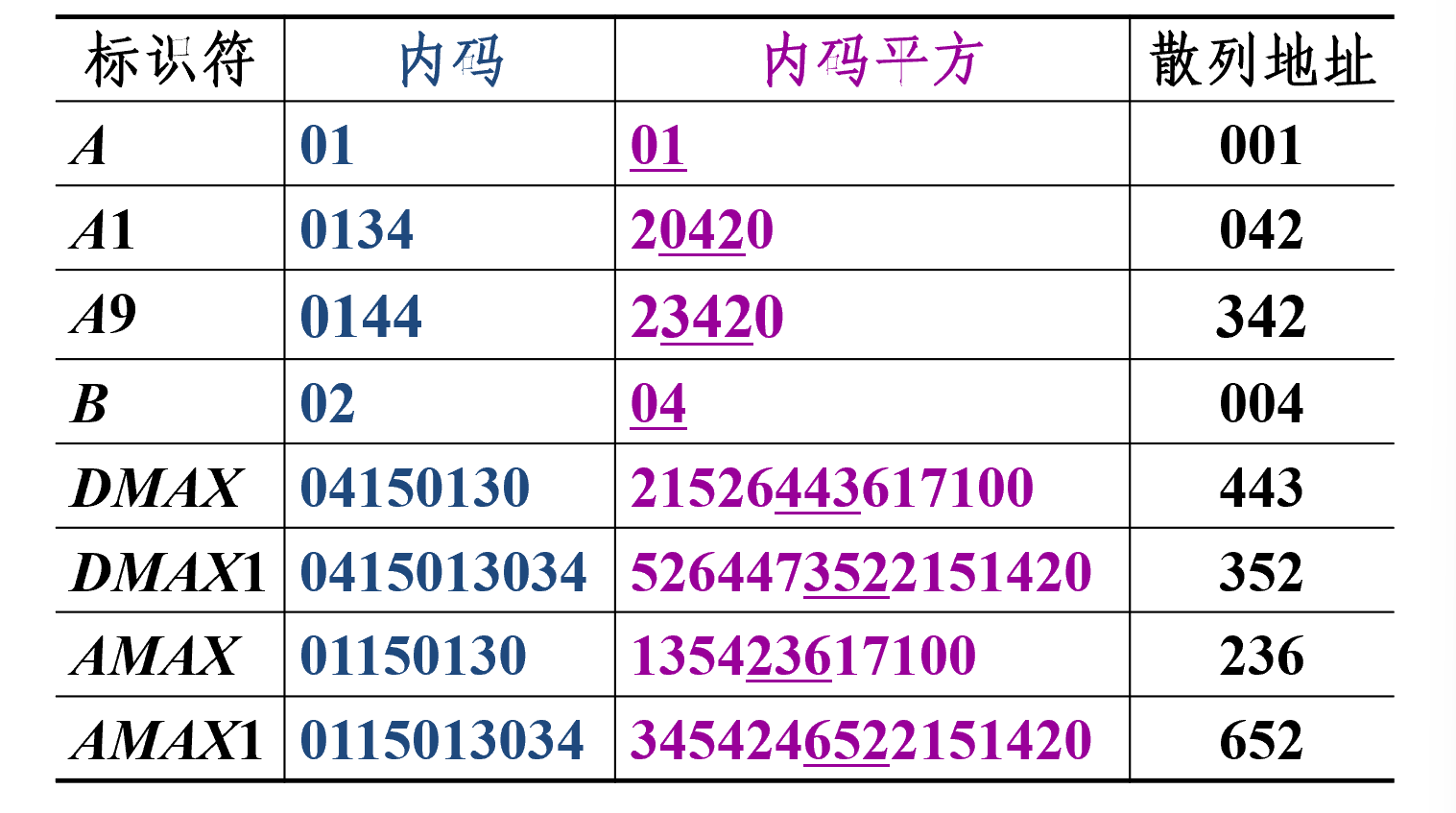
- 使用八进制表示
折叠法
此方法把关键码自左到右分成位数相等的几部分, 每一部分的位数应与散列表地址位数相同, 只有最后一部分的位数可以短一些。把这些部分的数据叠加起来, 就可以得到具有该关键码的记录的散列地址。
叠加方式
- 移位法：把各部分最后一位对齐相加；
- 分界法：各部分不折断，沿各部分的分界来回折叠, 然后对齐相加。
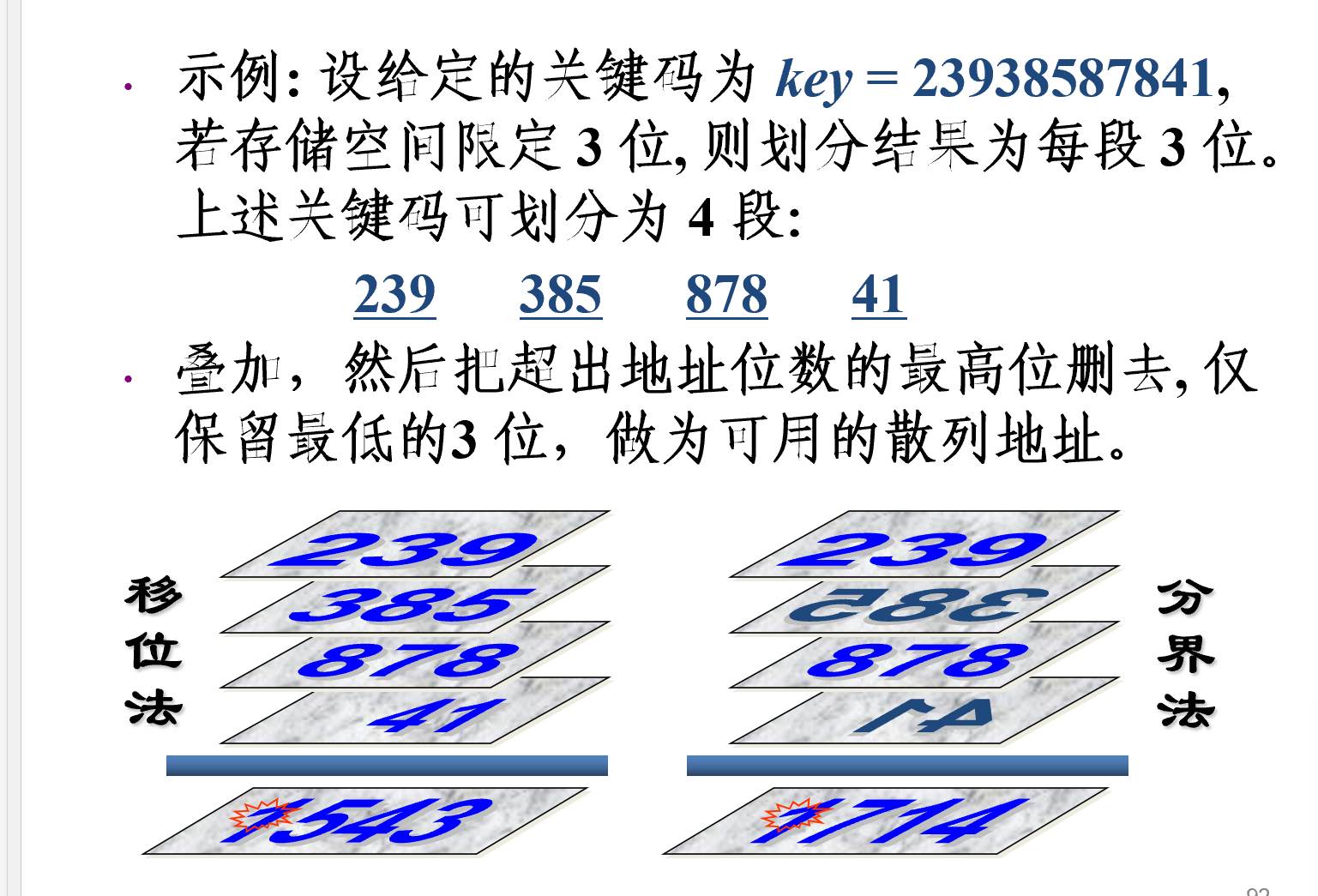
一般当关键码的位数很多，而且关键码每一位上数字的分布大致比较均匀时，可用这种方法得到散列地址。
假设地址空间为 HT[400]，利用以上函数计算，取其中 3 位，取值范围在0～999，可能超出地址空间范围，为此必须将 0～999 压缩到 0～399。可将计算出的地址乘以一个压缩因子 0.4，把计算出的地址压缩到允许范围。

难点¶

冲突处理¶

闭散列方式：线性探查法
发生冲突时顺次查找 \(H_i=(H_{i-1}+1)\%m,i=1,2,\dots,m-1\)
- 注意线性探测需要在到达数组末尾时回到数组开头
搜索成功的平均搜索长度（实际位置-散列位置+1）
搜索不成功的平均搜索长度为：
- 假设每种字母出现概率相同（这决定从什么位置开始搜索直到末尾空白）
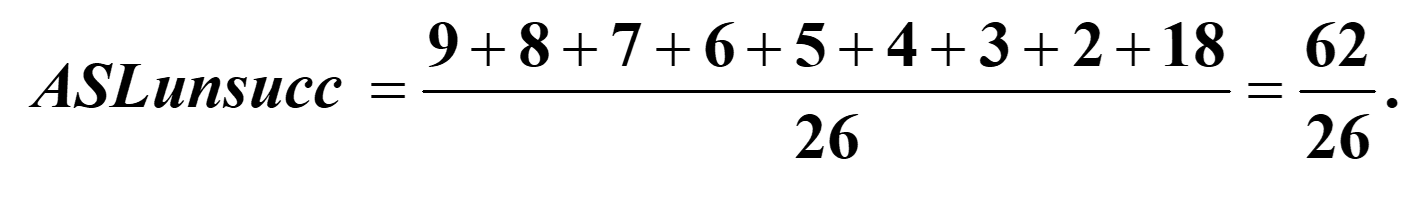
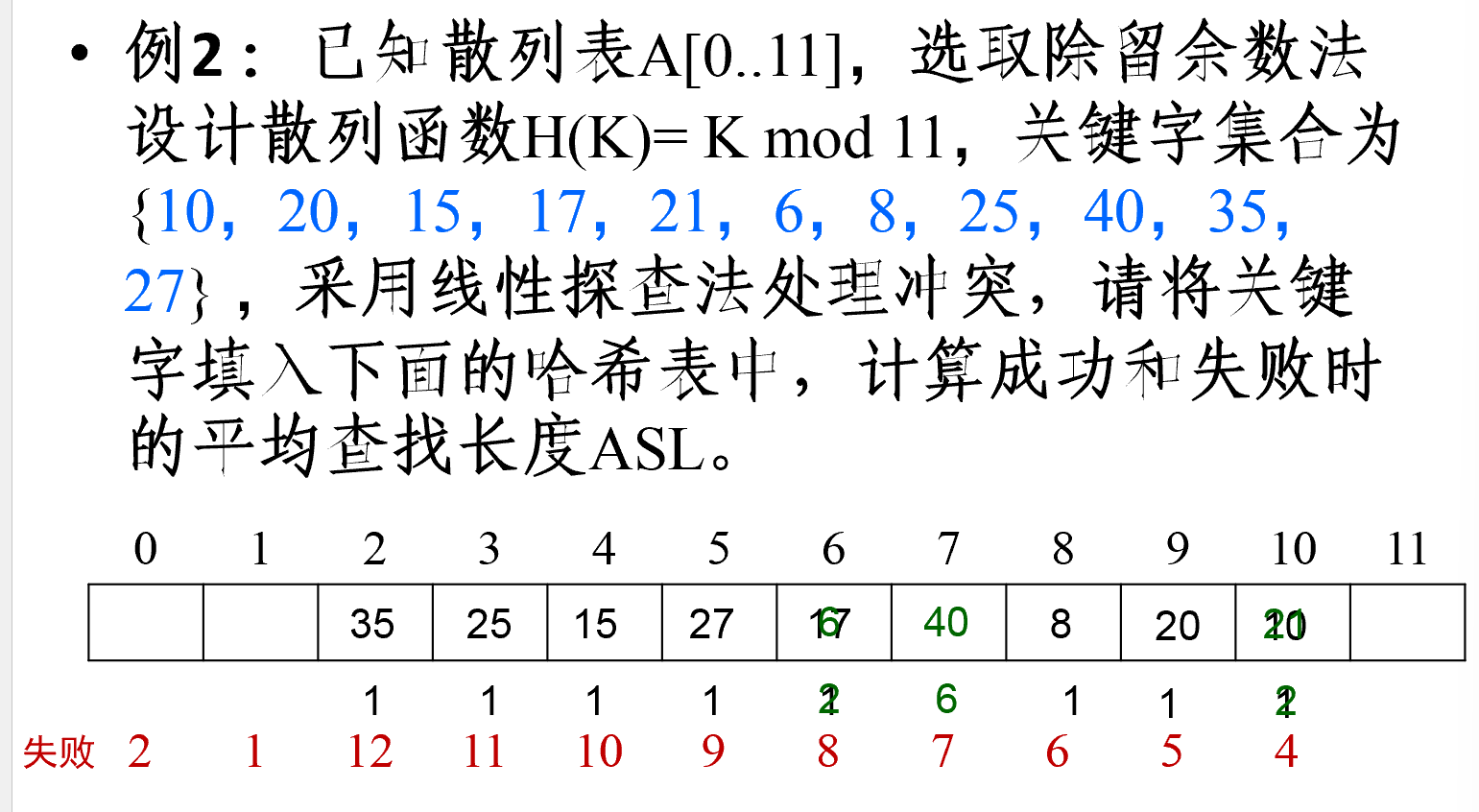
搜索成功的平均比对次数 \((1+1/(1-\alpha))/2\)
开散列方式：链地址法
若设散列表地址空间的位置从 0～m-1, 则关键码集合中的所有关键码被划分为 m 个子集，具有相同地址的关键码归于同一子集，通过一个单链表链接起来。我们称同一子集中的关键码互为同义词。每一个子集称为一个桶。
所有桶号相同的表项都链接在同一个同义词子表中，各链表的表头结点组成一个向量。向量的元素个数与桶数一致。桶号为 i的同义词子表的表头结点是向量中第 i 个元素。
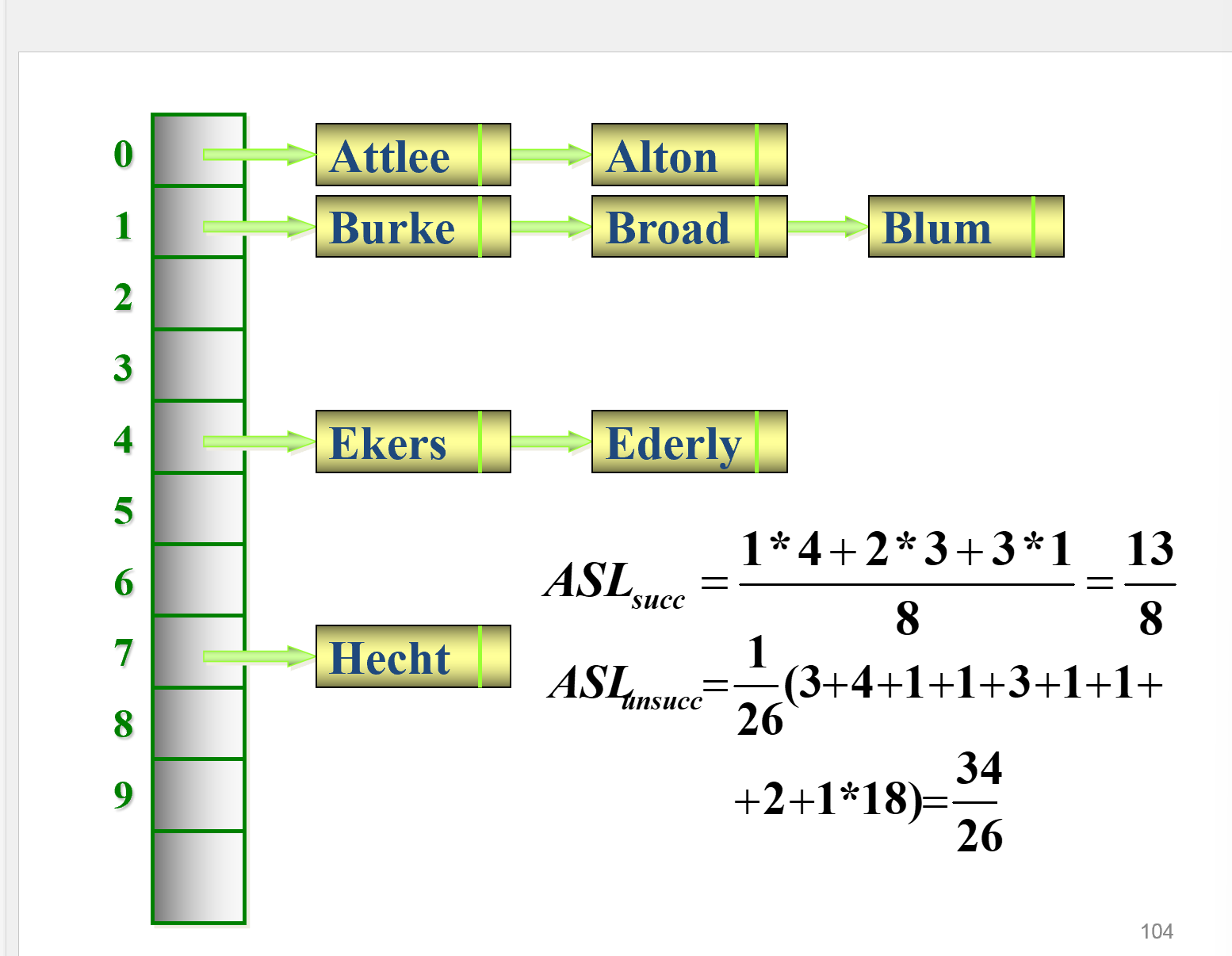
搜索成功的平均比对次数 \(1+\alpha\)
以搜索平均长度为 n / m 的同义词子表代替了搜索长度为 n 的顺序表，搜索速度快得多。

二叉搜索树¶

定义：二叉搜索树或者是一棵空树，或者是具有下列性质的二叉树
每个结点都有一个作为搜索依据的关键码 (key)，所有结点的关键码互不相同。
左子树（如果非空）上所有结点的关键码都小于根结点的关键码。
右子树（如果非空）上所有结点的关键码都大于根结点的关键码。
左子树和右子树也是二叉搜索树。
中序遍历可以得到从小到达的排序

二叉树的操作¶

搜索

template<class K, class E>
BSTNode<K, E>* BST<K, E>::
Search (const K x, BSTNode<K, E> *ptr) {
//私有递归函数：在以ptr为根的二叉搜索树中搜
//索含x的结点。若找到，则函数返回该结点的
//地址，否则函数返回NULL值。
    if (ptr == NULL) return NULL; 
    else if (x < ptr->key) return Search(x, ptr->left);
    else if (x > ptr->key) return Search(x, ptr->right);
    else return ptr;                //搜索成功
};

//非递归版本
template<class K, class E>
    BSTNode<K, E>* BST<K, E>::
Search (const K x, BSTNode<K, E> *ptr) {
    //叉搜索树中搜索含x的结点。若找到，则函数返
    //回该结点的地址，否则函数返回NULL值。
    if (ptr == NULL) return NULL; 
    BSTNode<K, E>* temp = ptr;
    while (temp != NULL) {
        if (x == temp->key) return temp;
        if (x < temp->key) temp = temp->left;
        else temp = temp->right;
    }
    return NULL;
};

搜索失败到达的空节点，就是应该插入元素的位置

插入

template <class K, class E>
    bool BST<K, E>::Insert (const K k1, const E& e1, BSTNode<K, E> *& ptr) {       
        //私有函数：在以ptr为根的二叉搜索树中插入值为
        //<k1,e1>的结点。若在树中已有含<k1,e1>的结点则不插入
        if (ptr == NULL) {     //新结点作为叶结点插入
            ptr = new BSTNode<K, E>(k1,e1); //创建新结点
            if (ptr == NULL)
            { cerr << "Out of space" << endl;  exit(1); }
            return true;
        }
        else if (k1 < ptr->key) Insert (k1,e1, ptr->left);      //左子树插入
        else if (k1 > ptr->key) Insert (k1,e1, ptr->right);     //右子树插入
        else return false;        //已在树中,不再插入
    };

为了向二叉搜索树中插入一个新元素，必须先检查这个元素是否在树中已经存在。即要先进行一次搜索，搜索成功测说明不需要再插入，搜索不成功则说明要将将新元素插入到操作停止的位置
利用二叉树的插入算法来建立二叉树
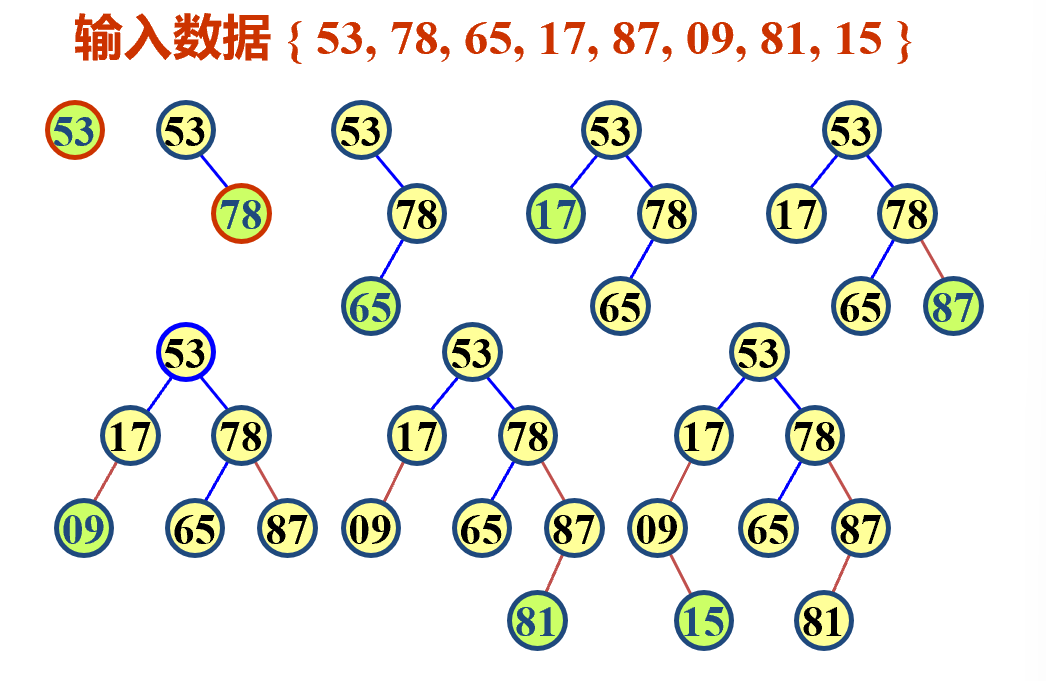
删除维护
删除叶结点，只需将其双亲结点指向它的指针清零，再释放它即可。
被删结点右子树为空，可以拿它的左子女结点顶替它的位置，再释放它。
被删结点左子树为空，可以拿它的右子女结点顶替它的位置，再释放它。

被删结点左、右子树都不为空，可以在它的右子树中寻找中序下的第一个结点 (关键码最小), (左子树最后一个即)用它的值填补到被删结点中，再来处理这个结点的删除问题。

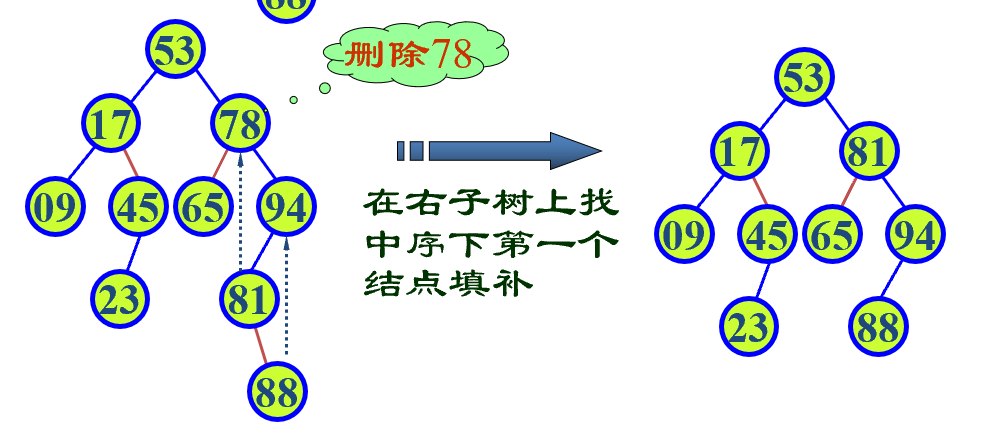
template <class K, class E>
    bool BST<K, E>::Remove (const K x, 
                            BSTNode<K, E> *& ptr) {
        //在以 ptr 为根的二叉搜索树中删除含 x 的结点
        BSTNode<K, E> *temp;
        if (ptr != NULL) {//为null表示不存在
            if (x < ptr->key) Remove (x, ptr->left);    
            //在左子树中执行删除
            else if (x > ptr->key) Remove (x, ptr->right);
            //在右子树中执行删除（找到目标了）
            else if (ptr->left != NULL && ptr->right != NULL)
            {       //ptr指示关键码为x的结点，它有两个子女
                temp = ptr->right;  
                //到右子树搜寻中序下第一个结点
                while (temp->left != NULL) 
                    temp = temp->left;
                ptr->key = temp->key;
                ptr->data = temp->data;
                //用该结点数据代替根结点数据（从右子出发去删除这个换上来的点）
                Remove (ptr->key, ptr->right);
            }
            //至少一个为空
            else {  //ptr指示关键码为x的结点有一个子女
                temp = ptr;
                if (ptr->left == NULL) ptr = ptr->right;
                else ptr = ptr->left;
                delete temp;
                return true;
            }
        }
        return false;
    };

难点¶

AVL 树¶

AVL 树是一种高度平衡的二叉树，或者是空树，或者满足左右子树都是 AVL 树，并且高度差绝对值不超过1
平衡因子
每个节点附加一个数字，给出右子树的高度减去左子树的高度所得的高度差，即节点的平衡因子 bf
取值：-1，0，1（否则就失去了平衡不是 AVL 树了）
高度和平均搜索长度可以保持在 \(O(log_2n)\)

平衡化旋转¶

插入或者删除后可能造成不平衡，需要通过旋转进行调整
左单旋转

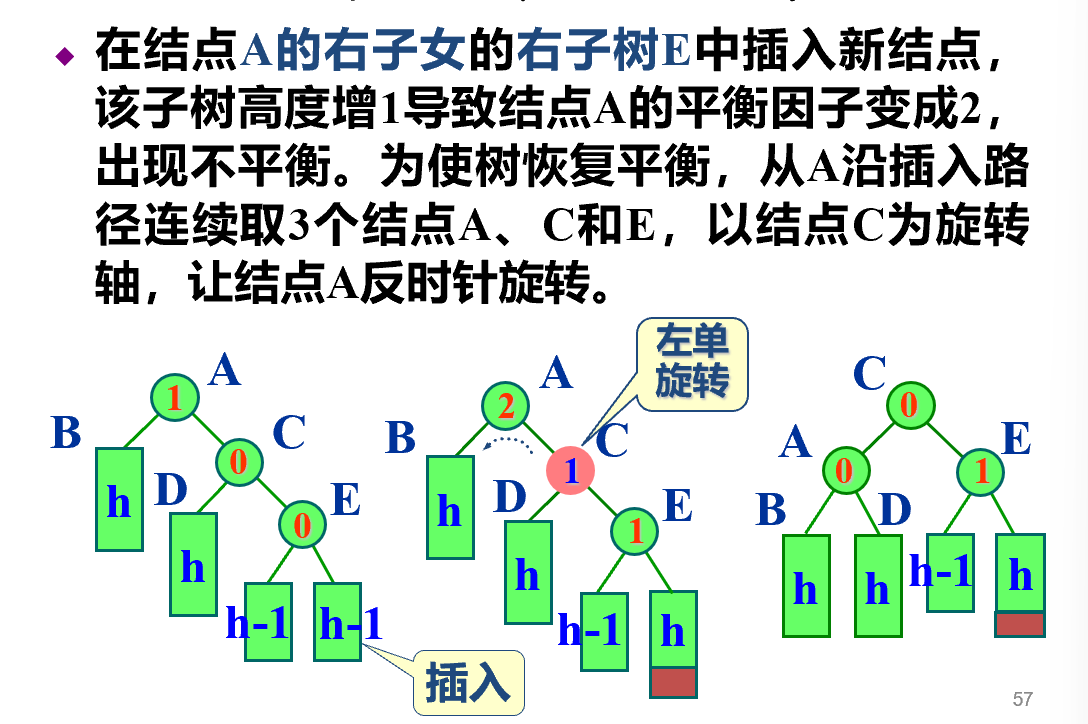
template <class K, class E> 
void AVLTree<K, E>:://ptr会返回为新的跟
RotateL (AVLNode<K, E> *& ptr) {
//右子树比左子树高: 做左单旋转后新根在ptr
     AVLNode<K, E> *subL = ptr;
    ptr = subL->right;
    subL->right = ptr->left;
    ptr->left = subL; 
    ptr->bf = subL->bf = 0;
};

右单旋转

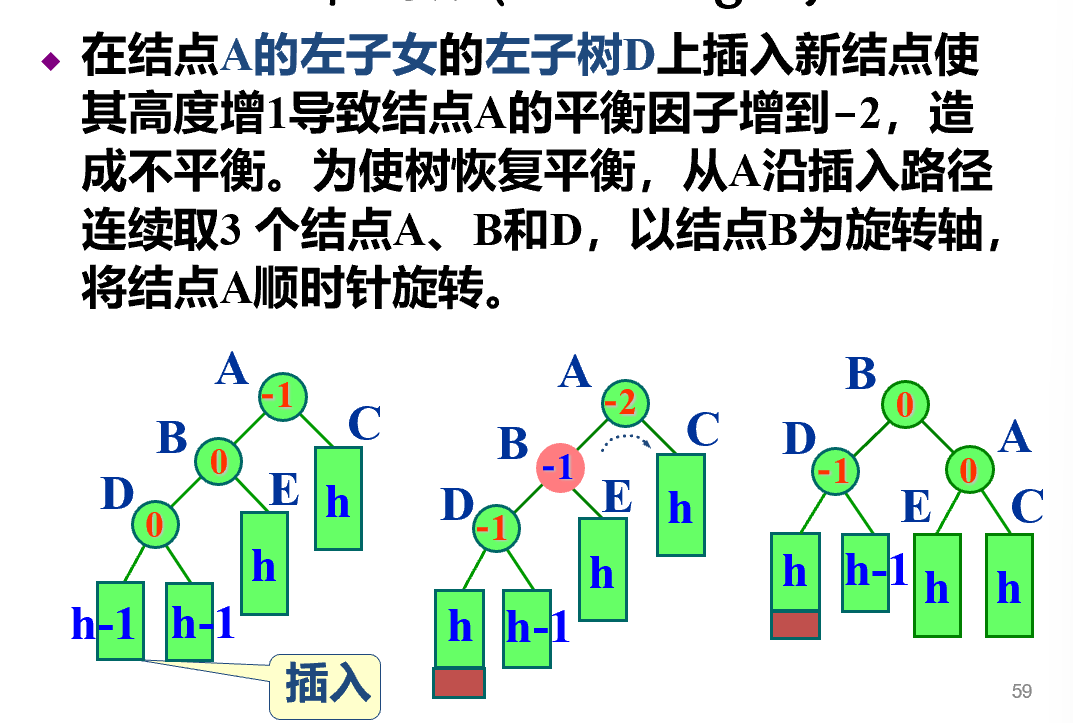
template <class K, class E>
void AVLTree<K, E>::
RotateR (AVLNode<K, E> *& ptr) { 
//左子树比右子树高, 旋转后新根在ptr
    AVLNode<K, E> *subR = ptr;   //要右旋转的结点
    ptr = subR->left;
    subR->left = ptr->right;    
    ptr->right = subR;      
    ptr->bf = subR->bf = 0;
};

先左后右
- 左旋右旋只能处理左侧和右侧的失衡，中间的无法处理，因此先进行一次旋转，将不平衡转移到左右两侧

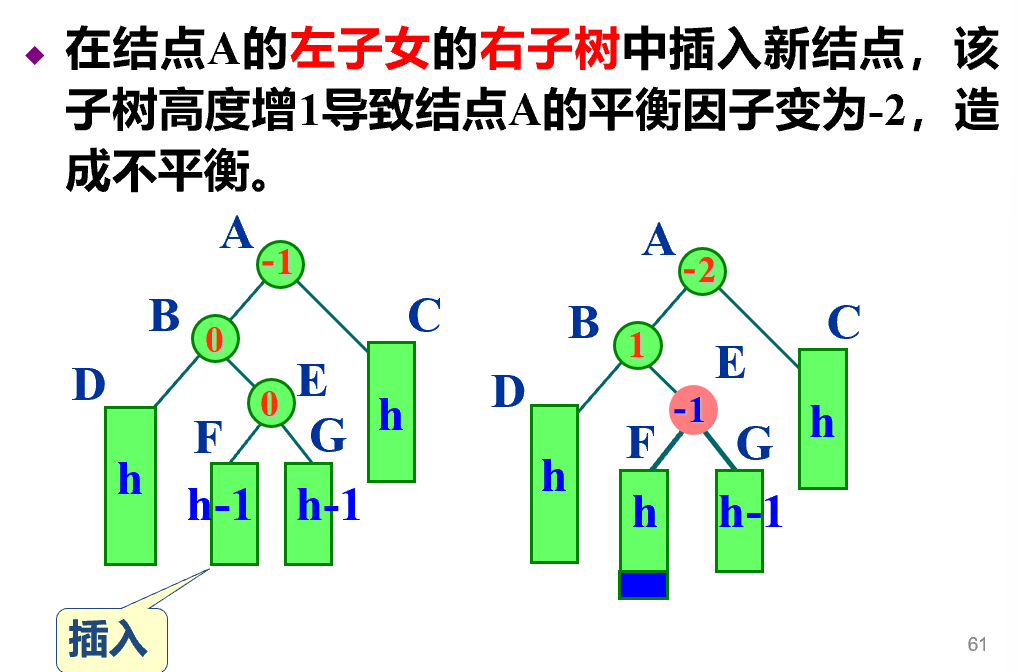
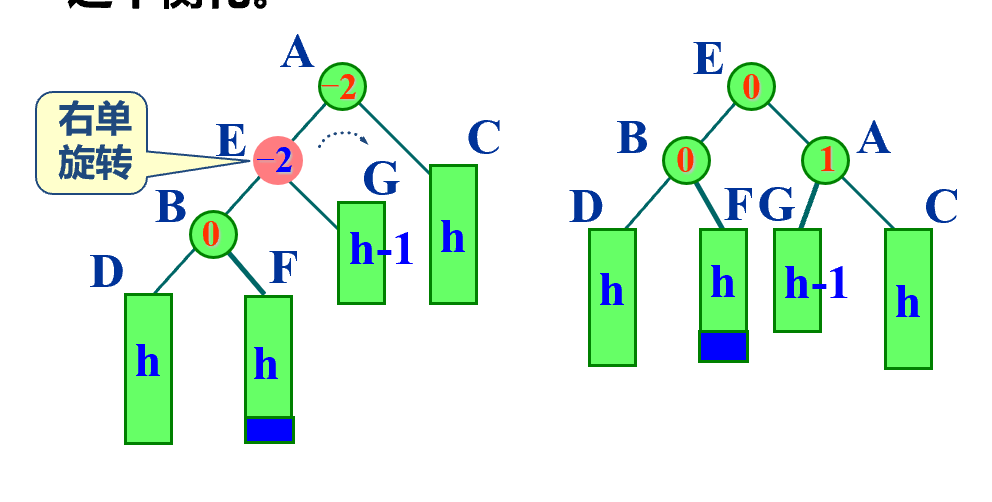
template <class K, class E>
void AVLTree<K, E>:: RotateLR (AVLNode<K, E> *& ptr) {
    AVLNode<K, E> *subR = ptr;
    AVLNode<K, E> *subL = subR->left;
    ptr = subL->right;
    subL->right = ptr->left;
    ptr->left = subL;
    if (ptr->bf <= 0) subL->bf = 0;
    else subL->bf = -1;
    subR->left = ptr->right;
    ptr->right = subR;  
    if (ptr->bf == -1) subR->bf = 1;
    else subR->bf = 0;
    ptr->bf = 0;
};

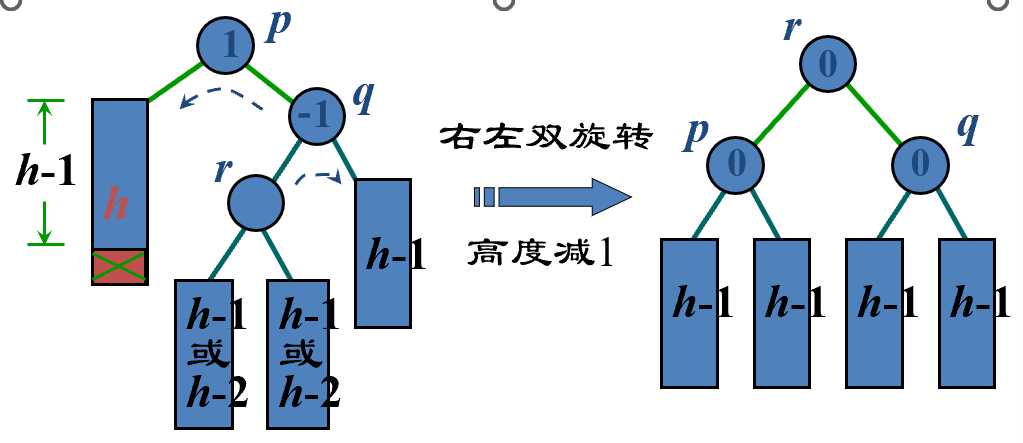
先右后左

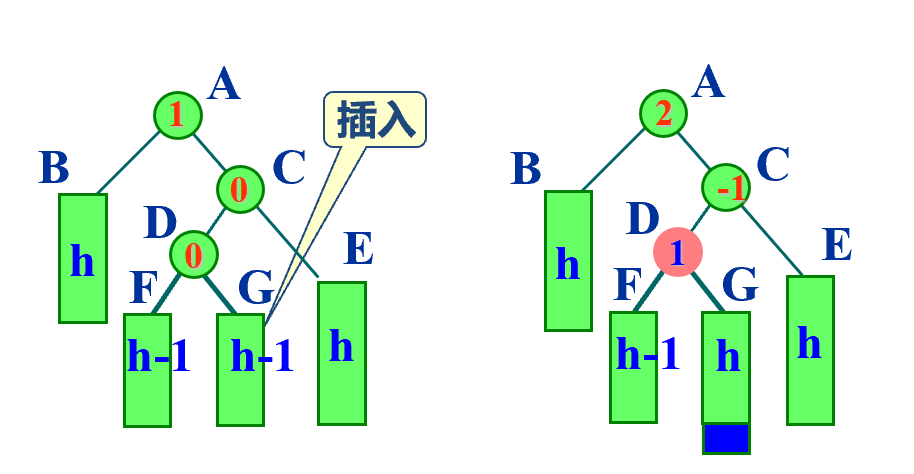
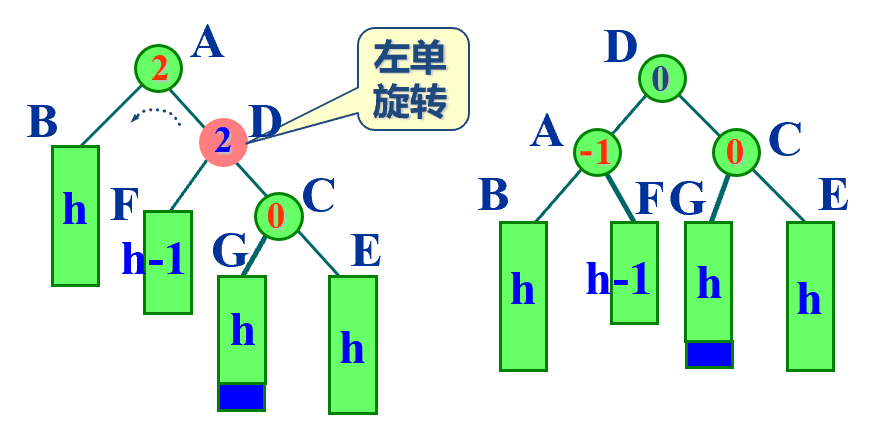
template <class K, class E>
void AVLTree<K, E>::
RotateRL (AVLNode<K, E> *& ptr) {
    AVLNode<K, E> *subL = ptr;
    AVLNode<K, E> *subR = subL->right;
    ptr = subR->left;
    subR->left = ptr->right; 
    ptr->right = subR;
    if (ptr->bf >= 0) subR->bf = 0;
    else subR->bf = 1;
    subL->right = ptr->left;
    ptr->left = subL;
    if (ptr->bf == 1) subL->bf = -1;
    else subL->bf = 0;
    ptr->bf = 0;
};

补充：旋转的原理*
单旋转
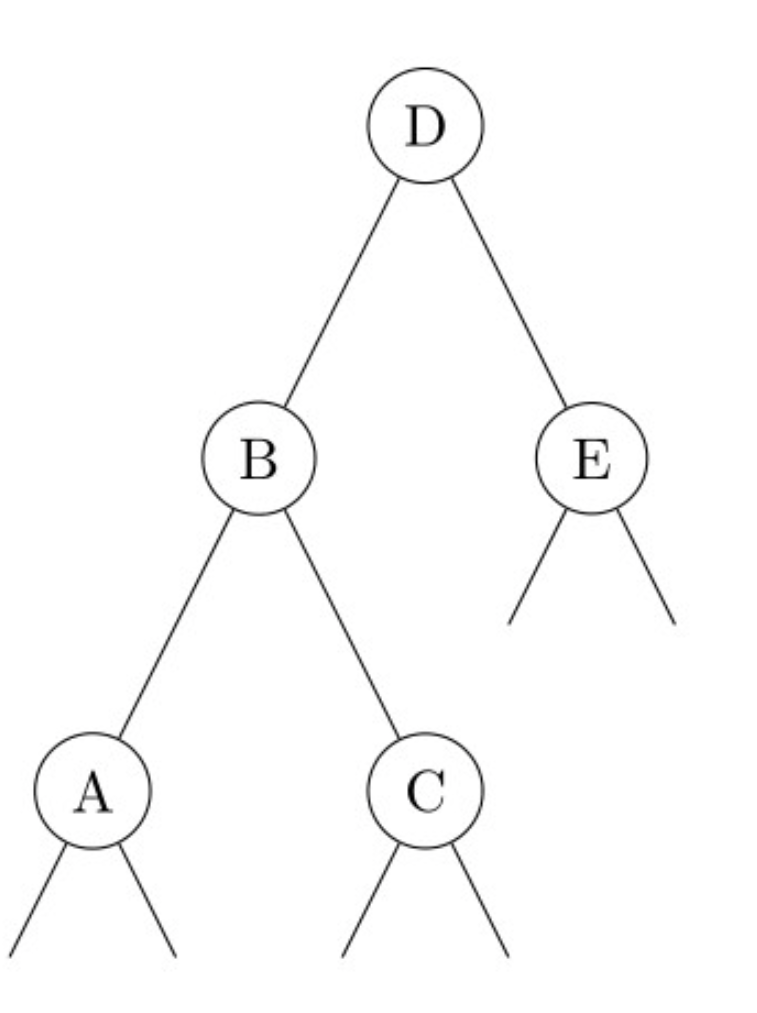
- 假设某次操作后哦 \(bf(D)=-2\) 假设 \(h(A)>=h(C)\)
- \[ 设h(E)=x,则 \begin{cases} h(B)=x+2\\ h(A)=x+1\\ x\leq h(C)\leq x+1 \end{cases} \]
- 对 D 向右旋转，则
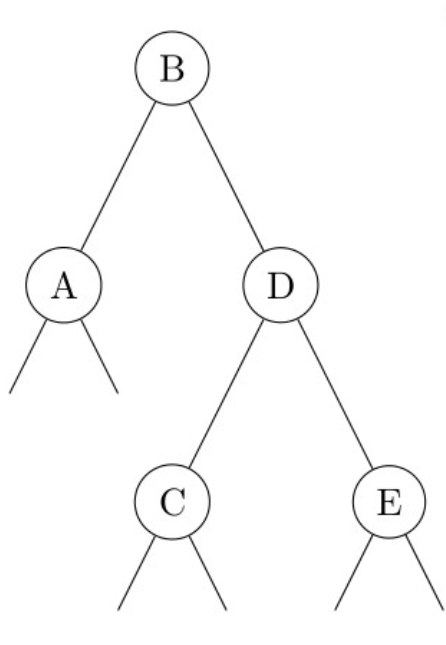
- \[ \begin{cases} 0\leq h(C)-h(E)\leq 1\\ x+1\leq h'(D)=\max(h(C),h(E))+1=h(C)+1\leq x+2\\ 0\leq h'(D)-h(A)\leq 1 \end{cases} \]
双旋转
- \(h(A)<h(C)\)
- \[ \begin{cases} h(B)=x+2\\ h(C)=x+1\\ h(A)=x \end{cases} \]
- 先对节点 B 进行一次左旋操作，再对节点 D 进行一次右旋操作
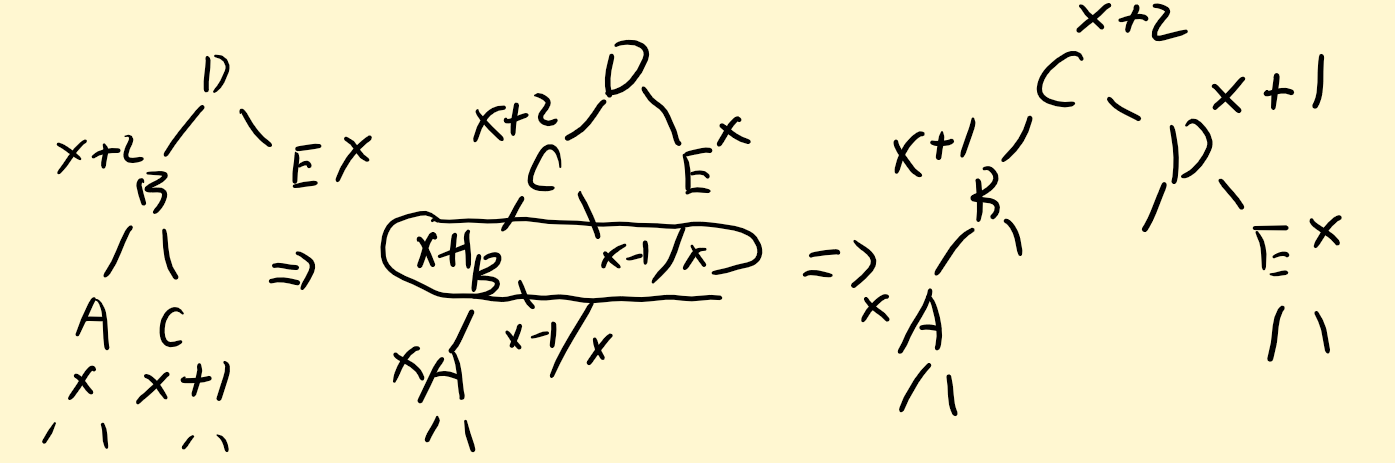
- \[ \begin{cases} x-1\leq h'(rs_B),h'(ls_D)\leq x\\ 0\leq h(A)-h'(rs_B)\leq 1\\ 0\leq h(E)-h'(ls_D)\leq 1\\ h'(B)=\max(h(A),h'(rs_B))+1=x+1\\ h'(D)=\max(h(E),h'(ls_D))+1=x+1\\ h'(B)-h'(D)=0 \end{cases} \]

插入¶

在插入新结点后（向二叉搜索树那样进行失败的查询后在原位置进行插入），需从插入结点沿通向根的路径向上回溯。如果在某一结点发现高度不平衡，停止回溯。从发生不平衡的结点起，沿刚才回溯的路径取直接下两层的结点。
如果这三个结点处于一条直线上，则采用单旋转进行平衡化。单旋转可按其方向分为左单旋转和右单旋转。如果这三个结点处于一条折线上，则采用双旋转进行平衡化。双旋转分为先左后右和先右后左两类。
插入新结点并修改 pr 的平衡因子值后，pr 的平衡因子值有三种情况：
结点 pr 的平衡因子为 0：什么也不需要做（说明向矮的树插入），树的高度不发生变化
\(|bf|=1\)
- 说明插入前 pr 的平衡因子是 0，不需要旋转，但是子树高度加一，需要继续考察双亲节点的平衡状态
\(bf=-2\)
- 在较高的子树插入，需要旋转转化
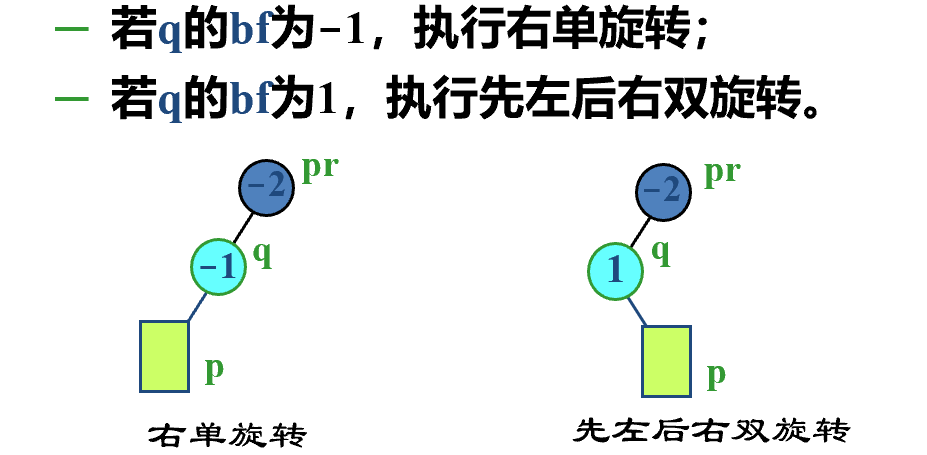
\(bf=2\)
- 右子树高

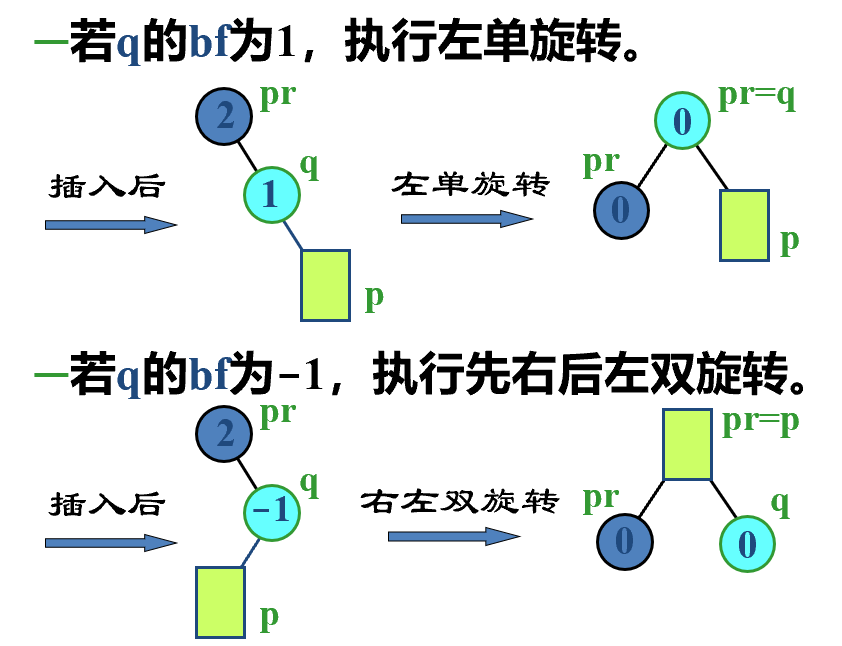
删除¶

如果被删结点 x 最多只有一个子女，可做简单删除:
将结点 x 从树中删去。
如果结点 x 有一个子女，可以简单地把 x 的双亲中原来指向 x 的指针改成指到这个子女结点；
如果结点 x 没有子女，x 双亲原来指向 x 的指针置为 NULL。
将原来以结点 x 的父结点为根的子树的高度减 1。
如果被删结点 x 有两个子女:
搜索 x 在中序次序下的直接前驱 y (同样也可以找直接后继)。
把结点 y 的内容传送给结点 x，现在问题转移到删除结点 y，把结点 y 当作被删结点。
因为结点 y 最多有一个子女，可以简单地用 1. 给出的方法进行删除。
删除 x 之后的维护（必须沿结点 x 的父结点通向根的路径反向追踪高度的变化对路径上各个结点的影响）
用 shorter（一个 bool 变量）指明子树高度是否缩短，初始为 True，在向上遍历检查中，如果 shorter 编程 false 算法终止，否则要进行检查及操作
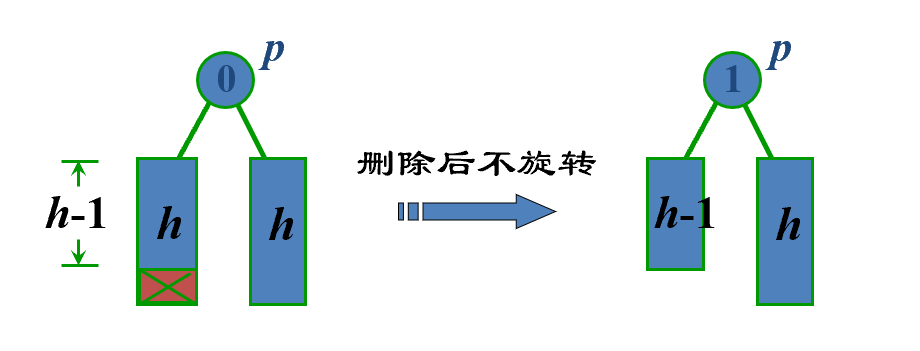
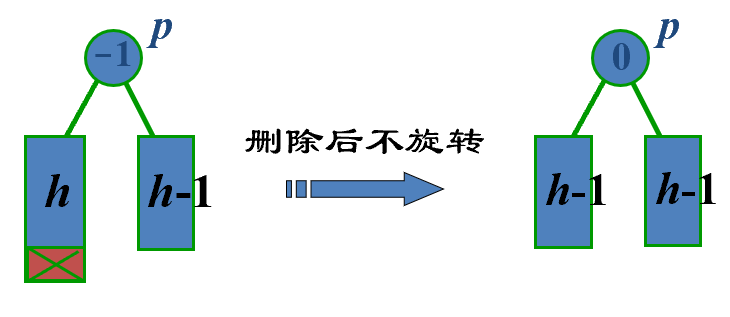
若节点的 bf 为 0，则有一个子树缩短，bf 变为-1/1，但是 shorter 为 false，停止向上
若 bf 不为 0 且较高的子树被缩短。则 p 的 bf 改为 0，同时 shorter 置为 True。还要继续检查上层结点的平衡因子。
结点 p 的 bf 不为 0，且较矮的子树又被缩短。则在结点 p 发生不平衡。需要进行平衡化旋转来恢复平衡。（假设高子树根为 q）
- 如果 q（较高的子树）的 bf 为 0，执行一个单旋转来恢复结点 p 的平衡，置 shorter 为 False。无需检查上层结点的平衡因子。
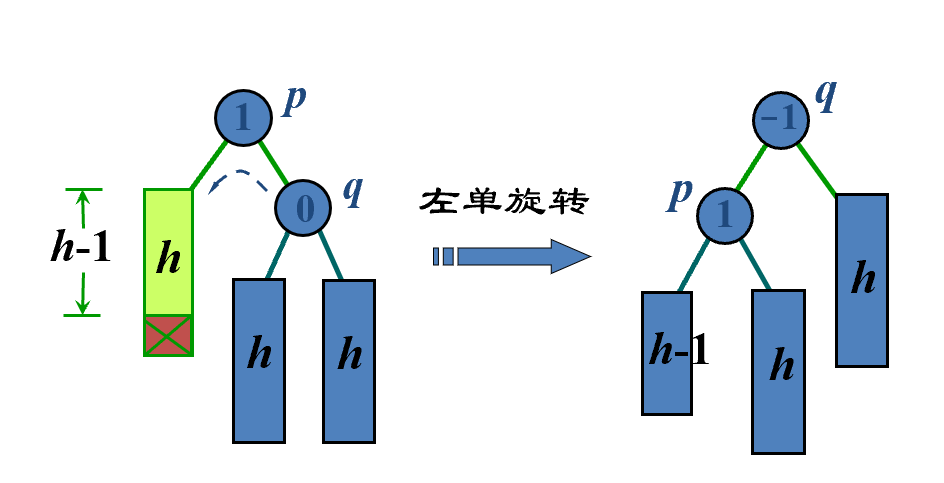
- 如果 q 的 bf 与 p 的 bf 同号，则执行一个单旋转来恢复平衡，结点 p 和 q 的 bf 均改为 0，同时置 shorter 为 True。还要继续检查上层结点的平衡因子。
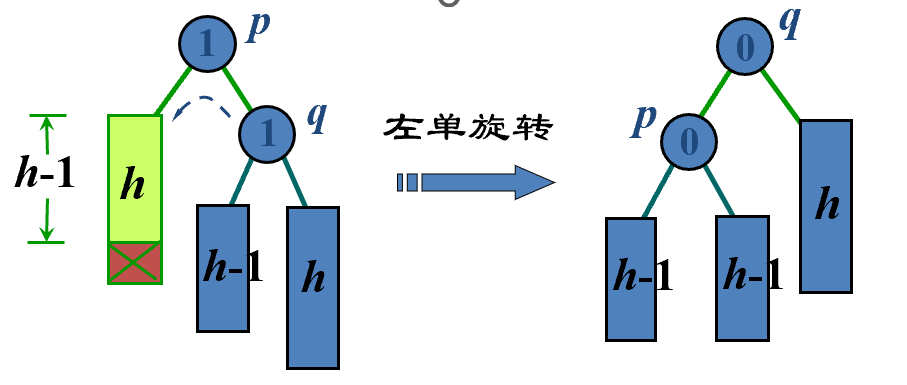
- 如果 p 与 q 的 bf 相反，则执行一个双旋转来恢复平衡。新根结点的 bf 置为 0，其他结点的 bf 相应处理，同时置 shorter 为 True。还要继续检查上层结点的平衡因子。