Skip to content

P13

姓名：田昊东 学号：211275022

编译原理作业 13

9.2.1 image.png image.png|328

^408300

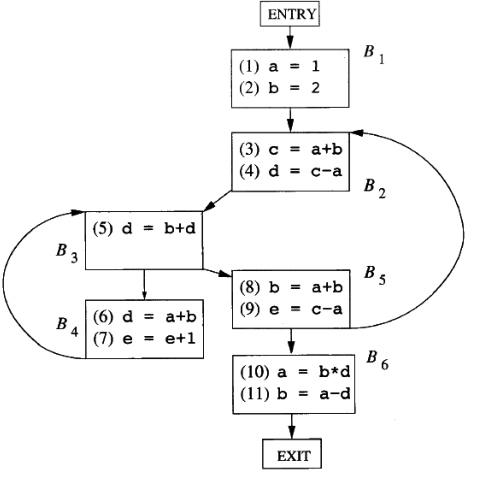
首先计算每个基本块的 \(gen\) 和 \(kill\) - \(gen_{B_{1}}=\{ 1,2 \}kill_{B_{1}}=\{ 8,10,11 \}\) - \(gen_{B_{2}}=\{ 3,4 \}kill_{B_{2}}=\{ 5,6 \}\) - \(gen_{B_{3}}=\{ 5 \}kill_{B_{3}}=\{ 4,6 \}\) - \(gen_{B_{4}}=\{ 6,7 \}kill_{B_{4}}=\{ 4,5,9 \}\) - \(gen_{B_{5}}=\{ 8,9 \}kill_{B_{5}}=\{ 2,7,11 \}\) - \(gen_{B_{6}}=\{ 10,11 \}kill_{B_{6}}=\{ 1,2,8 \}\) 下面通过迭代计算 \(IN\) 和 \(OUT\)

Block \(OUT_{0}\) \(IN_{1}\) \(OUT_{1}\) \(IN_{2}\) \(OUT_{2}\) \(IN_{3}\) \(OUT_{3}\) \(IN_{4}\) \(OUT_{4}\)
\(B_{1}\) 00000000000 00000000000 11000000000 00000000000 11000000000 00000000000 11000000000 00000000000 11000000000
\(B_{2}\) 00000000000 11000001100 11110001100 11001001100 11110001100 11101001100 11110001100 11101001100 11110001100
\(B_{3}\) 00000000000 00110110000 00101010000 11110111100 11101011100 11110111100 11101011100 11110111100 11101011100
\(B_{4}\) 00000000000 00001000000 00000110000 00101010000 00100110000 11101011100 11100111000 11101011100 11100111000
\(B_{5}\) 00000000000 00001000000 00001001100 00101010000 00101001100 11101011100 10101001100 11101011100 10101001100
\(B_{6}\) 00000000000 00000001100 00000000111 00001001100 00001000111 00101001100 00101000111 10101001100 00101000111
EXIT 00000000000 00000000011 00000000011 00000000111 00000000111 00001000111 00001000111 00101000111 00101000111

编译原理作业 14

9.2.3 image.png

首先计算每个基本块的 \(use\) 和 \(def\) - \(use_{B_{1}}=\{ \}def_{B_{1}}=\{ a,b \}\) - \(use_{B_{2}}=\{ a,b \}def_{B_{2}}=\{ c,d \}\) - \(use_{B_{3}}=\{ b,d \}def_{B_{3}}=\{ \}\) - \(use_{B_{4}}=\{ a,b,e \}def_{B_{4}}=\{ d \}\) - \(use_{B_{5}}=\{ a,b,c \}def_{B_{5}}=\{ e \}\) - \(use_{B_{6}}=\{ b,d \}def_{B_{6}}=\{ a \}\) 下面通过迭代计算 \(IN\) 和 \(OUT\)

Block \(IN_{0}\) \(OUT_0\) \(IN_{1}\) \(OUT_{1}\) \(IN_{2}\) \(OUT_{2}\) \(IN_{3}\) \(OUT_{3}\)
ENTRY 00000 00000 00000 00000 00000 00000 00000 00000
\(B_{1}\) 00000 00000 00000 11000 00000 11000 00000 11001
\(B_{2}\) 00000 00000 11000 01010 11000 11111 11001 11111
\(B_{3}\) 00000 00000 01010 11101 11111 11111 11111 11111
\(B_{4}\) 00000 00000 11001 01010 11001 11111 11101 11111
\(B_{5}\) 00000 00000 11100 11010 11110 11010 11110 11011
\(B_{6}\) 00000 00000 01010 00000 01010 00000 01010 00000