P2

姓名：田昊东学号：211275022

编译原理作业p2¶

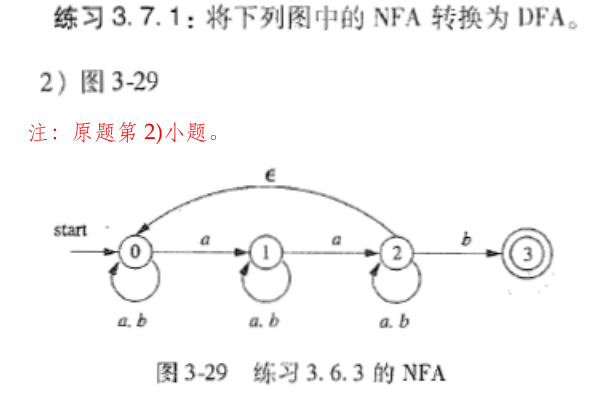
3.7.1

^5865eb

\[ A:\varepsilon-closure(0)=\{0\} \\ B:Dtran[A,a]=\varepsilon-closure(\{0,1\})=\{0,1\}\\ Dtran[A,b]=\varepsilon-closure(0)=\{0\}=A\\ C:Dtran[B,a]=\varepsilon-closure(\{0,1,2\})=\{0,1,2\}\\ Dtran[B,b]=\varepsilon-closure(\{0,1\})=\{0,1\}=B\\ Dtran[C,a]=\varepsilon-closure(\{0,1,2\})=\{0,1,2\}=C\\ D:Dtran[C,b]=\varepsilon-closure(\{0,1,2,3\})=\{0,1,2,3\}\\ Dtran[D,a]=\varepsilon-closure(\{0,1,2\})=\{0,1,2\}=C\\ Dtran[D,b]=\varepsilon-closure(\{0,1,2,3\})=\{0,1,2,3\}=D\\ \]

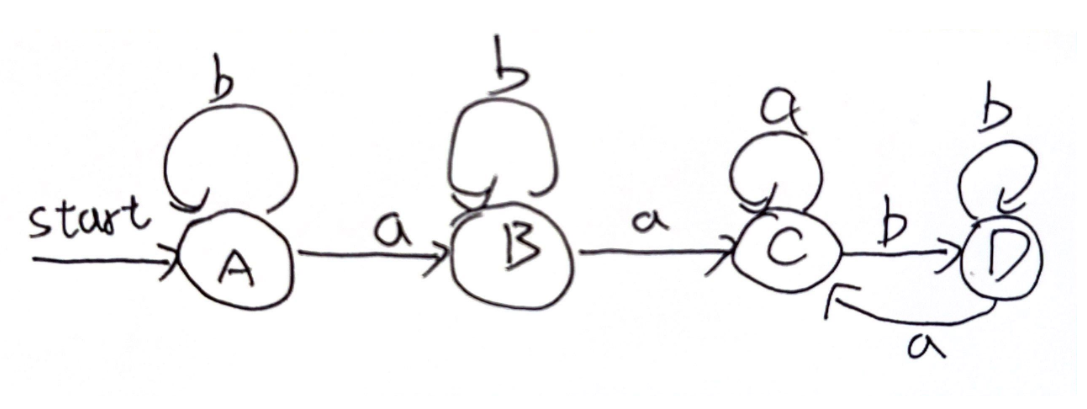
求出Dtran 转换表

NFA 状态	DFA 状态	a	b
{0}	A	B	A
{0,1}	B	C	B
{0,1,2}	C	C	D
{0,1,2,3}	D	C	D

画出DFA

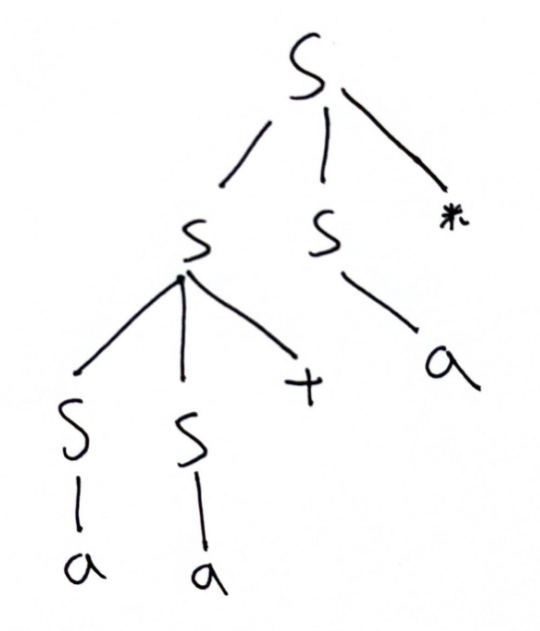
4.2.1

^7e4ebf

$S\to SS*\to SS+S*\to aS+S*\to aa+S*\to aa+a*$
$S\to SS*\to Sa*\to SS+a*\to Sa+a*\to aa+a*$
包含加法和乘法的后缀（逆波兰）表达式

4.4.4

^cc87a2

FIRST
对于产生式$S\to S(S)S|\varepsilon$
存在$S\to\varepsilon$因此加入$\varepsilon$
还存在$S(S)S\to\varepsilon(S)S$因此加入$($
故$FIRST(S) = [(,\varepsilon]$
FOLLOW
$FOLLOW(S)=FIRST(()\bigcup FIRST())\bigcup\$=[(,),\$]$

4.4.5

^1afc12

对于$aa$前两层都会先尝试$aSa$这样在第三层一定就会匹配失败，第二层会去尝试$aa$然后也会失败，最终第一层尝试$aa$匹配成功；
对于$aaaa$前四层都会尝试$aSa$然后再第5层失败，第四层尝试$aa$失败，第三层尝试$aa$会成功，但是之后第二层会发生失败（没有可以匹配右侧的$a$的了）因此第二层会尝试$aa$之后第一层检查，匹配成功
对于$aaaaaaaa$过程类似不再赘述
对于$aaaaaa$同样前六层先尝试$aSa$在第7层会失败，第6层尝试$aa$也会失败，第5层尝试成功，但是第4层失败（没有可以匹配右侧的$a$的了），第四层尝试$aa$成功，第三层成功，第二层失败（没有可以匹配右侧的$a$的了），第二层尝试$aa$成功，第一层成功，但是此时得到$aaaa$只匹配了前4位，并且整个搜索过程已经结束，匹配失败，即无法识别$aaaaaa$

def match_a(inp):
    return inp.read(1) == 'a'

def match_end(inp):
    return inp.read(1) == ''

def match_S(inp):
    fallback = inp.tell()
    if match_a(inp) and match_S(inp) and match_a(inp): return True
    inp.seek(fallback)
    if match_a(inp) and match_a(inp): return True
    return False

def match(inp):
    return match_s(inp) and match_end(inp)