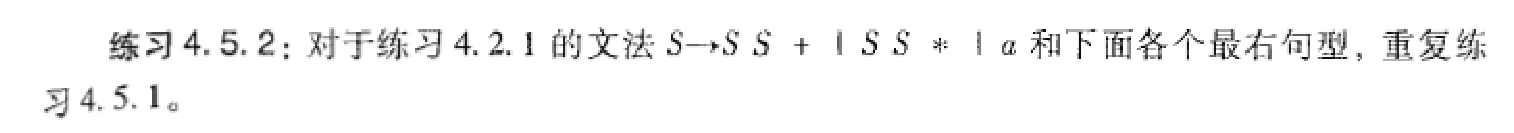P3

姓名：田昊东学号：211275022

编译原理作业 p 3

4.4.1

^4d0474

• 无左公因子，不需要进行提取
• 消除左递归：产生式1、2均存在左递归
• \(bexpr\to bterm \ bexpr'\)
• \(bexpr'\to or \ bterm \ bexpr' \ | \ \varepsilon\)
• \(bterm\to bfactor \ bterm'\)
• \(bterm'\to and \ bfactor \ bterm' \ | \ \varepsilon\)

• \(bfactor \to \ not \ bfactor \ | \ ( bexpr ) \ | \ true \ | \ false\)

• FIRST

• \(FIRST(bexpr)=FIRST(bterm)=FIRST(bfactor)=[not,(,true,false]\)
• \(FIRST(bexpr')=[or,\varepsilon]\)

• \(FIRST(bterm')=[and,\varepsilon]\)

• FOLLOW

• \(FOLLOW(bexpr)=FOLLOE(bexpr')[),\$]\)
• \(FOLLOW(bterm)=FOLLOW(bterm')[or,\$]\)

• \(FOLLOW(bfactor)=[and,\$]\)

• 预测分析表

非终符号/输入	and	or	not	true	false	(	)	$
bexpr			\(bexpr\to bterm \ bexpr'\)	\(bexpr\to bterm \ bexpr'\)	\(bexpr\to bterm \ bexpr'\)	\(bexpr\to bterm \ bexpr'\)
bexpr'		\(bexpr'\to or \ bterm \ bexpr'\)					\(bexpr'\to \varepsilon\)	\(bexpr'\to \varepsilon\)
bterm			\(bterm\to bfactor \ bterm'\)	\(bterm\to bfactor \ bterm'\)	\(bterm\to bfactor \ bterm'\)	\(bterm\to bfactor \ bterm'\)
bterm'	$bterm'\to and bfactor bterm' $	\(bterm'\to \varepsilon\)						\(bterm'\to \varepsilon\)
bfactor			$bfactor \to not bfactor $	$bfactor \to not bfactor $	$bfactor \to not bfactor $	$bfactor \to not bfactor $

4.4.2

^8d3c9c

• 提取公因子
• \(S\to SSop \ | \ a\)

• \(op\to \ + \ | \ *\)

• 消除左递归

• \(S\to aS'\)
• \(S'\to S \ op \ S' \ | \ \varepsilon\)

• \(op\to \ + \ | \ *\)

• FIRST

• \(FIRST(s)=FIRST(s')=[a]\)

• \(FIRST(op)=[+,*]\)

• FOLLOW

• \(FOLLOW(S)=FOLLOW(s')=[+,*,\$]\)

• \(FOLLOW(op')=[a,\$]\)

• 预测分析表

非终符号/输入	a	+	*	$
S	\(S\to aS'\)
S'	\(S'\to S \ op \ S'\)	\(S'\to\varepsilon\)	\(S'\to\varepsilon\)	\(S'\to\varepsilon\)
op		\(op\to+\)	\(op\to*\)

4.5.2

• \(a\)（使用\(S\to a\)）

4.5.3

^66eb46

栈中内容	剩余输入	句柄	操作
$	aaa*a++$		移入
$a	aa*a++$	a	规约 \(S\to a\)
$S	aa*a++$		移入
$Sa	a*a++$	a	规约 \(S\to a\)
$SS	a*a++$		移入
$SSa	*a++$	a	规约 \(S\to a\)
$SSS	*a++$		移入
$SSS*	a++$	SS*	规约 \(S\to SS*\)
$SS	a++$		移入
$SSa	++$	a	规约 \(S\to a\)
$SSS	++$		移入
$SS+	+$	SS+	规约 \(S\to SS+\)
$SS	+$		移入
$SS+	$	SS+	规约 \(S\to SS+\)
$S	$		接受