中间代码生成
中间代码表示¶
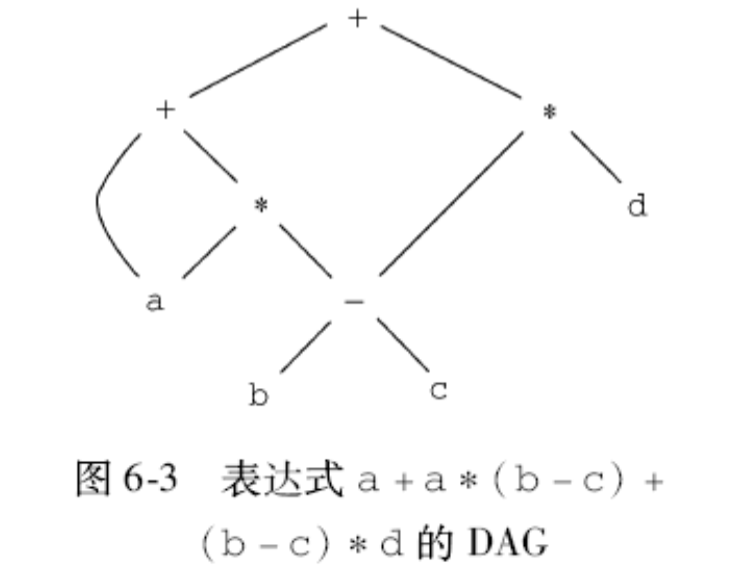
表达式的 DAG¶
- 语法树中,公共子表达式每出现一次,就有一颗对应的子树
- 表达式的有向无环图能够指出表达式中的公共子表达式,更简洁地表示表达式
- DAG 的构造
- 用和构造抽象语法树一样的 SDD 来构造
- 在函数 Leaf 和 Node 每次被调用时,构造新节点前先检查是否存在同样的结点 (值编码+散列表),如果已存在,则返回这个已有结点 docs/学校课程/课程/编译原理/作业/p6#^f11a36|6.1.2
三地址码表示¶
- 三地址码
- 每条指令右侧最多有一个运算符,即
x=y op z 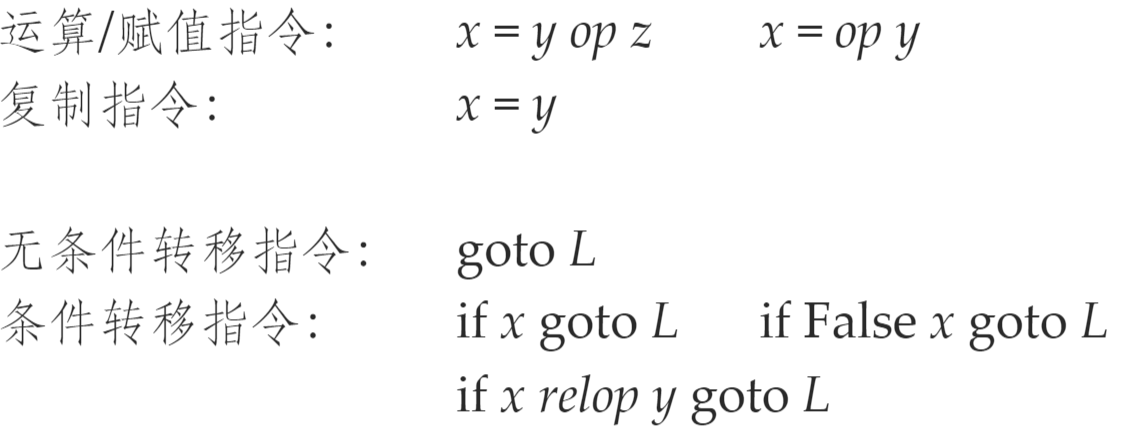

- 每条指令右侧最多有一个运算符,即
- 对于
do i = i + 1; while (a[i] < v);- [

- [
- 在实现时,可使用四元式/三元式/间接三元式/静态单赋值来表示三地址指令
-
三元式
op|arg1|arg2- x = y op z 需要拆分为两个式子
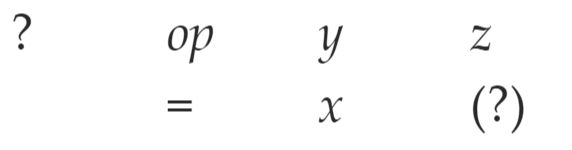
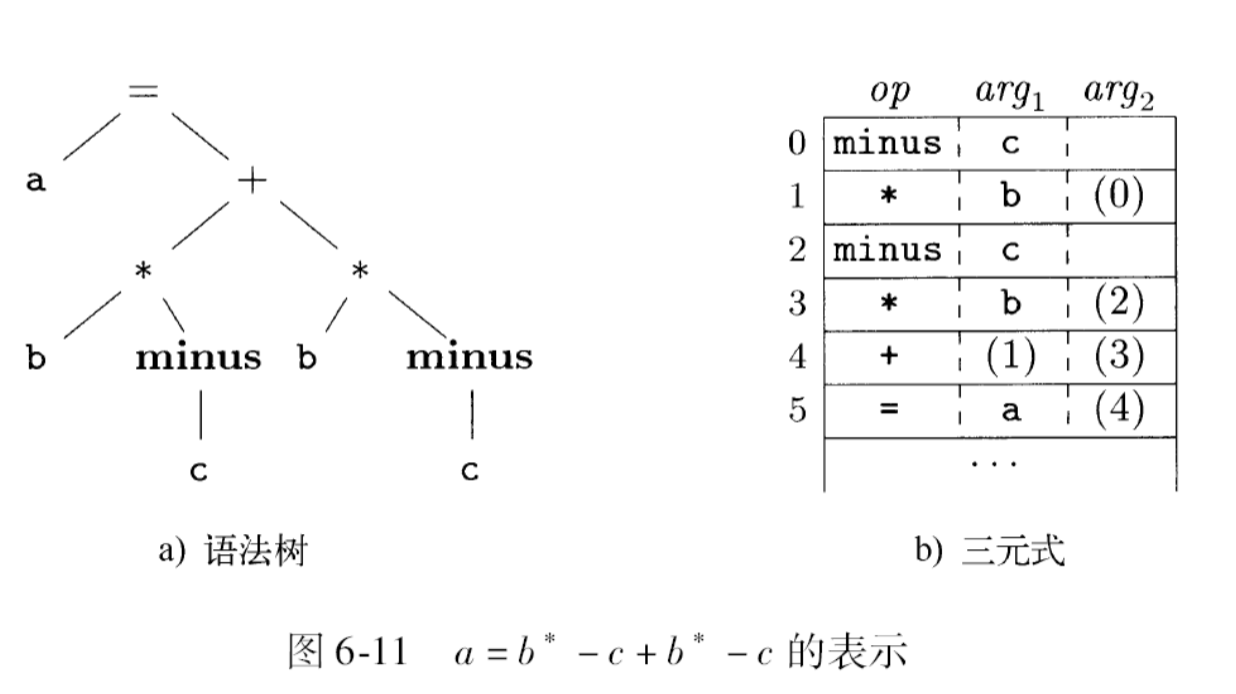
- 优化时经常需要移动/删除/添加三元式,导致三元式运算结果的位置变化
- x = y op z 需要拆分为两个式子
-
四元式

- 单目运算符不使用 arg2;
- param 运算不使用 arg 2 和 result
- 条件/非条件转移将目标标号放在 result 字段

-
间接三元式:解决三元式位置失效的问题
- 包含了一个指向三元式的指针的列表,可对该列表进行操作 (重新排序),完成优化功能,操作时不影响三元式本身

-
静态单赋值
- 所有赋值都是针对具有不同名字的变量
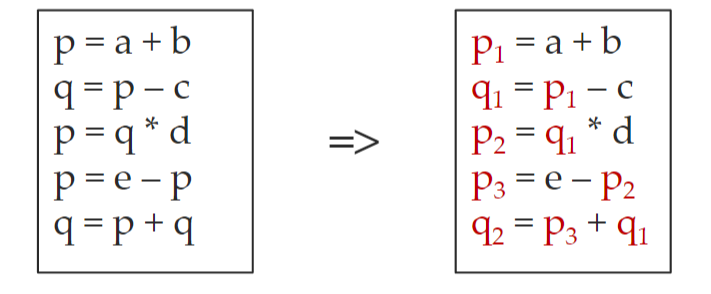
- 对于同一个变量在不同路径中定值的情况,可以使用φ函数来合并不同的定值
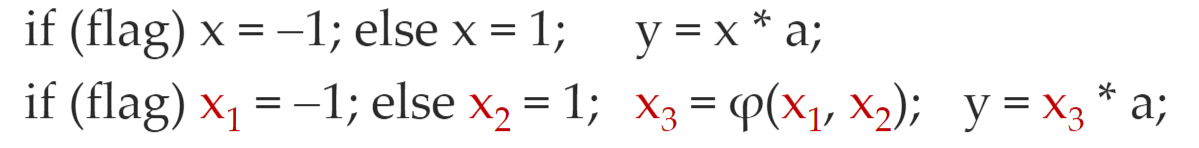
docs/学校课程/课程/编译原理/作业/p6#^a55c5f|6.2.2
类型和声明¶
- 利用一组规则来检查运算分量的类型和运算符的预期类型是否匹配
- 使用类型信息进行差错、确定内存空间、计算数组元素地址、类型转换、选择正确运算符等
类型的表示¶
- 类型表达式
- 基本类型+类型构造算子
- 数组表示:
array(2, array(3, integer))array 就是一个构造算子 - 基本类型是一个类型表达式
boolean,chair,...
- 记录
record包含名字段和数据结构,用于将字段名和类型构造得到记录表达式 - 如果 s 和 t 是类型表达式,其笛卡尔积 s × t 也是类型表达式 (描述列表或元组,如函数参数)
-
struct { int a[10]; float f; }表示为record((a × array(0..9, int)) × (f × real)) -
类型等价
- 结构等价:由相同基本类型;相同构造算子用于结构等价的类型得到;类型别名
- 名等价:类型名仅代表自身,两个类型如果拥有相同的名称,即被认为是名等价的。即使两个类型在结构上完全相同,如果它们的名称不同,它们在名等价的角度是不同的。
SDD 获取类型¶
- 变量的类型信息保存在符号表中
- 变量的类型确定了变量使用的内存(类型的宽度)
-
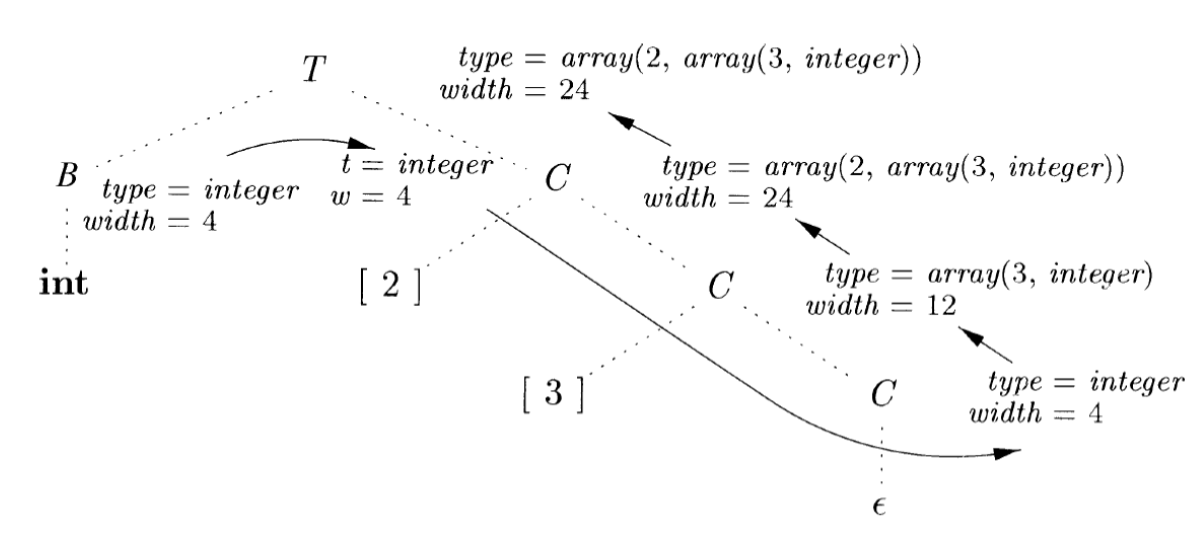
计算类型和宽度的 SDT
-
在处理一个过程/函数时,局部变量应该放到单独的符号表中去
-
这些变量的内存布局独立(相对地址即函数开始地址的距离从 0 开始,变量的放置和声明的顺序相同)
- 使用 offset 记录当前可用相对地址,当分配变量后 offset 增加相应的值

-
类型中的字段
- 一个记录中各个字段的名字必须互不相同
- 记录类型使用一个专用的符号表,对其各个字段的类型和相对地址进行编码

- 首先进入之前保存 top 指向的已有的符号表,然后创建新的符号表,并保存 offset,再重置为 0
- 结束之后通过顾浩表 top 构建记录,并通过 offset 获取宽度,之后恢复环境
类型转化和检查¶
- 给每个组成部分赋予一个类型表达式,通过逻辑规则表达类型表达式必须满足的条件
-
如果编译器中的类型系统能够保证它接受的程序在运行时刻不会发生类型错误,则该语言的这种实现称为强类型的(静态类型)
-
类型综合:根据子表达式类型构造出表达式类型
- 如果 f 的类型为 \(s\to t\) 且 x 为 \(s\) 则 \(f(x)=t\)
- 类型综合是一种自底向上的类型推断方法,它从字面量和变量的类型开始,通过表达式树向上推导到复杂表达式的类型。
-
类型推导:根据语言结构的使用方式来确定类型
- f (x)是一个表达式, 对于某些类型α和β,f 的类型为α \(\to\) β且 x 的类型为α
- 类型推导则是一种更全面的类型检测方法,它不仅仅局限于表达式的直接子元素,而是考虑整个程序的上下文来推导类型。
- 类型推导使得程序员可以在不显式声明类型的情况下编写代码
-
类型转换
- 简单的整数和浮点数计算的类型转化:

- 类型转化分为拓宽和窄化,编译器可以自动完成的为隐式转化,代码指定的为显示转化
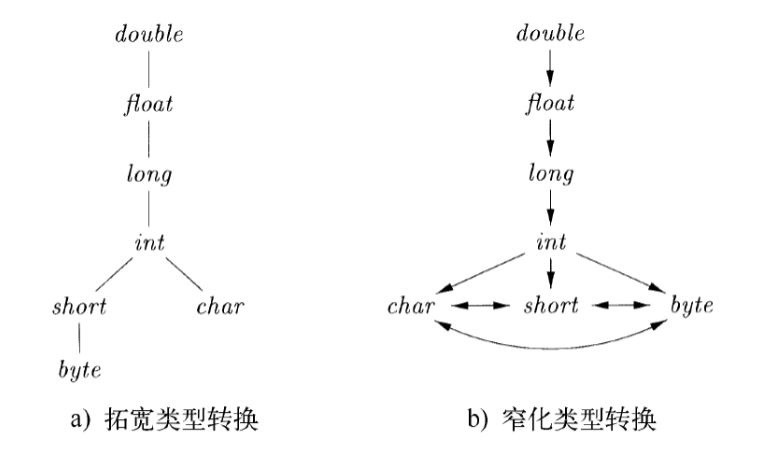
- 对两个类型运算时,可以使用最小公共祖先算法决定转化之后的类型
中间代码生成/翻译¶
- 将表达式翻译为三地址代码
- code 表示代码
- addr 表示存放表达式结果的地址
- newTemp 生成临时变量
- gen 生成指令

- 增量式翻译方案
- 不需要 code 指令保存已有的代码,而是对 gen 的连续调用生成一个指令序列
- gen 不仅构造新的三地址指令,还要将它添加到至今为止已生成的指令序列之后
数组¶
- 数组元素的寻址:如果下标不是从零开始要有
base + (i – low) * w - 数组引用的翻译
- 文法 \(L\to L[E]|id[E]\)
- L.array 是一个指向数组名字对应的符号表条目的指针 (L.array. base 为该数组的基地址)
- L.addr 指示一个临时变量,计算数组引用的偏移量
- L.type 是 L 生成的子数组的类 (宽度由L.type. width 给出, L.type. elem 给出其数组元素的类型)

- L 的代码只计算了偏移量, 数组元素的存放地址应该根据偏移量进一步计算,即 L 的数组基址加上偏移量

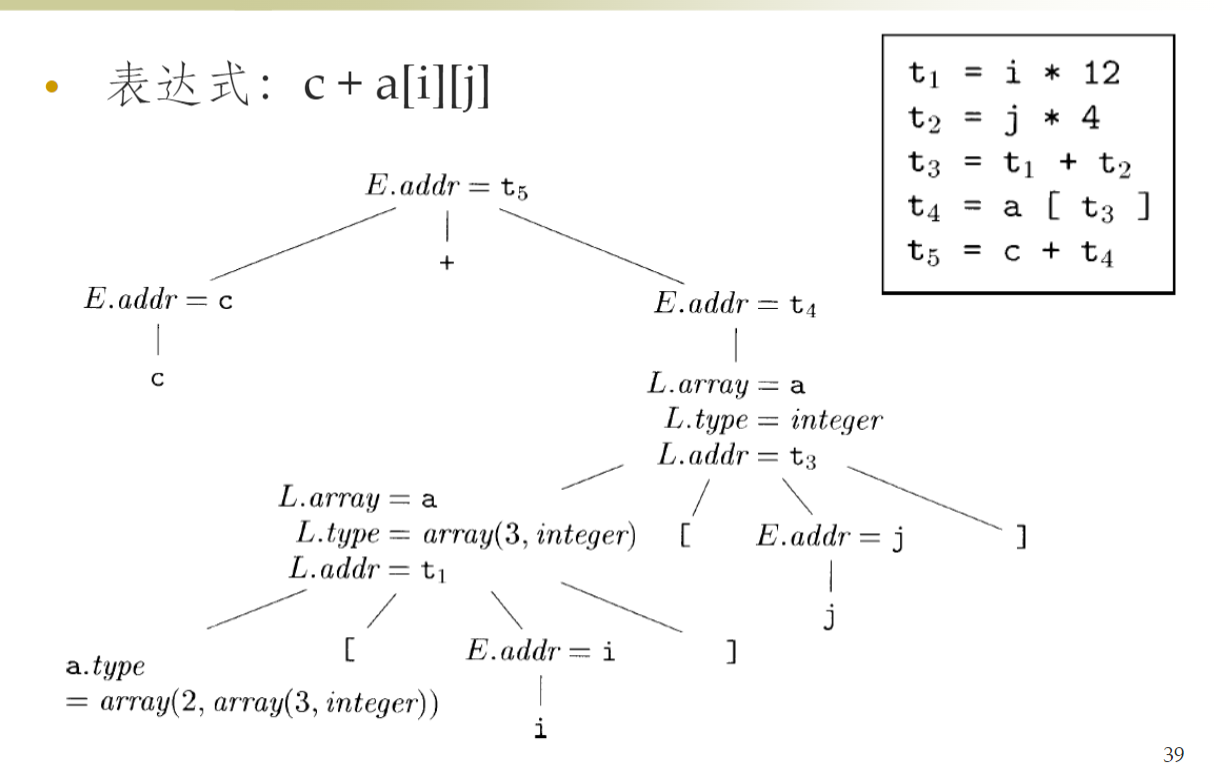
- docs/学校课程/课程/编译原理/作业/p7#^19c96a|6.4.3
控制流¶
- B.true:B 为真时的跳转目标
- B.false:B 为假时的跳转目标
- S.next:S 执行完毕时的跳转目标
- 要注意的是,这只是个属性,存储一下 next 的位置,但是并不是自动跳转,必要时(比如不是顺序)还是需要添加 goto
- B.true 和 B.false 同样如此
- 语法制导定义
- 即
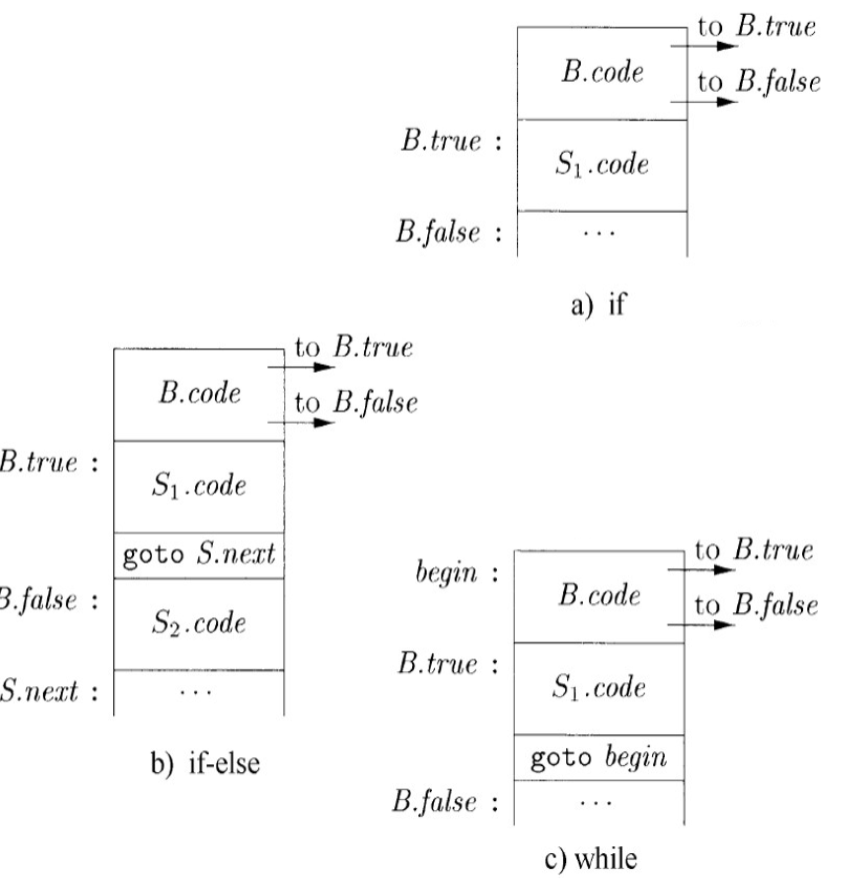 docs/学校课程/课程/编译原理/作业/p8#^690668|6.6.1
docs/学校课程/课程/编译原理/作业/p8#^690668|6.6.1
布尔表达式¶
- 布尔表达式可以用于改变控制流/计算逻辑值
- 文法:
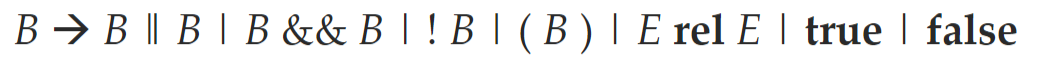
- 布尔表达式的短路求值需要通过跳转指令控制流实现
- 布尔表达式的SDD


- (rel 是比较)
-
生成中间代码
-
此外布尔表达式可能用于求值,此时不需要跳转进行流程控制,还应该根据表达式的不同角色来进行处理
回填¶
- 对于
if(B)S- 按照短路代码的翻译方法,B 的代码中有一些跳转指令在 B 为假时执行这些跳转指令的目标应该跳过 S 对应的代码,但生成这些指令时,S 的代码尚未生成,因此目标不确定
- 希望能一趟处理完成
-
思想:记录 B 中跳转指令
goto S.next的标号,但是先不生成跳转目标,先存储到 list,之后知道目标后统一填入 -
回填技术:
- 生成跳转指令时不指定跳转目标了,使用列表记录这些不完整指令的标号
- 等知道正确的跳转目标时再填写目标(同一个列表中的指令指向同一个目标)
-
综合属性
- truelist:包含跳转指令标号的列表,这些指令在取值 true 时执行
- falselist:包含跳转指令标号的列表,这些指令在取值 false 时执行
-
辅助函数
- makelist (i):创建一个包含跳转指令标号 i 的列表
- merge (p 1 , p 2 ):将 p 1 和 p 2 指向的标号列表合并然后返回
- backpatch (p, i):将 i 作为跳转目标插入 p 的所有指令中
-
添加非终结符 M 用于在需要时获取生成指令的标号

- 使用综合属性是为了在顶层(能看到 M 的位置)对下面 bool 语句跳转进行统一的回填
- 其中的 nextinstr 表示行号,即第几行的 goto 目标在等待填入
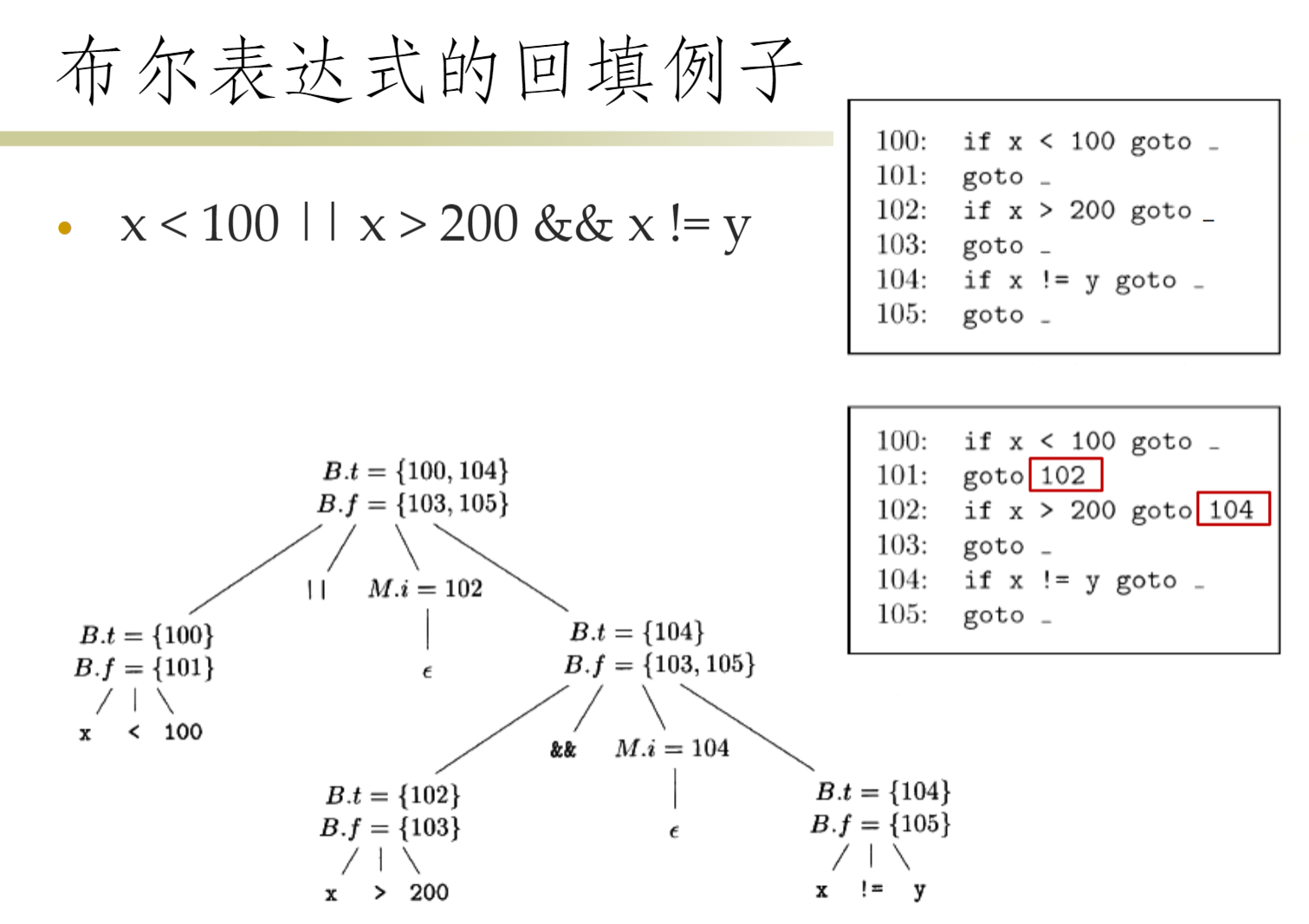
控制转移语句的回填翻译¶
-
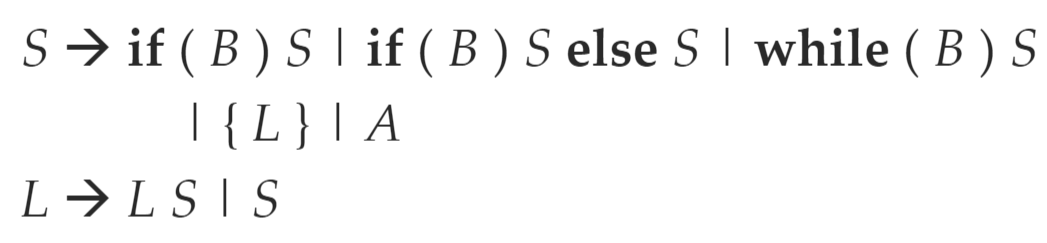
- 对上面布尔表达式回填结果进一步填写,得到完整的最终结果
-
M:同样用M.instr 记录下一条指令的标号
- N:生成 goto 指令坯,类似布尔表达式的回填
- 添加一个N.nextlist 包含该指令标号
- SDD 文法
-
对于 break 和 continue 也使用类似的方法:生成跳转指令胚,并插入到 nextlist 等 list 中
-
switch 语句