Skip to content

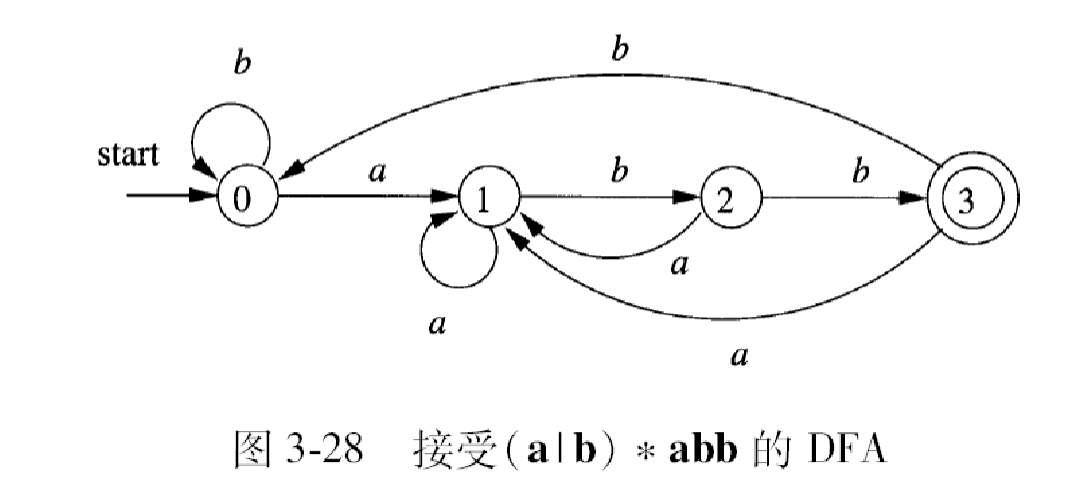
词法分析

词法分析器的作用

  • 读入字符流，组成词素，输出词法单元序列，并将词素提取到符号表
  • 过滤无用的如空白、换行、注释等

  • 词法分析器可以首先完成一些简单的处理工作，并且由于分析过程比语法分析更为简单，可以高效实现

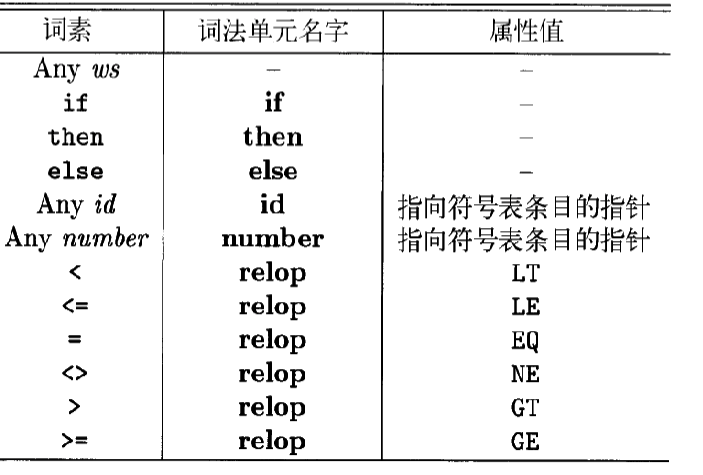
  • 词法单元：<词法单元名、属性值 (可选) >

    • 单元名是表示词法单位种类的抽象符号，语法分析器通过单元名即可确定词法单元序列的结构
    • 属性值通常用于语义分析之后的阶段
    • 一个模式匹配多个词素时必须通过属性来传递附加信息（用于区分），将用于语义分析代码生成等阶段
    • 属性值通常是一个结构化数据，如词素、类型、第一次出现位置等
  • 模式：描述了一类词法单元的词素可能具有的形式
  • 词素：
    • 源程序中的字符序列
    • 它和某个词法单元的模式匹配，被词法分析器识别为该词法单元的实例
  • image.png|500

词法单元的规约（正则表达式）

  • 字母表：有穷符号集合
    • 例子：{ 0, 1 }, ASCII, Unicode
  • 字母表中的串：表中符号的有穷序列
    • 空串：长度为 0 的串，ε
    • 连接：x = dog，y = house，xy = doghouse
    • 指数运算：\(x\) = dog，\(x^0\) = ε，\(x^1\) = dog，\(x^3\) = dogdogdog
  • 语言：某个字母表上串的可数集合
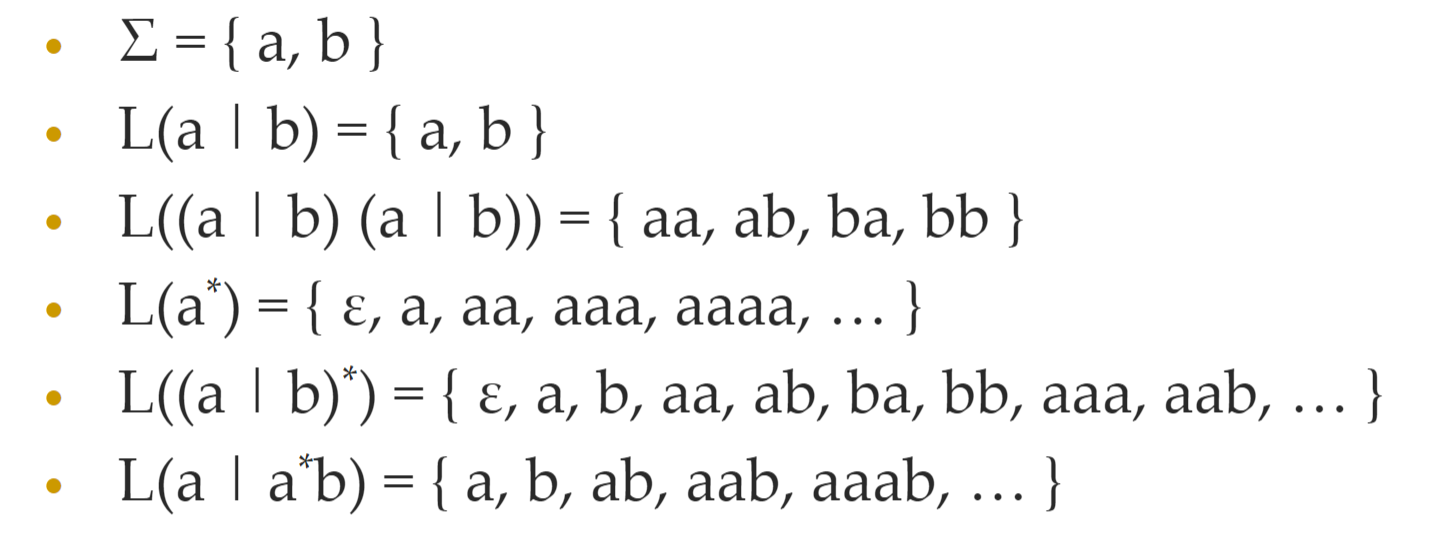
    • image.png|500

  • image.png|475

  • 优先级 * > 连接 > |

  • image.png|500
    • * 表示 0 个或多个相同字符
    • 如果 L (r) = L (s)，正则表达式 r 和 s 等价

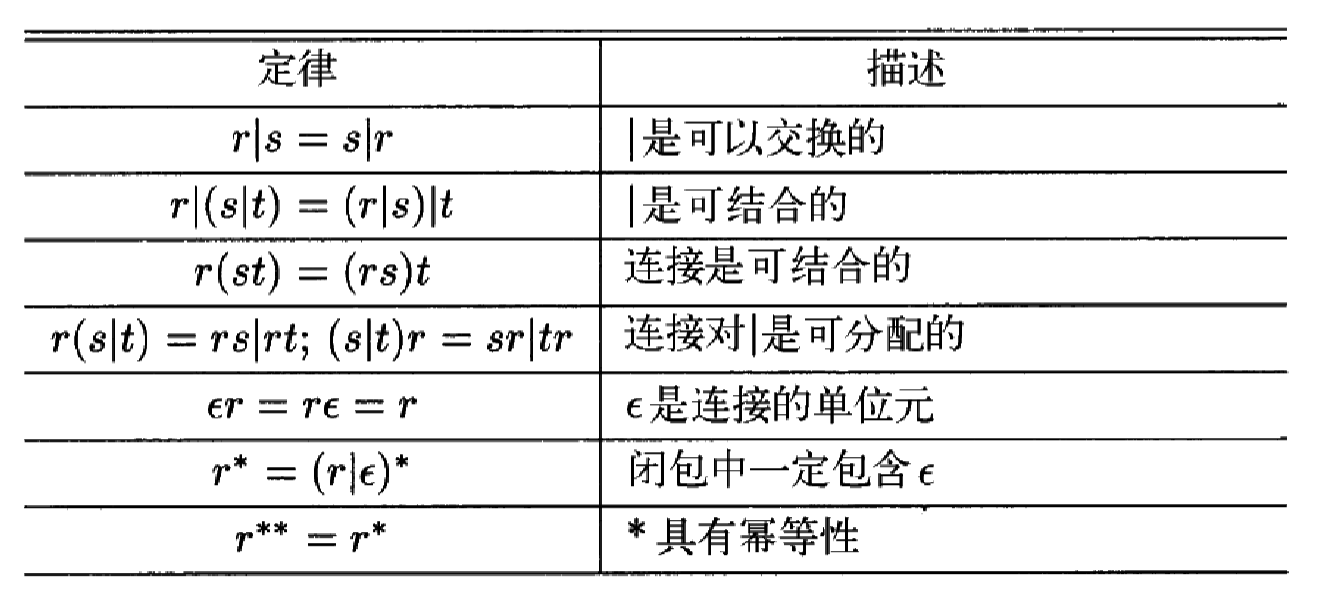
  • 代数定律

    • image.png|500

  • 正则定义（为复杂的正则表达式命名）

    • 一个正则定义是一系列定义的序列，每个定义都将一个名称（\(d_i\)）关联到一个正则表达式（\(r_i\)）
    • \(\sum\) 表示字母表，\(d_{i}\) 不在字母表中并且各不相同
    • \(r_{i}\) 是 \(\sum \cup {d_{1},\dots,d_{i-1}}\) 上的正则表达式（即所有可以用字母表或前面的正则表示的元素）
    • 逐步替换构建正则表达式：
      • 首先，\(d_1\) 的正则表达式就是 \(r_1\)。
      • 然后，为了得到 \(d_2\) 的正则表达式，你需要在 \(r_2\) 中将所有的 \(d_1\) 替换为 \(r_1\)。
      • 依此类推，为了构建 \(d_i\) 的正则表达式，你需要在 \(r_i\) 中将所有的 \(d_{1},\dots,d_{i-1}\) 替换为它们各自的正则表达式。
    • 通过正则定义可以自底向上逐步构建复杂的正则表达式
    • image.png|500

  • 正则表达式的扩展

    • \(r^+=rr^*\)
    • \(r?=ε |r\)
    • \[abcf]等价于 a | b | c | f
    • \[a−e]等价于 a | b | c | d | e

词法单元的识别（状态转换图）

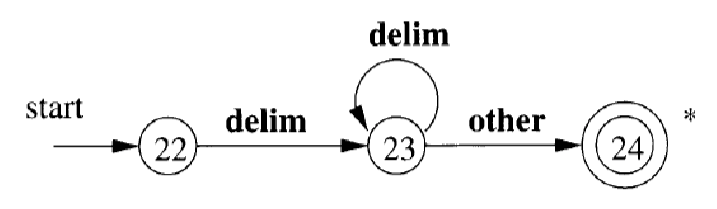
  • 定义 \(ws → (blank | tab | newline)^+\) 来消除空白

    • 词法分析器识别出这个模式时，不返回词法单元，继续识别其它模式
    • image.png|375

  • 一些词法单元的定义

    • image.png
    • image.png|500

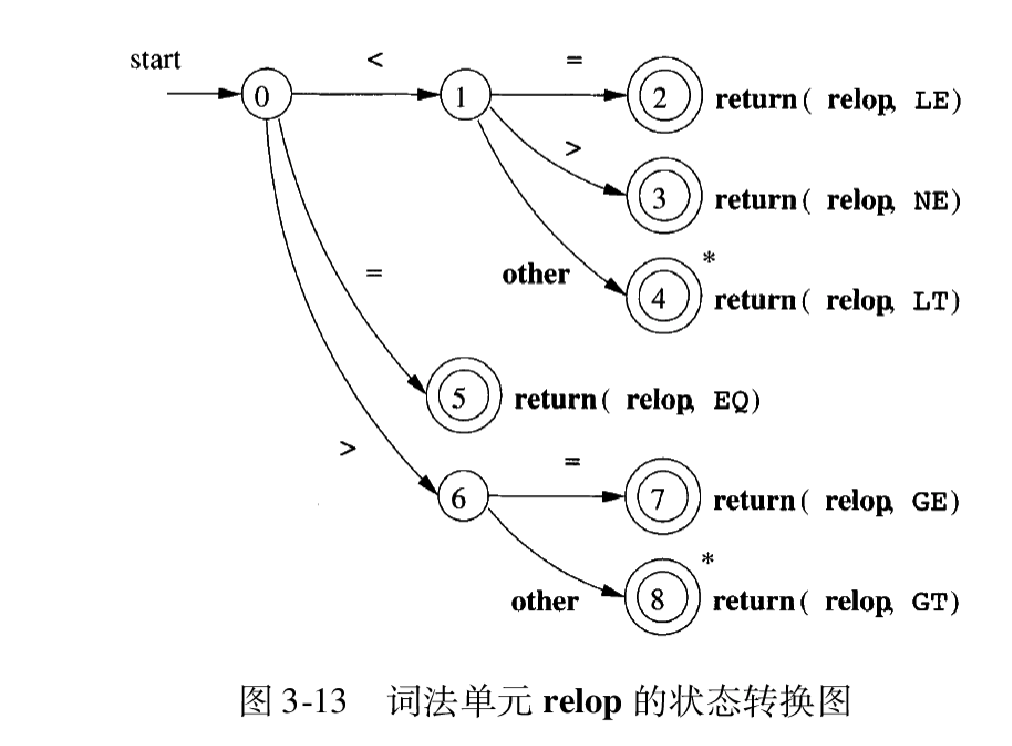
  • 状态转换图：

    • 状态：表示在识别词素时可能出现的情况
      • 某些状态为接受状态或最终状态，表明已找到词素
      • 加上*的接受状态表示最后读入的符号不在词素中
      • 开始状态 (初始状态)：用 Start 边表示
    • 边：从一个状态指向另一个状态
    • image.png|450

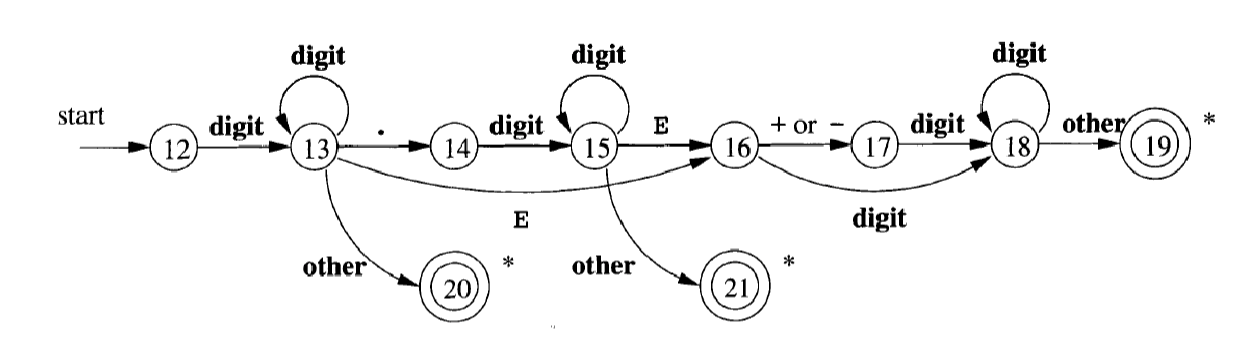
  • 识别无符号数（整数、小数、科学计数法）的状态转移图

    • image.png|475

  • 保留字的处理：

    • 一些解决保留字和标识符冲突的方法：在符号表中先填入保留字指明不是普通标识符；建立独立的高优先级的状态转换图
    • image.png|475

  • 处理多模匹配（实际处理保留字的方法）：

    • 按照优先级，顺序地尝试各个状态转换图，如果引发 fail ()，回退并尝试下一个状态图
    • 更好的方法：并行地运行各个状态转换图；通过 greedy 策略，识别最长的与某个模式匹配的输入前缀
    • 实际使用的方法：预先把各个状态转换图合成一个状态转换图，然后运行这个状态转换图

  • 工作方式：

    • Lex 生成的词法分析器作为一个函数被调用，不断读入余下的输入符号
    • 发现最长的、与某个模式匹配的输入前缀时：调用相应的动作，该动作进行相关处理；之后词法分析器继续寻找其它词素

  • 冲突解决方式：多个输入前缀与某个模式相匹配，或者一个前缀与多个模式相匹配

    • 多个前缀可能匹配时，选择最长的前缀
    • 最长的前缀与多个模式匹配时，选择列在前面的模式（因此字符表中按照优先级进行排序）

有穷自动机

  • 分类
    • 不确定的有穷自动机 NFA：
      • 存在多种选择的问题，一个符号可以出现在离开同一状态的多条边上，并且ε可以做标号
    • 确定的有穷自动机 DFA：
      • 对于每个状态及每个符号，有且只有一条边
    • 对于每个可以用正则表达式描述的语言，均可用某个 NFA 或 DFA 来识别

NFA

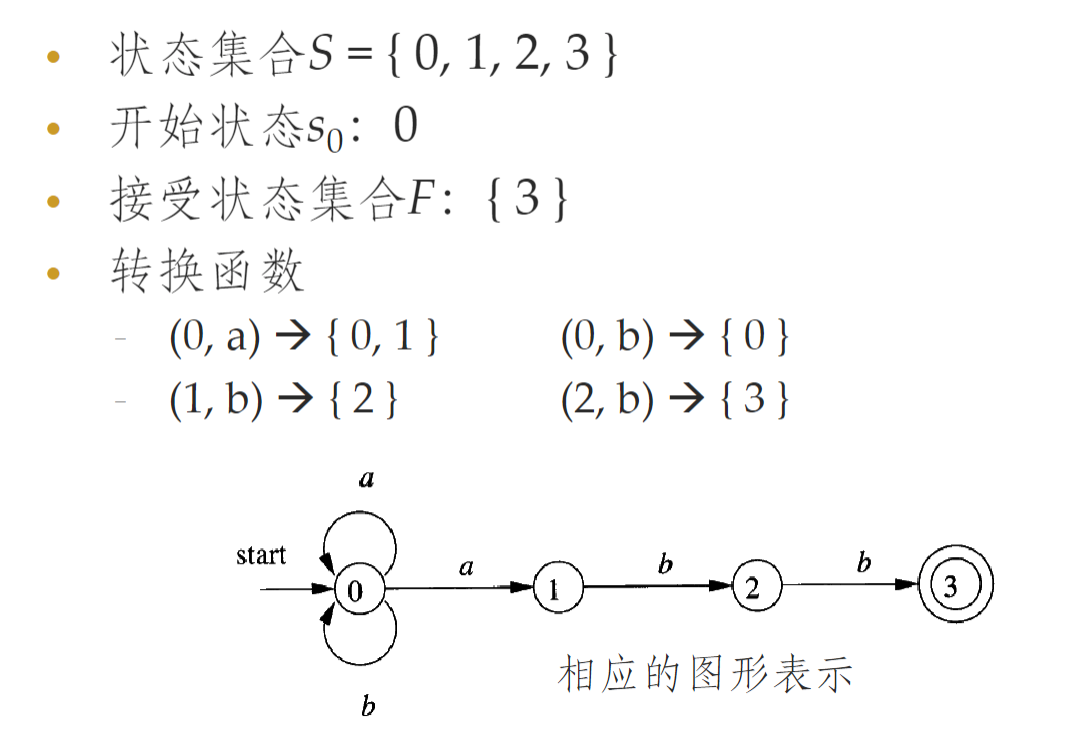
  • 定义：
    • 有穷状态集合 S
    • 输入符号集合 Σ （字母表）
    • 转换函数：对于每个状态给出后继状态的集合
    • S 中的 \(s_{0}\) 指定为开始状态
    • S 子集 F 接受状态集合

  • image.png|450

  • 转换表表示：用二维表表示

    • 每行一个状态，每列一个输入符号，每个条目对应后继状态集合
    • image.png|375
  • docs/学校课程/课程/编译原理/作业/p1#^bf07a9|3.6.5
  • NFA 接受输入字符串：当且仅当对应的转换图中存在一条从开始状态到某个接受状态的路径，且该路径各条边上的标号按顺序组成 x
  • NFA 接受的语言：从开始状态到达接受状态的所有路径的标号串的集合
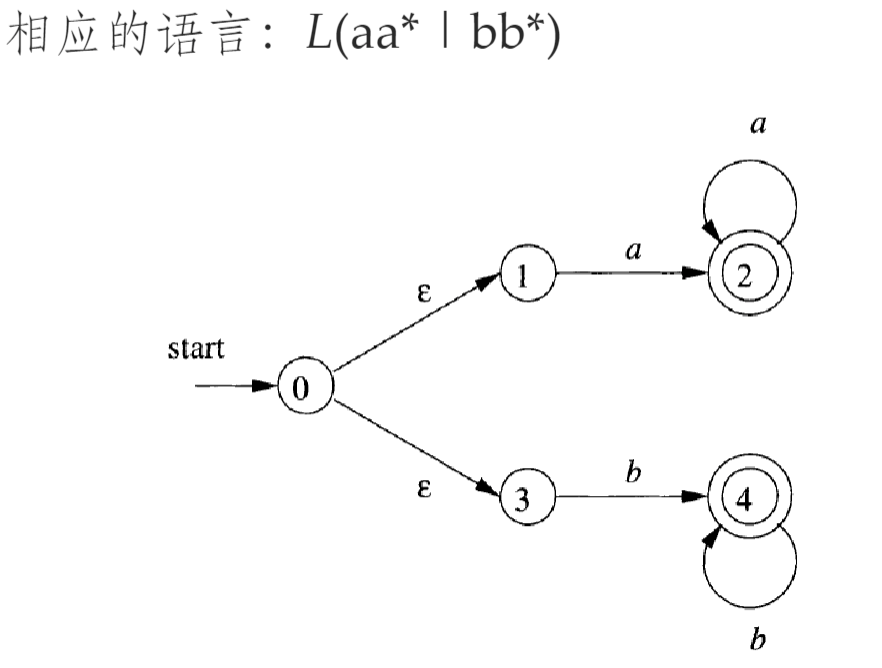
  • image.png|425

DFA

  • 注意 DFA 有唯一的初始状态
  • NFA 被称为 DFA，当：
    • 没有标号为ε的转换
    • 对于每个状态 s 和每个输入符号 a，有且仅有一条标号为 a 的离开 s 的边
  • 每个 NFA 都有一个等价的 DFA

  • DFA 可以更高效的进行模式匹配

  • DFA 的模拟运行

    • image.png|475

  • 从正则表达式到自动机：正则表达式->NFA->DFA

正则表达式 到 DFA 的转化

  • 子集构造法：

    • 构造得到的 DFA 的每个状态和 NFA 的状态子集对应
    • DFA 读入 a1, a2, …, an 后到达的状态对应于从 NFA 开始状态出发沿着 a1, a2, …, an 可能到达的状态集合
    • 在算法中“并行地模拟”NFA 在遇到一个给定输入串时可能执行的所有动作
    • 最坏情况下 DFA 的状态个数会是 NFA 状态个数的指数多个（但在大多情况下状态数目大致相同）

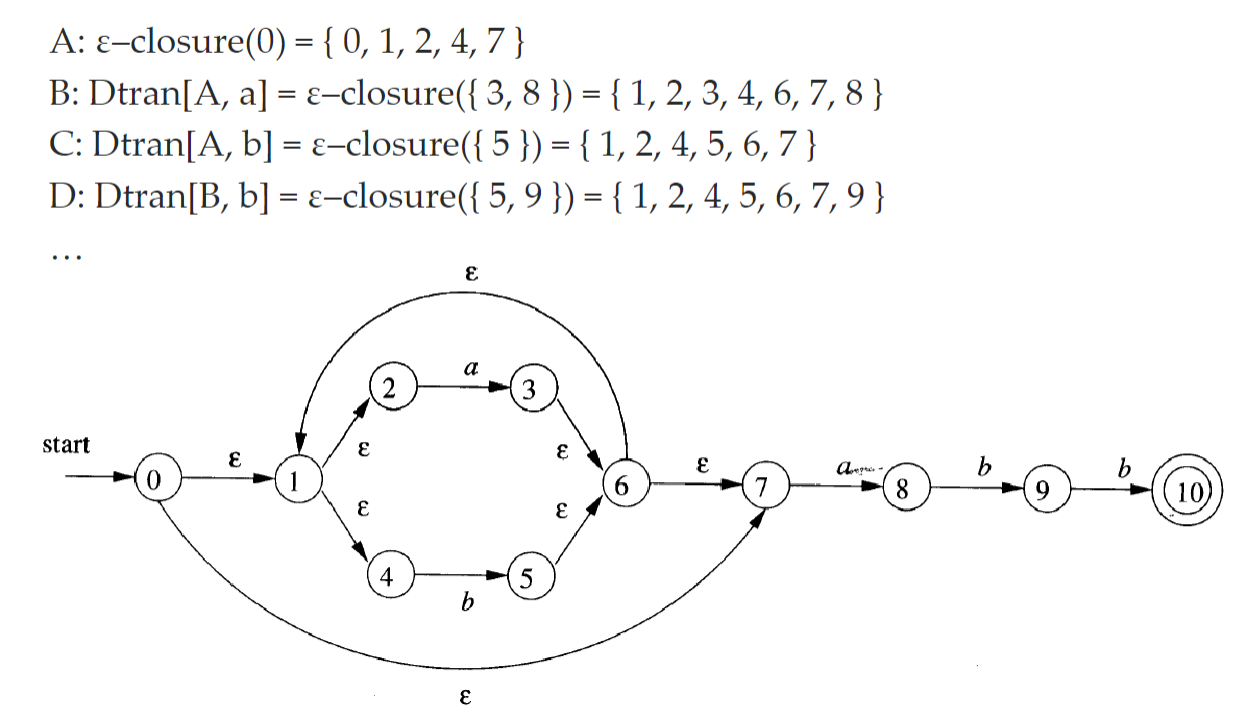
  • ε–closure (s)：从 NFA 状态 s 开始，只通过ε转换能到达的 NFA 状态集合

  • ε–closure (T)：从 T 中某个状态 s 开始，只通过ε转换能到达的 NFA 状态集合 （从子集找）
    • image.png|500
  • move (T, a)：从 T 中某个状态 s 出发，通过一个标号为 a 的转换能到达的 NFA 状态集合

  • Dtran [T, a]：Dtran[T, a]=ε–closure (move (T, a))

    • image.png|475

  • image.png|525

  • Dtran 转换表：

    • image.png|475

  • 正则表到时到 NFA

    • 根据正则表达式的递归定义，按照正则表达式的结构递归地构造出相应的 NFA
  • Chapter_3, page 60
  • docs/学校课程/课程/编译原理/作业/p2#^5865eb|3.7.1

NFA 合并（多模识别）

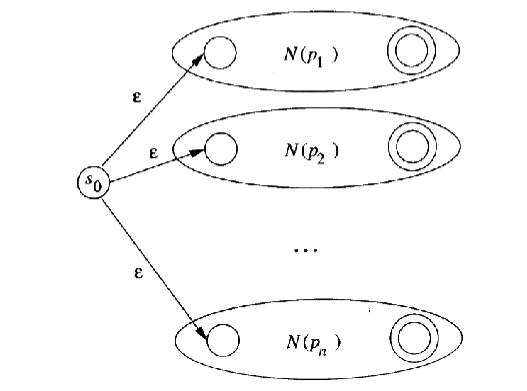
  • 引入新的开始状态，并引入从该开始状态到各个原开始状态的ε转换，得到的 NFA 所接受的语言是原来各个 NFA 语言的并集，不同的接受状态代表不同的模式
    • image.png|325
  • 对得到的 NFA 进行确定化，得到 DFA
    • 转化之后可能出现冲突：DFA 一个点对应 NFA 中的多个状态子集
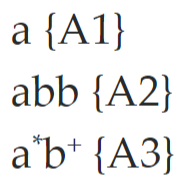
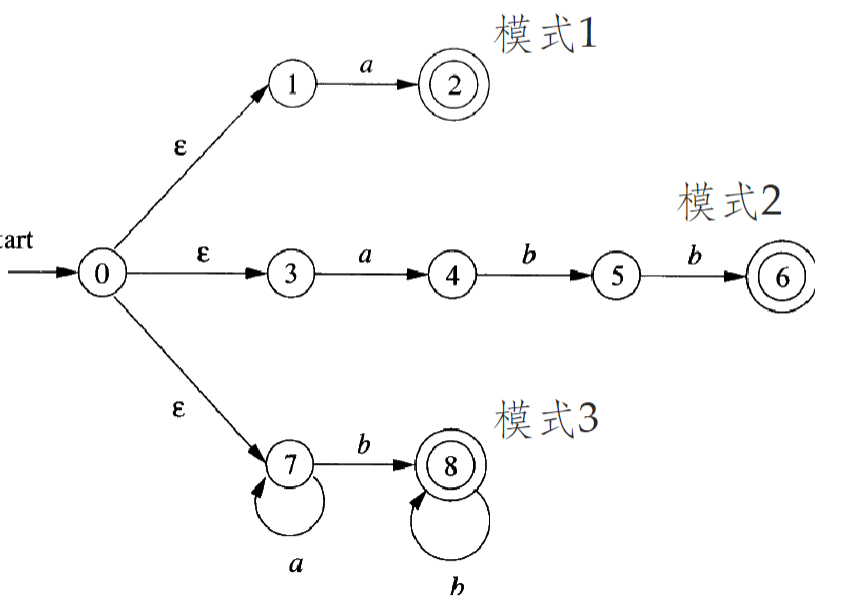
    • image.png|121 image.png|425
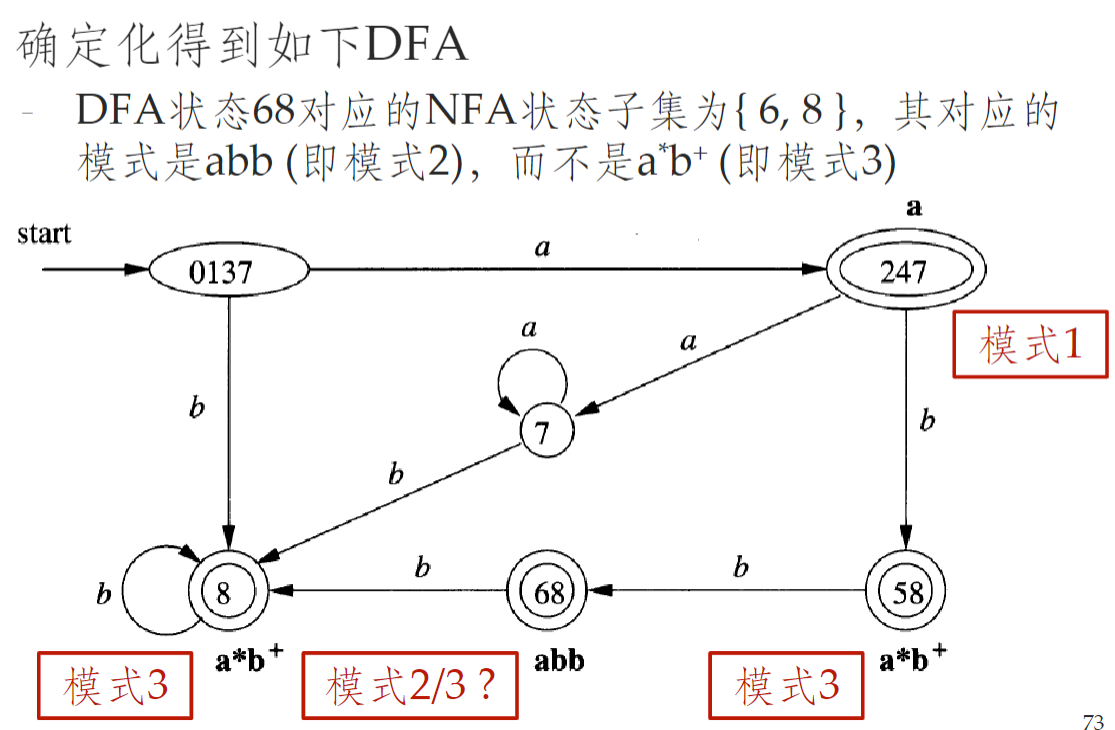
    • image.png|475
    • 通过设定状态优先级解决

DFA 最小化算法

  • 一个正则语言可对应于多个识别此语言的 DFA

  • 通过 DFA 的最小化可得到状态数量最少的 DFA (不计同构，这样的 DFA 是唯一的)

  • 状态的可区分：如果存在串 x，使得从状态 s1 和 s2，一个到达接受状态而另一个到达非接受状态，那么 x 就区分了 s1和 s2，即状态可区分

  • 不可区分的状态就是等价的，可以合并

  • 迭代法：

    • 基本步骤：先区分接受状态和非接受状态
    • 归纳步骤：如果 s 和 t 是可区分的，且 s'到 s、t'到 t 有标号为 a 的边，那么 s'和 t'也是可区分的
    • image.png|475
      • G 指的是集合，如 S-F, F
    • 最终没有区分开的状态就是等价的，从划分得到的等价类中选取代表，并重建 DFA
    • image.png|500

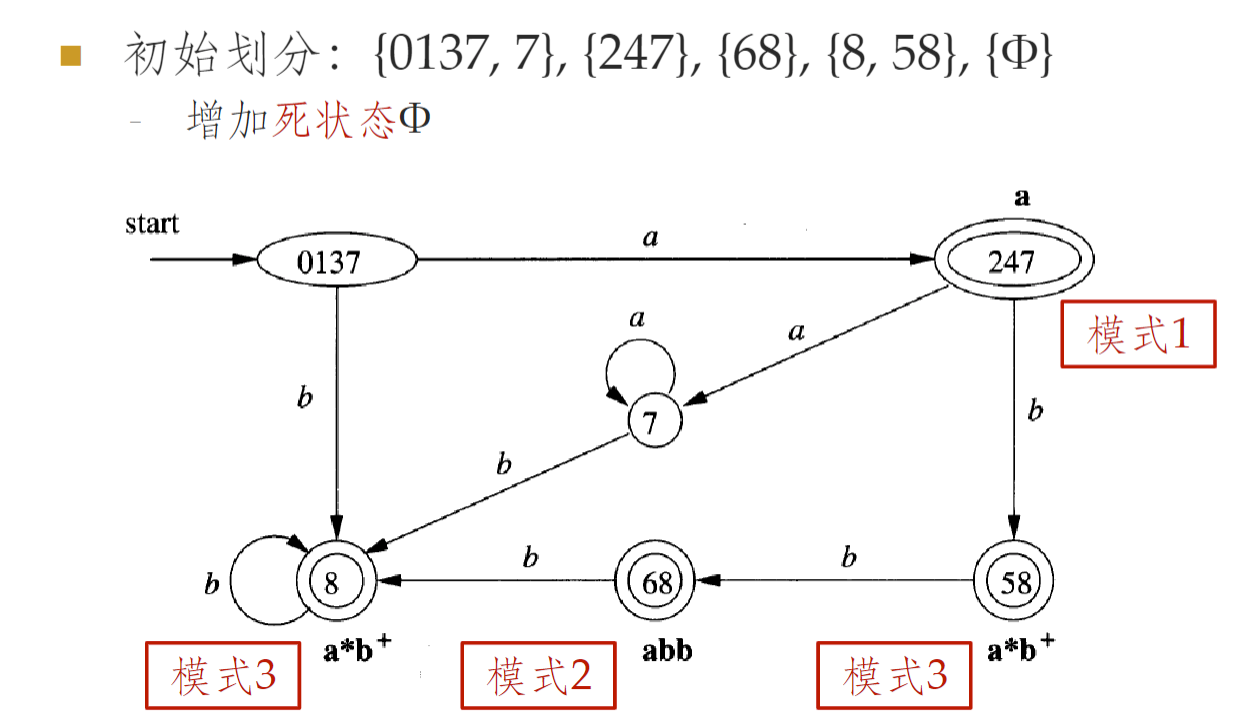
  • 例子

  • Chapter_3, page 77
  • 对于词法分析器的最小化，仅在初始化分时有所区别，对于接受状态集合内部还要根据不同的接受状态进一步划分 (对应不同模式的接受状态一定是不等价的)
    • 初始划分为所有非接受状态集合 + 对应各模式的接受状态集合
    • image.png|475