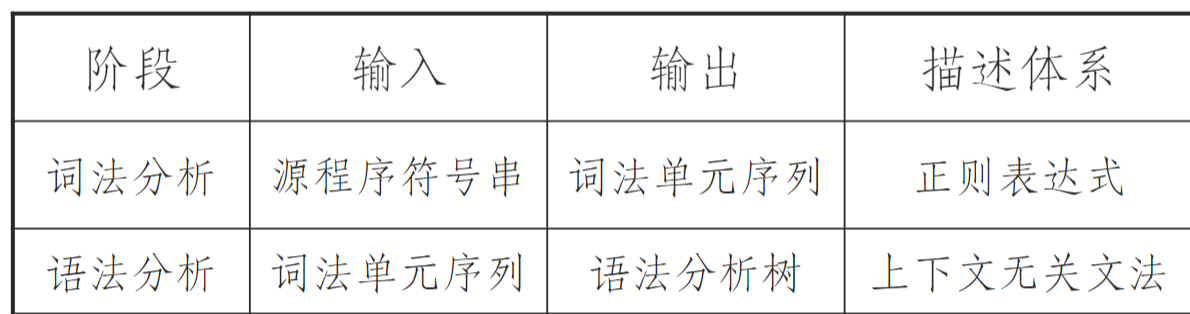
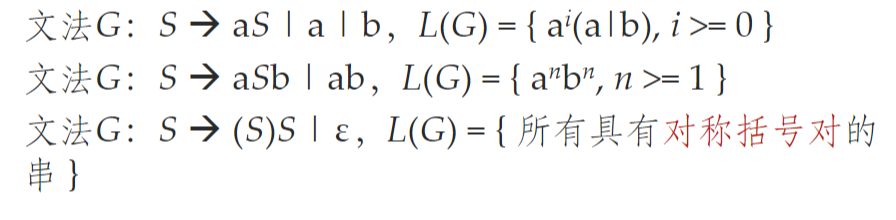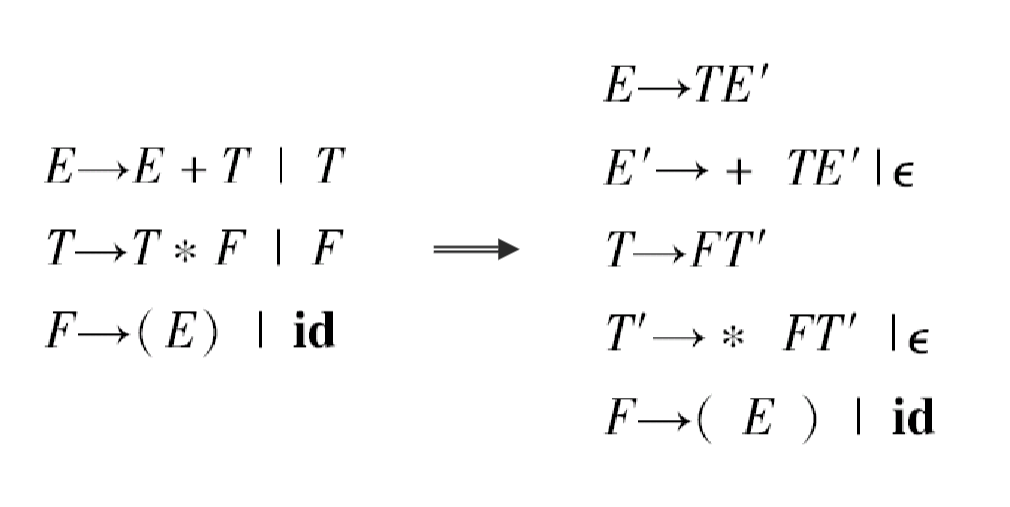语法分析
语法分析器¶
-
从词法分析器获得词法单元的序列,确认该序列是否可以由语言的文法生成
- 对于语法错误的程序,报告错误信息
- 对于语法正确的程序,生成语法分析树 (简称语法树)
-
上下文无关文法¶
- 程序设计语言构造的语法可使用上下文无关文法 (CFG) 或 BNF 表示法来描述
- 终结符号: 这些是文法中的基本符号,它们直接对应于语言的基本单位,即词法单元。
- 在编程语言中,终结符号可以是关键字、操作符、标识符、字面量等。
- 非终结符号: 非终结符号是文法中的变量,可以应用规则被替换为一系列终结符或非终结符的组合。
- 开始符号: 开始符号是一个特别指定的非终结符号,它代表整个文法的起点。
- 开始符号是我们用来生成所有有效字符串的起点。
- 产生式: 产生式定义了如何将终结符和非终结符组合成字符串。
- 产生式有一个头部(左部),头部是一个非终结符号;有一个体部(右部),体部是由终结符和非终结符组成的符号串。产生式表达了非终结符通过替换能变成什么样的符号串。
- 例如,产生式
expression → expression + term意味着非终结符expression可以被替换为由expression、加号+和term组成的序列。
-

- 简化表示
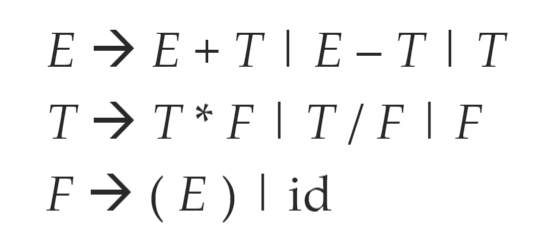
- 简化表示
-
推导:将待处理的串中的某个非终结符号替换为这个非终结符号的某个产生式的体。从开始符号出发,不断进行上面的替换,就可以得到文法的不同句型
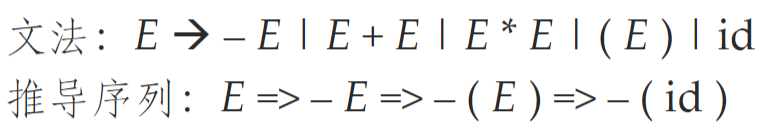
-

- 最左推导:替换最左边的非终结符。这意味着在每一步中,所有非终结符中最靠左的一个会被选中并用它的一个产生式进行替换。最左推导对应于自顶向下解析
-
句型: 如果 S =>* α,那么α就是文法 S 的句型. 可能既包含非终结符号,又包含终结符号,也可以是空串
- 句子:不包含非终结符号的句型
- 语言:文法 G 的语言就是 G 的句子的集合,记为 L(G)
- 如何验证文法 G 所确定的语言 L
- 证明 G 生成的每个串都在 L 中
- 证明 L 中的每个串都能被 G 生成
语法分析树¶
- 根结点的标号是文法的开始符号;叶子结点的标号是非终结符号、终结符号或ε;内部结点的标号是非终结符号,每个内部结点表示某个产生式的一次应用
- 树的叶子组成的序列是根的文法符号的一个句型,一棵语法分析树可对应多个推导序列
-
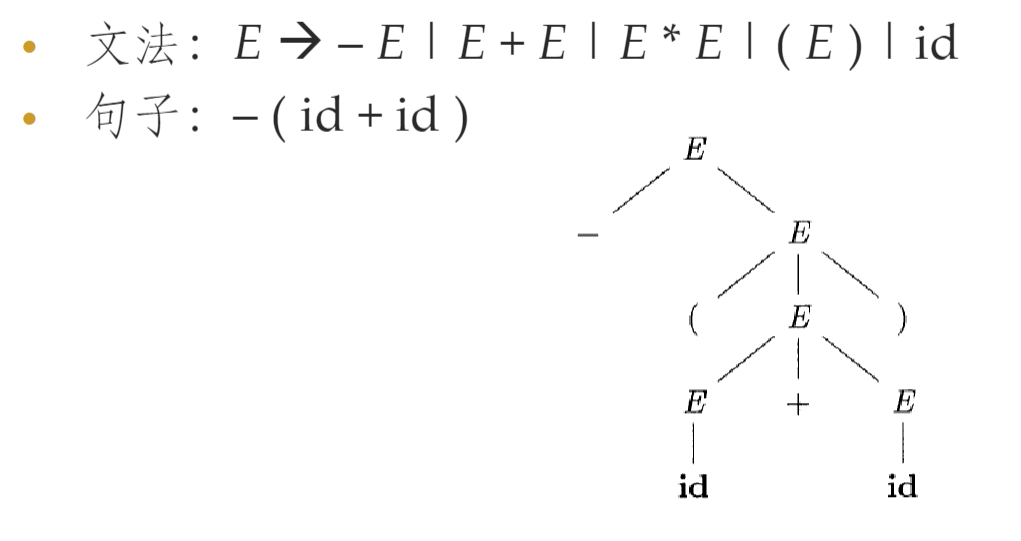
-
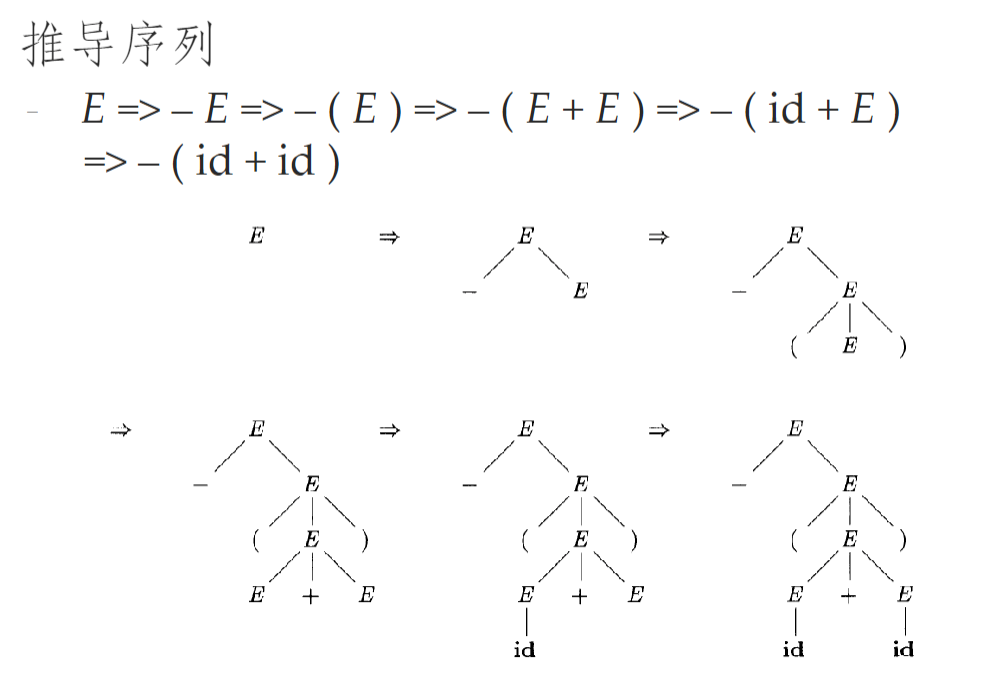
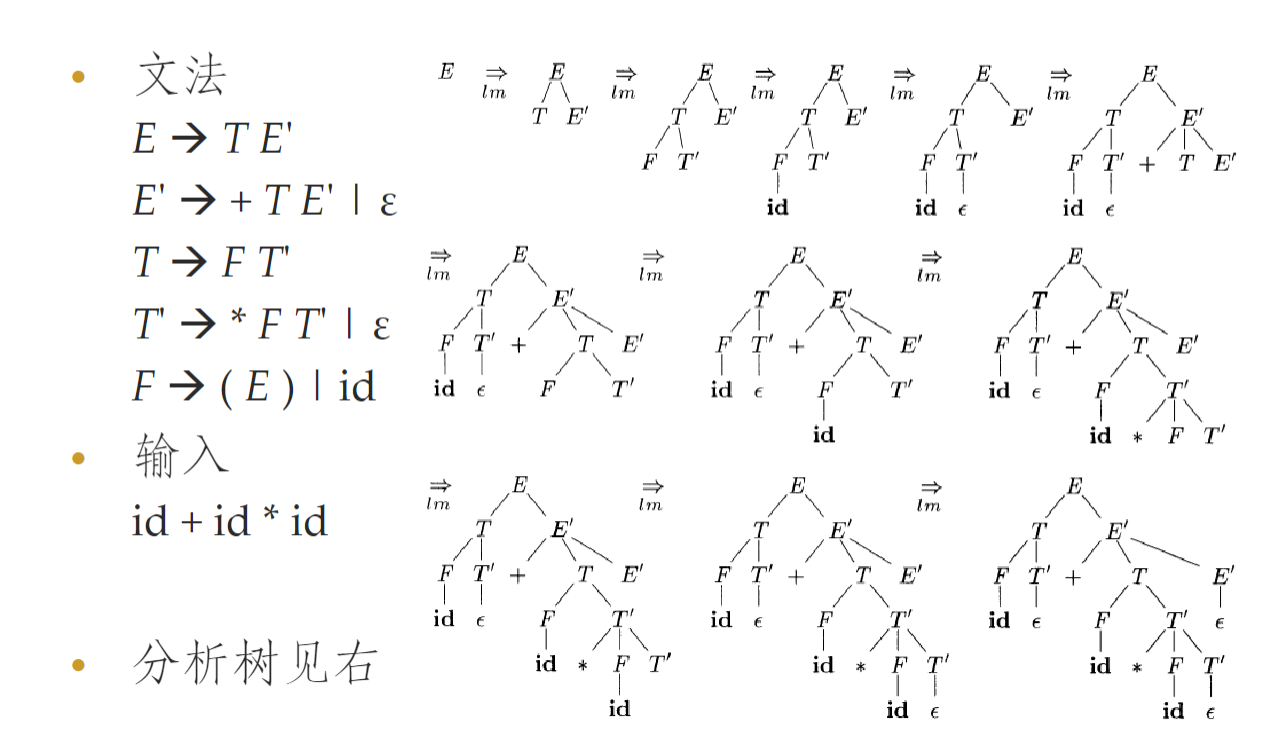
从推导序列构造分析树
-
二义性:如果一个文法可以为某个句子生成多棵语法分析树,这个文法就是二义的
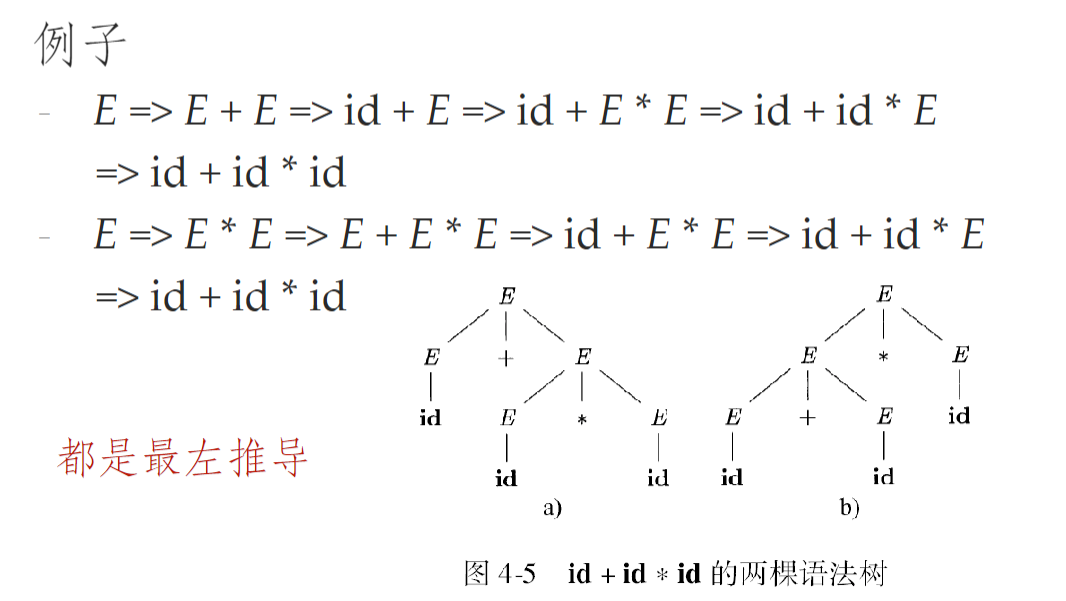
- 程序设计语言的文法通常是无二义的,否则就会导致一个程序有多种“正确”的解释
- 需要消二义性规则来剔除不要的语法分析树,需要更严格的文法限制
- docs/学校课程/课程/编译原理/作业/p2#^7e4ebf|4.2.1
上下文无关文法与正则表达式¶
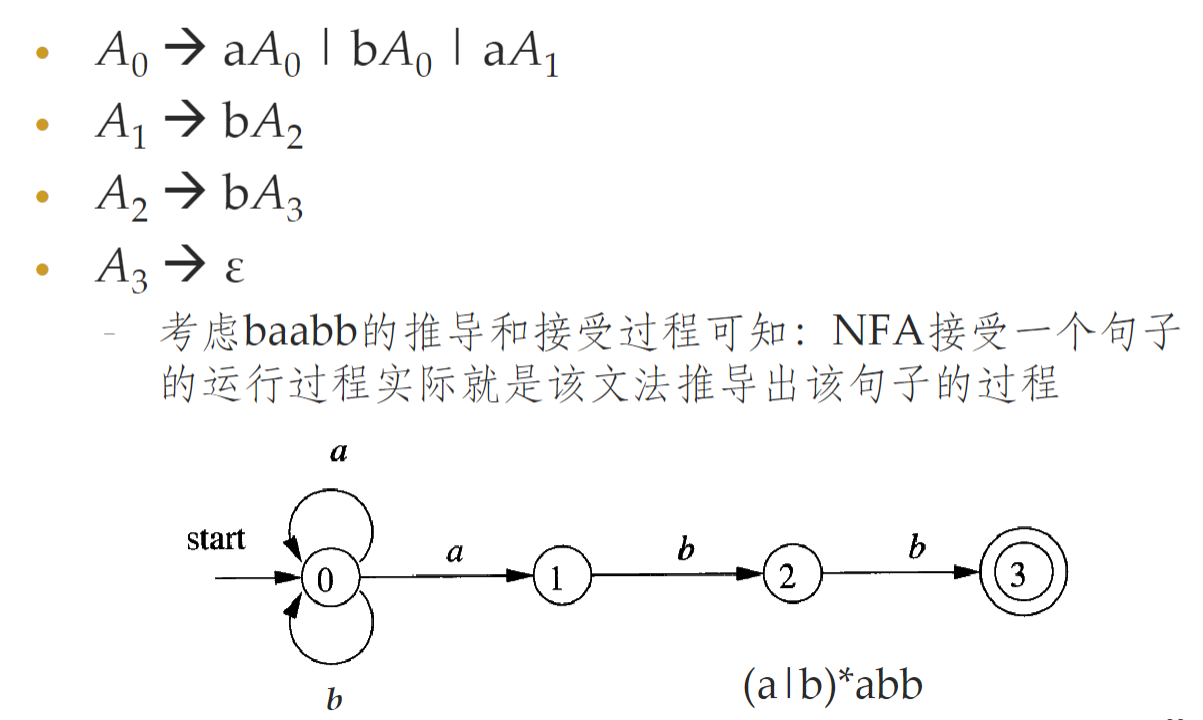
- 上下文无关文法比正则表达式的能力更强
- 所有的正则语言都可以使用文法描述
- 但有一些用文法描述的语言不能用正则表达式描述

- 有穷自动机只能有限计数
- 所有的正则语言都可以使用文法描述
设计文法¶
- 文法能描述程序设计语言的大部分语法,但是有部分无法描述,因此语法分析器接受的语言是程序设计语言的超集,还需要通过语义分析来剔除一些不合法的程序
-
文法的预处理:
- 消除二义性
- 消除左递归:文法中一个非终结符号 A 使得对某个串α 存在推导 \(A\overset{+}\rightarrow A\alpha\)
- 立即左递归 \(A\to A\alpha\)
- 提取左公因子
-
二义性的消除
- 一些二义性文法可被改成等价的无二义性的文法,二义性的消除方法没有规律可循
- 存在二义性的文法:
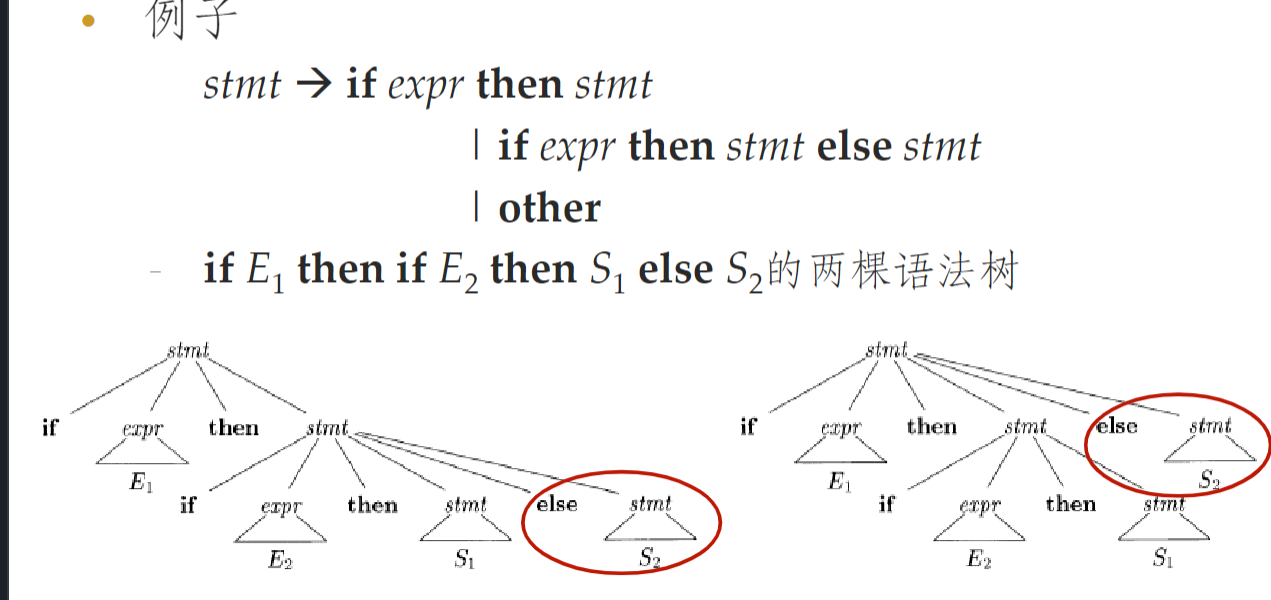

- 这里拆分为了两种类型,使得 ifthen 只能出现在末尾
-
左递归的消除
- 自顶向下的语法分析技术不能处理左递归的情况,因此需要消除左递归,但是自底向上的技术可以处理左递归
- 消除立即左递归:将左递归替换为右递归
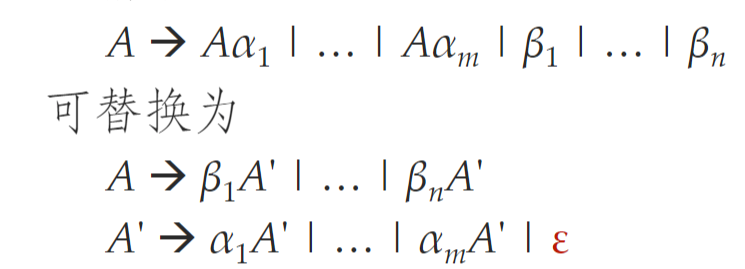
-
消除(多步)左递归
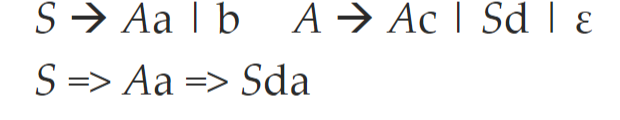
- 更加通用的左递归消除
- 基本思路是展开(合并多步骤)产生式,得到立即左递归式,再进行删除
- 更加通用的左递归消除
-
预测分析法
- 从开始符号推导出输入符号串,为最左边的非终结符号选择适当的产生式
- 当两个产生式具有相同前缀时(有多个可能的产生式)无法预测
- 提取左公因子: 用于解决预测分析法的冲突问题(提取前缀)
- 输入:文法 G;输出:等价的提取了左公因子的文法


语法分析技术¶
自顶向下¶
- 从语法分析树的根部按照先根次序开始构造语法分析树
- 通常用于处理 LL 文法
-
对应于最左推导
-
基本步骤:
- 确定对句型中最左边的非终结符号应用哪个产生式
- 后对该产生式与输入符号进行匹配
递归下降语法分析¶
-
递归下降语法分析:
- 每个非终结符号对应于一个过程,该过程负责扫描此非终结符号对应的结构

- 如果没有足够的信息来唯一确定可能的产生式,那么分析过程就产生回溯;这个过程是可能失败的,比如第 7 行(为终结符但是并不匹配);第 4 行也可能出错。
- 递归下降不能保证匹配成功(尽管存在结果)的原因是一层进行判断时不会考虑上一层(如 aSa 中后一个 a,这就是与暴搜的区别! 丢失了部分信息)这样回到上一层失败后上一层会直接尝试 aa 而不是更改下一层

-
为了解决信息不足,在自顶向下的分析技术中,使用向前看几个符号来确定产生式 (通常只看一个符号)
FIRST 和 FOLLOW¶
- FIRST(a)
- 可以从 a 推导得到的串的首符号的集合

- 计算方法
- FOLLOW(A)
- 可能在某些句型中紧跟在 A 右边的终结符号的集合
- 如果
A可以出现在句子的末尾,则还包括文法的结束符号EOF(通常表示为$)。 
- 计算方法:按照下面两个规则不断迭代,直到所有的 FOLLOW 集合都不再增长为止(由于规则二产生的迭代);将右端结束标记$加入 FOLLOW (S)中

- 这里计算的目标是 \(B\) 而不是 \(A\)

- docs/学校课程/课程/编译原理/作业/p2#^cc87a2|4.4.4
LL(1) 文法¶
- 可以构造出预测分析器,即不需要回溯的递归下降语法分析器。(可以根据当前输入的符号确定使用的产生式)
- 条件:对于 \(A\to \alpha|\beta\)
- \(FIRST(\alpha)\bigcap FIRST(\beta)=\Phi\)
- 若 \(\varepsilon \in FIRST(\beta)\) 则 \(FIRST(\alpha)\bigcap FOLLOW(A)=\Phi\) 反之亦然
- 即每次都有唯一的选择
- LL(1)文法的名称中的 "LL" 表示这是一种 "从左到右扫描,最左推导" 的文法,而 "1" 表示解析器在做决策时最多只需要查看输入的下一个符号。
预测分析算法¶
-
预测分析表构造算法:
- 输入:文法 G;输出:预测分析表;
- 对于每个生产式 \(A\to \alpha\)
- 对 \(FIRST(\alpha)\) 中的每个终结符 \(a\) ,将 \(A\to \alpha\) 加入到 \(M[A,a]\)
- 若 \(\varepsilon \in FIRST(\alpha)\),那么还要将 \(FOLLOW(A)\) 中的 \(b\) 将 \(A\to \alpha\) 加入到 \(M[A,b]\)
- 表示对于非终结符 \(A\) 以及下一输入 \(a\) 应该使用 \(M[A,a]\) 中的生产式

- LL (1)文法是无二义性的,因此一个格子内只会有一个生产式

-
非递归预测分析(只适用于 LL (1)语法)
- 自顶向下分析中:
- 先匹配掉句型中左边的所有终结符号;
- 对于最左边的非终结符号选择适当的产生式展开
- 匹配成功的终结符号不会再被考虑,只需要记住句型余下的部分以及尚未匹配的输入终结符号串
- 使用栈来处理
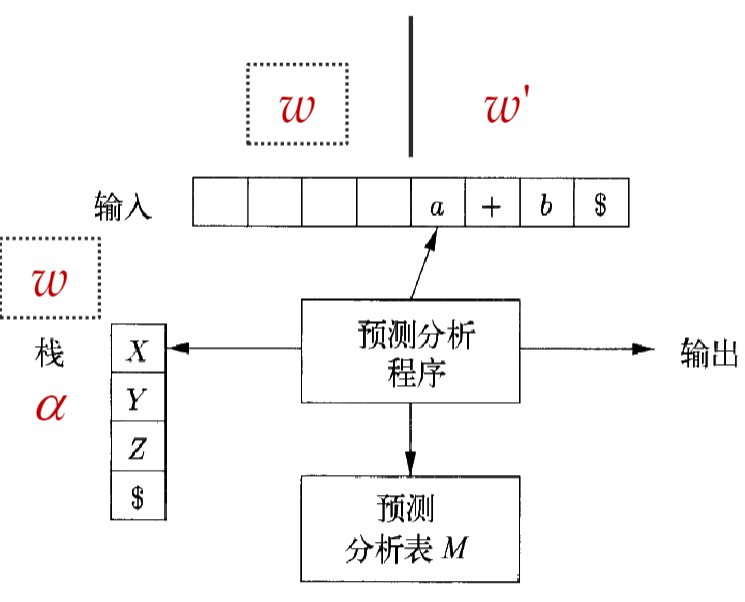

- 注意是将产生式的右部按倒序压入栈中
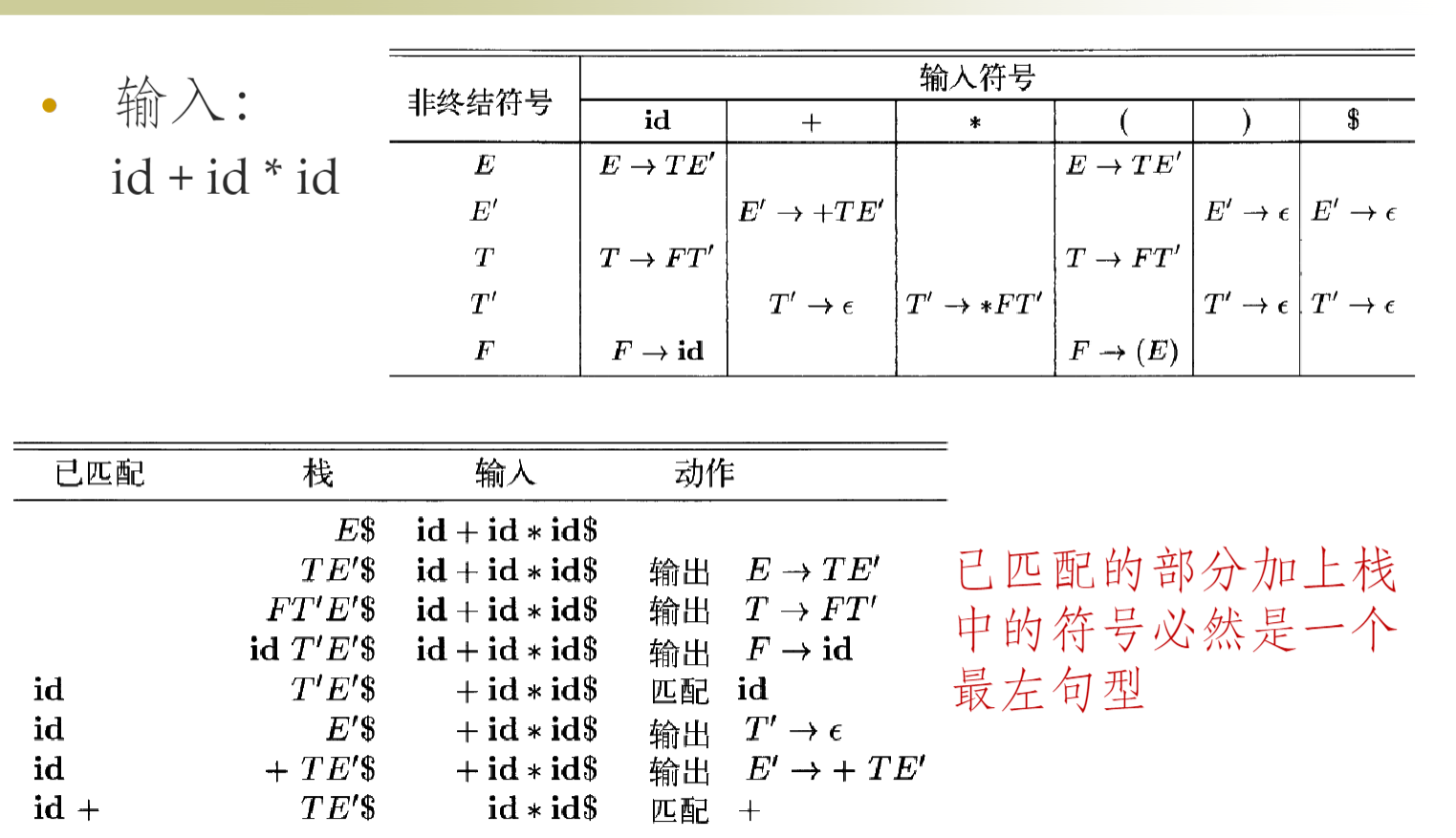
- 自顶向下分析中:
- docs/学校课程/课程/编译原理/作业/p3#^4d0474|4.4.1
- docs/学校课程/课程/编译原理/作业/p3#^8d3c9c|4.4.2
自底向上¶
- 从语法分析树的叶子开始构造语法分析树
- 使用移入-规约框架,通常用于处理 LR 文法(简单 LR 技术及 LR 技术)
-

-
自底向上语法分析的过程就可以看做从串归约到文法开始符号的过程
规约:一个与某产生式体相匹配的特定子串被替换为该产生式头部的非终结符号
-
如何规约到正确的开始符号?可能会规约到非句型
-
句柄
- 最右句型(句子经过一系列最右推导得到)中能够匹配某个生产式右侧的式子,并且这个匹配代表了从这个最右句型回到其直接前趋的最右推导的最后一步。
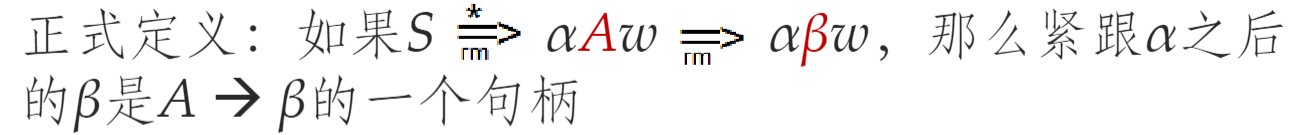
- 在一个最右句型中,句柄右边只有终结符号
- 如果文法没有二义性,那么每个句型有且只有一个句柄
- 整个过程其实就是反向

移入-归约分析技术¶
-

- 移入 (shift):将下一个输入符号移入到栈顶
- 归约 (reduce):将句柄归约为相应的非终结符号
- 句柄总是在栈顶
- 弹出句柄,压入被归约到的非终结符号
- 接受 (accept):宣布分析过程成功完成
- 报错 (error):发现语法错误,调用错误恢复子程序
-
冲突
- 对于有些不能使用移入-归约分析的文法,不管用什么样的移入-归约分析器都会到达这样的格局:即使知道了栈中所有内容、以及下面 k 个输入符号,人们仍然无法知道是否该进行归约 (移入-归约冲突),或者不知道按照什么产生式进行归约 (归约-归约冲突)


语法项集族¶
- LR (k)语法:
- L 表示最左扫描,R 表示反向构造出的最右推导,k 表示最多向前看 k 个字符
- 当 k 增大时,相应的语法分析器的规模急剧增大:当 k = 0, 1 时,已经可以解决很多语法分析问题,因此具有实践意义
-
优点:
- 表格驱动,可以自动生成
- 对于几乎所有程序设计语言只要写出上下文无关文法就能构造出识别语言的 LR 语法分析器
- 最通用的无回溯移入-规约分析技术
- 可以比 LL (k)分析更多的文法
-
项:文法的一个产生式加上在其中某处的 一个点
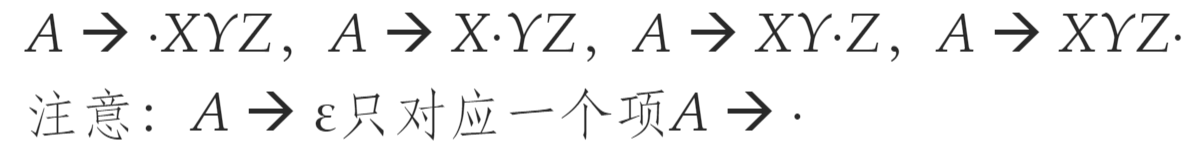

- 点的前面是已经解析了的部分,后面是还没内有解析的部分
- 增广文法
- G 的 G‘增广文法是在 G 中增加了新开始符号 S',并加入生产式 \(S'\to S\)
- 项集闭包 CLOSURE:如果 I 是文法 G 的一个项集,CLOSURE (I)就是根据下列两条规则从 I 构造得到的项集

- 之所以加入 \(B\to \cdot r\) 是因为想匹配 \(A\to \alpha \cdot B \beta\) 就需要 \(B\) 而新加入的式子给出了一种得到 \(B\) 的方法


-
GOTO 函数
- \(I\) 是一个项集,\(X\) 是一个文法符号,则 \(GOTO(I,X)\) 定义为 \(I\) 中所有形如 \([A\to \alpha \cdot X \beta]\) 的项所对应的项\([A\to \alpha X \cdot \beta]\) 的集合闭包

-
求 LR (0)项集的规范族算法:从初始项集开始,不断计算各种可能的后继,直到生成所有的项集

- 项集规范族构造
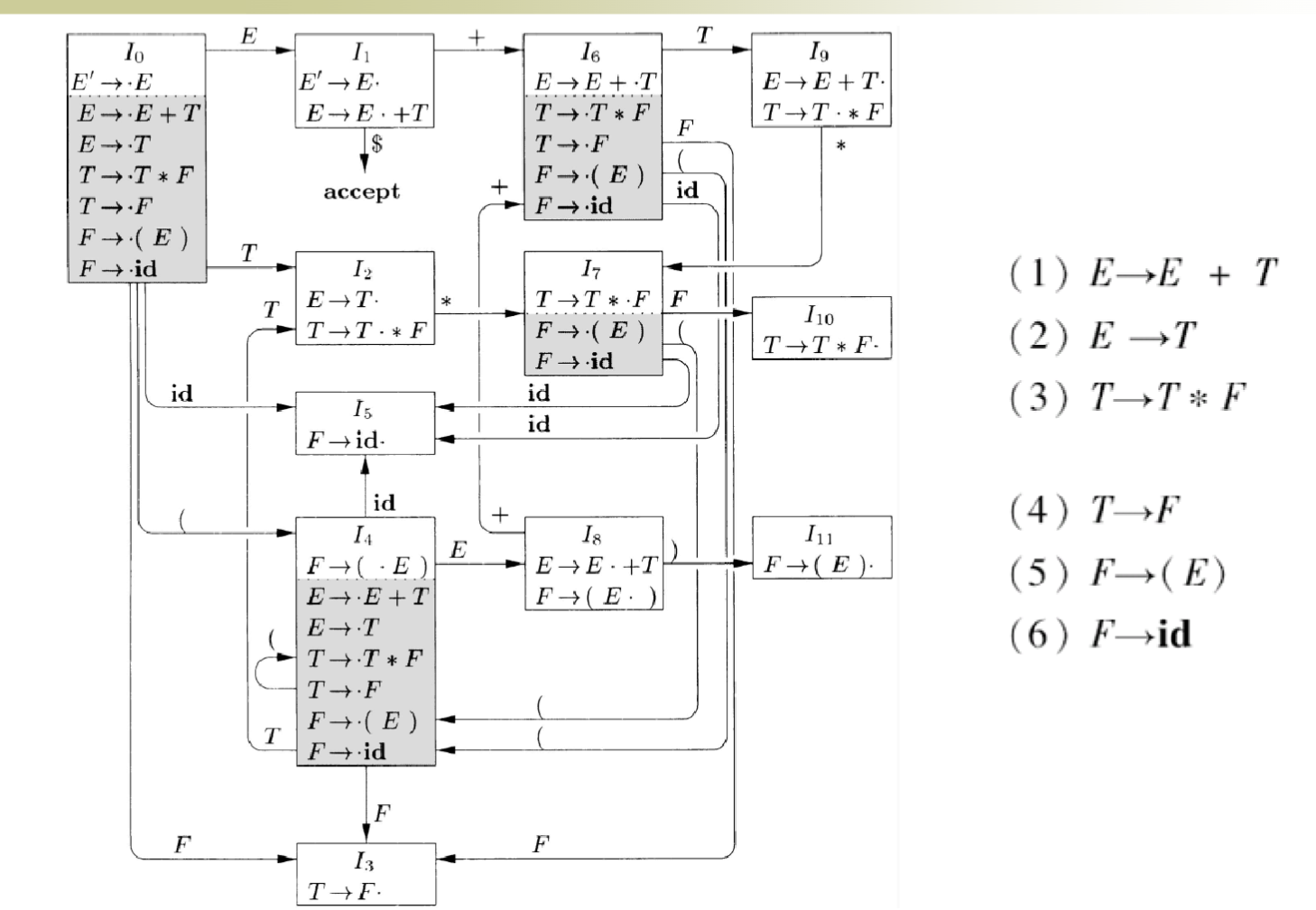
LR (0)项¶
- 构造
- 基于规范 LR (0)项集族可以构造 LR (0)自动机
- 规范 LR (0)项集族中的每个项集对应于 LR (0)自动机的一个状态
- 状态转换:如果 GOTO (I, X) = J,则从 I 到 J 有一个标号为 X 的转换
- 开始状态为 CLOSURE ({ S' → ·S })对应的项集
-
作用
-
LR(0)自动机的工作流程
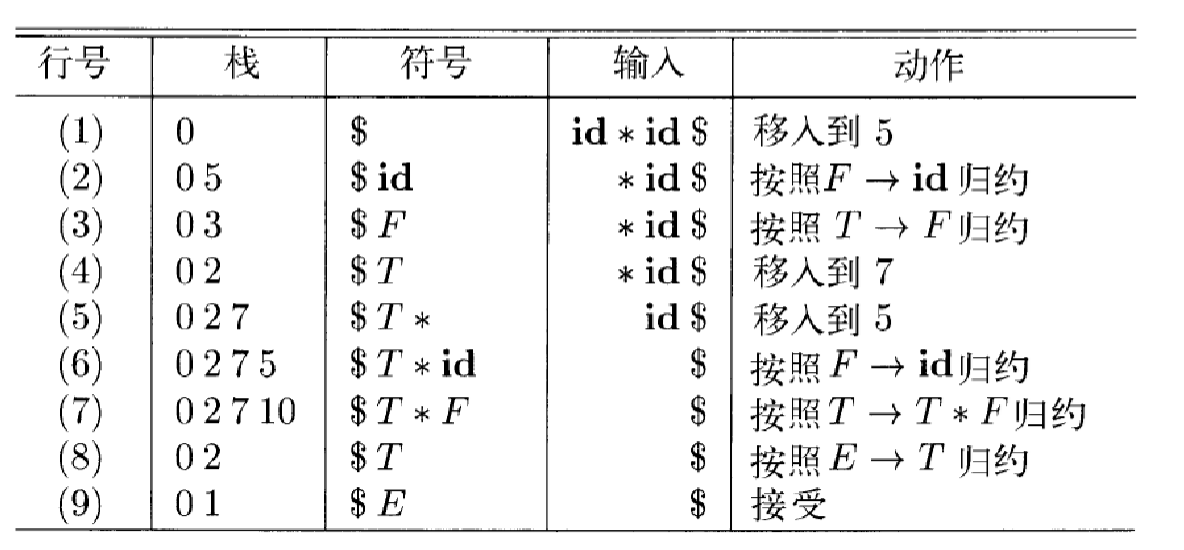
- 移入操作:会触发状态的转移
- 规约操作:按照规约生产式的规则先将栈顶的几个状态弹出,再将生产式左部的 A 移入栈

-
-
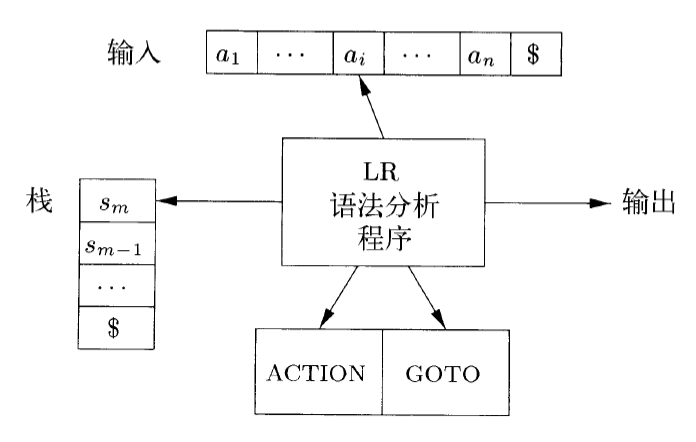
分析程序根据栈顶状态和当前输入通过分析表确定下一步动作
- 即语法分析器的格局包含栈中内容和余下输入
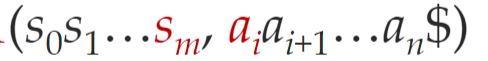
- 即语法分析器的格局包含栈中内容和余下输入
-
语法分析表的内容
- ACTION:指示操作:移入、规约、接受(完成分析)、报错(出现语法错误)
- GOTO:指导分析器在遇到非终结符后应该转移到的状态
- ACTION:指示操作:移入、规约、接受(完成分析)、报错(出现语法错误)
-
LR(0) 语法语法分析算法

- ACTION
- Shift(移入): 若 ACTION 表的某个单元格中有
Sx的指令,这表示当前看到的输入符号应该被“移入”。x代表一个状态号,分析器将这个符号推入栈中,并且状态x成为新的栈顶状态。 - Reduce(归约): 若单元格中有
Ry的指令,这意味着分析器应进行归约动作。y是产生式在文法中的编号,表示当前栈顶符号串应按此产生式的右部归约,并替换为产生式的左部非终结符。
- Shift(移入): 若 ACTION 表的某个单元格中有
- GOTO
- GOTO 表用于在归约动作之后确定下一个状态。
- 单元格中的数值表示新的状态。这个状态取决于当前的状态(即归约动作之前的状态)和归约后位于栈顶的非终结符。
- 注意:Action 中都是终结符,GOTO 中都是非终结符
- ACTION
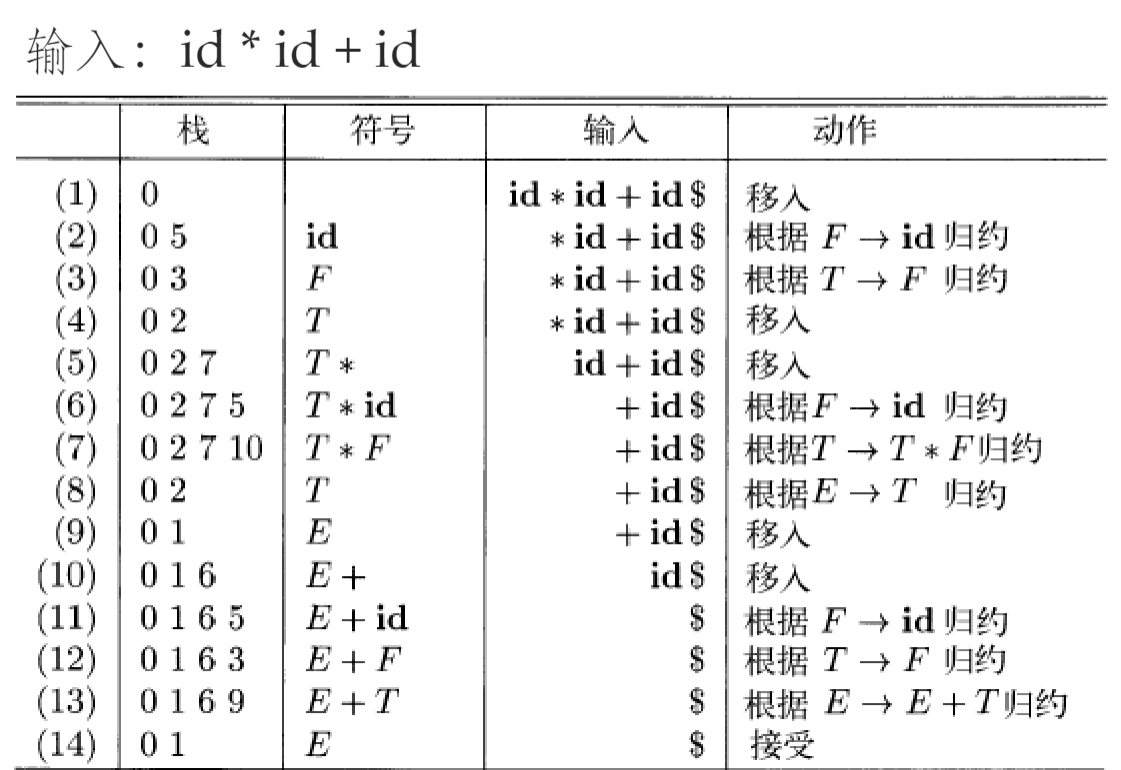
- 在 (2)->(3)后先看 ACTION 得 R 6 进行规约,栈顶出栈变成 0(弹出元素的数目等于生成式右侧元素数目),并且规约之后得到 F,根据 GOTO(0, F)=3 ,得到新状态 3 并入栈
- 即规约时先使用 ACTION 确定使用的产生式,之后再使用 GOTO 进行状态转移
- 如 0135 (S->SS)那么就要出栈 3* 个元素 (0),再根据 GOTO 入栈新元素
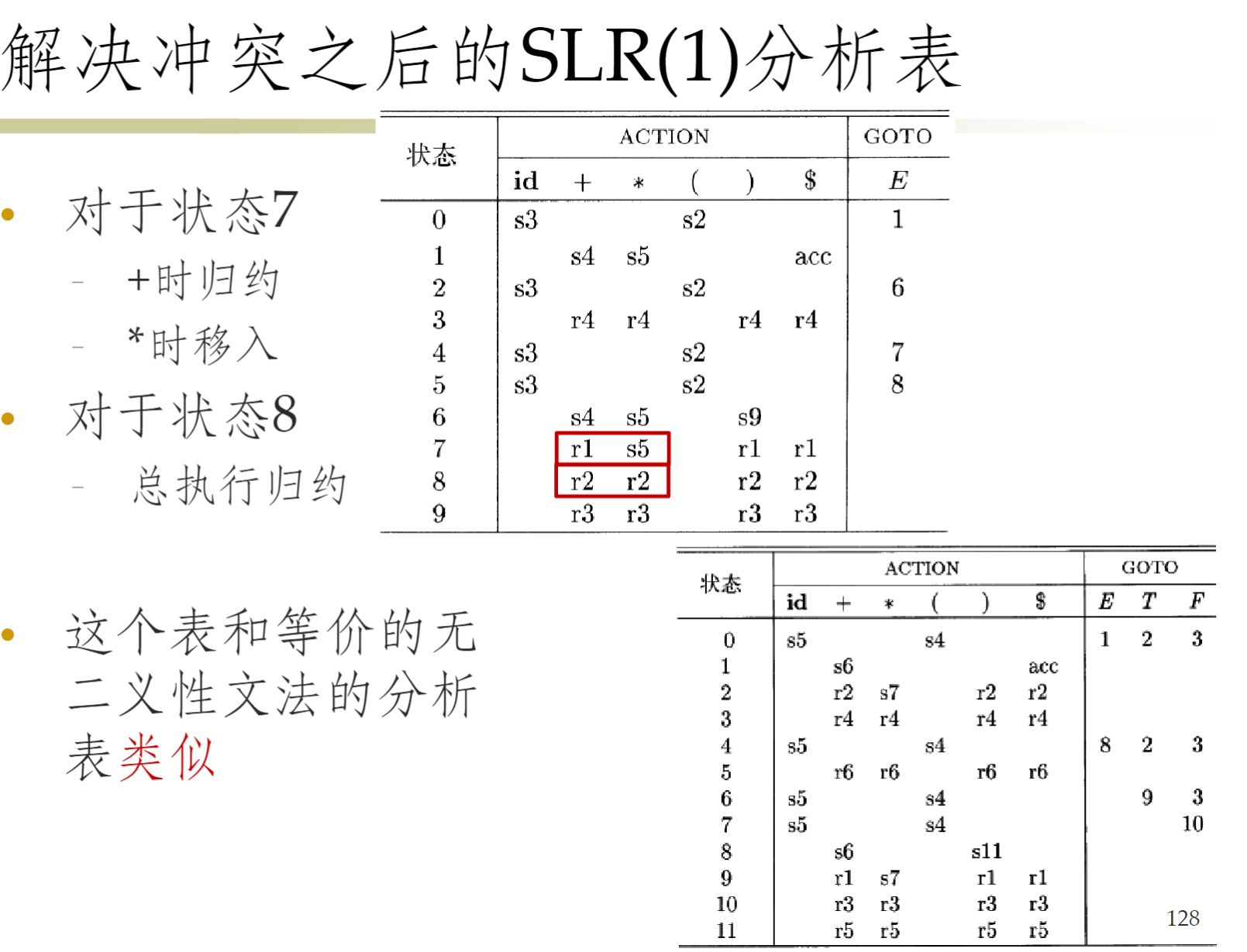
SLR (1) 语法语法分析¶
- 以 LR(0)自动机为基础
- SLR 语法分析表的构建
- 构造增广文法
S' → S的 LR (0)的项集规范族{\(I_0,\dots,I_{n}\)} - ACTION 填写:
- 如果项集
Ii中包含形如A → α·aβ的项目,并 且有一个状态转移GOTO(Ii, a) = Ij,那么在 ACTION 表的第i行、对应a列的位置上填入"移入j"。 - 如果项集
Ii中包含形如A → α·的项目,表示我们可以用产生式A → α进行归约,那么对于文法的 FOLLOW(即所有可以出现在 A 后面的元素) 集合中的每个终结符a,在 ACTION 表的第i行、对应a列的位置上填入"按A → α归约"。 - 如果项集
Ii中包含增广产生式S' → S·,即识别出整个输入串,那么在 ACTION 表的第i行、对应结束符号$的位置上填入"接受"。 - 空白的条目设为"error"
- 如果项集
- 对于每个状态转移
GOTO(Ii, A) = Ij,其中A是非终结符,将GOTO表的第i行、对应A列的位置上填入j - 如果 SLR 分析表没有冲突(ACTION 的格子里只能有一个指令),该文法就是 SLR 的, 否则需要使用更复杂的方法如 LALR、LR(1)处理

- 构造增广文法
SLR 对冲突的处理
- 可行前缀:可以出现在语法分析器栈中的最右句型的前缀,且没有越过该句型的句柄的右端(不可能越过,越过就先进行规约转化了)
- 有效项(候选规约)
- 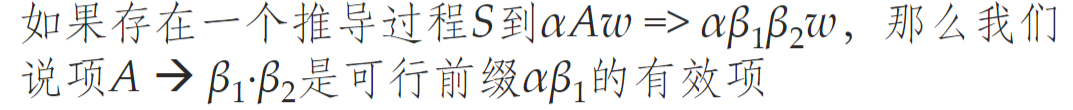 - 可行前缀与动作的关系
- 移入:如果有效项中的
- 可行前缀与动作的关系
- 移入:如果有效项中的 β2 不为空,即形如 A → β1·β2,这表明当前句柄还没有完全出现在分析栈中,我们期待更多的符号来完成句柄。在这种情况下,下一步应该是移入操作。
- 归约:如果 β2 为空,即形如 A → β1·,这表示当前句柄已经完整地出现在分析栈中,接下来应该执行归约操作。
- 如果有两个有效项要对一个可行前缀进行不同动作,那么就发生冲突
- 冲突实际上表示该可行前缀可能是两个最右句型的前缀,第一个包含了句柄,而另一个尚未包含句柄;也可能都认为包含句柄,但是规则不一样
- SLR 解决冲突:假如要按照 A → β进行归约,只有当下一个输入符号在 FOLLOW (A)中时才可以归约(不能解决所有冲突)
- 
- SLR 语法分析器的问题:并不能完全确定什么时候应该进行规约
LR(1)项(规范 LR 方法)¶
-
添加项 [A → ·α]时,把期望的向前看符号也加入项中 (成为 LR (1)项集)
- 即还需要考虑向前看( Follow )符号,在某一点基于接下来的输入符号来决定解析动作的机制。如 [A → α•β, a]
- a 就是向前看符号,可以是终结符号或者$
- 表示将来如果按照 A → αβ• 规约,规约时的下一个输入符号必须是 a
- 当β非空时,移入动作不考虑 a,a 传递到下一状态
在之前的 SLR 中只有移入会考虑当前的下一个输入,而规约只根据 follow 进行限制。而 LR(1)对每一种情况能否进行规约做出了明确的说明
-
LR (1)项中包含更多信息来消除一些归约动作,更加精确的指明何时应该进行归约
-
LR (1)与可行前缀
- 说一个 LR(1) 对可行前缀有效,主要是指这个 LR(1) 项能够正确地反映出在某个特定的语法分析过程中,当分析器读入了一个可行前缀之后,下一个输入符号是什么,并且能够根据这个信息做出正确的语法分析决策。

-
CLOSURE 的计算
- 由项 [A → α·Bβ, a]生成新项[B → ·θ, b]时,b 必须在 FIRST (βa)中
- 对 LR (1)项集中的任意项[A → α·Bβ, a],总有:a 在 FOLLOW (A)中 (初始项满足这个条件,新产生的项也满足)

-
GOTO 的计算 (和 LR (0)项集的 GOTO 算法基本相同)
-
LR(1)项集族的构造算法
-
构造语法分析表
- 首先构造得到 LR(1)的项集族 \(C=\{I_{0},\dots,I_{n}\}\)

- 没有填写的条目为 error
- 如果条目有冲突,说明不是 LR (1) 的
- 初始状态对应于 [S'->·S,$]所在项集
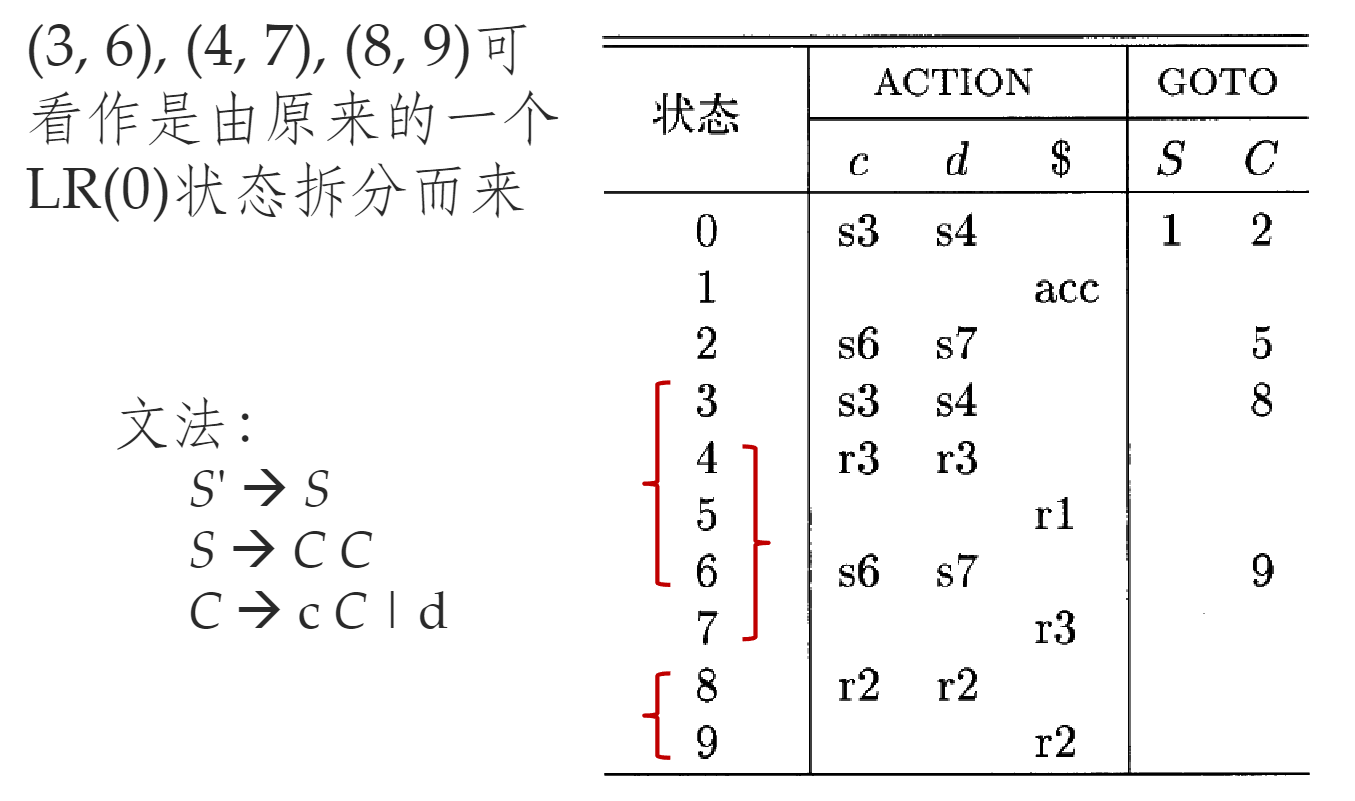 docs/学校课程/课程/编译原理/作业/p4#^266be1|4.7.1(1)
docs/学校课程/课程/编译原理/作业/p4#^266be1|4.7.1(1)
LALR 语法分析(向前看 LR)¶
- 基于 LR (0)项集族,但每个 LR (0)项都带有向前看符号
- 分析能力强于 SLR 方法,且分析表和 SLR 分析表一样大
-
LALR 已经可以处理大部分的程序设计语言
-
SLR (1) 分析能力较弱,而 LR(1)得状态数量又很大,LALR (1)才是实践中常用得方法,状态数量较少得同时能方便得处理大部分常见程序设计语言得构造
-
寻找具有相同核心的 LR (1)项集,并把它们合并成为一个项集
- 核心指的是项的第一分量的集合(即不含向前看符号)
- 一个 LR (1)项集的核心是一个 LR (0)项集
-
原来无冲突的 LR (1)分析表在合并之后得到 LALR (1)分析表,新表中可能存在冲突
- 因为被合并的项具有相同的核心 (即移入相同次后同时规约),因此不存在移入-规约冲突
- 但是可能引起规约-规约冲突

-
分析表构造算法
- 首先构造得到 LR(1)项集族
- 对于 LR(1)中得每个核心,找出具有该核心的项集,并把这些项集替换为他们的并集
- 如果合并之后存在冲突,那么说明这个语法不是 LALR 的
- GOTO 的构造:设 J 是一个或者多个 LR (1)项集 (包括 I 1)的并集,令 K 是所有和 GOTO (I1, X)具有相同核心的项集的并集,那么 GOTO (J, X) = K

docs/学校课程/课程/编译原理/作业/p4#^253900|4.7.1(2)
二义性文法的使用¶
- 二义性文法都不是 LR 的
- 某些二义性文法是有用的:某些二义性文法可以更加简洁的描述结构,隔离某些语法结构,对其进行特殊处理
-
对于某些二义性文法:可以通过消除二义性规则来保证每个句子只有一棵语法分析树(可以在 LR 分析器中实现这个规则)
-
使用优先级、结合性消除冲突
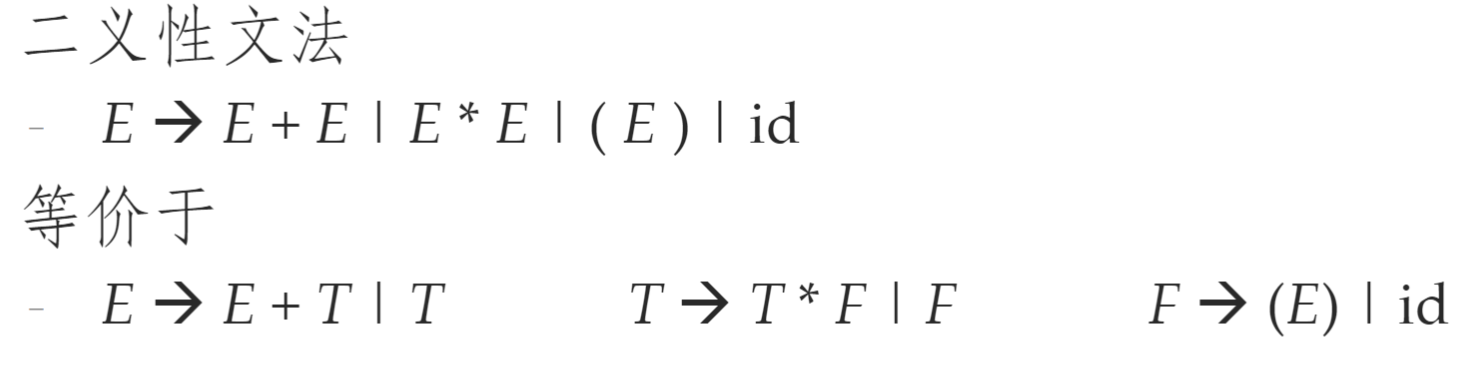
- 使用二义性文法可以容易的修改运算符的优先级和结合性,并且避免引入太多的非终结符号
-

-

语法错误的处理¶
-
语法分析器中错误处理程序的设计目标
- 清晰准确地报告出现的错误,并指出错误的位置
- 能从当前错误中恢复,以继续检测后面的错误
-
错误恢复
- 报错说明输入的串不是句子
- 使用者希望预测分析器能够进行恢复处理后继续语法分析过程,以便在一次分析中找到更多的语法错误
- 可能恢复得并不成功,之后找到的语法错误是假的
- 使用栈里面的符号以及待分析的符号进行错误处理
-
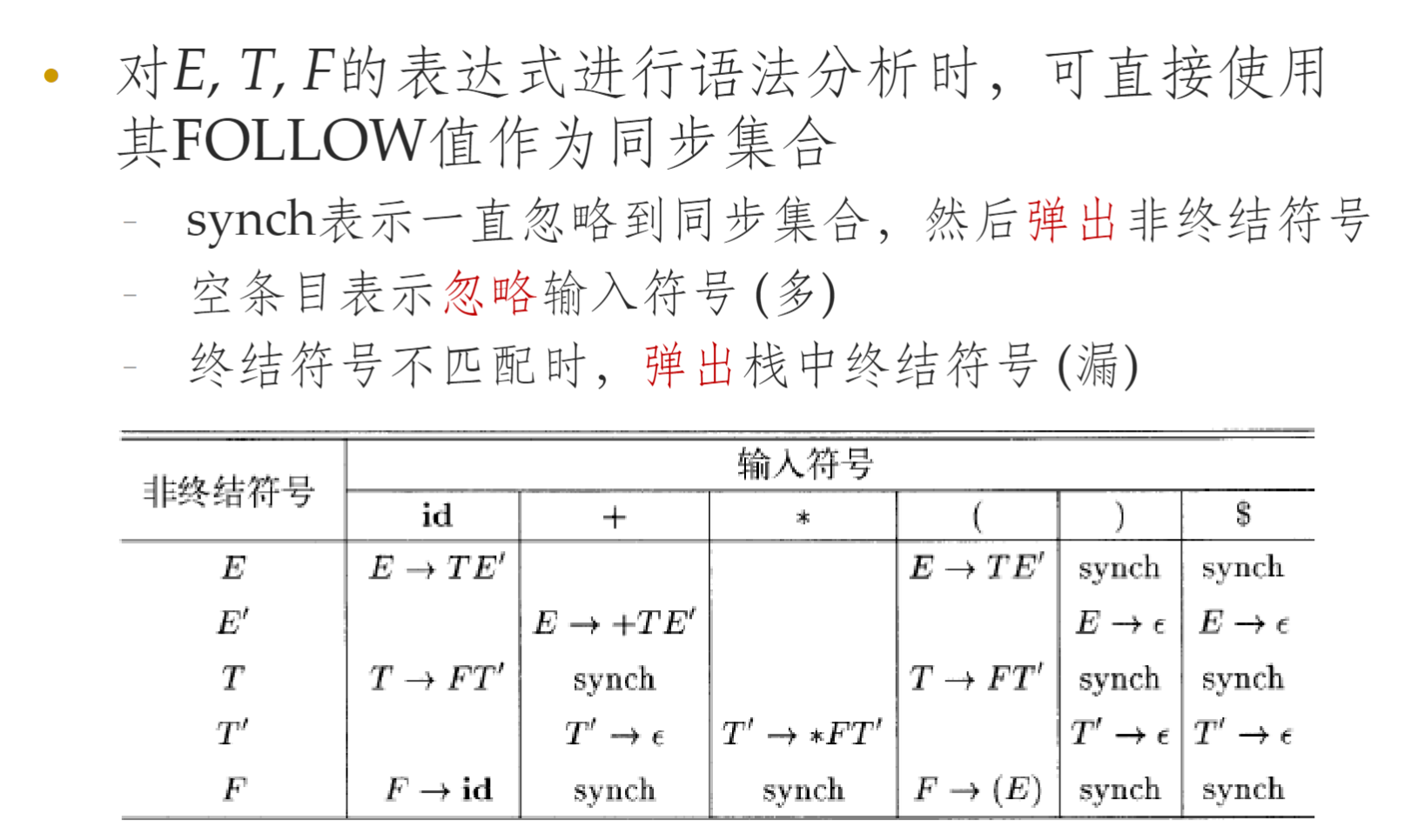
恐慌模式
- 语法分析器遇到错误后,忽略输入中的一些符号,直到出现由设计者选定的某个同步词法单元(这个程序结构结束的标志,比如;)
- 语法分析过程出现错误就是不可能找到对应这个非终结符的串了,考虑跳过它,然后继续进行语法分析处理
- 同步词法单元的启发式规则
-

-
短语层次的恢复
- 在预测语法分析表的空白条目中插入错误处理例程的函数指针