数据的表示和运算¶

进制转化¶

2<=>10 -整数部分除2取余数（低位到高位），小数部分乘2取整数（高位到低位）
8/16<=>2
一位转化为一组为3/4位的2进制组

数值数据的表示¶

补码：一个负数的补码等于模减该负数的绝对值。对于某一确定的模，某数减去小于模的另一数，总可以用该数加上另一数负数的补码来代替。
即补码为：对应正数各位取反、末位加1
- 将补码还原为原码就是求补码的补码：各位取反（符号位不变），末位加一
- [X]补=2^n+X(mod 2^n)（n是码的长度位数）
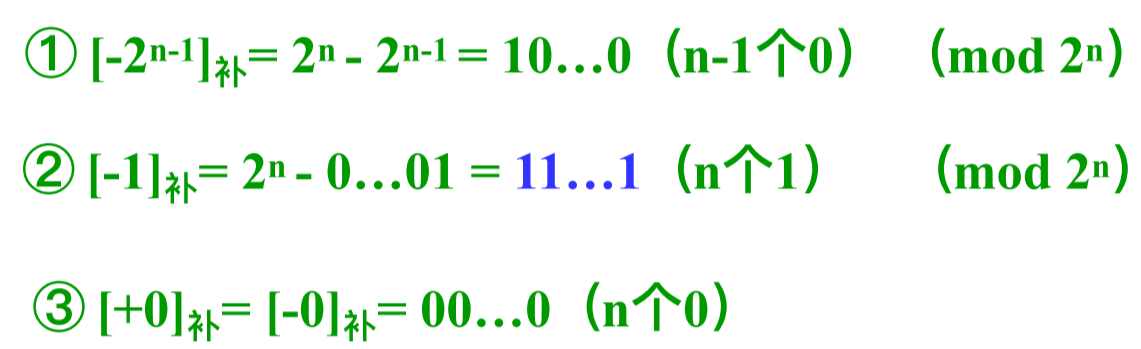
一些常见的特殊值
- 0:0000...
- -1:1111...
- -2147483648:1000...
- 2147483647:0111...
补码的补码是原码
- 因此通过补码求原码的方式和求补码的方式是相同的
\([x]_补\)和\([-x]_补\)的转化是各位取反（包括符号位），末尾加一
c中数据表示与转化
c90中-2147483648与-2147483647-1
- -2147483648 不是一个整数常量，而是一个表达式，它将一元减号运算符应用于 2147483648 这个整数常量。
- 由于 2147483648 超出了有符号整数的范围，它被视为无符号长整型 (unsigned int) 类型。
- 因此，-2147483648 实际上是对 2147483648 进行无符号算术运算的结果，它的值仍然是 2147483648非常特殊的一个值。
- 而 -2147483647-1 是一个有符号整型 (int) 类型的常量，它的值是 -2147483648。
- 而对于“int i=-2147483648;”，则“i <2147483647”的执行结果为true，因为是按照int类型来处理的
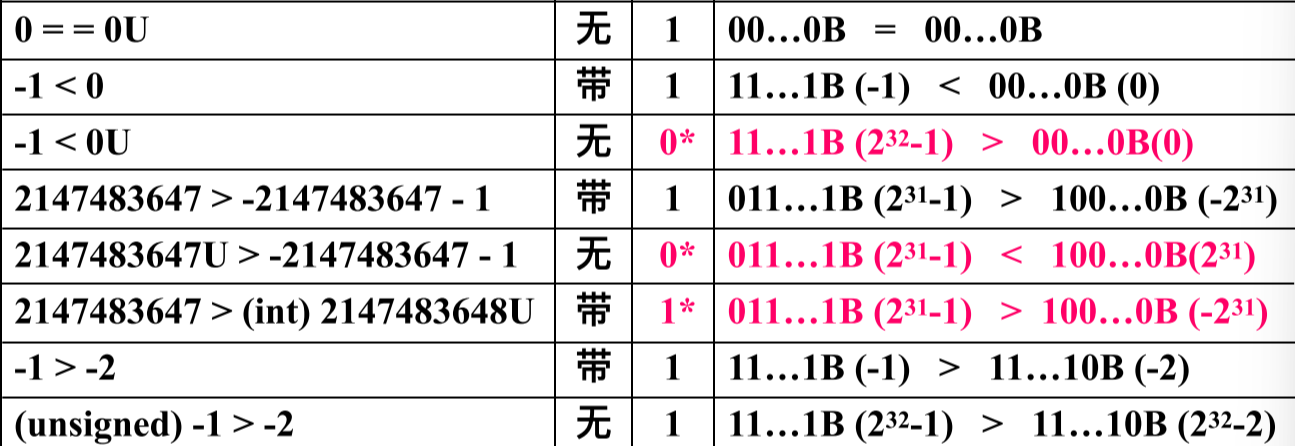
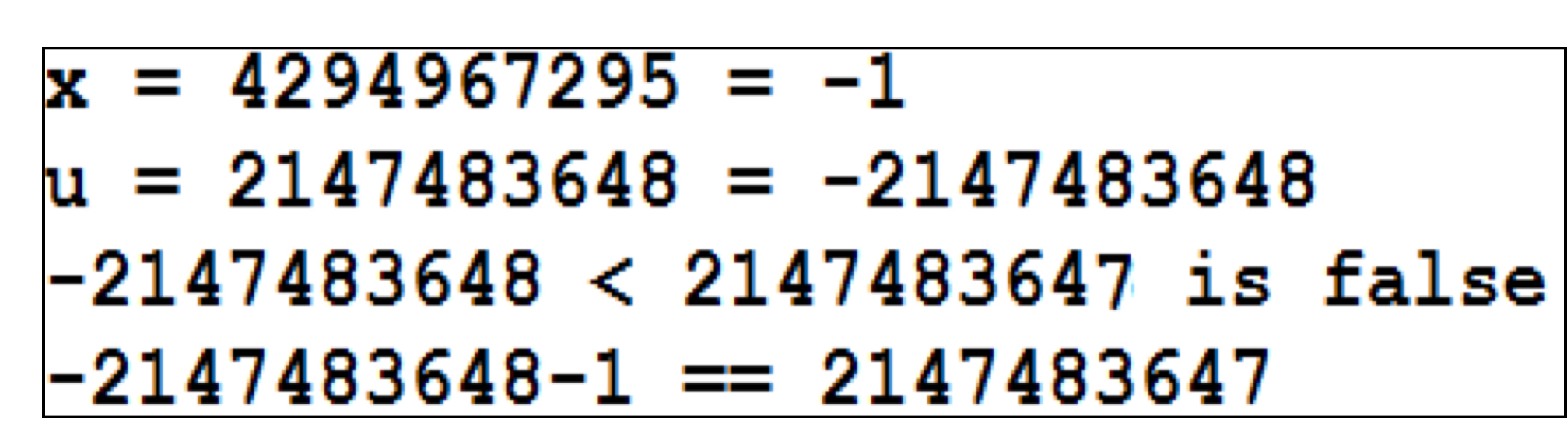
- 例：
- 造成不同的原因是第一次比较都转化为unsigned int（那么-1就变成了一个非常大的无符号整数）
- 第二次比较时转化为了int

科学计数法与浮点数¶

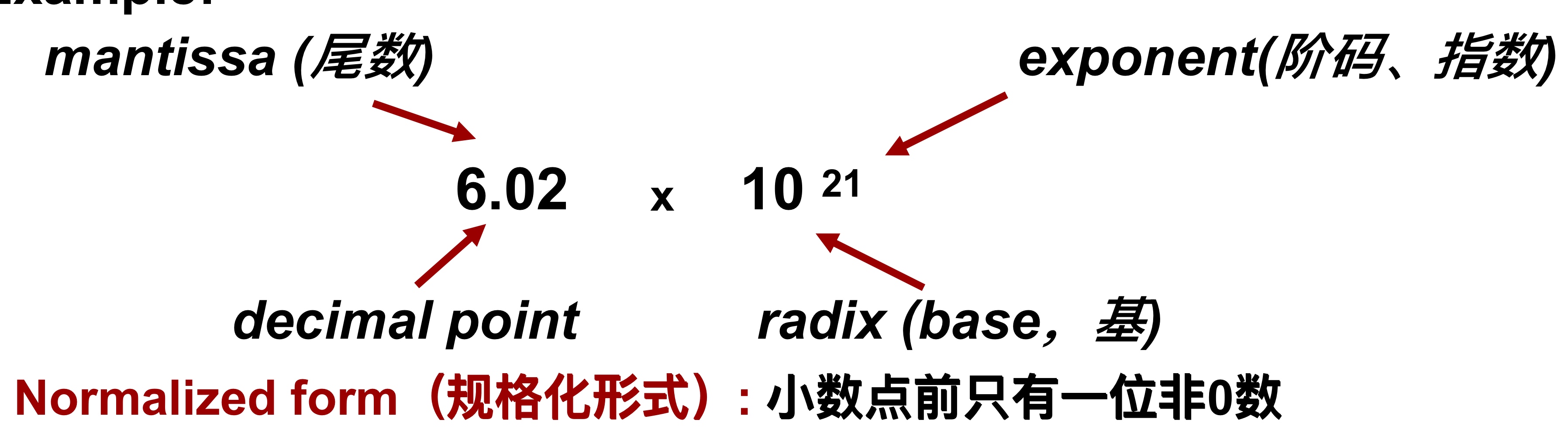
阶码用移码表示，就是补码第一位取反，即1表是正，0表示负
最大正值：0111111 … （23个1）= (-1)^0 * (2 - epsilon) * 2^(127)
00000000 00000000 … （23个0）= (-1)^0 * (0.5) * 2^(-126)
阶码0000 0001(-126)~1111 1110(127)，全0全1表示特殊值
- tip：可以这样理解，全零到全1是一个逐渐增大的过程（0～256）用中位数127均分为正负两部分
- 阶码的值减去偏置常数（127）可以得到真实值·
划分1｜8｜23；1｜11｜52
例：
特殊值
补充==为什么非规格化的数是-126而不是-127==：因为非规格化数时偏置常数为126而不是127！这样实现了数据大小的平滑过渡
符号位为1/0，尾数阶数全为0表示0
阶数为0，尾数不为0表示非规格化浮点数，即为了可以表示更小的浮点数，通过去掉前导的1来实现。
尾数为0，阶数全1表示正负无穷inf
尾数不为零，阶数全为1表示非数字NaN
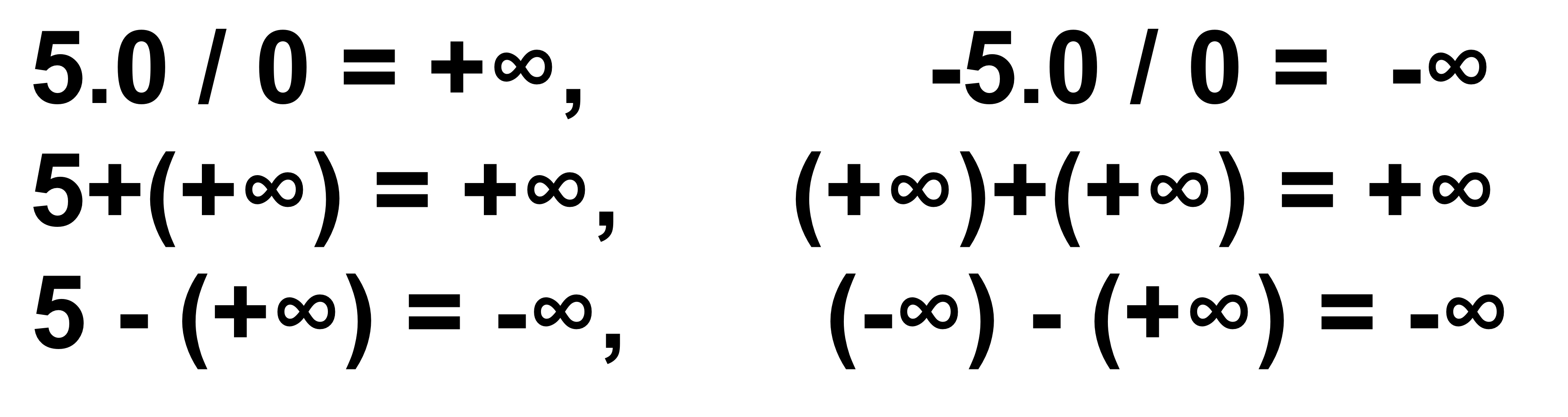
向系统输入一个不可表示的数时，系统会将其转化为最近的可表示数字。
例：浮点数转化：
先把10进制数分为整数部分和小数部分，然后分别转化为2进制数。
- 整数部分用除以2，反向取余数的方法，直到商为0终止。例如987转化为二进制数是1111011011。
- 小数部分用乘以2，取整数部分的方法，直到小数部分为0或者位数足够多。例如0.25转化为二进制数是0.01。
- 然后把整数部分和小数部分拼接起来，得到一个完整的二进制数。例如987.25转化为二进制数是1111011011.01。
接着把二进制数规格化，即把小数点移动到最高位之后，并记录移动了多少位。例如1111011011.01规格化后是1.11101101101*2^9。
最后把符号位、阶码和尾数提取出来并拼接起来，得到32位2进制浮点数。符号位是0表示正号；阶码是移动的位数加上偏移量127，即9+127=136，再转化为二进制得到10001000；尾数是小数部分的23位，不足的用0补齐，得到11101101101000000000000。所以最终结果是01000100011101101101000000000000。

非数值数据的表示¶

逻辑数据¶

用一位表示

西文字符¶

ascll码，不超过256个，7/8个二进制表示
包含数字、字母、专用符号、控制字符
8859

汉字字符¶

输入码:对汉字用相应按键进行编码表示，用于输入
内码:用于在系统中进行存储、查找、传送等处理
字模点阵或轮廓描述: 描述汉字字模点阵或轮廓，用于显示/打印
为与ASCII码区别，将国标码的两个字节的第一位置“1”后得到一种汉字内码
gb2312，gbk...

发展¶

Unicoide 的全称是 Universal Multiple-Octet Coded Character Set（通用多八位字符集，简称 UCS）。Unicode 在一个字符集中包含了世界上所有文字和符号，统一编码，来终结不同编码产生乱码的问题。
UTF-8:一个uncode占用4个字节，utf8对不同序号的字符用不同（1-4）个字节进行存储，节约空间，是一种变长编码方式。

显示¶

字形描述：
点阵描述
轮廓描述（矢量字体）

数据的宽度和存储¶

宽度和单位¶

二进制中的一位（0/1）是计算机中信息的最小单位，记为bit比特
8个bit（b）组成一个字节（位组），记为Byte（B）
字：不同计算机中一个字代表的长度不同（2、4...个字节）
字长：等于CPU内部总线的宽度、运算器的位数、通用寄存器的宽度等。数据通路的宽度。

存储和排列¶

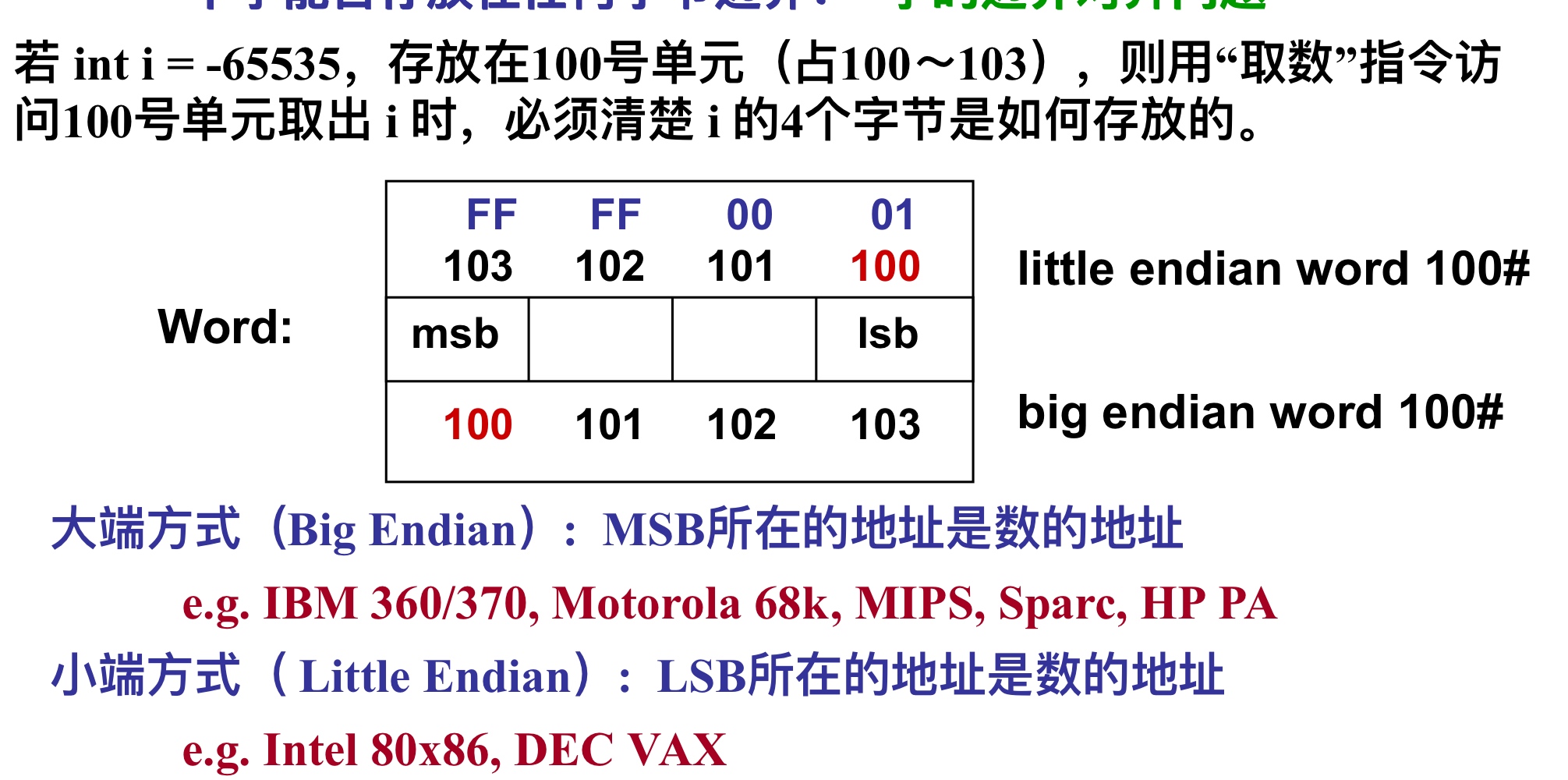
最低有效位lsb和最高有效位msb表示数的高地位（对于带符号数msb就是符号位）
小端lsb对应低地址，msb对应高地址
如：FF AF 00 23
从大端还原：FF AF 00 23
从小端还原：23 00 AF FF
- 一个字节八个比特即两个十六进制位
- 块内元素顺序保持不变
大端小端需要统一数据格式才能相互传递信息

例题¶

p58 2.26（综）

数据的运算¶

移位运算：
逻辑移位（无符号数）：移出、补零
算术移位（带符号数）：左移补零、右移补符号位
移动时舍去1可能发生溢出
扩展、截断：（类型转化时可能需要）
扩展：无符号数前面补0，有符号数补符号
截断：直接舍去高位

整数加减¶

机器（加法器）在运算时不会区分有/无符号数，得到的结果的机器数是相同的，标志位也是相同的，只是高级语言对数据的真值以及符号位（检查CF还是OF）的解释会受到数据类型的影响
有时可能无符号溢出但有符号不溢出，有时又恰好相反
整数在计算机中的表示形式（机器数）是其补码，并且用补码可以统一加减法
\([-y]_补\)=~\([y]_补\)+1（包含符号位也取反）
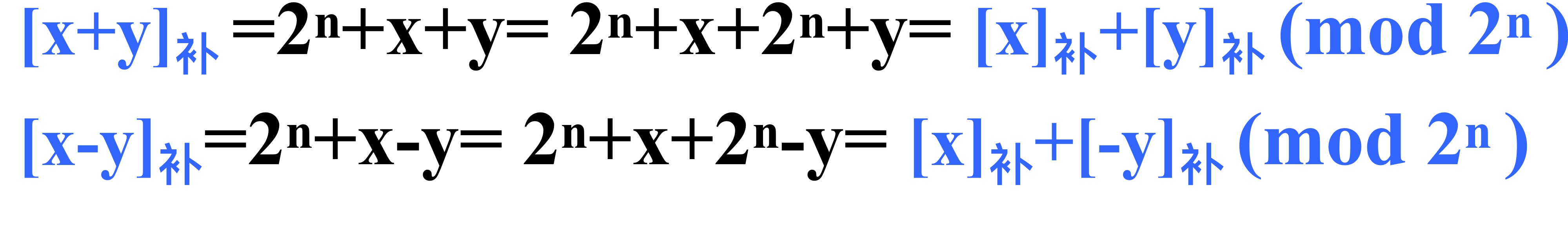
实现减法主要需要求出\([-y]_补\)
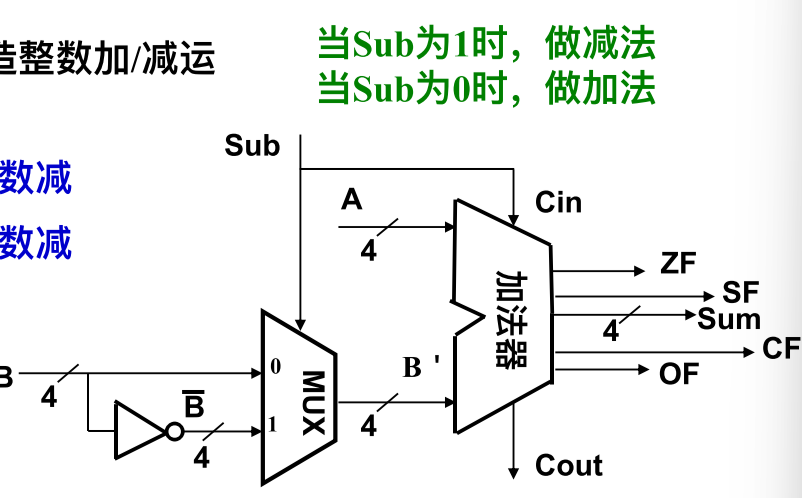
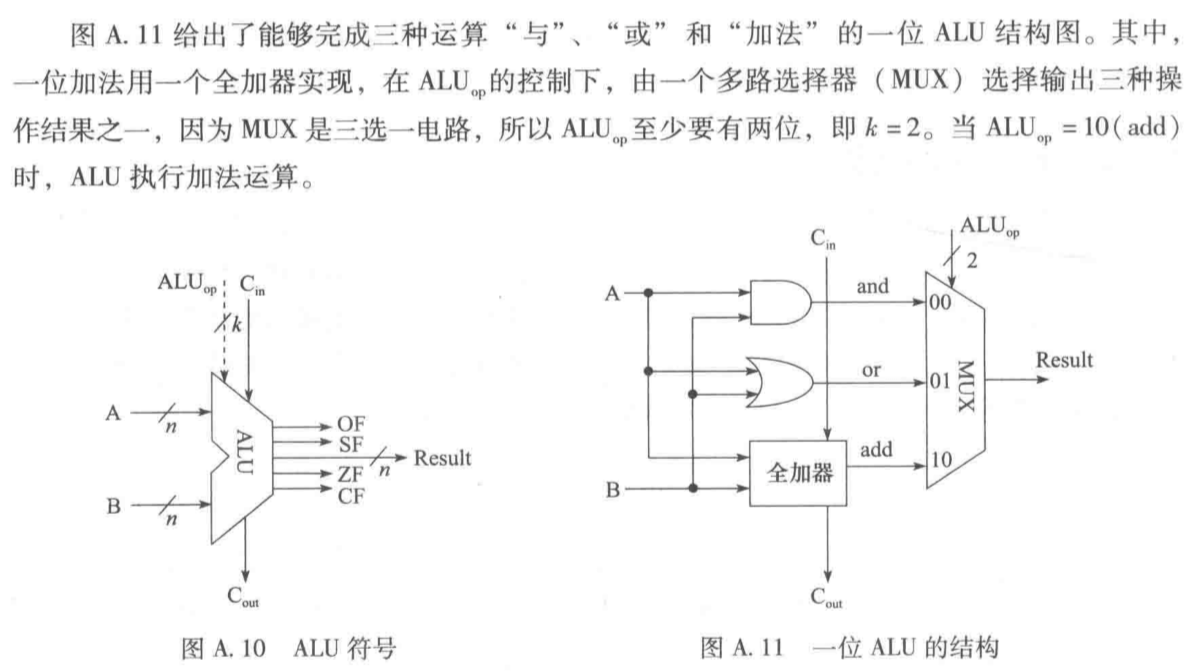
封装后的ALU可以实现
⽆符号整数加、减
带符号整数加、减
与、或、⾮、异或等逻辑运算
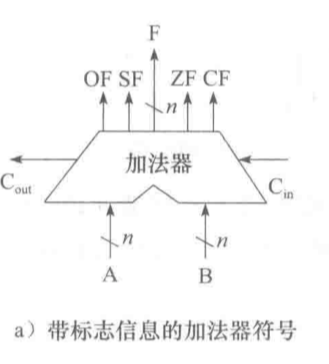
输出标志信息
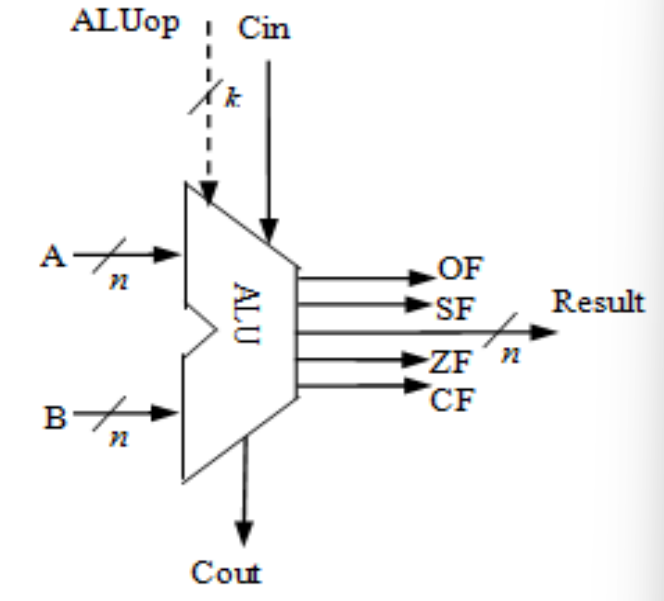
- 有⼀个操作控制端（ALUop），⽤来决定ALU所执⾏的处理功能。 ALUop的位数k决定了操作的种类，例如，当位数k为3时，ALU最多只有23=8种操作。
标志位
溢出OF：OF=Cn^Cn-1(最高位和次高位的进位的异或)，有符号数同符号相加结果变号说明发生了溢出（针对有符号整数，指的是进位到了符号位），当最高位和次高位进位数目不同时就说明最高位（符号位）的大小发生了变化（和的符号位和加数的符号位不同），故说明发生了溢出
- 两个同符号数相加发生变号
进（借）位CF：cout^cin（针对无符号整数，如果输出的结果比输入的数字还要小就说明发生进位，CF=1）
- 可以这样区分：OF发生时是最高位发生变化，CF是OF向前又进了一位
- 减法中代表发生借位
- C表示进位(借位)位的状态，Sub表示运算类型（0表示加法，1表示减法），CF=C^Sub
符号位SF
零标志ZF：当数为0时ZF为1
计算机中所有算术运算都基于加法器实现！
加法器不知道所运算的是带符号数还是⽆符号数。
加法器不判定对错，总是取低n位作为结果，并⽣成标志信息。
使用减法结合符号位比较元素大小
unsigned：CF=0说明大于（不需要借位）
signed：OF=SF说明大于

举例¶

整数乘除¶

乘法¶

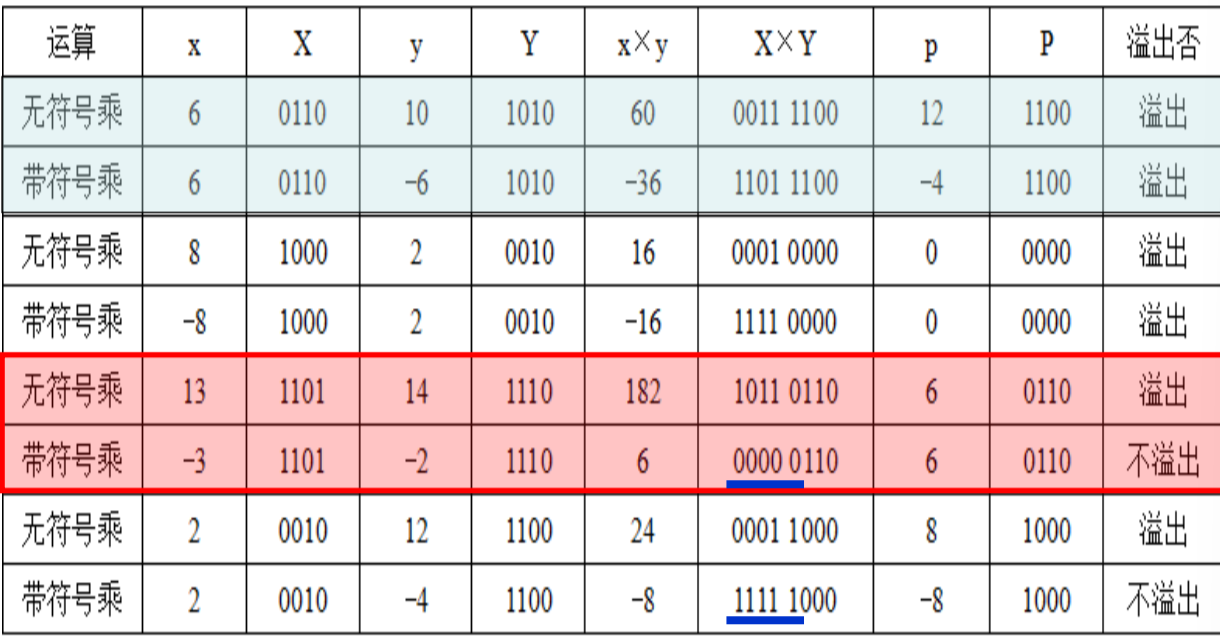
两个n位数相乘得到得到2n位数，其中高n位会被舍弃，但可以用于判断是否发生了溢出
无符号：若⾼n位全0，则不溢出，否则溢出
带符号：若⾼n位全0或全1且等于低n位的最⾼位，则不溢出。
注意：在开始乘法之前要先对数进行拓展，拓展到2n位，有符号数前面补符号位，无符号数补0！然后直接进行无符号乘法即可
编译器在处理变量与常数相乘时，往往以移位、加法和减法的组合运算来代替乘法运算。
把n位数的乘法转化为1位（布斯算法）
对于带符号乘，若积只取低n位，则和无符号相同；若取2n位，则采用“布斯”乘法
- 不能直接用无符号乘法处理有符号乘法
- 使用布斯乘法处理有符号数乘法：
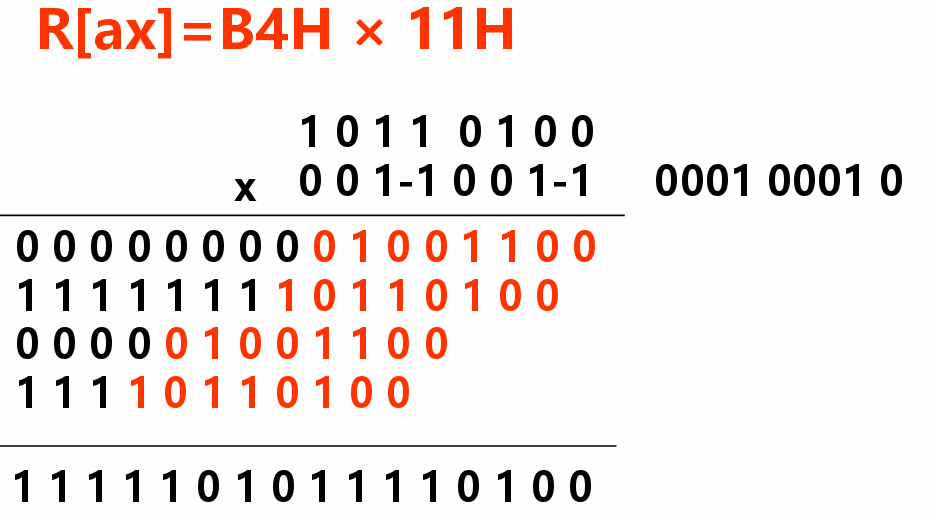
- 将乘数末尾添0，y_i=y_i-1-y_i()每一位等于低位点减去该位，如果是1就做加法，如果是-1就做减法（被乘数各位取反末尾加一）

整数除法¶

对于带符号整数来说，n位整数除以n位整数，除-2^n-1/-1= 2^n-1会发⽣溢出外，其余情况（除数为0外）都不会发⽣溢出。
因为整数除法，其商也是整数，所以，在不能整除时需要进⾏舍⼊，通常按照朝0⽅向舍入
为了缩短除法运算的时间，编译器在处理⼀个变量与⼀个2的幂次形式的整数相除时，常采⽤右移运算来实现。
⽆符号：逻辑右移；带符号：算术右移
能整除时，直接右移得到结果，移出的为全0
不能整除时，右移移出的位中有⾮0，需要进⾏相应处理
- ⽆符号数、带符号正整数：移出的低位直接丢弃
- 带符号负整数：加偏移量(2^k-1)(避免向-inf舍入)，然后再右移k 位，低位截断
- 若不加偏移量则右移总是向-inf舍入

浮点数的运算¶

浮点数除以0会返回特殊值（NAN或inf）不会报错

加减¶

对阶-加减-规格化-舍入
运算之前要先进行对阶操作（使两数阶码相等）
⼩阶向⼤阶看⻬，阶⼩的那个数的尾数右移，右移位数等于两个阶码差的绝对值（二进制右移时别忘了规格化隐含的1），结果的阶码取参与运算数的阶码的较大值
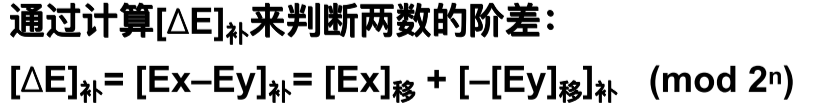
- 补码运算溢出时得不到正确的阶差
运算完成之后进行规格化：
当尾数⾼位为0，则需左规：尾数左移⼀次，阶码减1，直到MSB为1或阶码为00000000（-126，⾮规格化数）
当尾数最⾼位有进位，需右规：尾数右移⼀次，阶码加1，直到MSB为1或阶码上溢
以为过程中注意是否发生溢出：阶码溢出异常处理：阶码上溢，则结果溢出；阶码下溢到⽆法⽤⾮规格化数表示，则结果为0
如果尾数⽐规定位数⻓（有附加位），则需考虑舍⼊
若运算结果尾数是0，则需要将阶码也置0。
例

附加位¶

为了减少浮点数计算过程中造成的精度的损失
IEEE754规定: 中间结果须在右边加2个附加位
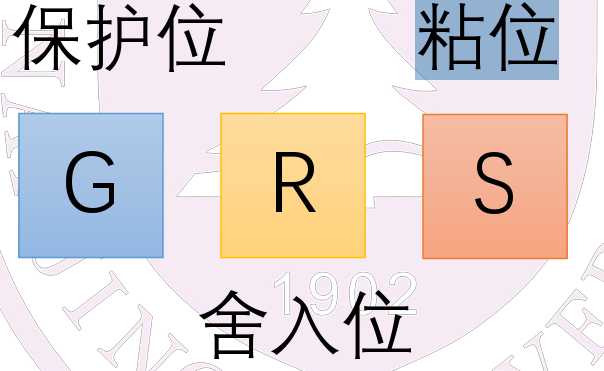
Guard (保护位)：在significand右边的位
Round (舍⼊位)：在保护位右边的位
sticky粘位（只要舍入位右边有1，粘位就置1）
附加位的作⽤：⽤以保护对阶时右移的位或运算的中间结果。
附加位的处理：
左规时被移到significand中;
作为舍⼊的依据。
舍入规则
分类：
- 就近舍入（向偶数舍入）：即十进制下的“四舍五入”，如果多余数字等于0.5，则取最低位为偶数的值。
- 如果 G = 0 ，向下舍入（什么都不做）
- 如果 G = 1 ， RS == 10 或 RS == 01或11 ，向上舍入（向尾数添加一个）
- if GSR = 111，round to even(二分之一概率+1)
- 向上舍入（向正无穷舍入）：即如果多余数字大于0，则最低位进1。
- 向下舍入（向负无穷舍入）：即直接舍掉多余数字。
- 向零舍入（截断）：即如果多余数字大于0，则直接舍掉多余数字，否则最低位进1。

乘除¶

类型转换¶

从int转换为float时，不会发⽣溢出，但可能有数据被舍⼊
从int或 float转换为double时，因为double的有效位数更多，故能保留精确值
从double转换为float和int时，可能发⽣溢出，此外，由于有效位数变少，故可能被舍⼊
从float 或double转换为int时，因为int没有⼩数部分，所以数据可能会向0⽅向被截断

补充¶

数字逻辑电路基础¶

基本原件¶

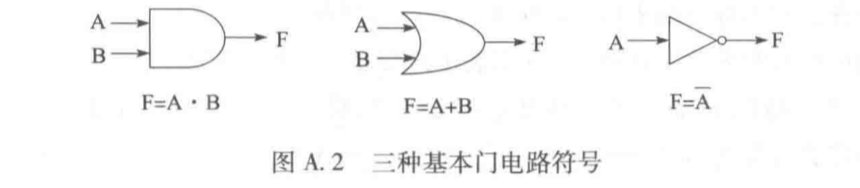
与门，或门，非门
有存储功能的电路成为时序逻辑电路，没有的称为组合逻辑电路
n位逻辑运算

数据的表示和运算¶

进制转化¶

数值数据的表示¶

科学计数法与浮点数¶

非数值数据的表示¶

逻辑数据¶

西文字符¶

汉字字符¶

发展¶

显示¶

数据的宽度和存储¶

宽度和单位¶

存储和排列¶

例题¶

数据的运算¶

整数加减¶

举例¶

整数乘除¶

乘法¶

整数除法¶

浮点数的运算¶

加减¶

附加位¶

乘除¶

类型转换¶

补充¶

数字逻辑电路基础¶

基本原件¶

组合逻辑部件¶

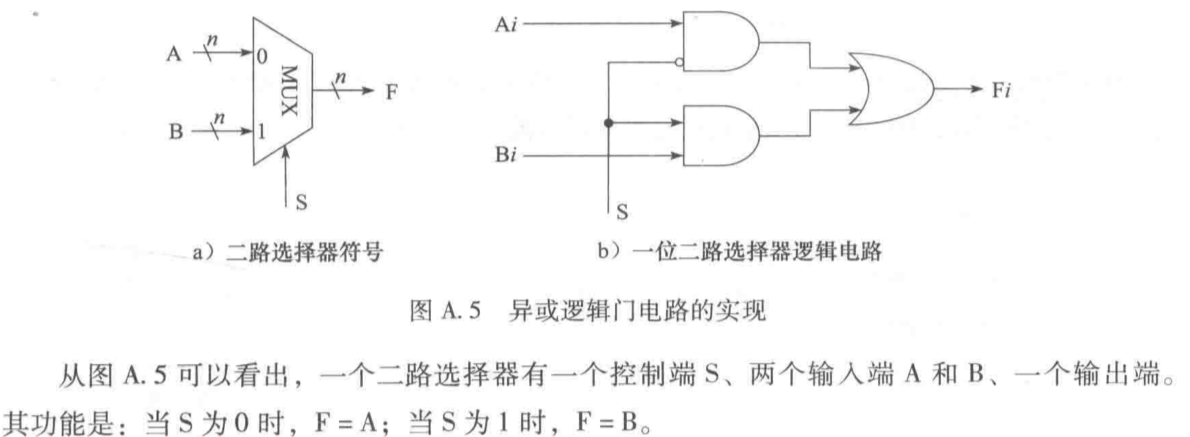
多路选择器¶

无符号数加法器¶

算数逻辑部件ALU¶