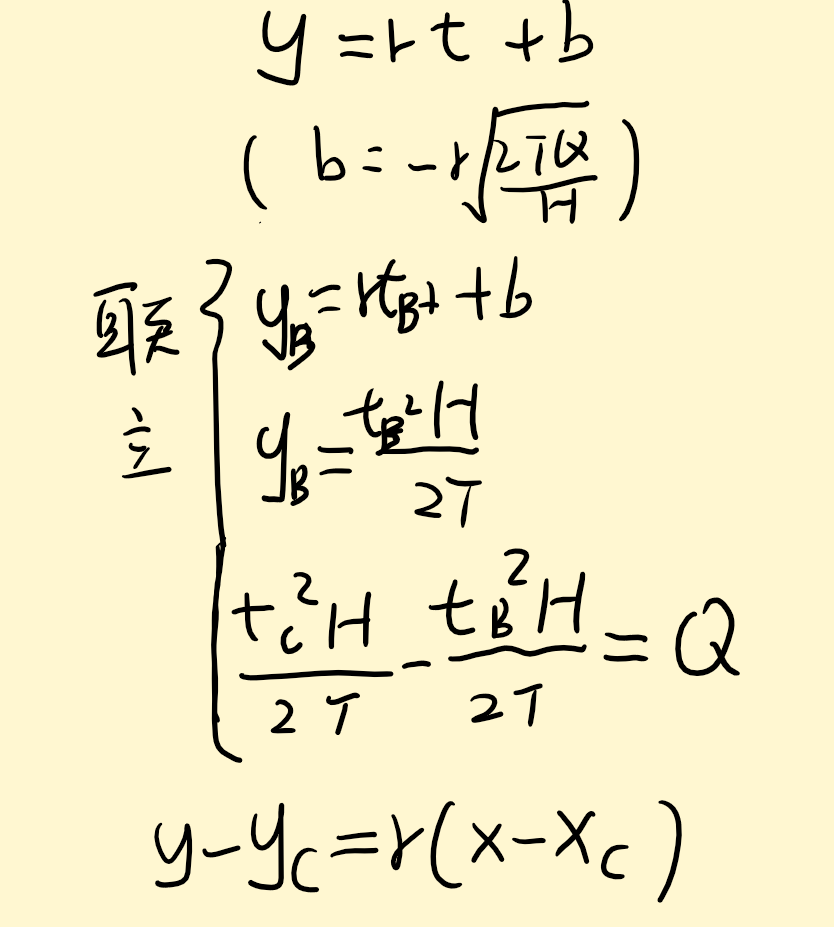作业六
211275022田昊东
P1
- 一共有4块可以及时到达正常播放,分别为1、4、5、6

- 如图所示,有6块可以及时到达以供播放
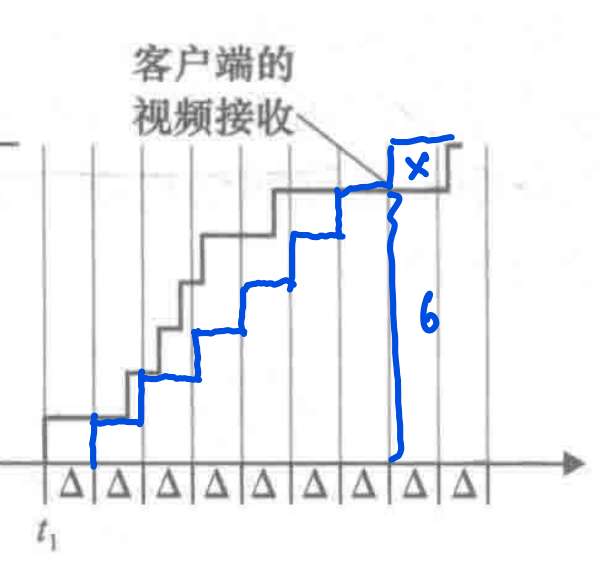
- 在\(t_1\)后第四区间中达到最大值2
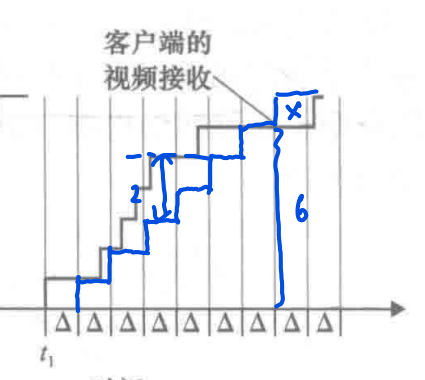
- 如图,当时延为3时刚好能使得所有块及时到达以共发送
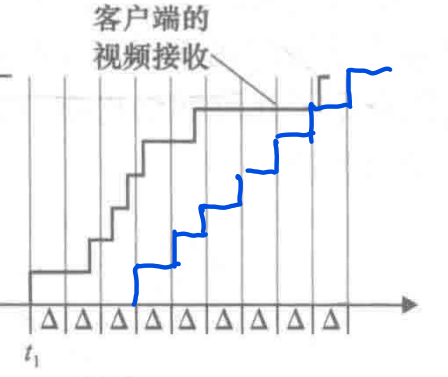
P3
- 由于速度均匀变化,因此平均速率为\(\frac{H}{2}\)
-
- 当\(r>\frac{H}{2}\)时数据接收的速度在大部分情况都会小于播放的需求,因此用户面临严重的播放卡顿
- 当\(r=\frac{H}{2}\)时可能会出现周期性间歇卡顿
- 当\(r<\frac{H}{2}\)时在前几个区间由于到达速率的波动可能会存在不时卡顿的现象,但随着播放的进行,卡顿现象会逐渐消失
-
- 一个周期可以缓存的比特数目为\(\frac{TH}{2}\),在一个周期内t时间可以缓存的数目为\(\frac{t^2H}{2T}\)
- 不妨设\(kT<Q<(k+1)T\),那么\(t=kT+\sqrt{\frac{2T(Q-kT)}{H}}\)
- 当\(Q=\frac{T}{2}\)时说明刚好需要一个周期来缓存数据,而缓存的数据至少够一个周期内视频播放,而每播放一个周期,就又至少缓存够一个周期播放的数据,由此缓存永远不会用完,视频可以流畅的播放。
-
- 求\(Q\)的最小值,就是求解对应视频播放消耗比特的直线与数据达到的曲线的切点(令\(H=2r\)),最终计算得到\(Q\)的最小值
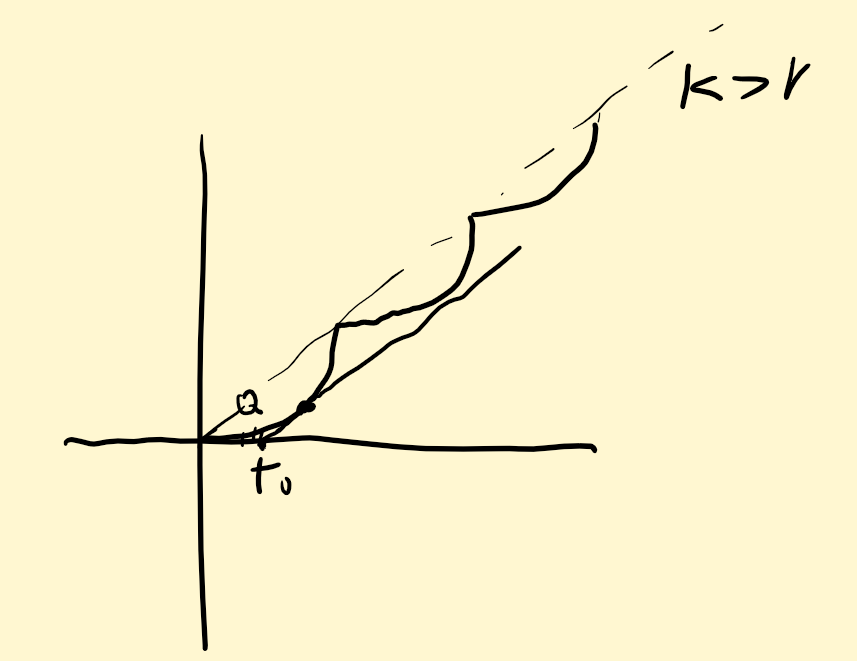
- 联立方程\(\begin{numcases}{}y=rt+b\\y=\frac{t^2H}{2T}\\\frac{tH}{T}=r\end{numcases}\)
- 解得\(\begin{numcases}{}t=\frac{rT}{H}\\b=-\frac{r^2T}{2H}\end{numcases}\)
- 与x轴联立得到\(t_0=\frac{rT}{2H}\)
- 带入得到\(Q_{min}=\frac{r^2T}{8H}\)
-
- 当\(Q>=Q_{min}\)时,缓存始终大于0,就是要找到何时缓存量第一次到达\(B\)

- 仍作出假设\(kT<t_f<(k+1)T\)
- 不妨假设\(Q<=\frac{TH}{2}\)
- 那么带入坐标解出\(b=-r\sqrt{\frac{2TQ}{H}}\)
- 即有\(B=\frac{kTH}{2}+\sqrt{\frac{2T(Q-kT)}{H}}-rt-b\)
- 解出\(t_f=kT+t\)
- 当\(Q<Q_{min}\)时,会发生卡顿(不妨假设只发生了一次)
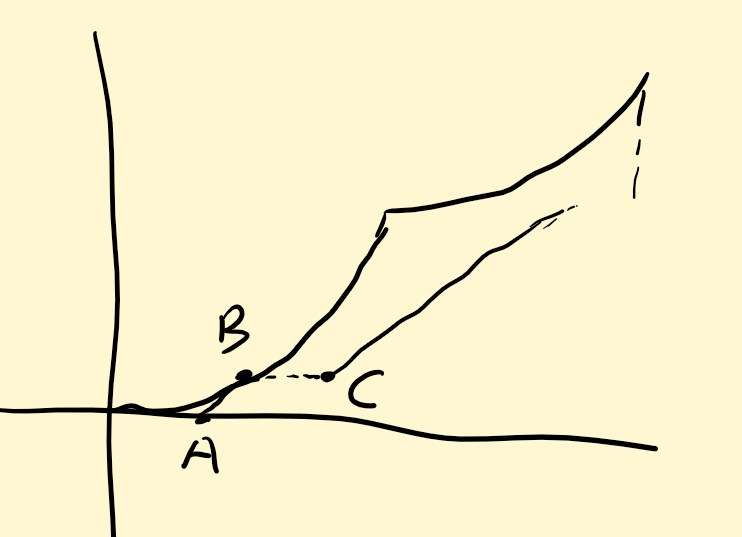
- 如图所示,延时加载完成后开始播放,到达B后出现卡顿,又进行延时加载,到c处完成,开始继续播放
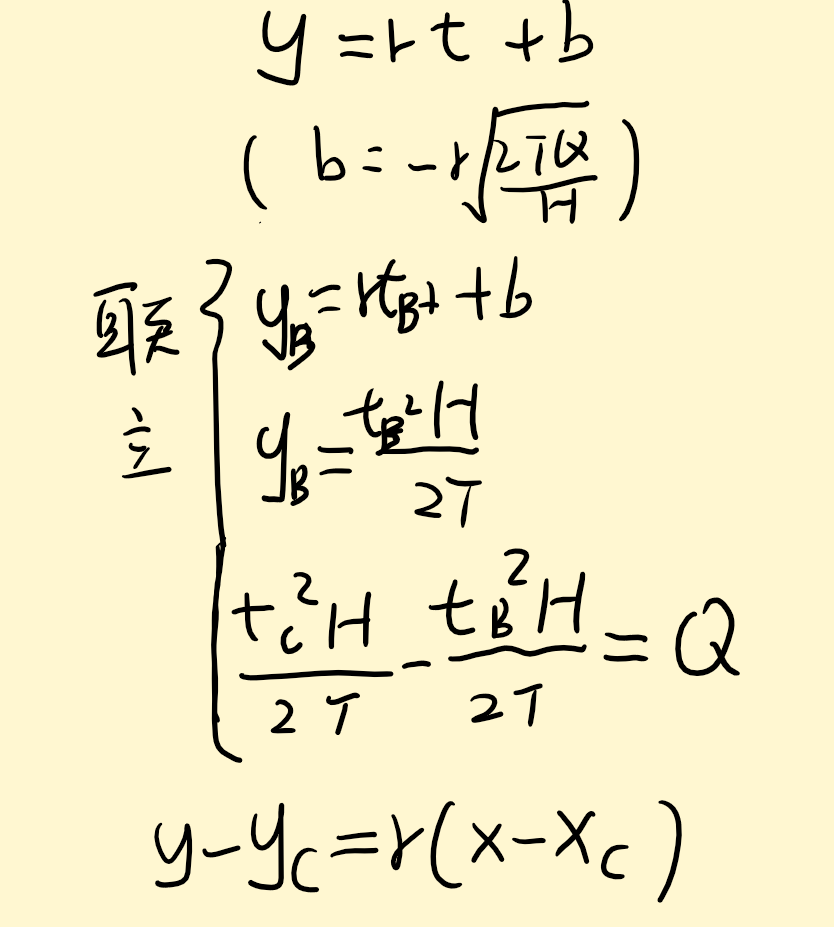
- 得到缓冲后的方程\(y=rt+b_c\),且有\(B=\frac{kTH}{2}+\sqrt{\frac{2T(Q-kT)}{H}}-rt-b_c\)
- 得到最终结果\(t_f=kT+t\)
P5
- 需要存储所有组合\(N^2\)
- 只需要分别进行存储\(2N\)
P20
- 桶长度为p,令牌生产速率也为p
- 第一个漏桶限制了平局速率和突发长度,使用第二个漏桶来限制峰值速率。
- 桶长度为p表示短时最多只能发送p个包,即实现了峰值速度的限制
- 令牌生产速率也为p,则保证能快速恢复,使得峰值的限制始终为p