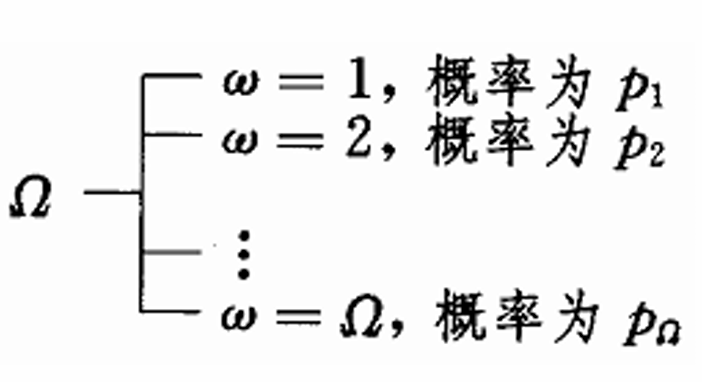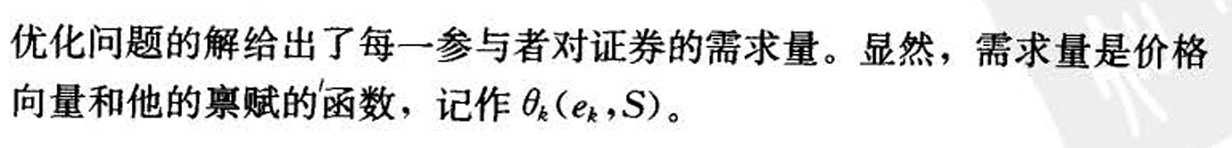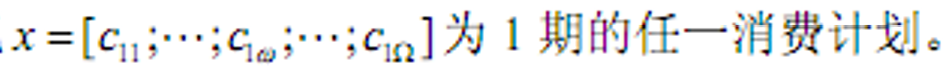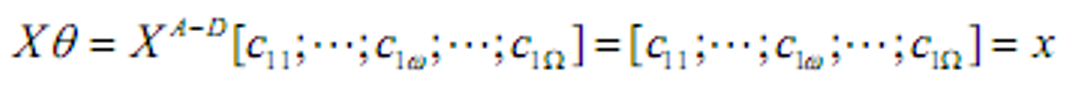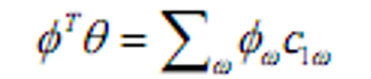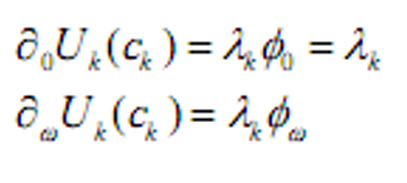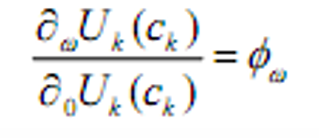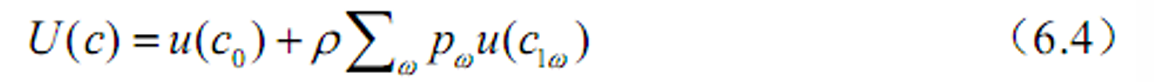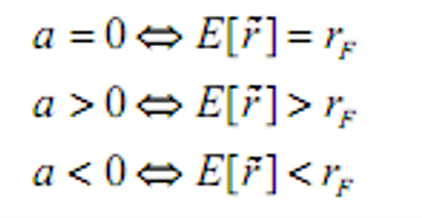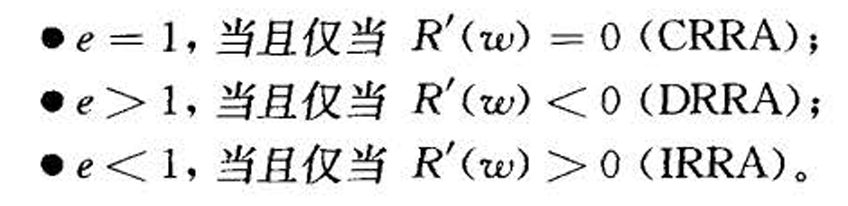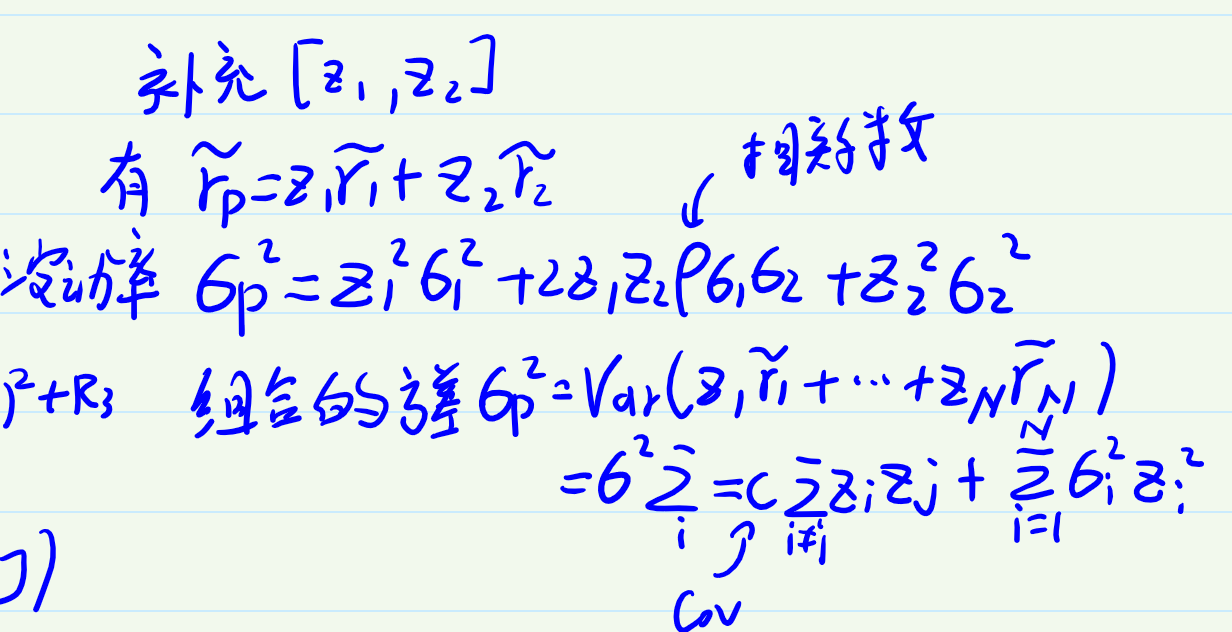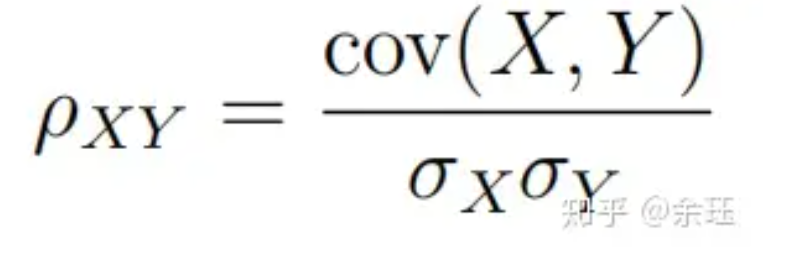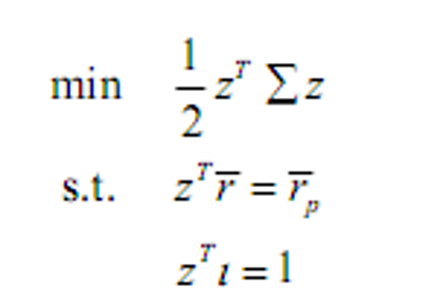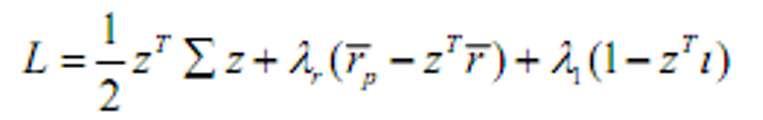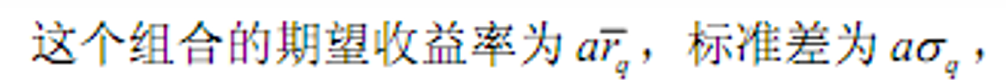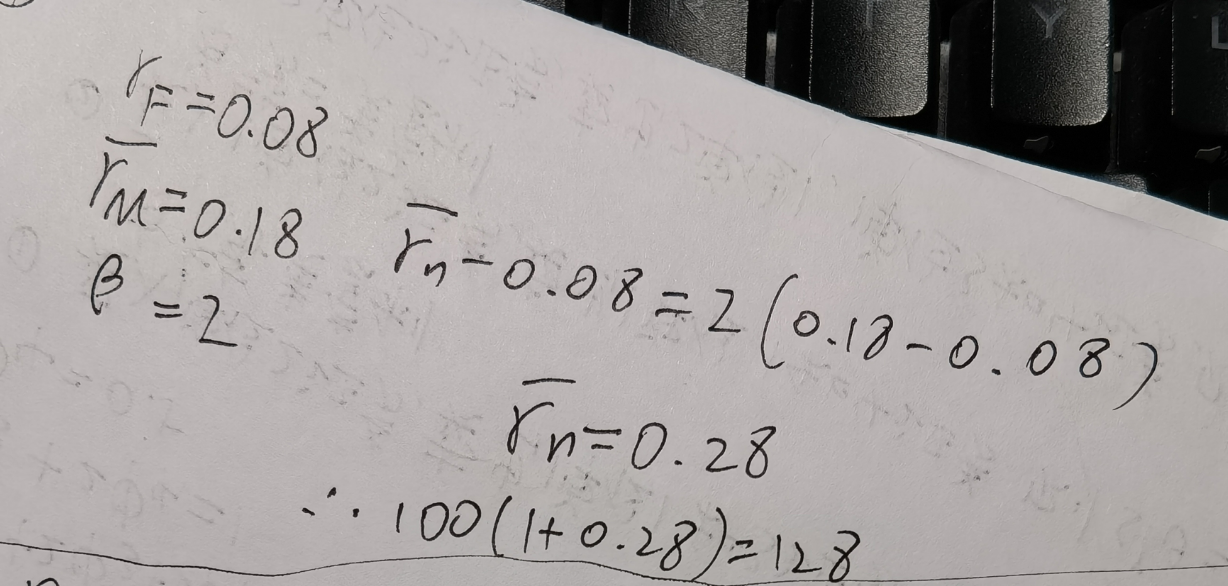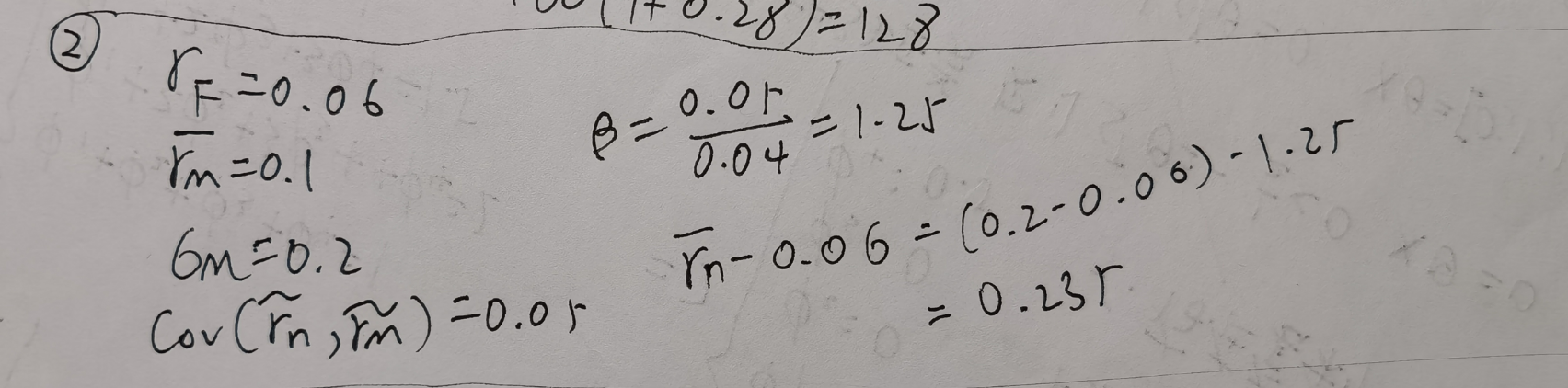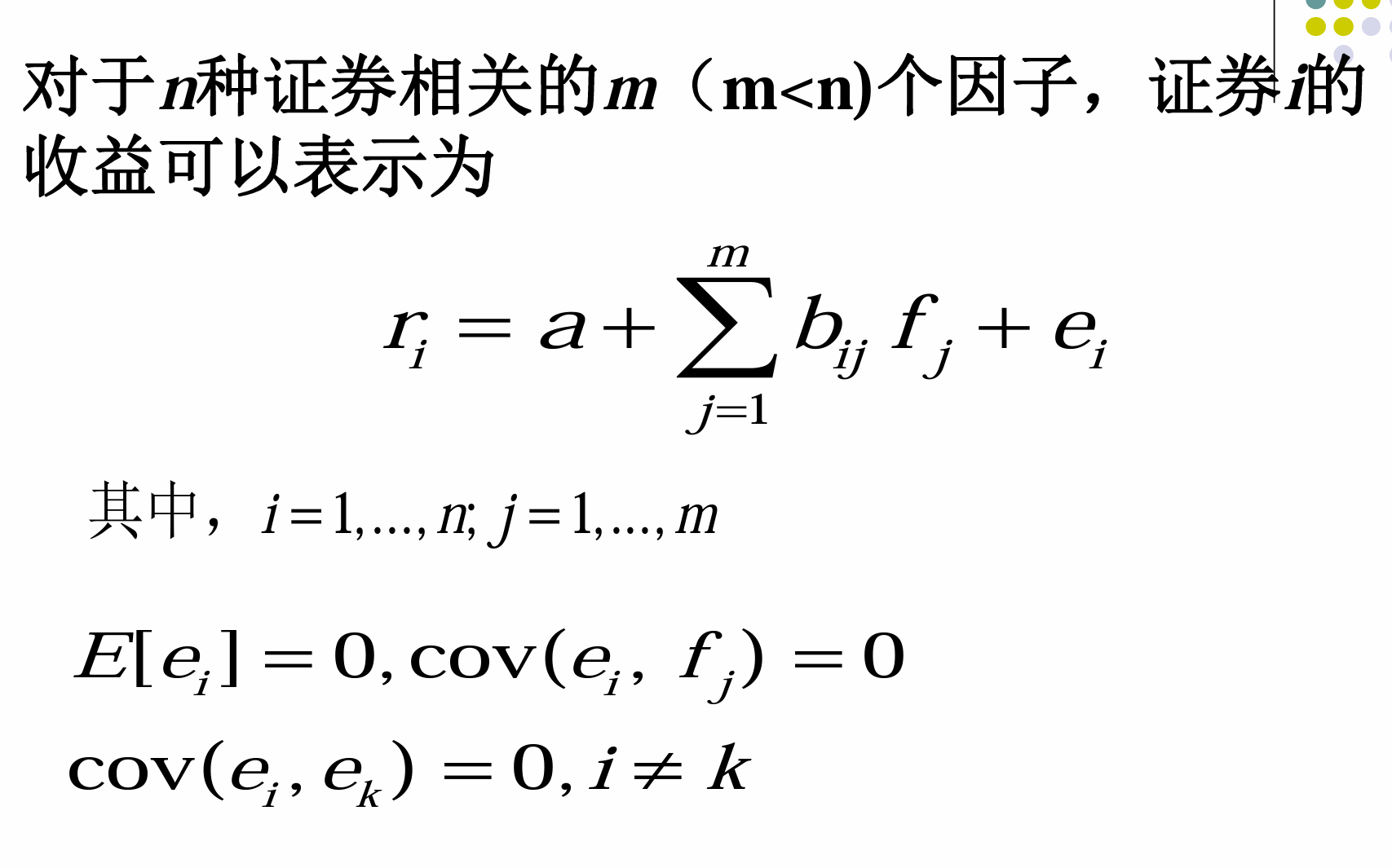考试类型¶
- 名词解释20
- 重点看书,定义1.1、1.2...如偏好、效应函数,定理结论
- 选择题20
- 简答题20
- 综合题40
- 后三章为主,计算
考试内容¶
- 证明思路要了解
- 定义+定理结论(性质)
- 注意对照勘误
- 注意看作业
u2(市场框架的定义、结论)¶
- 经济环境:状态、不确定性(了解一下)
- 参与者禀赋的数学性质(记住)
- 证券、市场、交易过程、无摩擦市场、什么叫经济、证卷市场经济
- 框架:环境、参与者、市场、均衡等(经济的组成)
- 市场出清、帕丽特最优,市场均衡、价格
- 偏好的定义,参与函数的定义
- 定理2.1
- p21定义市场化
- 定义2.5
u3¶
-
什么叫ab证券
-
知道优化问题如何建立、限制,不用会计算拉格朗日,以及得到的解、性质(定理3.3均衡性)(不用会解)
-
什么是市场完全(定义3.4,3.2,3.3结论)
u4¶
- 套利(4.1)三类
- 无套利原理
- 资产定价基本定理(4.7)
- 风险中性定价
u6¶
- 期望效应函数及简化6.1、6.4(勘误)时间可加、状态独立
- 时间可加。。。各种希望效应函数
- 独立
- 拓展了解一下
u7¶
- 理性消费者风险厌恶->效应函数凹形
- 风险厌恶定义
- 7.2风险厌恶特征
- 7.3度量绝对相对
- 例子看一下即可
- 定理7.4,条件等价推到
- 7.5比较结论会应用
u8¶
- 8.23456最优组合的性质,投资不投资的条件
- 定理8.234及56(课件上的5‘)的应用
u9¶
- 随即占优,判别(不同阶)
- 基金分离
u12&&¶
- capm公式,计算价格等等,
- 资本市场线、证卷市场线、画图
- 均值标准差前沿组合图及性质
u13&&¶
- 模型是什么,给出参数的计算(看例子,了解推倒思路)
u14&&¶
- 以课件为主
知识点整理¶
U2-基本框架¶
基本概念¶
-
经济结构
-
所处的自然环境
-
经济中各参与者的经济特征
-
金融市场
-
经济环境:
-
时间01
- 状态(风险)(卢卡斯经济)
-
经济参与者
-
集合\(K=1,...,k\)
- 因素:经济资源(禀赋,信息,生产技术);经济需求
- 禀赋(初始占有的资源,可以用作消费生产)
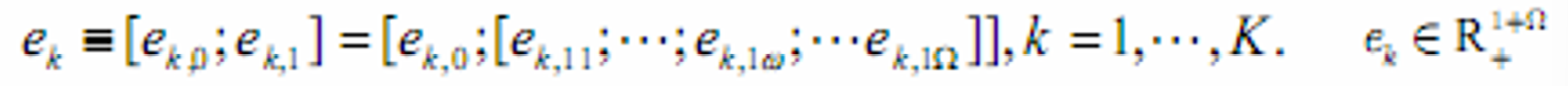
- 信息:公共、私有信息(不考虑不对称的情况)
- 经济需求(基于他在不同时期和未来不同状态下的消费)
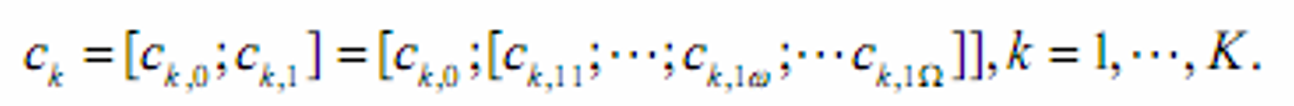
- 消费集(参与者所有可能的消费计划)
- 消费选择(计划):[c0;c1]
- 不同状态下消费单一消费品的单位数
- 消费路径:[c0;c1w]

- &&偏好
- 参与者的经济需求是由他对于不同消费计划的喜爱来描述的。偏好是参与者对所有可能消费计划中的一个排序,这样的排序定义了他的经济需求。

- 排除了消费计划之间无法比较的可能性。
- 排除了非理性的问题
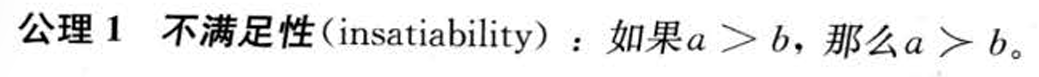
- 如果a>b,即在所有时期和状态下a都不比b提供的消费少且在有些状态下提供更多的消费,那么a优于b
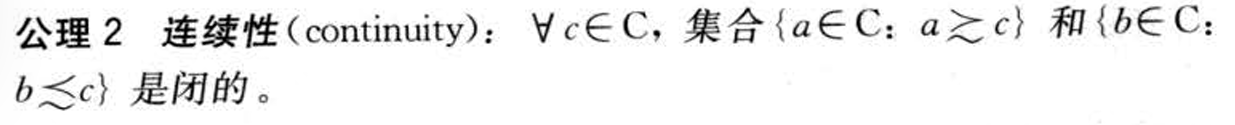
- 如果两个消费计划非常接近,即它们在所有时期和状态下都提供相似的消费,那么它们的排序应该是“接近的“
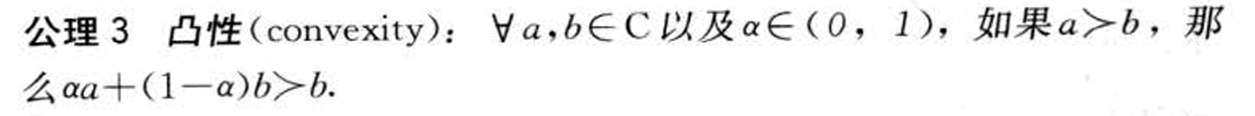
- &&效用函数
- 对于给定的偏好关系,可以给每一个消费计划一个实数作为效用,这个从消费计划到实数的映射称为效用函数(偏好定量化)
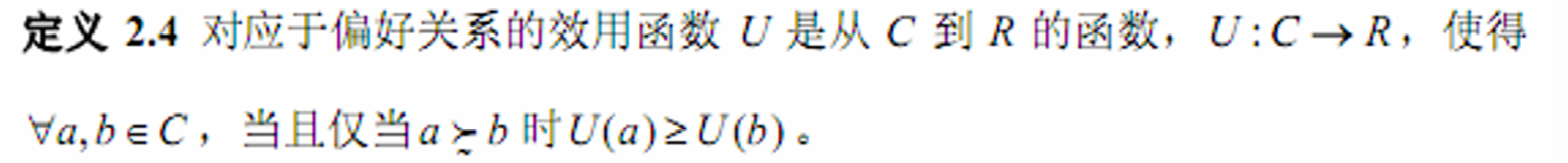
- &&

- 正单调变换后的效用函数在排序&比较上是等价的
- 证卷市场
- 金融市场由一组证券构成
- 支付树:

- 它的支付只取决于未来的实际经济状况。
- 它的支付是外生给定的且不受经济中参与者行为的影响
- 因为所有参与者都知道可能状态的集合和对应的概率,他们也知道且一致认同证券支付的概率分布。
-
市场结构,支付矩阵(N只证券在未来的支付)
-
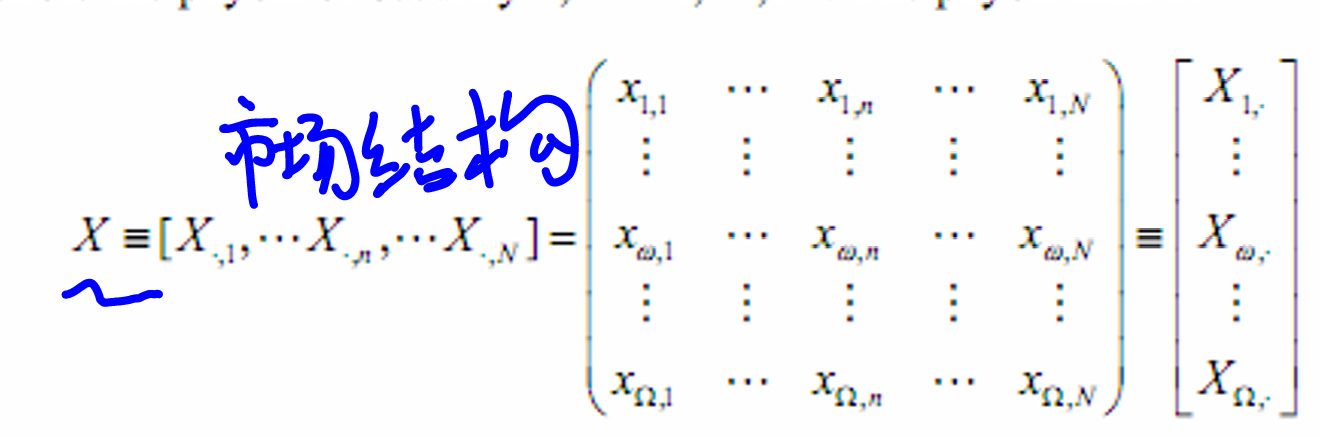
-
证卷组合(证券的持有数目)
-
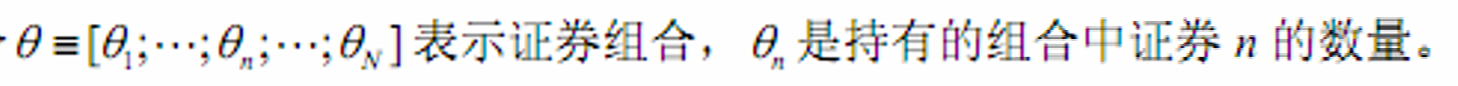


-
&&市场化支付集合

-
即由组合可以产生的支付
- 价格向量

-
&&无摩擦市场:
-
所有参与者都可以无成本地参与证券市场
- 没有交易成本
- 对于参与者的证券持有量没有头寸限制
- 个体参与者的交易不会影响证券价格
- 没有税收
- &&经济的定义(特定的三部分组成)

- 证券市场经济
- 市场均衡
- 参与者持有量取决于这些证券的价格。
- 参与者对证券的需求会共同影响证券的价格。
- 如果价格使得对证券的需求恰好等于它的供给,市场达到了均衡
- 参与者优化
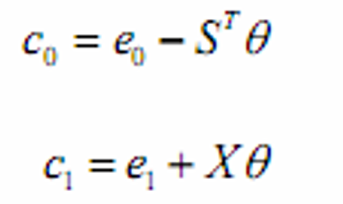
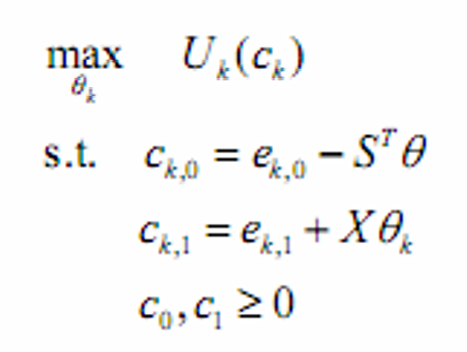
- 给出了最优时每一参与者对不同证券的需求量
- 市场出清:总需求等于总供给
- 市场出清条件,参与者的总需求等于总供给
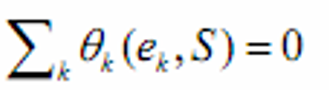
- 即商品市场出清(Walras法则)
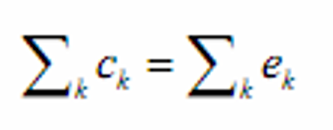
- pareto最优

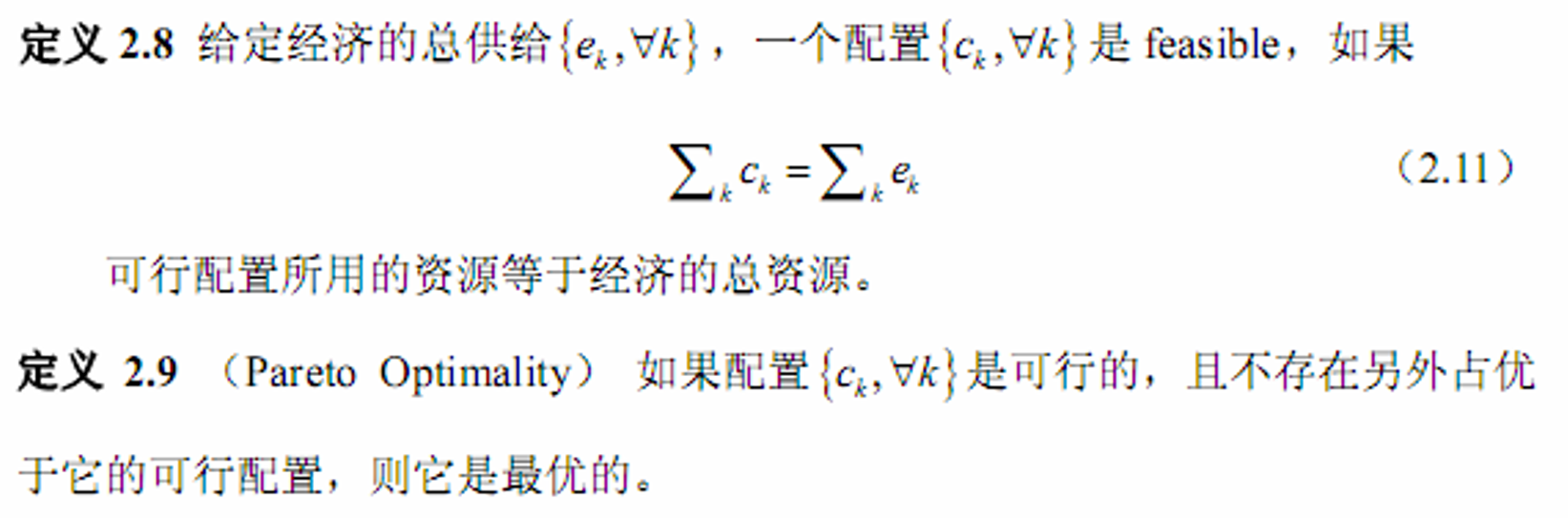
- 即在不牺牲其他参与者的福利或使用更多资源的前提下,不 能改进任意一个参与者的福利。
例题¶
U3-AD市场¶
基本概念¶
- 状态价格

- &&(A-D证券)
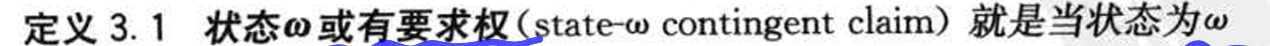

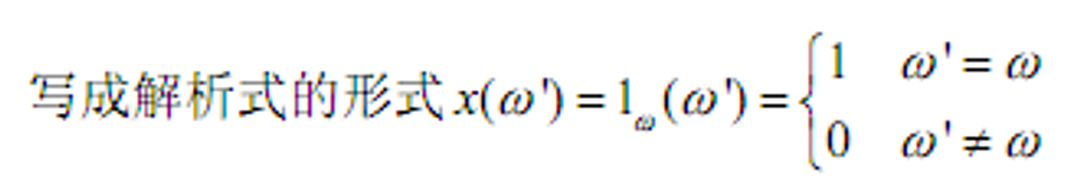
- A-D证券市场:
- &&市场完全性
- 可以用状态或有要求权的组合为任意未来消费计划融资。

- A-D市场一定是完全的
- 参与者优化(针对单个参与者)
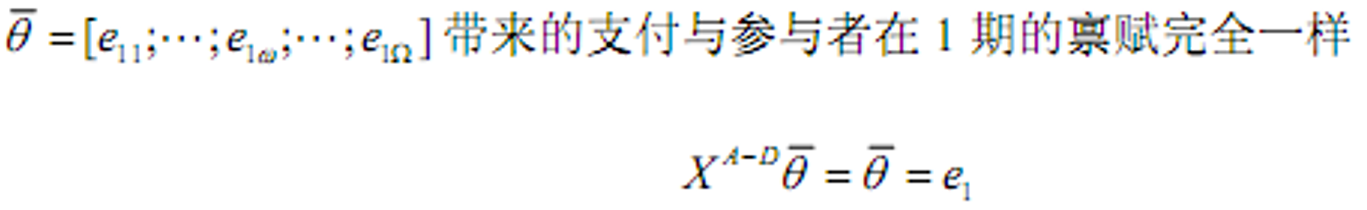
- 参与者0期加1期的禀赋为
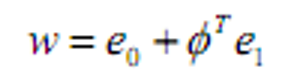 有
有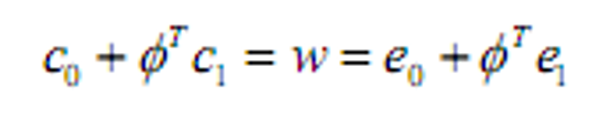

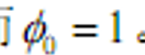
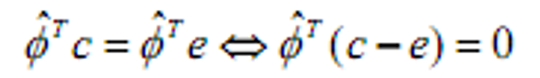
- &&得到
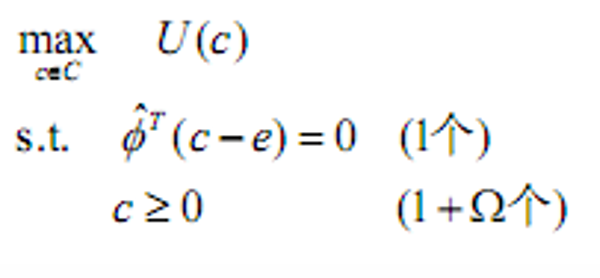
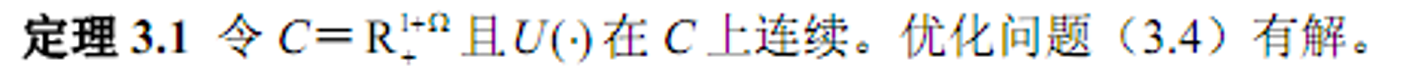
- &&解的性质
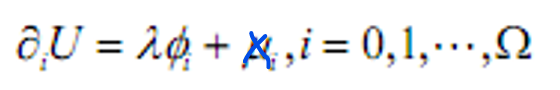
- 市场均衡(针对多个参与者)
- 条件
- 投资者最优
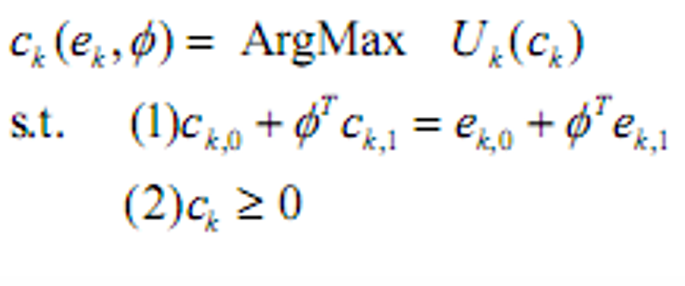
- 市场出清(每个时期的消费=禀赋)
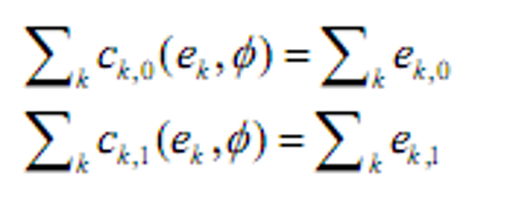
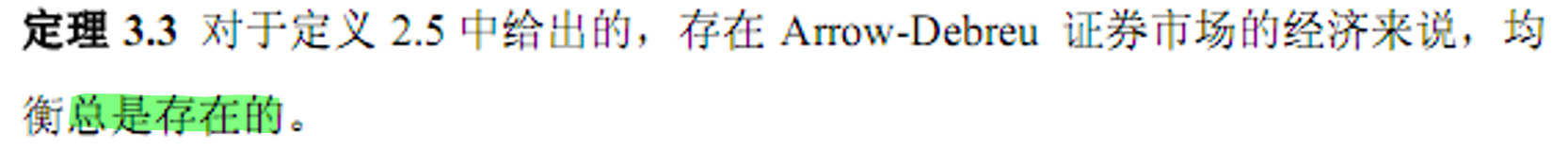
- &&性质:
- 均衡时,参与者根据市场价格选择最优的消费/组合计划。他在1期任意状态下的相对边际效用等于状态价格。并且,所有参与者在市场出清价格下达到他们的最优。


例题¶


-

- 预算集:消费总额等于禀赋总额
-
市场均衡


U4-套利和资产定价¶
基本概念¶
- 复合证券:它们的支付都可以看成是由状态或有证券的组合而产生的。
- 冗余证券:支付可以表示成其他证券支付的线性组合,没有它我们也可以生成相同的支付
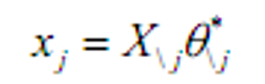 (市场不满秩)
(市场不满秩) - 如果市场没有摩擦,冗余证券的存在与否没有任何经济意义。但当市场 存在摩擦时,即使某个证券的支付与其他证券的支付是相关联的,它也 不再是冗余证券了,因为要用其他证券来实际复制它是有额外成本的 。
- 满秩
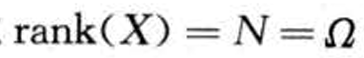 的证券市场结构与Arrow-Debreu证券市场之间是等价的(满秩的金融市场结构和A-D经济之间有了一一对应)
的证券市场结构与Arrow-Debreu证券市场之间是等价的(满秩的金融市场结构和A-D经济之间有了一一对应) - &&

- 行线性无关
- 可以转化为状态或有组合(A-D)
- &&套利
- 无成本、无风险、有收益

- 无套利原理

- &&
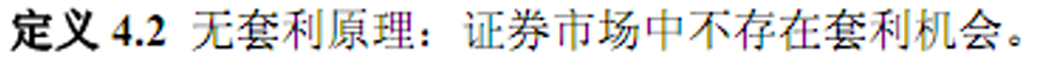
- 不存在市场套利机会依赖于两个假设: 市场参与者的不满足性,市场无摩擦 。
- &&资产定价基本定理
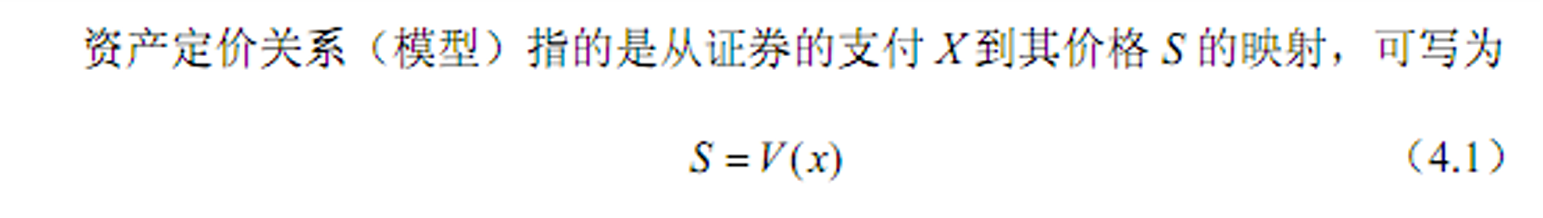
- (一价定律)两个具有相同支付的证券(或组合)的价格必定相同。
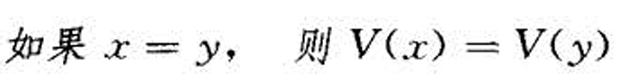
- 支付为正的证券或证券组合的价格为正
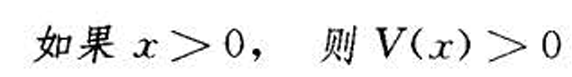
- 给定两只证券1和2'如果证券1的支付总是大于证券2' 那么证券1的价格必高于证券2的价格。
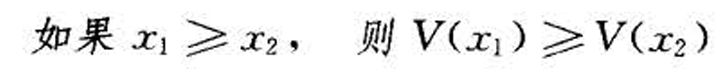
- &&


- &&

- 不存在套利的充要条件

- 注意是>>全部严格大于0
- 风险中性定价和鞅
- 存在无风险债券,1期支付全部为1
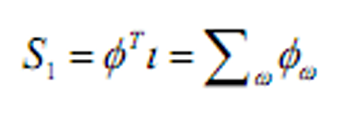
- 无风险利率
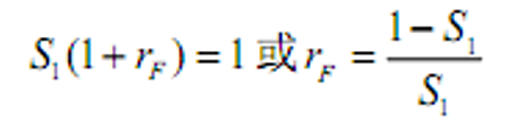
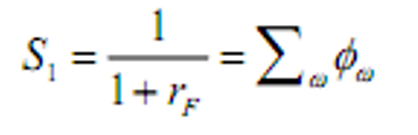


- 令
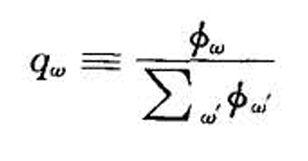 则
则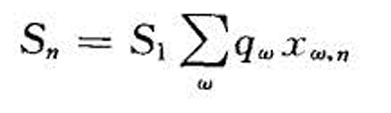 (
(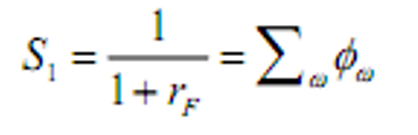 )
) - &&风险中性定价即
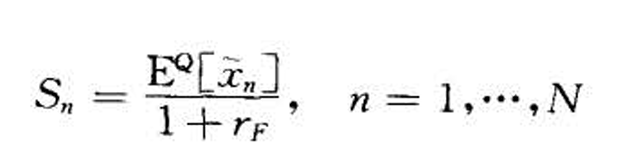

- 令

- &&

例题¶
- 套利分类


- 资产定价


- 风险中性定价



- 判断套利!
U6-期望效应函数¶
基本概念¶
-
效应函数依赖于未来的概率分布以及各状态下的消费偏好
-
&&不同消费路径的原始形式:
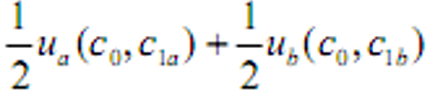
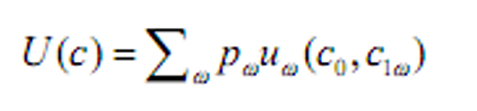
- &&

- 模型简化
- &&状态独立:
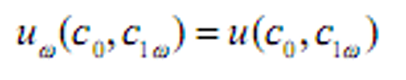
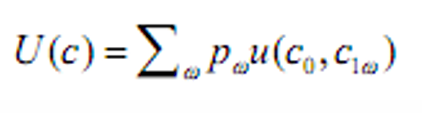
- &&时间可加性:
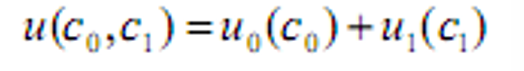
- 即:
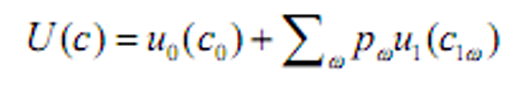
- 添加一个常系数进一步化简:
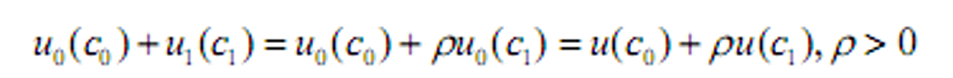
- 不支持正单调变换(不满足序数性)
U7-风险厌恶¶
基本概念¶
- 凹函数(其实是上凸函数)
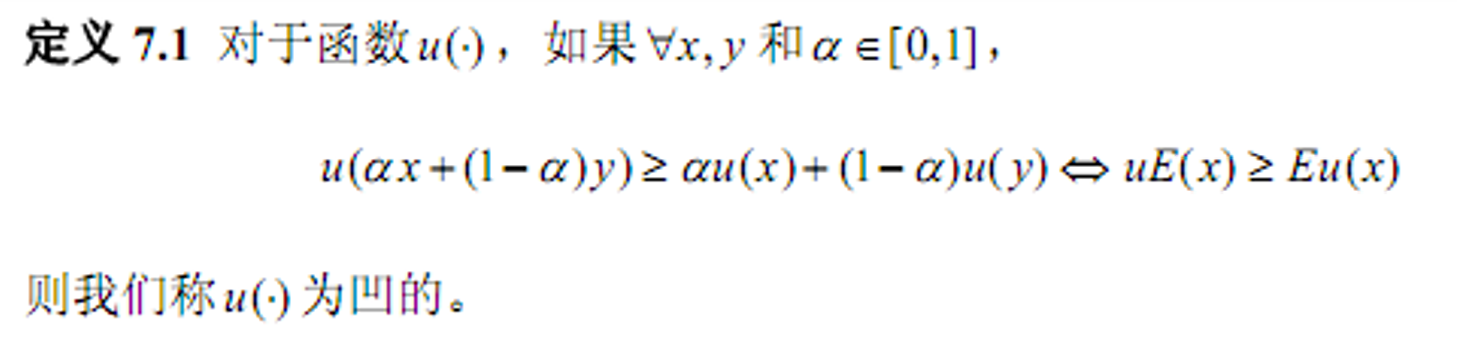
- &&

- 风险厌恶定义
- &&


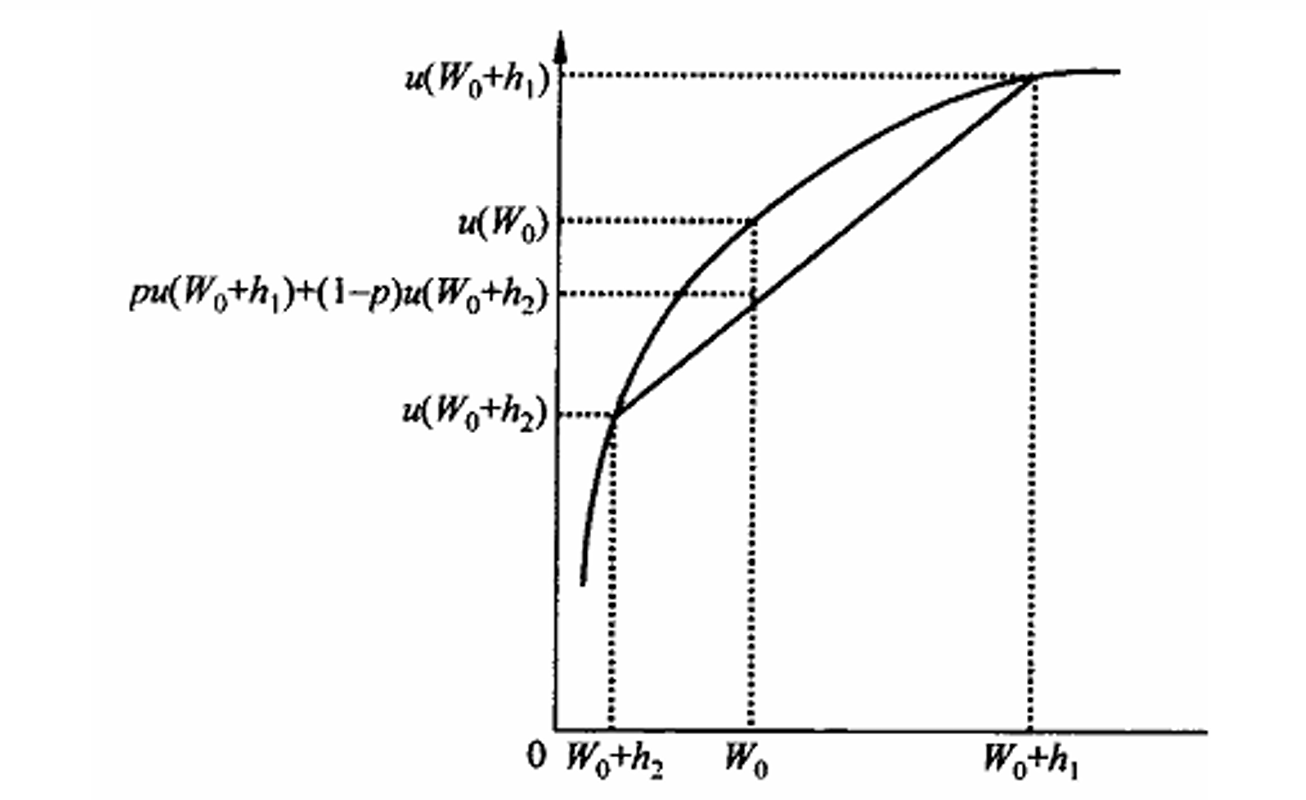
- 绝对风险厌恶

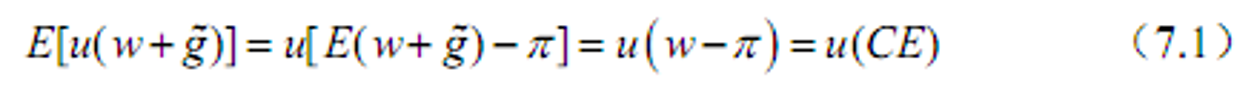
- &&风险溢价(风险赌博的确定性等值)是参与者为了消除风险而愿意放弃的财富值
- >0风险厌恶
- =0风险中性
- <0风险偏好
- CE为完全确定的收入量
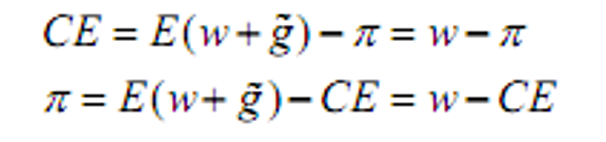
- &&
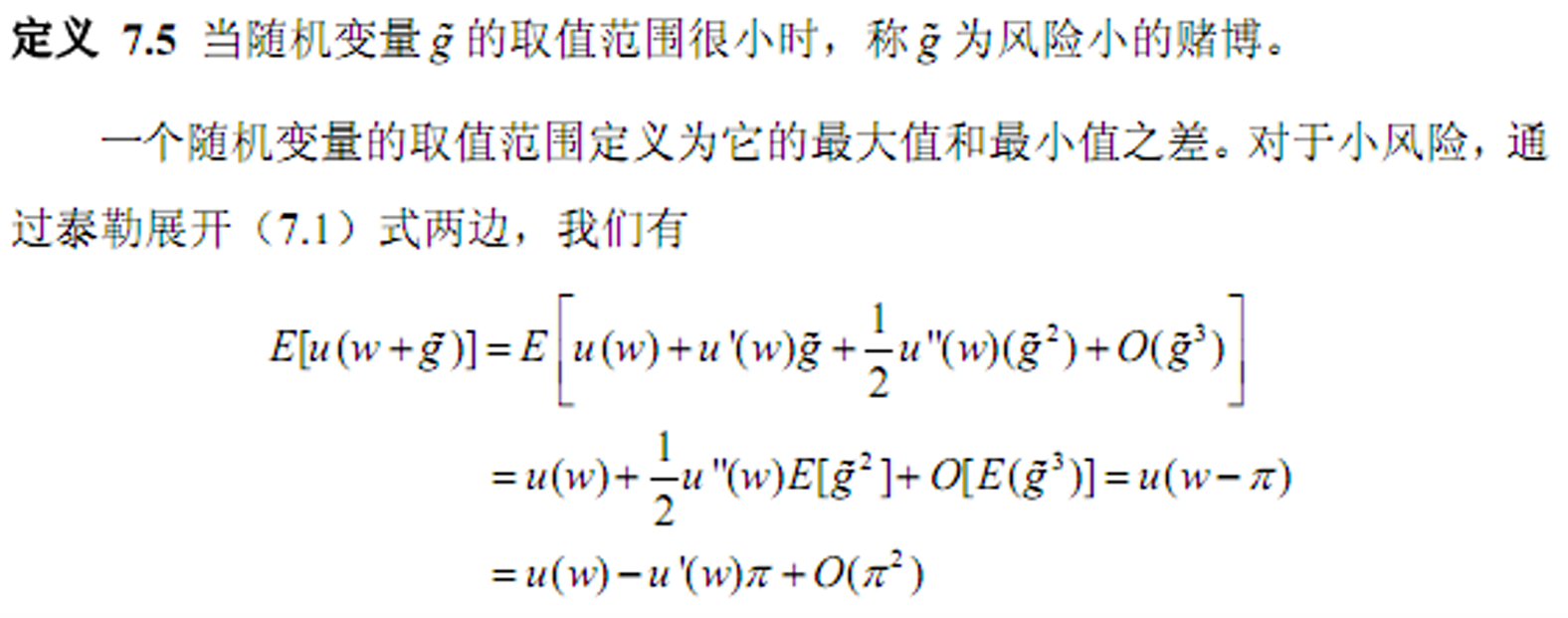

- 绝对风险厌恶系数
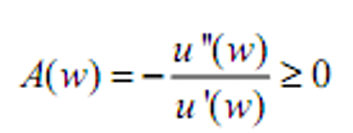
- 风险容忍度
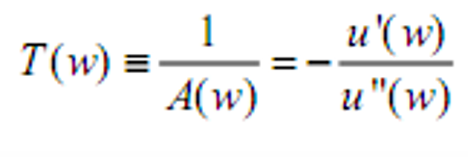
- 相对风险厌恶
- 考虑以总财富作为基数的赌博和风险溢价(即盈亏与风险溢价与总财富成比例)
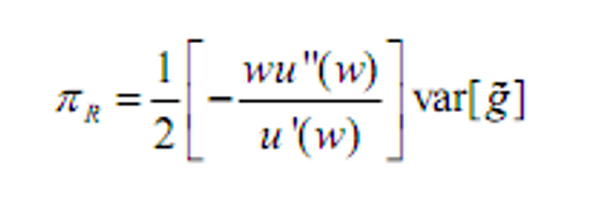
- 相对风险厌恶系数
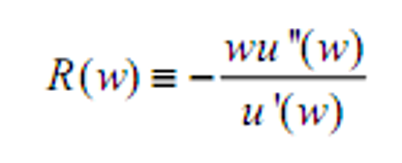
- *分类
- CARA:常数绝对风险厌恶,相对风险厌恶随财富递增
- CRRA:常数相对风险厌恶,绝对风险厌恶递减
- IARA DARA IRRA DRRA
- &&

U8-组合选择1¶
基本概念¶
-
针对单个资产最优选择展开
-
解决消费/投资组合的问题
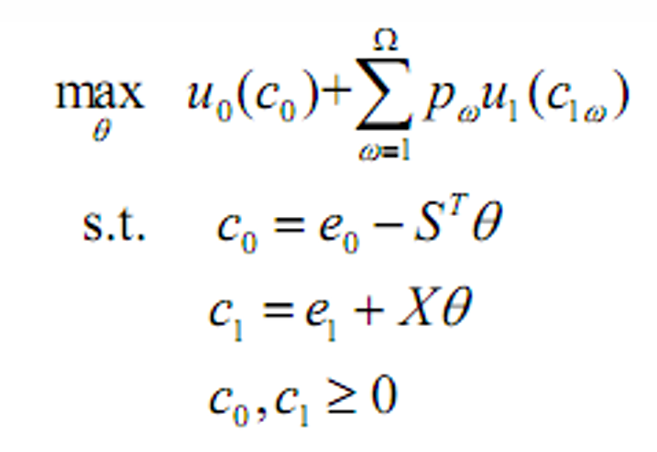
-
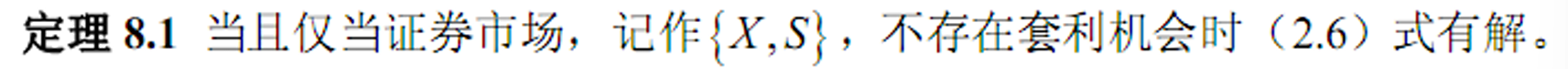
-
Euler方程(单只证券的最优数目)
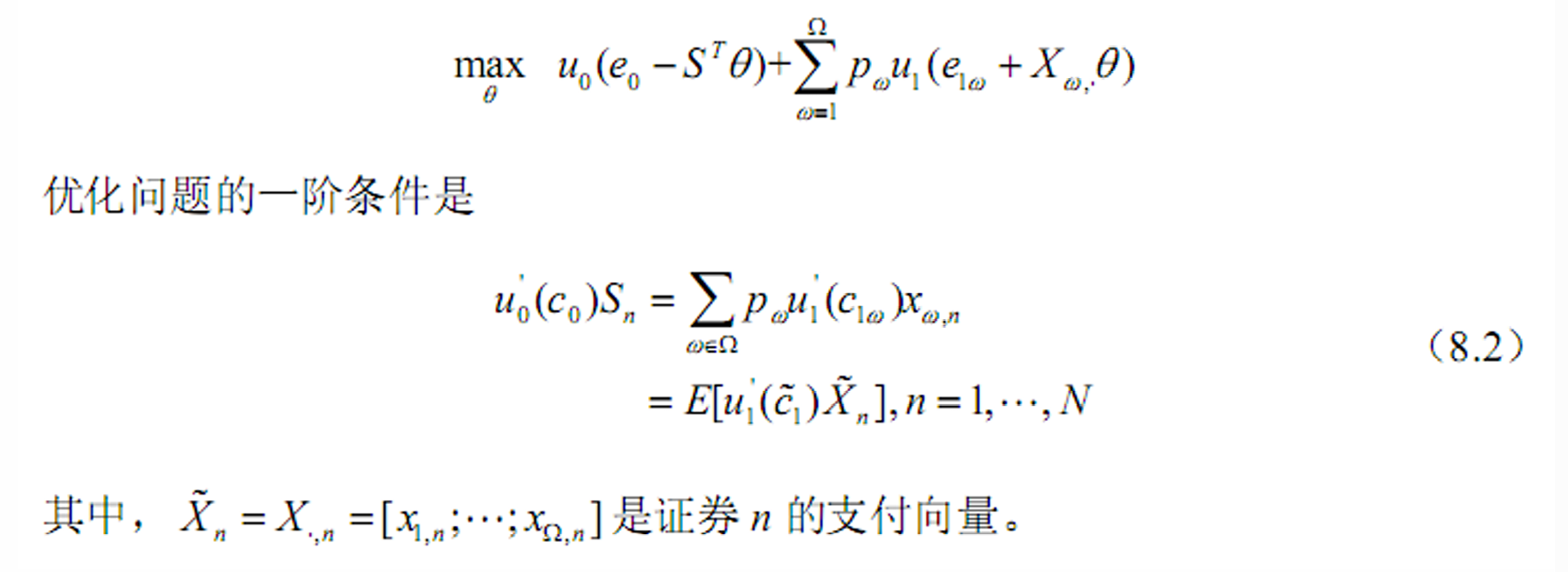
- 是左右对
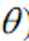 求导
求导 - 投资1单位证券未来消费增加的边际效用=付出价格而当前消费减少的边际效用
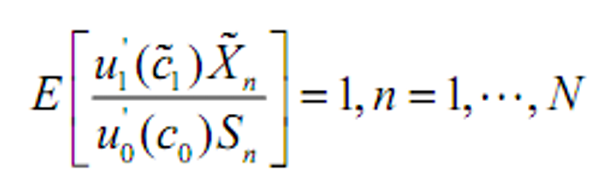
- 是左右对
- 投资组合选择
- 将问题拆分为0期储蓄数目,以及投资的配置
- 投资者投资于证券组合的0期储蓄
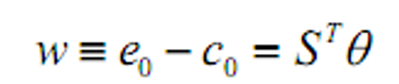
- 给定投资总额时0期消费的数目固定,问题可以表示为
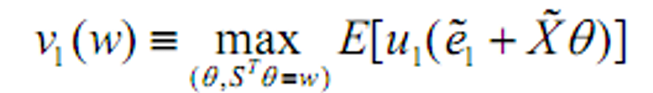
- 表述为
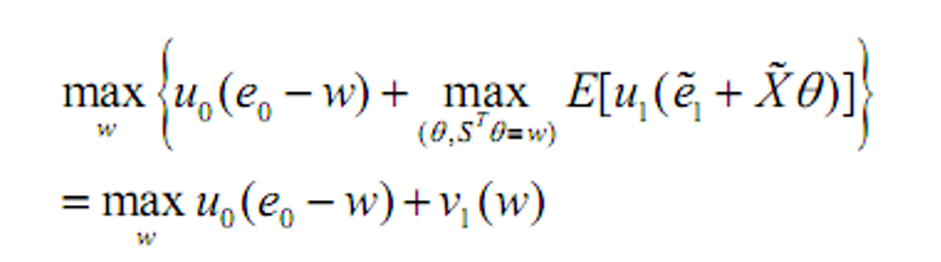
-
可以令\(e_1=0\)即参与者的禀赋只包括当前消费以及对交易证券的持有(不包括任意形式的将来的消费)
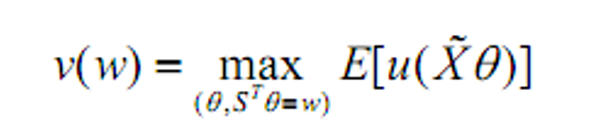
- 投资w可以获得的最大收益
-
利用无风险证券进一步简化
- 是第n只证券无风险,利率为\(r_F\)
- 总收益率
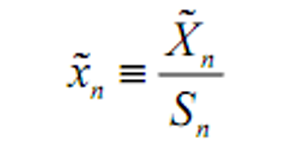 ;净收益率
;净收益率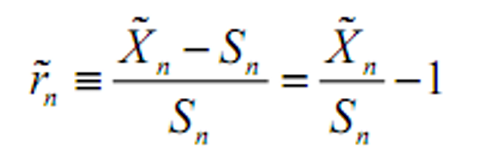 ;
; - &&那么有
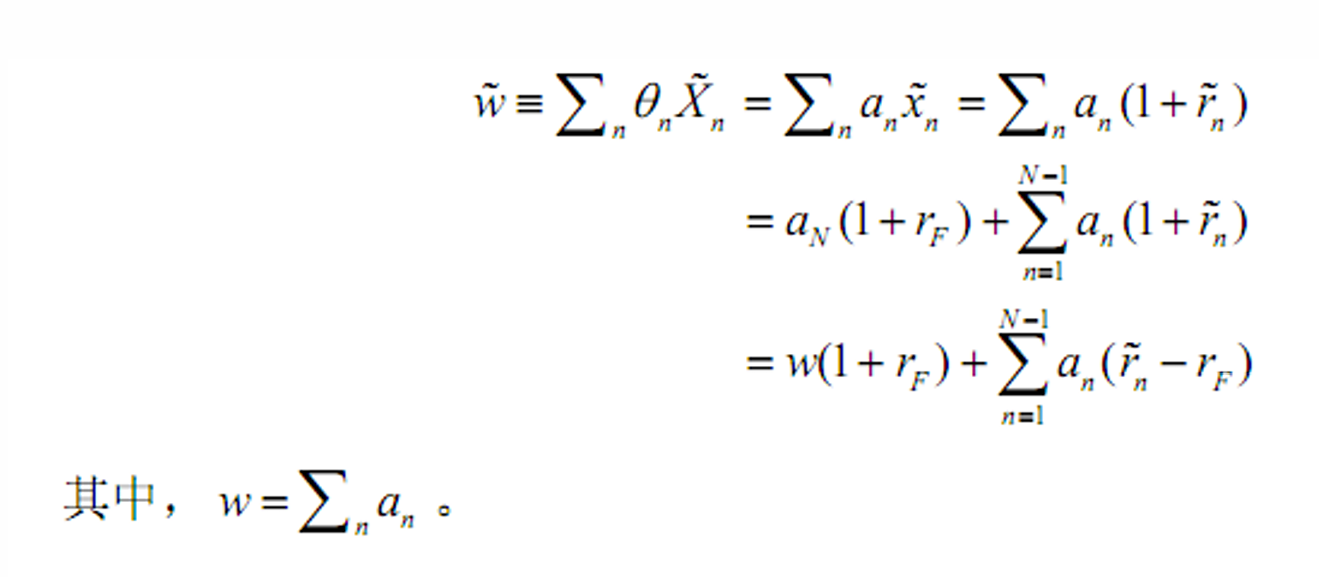
- &&超额收益
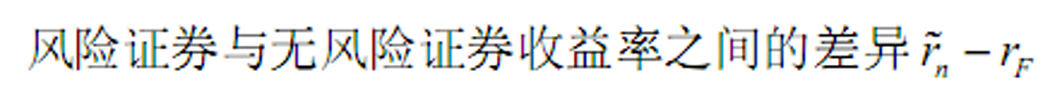

- &&
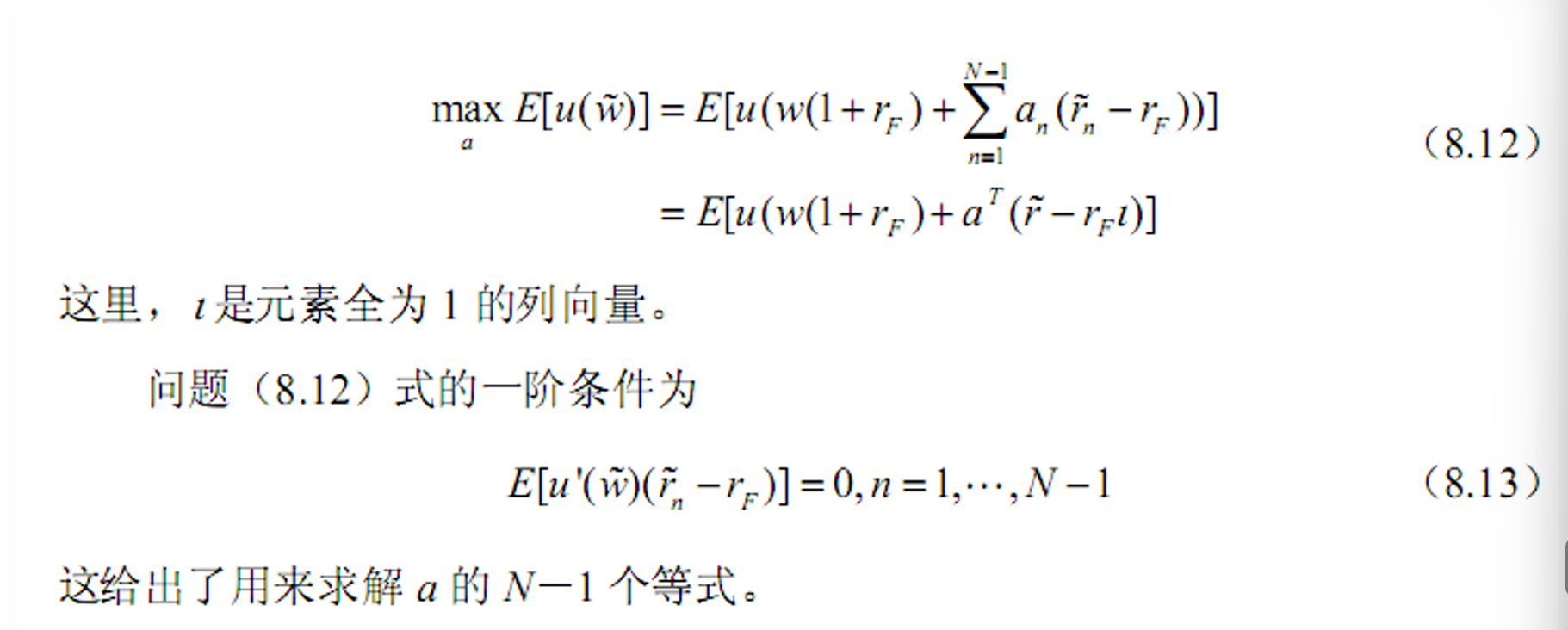
-
&&最优组合性质
-
有一只风险证券时:
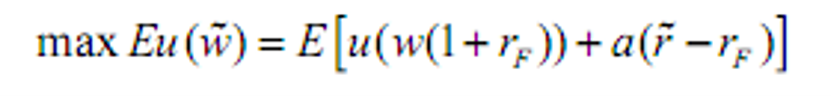
-
购买风险资产的倾向与绝对风险厌恶系数之间的关系
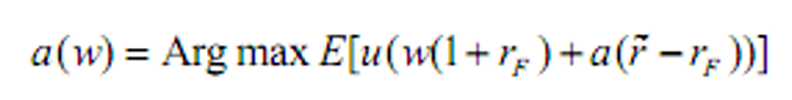
-
风险资产占比变化(总财富w增加,风险资产投资会增加多少?占比是否会发生变化)
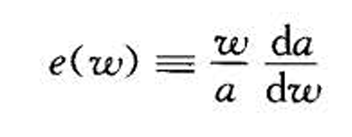
-
存在多支风险证券时的性质

- 与无风险证券进行比较
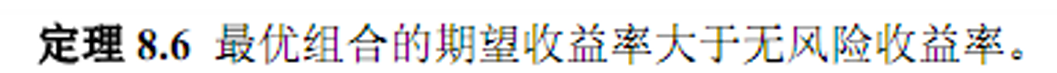
例题¶
- Euler方程(单支证券)

- \(u_0(x)=logx\) \(u_1(x)=plogx\)
- wuler方程本质上就是对
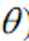 左右分别求导
左右分别求导 - 最优组合计算


U9-组合选择2¶
基本概念¶
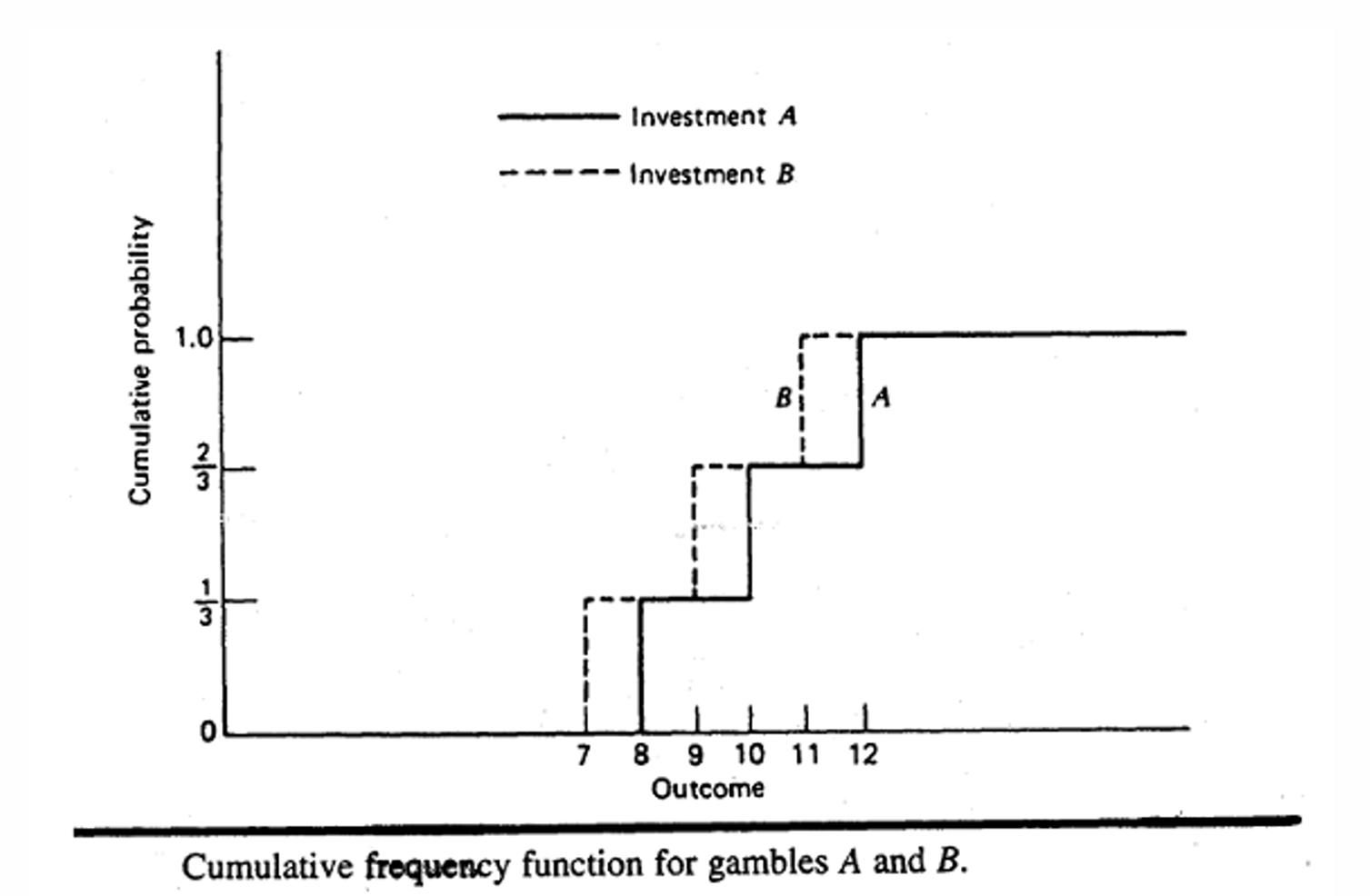
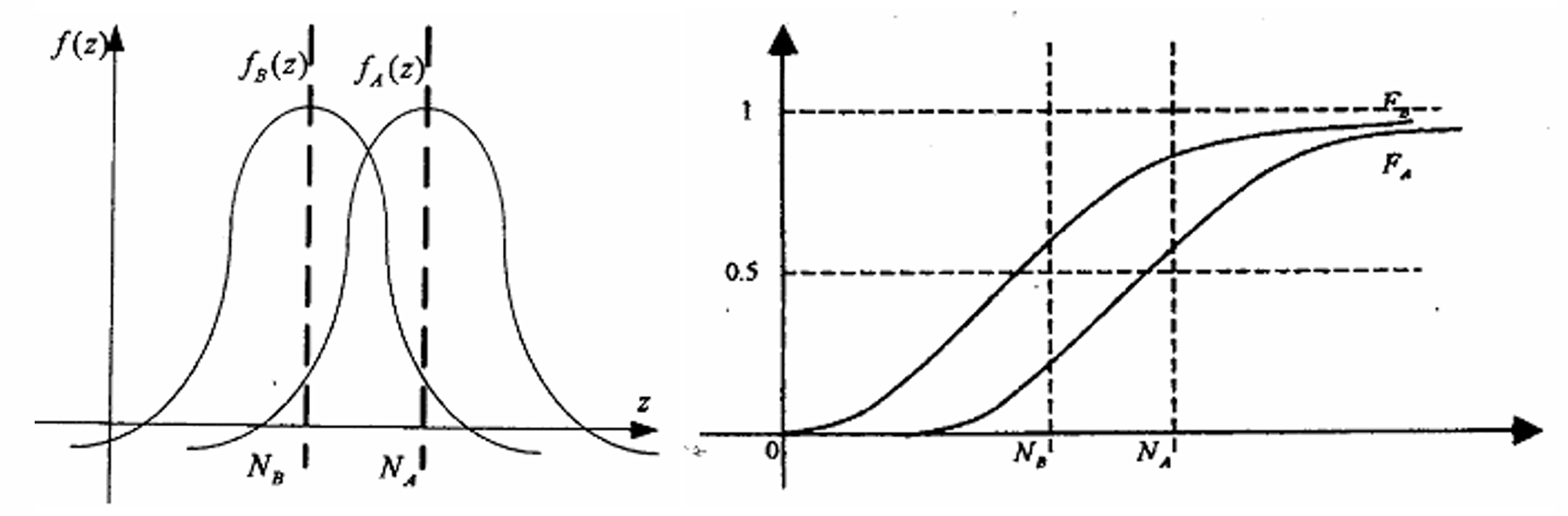
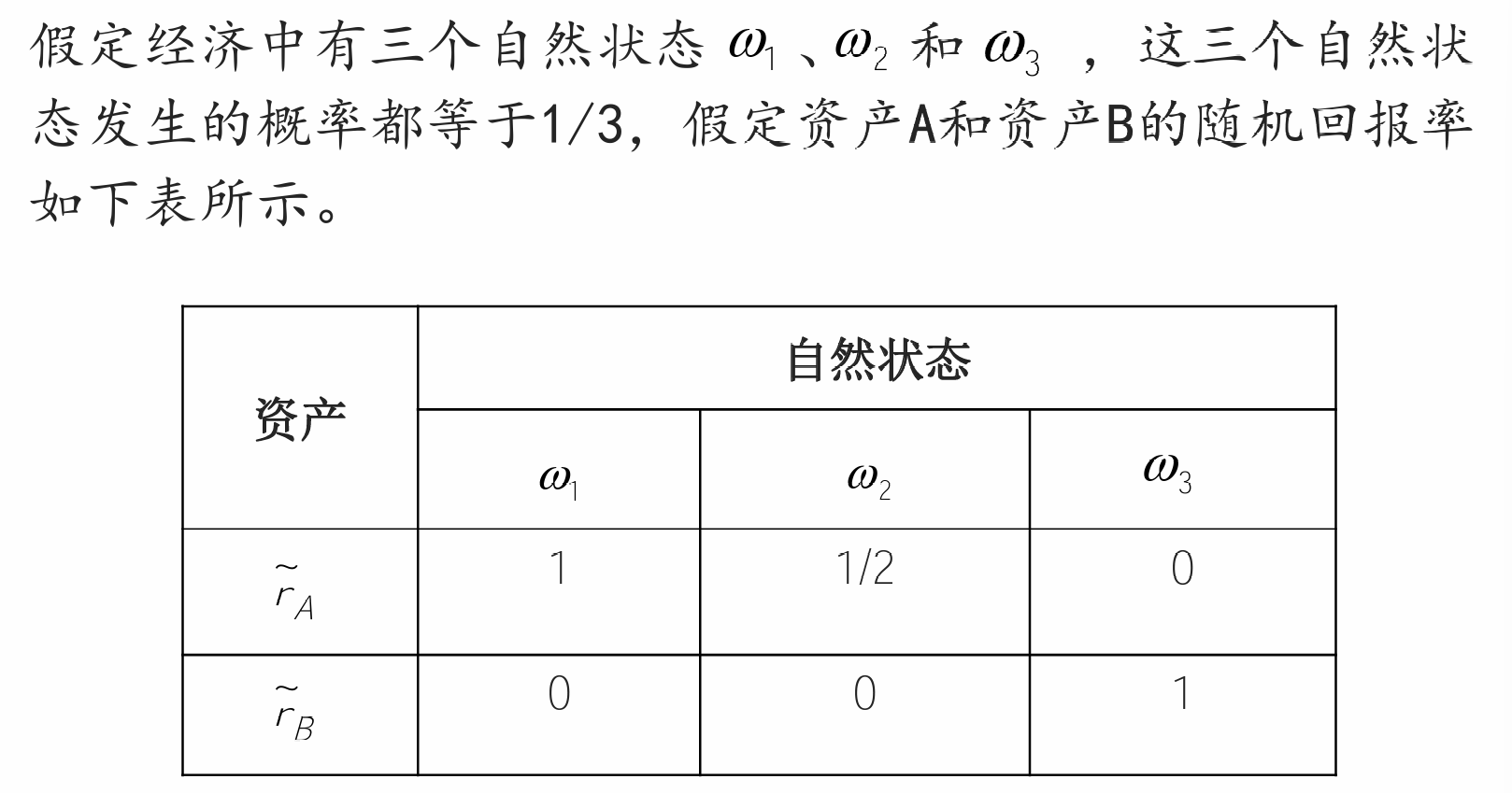
- 一阶随即占优(收益FSD)

- 比较的是全投资A或B而不是组合
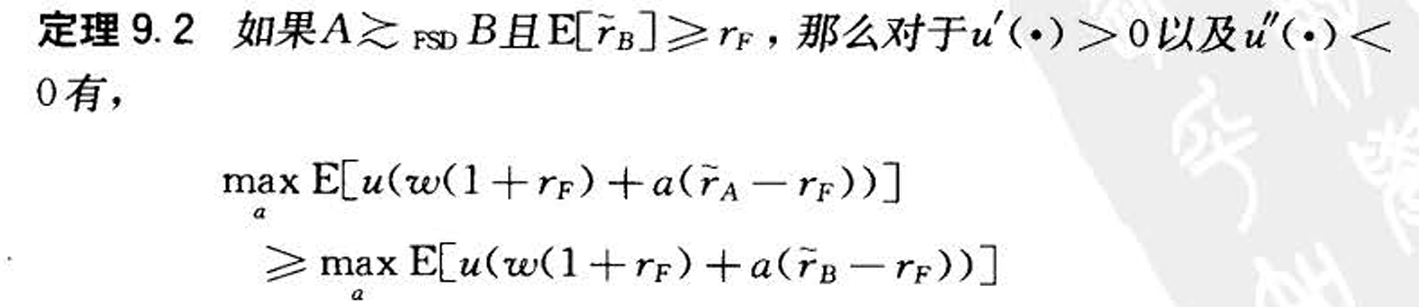
- 如果A一阶随机占优于B,那么参与者选择其中之 一与无风险证券构造投资组合,选择A要比选择B好。(不适用于风险证券之间的组合)
- 二阶随即占优(风险SSD)
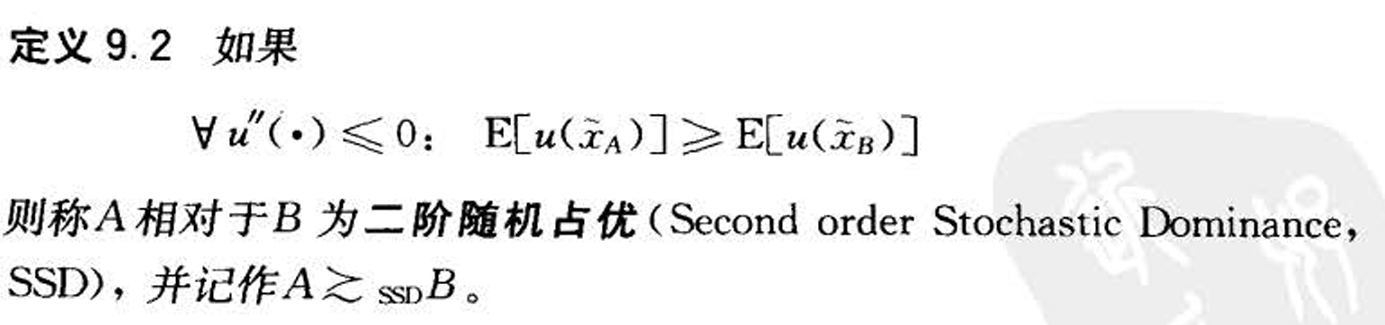
- 在期望相同
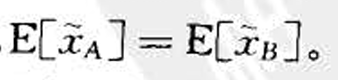 的情况下考虑方差
的情况下考虑方差 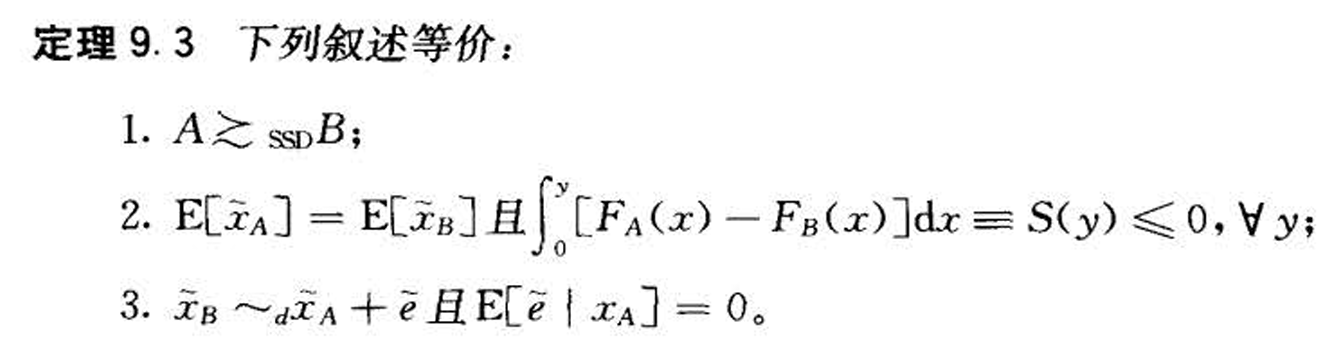
- 占优

- 占优一定随机占优,但是占优代表出现了套利的可能,因此无套利原理排除了占优存在的可能性
- 随机占优是可以出现的,表示的是在概率意义上的更好
- 组合分离
- 使用相对权重定义组合
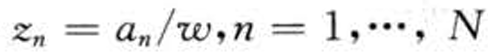 (
( )
)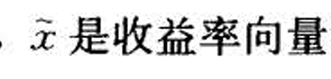 组合收益率为
组合收益率为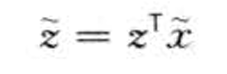
- 表示为投资比例的函数
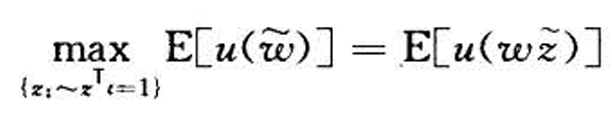 即
即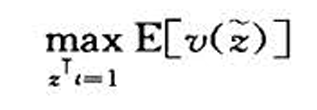 (假设投资资产的数目为定值)
(假设投资资产的数目为定值) 
- 分离为投资金额和最高效益
- 共同基金分离
- &&
 (即股票不全线性无关)
(即股票不全线性无关)- 对投资方案进行化简(股票组合->基金)
- 每一个参与者的最优组合都是F只基金的线性组合。参与者只需要考虑F支基金的组合,这F支基金就叫做分离基金,这种情形叫共同基金分离
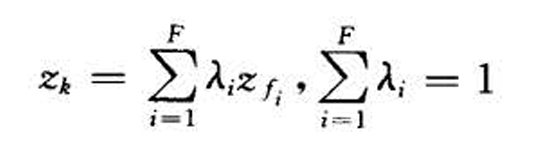
- 分离基金的集合不是唯一的,给定一个分离基金的集合, 这些基金的线性组合也可以作为分离基金。
- 无风险证券作为分离基金之一时的情况也称为货币分离

- 两基金分离


- &&

- &&


- 单基金分离
- &&


例题¶
- 一阶随即占优
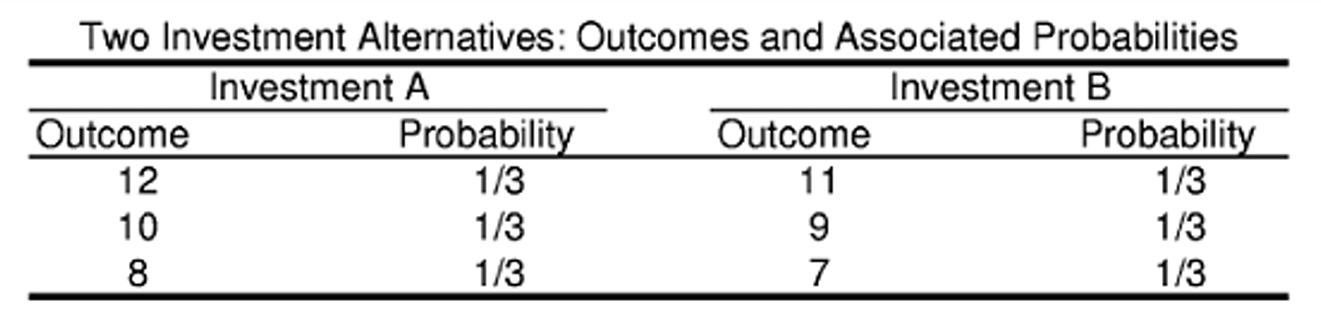

- (随即回报率还要加1)
- 二阶随即占优
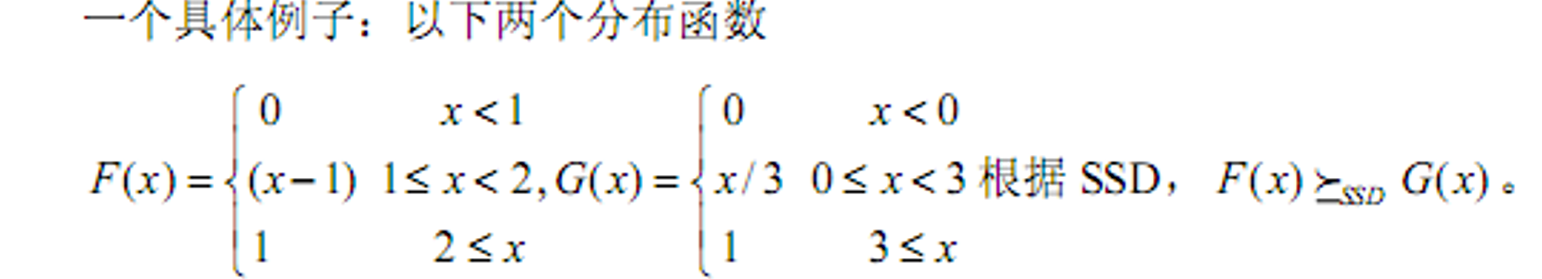
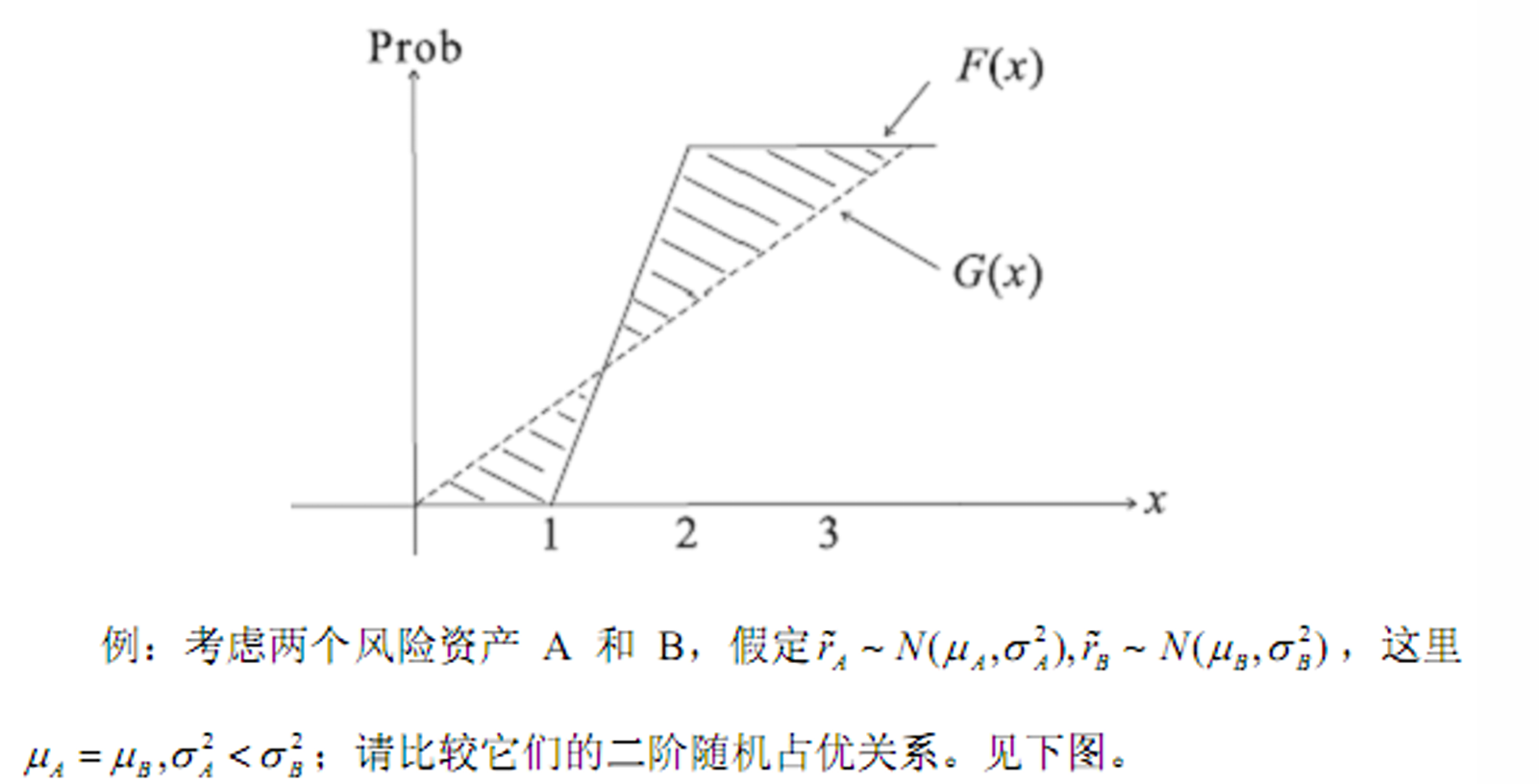
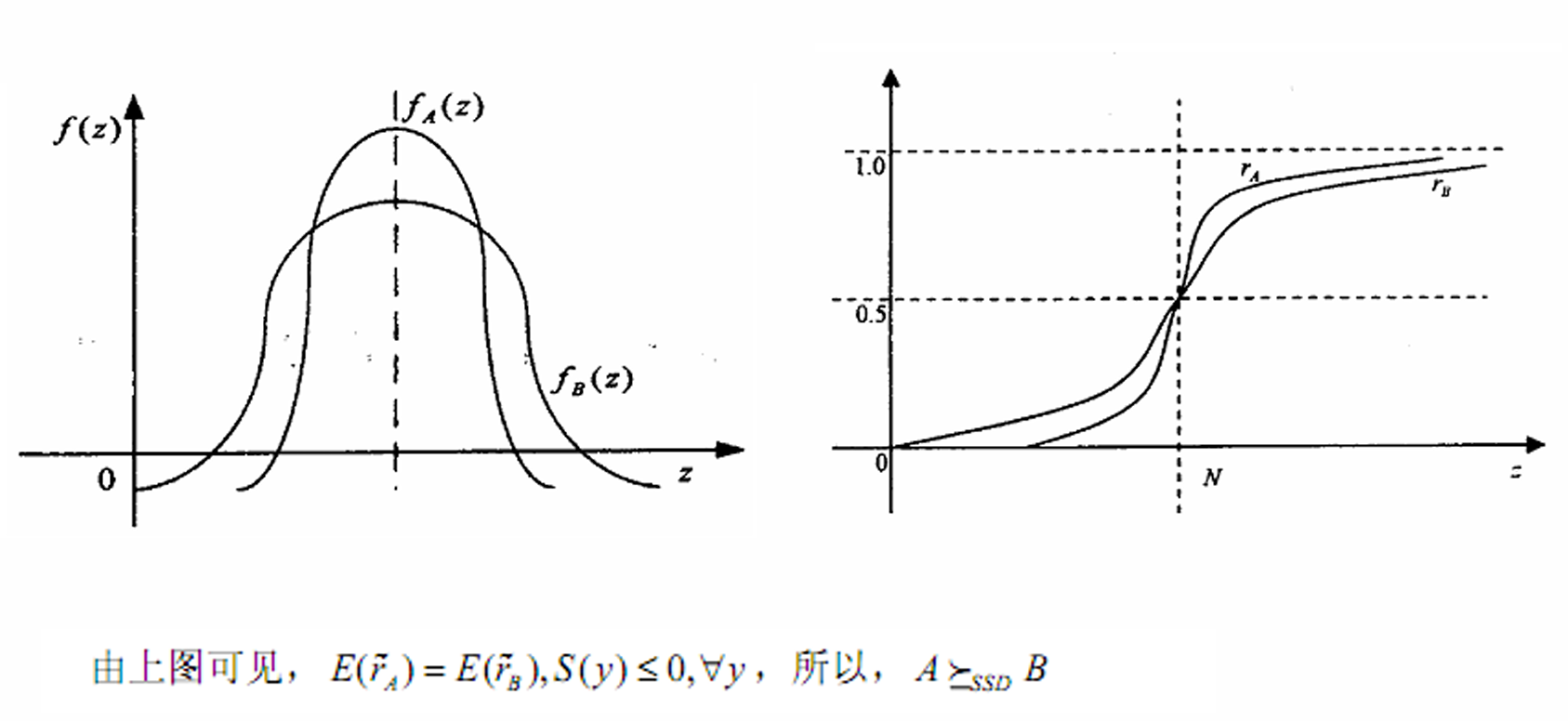

- 这么构造是为了使得条件期望为0

U12-均值方差模型¶
基本概念¶
- 将期望效应函数使用泰勒展开
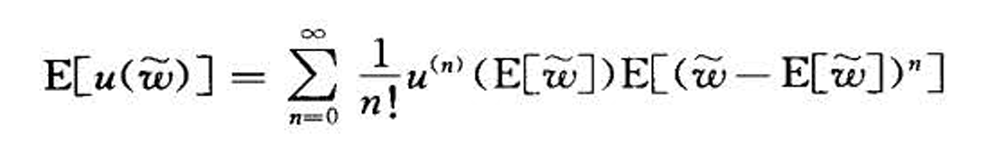
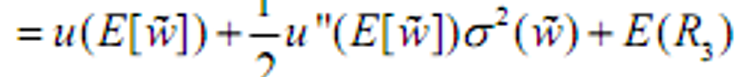
- 存在特定的条件,使得函数满足
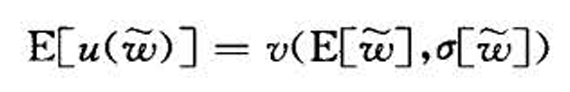
- 补充组合的均值方差求法
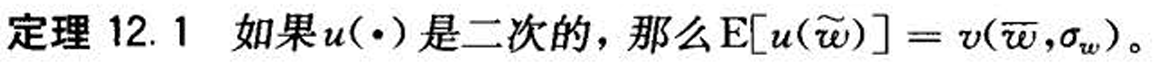
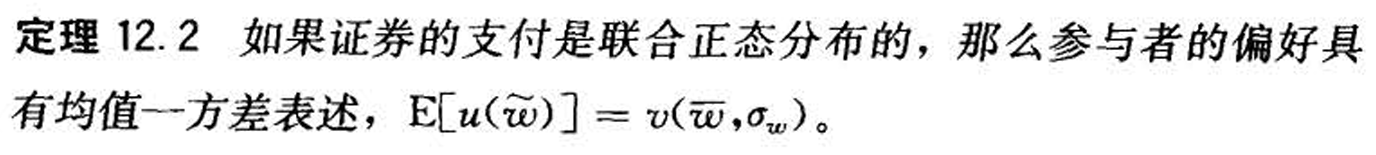

- 效应函数随着收益期望增加而增加,方差增加而减少,并且都是凹的
- 均值方差前沿组合

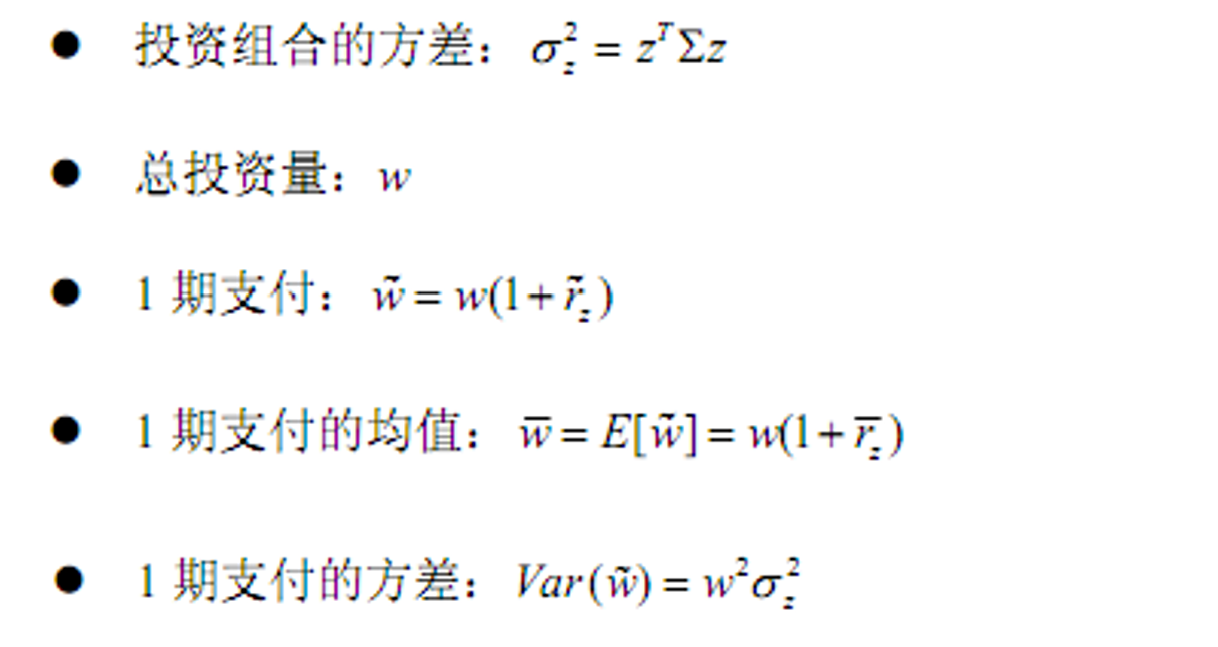
- 均值方差前沿组合MVF:达到指定的期望收益率而方差最小
- &&解
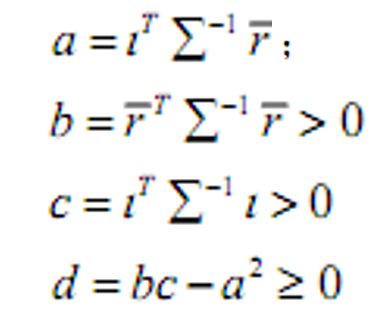
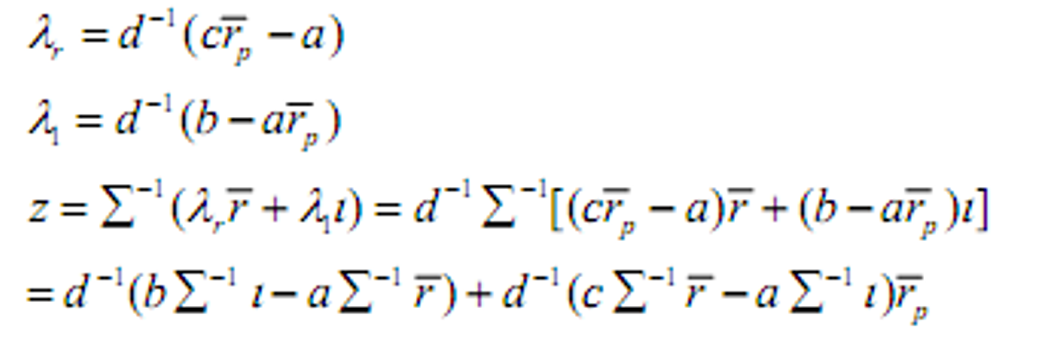
- &&均值方差前沿组合性质

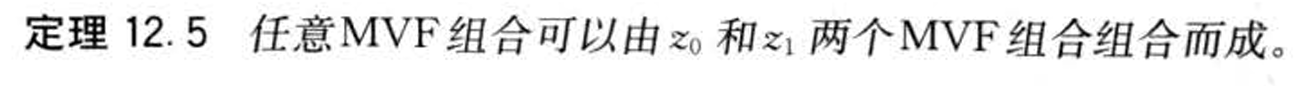
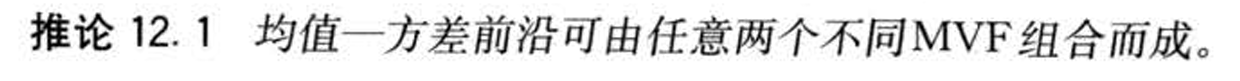
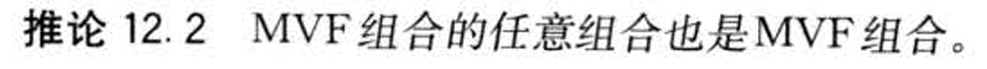
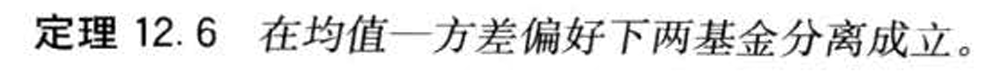
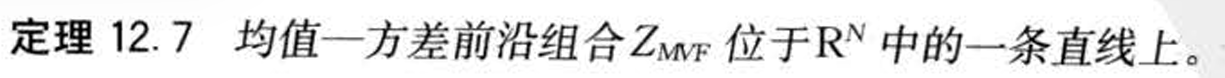
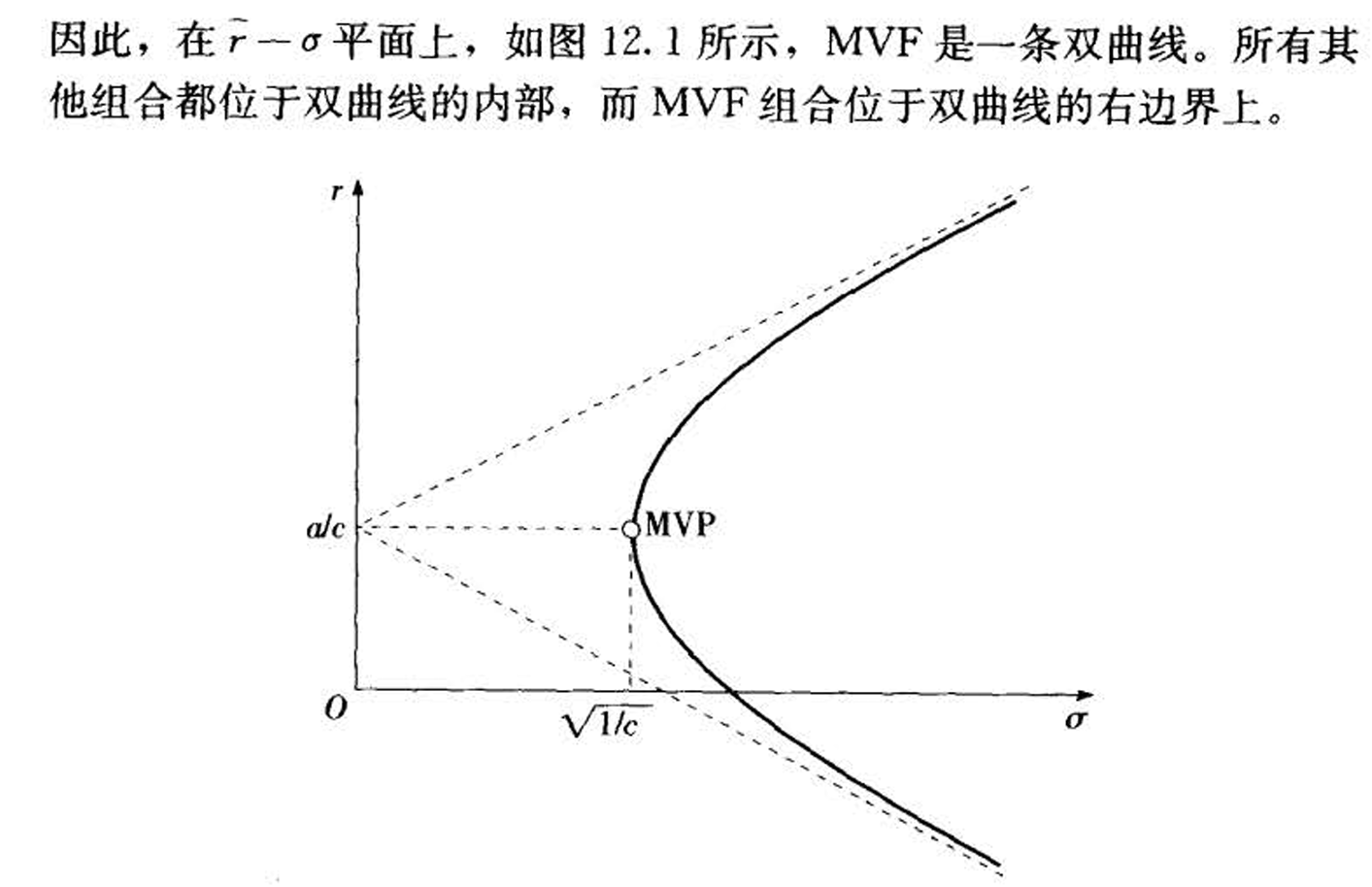
- &&

- 两种坐标轴(标准差/方差,对应双曲线格式和抛物线格式)
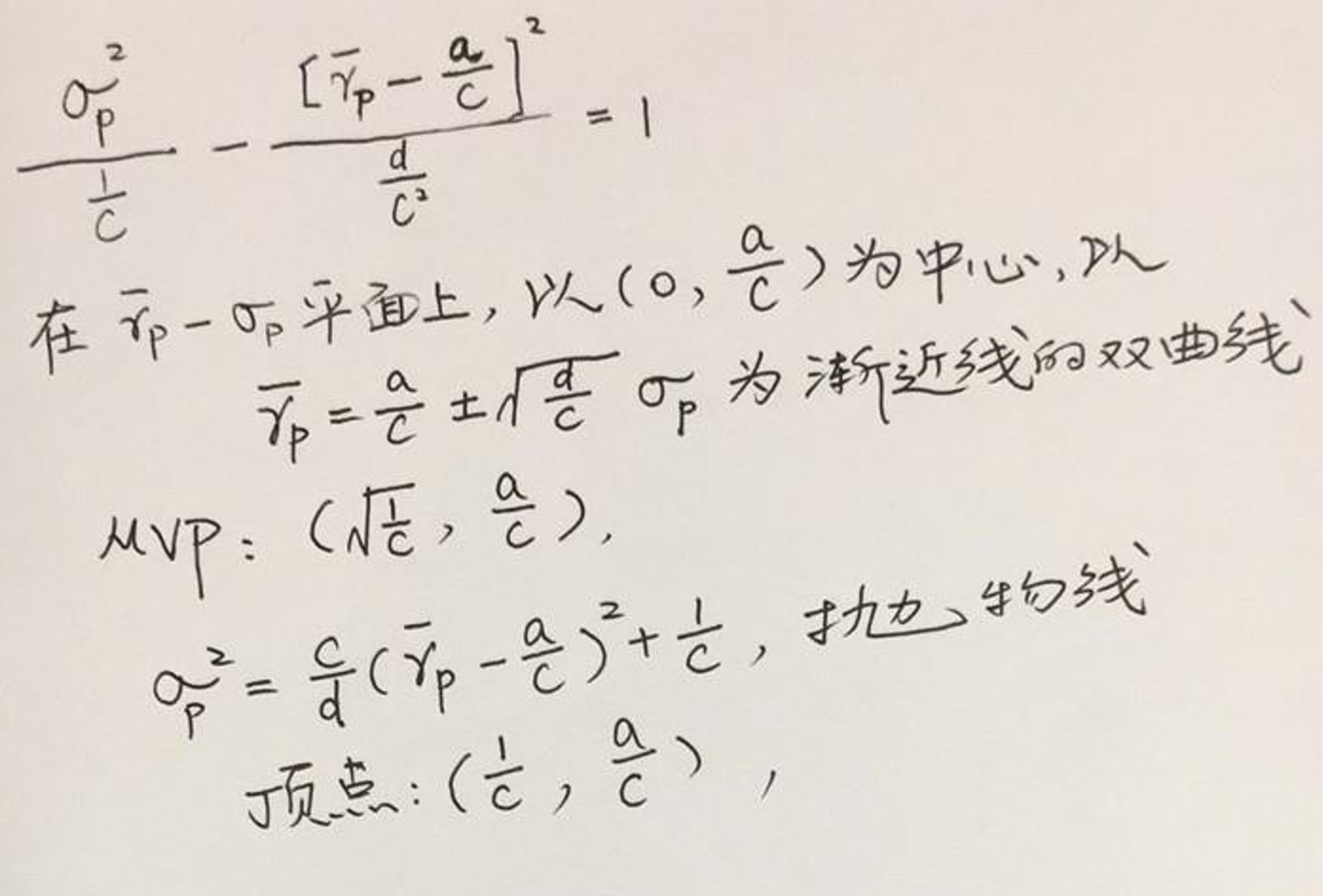
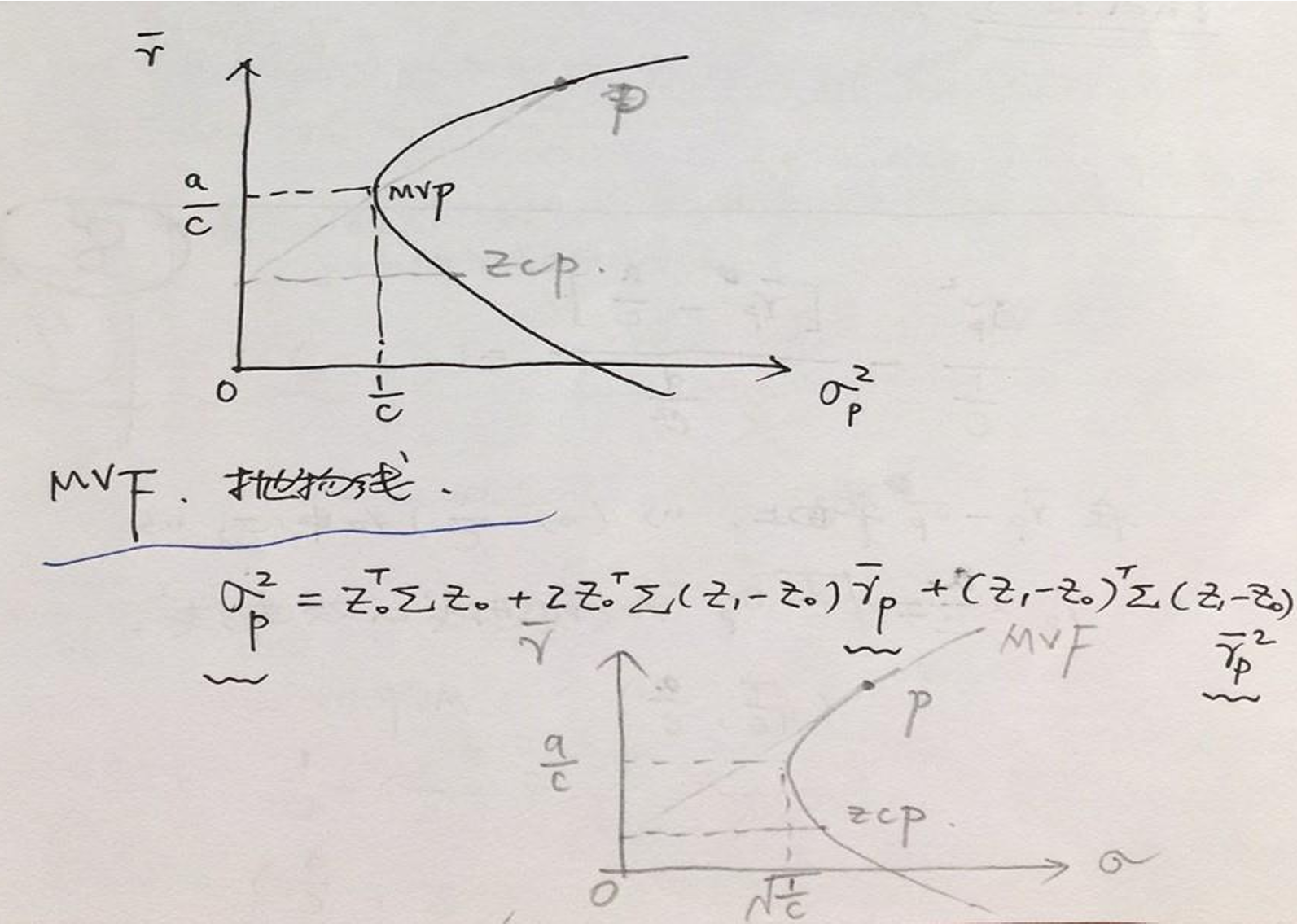
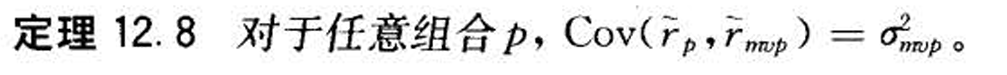 =1/c
=1/c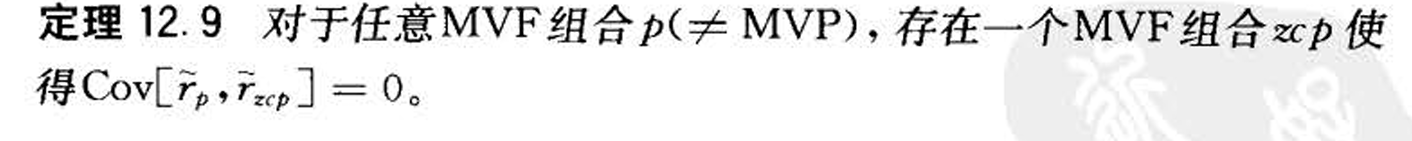


- 双曲线中切线在y轴的截距为zcp,抛物线中为连线

- 存在无风险资产
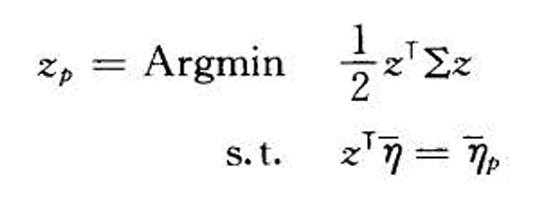
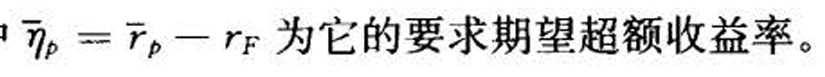
- 解
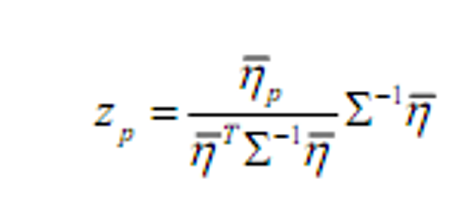
- 切点组合

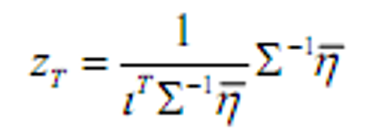
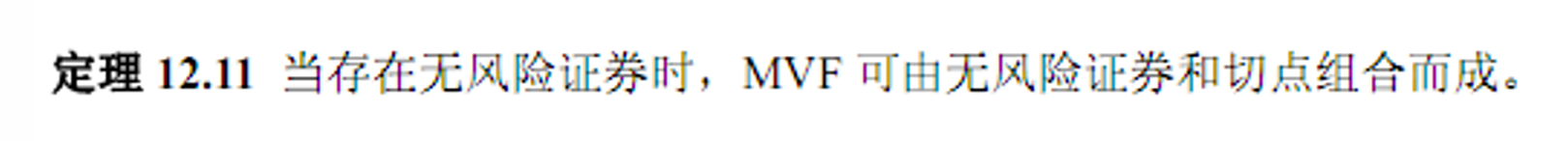
- 夏普比



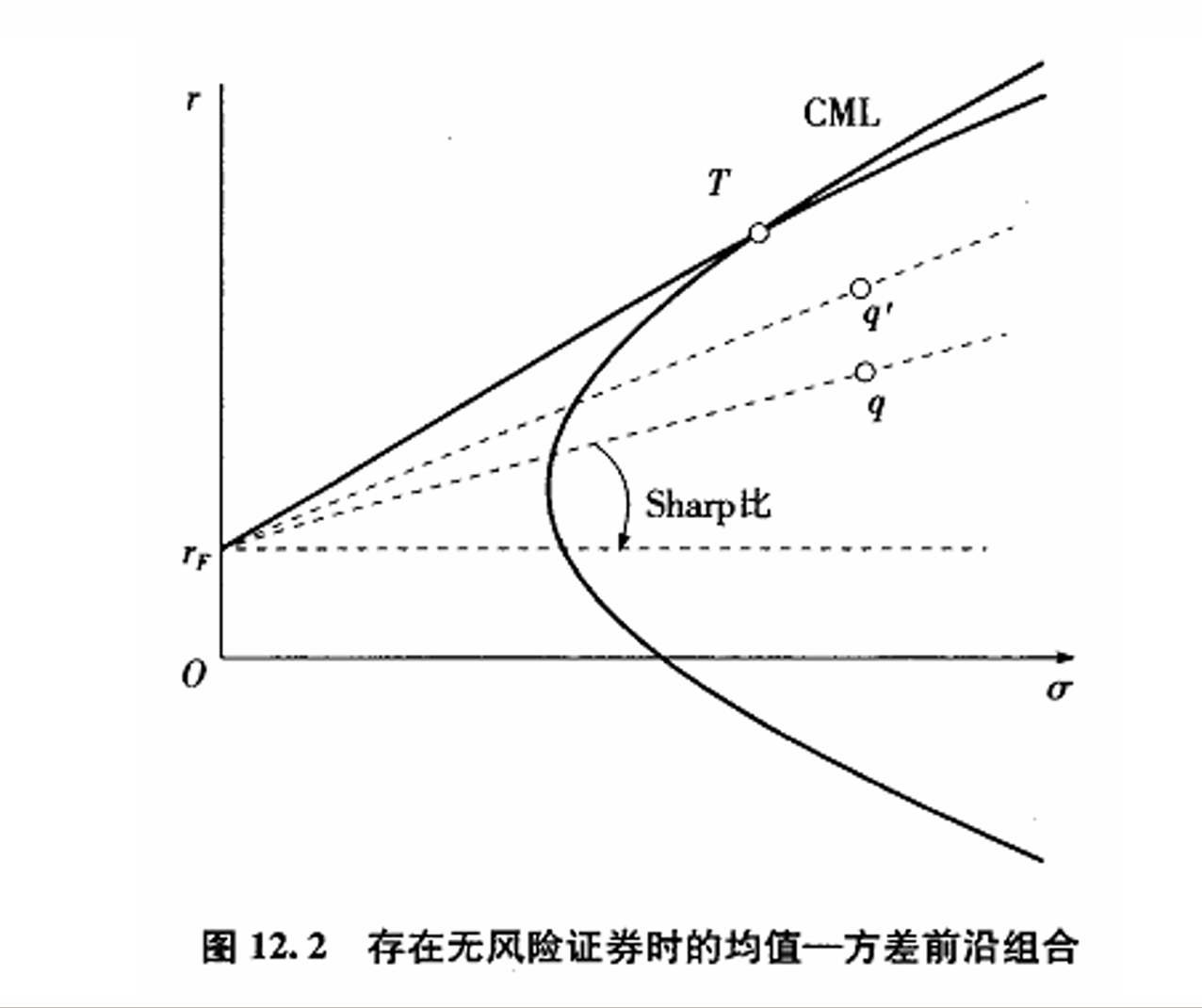
- 存在无风险证券时可以到达双曲线左侧的直线上!
- &&这条线(CML)被称为资本市场线,所有具有均值方差偏好的参与者的组合选择都来自于CML
- 夏普比

- 同一条直线上恒定(斜率)
- 切点组合的夏普比最大

- 风险证券与夏普比

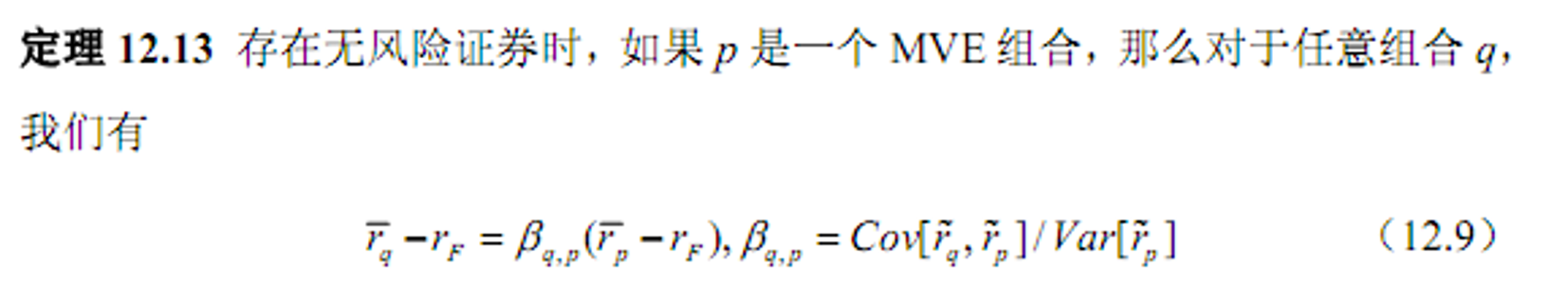


例题¶
- &&MVF曲线计算
-
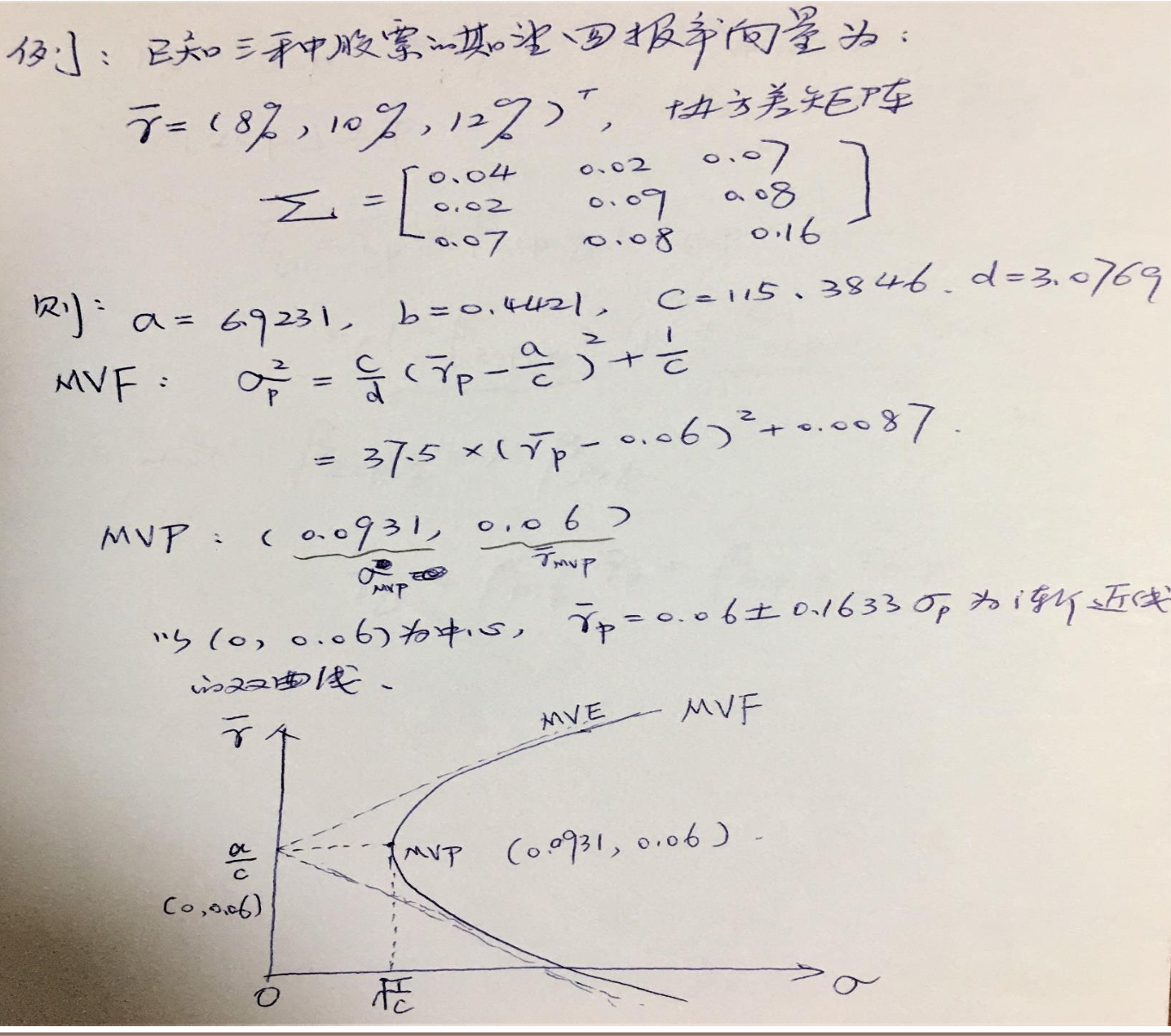
-
波动率计算





U13-资本资产定价模型(CAPM)¶
基本概念¶
- 在均值-方差偏好的基础上(两基金分离成立),CAPM 给出了均衡时风险和收益之间的关系,将单个投资者拓展到多个投资者。
- 市场组合

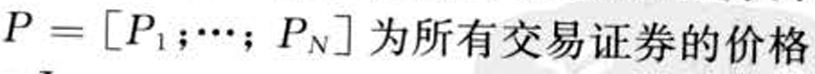
- 证券n的市值(市场资本化):
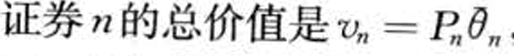
- 市场组合的总市值
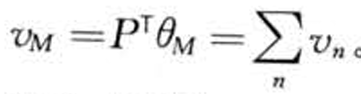
-
各证券所占的比例
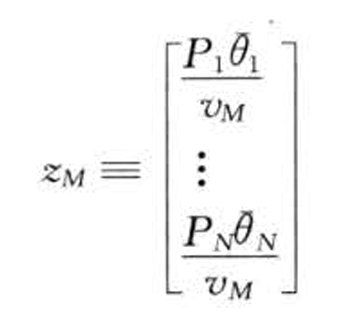
-
市场均衡
-
&&
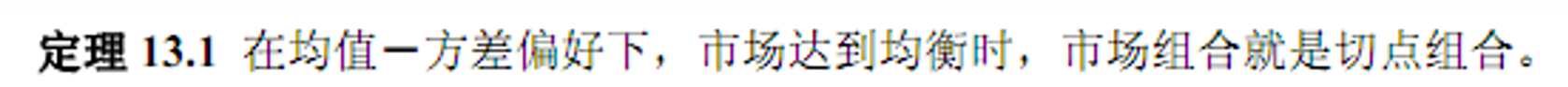
-
资产定价关系
-
&&


- 风险溢价=风险数目*风险价格
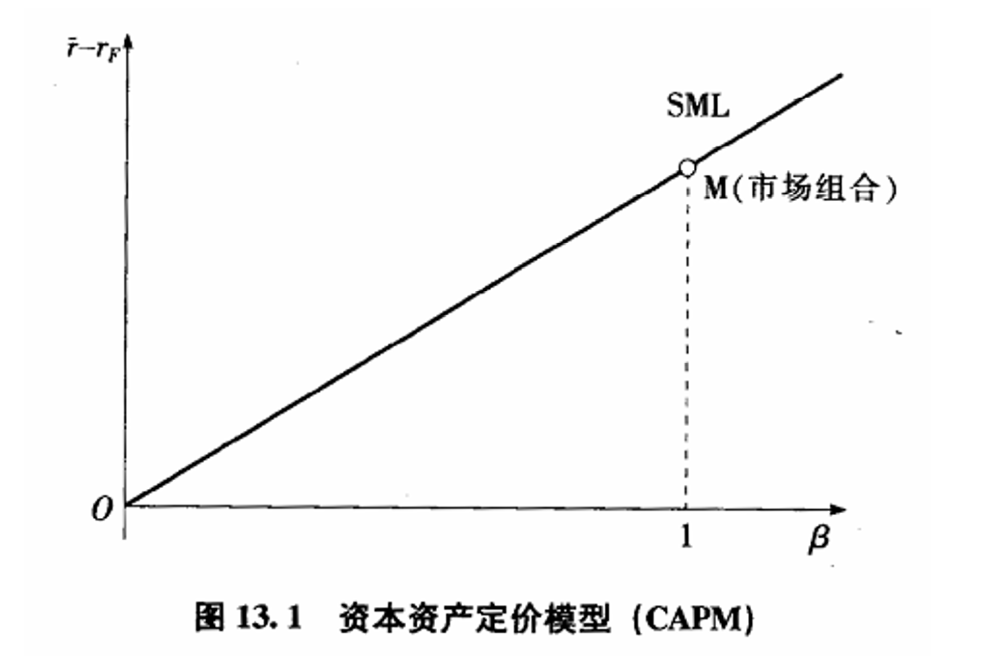
- &&证券市场线SML:横轴表示每个资产相对于市场组合的B值,纵轴表示 它的风险溢价。由CAPM可知,所有资产都应位于通过原点的一条直线上,它的斜率为市场组合的风险溢价。
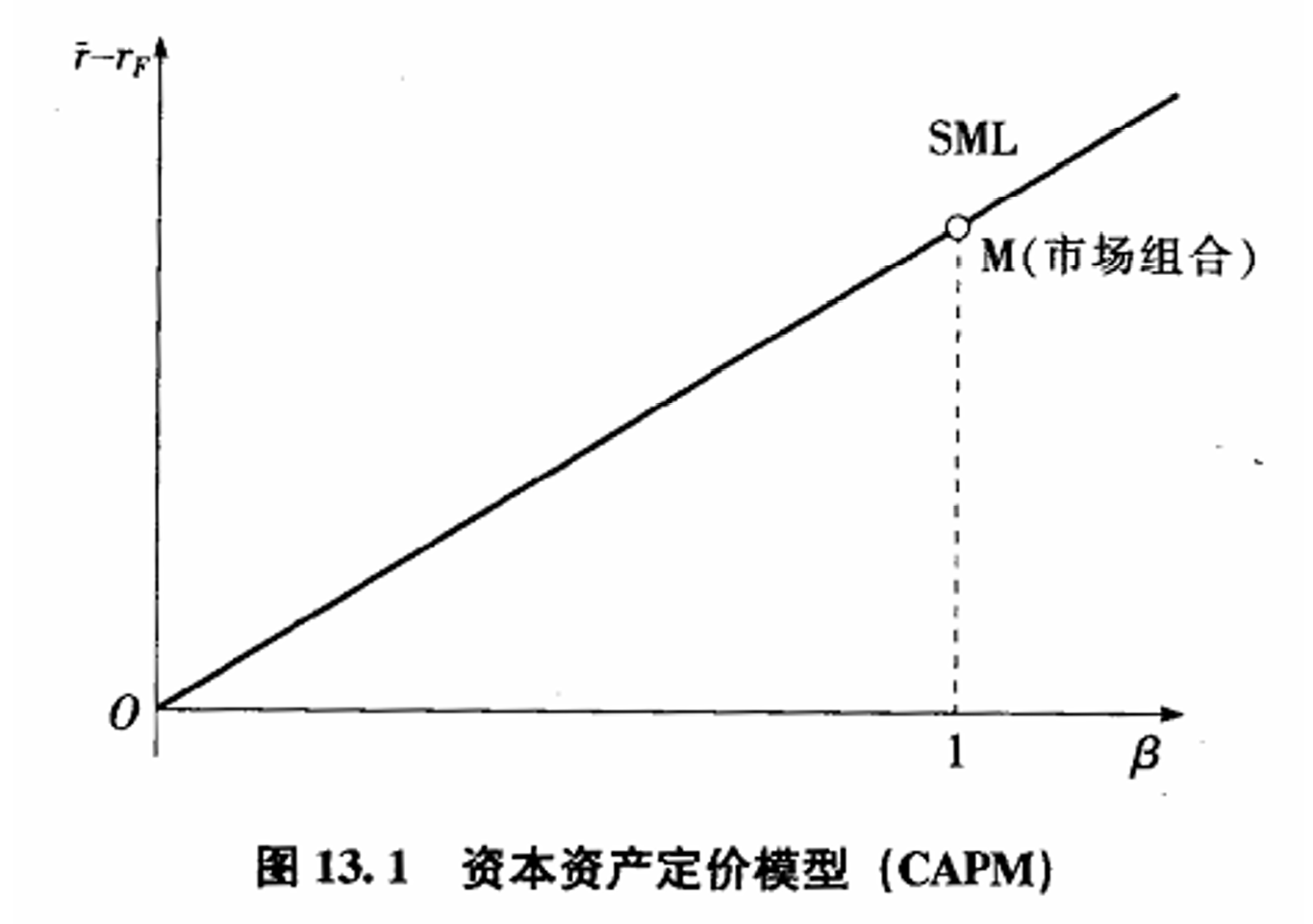
-
对市场收益\(r_M\)做线性回归
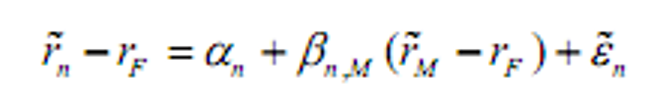
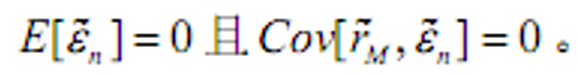
- 把资产收益投影到市场收益上并得到一个与市场收益不相关的残差项。由于CAPM要求截距(\(a_n=0\)),因此把资产收益率的风险分解成两个部分:第一个部分是它所负载的市场风险(系统风险)。由市场组合收益的风险定义, 负载的大小由资产的市场B值来确定。第二个部分是剩余风险,即剩下的与市场无关的风险(非系统风险)。
- 承担市场风险会产生一个与由B度量的总负载成正比的溢价。而承担剩余风险没有溢价。
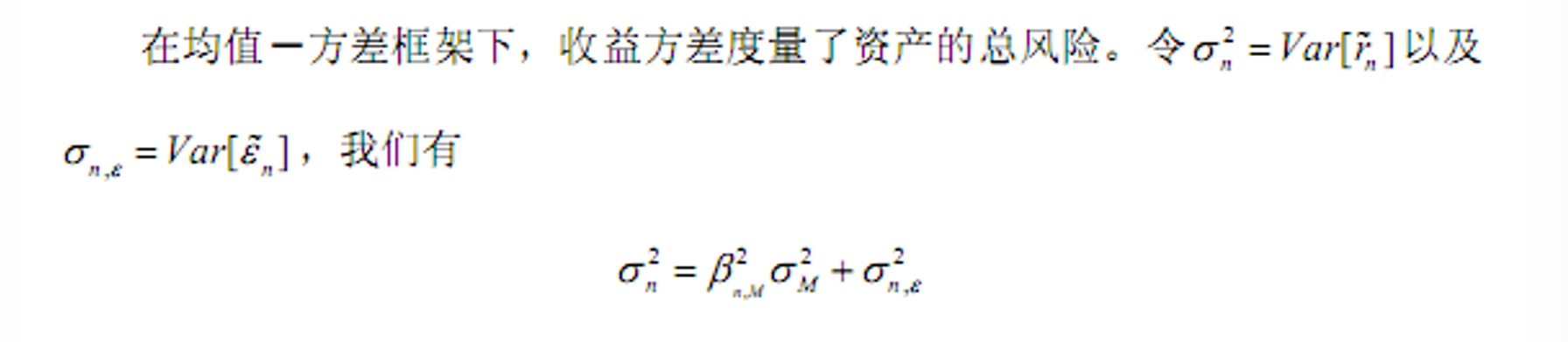
- 市场回归式\(R^2\)(市场风险的相对比例)
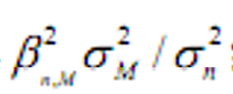
-
不存在无风险资产的CAPM
- 市场组合是一个MVF组合,因为每一个参与者都持有一个

- 即
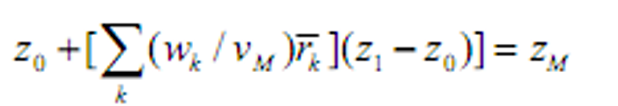
- &&

- 是切点组合的“zcp”(y轴截距)
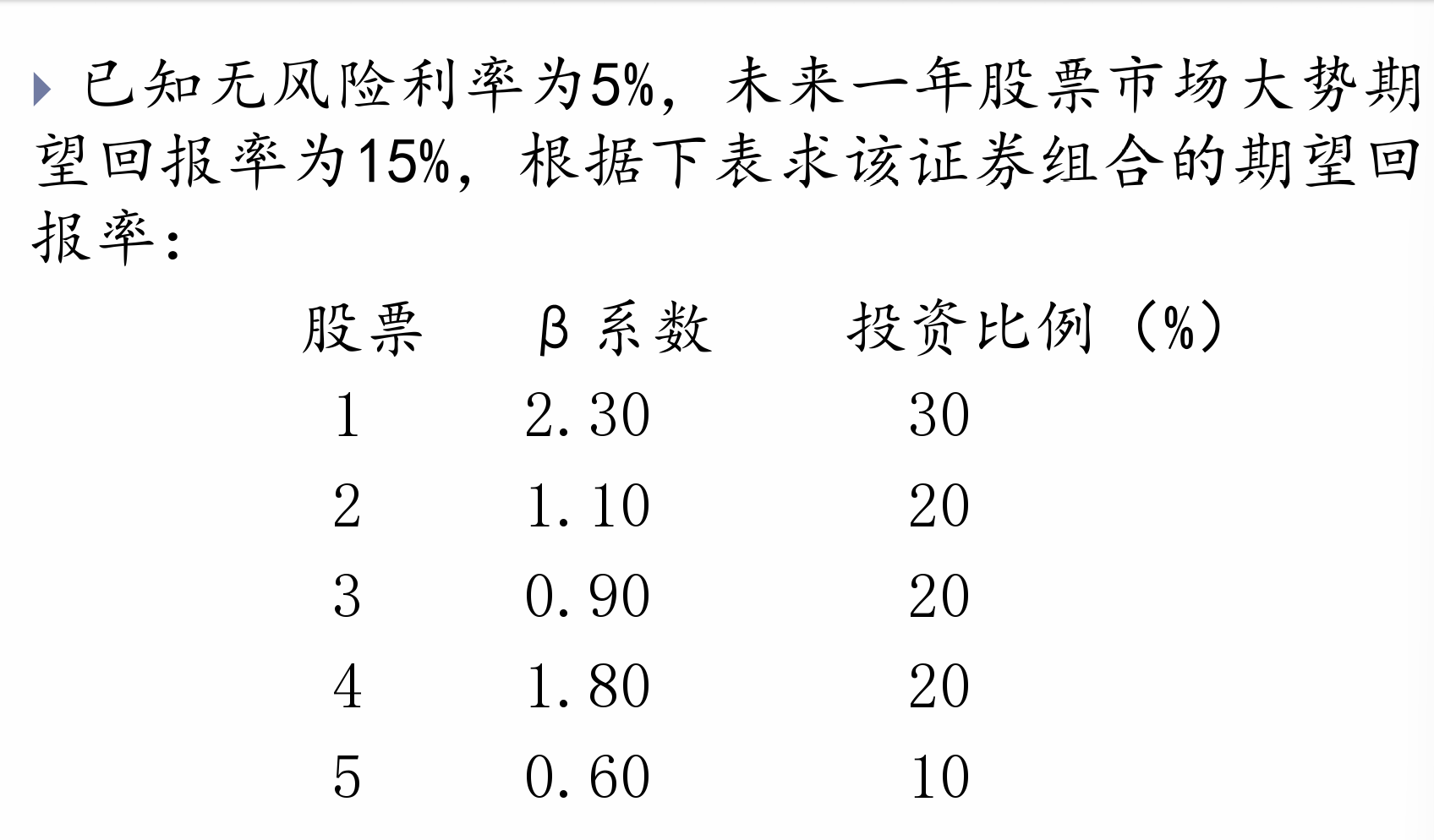
例题¶
- 有无风险证券的资产定价

-

-

-
U14-套利定价理论APT¶
基本概念¶
- &&用多个因素来解释风险资产收益,并根据无套利原则,得到风险资产均衡收益与多个因素之间存在 (近似的)线性关系这一结论
- 分为因子模型和无套利均衡两部分
-
因子模型是一种假设证券的回报率只与不同的因子或者指标的运动有关的经济模型
-
单因子模型
- &&单因子模型 :证券的回报率生成过程只取决于唯一的因子。建立以这个唯一因子变化为自变量,以证券回报率为因变量的单因子模型。
-
如证券 A 的回报率与 增长率之间的关系可以表示如下:

- 回归模型
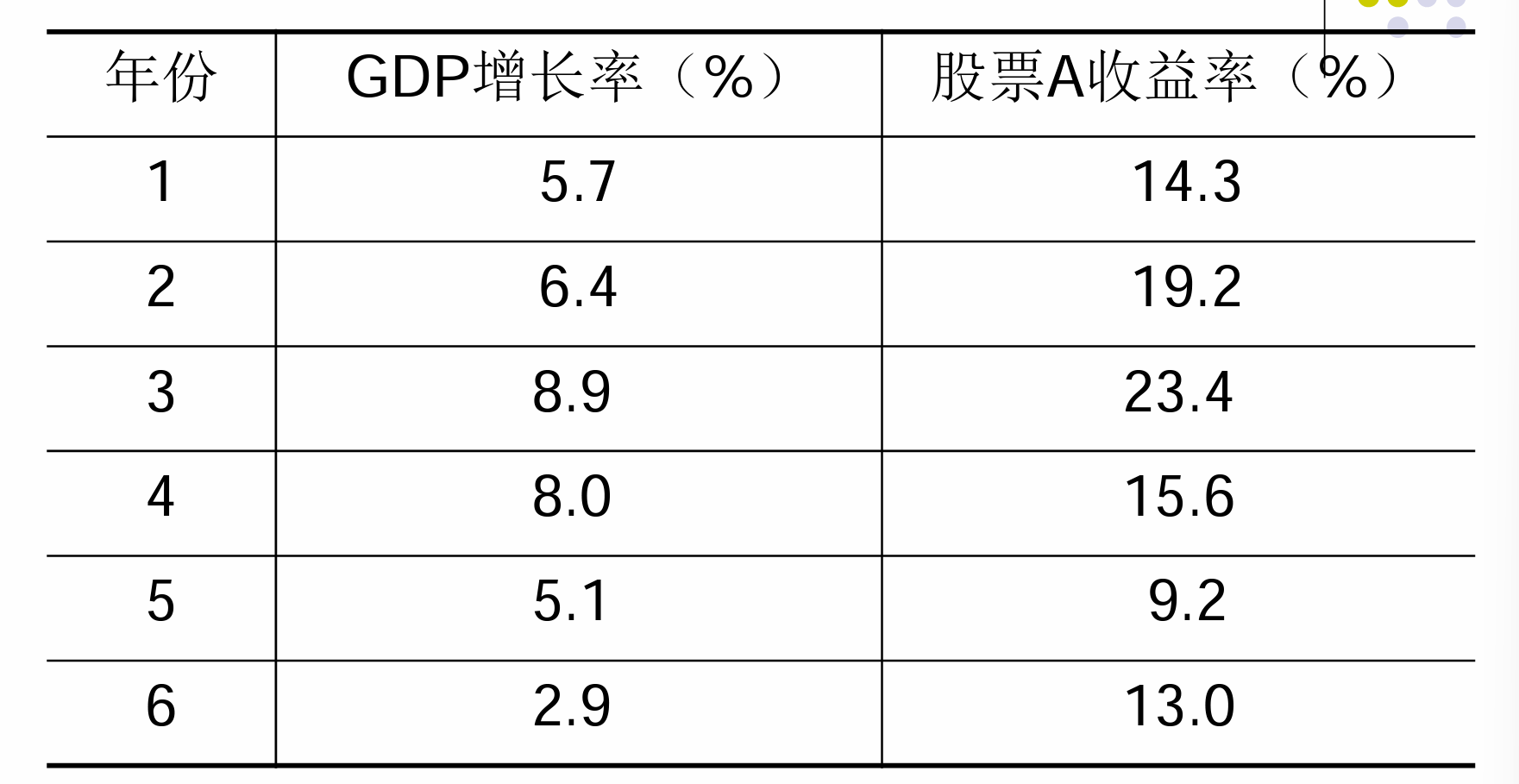
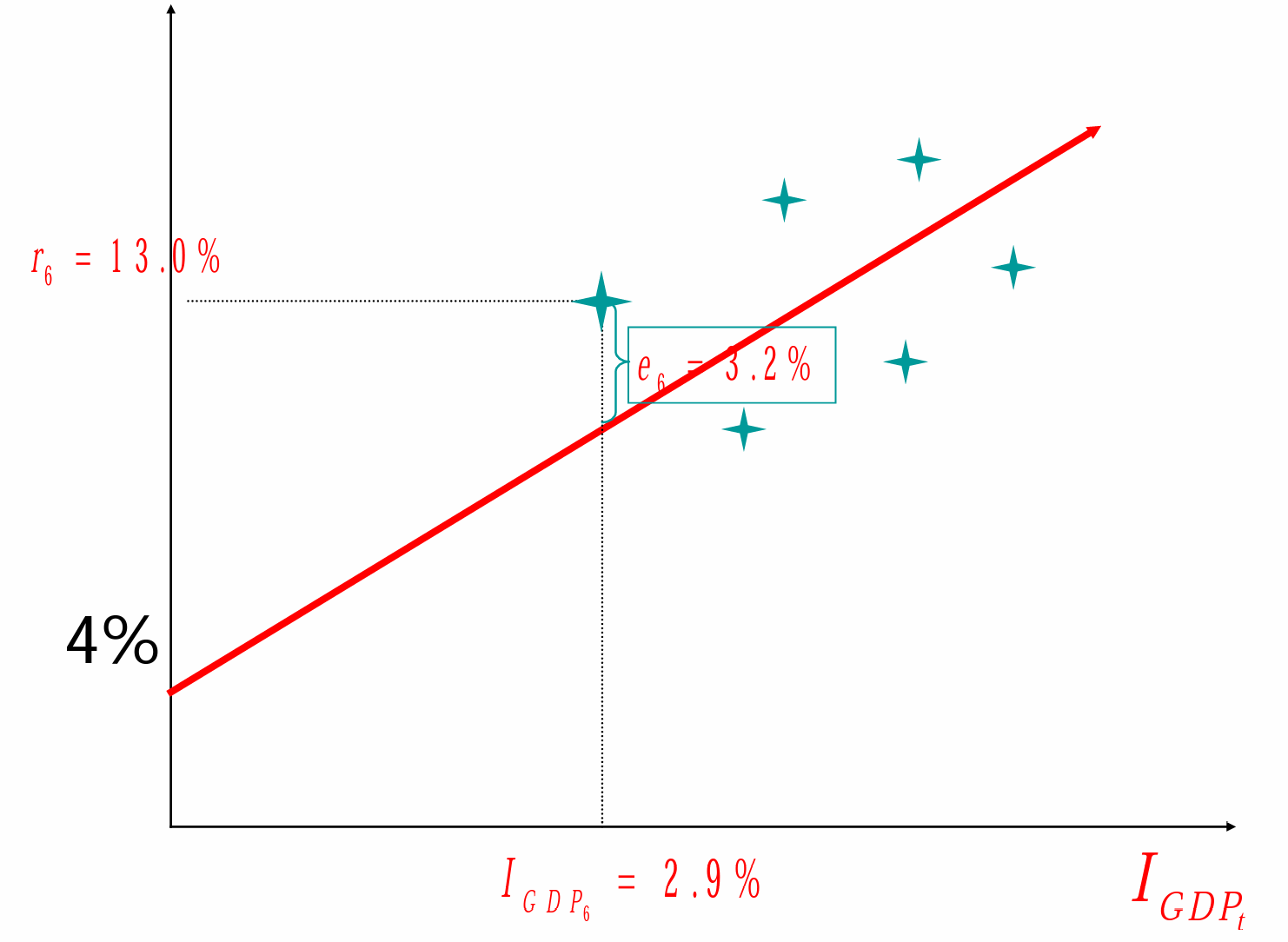
- 得到
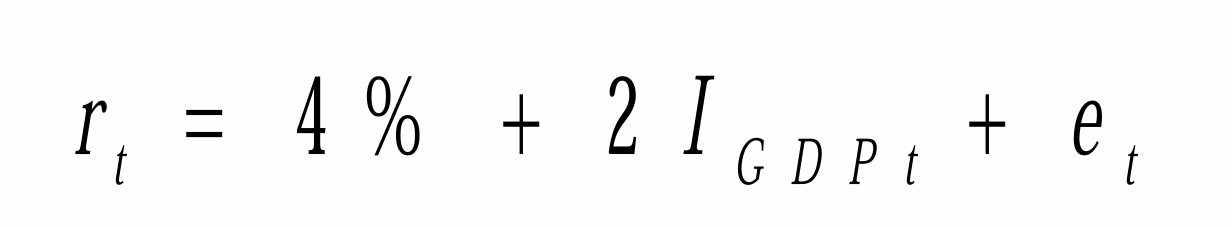

-
单因子模型通式

- 只考虑特定时间
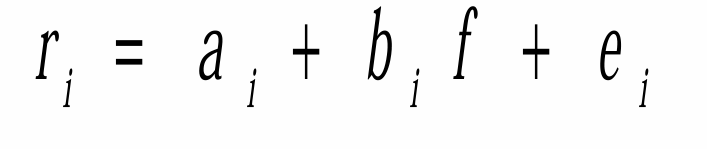
- 假设 (1) :因子 f 具体取什么值对随机项没有影响, 即因子 f 与随机项是独立的,这样保证了因子 f 是 回报率的唯一因素。

- 假设 (2) :一种证券的随机项对其余任何证券的随机项没有影响,换言之,两种证券之所以相关, 是由于它们具有共同因子 f 所致。
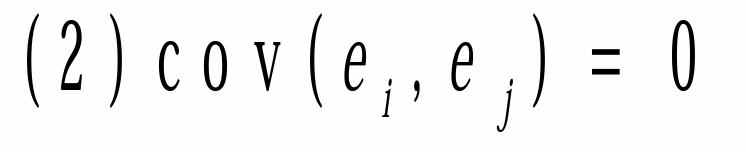
- 因而回报率均值为
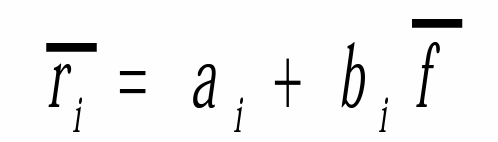
- 方差为
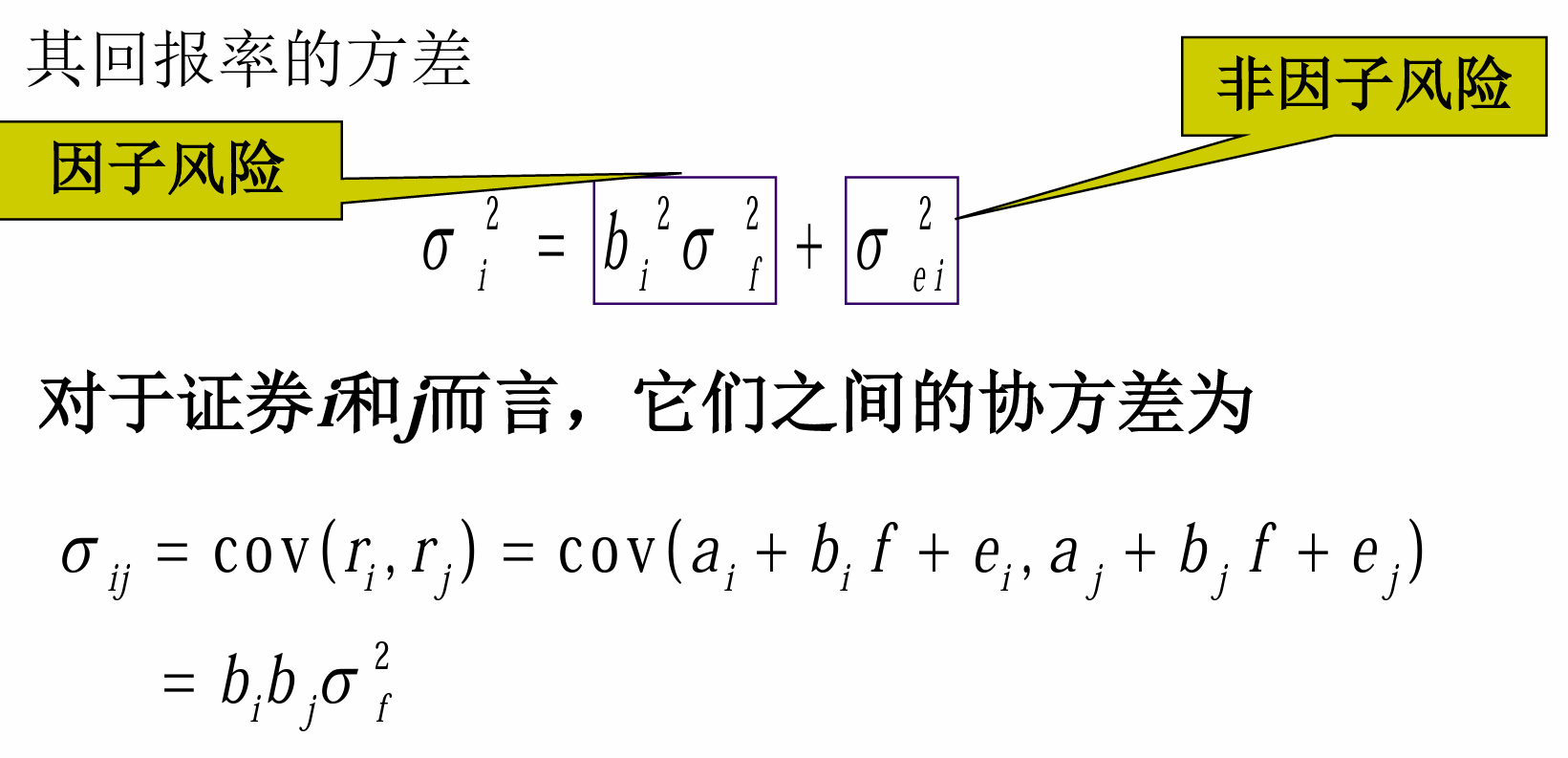
-
&&单因子模型优点


- n足够大时有
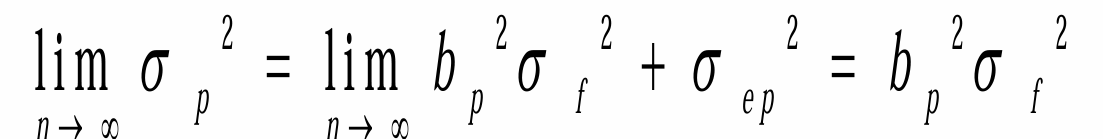
-
CAPM模型为证券回报仅仅与市场因子回报 有关的单因子模型
-
多因子模型
- 现实中存在市场因素以外的其他因素 引起股票价格的共同移动。单因素模型难以把握公司对不同的宏观经济因素的反应。
-
两因子模型
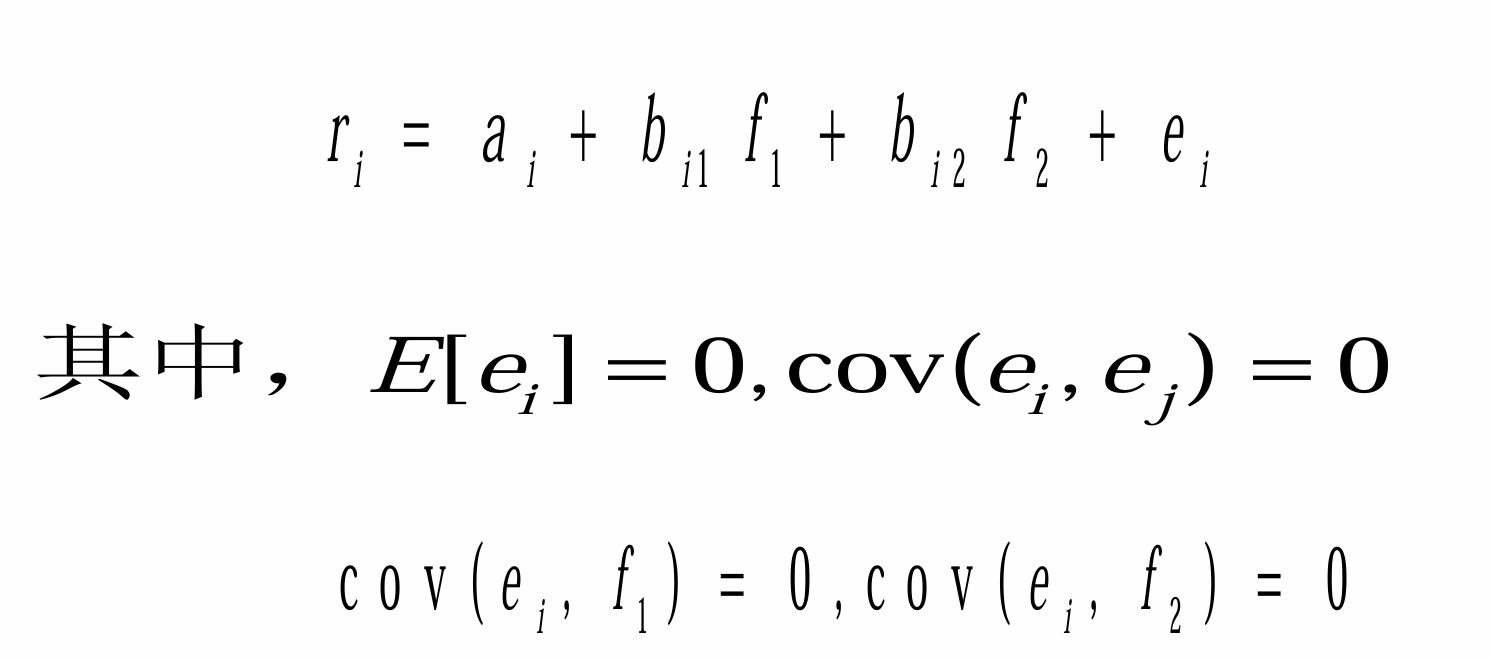

- 优点

-
多因子模型
-
套利机会
- 套利(Arbitrage)是同时持有一种或者 多种资产的多头或空头,从而存在不承担风险 的情况下锁定一个高于无风险利率的收益。
-

-
套利定价理论APT
- 基本原理:由无套利原则,在因子模型下,具有相同因子敏感性的资产( 组合 ) 应提供相同的期望收益率 。

-

- 所有具有等因子敏感度的证券 或证券组合,除去非因子风险外,其行为是一 致的。因此,所有具有等因子敏感度的证券或者证券组合的期望回报率是一样的。 否则就存在第二类套利机会,投资者就会利用它们,直到消除这些套利机会为止。 这就是 APT 的实质。
-
&&套利的数学表示
-
无套利


- 对于不同的b存在相同的参数
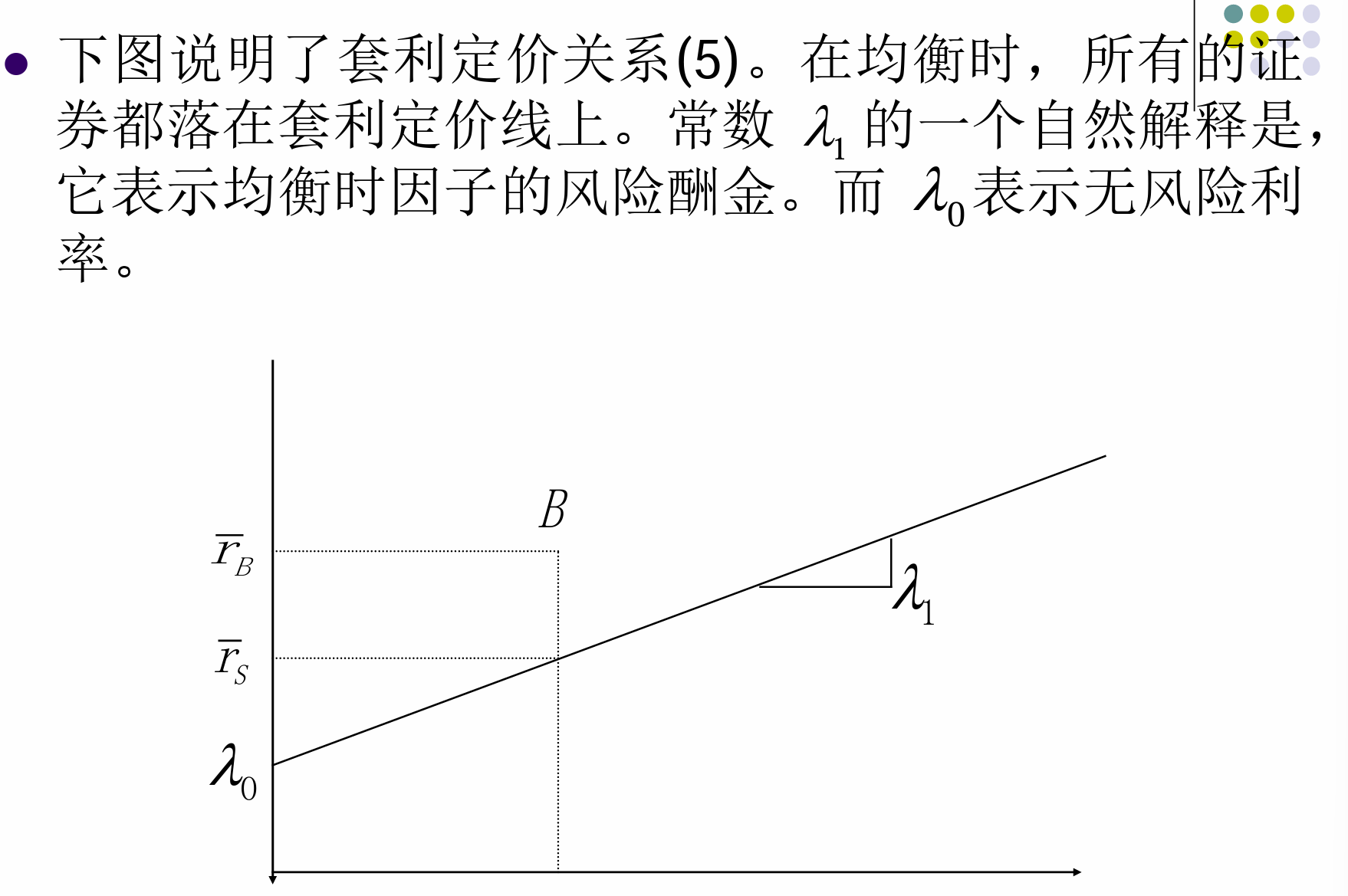
- &&

-
APT的意义

-

- 对于不同的证券这是一个定值
-

-
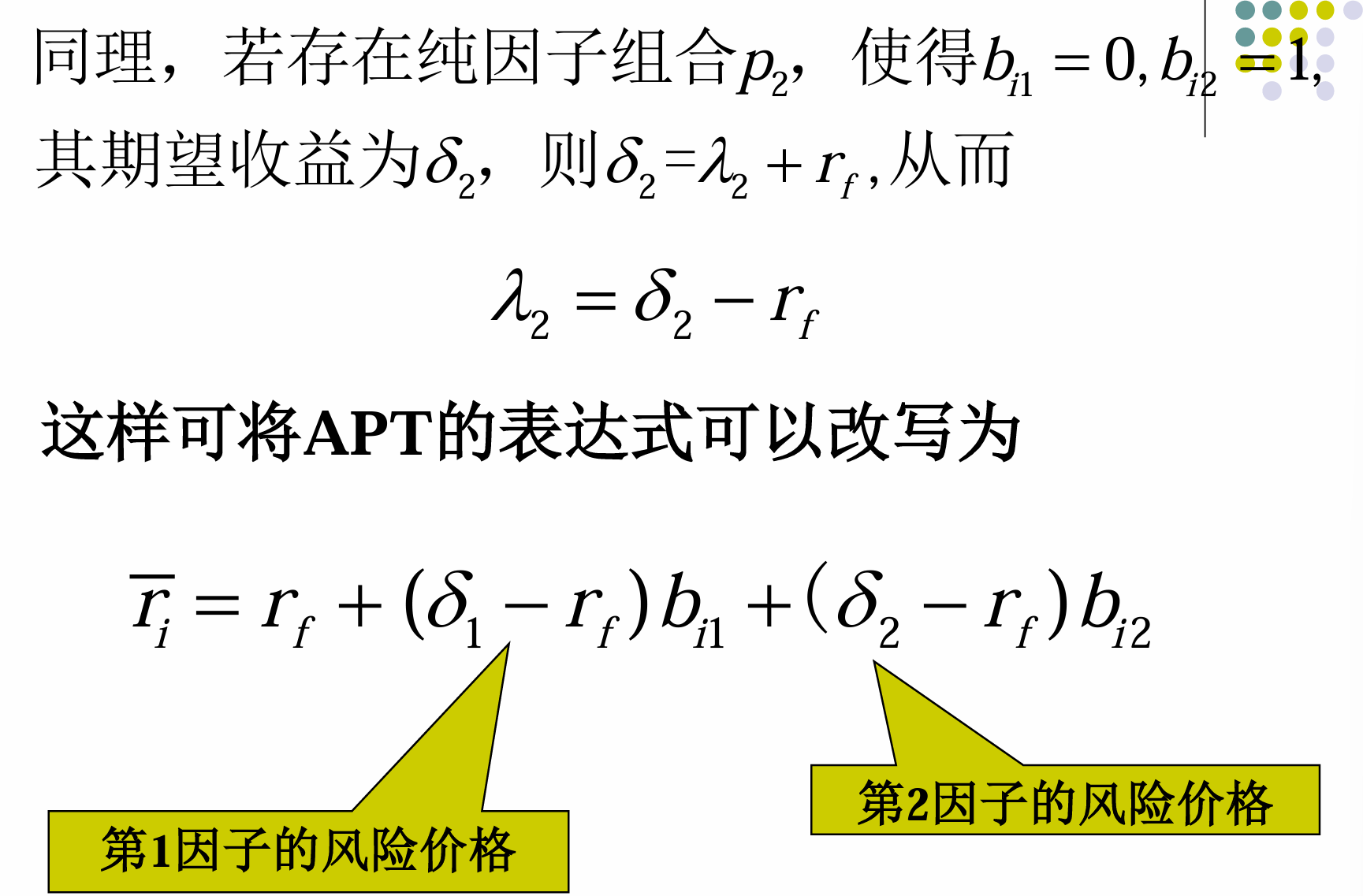
&&APT的另一种表示纯因子组合


-

-
&&APT与CAPM的区别和联系

-

-

-
&&APT对资产组合的指导意义

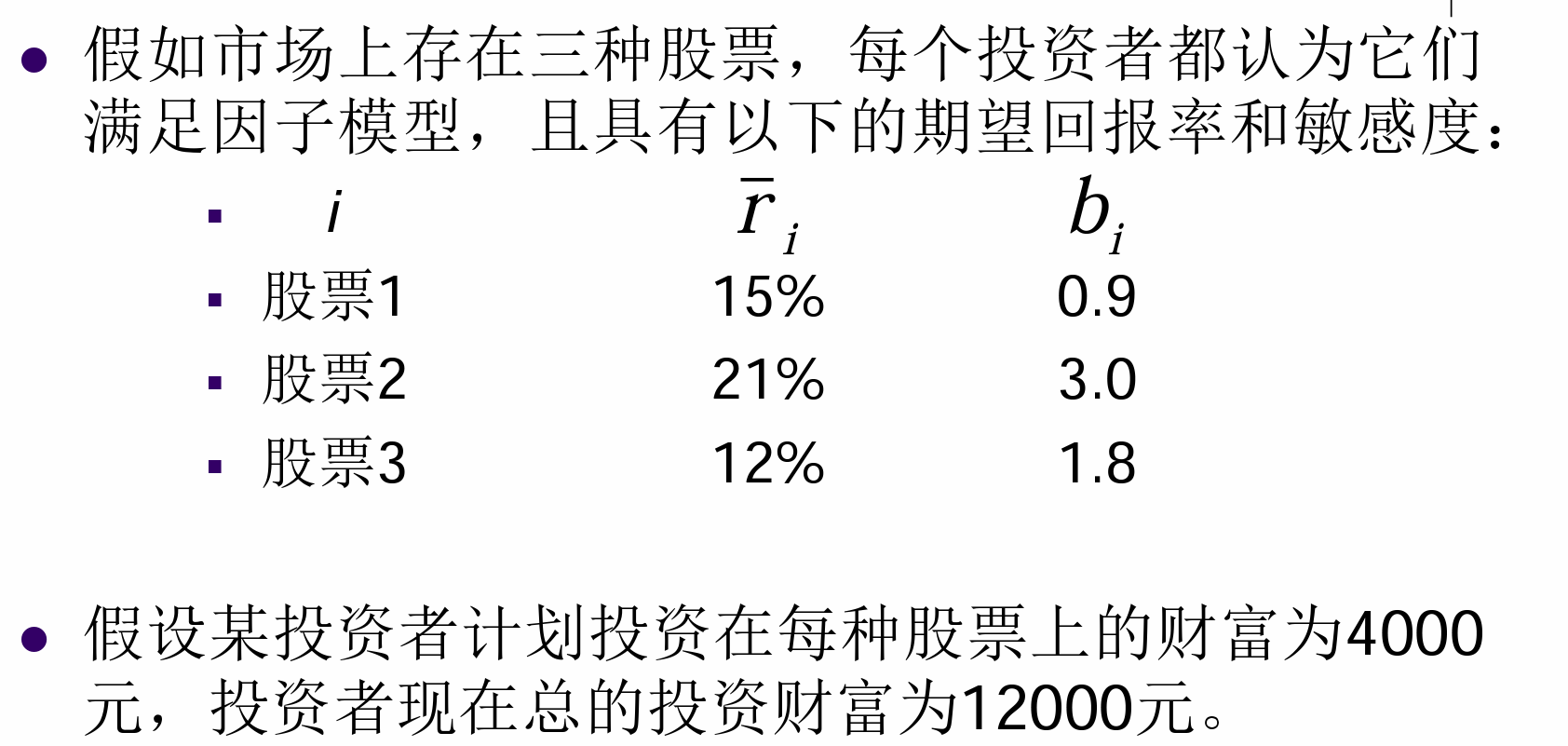
例题¶
- 寻找套利

-

-
使用APT进行定价



补充¶
-
cml与sml
-
资本市场线是沿着投资组合的有效边界,由风险资产和无风险资产构成投资组合。资本市场线上的每一点,都代表着一个完整的投资组合。此外,纵轴和横轴分别是期望收益和标准差。CML的斜率表示市场风险,即市场投资组合的回报率和风险之间的关系。
- 证券市场线表明证券或证券组合收益与贝塔系数之间的关系。首先,横轴的标志是贝塔系数。SML上的每个点代表一个证券,其风险是通过贝塔来度量的,贝塔衡量了该证券相对于整个市场的波动性。SML的斜率表示市场风险溢价,即每单位贝塔所获得的额外期望回报
-
处于SML下方的任何资产或投资组合代表资产价值被高估。
-
处于SML上方的任何资产或投资组合代表资产价值被低估。