离散数学
时间紧迫,以概念为主,附加简单例子。限于之前笔记形式,图片质量较低
逻辑与推理¶
命题逻辑¶
- 命题:
- 是一个陈诉事实的句子
- 要么为真要么为假
- 使用小写字母(命题变元)代表命题,取值范围为 \(\{T,E\}\)
- 命题表达式:命题表达式由命题变元和运算符组成
-
运算符
- 非 \(\neg\)
- 合取 \(\wedge\)
- 析取 \(\vee\)
- 蕴含 \(p\to q\):p=1 q=0 是为 false,其他时候为 true
- 双蕴含 \(p\leftrightarrow q\):“当仅当“,具有相同值时为 true(也称 pq 逻辑等价)
- 优先级:\(\neg, \wedge,\vee,\to,\leftrightarrow\)
-
将自然语言翻译为命题表达式(例子)
-
特殊的命题表达式
- 永真式
- 矛盾式
- 可能式
-
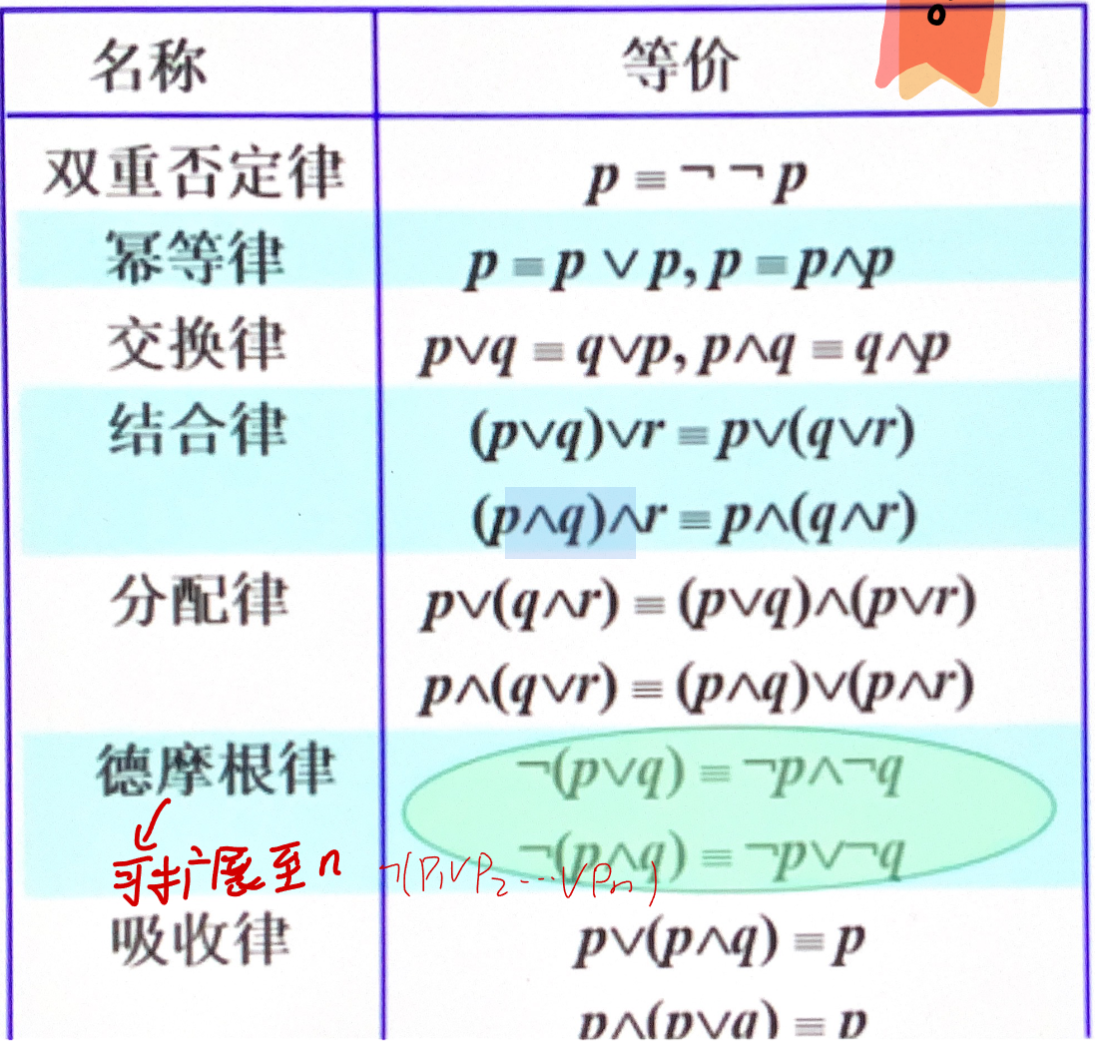
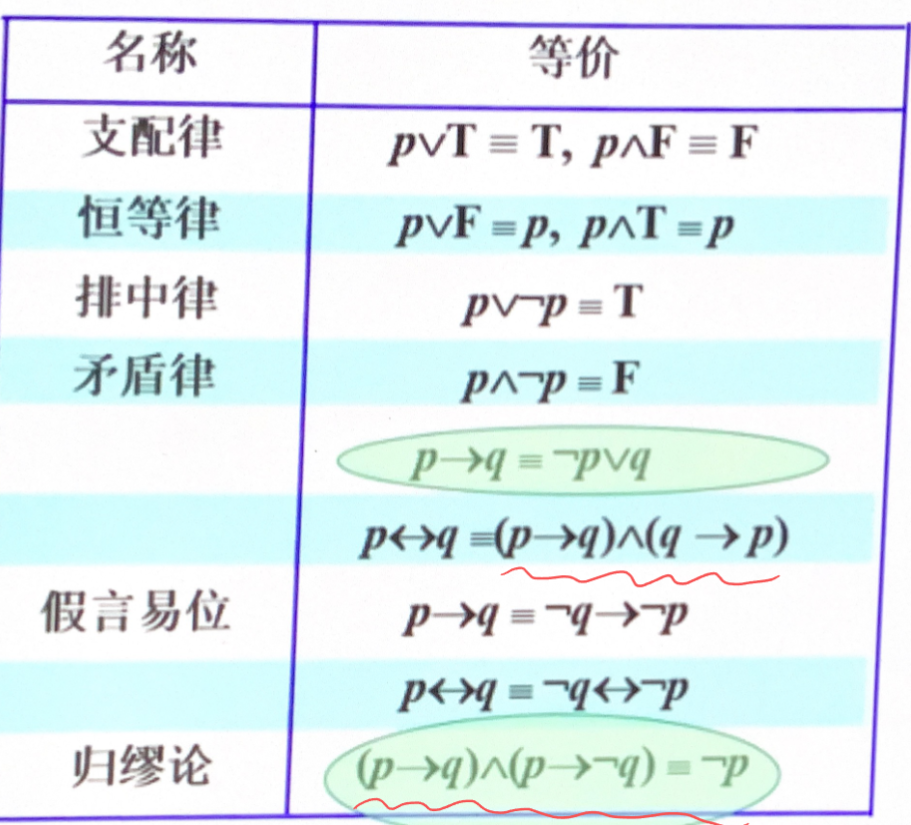
逻辑等价
-
合取范式 CNF
- 可以用于判断满足性,求解假指派
- 析取范式 DNF
- 可以用于求解真指派
- 直接化简表达式较麻烦,可以用真值表求解范式
- 合取取成假的,即出现一个这种取值就为 false
- 析取取成真的,出现一个这种取值就为 true
- 主范式:每个括号内都出现所有命题变元,并按照自然顺序进行排序
- 使用真值表求解的例子
- \(A\vee(B\wedge C)\)
- CNF:\((A\lor B\lor C)\land(A\lor B\lor\lnot C)\land(A\lor\lnot B\lor C)\)
- DNF:\(A \lor (\neg A \land B \land C)\)
| A | B | C | B ∧ C | A ∨ (B ∧ C) |
|---|---|---|---|---|
| F | F | F | F | F |
| F | F | T | F | F |
| F | T | F | F | F |
| F | T | T | T | T |
| T | F | F | F | T |
| T | F | T | F | T |
| T | T | F | F | T |
| T | T | T | T | T |
- 命题推理
| 逻辑关系 | 表达式 | 结果 |
|---|---|---|
| 假言推理 | p, p→q |
q |
| 取拒式 | ¬q, p→q |
¬p |
| 假言三段论 | p→q, q→r |
p→r |
| 析取三段论 | ¬p, p∨q |
q |
| 附加律 | p |
p∨q |
| 化简律 | p∧q |
p |
| 合取律 | p, q |
p∧q |
| 消解律 | p∨q, ¬p∨r |
q∨r |
-  |
||
| #### 谓词逻辑 | ||
| - 允许使用量词来表达某些属性或关系适用于一些或所有可能的对象。谓词逻辑比命题逻辑表达能力更强,因为它能详细描述事物之间的关系以及事物的属性。 | ||
| - 全称量词:\(\forall\) | ||
| - 存在量词:\(\exists\) | ||
| - 谓词: | ||
| - 一元谓词 :\(P (x)\) | ||
| - 二元谓词:\(P(x,y)\) | ||
| - 约束变元:受到量词约束;自由变元:不受到两次约束 | ||
| -  | |
| - 量词公式 | ||
| - \(\forall x\forall y=\forall y\forall x\) | ||
| - \(\exists x\exists y=\exists y \exists x\) | ||
| - 对于混合 \(\forall \exists\) 的情况不能随意调换顺序 | ||
| -  |
- 等价式
- \(\neg\forall xp(x)\equiv\exists x\neg p(x)\) \(\neg\exists xp(x)\equiv\forall x\neg p(x)\)
- \(\begin{aligned}\forall x(P(x)\wedge Q(x))\equiv(\forall x P(x))\wedge(\forall xQ(x))\\\exists x(P(x)\vee Q(x))\equiv(\exists xP(x))\vee(\exists xQ(x))\end{aligned}\)
- \(\begin{aligned}(\forall xP(x))\vee(\forall xQ(x))\to\forall x(P(x)\vee Q(x))\\\exists x(P(x)\wedge Q(x))\to(\exists xP(x))\wedge(\exists xQ(x))\end{aligned}\)
- \(\begin{aligned}\forall x(P(x)\vee R)\equiv(\forall xP(x))\vee R\\\exists x(P(x)\wedge R)\equiv(\exists xP(x))\wedge R\end{aligned}\)
- \(\begin{aligned}\forall x({R}\rightarrow p(x))\equiv{R}\rightarrow\forall xP(x)\quad\exists x({R}\rightarrow{P}(x))\equiv{R}\rightarrow\exists xP(x)\\\forall x(P(x)\rightarrow{R})\equiv(\exists xP(x))\rightarrow{R}\quad\exists x({P}(x)\rightarrow{R})=(\forall xP(x))\rightarrow{R}\end{aligned}\)
-
前束范式:将 \(\forall \exists\) 放在表达式最前面
-
自然演绎规则
- 全称例示 \(\forall p(x)\to p(c)\)
- 全称生成 \(p(c)对任意 c\to\forall xp(x)\)
- 存在例示 \(\exists xp(x)\to p(c)对于某个c\)
- 存在生成 \(p(c)对某个 c\to \exists xp(x)\)
-

-
谓词逻辑具有:不可判定性和推理复杂性
- 不存在一个通用的算法能够判定任意给定的逻辑陈述是否是可证的
- 在谓词逻辑中,推理任务通常是非常复杂的,它们可以是NP-难的
证明方法¶
- 定理:能被证明为真的陈述
- 证明:表明陈述为真的有效论证
- 定理证明中可以使用的陈述:定理前提、术语定义、公理、已经证明的定理
- 直接证明
- 反证法 \(\neg q \to\neg p\) 推导出 \(p\to q\)(是归谬法的特例,通常用于证明命题的真实性)

- 广义反证法:\(p_{1}\wedge\dots\wedge p_{n}\to q\equiv\neg q\wedge p_{1}\dots\to F\)
- 归谬法:通过假设某个命题为真,然后从这个假设出发逻辑推导,直至推出一个矛盾或荒谬的结论,从而证明这个命题实际上是假的
- 等价性证明
- 分类讨论
- 存在性证明
- 构造性证明(构造说明给出具体示例)
- 非构造性性证明(说明存在,但是不给出具体实例)
- 唯一性证明
- \(\begin{aligned}&\exists x\left(P(x)\wedge\forall y\left(y\neq x\rightarrow\neg P(y)\right.\right)\\&\exists x\left.P(x)\wedge\forall y\right.\forall z\left(P(y)\wedge P(z)\rightarrow y=z\right)\end{aligned}\)
- 寻找反例
- 找出一个反例进行否定
数学归纳法与良序原理¶
-
数学归纳法的基本过程
- 基础步骤:证明 \(P(0)\)
- 归纳步骤: 归纳假设 \(P(k)\) 证明 \(P(k+1)\)
-
强数学归纳法
- 归纳步骤改为假设 \(P(0)\dots P(k)\) 成立,证明 \(P(k+1)\) 成立
-
良序原理:自然数 \(N\) 的任何非空子集 \(S\) 均有最小元素\(\exists a\in S(\forall b\in S(a\neq b\to a<b))\)
- 数学归纳法实际上是基于自然数集的良序性质。由于自然数集是良序的,我们可以确定序列的起点,并且可以保证每个数都有一个后继数,即 𝑘 之后有 𝑘+1。这就提供了数学归纳法中从 𝑘 到 𝑘+1 这一步骤的逻辑基础。(并且保证证明是完全的不会有遗漏)
-
结构归纳法
- 结构归纳法不局限于自然数,适用于任何可以递归定义的结构,适用于逻辑表达式、树、图等数据结构
- 基础步骤:证明对于初始元素来说命题成立
- 递归步骤:针对生产新元素的规则,若相关元素满足命题,则新元素也满足命题
-
程序的正确性
- Hoare 三元组 \(\{ P \}S\{ Q \}\):\(S\) 是一段程序,\(PQ\) 是程序中变量的断言,分为前置断言和后置断言
- 如果 \(S\) 执行之前 \(P\) 成立,那么就有 \(S\) 运行完之后 \(Q\) 成立
- 这就满足了部分正确性,完全正确性还要求程序能在有限步内终止
数学¶
数论¶
数及运算¶
- 皮亚诺公理
- 零是自然数
- 每个自然数都有一个自然数后继
- 零不是任何自然数的后继
- 不同自然数有不同的后继
- 若由自然数组成的某个集合含有零,并且每当该集合含有某个自然数时便也同时含有这个自然数的后继,那么该集合定义所有自然数
- 自然数的集合表示:\(0\) 表示 \(\phi\);\(S(x)=x\cup \{ x \}\) \(\begin{aligned}1&=S(0)=S(\emptyset)=\emptyset\cup\{\emptyset\}=\{\emptyset\}=\{0\}\\2&=S(1)=S(\{0\})=\{0\}\cup\{\{0\}\}=\{0,\{0\}\}=\{0,1\}\\3&=S(2)=S(\{0,1\})=\{0,1\}\cup\{\{0,1\}\}=\{0,1,\{0,1\}\}=\{0,1,2\}\end{aligned}\)
- 加法定义:\(m+0=m\),\(m+S(n)=S(n+m)\)
- 乘法定义:\(m\times{0}=0\),\(m\times S(n)=S(m\times n)\)
- 减法不封闭:将自然数扩展至整数
- 除法扩展至实数
数论初步¶
- 整除:\(b=ac\) 称 \(a\) 整除 \(b\) 记作 \((a|b)\)
- \(a\mid b\) 则 \(a\mid bc\)
- \(a\mid b\) 且 \(b\mid c\) 则 \(a\mid c\)
- \(a\mid b\) 且 \(a\mid c\) 则 \(a\mid(mb+nc)\)
- 带余除法
- \(a\) 为整数,\(d\) 为正整数,则存在唯一的整数 \(0\leq r<d\) 满足 \(a=dq+r\),记 \(q=a\ div\ d\),\(r=a\ mod\ d\)
- 同余:\(a,b\in Z;m\in Z^+\) 若 \(m|(b-a)\) (即 \(a=b+km\))则称 \(a\) 与 \(b\) 模 \(m\) 同余,记为 \(a\equiv b(mod\ m)\) ,同余具有传递性和对称性
-
同余算术:在模 \(m\) 同余的情况下将算术范围限制在 \(Z_{m}=\{ 0,\dots,m-1 \}\)
- 模 \(m\) 加:\(a+_{m}b=(a+b)mod\ m\)
- 模 \(m\) 乘:\(a·_{m}b=(a·b)mod\ m\)

-
对于 \(a_{1}\equiv b_{1}(mod\ n)\) 和 \(a_{2}\equiv b_{2}(mod\ n)\)
- 支持加减乘除以及幂运算(即任意整系数多项式)
- \(p(a)\equiv p(b)(mod\ n)\)
- 应用 \(32^{68}mod\ 31\to 1\dots 1mod\ 31\)
- (因为 \(32\equiv 1(mod/ 31)\))
- 但注意 \(k^a!\equiv k^b(mod\ n)\)
- 若 \(d\mid m\) 则 \(a\equiv b(mod\ m)\to a\equiv b(mod\ d)\)
- \(a\equiv b(mod\ m)\iff da\equiv db(mod\ dm)\)
- \(c,m\) 互素 \(a\equiv b(mod\ m)\iff ca\equiv cb(mod\ m)\)
-
算术基本定理:每个大于 1 的正整数都可以唯一的写为一个素数或若干素数的乘积,其中素数因子以非递减出现 \(n=p_{1}^{\alpha_{1}}\dots p_{k}^{\alpha_{}k}\)
- 最大公约数(能整除两个整数的最大正整数):\(gcd(a,b)=min\{ d\in N^+\mid d\mid a,d\mid b \}\);另一种表述:若 \(a=p_{1}^{\alpha_{1}}\dots p_{k}^{\alpha_{k}}\),\(b=p_{1}^{\beta_{1}}\dots p_{k}^{\beta_{k}}\) 有 \(gcd(a,b)=p_{1}^{\gamma_{1}\dots p_{k}^{\gamma_{k}}},\gamma_{i}=min(\alpha_{i},\beta_{i})\)
- 最小公倍数就是换成 \(max\)
- 辗转相除法求最大公约数
- 利用 \(a\) 除 \(b\) 余 \(c\),有 \(gcd(a,b)=gcd(b,c)\)

-
裴蜀定理:\(gcd(a,b)\) 一定是 \(a\) 和 \(b\) 的线性组合,即 \(\forall a,b\in Z^+(\exists s,t\in Z(gcd(a,b)=sa+tb))\)
- 即 \(ax+by=c\) (即 \(ax\equiv c(mod\ b)\))有整数解当仅当 \(gcd(a,b)\mid c\)
-
同余方程: \(ax\equiv b(mod\ m)\) 称为线性同余方程
-
中国剩余定理:求解线性同余方程组
- \(\left\{\begin{matrix}x\equiv a_1\pmod{m_1}\\x\equiv a_2\pmod{m_2}\\\vdots\\x\equiv a_n\pmod{m_n}\end{matrix}\right.\)
- 假设 \(m_{1}\dots m_{n}\) 两两互素,则一元线性同余方程组在模 \(M\) 下有唯一解 (\(M=\prod_{{i=1}}^nm_{i}\))
- 令 \(M_{i}=\frac{M}{m_{i}}\),\(t_{i}=M_{i}^{-1}\)(模 \(m_{i}\) 下的逆 \(t_{i}M_{i}\equiv 1(mod\ m_{i})\))
- 方程组的解为 \(x=a_{1}t_{1}M_{1}\dots+a_{n}t_{n}M_{N}+kN\)

-
费马小定理:设正整数 \(a\) 不是素数 \(p\) 的倍数 (\(gcd(a,p)=1\))有 \(a^p\equiv a(mod\ p)\) 即 \(a^{p-1}\equiv 1(mod\ p)\)
- 如 \(5^{116}\equiv 1(mod\ 59)\)
- 费马小定理实际上是欧拉定理的特例
- 欧拉定理
- 若 \(a\) 与 \(n\) 互素,则 \(a^{\varphi(n)}\equiv 1(mod\ n)\)
- \(\varphi(n)\) 称为欧拉函数,为不大于 \(n\) 且与 \(n\) 互质的正整数的个数,即 \(\varphi(n)=\mid \{ k\mid{1}\leq k\leq n,gcd(k,n)=1 \}\mid,n\in N^+\)
- 欧拉函数的计算 \(\varphi(n)=\prod_{i=1}^kp_{i}^{\alpha_{i}}\left( 1-\frac{1}{p_{i}} \right)\)
- 如 \(\varphi(12)=12\left( 1-\frac{1}{2} \right)\left( 1-\frac{1}{3} \right)=4\)
- \(\varphi(p)=p-1\)(p 是素数)(费马小定理)
- 若\(m\)与\(n\)互素,则\(\varphi(mn)=\varphi(m)\varphi(n)\)
组合数学¶
基本公式¶
- 乘法原则:做一件事有多个步骤,第一步 n 种,第二部 m 中,则完成需要 \(m\times n\) 种
- 加法原则:一件事有两种做法,第一种做法有 \(n\) 种,第二种有 \(m\) 种,则总共有 \(m+n\) 种方法
- 排列:\(P(n,r)=\frac{n!}{(n-r)!}\) (\(P(n,n)\) 是一个集合上的双射),从 n 个元素有序取出 r 个
- 组合:\(C(n,r)=\frac{P(n,r)}{P(r,r)}=\frac{n!}{r!(n-r)!}\)
- \(C(n,r)=C(n,n-r)\)
- \(C(n,k)=C(n-1,k-1)+C(n-1,k)\) 即 \(\sum^n_{j=r}C(j,r)=C(n+1,r+1)\)
- \(kC(n,k)=nC(n-1,k-1)\)
-
二项式系数
- \((x+y)^n=\sum^n_{j=0}C(n,j)x^{n-j}y^j\)
- \(\sum^n_{k=0}(-1)^kC(n,k)=0\),\(\sum^n_{k=0}2^kC(n,k)=3^n\);分别对应 \((1-1)^k(2+1)^k\)
- 扩展到多项式 \((x_{1}\dots x_{m})^n=\sum_{k_{1}+\dots+k_{m}=n}C(n,k_{1}\dots k_{m})\prod_{t=1}^mx_{t}^{k_{t}}\) ;其中 \(C(n,k_{1}\dots k_{m})={\frac{n!}{k_{1}!\dots k_{m}!}}\)
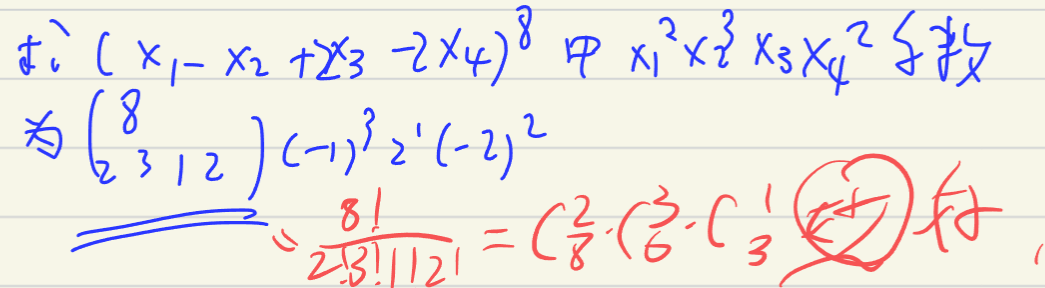
-
范德蒙恒等式
- \(C(m+n,r)=\sum^r_{k=0}C(m,r-k)C(n,k)\)
- \(C(2n,n)=\sum_{k=0}^n C(n,k)^2\)
计数原理¶
- 容斥原理:
- \(\bigcup_{i=1}^nA_i=S_1-S_2+S_3-...+(-1)^{k+1}S_k+...+(-1)^{n-1}S_n\) 其中 \(S_k=\sum_{1\leq i_1\leq i_2\leq..\leq i_k\leq n}\lvert A_{i_1}\cap A_{i_2}\cap...\cap A_{i_k}\mid\quad k=1,2,...,n\)
- 错位排列:有 \(n\) 个普通的数,重新排列使得所有数都不在原先的位置,有多少方案
- 称满足 \(i_{k}=k\) 的排列为性质 \(A_{k}\) ,那么错位排列个数有 \(N(\overline {A_{1}}\dots \overline{A_{n}})=n!-S_{1}+S_{2}\dots\) 其中 \(\sum_{1\leq i_1\leq i_2\ldots\leq i_k\leq n}\lvert A_{i_1}\cap A_{i_2}\cap...\cap A_{i_k}\rvert\) 有 \(S_{k}=\binom{n}{k}(n-k)!=\frac{n!}{k!}\)
- 这样 \(P=\begin{aligned}n!\sum_{k=0}^n\frac{(-1)^k}{k!}\end{aligned}\to \frac{n!}{e}\)
- \(D_{1}=0,D_{2}=1,D_{3}=2\dots\) 存在递推 \(D_{n}=(n-1)(D_{n-1}+D_{n-2})\)
- 假设第一个元素 a 放在 b 位置上,b 有两种选择:放在 a(\(D_{n-2}\));不放在 a(此时每个元素有一个位置不能放,就是 \(D_{n-1}\))
- 鸽笼原理
- 将 n 只鸽子放到 m 个笼子中,若 \(m<n\) 则至少有一个笼子要装 \(2\) 个或更多鸽子(即 \(\mid A\mid>\mid B\mid\) 则不存在 \(A\to B\) 的单射)
- 推广:\(n\) 只鸽子置于 \(m\) 个笼子,至少有一个有至少 \(\left\lfloor \frac{n-1}{m} \right\rfloor+1\) 只鸽子
- 拉姆齐数
- \(R(k,l)=n\) 表示最小的 \(n\) 使得必有 \(k\) 个人相识或 \(l\) 个人互不相识
- \(R(3,3)=6\)
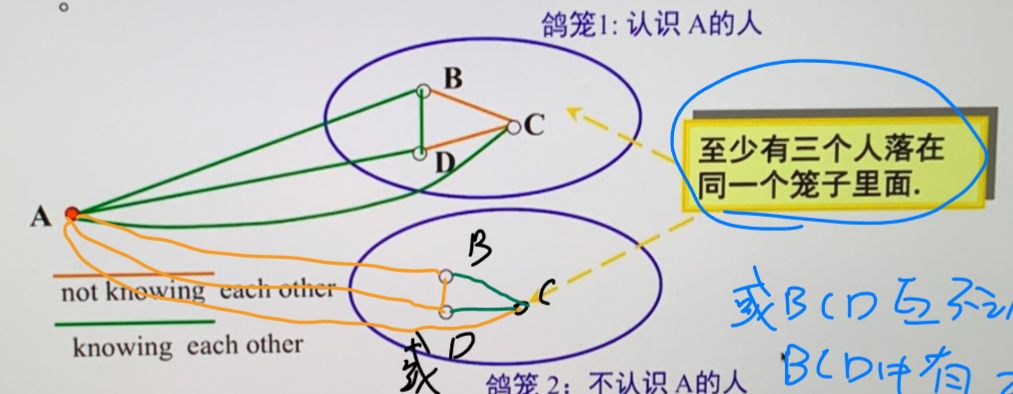
- 依据是否认识 A 进行划分,其中一组至少有 3 个人,(以认识 A 为例)这三个人只要两个互相认识,那么就闭合得到三个人互相认识,如果全不认识,那就得到 3 个人互相不认识
典型排列/组合¶
- 圆排列:从 \(n\) 个不同元素中,取 \(r\) 个不重复的元素排成一个圆圈 \(\frac{P(n,r)}{r}\)
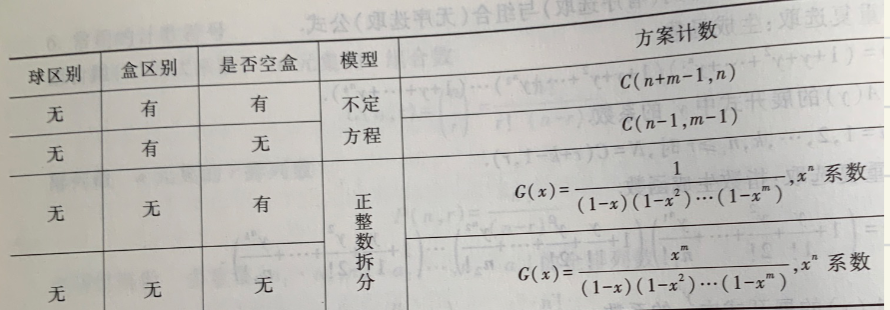
- 隔板法:将一组相同物品分配到不同的容器,并且可以处理容器可以/不可以为空的情况
- 假设不可以为空,有 k 个桶,n 个物品,分配方式数目有 \(C(n+k-1,k-1)\)
- 应用:三种水果(足够多),选 4 个有多少方案:\(C(6,2)\) 即 4 个物品 3个桶
-
有重复元素的排列:\(n\) 个元素,\(m_{i}\) 是第 \(i\) 个重复项的重复次数,这 \(n\) 个元素的排列结果有 \(\frac{P(n,n)}{\prod m_{i}!}\)
-
第二类斯特林数 \(S(n,k)\) 记 \(\left\{\begin{matrix}n\\k\end{matrix}\right\}\)
- 将 n 个不同元素的集合划分为 k 个非空子集
- \(S(n+1,k)=kS(n,k)+S(n,k-1)\) 前一项表示新元素和原先某一组一起,后一项表示自己一组
- 斯特林数没有简单的通项公式,难以求解

概率论¶
- 试验:从一组可能的结果中得到一个结果的过程
- 样本空间:所有可能的结果的集合,表示随机试验可能出现的所有结果
-
概率分析的基本步骤:选定样本空间,定义相关事件,确定结果概率,计算事件概率
-
古典概率:实验结果数目有限;等可能性;互斥性;可加性
-
频率主义概率:试验次数无穷多时得到结果概率
-
概率空间:基于集合论的概率定义
- 样本空间 \(S\) 中的一个元素 \(w\) 称为一个结果
- 在 \(Pr: S\to R\) 的函数满足 \(\forall_{w\in S}Pr[w]\geq 0,\sum_{w\in S}Pr[w]=1\) 则为一个样本空间 \(S\) 上的概率函数:描述随机变量取值的概率分布的函数
- \(S\) 的一个子集 \(E\) 称为一个事件(部分结果的集合)\(Pr[E]=\sum_{w\in E}Pr[w]\)
-
均匀分布:指每个结果的概率相同,为 \(\frac{1}{\mid S\mid}\),可以通过计数计算概率
-
条件概率:给定 \(F\) 条件下 \(E\) 的概率 \(Pr[E\mid F]={\frac{Pr[E\cap F]}{Pr[F]}}\)
-
贝叶斯定理:\(Pr[F\mid E]=\frac{Pr[E\mid F]Pr[F]}{Pr[E\mid F]Pr[F]+Pr[E\mid\overline F]Pr[\overline F]}\)
-
事件独立性:EF 为相互独立当仅当 \(Pr[E\cap F]=Pr[E]\cdot Pr[F]\)
- 随机变量:将样本空间中的每个结果映射到实数的函数 (便于进一步计算期望等统计信息) \(X: S\to R\)
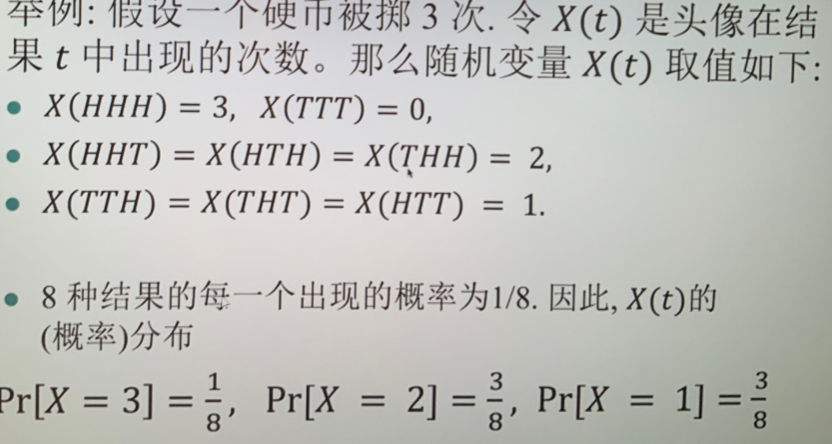
- 随机变量的分布:\((r,Pr[X=r])\) 其中 \(r\in X(S)\),\(Pr[X=r]\) 为 \(X\) 取值 \(r\) 的概率
- 期望:\(Ex[x]=\sum_{w\in S}X(w)Pr[w]\),记 \(X\) 在 \(w\) 的偏差为 \(X(w)-Ex[X]\)
-
条件期望:一个随机变量在条件下的结果的取值的概率加权平均
- \(Ex[R\mid A]=\sum r·Pr[R=r\mid A]\)
- 全期望公式:\(A_{1}A_2\dots\) 为 \(S\) 的一个划分,则 \(Ex[R]=\sum_{i}Ex[R\mid A_{i}]Pr[A_{i}]\)


-
期望的性质
- 线性(可加性):\(E[X+Y]=E[X]+E[Y]\),\(E[ax+b]=aE[x]+b\)
- 对于独立事件还有:\(E[XY]=E[X][Y]\)


-
方差:\(Var[X]=Ex[(X-Ex[X])^2]\)
- 使用期望计算 \(Var[X]=E[X^2]-E[X]^2\)
- 标准差 \(\sigma_{X}=\sqrt{ Var[X] }\)
- 对于独立随机变量有 \(Var[X+Y]=Var[X]+Var[Y]\)
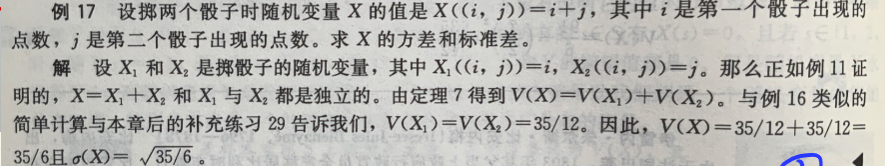
关系代数¶
集合¶
- 集合是一组无序、确定的(要么属于,要么不属于)相互区分的对象,这些对象成为集合的元素
- 集合相等 \(A=B\iff\forall x(x\in A\leftrightarrow x\in B)\)
- 子集 \(\subseteq\) 有 \(\forall (x\in A\to x\in B)\)
- 真子集 \(\subset\) (\(A\neq B\))
- 有限集合:若集合 S 有 n 个不同元素,且 n 为自然数,那么就称 S 为有限集合,基数为 \(\mid S\mid =n\)
- 否则为无限集合
- 空集 \(\phi\)
- 是所有集合的子集
- 空集是唯一的
- 注意 \(\{ \phi \}\) 不是不是空集
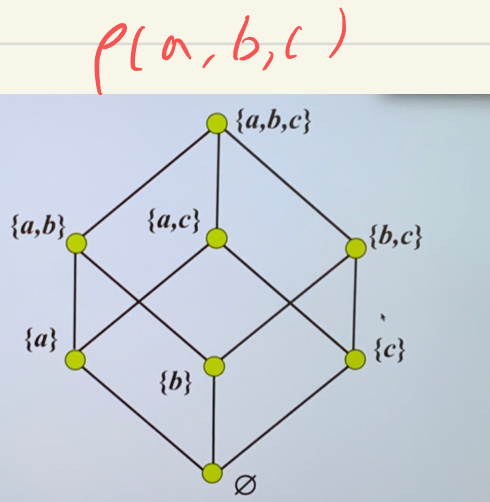
- 幂集:
- 对于集合 \(S\),幂集为 \(S\) 的所有子集的集合\(\rho(S)=\{ x\mid x\subseteq S \}\)
- \(\rho(\{a,b\})=\{\phi,\{ a \},\{ b \},\{ a,b \}\}\)
- 若 \(\rho(A)\subseteq\rho(B)\) 则 \(A\subseteq B\)
- 若集合的基数为 \(n\) 则 \(\mid\rho\mid=2^n\)
- \(x\in P(A)\iff x\subseteq A\)
- 归纳集 \(\phi\in A\),\(\forall a(a\in A\to S(a)\in A)\)
集合运算¶
- 差集 \(A-B\to a\in A\wedge a\notin B\)
- 对称差 \(A\oplus B=(A-B)\cup(B-A)=(A\cup B)-(A\cap B)\)
- 广义并:集合 A 的所有元素的并为 \(\cup A=\{ x\mid\exists y(y\in A\wedge x\in y) \}\)
- 广义交:集合 A 的所有元素的交为 \(\cap A\{ x\mid\forall y(y\in A\to x\in y) \}\)
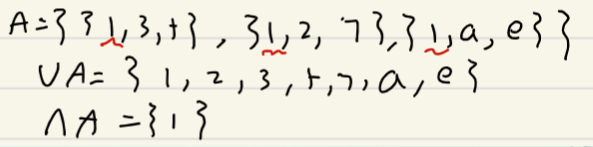
集合的基数¶
- 等势:如果存在集合 A 到 B 的双射,称集合 A 与 B 等势,记为 \(A\approx B\)(元素间一一对应,有 \(\mid A\mid=\mid B\mid\))
- 若存在 \(n(n\in N)\)(自然数集合子集) 与 \(S\) 等势,则称 \(S\) 为有限集,否则称为无限集
- 可数集即存在集合到 N 的一个单射
- 与自然数集 N 等势的集合称为可数无限集
- 有限集都是可数集,都可以与一个 \(n\) 等势
- \(S\) 是无限集 iff 存在 S 的真子集 S' 使得 S 与 S‘等势、
- 整数集与自然数集等势
- 可数个可数集的并集仍然是可数集
- \((0,1)\) 不可数

- 无法数清(总是能构造一个没数到的情况)
-
不是所有无限集都等势
- 等势的无限集:\((0,1)\to R\);直线上点 \(\to\) 平面内点;
- 康托尔定理:任何集合与其幂集不等势 \(A\neq\rho(A)\)
- 证明思路与上面 \((0,1)\) 不可数类似,构造出于与每一行都不一样的集合,说明不是双射
-
优势关系:
- 如果存在从 A 到 B 的单射,称 B 优势于 A,记为 \(\mid A\mid\leq\mid B\mid\) 或 \(A\preceq·B\)
- 若 AB 不等势,则记为真优势 \(\mid A\mid<\mid B\mid\) 或 \(A\prec B\)
- 对于任何集合 A 都有 A 的幂集真优势于 A
- 实数集真优势于自然数集
- 使用优势关系说明等势 \(\mid A\mid\leq\mid B\mid,\mid B\mid\leq\mid A\mid\to\mid A\mid=\mid B\mid\),即找到正反两个单射就可以说明等射(这往往比直接找双射更为简单)
- 实数集与幂集等势

- 实数集与幂集等势
- 连续统假说
- 自然数集合基数记为 \(\aleph_{0}\),其幂集(或实数集)记为 \(\aleph_{1}(=2^{\aleph_{0}})\) (连续统基数 \(c\))
- \(\aleph_{2}\) 平面上的曲线的基数
- 连续统假说就是说:不存在 \(A\) 使得 \(\aleph_{i}<\mid A\mid<\aleph_{i+1}\)
关系与函数¶
- 有序对 \((a,b)\) 是集合 \(\{ \{ a \},\{ a,b \} \}\) 的缩写
- \((x,y)==(u,v)\iff x=u\&\&y=v\)
- 笛卡尔积
- 对于集合 \(A,B\) 有 \(A\times B=\{ (a,b), a\in A,b\in B\}\)
- 若均为有限集合则 \(\mid A\times B\mid=\mid A\mid\times\mid B\mid\)
- \(A\times B=B\times A\iff[(A=\phi)\vee(B=\phi)\vee(A=B)]\)
- 支持分配率 $$\begin{aligned}&A\times(B\cup C)=(A\times B)\cup(A\times C)\&A\times(B\cap C)=(A\times B)\cap(A\times C)\&(B\cup C)\times A=(B\times A)\cup(C\times A)\&(B\cap C)\times A=(B\times A)\cap(C\times A)\end{aligned} $$
-
二元关系:两类对象建立联系
- 若 \(A,B\) 是集合,则从 \(A\) 到 \(B\) 的关系是 \(A\times B\) 的一个子集(二元关系是笛卡尔积的一个子集)
- 全域关系:\(\{ (x,y)\mid x,y\in A \}\)
- 恒等关系:\(\{ (x,x)\mid x\in A \}\)
- 控关系:\(\phi\subseteq A\times A\)
- 对于 \((a,b)\in R\) 记为 \(aRb\)
- \((a,b)\notin R\) 记为 \(\neg aRb\)
-
关系 R 的重要集合,设 \(R\subseteq A\times B\)
- \(R\) 的定义域:\(Dom(R)=\{ x\mid(\exists y\in B)(x,y)\in R \}\)
- \(R\) 的值域:\(DRan(R)=\{ y\mid(\exists x\in B)(x,y)\in R \}\)
- \(R\) 的域:\(Fld(R)=Dom(R)\cup Ran(R)\)
- 关系的逆 \(R\subseteq A\times B\) 即 \(R^{-1}=\{(x,y)|(y,x)\in R\}\)
-
关系矩阵可以用来表示二元关系,\(m_{ij}\) 就表示存不存在 \((i,j)\)
-
复合关系:\(S \subseteq A\times B\),\(R\subseteq B\times C\) ,复合为 \(R\circ S=\{(x,y)|(\exists t\in B)((x,t)\in S\wedge(t,y)\in R)\}\)
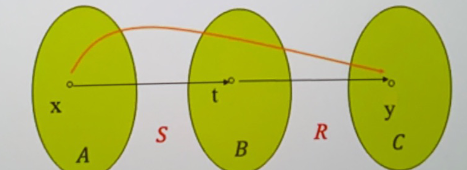
- 要注意的是,复合关系从右向左 \(xStRy\)
- \(R_1\circ(R_2\circ R_3)=(R_1\circ R_2)\circ R_3\)
- \((R\circ S)^{-1}=S^{-1}\circ R^{-1}\)

- 对应到矩阵上就是右边的关系矩阵乘左边的关系矩阵
-
关系的幂
- 对于 \(R\subseteq A\times A\),关系 \(R\) 的 \(n\) 次幂定义为 \(R^0=I_{A},R^{n+1}=R\circ R^n\)
- 通过关系矩阵计算较为方便
- \({R^m\circ R^n=R^{m+n}},({R}^m)^n={R}^{mn}\)
- 若 \(R^S=R^{S+T}\) 则 \(\forall k\geq S,R^k=R^{k+T}\) 以及 \(R^k=R^{k+nT}\)
- 由鸽笼原理还能得到 \(\mid A\mid=n\) 则 \(R^{s}=R^{t}\wedge0\leq s<t\leq2^{n^{2}}\)
-
函数(映射) \(f: A\to B如R=\{ (x,f(x))\mid x\in A \}\)
- 函数是一种特殊的二元关系,对集合 \(A\) 中的每一个元素,存在唯一一个 \(B\) 中的元素与之对应
- 函数具有决定性,同一输入总是对应同一输出
- \(A\) 为定义域,\(B\) 为伴域
- 存在 \(\mid B\mid^{\mid A\mid}\) 种函数
- 对于 \(f(a)=b\) 称 \(b\) 为 \(a\) 的像;\(a\) 为 \(b\) 的反像;\(b\) 的集合构成 \(f\) 的值域,是伴域的一个子集
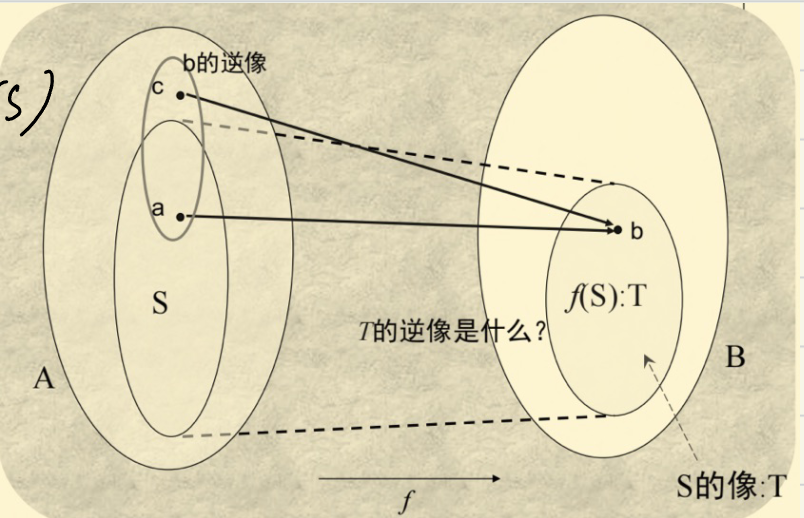
- \(X,Y\) 为 \(A\) 的子集
- 并集的像:\(f(X\cup Y)=f(X)\cup f(Y)\)
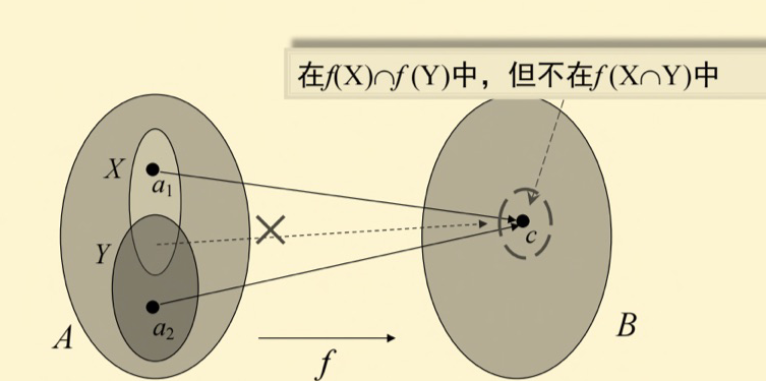
- 交集的像:\(f(X\cap Y)\subseteq f(X)\cap f(Y)\)
-
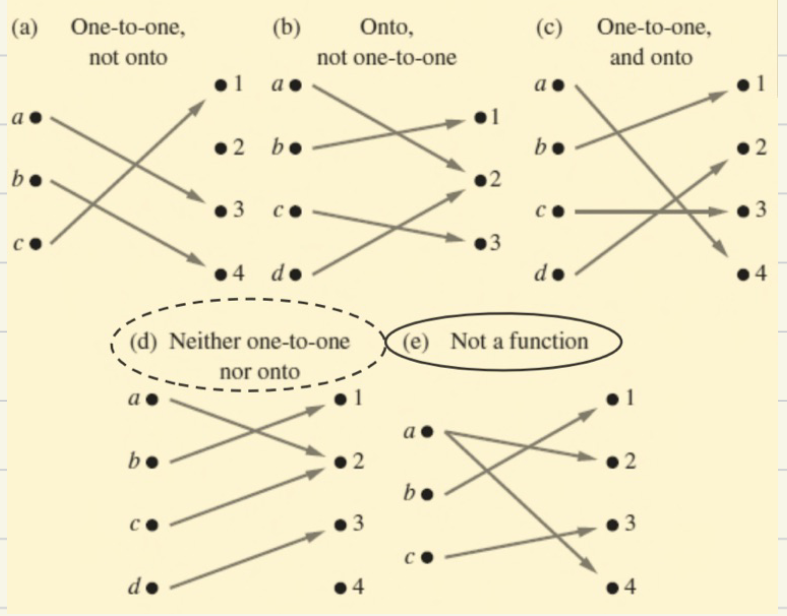
函数的分类
- 单射:一对一的,\(\forall x_{1}x_{2}\in A,如果f(x_{1})=f(x_{2})则x_{1}=x_{2}\)
- 满射:映上的,\(\forall y\in B\exists x\in A使得f(x)=y\)
- 双射:一一对应的,满射+单射(或者双向单射)
-
函数的比较与运算
- \(f=g\iff dom(f)=dom(g) \forall x(x\in dom(f)\to f(x)=g(x))\)
- \((f_1+f_{2})(x)=f_{1}(x)+f_{2}(x)\)
- \((f_{1}f_{2})(x)=f_{1}(x)f_{2}(x)\)
-
反函数:仅有双射函数才存在反函数 \(f(a)=b,f^{-1}(b)=a\)
-
复合函数 \((fog)(a)=f(g(a))\),\(g\) 的值域为 \(f\) 定义域的子集
- 满足结合率到那时不满足交换律
- \(fog\) 是满射:\(f\) 一定是满射,但是 \(g\) 不一定是
- \(fog\) 是单射,\(g\) 一定是单射,但是 \(f\) 不一定是
- 满射的复合是满射
- 单射的复合是单射
- 双射的复合是双射
-
序列:
- 一个序列是从 Z 的一个子集到集合 S 的一个函数,用 \(a_{n}\) 表示 n 的像,称为序列的项
- 主要限制了离散整数定义域(有点类似一个数组)
关系的性质¶
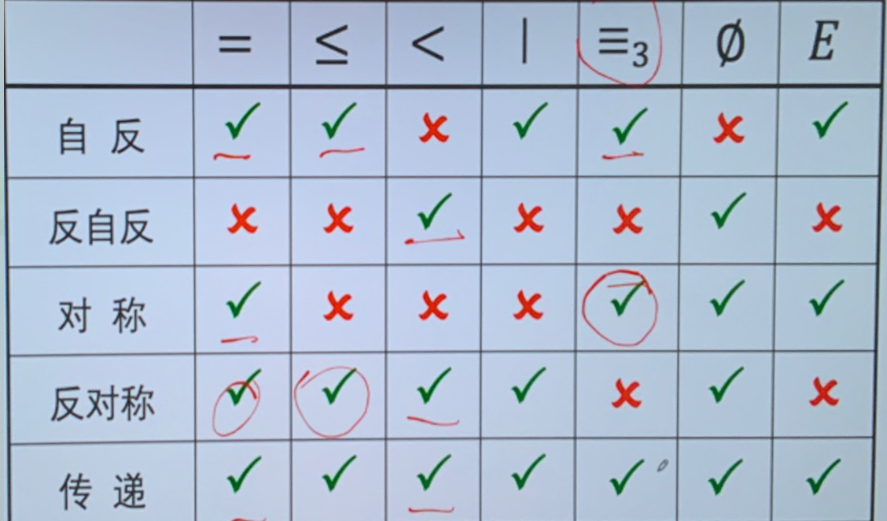
自反性
- 自反 \((\forall x\in A)(xRx)\)
- 反自反 \((\forall x\in A)(\neg xRx)\)
- 非自反:既不是自反也不是反自反
-  - 自反的充要条件 \(I_{A}\subseteq R\),反自反充要条件 \(R\cap I_{A}=\phi\)
- 关系矩阵对角线为全 1
-
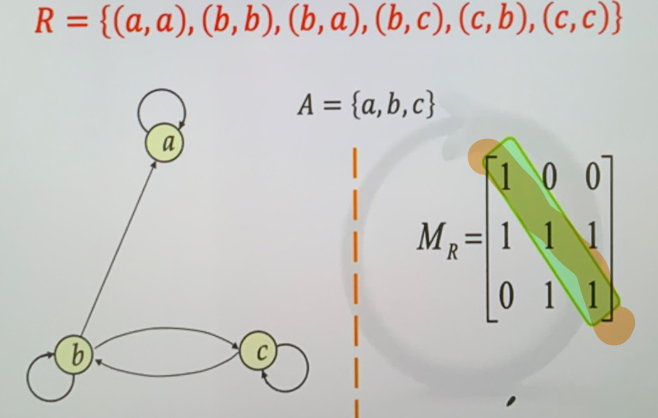
- 自反的充要条件 \(I_{A}\subseteq R\),反自反充要条件 \(R\cap I_{A}=\phi\)
- 关系矩阵对角线为全 1
- 
对称性
- 对称 \((\forall x,y\in A)(xRy\to yRx)\)
- 反对称 \((\forall x,y\in A)(xRyRx\rightarrow x=y)\) 即只允许 \((x,x)\) 这种对称
- 如果不存在 \(xRyRx\) 也是反对称的!
- 强反对称 \((\forall x,y\in A)(xRy\rightarrow\neg yRx)\),不允许一切对称
-  - \(\phi\) 属于上面全部三种对称
- 对称关系的充要条件 \(R=R^{-1}\)
- 反对称充要条件 \(R\cap R^{-}\subseteq I_{A}\)
- 对称的关系矩阵有 \(M_{R}=M_{R}^T\)
-
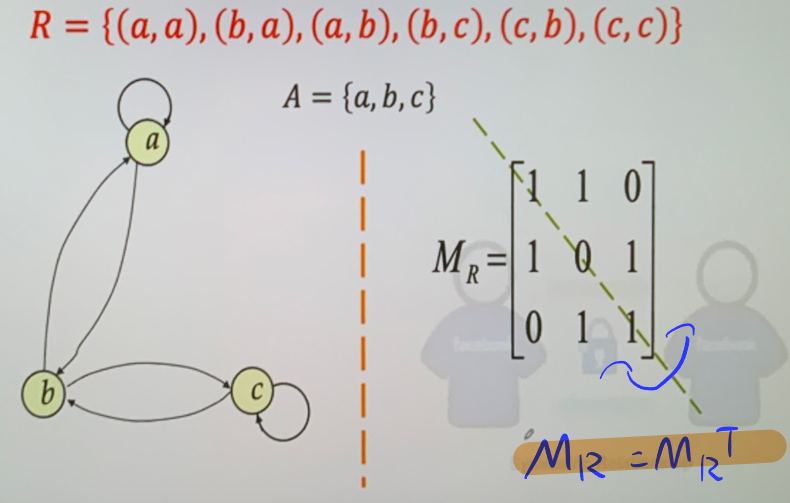
- \(\phi\) 属于上面全部三种对称
- 对称关系的充要条件 \(R=R^{-1}\)
- 反对称充要条件 \(R\cap R^{-}\subseteq I_{A}\)
- 对称的关系矩阵有 \(M_{R}=M_{R}^T\)
- 
传递性
- 传递是指 \(\left(\forall x,y,z\in A\right)\left(xRyRz\rightarrow xRz\right)\)
-  - 传递的充要条件 \(R^n\subseteq R\)
- 关系矩阵有 \(M_{R}\times M_{R}\leq M_{R}\)
-
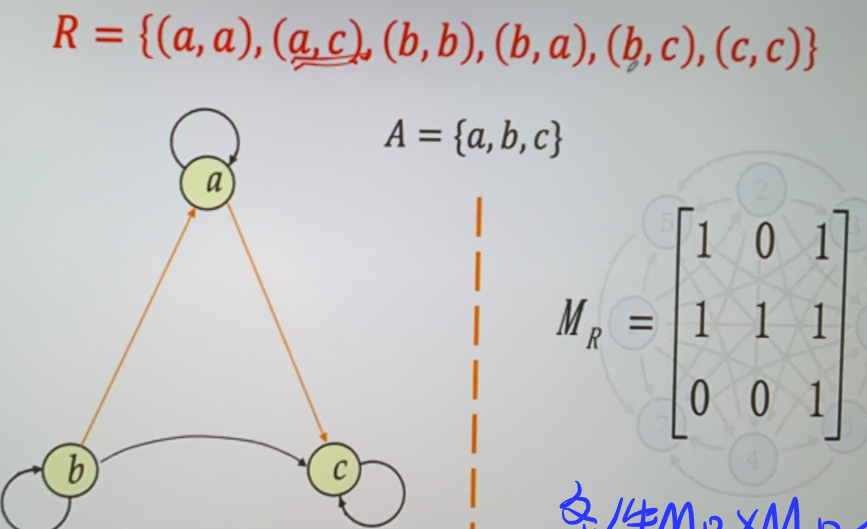
- 传递的充要条件 \(R^n\subseteq R\)
- 关系矩阵有 \(M_{R}\times M_{R}\leq M_{R}\)
- 
等价关系¶
- 同时满足自反、对称、传递的为等价关系,记 \(x\sim y\)
- 等价类:
- 对于 \(R\) 为 \(A\) 上的等价关系,\(a\) 关于 \(R\) 的等价类为 \([a]_{R}=\{ b\in A\mid aRb \}\),称 \(a\) 为这个等价类的代表元素(等价类中每个元素都可以作为代表元素)
- 比如对于模 n 同余关系,有 \([x]=\{ y\mid x\equiv y(mod\ n) \}=\{ x+kn\mid k\in Z \}\)
 \(\(\begin{aligned}&(1)\:(\forall x\in A)(x\in[x])\\&(2)\:(\forall x,\:y\in A)(x\sim y\mapsto[x]=[y])\\&(3)\:(\forall x,\:y\in A)(\neg(x\sim y)\hookrightarrow[x]\cap[y]=\emptyset)\\&(4)\:(\forall x,\:y\in A)([x]=[y]\:\text{与 }[x]\cap[y]=\emptyset\text{恰具其一}\\&(5)\:\cup\{[x]\mid x\in A\}=A\end{aligned}\)\)
\(\(\begin{aligned}&(1)\:(\forall x\in A)(x\in[x])\\&(2)\:(\forall x,\:y\in A)(x\sim y\mapsto[x]=[y])\\&(3)\:(\forall x,\:y\in A)(\neg(x\sim y)\hookrightarrow[x]\cap[y]=\emptyset)\\&(4)\:(\forall x,\:y\in A)([x]=[y]\:\text{与 }[x]\cap[y]=\emptyset\text{恰具其一}\\&(5)\:\cup\{[x]\mid x\in A\}=A\end{aligned}\)\)
-
商集:以关系 \(R\) 的所有等价类作为元素的集合称为 A 关于 \(R\) 的商集 \(A/R=\{ [x]_{R}\mid x\in A \}\)

- 非空集合的每一商集对应 \(A\) 的唯一划分(因此有几种等价关系就有几种划分),划分中的元素称为划分块(\(\cap\) 为 \(\phi\);\(\cup\) 为 \(A\))
-
闭包:\(R\) 的 \(P\) 性质的闭包,存在 \(S\subseteq A\times A\)
- \(R\subseteq S\)
- \(S\) 具有性质 \(P\)
- \(\forall T(R\subseteq T\wedge T有性质P\to S \subseteq T)\)(表示闭包是最小的,符合性质的关系)
- \(S\) 就是 \(R\) 的 \(P\) 闭包(存在且唯一)
- 构造方式
- 自反闭包:\(r(R)=R\cup I_{A}\)
- 对称闭包:\(s(R)=R\cup R^{-1}\)
- 传递闭包:\(t(R)=\cup \{ R^n\mid 1\leq i\leq\mid A\mid \}\)
- 对应到矩阵运算
- \(M_{r(R)}=M_{R}\vee M_{I_{A}}=M_{R}\vee I_{A}\)
- \(M_{S(R)}=M_{R}\vee M_{R}^{T}\)
- \(M_{t(R)}=M_{R}\lor M_{R}^{[2]}\lor\cdots\lor M_{R}^{[n]}\)
- 闭包运算
- 传递闭包 Warshall 算法
- 迭代的使用 \(W_{i-1}\) 计算 \(W_{i}\)
- \(W_{0}=M_{R}\)
- \(W_k[i,j]=1\iff W_{k-1}[i,j]或 W_{k-1}[i,k]=1\ and\ W_{k-1}[k,j]=1\)
- \(W_{n}\) 就是结果
- 使用 \(R^{(i)}\) 表示使用前 \(i\) 个点作为中间结点
- \(R_{ij}^{(k)}=R_{ij}^{(k-1)}\vee(R_{ik}^{(k-1)}\wedge R_{kj}^{(k-1)})\)
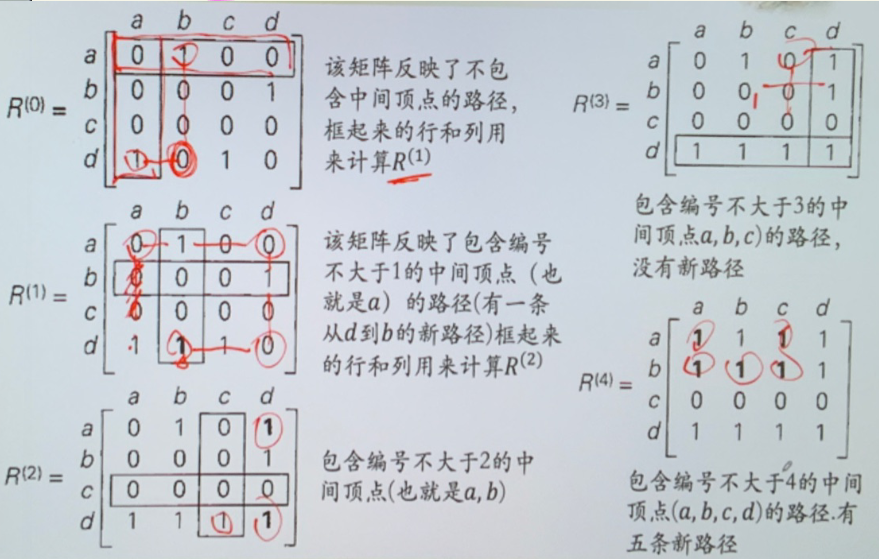
偏序集¶
- 偏序:自反、反对称、传递关系称为偏序关系,记作 \(a\preceq b\)(这种偏序也称为自反偏序、非严格偏序)
- 严格偏序、反自反偏序:将自反更换为反自反
- 偏序集:集合 \(A\) 及其上的偏序关系 \(\preceq\) 一道称为偏序集,记作 \((A,\preceq)\)
- 偏序集是他的覆盖关系的传递自反闭包
- 可比:对于 \(A\) 中的元素,有 \(x\preceq y\) 或者 \(y\preceq x\) 则称 \(x\) 与 \(y\) 可比
- 不可比的情况:\((\{ 1,2,4,6,8 \},\mid)\) 中的 \(4,6\) 就是不可比的
- 全序:若 \(A\) 中任何两个元素都是可比,称 \(R\) 为 \(A\) 上的全序关系
- 覆盖:\(y\) 覆盖 \(x\) 当仅当 \(x\prec y\) 并且不存在 \(z\in A\) 使得 \(x\prec z\prec y\)
- 良序:\(A\) 的任意非空子集都有最小元素,则称为良序
- 良序必为全序
- 良序上支持数学归纳法
- 全序不一定是良序(如 \(A\) 为无穷集合 \((R,\leq)\))
- 良基:存在极小元
哈斯图¶
-
利用特定性质简化图的表示
- 利用自反性质省略圈
- 利用反对称省略箭头
- 利用传递性省略部分连线(覆盖)
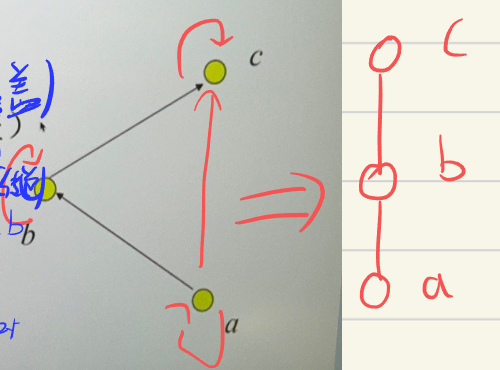
-
特殊元素 (\(x\),\((A,\preceq)\))
- 极大元素:没有更大元素了 \(\forall y\in A\) 若 \(x\preceq y\),那么 \(x=y\)
- 极小元素:没有更小元素了 \(\forall y\in A\) 若 \(y\preceq x\),那么 \(x=y\)
- 最大元素:比所有元素都大 \(\forall y\in A\) 有 \(y\preceq x\)
- 最大最小是不一定存在的,但是由穷集合一定有极大极小元
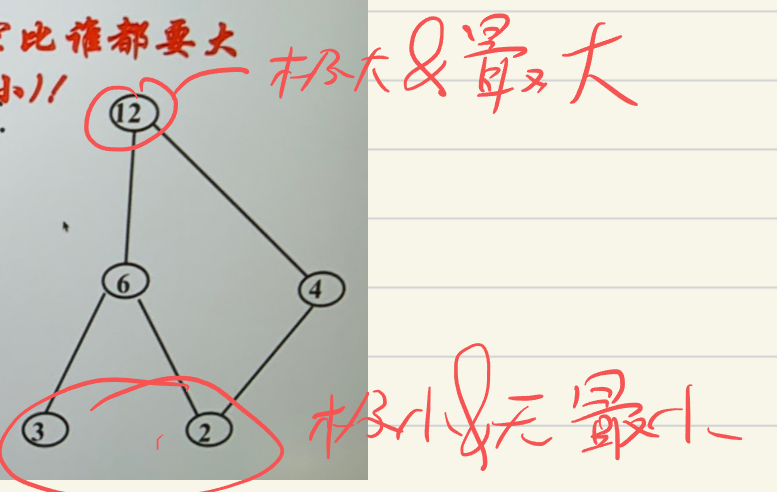
- 最小元素:比所有元素都小 \(\forall y\in A\) 有 \(x\preceq y\)
- 上界:对于偏序集的子集 \(B\) 若存在 \(y\in A\) 对 \(\forall x\in B\) 有 \(x\preceq y\) 则 \(y\) 是 \(B\) 的上界
- 最小上界(上确界):如果上界构成的偏序集有最小元,则该最小元为 \(B\) 的最小上界(上确界)
- 不一定存在,若存在则唯一
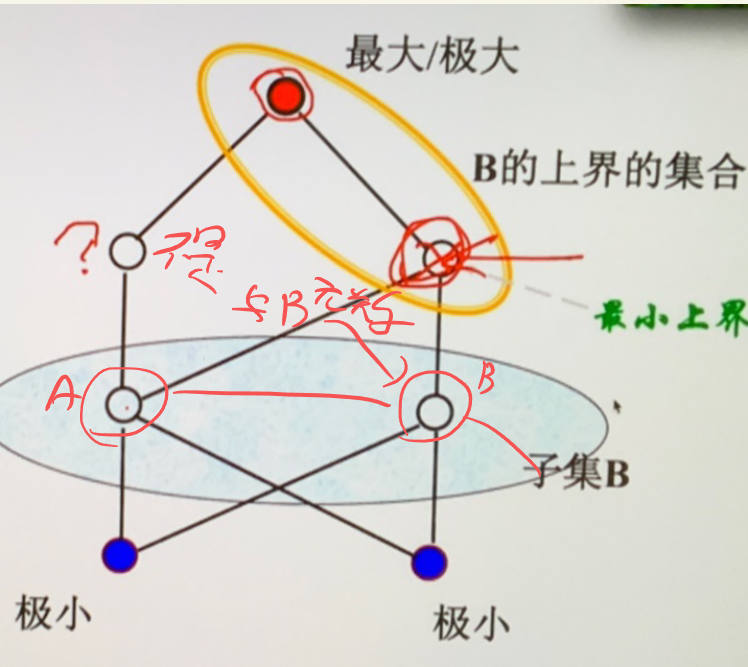
- 极大元素:没有更大元素了 \(\forall y\in A\) 若 \(x\preceq y\),那么 \(x=y\)
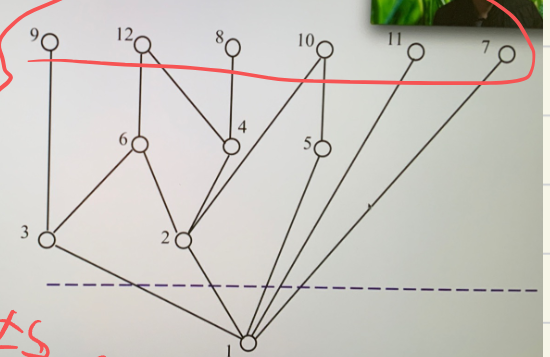
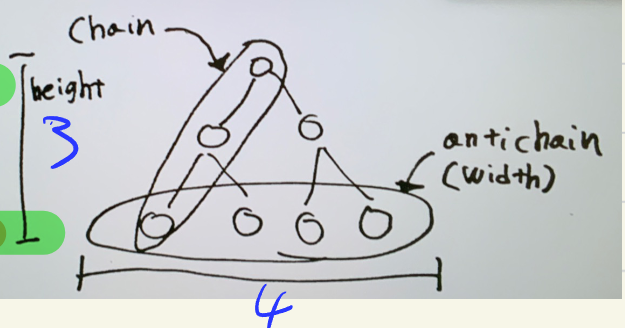
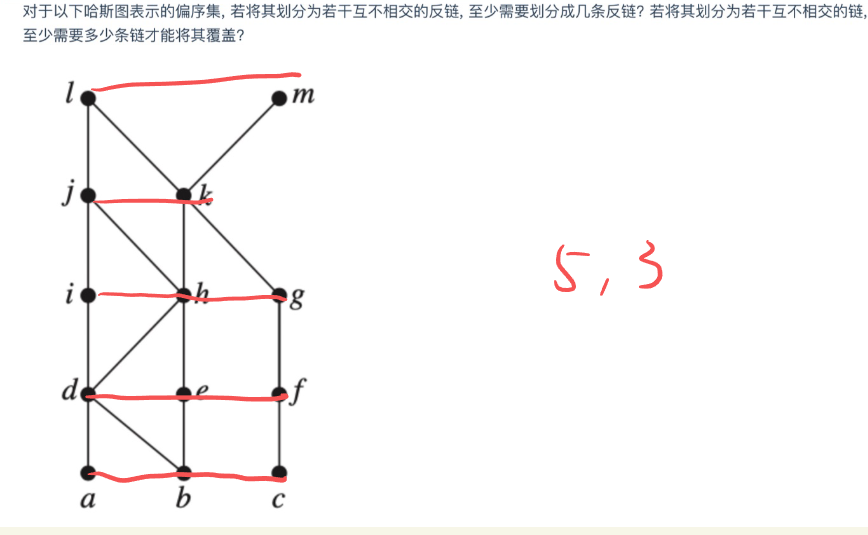
链与反链¶
- 链:\(C\) 为偏序集的一个子集,如果 \(C\) 中任何两个元素均可比,则 \(C\) 构成一个链
- 如果不是任何其他链的子链,则称为极大化链(即 \(C\) 之外不存在一个元素与 \(C\) 中所有元素都可比)
- 反链:\(C\) 中任何两个元素均不可比,那么构成一个反链
- 同样如果 \(C\) 不是其他反链的子链,那么就是极大化的(\(C\) 外没有一个元素与 \(C\) 中每一个元素都不可比)
- 高度:有限偏序集中最长的链的节点个数
-
宽度:最大反链的元素个数
-
偏序集的划分
- 若高度为 \(t\) 则可以划分为 \(t\) 个反链
- 要么一条长度至少为 \(t\) 的链,一条长度至少为 \(\frac{\mid A\mid}{t}\) 的反链
- 链覆盖:一组互不相交的链,包含了偏序集中的所有元素
- 宽度为 \(w\) 的偏序集可以划分成 \(w\) 个链,即覆盖的最小链数等于最长反链的长度
格¶
-
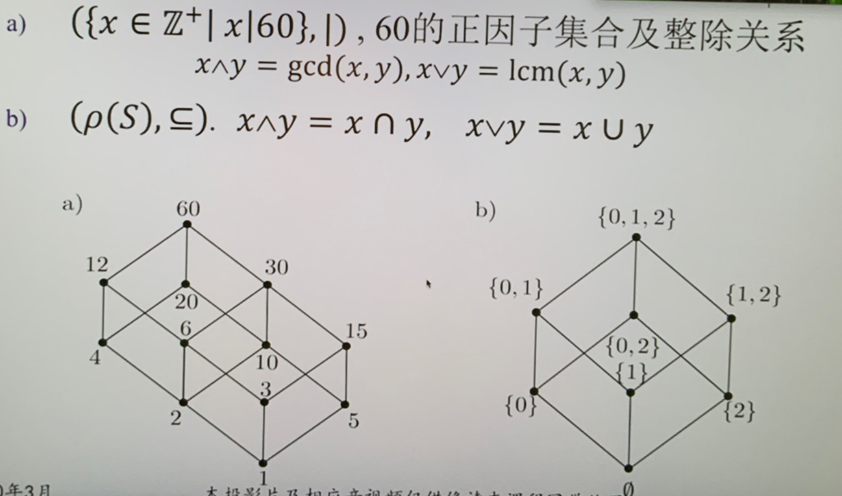
偏序格:\((L,\preceq)\) 为偏序集
- 对于 \(\forall x,y\in L\) 均存在最小上界 \(lub\{ x,y \}\) 记为 \(x\vee y\)
- 对于 \(\forall x,y\in L\) 均存在最大下界 \(glb\{ x,y \}\) 记为 \(x\wedge y\)
- 格上支持两种二元运算 \(\vee\wedge\)
- 支持结合律,交换律,幂等律,吸收律 (\(a\wedge(a\vee b)=a,\:a\vee(a\wedge b){=}a\))
- 则称 \(L\) 关于 \(\preceq\) 构成一个格

-
性质
- \(a\leq c,b\leq c\Rightarrow a\lor b\leq c\)
- \(c\leq a,c\leq b\Rightarrow c\leq a\wedge b\)
- \(a\leq c,b\leq d\Rightarrow a\lor b\leq c\lor d,a\land b\leq c\land d\)
- \(a\leq b\iff a\wedge b=a\iff a\vee b=b\)
- 对偶命题
- 如果命题对一切格为真,那么对偶命题也对一切格为真
- \(P*\) 对偶命题是将 \(P\) 中的 \(\leq\geq\vee\wedge\) 分别替换为 \(\geq\leq\wedge\vee\)
代数格¶
- 代数格是满足结合律、交换律、吸收率(针对 \(\vee\wedge\) 操作)
- 代数格与偏序格是等价的(代数格是从满足运算性质的角度出发定义;偏序集则是从偏序关系,上下界的角度出发定义的)
-
子格
- 对于非空集合 \(S\subseteq L\),若 \(S\) 关于 \(\vee \wedge\) 仍然构成格,则称 \((S,\vee,\wedge)\) 构成 \(L\) 的子格(即任意两点的上确界和下确界均在子集中)

-
假设有两个格 \((L_1,\wedge_{1},\vee_{1})\) 和 \((L_{2},\wedge_{2},\vee_{2})\)
- 格同态
- 存在 \(f: L_{1}\to L_{2}\) 使得对 \(\forall a,b\in L_{1}\) 有 \(\begin{aligned}f\left(a\wedge_{1}b\right)=f\left(a\right)\wedge_{2}f\left(b\right)\\f\left(a\vee_{1}b\right)=f\left(a\right)\vee_{2}f\left(b\right)\end{aligned}\)
- 称 \(f\) 为从 \(L_{1}到\) \(L_{2}\) 的同态映射,即格同态
- 格同态不改变偏序关系 \(\forall x,y\in L_{1}(x\leq_{1}y\to f(x)\leq_{2}f(y))\)
- 逆命题不一定成立
-
格同构
- 若同态映射 \(f\) 为一个双射,则称为格同构
- \(格同构 \iff \forall x,y\in L_{1}\left(x\leq_{1}y\Leftrightarrow f\left(x\right)\leq_{2}f\left(y\right)\right)\)

-
典型的格
- 链、钻石格(M3)、五角格(N5)
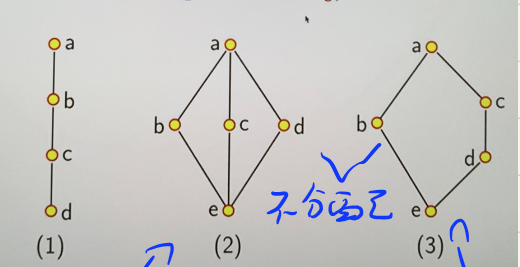
- 钻石格和五角格均不具有分配性 (如 bcd)
-
分配格,对于 \(\forall a,b,c\in L\) 有
- \(\begin{aligned}a\wedge(b\vee c)&=(a\wedge b)\vee(a\wedge c)\\a\vee(b\wedge c)&=(a\vee b)\wedge(a\vee c)\end{aligned}\)
- 要注意对于所有的格都有 \(\begin{aligned}a\wedge(b\vee c)&\leq(a\wedge b)\vee(a\wedge c)\\a\vee(b\wedge c)&\geq(a\vee b)\wedge(a\vee c)\end{aligned}\)
- 分配格的判定定理
- 当仅当不含有与 \(M_3,N_5\) 同构的子格(注意区分子图和子格)
- 当仅当 \(\left(a\wedge b=a\wedge c\right)\wedge\left(a\vee b=a\vee c\right)\rightarrow b=c\)
- 有界格
- 若存在 \(b\in L\) 使得 \(\forall x\in L\) 有 \(b\leq x\) 则 \(b\) 为 \(L\) 的全下界,也记为 \(0\)
- 相反地 \(t\in L\) 使得 \(\forall x \in L\) 有 \(x\leq t\) 则称 \(t\) 为全上界, 也记为 \(1\)
- 若存在格中存在全上界或全下界则一定唯一,有界限格也可以记为 \((L,\wedge,\vee,0,1)\),有介格的对偶命题还需要对 \(0,1\) 进行调换
- 对于 \(0,1\) 有界格也满足同一律及支配律
- 有限格都是有界格,求法:\(\frac{a_1\wedge a_2\wedge\cdots\wedge a_n\text{是L的全下界}}{ a _ 1 \vee a _ 2 \vee \cdots \vee a _ n\text{是}L\text{的全上界}}\)
- 补元(有界格才有补元)
- \(a\in L\) 的补元 \(b\) 为 \(a\wedge b=0,a\vee b=1\) (0,1 就是一组补元)
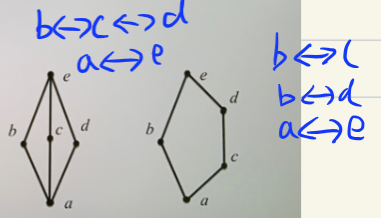
- 有界分配格的补元存在且唯一
- 有补格
- 对于有界格,如果所有元素均存在补元,则称其为有补格
- \(M_{3}N_{5}\) 就都是有补格
布尔代数¶
- 布尔代数是一种分配有补格,具有封闭性质的代数系统
- 三种运算 \(\sim\),\(\vee(+)\),\(\wedge(·)\)
- 同态
- \(\begin{aligned}f(x\wedge y)&=f(x)\cap f(y),\\f(x\vee y)&=f(x)\cup f(y),\\f(x^{\prime})&=\sim f(x),\\f(0)&=\theta,f(1)=I\end{aligned}\)
- 若 \(f\) 为一个满射,则称为满同态
- 同构
- 如果同态 \(f\) 是一个双射,那么称为同构,记 \(B\cong P\)
- \(B=(\{0,1\},+,\cdot,^{-},0,1)\) 为布尔代数
- \(B^{n}=\{(x_{1},\ldots,x_{n})|x_{i}\in{B},i=1,\ldots,n\}\)构成布尔代数
- 幂集也构成了一个布尔代数
- 原子:\(a\neq 0\) 对 \(\forall x\in L\) 有 \(0<x\leq a\to x=a\)
- 对于原子 \(a\neq b\) 有 \(a\wedge b=0\)
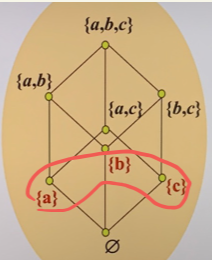
- 有限布尔代数表现代理
- 对于任意有限布尔代数 \(B\) 同构与 \(B\) 中所有原子构成的集合 \(A\) 的幂集 \(\rho(A)\)
- \((B,\wedge,\vee,-,\mathbf{0},\mathbf{1})\cong(P(A),\cap,\cup,\tilde{\mathbf{0}},A)\)
- 推论:任何有限布尔代数的基数均为 \(2^n\),所有等势的布尔代数均同构
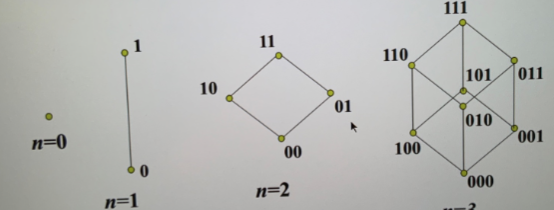
- 布尔函数
- \(B^n\to B\) 的函数(即 n 格输入一个输出的逻辑电路)
- 举止范围为 \(B\) 的变元称为布尔变元
- 布尔和:\((f+g)(x_{1}\dots x_{n})=f(x_{1}\dots x_{n})+g(x_{1}\dots x_{n})\)
- 布尔积:\((\mathrm{f·g})(x_1,\ldots,x_n)=\mathrm{f}(x_1,\ldots,x_n)\cdotp\mathrm{g}(x_1,\ldots,x_n)\)
- 补函数:\(\overline{f}(x_1,\ldots,x_n)=\overline{f(x_1,\ldots,x_n)}\)
- n 元布尔函数全体也构成了一个布尔代数
- 卡诺图化简
- 相邻元素只有一项不同

代数系统¶
- 函数 \(A^n\to B\) 称为从 \(A\) 到 \(B\) 的的 \(n\) 元运算
- 若 \(B\subseteq A\) 则称则称运算在集合 \(A\) 上封闭
- 在有限集合上 \(m\) 元运算的个数是确定
-
运算表
- 用于定义有限集合(元素较少)上的一元或二元运算
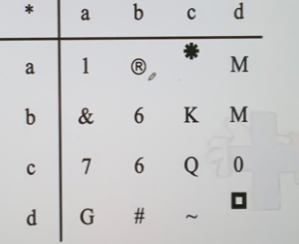
-
代数系统:
- 给定一个非空集合,以及 1 个或若干个运算,并且运算对上述集合封闭
- 如 \(<Z,+>\)
- 结合性:保持次序不变的前提下可以按照任何的顺序进行计算
- 分配性:运算 \(·\) 对 \(*\) 满足分配性即 \(\forall x,y,z\in A,x\circ(y*z)=(x\circ y)*(x\circ z)\)
-
交换性:可以重新排列先后次序
-
单位元:\(\forall x\in S,e\circ x=x\circ e=x\) 则称 \(e\) 为单位元,简记 \(1\)
- 左单位元 \(e_L\circ x=x\)
- 右单位元 \(x\circ e_{R}=x\)
- 左右单位元不一定存在,如果存在则一定唯一
- 如果一个代数系统同时有做单位元和右单位元,那么相等且唯一(即为单位元)
- 子代数:子集、运算封闭,具有相同的代数常数(单位元,零元)
- 逆元
- 只有存在单位元的代数系统才有逆元
- 左逆元 \(a^{-1}_{L}\circ a=1\)
- 右逆元 \(a\circ a^{-1}_{R}=1\)
- 逆元 \(a^{-1}\circ a=a\circ a^{-1}=1\),两个元素互为逆元
- 当代数系统具有结合性时:
- 既有左逆又有右逆,则二者必相等且唯一
- 如果每个元素都有左逆,那么左逆即右逆且逆元唯一
- 零元
- \(\forall x\in S,t\circ x=x\circ t=t\)
-

-
同构映射:代数系统 \(<S_{1},\circ>\) 和 \(<S_{2},*>\) 同构 \(S_{1}\cong S_{2}\) 当仅当 \(\forall x,y\in S_1,f({x}\circ y)=f(x)*f(y)\),其中双射函数 \(f\) 称为同构映射
- 同构关系是一种等价关系
- 只有两个代系统集合等大才可能同构
- 同态映射:\(S_{1}\sim S_{2}\)
- 不要求双射,如果是满射称为满同态
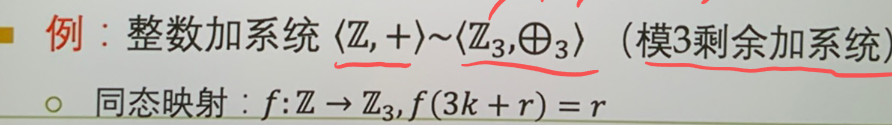

群论¶
- 半群 (Semigroup):代数系统(运算封闭)+结合性
- 幺半群(monoid):半群+单位元
- 群:幺半群+逆元
- 即:代数系统+结合性+单位元+逆元(群论公理)

- 根据集合是否有穷还划分为有限集和无限集
- 如果还满足交换律则称为交换群(abelian 群)
- 群的性质
- 群是满足消去律的(由于有逆元)\(ac=ab\iff c=b\)
- \(ax=b\) 及 \(ya=b\) 均有唯一解
-
群的阶数
- 三阶群唯一
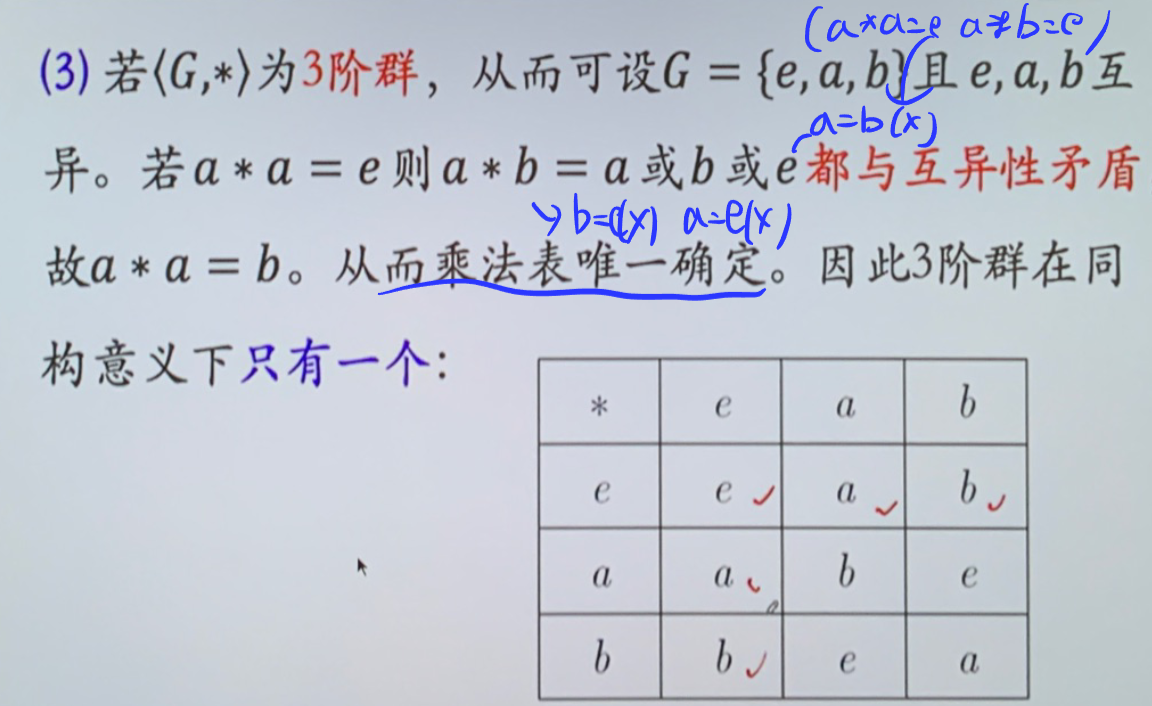
- 四阶群只有两种 \(Klein\) 四元群和 \(<Z_4,\oplus_4>\) ,并且均为交换群
- 1-5 阶均为阿贝尔群
- 三阶群唯一
-
子群
- 子集
- 运算封闭
- 单位元封闭(还在集合中)
- 逆元封闭
- 记为 \(<H,*>\leq<G,*>\)
- 平凡子群:两个特殊的子群,\(\langle\{e\},*\rangle,\langle G,*\rangle\) 单位元和自身
-
子群的判定

- 对于有限子群(非空有穷子集),进一步简化为 \(\forall a,b\in H,ab\in H\)
- 一定存在 \(a^{-1}\),因为根据鸽笼原理一定有 \(a^i=a^j\)
-
元素的阶
- \(a^n\): \(n<0\) 时 \(a^n=(a^{-n})^{-1}\)
- 若 \(\exists n\in N^+,a^n=e\) 则称阶有穷为 \(\mid a\mid=min\{ n>0\mid a^n=e \}\),否则称阶无穷 \(\mid a\mid=\infty\)
- \(\begin{aligned}&(1)\:\text{对}k\in\mathbb{Z}^+,\:a^k=e\Leftrightarrow\mid a\mid\mid k\\&(2)\:|a|=|a^{-1}|\\&(3)\:|ab|=|ba|\\&(4)\:|b^{-1}ab|=|a|\end{aligned}\)
- 阶大于 2 的元素一定有偶数个
- 如果只有 1,2 阶元,则是阿贝尔群
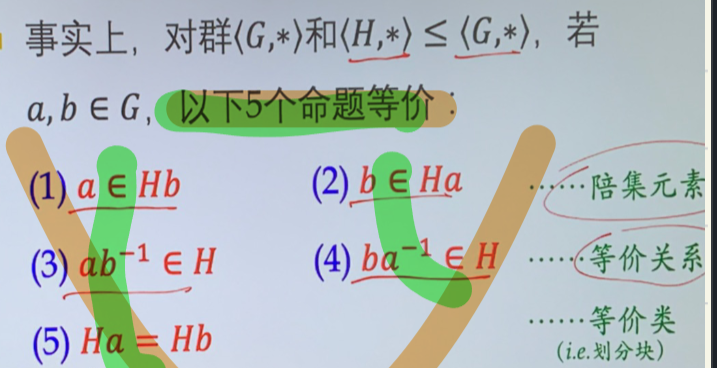
陪集¶
- 陪集:子群将群分解为培集
- 对于 \(<H,*>\leq<G,*>,a\in G\),令 \(H{a}=\{ha|h\in H\},\:aH=\{ah|h\in H\}\) 称为右/左陪集,H 在 G 中陪集的个数,称为 \(H\) 在 \(G\) 中的指数 \([G:H]\)

- 右陪集关系(等价关系):\((\forall a,b\in G)aRb\Leftrightarrow ab^{-1}\in H\),\(R\) 是 \(G\) 上的等价关系,\([a]_{R}=Ha\)
- 相似的左陪集关系:\(\left(\forall a,b\in G\right)a\boldsymbol{R}^{\prime}b\Leftrightarrow b^{-1}a\in H\)
- 陪集与划分
- \(\begin{aligned}&(1)He=H\\\\&(2)(\forall a\in G)(a\in Ha)\text{ 从而 U}\{Ha|a\in G\}=G\\\\&(3)(\forall a,b\in G)(Ha=Hb\lor Ha\cap Hb=\emptyset)\\\\&(4)\left\{Ha|a\in G\right\}\text{为}G\text{之划分}\end{aligned}\)
- 陪集的势
- \(\text{设}\langle H,*\rangle\leq\langle G,*\rangle,\quad a\in G,\quad\text{则}H\approx Ha\approx aH\)
- Lagrange 定理:若 \(<G,*>\) 为有限群:\(|G|=|H|\cdot[G:H]\)
- 子群的阶数是原先群的阶数的因子
- 元素的阶数也是原先群的阶数的因子(元素的阶数决定生成子群 \(<a>\) 的元素数目)
- 若群的阶数为质数,则 \((\exists a\in G)(\langle a\rangle=G)\)

循环群¶
- 若 \((\exists a\in G)(G=<a>)\) 则 \(<G,*>\) 为循环群
- 其中 \(<a>=\{ a^n\mid n\in Z \}\),则 \(a\) 称为 \(G\) 的生成元
- 充要条件为 \(\exists a\in G,\mid a\mid=\mid G\mid\)
- 有限循环群:若生成元的阶为 \(n\) 则为 \(n\) 阶有限循环群 \(G=\{ a^0,a^1\dots a^{n-1}\}\)

- 若 \(\mid a\mid=n\) 则对不大于 \(n\) 的正整数 \(r\) 也有,\(G=<a^r>\iff gcd(n,r)=1\),也就是说 \(n\) 阶循环群的生成元的数目刚好等于不大于 \(n\) 并且与 \(n\) 互质的正整数数目 (欧拉函数 \(\phi(n)\))
- 对于有限群均有 \(<G,*>\cong <Z_{n},\oplus_{n}>\)
-
无限循环群:\(a\) 为无限阶元 \(G=a^0,a^{\pm 1}\dots\)
- 若 \(a\) 是无限循环群的生成元,则 \(a^{-1}\) 也是,并且无限循环群有且仅有这两个生成元
- 对于所有无限群均有 \(<G,*>\cong <Z,+>\)

-
循环群的子群
- 循环群的子群为循环群
- 无限循环群的子群除 \(\{ e \}\) 之外都是无限循环群
- 对 \(n\) 的每一个因子 \(d\),循环群中都恰有一个 \(d\) 阶子群
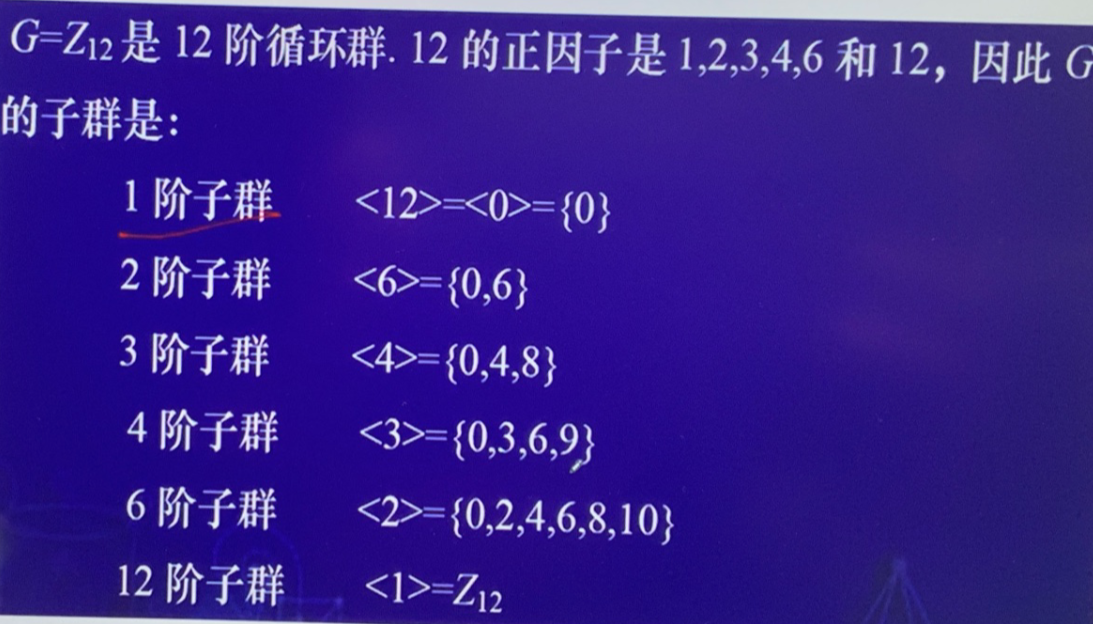
-
\(\text{设}f\text{为从群}\langle G,*\rangle\text{到群}\langle H,0\rangle\text{的同态}\)
- \(f(e_G)=e_H\) 同构下可以保证唯一
- \(f\left(a^{-1}\right)=\left(f\left(a\right)\right)^{-1},\forall a\in G\)
- 群同构的证明过程:
- 构建 \(\forall x,y\in G_{1},\:f(x\circ y)=f(x)*f(y)\)
- 证明双射
- 循环群都是阿贝尔群
图论¶
图的定义和表示¶
- 图 \(G\) 是一个三元组 \(G=(V,E,\varphi)\)
- 分别表示顶点集合、边集 (\(V\bigcap E=\phi\))、边对应的端点集
- 简单图:\(\forall e\in E,|\varphi(e)|=2\) 并且 \(e_{1}\neq e_{2}\to \varphi(e_{1})\neq \varphi(e_{2})\) 即不含自环和多重边
- 伪图正相反
- 有向图的底图:把每一条有向边替换为无向边(简单有向图的底图不一定是简单无向图)
- 使用 \(d_{G}^+\) 和 \(d_{G}^-\) 表示入度和出度,注意自环会共享两个边
-
平凡图:只有一个点没有边的图
-
弱连通有向图:底图为连通无向图
-
强连通有向图:对任意 ab 有 \(a\to b,b\to a\)
-
握手定理:因为 \(\sum d=2m\),因此无向图中奇数点的个数一定是偶数个
- 子图
- \(G=<V,E>,G'=<V',E'>\) 若 \(V'\subseteq V,E'\subseteq E\) 则称 \(G'\) 为 \(G\) 的子图(若边/点不完全相同,则为真子图)
- 导出子图:保留了原图中选定顶点之间的所有连接关系(即子图中两点有边当今当原图中两点之间有边)
特殊简单图¶
- 完全图 \(K_n\):简单图中任意两点都相连,即每个顶点为 \(n-1\) 度
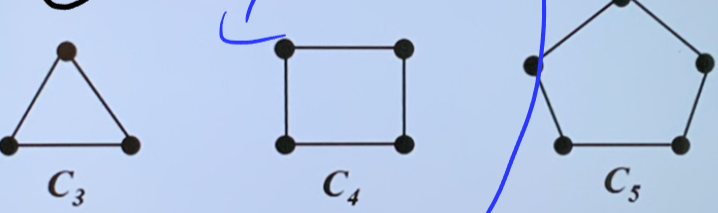
- 圈图 \(C_{n}\)
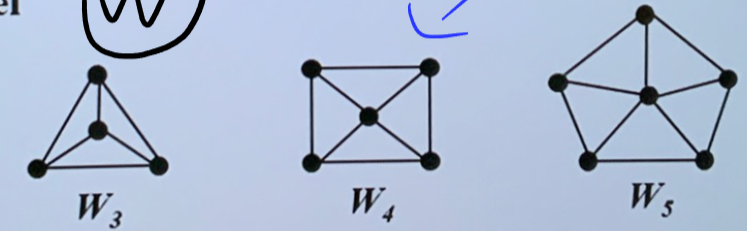
- 轮图 \(W_{n}\)
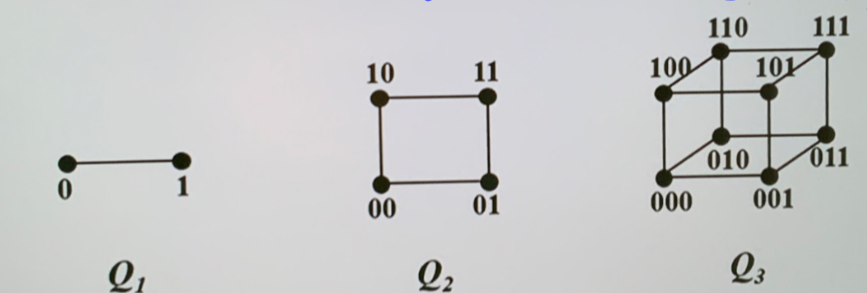
- 立方体图 \(Q_{n}\)
- 正则图:各点度相同
图的表示与同构¶
- 邻接矩阵、邻接表
-
关联矩阵:是点与边的关联关系(邻接矩阵是点与点)
- 设有 n 个点 m 条边,就有一个 \(n\times m\) 阶矩阵,\(m_{ij}=1\iff e_{i}关联v_{i}\)
- 适用于无向图,不能表示边的方向
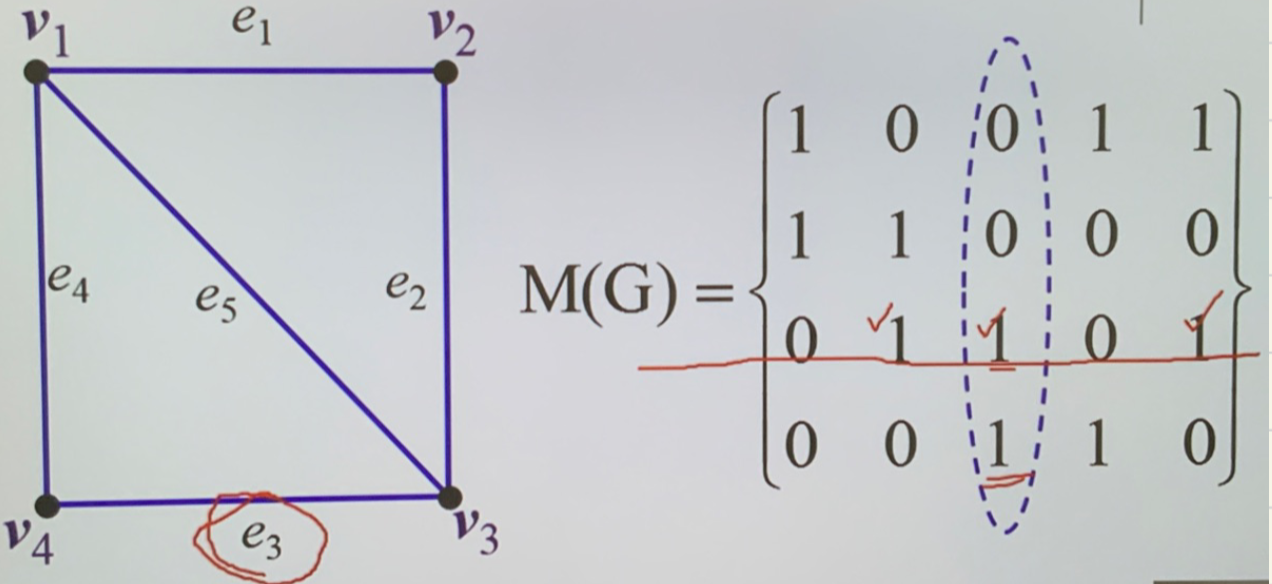
-
邻接矩阵的运算
- 行中的 1 的个数表示出度;列中的 1 的个数表示入度
- 逆图的邻接矩阵就是原图的邻接矩阵的转置
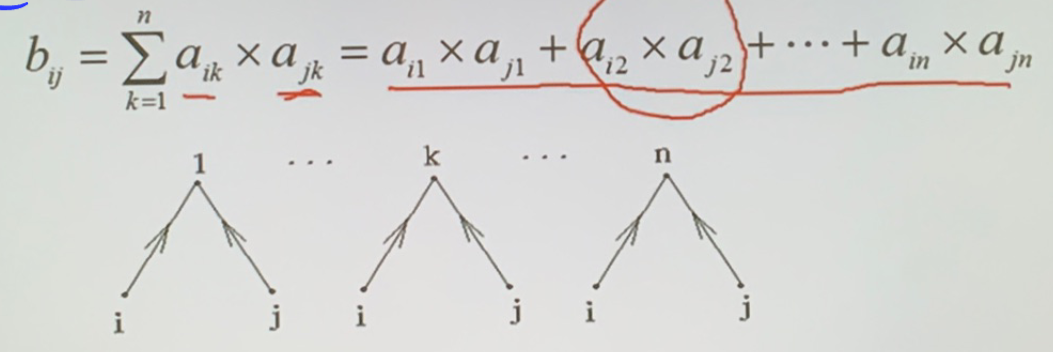
- \(A\times A^T\),\(b_{ij}\) 表示顶点 \(i\) 和顶点 \(j\) 均有边指向的那些顶点的个数
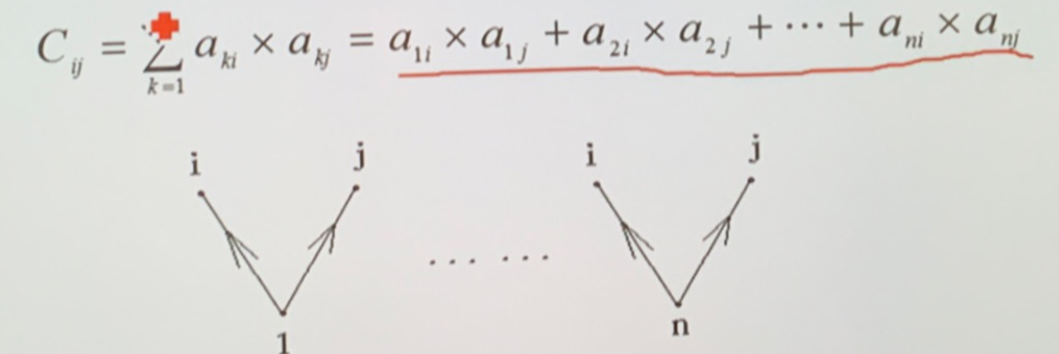
- \(A^T\times A\),\(b_{ij}\) 表示同时有边指向顶点 \(i\) 和 \(j\) 的顶点个数
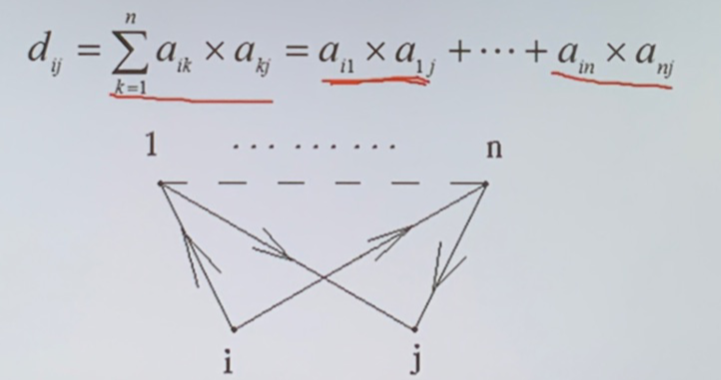
- \(A\times A\),\(b_{ij}\) 表示 \(i\) 和 \(j\) 之间具有的长度为 \(2\) 的通路的数目
-
应用:
-
图的同构
- \(\mathbf{G}_{1}=(\mathbf{V}_{1},\mathbf{E}_{1},\mathbf{\varphi}_{1})\text{和}\mathbf{G}_{2}=(\mathbf{V}_{2},\mathbf{E}_{2},\mathbf{\varphi}_{2})\)
- 若存在双射 \(f{:}V_{1}{\to}V_{2},g{:}E_{1}{\to}E_{2}\) 使得 \(\forall e{\in}{E}_1,\varphi_1(e){=}\{u,v\}\iff g(e){\in}\mathbb{E}_2,\varphi_2(g(e)){=}\{f(u),f(v)\}\)
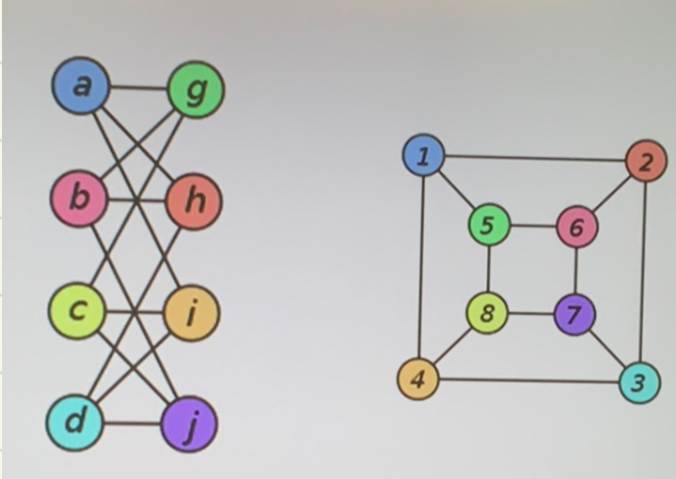
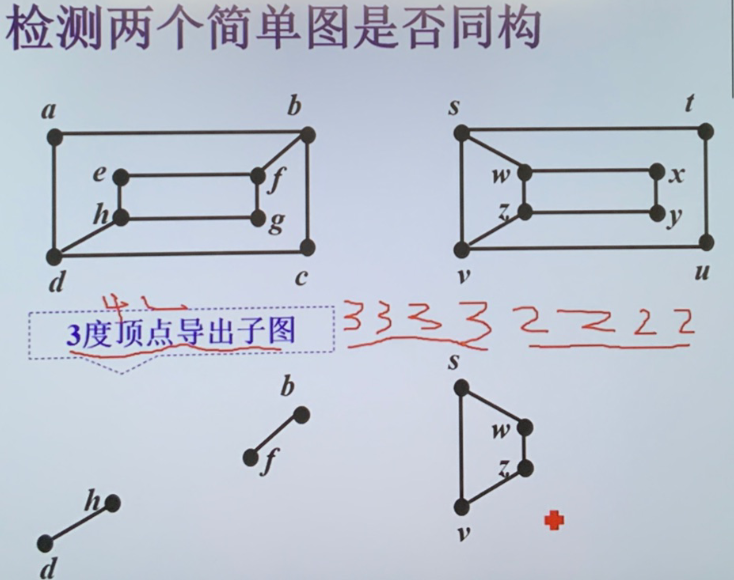
- 检测图是否同构:
- 考察图的不变量:如长度为 \(k\) 的回路的存在性
- 若 \(G\) 和 \(H\) 同构,则 \(G\) 的 \(k\) 度点导出子图与 \(H\) 的 \(k\) 度点导出子图同构
图的运算¶
- \(G\bigcup G'\):以 \(V(G)\bigcup V(G')\) 作为点集,\(E(G)\bigcup E(G')\) 作为边集
- \(G*G'\):对于不想交的无向图,以 \(V(G)\bigcup V(G')\) 作为点集,以 \(E (G)\cup E (G^{\prime})\cup\{\{x, y\}|x\in V (G), y\in V (G^{\prime})\}\) 为边集, 如 \(K_{2}*K_{3}=K_{5}\)
- \(\overline G\) 补图:\(G({V},[{V}]^2\setminus{E})\)
连通图¶
-
通路:从 \(v_{0}\) 到 \(v_{n}\) 的长度为 \(n\) 的通路(\(n\) 条边 \(e_{1}\dots e_{n}\) 的序列)
- 不区分多重边时可以直接用顶点的序列表示
- 回路:起点与终点相同(长度大于 0)
- 简单通路:边不重复;
- 初级通路(路径):点不重复(边更不重复)
-
对于无向图,如果图中任意两点之间都有通路(这是一个等价关系),那么称无向图 \(G\) 为连通的
-
连通分支:极大连通子图,每个无向图是若干个不相交的连通分支的并
- \(p(G)\) 表示 \(G\) 的连通分支的数目
- 删除一个点之后,连通分量数目可能不变,减少(-1), 增加(可能增加多个)
- 删除一条边后有 \(p(G)\leq p(G-e)\leq p(G)+1\)
-
割点:对于 \(v\in V_{G}\),若 \(p(G-v)>p(G)\) 则称 \(v\) 为割点,三个等价命题:
- \(v\) 是割点
- 存在 \(V-\{v\}\) 的划分 \(\{ V_{1},V_{2} \}\) 对于 \(\forall u\in V_{1},w\in V_{2}\), \(uw\) -通路均包含 \(v\)
- 存在顶点 \(u,v\) 使得任意 \(uw\) 通路都包含 \(v\)
- 割边:\(p(G-e)>p(G)\) 则称 \(e\) 是 \(G\) 中的割边,四个等价命题
- \(e\) 是割边
- \(e\) 是割边当仅当 \(e\) 不在 \(G\) 的任一简单回路上
- 存在 \(V-\{v\}\) 的划分 \(\{ V_{1},V_{2} \}\) 对于 \(\forall u\in V_{1},w\in V_{2}\), \(uw\) -通路均包含 \(e\)
- 存在顶点 \(u,v\) 使得任意 \(uw\) 通路都包含 \(e\)
- 点连通图:
- 使非平凡连通图 \(G\) 成为不连通图或者平凡图需要删除的最少(不是说删除了这么多就不连通了)定点数称为点连通度,记为 \(\kappa(G)\)
- 不连通图的连通度为 0,\(\kappa (K_{n})=n-1\)
- 若 \(\kappa (G)\geq k\) 则称 \(G\) 是 \(k\) 连通图(删除少于 \(k\) 个点仍然连同)
-
边连通图:与点联通图的定义类似,记为 \(\lambda(G)\)
-
连通度的上限
- 对于非平凡简单图有 \(\kappa(G)\leq\lambda(G)\leq\delta (G)\)(最小顶点度)
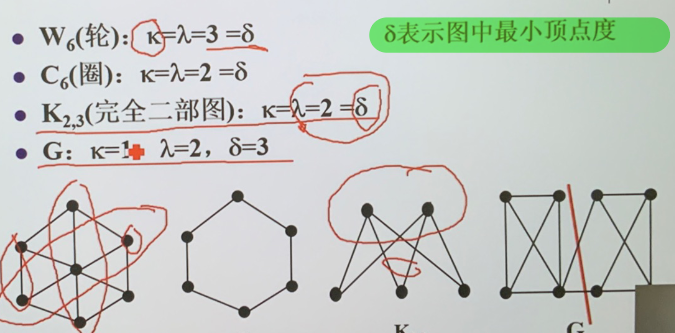
- 设 \(G\) 为简单图 \(\mid G\mid=n\geq 3\) 且 \(\delta_{G}\geq n-2\) 则 \(\kappa(G)=\delta_{G}\)
- 图 \(G\) 是 \(k\) 连通图,当仅当 \(G\) 中任意两点至少被 \(k\) 条除端点外顶点不想交的路径路径所连接
- 图 \(G\) 是 \(k\) 边连通图,当仅当 \(G\) 中任意两点被至少 \(k\) 条边不相交的路径所连接
- 一个图是 2 连通的 \(\iff\) 是一个回路互是在一个已有的 2 连通图上一次增加路径(连接两个点)
欧拉图¶
- 包含图中每一条边的简单通路为欧拉通路(简单回路为欧拉回路)
- 若一个图中有欧拉回路,则称为欧拉图,如果只有欧拉通路没有欧拉回路,那么称 G 为半欧拉图
- 连通图为欧拉图,当仅当所有顶点的度均为偶数
- 与命题“图中所有边包含在若干个相互没有公共边的简单回路中”等价
- 连通图为半欧拉图,当仅当恰有两个奇度点(必须以这两个点为简单通路的起始点)
-
有向欧拉图:有向图中含所有边的有向简单回路称为有向欧拉回路,对应的图为有向欧拉图
-
构造欧拉回路 Fleury 算法(输入欧拉图,输出一个欧拉回路)
- 任取 \(v_{0}\in V_{G}\) 令 \(P_{0}=v_{0}\)
- 设 \(P_{i}=v_{0}e_{1}v_{1}\dots e_{i}v_{i}\) 按照下列规则从剩下的点中选择 \(e_{i+1}\)
- 要求 \(e_{i}\) 与 \(v_{i}\) 关联,除非别无选择,否则不应该选择割边(删除这条边之后剩下的边应该在同一个连通分量)
-
随机欧拉图:从 \(v\) 开始,每次从当前点关联的边种随机选一条边,均可以构造欧拉回路,\(G\) 为以 \(v\) 为始点的随机欧拉图
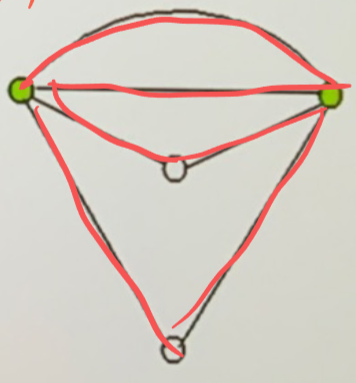
- \(G\) 为欧拉图当仅当 \(G\) 中任一回路都包含 \(v\)
哈密顿图¶
- 哈密顿通路 (哈密顿图):包含所有顶点,通路上各顶点不重复
- 哈密顿回路:起点重终点相同(与环同构)
-
若有点的度为 1 则没有哈密顿回路,并且不能存在割点;对于每一个顶点只会使用其两条边;n 个顶点的哈密顿回路有 n 调边
-
必要条件:对于任意 \(S\subseteq V\) 有 \(P(G-S)\leq\mid S\mid\)
-
充分条件(Ore 定理):对于无向简单图 \(\mid G\mid=n\geq 3\),若任意不相邻的顶点对都满足 \(d(u)+d(v)\geq n\) 则有哈密顿回路(或者是 \(\delta(G)\geq \frac{n}{2}\))
- G 的闭合图,\(C(G)\) 连接 \(G\) 中不相邻并且度之和不小于 \(\mid G\mid\) 的点对,直到没有哦,\(G是哈密顿\iff C(G)是哈密顿\)
- \(d(u)+d(v)\geq n-1\) 则说明有哈密顿通路(哈密顿图)
-
竞赛图:底图为完全图的简单有向图
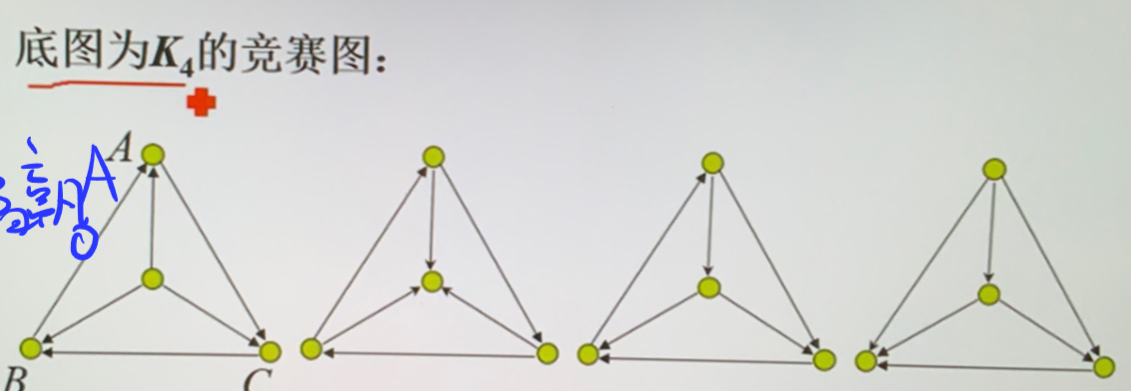
- 可以看做 \(n\) 个选手循环赛的结果
- 竞赛图一定有哈密顿通路


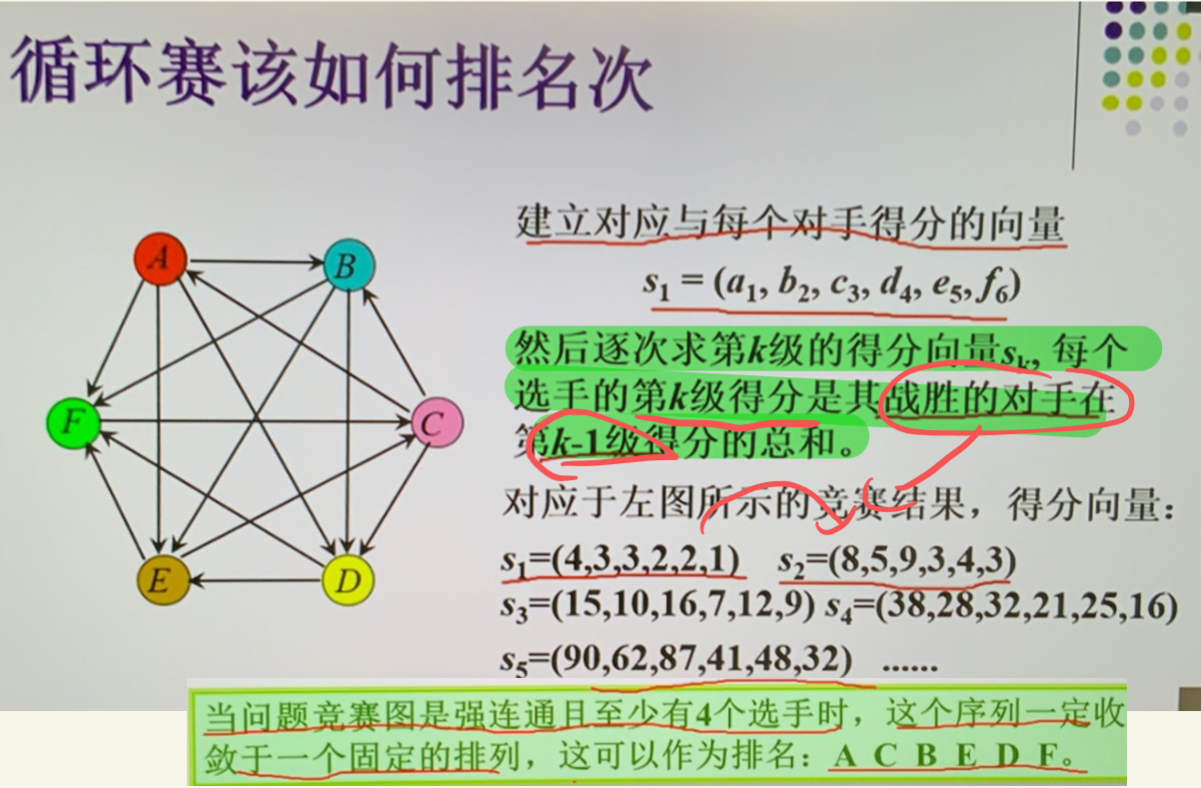
-
*旅行商问题
- 找最短哈密顿回路(找哈密顿回路本身就是 NPC)
- 对于完全图,有 \(\frac{(n-1)!}{2}条\) 是一个 NPC 问题
- 近似算法:总是选择最近的点
二部图¶
- 二部图
- 顶点集划分为两个集合, 边端点位于不同类别
- 完全二部图 \(K_{n,m}\):来自不同类别的两个顶点之间均有边
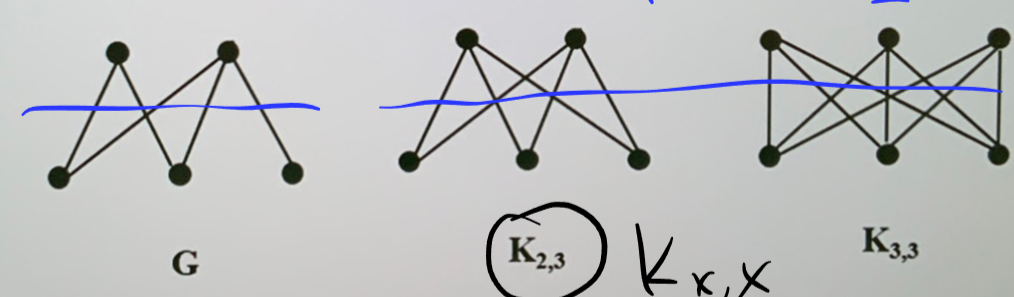
-
\(G\) 为二部图当仅当不含奇圈
-
匹配:\(E^*\subseteq E\) 为 \(G\) 的匹配,其中 \((\forall e_{1},e_{2}\in E^*)\) 均有 \(e_{1},e_{2}\) 不相邻
- 极大匹配:再加一条边就是非匹配了
- 匹配数:图 \(G\) 的匹配数为 \(\beta_{1}(G)=max\{ \mid E^*\mid\mid E^*为G的匹配 \}\)
- 最大匹配:即 \(\mid E^*\mid=\beta_{1(G)}\)
- \(v_{i}\) 与 \(v_{j}\) 被 \(M\) 匹配:\((v_{i},v_{j})\in M\)
- \(v\) 为 \(M\) 饱和点:有 \(M\) 中边与 \(v\) 关联(非饱和点正好相反)
- 完美匹配:\(G\) 中无 \(M\) 非饱和点
- 交错路径:\(M\) 与 \(E-M\) 中交替取边构成的 \(G\) 中路径
-
可增广路:起点和终点都是非饱和点的交错路径
- 增广路:将可增广路的匹配边变为非匹配边,非匹配边变为匹配边,得到的新路径为增广路
- 最大匹配 \(\iff\) 不含可增广路
-
对于二部图中两个点集 \(V_{1},V_{2}(\mid V_{1}\mid<\mid V_{2}\mid)\) 若 \(V_{1}\) 中全部为饱和点,则为完备匹配(当 \(\mid V_{1}\mid=\mid V_{2}\mid\) 时为完美匹配)
- 完备匹配一定是极大匹配
- Hall 定理:对于上述二部图有完备匹配当仅当 \(V_{1}\) 中任意 \(k\) 个点至少与 \(V_2\) 中任意 \(k\) 个顶点相邻
- 推论:二部 k-正则(k 一定偶数)图总是有完美匹配;\(V_{1}\) 中每个顶点至少关联 \(t\) 条边,若 \(V_{2}\) 中每个顶点至多关联 \(t\) 条边,则存在完备匹配
树¶
- 不含回路的连通简单图为树,是边最少的连通图(每条边都是割边),边最多的无回路图 (加一条边产生唯一回路)
- 树中任意两点之间存在唯一路径
-
\(n=\left|V(T)\right|,\:m=\left|E(T)\right|\) 有 \(m=n-1\) (因此连通图有 \(m\geq n-1\))
- 树等价与:不含回路并且 \(m=n-1\);连通并且 \(m=n-1\)
-
生成子图:保留点,减少边
- 若生成子图为树,则为生成树,无向图有生成树当仅当连通
- 图有唯一的生成树当仅当自身就是树
-
生成树的个数
- 对于完全图 \(n^{n-2}\)
- 对于完全二部图 \(p^{q-1}q^{p-1}\)
-
有向树:底图为有向图
-
根树
- 有向树,恰有一个入度为 0 的顶点(根),其他节点入度都为 1,
- 存在从根到其他点的唯一通路
-
m 元树:每个内点至多 m 个子女(m 叉)
- \(m^{h-1}<l\leq m^{h}\)
- 完全 m 元树:每个内点恰好 m 个子女(m 叉正则)
- \(n-1=m\times i\) 入度等于出度,因此 \(\frac{{n-1}}{m}\) 个内点 \(n-\frac{{n-1}}{m}\) 个叶节点
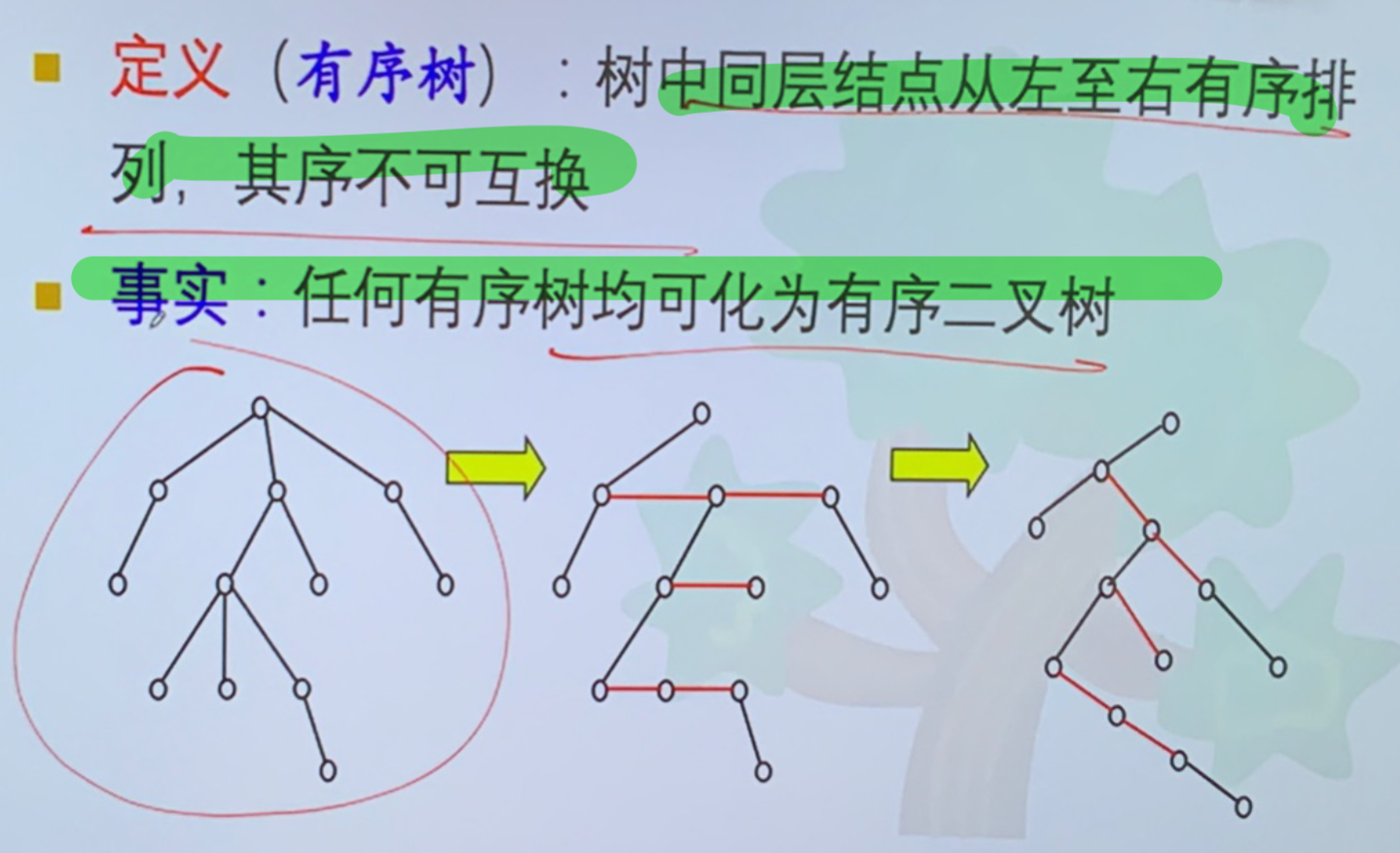
- 平衡:树叶都在 h、h-1
- 有序:同层顶点固定次序