离散数学
url: https://blog.csdn.net/unseven/article/details/110876249?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522171585914516800185862424%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=171585914516800185862424&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2alltop_positive~default-1-110876249-null-null.142v100control&utm_term=%E7%A6%BB%E6%95%A3%E6%95%B0%E5%AD%A6%E9%80%89%E6%8B%A9%E9%A2%98&spm=1018.2226.3001.4187 title: - 离散数学 - 期末练习题解析_xa(x) 等价命题 - CSDN 博客 date: 2024-05-16 20:32:33 tag: summary:
一、 选择题¶
- 下列句子中,( )是命题。
A . 2 是常数
B. 这朵花多好看啊!
C. 请把们关上!
D. 下午有会吗?
A
命题是能判断真假的陈述句
B 是感叹句、C 是祈使句,D 是疑问句
- 令 p: 今天下雪了,q: 路滑,r:他迟到了。则命题 “下雪路滑,他迟到了” 可符号化为( )
A. p∧q→r
B. p∨q→r
C. p∧q∧r
D. p∨q↔r
A
运算优先级为 ¬,∧, ∨,→,↔,
A 可看成 (p∧q)→r
- 令 p:今天下雪了,q:路滑,则命题 “虽然今天下雪了,但是路不滑” 可以符号化为( )
A. p∧¬q
B. p∧q
C. p∨¬q
D. p→¬q
A
- 设 P(x):x 是鸟,Q(x):x 会飞,命题 “有的鸟不会飞” 可符号化为( )
A. ¬(∀x) ( p(x) →Q(x) )
B. ¬(∀x) ( p(x) ∧ Q(x) )
C. ¬(∃x) ( p(x) →Q(x) )
D. ¬(∃x) ( p(x) ∧ Q(x) )
A
有的鸟不会飞,即可译为不是所有鸟都会飞
在全称量词∀后面用→联接词
在存在连词∃后面用 ∧ 联接词
- 设 p(x):x 是整数,f(x):x 的绝对值,L(x,y):x 大于等于 y;命题 “所有整数的绝对值大于等于 0” 可以符号为( )
A. ∀x(p(x) ∧ L(f(x),0) )
B. ∀x(p(x)→L(f(x),0) )
C. ∀xp(x) ∧ L(f(x),0)
D. ∀xp(x)→L(f(x),0)
B
所有整数的绝对值大于等于 0,用到的为全称量词∀,整个命题应该是同一个 x,在全称量词∀后面用→联接词,所以整个命题可符号为∀x(p(x)→L(f(x),0) )
- 设 F(x):x 是人,G(x):x 犯错误,命题 “没有不犯错误的人” 符号为( )
A. ∀x(F(x) ∧ G(x) )
B. ¬∃x(F(x) →¬G(x) )
C. ¬∃x(F(x) ∧ G(x) )
D. ¬∃x(F(x) ∧ ¬G(x) )
D
A 和 B 的联接词使用错误
D,不存在人不犯错误
-
下列命题公式不是永真式的是( A )
A. (p→q)→p
B. p→(q→p)
C. ¬p∨(q→p)
D. (p→q)∨p
-
设 R(x):x 为有理数; Q(x):x 为实数。命题 “任何有理数都是实数” 的符号化为 ( C )
A.(彐 x) ( (R(x)∧Q(x) )
B.(∀x)( (R(x)∧Q(x) )
C.(∀x)( (R(x)→Q(x) )
D. 彐 x(R(x)→Q(x) ) -
设个体域 D={a,b}, 与公式∀xA(x) 等价的命题公式是 ( A )
A. A(a)∧A(b)
B. A(a)→A(b)
C. A(a) ∨ A(b)
D. A(b)→A(a)
已知个体域,消去量词,∀xA(x) 中有全称量词,则把所有 x 的取值全列出来
应该为 A(a)∧A(b)
- 下列等价式不正确的是 (A)
A. ∀x((P(x) ∨ Q(x) ) ⇔ ∀xP(x) ∨ ∀xQ(x)
B. ∀x(P(x) ∧ Q(x)) ⇔ ∀xP(x) ∧ ∀xQ(x)
C. ∃x(P(x) ∨ Q(x) ) ⇔ ∃xP(x) ∨ ∃xQ(x)
D. ∀x(P(x)∧Q) ⇔ ∀xP(x)∧Q
A

-
设个体域 D={a,b}, 与公式彐 xA(x) 等价的命题公式是 ( C )
A.A(a) ∧A(b
B.A(a)→A(b)
C. A(a) ∨ A(b)
A(b)→A(a) -
设 X={Ø,{a}{a,Ø}}, 则下列陈述正确的是 (
A. a∈X
B. {a,Ø}⊆X
C. {{a,Ø}}⊆X
D. {Ø}∈X
C
元素与集合的关系用属于
集合与集合的关系用包含
A 中用的是属于,但 a 不是 X 的元素,因为需要把整个集合 {a} 看成 X 的 一个元素
B 用的是属于,说明得把 {a,Ø} 看成一个集合,a 和 Ø 都得是 X 的元素,a 不是 X 的元素,所以不正确,也可解释作 {a,Ø} 只是 X 的一个元素,并不是指一个集合
C 正确,有两重括号,第一个括号内的 {a,Ø} 就是 X 的一个元素,{{a,Ø}}就是 X 的一个子集
D 中用的是属于,说明整个 {Ø} 被看成是一个元素,但 X 中只有 Ø 而没有{Ø}
- 有向图 D 是连通图, 当且仅当 ( D )
A. 图 D 中至少有一条通路
B. 图 D 中有通过每个顶点至少一次的通路
C. 图 D 的连通分支数为一
D. 图 D 中有通过每个顶点至少一次的回路
D
这里的连通图应该指的是强连通图
对 C 要特别注意一下,有第一章的命题逻辑我们知道 “当且仅当” 指的是充要条件,连通图的连通分支数确实为一,但连通分支数为一的并不代表是连通图,所以 C 是错的
- 设 A={a,b,c}, 则下列是集合 A 的划分的是 ( B)
A. {{b,c},{c}}
B. {{a},{b,c}}
C. {{a,b},{a,c}}
D. {{a,b},c}
B

我们可以知道π是一个子集族,里面都应该是子集,D 错误
然后每个子集不能有重复的元素,AC 错误
- 下列谓词公式中是前束范式的是 (D)
A. ∀xF(x)∧¬(∃x)G©
B. ∀xP(x) ∧ ∀yG( y)
C. ∀x(P(x)→∃yQ(x,y)
D. ∀x∃y(P(x)→Q(x,y))
D
前束范式就是所有的量词都在前面
- 设 M={x | f1(x)=0},N={x | f2(x)=0}, 则方程 f1(x)*f2(x)=0 的解为( B )
A. M∩N
B. M∪N
C. M⊕N
C. M-N
f1(x)*f2(x)=0 只有 = 要有一个为 0 其结果就为 0
显然是 M 和 N 的并集

在数学中,群表示一个拥有满足封闭性、满足结合律、有单位元、有逆元的二元运算的代数结构,包括阿贝尔群、同态和共轭类。
设 G 是一个群,则
- G 满足消去律(左消去和右消去),即∀a,b,c∈G, 若 ab=ac, 则 b = c
- 任意一个元素的逆元的逆元是其本身, A 正确
-
(ab)^-1 = b ^-1 * a ^-1, C 错误
其余请看群的详细介绍 -
在整数集合 Z 上,下列定义的运算满足结合律的是( )
A. a_b=b+1
B. a_b=a-1
C. a_b=ab-1
D. a_b=a+b+1
D
如果满足结合律,则 (a*b)*c=a*(b*c)

- 设简单图 G 所有的结点的度数之和为 50,则 G 的边数为( )
A. 50
B. 25
C. 10
D. 5
B
既不含平行边也不含环的图为简单图
由握手定理:度数之和为变数的 2 倍,变数为 25
- 设简单无向图 G 是一个有 5 个顶点的 4 - 正则图,则 G 有( )条边。
A. 4
B. 5
C. 10
D. 20
C
正则图是指各顶点的度均相同的无向简单图
有题意,度数之和为 5*4=20,边数 = 20 / 2 = 10
- 设集合 A={1,2,3,4},A 上的等价关系 R= {<1,1>, <.3,2>,<2,3>,<4,4>} U IA (恒等关系), 则对应于 R 的划分是( )
A. {{1},{2,3},{4} }
B. {{1,3},{2,4} }
C. {{1,3},{2},{4} }
D. {{1},{2},{3},{4} }
A
IA 表示恒等关系,设 A={a,b,c},则其上关系 R={
本题中 IA 中应该是补齐 <2,2><3,3>,2 和 3 应该被分到了另外一块,应该选 A

D
在数学中,若对某个集合的成员进行一种运算,生成的仍然是这个集合的元素,则该集合被称为在这个运算下闭合。
比较最大数,得到的结果还是在 A 中
比较最小数,结果还是在 A 中
最大公约数,1 和 10 的最大公约数为 1,L 为任意数字,与其他的数求最大公约数,都可以在 1,2,10,L 中取得
若 L 为 3,3 和 10 的最小公倍数为 30,不在 A 中,D 不是封闭的

C
先看看满射,单射和双射的定义

F 的关系是一一对应的,满足单射,但f的值域中没有d,不满足满射的条件

B
割点和割边指拿掉某个点或某些边,连通分支数增加
割点集和桥指拿掉某些点或某条边,连通分支数增加

D
经过图的每一条边且仅一次并且行遍图中的每个顶点的回路(通路),称为欧拉回路(欧拉通路),存在欧拉回路的图,称为欧拉图
无向图 G 有欧拉回路当且仅当 G 是连通图且无奇度顶点
只有欧拉通路当且仅当图 G 恰有2个奇度顶点,这两个点为欧拉通路的端点

A
叶子结点度数只有1,显然不对
其余都是树的等价条件

A
幂集的个数为 2^n

C
握手定理的推论:任何图中的度数为奇数的顶点的个数为偶数
可以排除 A 和 D
对 B 选项,总共有 6 个点,有两个度数为 5 的点,而度数为 5 说明它与其他顶点都相连,反过来其它每个点都会与这两个点相连,度数不可能小于 2,B 错误

欧拉图中没有奇度顶点,排除 A,C
哈密顿图中任意两个不相邻的顶点度数之和 >=n-1
D 中选择右边的两个度数为 2 的顶点,度数之和为 4<6,D 不存在哈密顿回路


C
共有 6*3=18 度
边数 = 度数之和 / 2 = 9

B
自反是全部顶点都有自环
反自反是全部顶点都没有自环
对称是顶点之间有边的话,全是双向边
反对称是顶点之间有边的话,全单向边

B

R2 是将 R1 的单向边补成了双向边,应该是对称闭包
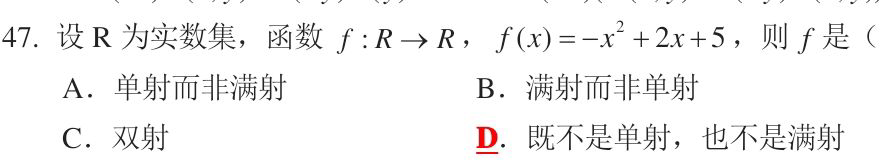
D
f(x) 中 x 与 y 并不是一一对应,所以不是单射,f(x) 的最大值 6,并不是实数集 R,不是满射

C
A,B,D 中都有奇度顶点,无法构成欧拉图
二. 填空题¶
- 命题公式 ¬(p→q) 的成真赋值_, 成假赋值__.
真:1 0 , 假: 0 0, 0 1, 1 1.
- 命题公式 (p ∨ q)→p 的成真赋值_, 成假赋值_.
真:0 0, 0 1 , 1 1. 假:1 0.
- 命题公式 p→(p∧q) 的成真赋值_, 成假赋值__.
真:00,01,11,假:10
- 公式 (∀x)( ∀x)( P(y)→Q(x,z) ) ∧ (∃y)R(x,y) 约束变元为_, 自由变元为_.
x,y x,z
对左边部分 ∀x ∀y 说明 x,y 是约束出现的,z 是自由的
对右边∃y 说明 y 是约束的,x 是自由的
- 公式 ∀x(P(x) ∨ ∃yR(x) )→Q(x,z) 约束变元为_, 自由变元为__.
约束: x,y
自由: x,z
- 设 A = {a,b,{a,b} }, B={a,b}, 则 B-A=_,A⊕B=__.
B-A=Ø
A⊕B={{a,b} }
- 设 A={1,2,3},A 上的关系 R={<1,2>,<2,1>}, 则对称闭包 s( R ) = __, 传递闭包 t( R )= ___。
s(R) = {<1,2>,<2,1>} // 本身就是双向边,无需改动
t(R)={<1,2>,<2,1>,<1,1>,<2,2>} //<1,2><2,1 > 添加 < 1,1>, 同时也可以看成 < 2,1>,<1,2 > 要添加 < 2,2>
- 设 A={a,b,{a,b} },B= {a,b,c},则 A⊕A= __,A⊕B=____.
则 A⊕A=Ø
A⊕B={{a,b},c}
- 一颗无向树的顶点数 n 与边数 m 的关系是_,6 阶无向连通图至多有_颗不同的生成树。
m = n-1
6 颗
- 设 f(x)=x-1,g(x)=x^2, 则复合函数 (f g)(x)=_,(g f)(x) =__.
统一规定为右复合
(f g)(x) = g(f(x))=(x-1)^2
(g f)(x) =f(g(x))=x^2-1
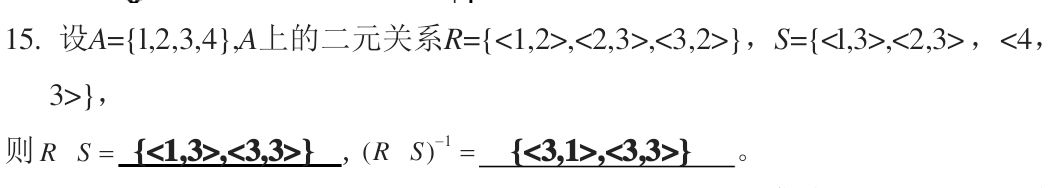
合成
R°S={
- 一颗无向树的顶点数 n 与边数 m 的关系是_, 设 G 是具有 8 个顶点的数,则 G 增加__条边才能把 G 变成完全图。
m =n-1
21 条
无向完全图 边数 m = (n(n-1))/2
有向完全图 边数 m = (n(n-1))
总边数 m = 8*7/2=28,树 G 有 7 条边
增加 28-7=21 条

