线性代数
超级简要的知识点复习,针对面试的简单问题
行列式¶
计算行列式¶
- 行列式的计算公式:\(\det(A)=\sum_{j=1}^n(-1)^{1+j}a_{1j}M_{1j}\)
- 余子式:余子式是一个矩阵通过删去某一行和某一列后得到的子矩阵的行列式。\(M_{ij}\) 就是阐述第 \(i\) 行和第 \(j\) 列得到的子矩阵的行列式
- 代数余子式:在余子式上乘以一个符号因子 \(C_{ij}=(-1)^{i+j}M_{ij}\)
行列式的性质¶
- 对于上三角、下三角、对角矩阵其值为 \(a_{11}\dots a_{nn}\)
- \(\mid D\mid=\mid D^T\mid\)
- 对调两行/列符号取反
- 可以提取一行/列公因子到行列式外面
- 因此若行列式中两行/列成比例,那么值为 0
- 可以把行列式一行的倍数加到令一行
矩阵¶
矩阵运算¶
- 加法:同型矩阵才能相加
- 点乘
- 乘法:不满足交换律
- \(EA=AE=A\)
- 方阵相乘,有:\(\mid AB\mid=\mid A\mid\mid B\mid\)
- 幂:\(A^0=E\);\(\mid kA\mid=k^n\mid A\mid\)
- 只有 \(n\) 阶方阵才能计算幂
转置与共轭¶
- 矩阵转置
- \((A+B)^T=A^T+B^T\)
- \((AB)^T=B^TA^T\)
- 对称矩阵有 \(A^T=A\) 反对称矩阵有 \(A^T=-A\)
- 有 \(A+A^T\) 为对称矩阵 \(A-A^T\) 为反对称矩阵
- 共轭矩阵
- 求中的 \(a_{ij}\) 为复数,共轭矩阵为 \(\overline A=(\overline {a_{ij}})_{m\times n}\)
- \(\overline{A+B}=\overline A+\overline B\)
- \(\overline{AB}=\overline A \ \overline B\)
初等矩阵与初等变换¶
- 初等变换
- 调换行/列
- k 乘以某一行/列
- 把矩阵的一行/列的 k 加到另一行/列
- 初等矩阵:对单位矩阵进行一次初等变换得到的矩阵为初等矩阵
- 对矩阵进行初等行变换等同于左乘相应的初等矩阵
- 对矩阵进行初等列变换等同于右乘相应的初等矩阵
- 如果能经过有限次初等行/列变换从 A 得到 B 则称 AB 行/列等价
秩¶
- \(k\) 阶子式:任取矩阵的 \(k\) 行和 \(k\) 列,位于其交点上的 \(k^2\) 个元素,按照原来的顺序构成的 \(k\) 阶行列式
- 对于矩阵 \(A(m\times n)\), 存在一个不为 \(0\) 的 \(k\) 阶行列式,并且所有 \(k+1\) 阶行列式均为 \(0\),则矩阵的秩为 \(r(A)=k\)
- 若 \(k=m\) 则为行满秩;\(k=n\) 为列满秩;\(k=m=n\) 为满秩矩阵(\(\iff\mid A\mid\neq 0\))
- 行阶梯矩阵的秩就等于其非零行的数目
- 初等变换不改变矩阵的秩
- 对于任何矩阵都有行秩等于列秩
特殊矩阵¶

- 基本矩阵:只有一个元素为 1 ,其他均为 0,记为 \(E_{ij}\)
阶梯矩阵¶
- 行阶梯矩阵:
- 所有非零行的行号都小于零行的行号
- 每个非零行的第一个元素的位置 \(t_{i}\) 有 \(t_{1}<t_{2}\dots t_{r}\) (注意必须是严格小于)
- 行简化阶梯矩阵:
- 是行阶梯矩阵
- 每个非零行的第一个元素为 1,剩下所有元素都为 0
- 标准型矩阵:既是行简化阶梯矩阵,又是列简化阶梯矩阵,其左上角是一个单位矩阵 \(\left(\begin{array}{cc}E&0\\0&0\end{array}\right)\)
- 一个矩阵总是可以通过初等变换得到一个行/列简化阶梯矩阵及标准型矩阵
可逆矩阵¶
- 只有方阵才可能是可逆矩阵
- 若存在同阶方阵 \(B\) 使得 \(AB=BA=E\) 则称 \(A\) 为可逆矩阵,\(B\) 为其逆矩阵
- 可逆矩阵的是满秩矩阵,可以表示为初等矩阵的乘积(可以通过初等变换得到单位矩阵)
- 一个矩阵乘以可逆矩阵就相当于进行了一系列初等变换(即秩不发生变化)
- 使用伴随矩阵求解逆矩阵
- 伴随矩阵 \(A^*\) 是 \(A\) 的代数余子式组成的矩阵的转置,有 \(\mathcal{A}^*=A^*A=\mid A\mid E\)
- 因此有 \(A^{-1}=\frac{1}{\mid A\mid}A^*\)
- 基于初等变换的求解方式 \([A|E]\to[E|A^{-1}]\)
相似矩阵¶
- 对于同阶方阵 \(A\) 与 \(B\),如果存在可逆矩阵 \(P\) 使得 \(B=P^{-1}AP\) 则称 \(A\) 相似于 \(B\) 即 \(A\sim B\),\(B\) 为 \(A\) 的相似矩阵,\(P\) 为相似变换矩阵(这是一种等价关系)
- 若相似有 \(|A|=|B|\)
- \(f(A)\sim f(B)\) 多项式函数
- 相似三角形具有相同的特征值
特征值与特征向量¶
- \(A\alpha=\lambda_{0}\alpha\)
- \(\lambda_{0}\) 为 \(A\) 的特征值(一个标量)
- \(\alpha\) 为 \(A\) 的特征向量(零向量除外)特征向量 𝑣 是一个在矩阵 𝐴 作用下方向不变的向量,即矩阵 𝐴 对它的作用仅仅是拉伸或缩放(由特征值 𝜆 确定)。
- 属于不同特征值的特征向量线性无关
- 求解特征值与特征向量
- 原式可以变换为 \(|\lambda_{0}E-A|\alpha=0\)
- 当 \(|\lambda_{0}E-A|=0\) (特征多项式)时 \(\alpha\) 为一个非零解
- 即先通过行列式求解特征值,再高斯消元得到特征向量
- 主对角线上元素和称为迹 \(tr(A)=a_{11}+\dots+a_{nn}\)
- \(\sum^n_{j=1}\lambda_{j}=tr(A)\)
- \(\prod_{j=1}^{n}\lambda_{j}=|A|\)
矩阵对角化¶
- 若矩阵相似于一个对角矩阵,则称 \(A\) 可以对角化
- 充要条件就是 \(n\) 阶矩阵有 \(n\) 个线性无关的特征向量
- 代数重数是指特征值作为多项式(特征多项式)的根出现的次数。
- 几何重数是指对应于特征值的线性独立特征向量的个数。
- 一个矩阵是对角化的,当且仅当其每个特征值的几何重数等于代数重数。
内积与正交¶
- \(\alpha\:=(a_{1},a_{2},\cdots,a_{n})^{T},\:\beta=(b_{1},b_{2},\cdots,b_{n})^{T}\) 内积为 \((\alpha,\beta)= \alpha^T\beta=a_1b_1+a_2b_2+\cdots+a_nb_n\geq 0\)
- 长度(模):\(\|\alpha\|=\sqrt{(\alpha,\alpha)}\)
- 模为 1 的称为单位向量
- 若 \((\alpha,\beta)=0\) 则说 \(\alpha,\beta\) 正交
- 不含零向量并且两两正交的向量组为正交向量组,一定线性无关(标准化后为标准正交向量组)
- 若 \(A^TA=E\) 则称 \(A\) 为正交矩阵
- 使用正交矩阵进行线性变换称为正交变换
向量¶
线性相关与无关¶
- 线性组合:\(\beta=k_{1}\alpha_{1}+\dots+k_{s}\alpha_{s}\) 则 \(\beta\) 为 \(\alpha_{i}\) 的线性组合
- 对于向量组 \(\beta={\beta_1\dots \beta_{n}}\) 都可以由 \(\alpha=\alpha_{1}\dots \alpha_{n}\) 表示,则称 \(\beta\) 可以由 \(\alpha\) 线性表示,如果反之也成立,则称两者等价
- 若存在 \(k_{1}\alpha_{1}+\dots+k_{m}\alpha_{m}=0\) 有非全 0 解时称 \(\alpha_{1}\dots \alpha_{m}\) 线性相关
- 如果一个向量组中有 0 向量,则向量组线性相关
- 部分相关->整体相关;整体无关->部分无关
- 向量组线性相关 \(\iff\) 至少有一个向量可以由向量组中其他向量线性表示
-
对于 \(\alpha_{1}\dots \alpha_{S}\) n 维列向量线性相关 \(\iff r(A)<S\)
-
向量组的一个部分子向量组线性无关,并且加入任何一个其他向量后都是线性相关,则为一个极大线性无关组
- 向量组与其极大线性无关组等价,不同极大线性无关组之间也等价
- 等价线性无关向量组的秩相同,向量组的秩就是其极大线性无关组元素的数目
线性方程¶
克莱姆法则¶
- 求解 n 元线性方程组:\(Ax=b\)
- \(A\) 为 \(n\times n\) 的系数矩阵,\(x\) 为有 \(n\) 个未知数的列向量,\(b\) 是常数向量
- \(\mid A\mid\neq 0\) 时有解且唯一
- \(A_i\) 表示把第 \(i\) 列换成 \(b_1\dots b_{n}\) 有 \(x_i=\frac{\det(A_i)}{\det(A)}\)
- \(b\neq 0\) 为非齐次线性方程组,\(b=0\) 为齐次线性方程组
- 当 \(\mid A\mid=0\) 时存在(无数个)非零解
- 克莱姆法则是一种基于行列式的解析方法,用于求解具有唯一解的小规模线性方程组。
高斯消元¶
- 高斯消元法适用于较大规模的线性方程组,通过矩阵变换和回代求解,具有较好的数值稳定性和较低的计算复杂度。
- 求解 n 元线性方程组:\(Ax=b\)
- 可以使用增广矩阵 \(B=(A \ b)\) 表示线性方程组

- 前向消元
- 选择主元:从矩阵的第一列开始,选择一个非零元素作为主元。
- 消去变量:使用主元,通过初等行变换将主元所在列的其他元素变为零。
- 重复步骤:对矩阵的每一列重复上述过程,直到所有列都处理完毕,最终得到一个上三角矩阵。
二次型¶
- 二次型是 \(n\) 个变量在某个数域上的二次齐次多项式
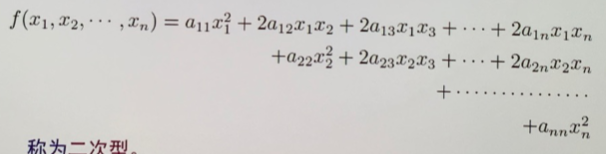
- 即 \((x_1x_2\cdots x_n)\left(\begin{array}{cccc}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{array}\right)\left(\begin{array}{c}x_1\\x_2\\\vdots\\x_n\end{array}\right)\)
- 可以改写为 \(f(x_{1},\dots x_{n})=X^TAX\) ,其中 \(A\) 为一个对称矩阵,A 的秩就是二次型的秩
- 通过对 \(X\) 进行线性变换得到的只包含平方项的二次型为原二次型的标准型
- 合同变换:\(B=P^TAP\) 则称 \(B\) 为 \(A\) 的合同变换
- 若 \(|P|\neq0\) 则为非退化线性变换
- 否则为退化线性变换
正定矩阵¶
- 前提为 \(A\) 是一个实对称矩阵
- 对于 \(x\neq 0\) 都有 \(x^TAx>0\) 则 \(f\) 为正定二次型 \(A\) 为正定矩阵
- 同理 \(x^TAx<0\) 为负定矩阵
- \(\geq\) 为半正定矩阵;\(\leq\) 为半负定矩阵
- 合同变换不改变正定性
- 正定矩阵的特征值全大于零,或顺序主子式均大于零
主子式¶
- 顺序主子式:矩阵左上角连续的 \(i\) 行 \(i\) 列
- 主子式:不一定连续的 \(i\) 行 \(i\) 列
线性空间¶
- 数环和数域的区别:都是一个具有加法和乘法的代数结构,区别在于数域要求每个非零元素都有乘法逆元(如整数构成数环,但是有理数就构成数域)
-
定义:集合 \(V\) 连通向量加法、标量乘法两个运算,并且,满足一下条件
- 封闭性
- 结合律
- 交换律
- 存在单位元
- 存在零元
- 存在逆元
- 分配律
-
如果在 \(V\) 中可以找到任意多个线性无关的向量,则其为无限维线性空间
-
如果存在一组 \(n\) 个向量线性无关,并且其他向量都可以由这 \(n\) 个向量来表示,那么这 \(n\) 个向量就是 \(V\) 的一组基,记为 \(d\mathrm{Im}(V)=n\) 称为线性空间的维数(不同基具有相同的维数)
-
子空间:首先 \(W\) 是线性空间 \(V\) 的一个非空子集,如果他也对加法和乘法构成一个线性空间,那么他就是 \(V\) 的一个线性子空间
- 至少有两个子空间(平凡子空间):零子空间、全子空间
- \(n\) 维线性空间的子空间的维数都小于等于 \(n\)