Skip to content

前缀和与差分

前缀和

  • 前缀思想本质上是动态规划的一种

二维前缀和

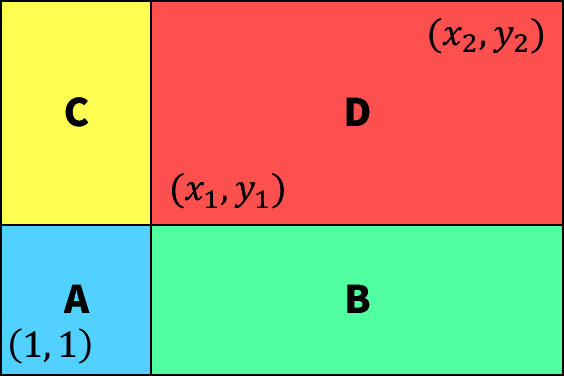
//生成
vector<vector<int>>arr(mat.size()+1,vector<int>(mat[0].size()+1));
for(int i=1;i<=mat.size();i++)
{
    for(int j=1;j<=mat[0].size();j++)
        arr[i][j]=arr[i-1][j]+arr[i][j-1]+mat[i-1][j-1]-arr[i-1][j-1];
}
//查询
int getnum(vector<vector<int>>&arr,int x1,int y1,int x2,int y2)
{
    return arr[x2+1][y2+1]-arr[x2+1][y1]-arr[x1][y2+1]+arr[x1][y1];
}

例题

特殊前缀和

例题

其他前缀

  • 前缀积
  • 对于前缀积，我们可以用除法消去前 l−1 个数对结果的影响
  • 如果有零不能直接除法，需要根据0进行特殊处理
  • 前缀异或
  • 可以再次异或消去前 l−1 个数对结果的影响
  • 前缀与
  • 可以对每一位取前缀，一个区间如果全部是1，那么与就是1，否则是0

例题

差分

  • 差分数组方便修改，但是每次查询都需要遍历一遍差分数组（做一遍前缀和）来获得原数组。
  • 可以快速对元素进行范围修改O(1)，但是查询性能较差O(n)
  • 若将al~ar之间的元素全部加上k，只有al-al-1会增大k，ar+1-ar会减小k
  • dif[l]+=k dif[r+1]-=k

二维差分

  # 生成差分
  state[r1][c1] += 1
  state[r1][c2 + 1] -= 1
  state[r2 + 1][c1] -= 1
  state[r2 + 1][c2 + 1] += 1

三维差分*

D[num(x1[i],  y1[i],  z1[i])]   += d[i];
D[num(x2[i]+1,y1[i],  z1[i])]   -= d[i];
D[num(x1[i],  y1[i],  z2[i]+1)] -= d[i];
D[num(x2[i]+1,y1[i],  z2[i]+1)] += d[i];
D[num(x1[i],  y2[i]+1,z1[i])]   -= d[i];
D[num(x2[i]+1,y2[i]+1,z1[i])]   += d[i];
D[num(x1[i],  y2[i]+1,z2[i]+1)] += d[i];
D[num(x2[i]+1,y2[i]+1,z2[i]+1)] -= d[i];

  • 三维前缀和还原

  • 分维度分别求和（二维前缀和同样可以使用这种方式）

```c++ for (int i=1; i<=A; i++) for (int j=1; j<=B; j++) for (int k=1; k<C; k++) //把x、y看成定值，累加z方向 D[num(i,j,k+1)] += D[num(i,j,k)]; for (int i=1; i<=A; i++) for (int k=1; k<=C; k++) for (int j=1; j<B; j++) //把x、z看成定值，累加y方向 D[num(i,j+1,k)] += D[num(i,j,k)]; for (int j=1; j<=B; j++) for (int k=1; k<=C; k++) for (int i=1; i<A; i++) //把y、z看成定值，累加x方向 D[num(i+1,j,k)] += D[num(i,j,k)];

```

例题

c++ class Solution { public: vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) { vector<int>ans(n); for(auto &a:bookings)//构建差分数组 { ans[a[0]-1]+=a[2]; if(a[1]<n) ans[a[1]]-=a[2]; } for(int i=1;i<n;i++)//还原元素 { ans[i]+=ans[i-1]; } return ans; } };

```python

 # 前缀还原
 for i in range(1, len(state) - 1):
              for j in range(1, len(state[0]) - 1):
                  state[i][j] += state[i][j - 1] + state[i - 1][j] - state[i - 1][j - 1]
 ```