博弈¶
公平游戏¶
ICD公平组合游戏¶
- 有两个玩家,游戏规则对两人公平
- 游戏状态优先,能走的步数有限
- 两人轮流走,一个玩家不能走步时游戏结束
- 游戏的局势不能区分玩家身份
- 给定初始局势,并且指定先手玩家,如果双方都采用最优策略那么获胜者是确定的,即ICG问题存在必胜策略

简单游戏¶
简单巴什游戏¶
- 有n个石子,一次最多取m个:
- 若n%(m+1)=0则后手获胜,先手取k个,后手可以通过取n-k个维持这个状态
- 其他情况下先手获胜,因为先手可以用一次操作让局势转移到n%(m+1)=0
- 每次只能取pk个,p是素数,k为自然数
- 首先1~5都可以使用素数的幂来表示,而6不可以
- 如果剩余的数是6的倍数则后手赢
- 如果不是则可以取一次后转化为是的条件
威佐夫游戏¶
-
有两堆石子,一次可以从一堆取走任意石子或者在两堆种取走相同数目的石子。
-
先手必输的局面为奇异局势\((0,0)、(1,2)、(3,5)、\dots\)
-
插值递增,且每个局势的第一个值是在钱没没有出现过的最小自然数,实际上第一个数就是局势的差值乘以1.618取整
-

-
```c++ int main(){ int n, m; double gold = (1 + sqrt(5))/2; //黄金分割=1.618033988749894…精确到小数15位 while(cin >> n >> m){ int a = min(n, m), b = max(n, m); double k = (double)(b – a); int test = (int)(k*gold); //乘以黄金分割数,然后取整 if(test == a) cout << 0 << endl; //先手败 else cout << 1 << endl; //先手胜 } return 0; }
```
P-position N-position 动态规划¶
- P-position表示前一个玩家(刚走过)的必胜位置,N-position表示下一个玩家的必胜位置(当前状态)
- 对于当前玩家P表示先手必败,N表示先手必胜
巴什游戏¶
- 巴什游戏的通用方法,如可以取的数为集合\(\{a_1,\dots,a_k\}\)
- 以{1,4}为例

- 可以从左到右计算,使用递推(动态规划)
- 如2时只能选择拿1个,那就转化为对手的N就是自己的P
- 当一个点存在多种选择方案时,如5,可以选择1,4,只有有一种方案可以使得对手是p,那么自己就是n,否则说明无论选什么都必败,故为p。
- 通常来说pn表的变化存在周期性如该问题周期为5
尼姆游戏¶
- 有n堆石子\(\{a_1,\dots,a_n\}\),两个玩家每次从任一堆中取走任意数量的石子,拿走最后一堆的人获胜
- 若\(a_1\bigoplus\dots\bigoplus a_n!=0\)则先手必胜即N,否则先手必败即P
- 平衡态与非平衡态,最终所有石子堆都为0,异或为0,将这种局势称为平衡态,由于只需要一次操作就一定可以将不平衡态转化为平衡态,因此处于平衡态的必败,处于非平衡态的必胜
- 对于两堆的特殊情况,可以这样理解:
- 两个必败态游戏组合成的游戏是必败态。因为先手必然会把游戏变成必胜态和必败态的组合给后手,后手可以通过聪明的操作把其中的必胜态变成必败态给先手,这样先手拿到的一直是两个必败态,先手输。
- 必败态和必胜态的组合成的游戏是必胜态。先手可以通过聪明的操作把必胜态变成必败态给对手,这样对手就会作为两个必败态组合的游戏的先手,根据上一条结论,我们知道对手必败,也就是先手必胜。
- 两个必胜态组合生成的游戏可能是必胜态,也可能是必败态。首先先手肯定不能把其中一个必胜态变成必败态,因为这样会给后手一个(必败态,必胜态)的局势,这样后手拿到必胜态,后手必胜,所以只能把其中一个必胜态再变成另外一种必胜态。当然,对手也不傻,也会把继续把其中一个必胜态变成另一种必胜态维持下去,但我们这样讨论的默认都是一定会结束的游戏,所以关键节点在于:什么必胜态没办法转换为另一种必胜态,只能转换为必败态。
- N->P:选择一堆具有k个石子的堆,其他n-1堆异或的结果为H,若H<k则可以从k中取出石子,使得k=H即总异或变为0,也就转化为了P(存在多少对k<H就是存在多少可能的方案数)
-
进入P后,取任意石子都至少会使得二进制的一位发生变化,即转化为N
-
c++ int sum=0, ans=0; //sum是Nim-sum,ans是第一步可行方案数 for(int i=0; i<n; i++) sum ^= a[i]; //异或计算,求Nim-sum if(sum==0) cout<<0<<endl; //开始局面是P-position,先手必败 else{ //开始局面是N-position,先手胜 for(int i=0; i<n; i++) if((sum^a[i]) <= a[i]) //计算第一步所有可能方案 ans++; cout<<ans<<endl; }
SG¶
图游戏¶
- 给定一个有向无环图,起点放置棋子,两个玩家交替沿有向边移动棋子,无法移动者判负
- 严格定义:
- 一个DAG\(G(X,F)\),\(X\)是局势的非空集合,F表示对于\(x\in X\)有\(F(x)\subset X\),一个玩家从\(x_0\)先走。然后两个人交替走,在x处可以选择移动到\(y\in F(x)\)
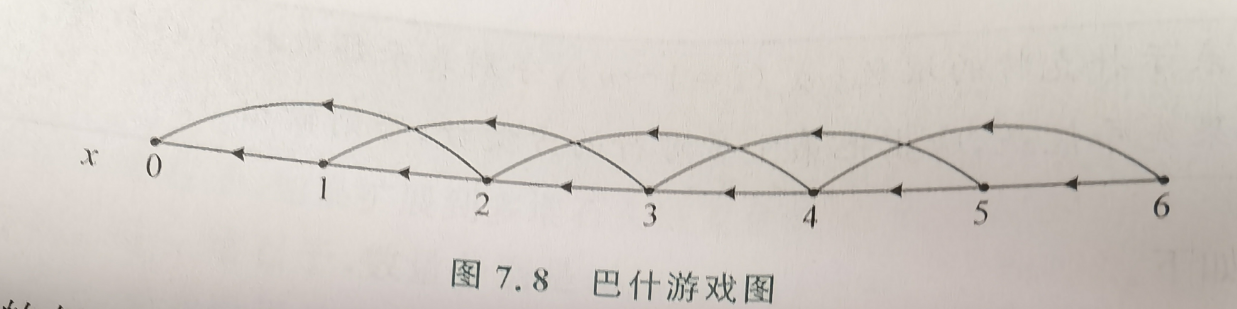
- 巴什游戏、尼姆游戏等ICG问题都可以用图游戏来表示,把每个局势作为一个点,每个局势和后继局势之间连一条有向边就抽象成了图游戏
- 如巴什游戏:\(X=\{0,\dots,n\}\)一次可以拿的石子为\(\{1,2\}\)则可以画出
- 对于尼姆游戏,状态的数目多得多,对于三堆\(\{5,7,9\}\)有\(6*8*10=480\)种局势(三元组)
SG函数¶
-
\(sg(x)\)表示不等于其后继节点得\(sg\)值得最小非负整数(MEX)
-
\(SG(x)=MEX\{SG(y)|y\rightarrow x\}\)
-
我们将必败点称作0级必胜点,\(n\)级必胜点可以一步走到\([0,(n-1)]\)级必胜点
-
\(SG(x)\)就是表示一个点的必胜点的级别
-
同级必胜点组成的游戏是必败的(先手降低一个,后手也可以降低一个),不同级必胜点组成的游戏是必胜的(先手可以将其转化为同级必胜点),可以通过异或来判断必胜级别是否全部相同,若\(sg(x_1)\bigoplus,\dots\bigoplus sg(x_n)=0\)先手必败,否则先手必胜(尼姆游戏实际上就是升维的组合巴什游戏)
-
```c++ const int MAX = 1001; int n, m, sg[MAX], s[MAX]; void getSG(){ memset(sg, 0, sizeof(sg)); for (int i=1; i<=n; i++){ memset(s, 0, sizeof(s)); for (int j=1; j<=m && i-j>=0; j++) s[sg[i-j]] = 1; //把i的后继点放到集合s中(如果取值离散,在一个集合种取值,只需要用arr[]数组中元素替代j) for (int j=0; j<=n; j++) //计算sg[i](MEX) if(!s[j]){ sg[i]=j; break;} } }
```
例子¶
- 巴什游戏为例
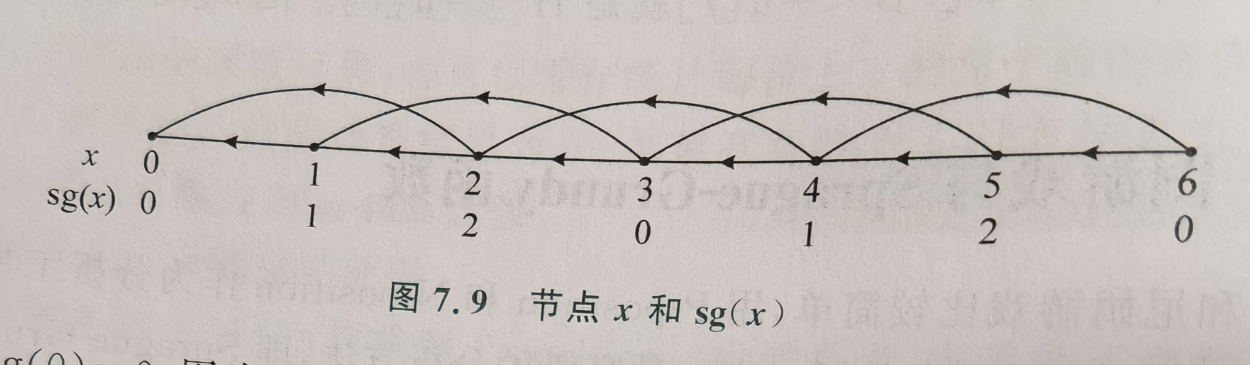
- \(sg(x)=0\)的点就是必败点
-
对于\(x=0\)该点显然是一个p点,所有点最终都会通向这个点(游戏会结束),当玩家处于\(sg(x)=0\)的点时一定可以移动到\(sg(x)!=0\)的点之后又一定移动到\(sg(x)=0\)的点
-
解决尼姆游戏
- 计算每一堆石子的sg值,若\(sg(x_1)\bigoplus,\dots\bigoplus sg(x_n)=0\)先手必败,否则先手必胜
例题¶
- 464. 我能赢吗
- 状态压缩+记忆化搜索
- 294. 翻转游戏 II
- 877. 石子游戏
- 用dp[i] [j]记录剩余石子状态为i-j时,当前玩家领先的分数
- dp[i][j]=max(piles[i]−dp[i+1][j],piles[j]−dp[i][j−1]),每个玩家都希望自己领先尽可能多的分数
- P5675 取石子游戏
- 方案计数:异或为0的组合种选择任意一堆;异或不为0,选择其中一堆x满足x小于组合中其他堆的异或(这样可以保证无法通过一次操作使得异或为0)
-
可以先枚举第一个选择的堆,然后寻找异或大于等于该堆的组合,就可以得到结果
- 对点i的可访问次数\(a_i\)分析,若\(a_i\)为偶数则该点必胜(拥有一次翻转机会),如果为奇数必胜当且仅当后面m个数存在必败态,否则就为必败态;此外一个必败态可以使得前面m个位置都是必生态;并且区间最右侧的奇数点一定是必败态
- 用g[i]表示[1,i]内最右奇数点,i=g[r]为必败态,前面m个必胜,因此上一个必败态在g[i-m-1],如果这样能跳到l,l就是必败点
- 可以连接所有的i和g[i-m-1],者样问题就变成了查询l与g[r]是否存在后继关系
- 通过预处理建树,每次查询比较时间戳,复杂度为\(O(q)\)