Skip to content

哈希

概念

  • 分类
    • 闭散列表：闭散列也称为开放地址法，是在线性存储空间上的解决方案。当发生冲突时，采用冲突处理方法在线性存储空间上探测其他的位置。根据增量序列的不同，开放地址法又分为线性探测法、二次探测法等等。
      • 问题：容易产生堆积问题；需要额外的字段表示节点状态，记录数据是被删除的而不是空白的。下次查找的时候继续向后走
      • hash‘(key) = (hash(key) + d) % m
    • 开散列表：开散列的方案是建立一个邻接表结构，以哈希函数的值域作为邻接表的表头数组，映射后的值相同的原始信息放到同一个桶对应的链表里，插到相应的表头上。相当于在哈希表每一个节点持有一个链表，某个数据项对的关键字还是像通常一样映射到哈希表的节点中，而数据项本身插入到节点持有的链表中。发生冲突时，在链表后面追加数据。
      • 问题：存储的记录是随机分布在内存中的，这样在查询记录时，相比结构紧凑的数据类型，哈希表的跳转访问会带来额外的时间开销。

应用

分桶算法

  • 分桶法是把一排元素(key)按照某种标准放到各个桶中，每个桶分别维护自己内部的信息，外部只需要管理各个桶即可，提高计算的效率。

桶排序

分桶依据：频率、斜率及数字特征等等

前缀和加哈希表

与其他数据结构结合

  • 由于哈希表中的元素排列具有无序性，为了实现按照一定的顺序添加和删除元素，可以使用vector、list、deque等辅助记录元素顺序。
  • 与平衡树结合：set、map
    • 利用其有序性方便高效的解决问题，并使用成员函数lower_bound,upper_bound二分搜索加速。
    • 911. 在线选举
      • 结合动态规划思想，预处理出所有结果
    • 1146. 快照数组
    • 981. 基于时间的键值存储
    • 1348. 推文计数 
      class TimeMap {
public:
    TimeMap() {

    }

    void set(string key, string value, int timestamp) {
        check[key][timestamp]=value;
    }

    string get(string key, int timestamp) {
        auto it=check[key].upper_bound(timestamp);//找到第一个更大的时间
        if(it==check[key].begin())//不存在<=的元素
            return "";
        else
        {
            it--;
            return it->second;
        }
    }
    unordered_map<string,map<int,string>>check;//外层不需要有序，内层按照时间顺序进行排列
};

与双向链表构建有顺序的字典

  • 带顺序的字典
  • 可以在O（1）时间完成增删改查
  • 不同排序顺序主要体现在对链表的调整不同

模板

  • c++中要用unordered_map和list来实现
  • 带更新顺序的字典，就是在字典的基础上，在维护数据过程中需要维护数据的更新顺序。这里的更新顺序与前面提到的插入顺序的区别是，插入一个已经存在的元素的时候也算是一次更新。
  • 链表是天然地具有先后顺序的线性结构，插入的时候直接在末尾插入即可，链表中的元素直接保持了插入的顺序。删除的时候我们需要查找待删除的元素在链表中的位置。链表的查找性能不好，但是可以将数据的 key 和链表节点分别作为哈希映射的键和值。这样查询的需求就可以通过哈希映射找到链表中的节点，而插入顺序直接由链表的插入维护。
  • 思想：用双向链表辅助哈希表来维护一个顺序。 
    class OrderedDict {//以更新顺序为例
public:
    int size() {
        return linkedlist.size();
    }

    int get(char key) {//查看元素的value
        auto it = mapping.find(key);
        if(it == mapping.end())
            return -1;
        else
            return (it -> second).first;
    }

    void put(char key, int index) {//插入元素，如果已经有了就删除重新插入、
        auto it = mapping.find(key);
        if(it != mapping.end())
            remove(key);
        linkedlist.push_front(key);
        mapping.insert(pair<char, pair<int, list<char>::iterator>>(key, pair<int, list<char>::iterator>(index, linkedlist.begin())));
    }

    void remove(char key) {
        auto it = mapping.find(key);
        if(it != mapping.end())
        {
            auto iter = (it -> second).second;
            linkedlist.erase(iter);
            mapping.erase(it);
        }
    }

    int remove_bottom()//移除最先插入的元素
    {
        char key = linkedlist.back();
        int index = mapping[key].first;
        mapping.erase(mapping.find(key));
        linkedlist.pop_back();
        return index;
    }

private:
    unordered_map<char, pair<int, list<char>::iterator>> mapping;//<key,<value,链表迭代器>>(我觉得//<key,iterator>就够了)
    list<char> linkedlist;
};

带更新顺序的字典

  • 首先是常规的插入、删除、查询功能，与哈希表的插入、删除、查询一样，只是有一点变化：在插入时，如果 key 已经存在，则将对应的链表节点调度到表头。（在put时放在头）
  • 340. 至多包含 K 个不同字符的最长子串
    • 也可以用multiset代替，但是效率更高。

带访问顺序的字典

  • put 中如果达到 capacity 需要删除链表的尾部节点；get 时，如果有值，则需要将对应的链表节点调度到表头。（在put和get时放在头）
  • 146.LRU缓存

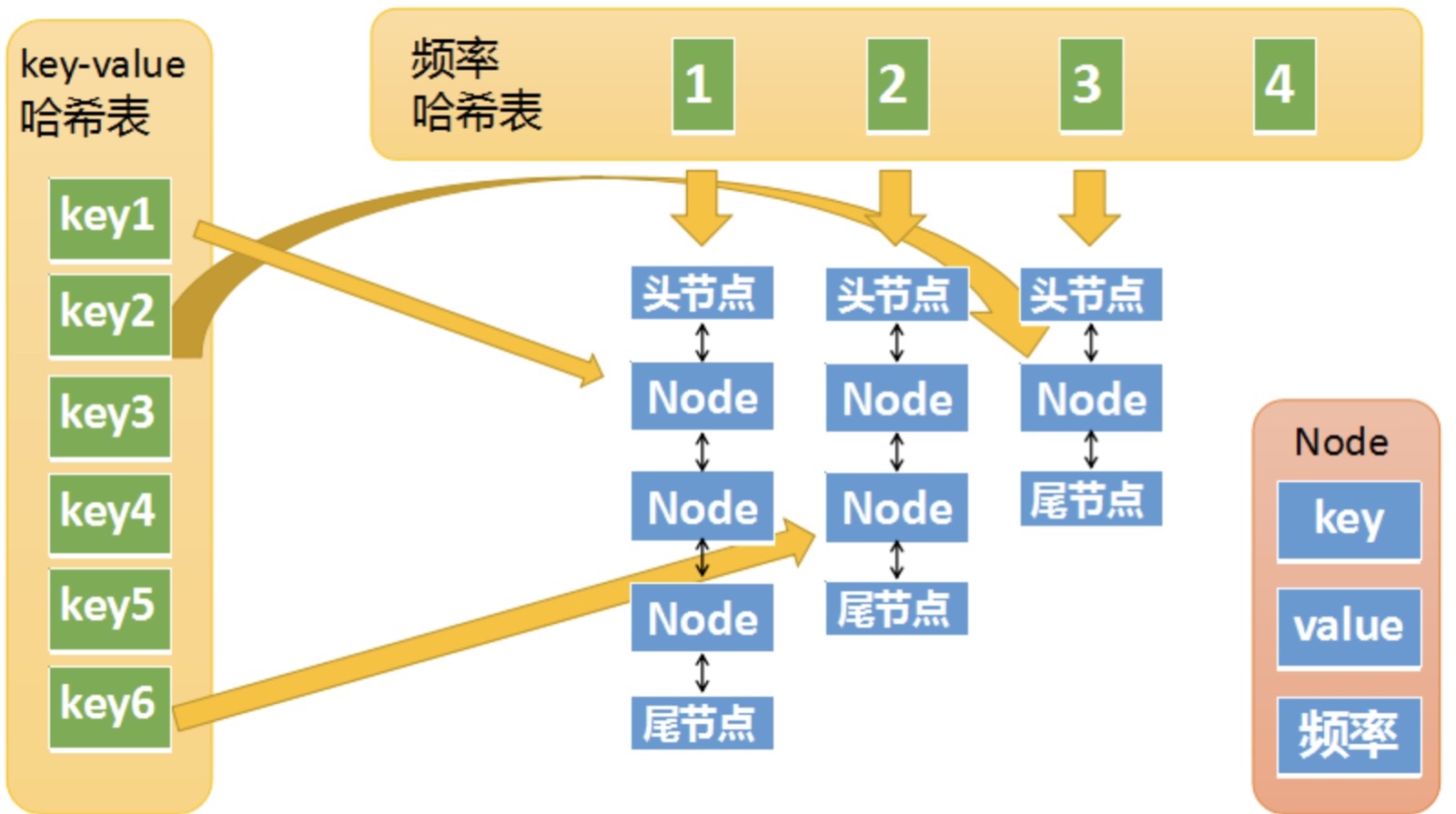
带频率顺序的字典（难）

  • put 中如果达到 capacity 需要删除访问次数最低的节点，当访问次数最低的节点有多个时，删最早访问的那个；get 时，如果有值，则需要将访问次数加 1 并将对应的链表节点调度到表头
  • LFU与LRU原理
  • 460. LFU 缓存
    • 使用双哈希表，与LRU相比用一个哈希表维护出现频率<频率,双链表>，实际上对于同一出现频率内的元素相当于用许多LRU机制进行维护；另一个hash表则维护所有的元素（这与LRU是一致的）
  • 432. 全 O(1) 的数据结构
    • 数据结构微调（内层哈希表，外层双链表）
  • 1224. 最大相等频率
    • 类似思路（双hash表）

stl库

自定义hash函数

  • 包含：hash\哈希函数和 equal_to\比较规则(注意：自定义的两个函数必须都是双 const 的)
    • 哈希函数的作用: 根据各个键值对中键的值，计算出一个哈希值，哈希表可以根据该值判断出该键值对具体的存储位置。
    • 比较函数的作用: 当键是自定义对象或容器时，定义什么叫两个键相等，两个不相等的键的哈希值可能是一样的，这是哈希冲突的来源。
    • STL 中的哈希函数不是普通函数，而是一个函数对象类。因此想要自定义哈希函数，需要自定义一个函数对象类。
  • hash\
    • 可以用提供的现成的进行组合，也可以自定义
    • 如 hash\()(s)+hash\()(n) 
      class MyHash {
public:
    int operator()(const Point &A) const {
        return A.get_slope();//返回值自定义
    }
};
//使用
unordered_set<Point, MyHash> point_setting;//传入hash函数对象
  • equal_to\
    • 如果类型定义了==则不需要再去定义 equal_to\
    • 也可以通过直接定义 equal_to\来实现

例

  • 1128. 等价多米诺骨牌对的数量 
    class Solution {
public:
    struct item{
        item(int x,int y):x(x),y(y){}
        int x,y;
        bool operator==(const item&a)const//自定义比较（什么时候对应同一个键，注意为双const）
        {
            return (x==a.x&&y==a.y)||(x==a.y&&y==a.x);
        } 
    };
    struct myhash{
        int operator()(const item&a)const//用系统提供的哈希函数
        {
            return hash<int>()(a.x)+hash<int>()(a.y);
        }
    };
    int numEquivDominoPairs(vector<vector<int>>& dominoes) {
        int ans=0;
        unordered_map<item,int,myhash>check;
        for(auto&a:dominoes)
        {
            check[item(a[0],a[1])]++;
            ans+=check[item(a[0],a[1])]-1;
        }
        return ans;
    }
};

扩展

字符串（数组）哈希(Rabin-Karp 算法)

  • 把任意长度的数组映射成一个非负整数
  • 哈希函数：
    • base：进制基数
    • mod：可以为一个具体值如1e9+7或通过unsigned类型自动实现。

ull a[10010];
char s[10010];
ull BKDRHash(char *s){             //哈希函数
    ull P = 131, H = 0;            //P是进制，H是哈希值
    int n = strlen(s);
    for(int i=0;i<n;i++)
        H = H * P + s[i]-'a'+1;    //H = H * P + s[i];  //两种方法
 //上面三行可以简写为一行：
 // while(*s)   H = H*P + (*s++);
    return H;                      //隐含了取模操作，等价于 H % 264
}
- 计算单个字符串的哈希值

计算全部字串哈希

  • 可以使用前缀和进行计算
  • 前缀计算哈希值进行哈希，比使用 unordered_set\取子串快速的多
  • 例如要长度为 l 的子字符串, (总长为 n)，那么 RK 算法 O (n)而普通 unordered_set\为 O(nl) 
    //base常用31（对字符串来说），mod:1e9+7
//定义为int类型
for (int i = 1; i <= n; ++i) {
            pre[i] = ((LL)pre[i - 1] * base + text[i - 1]) % mod;
            mul[i] = (LL)mul[i - 1] * base % mod;//计算base的i次幂
        }
hash = (pre[r + 1] - (LL)pre[l] * mul[r - l + 1] % mod + mod) % mod;
//unsigned long long定义，操作方便可以自动取余并且发生哈希冲突的可能性更小（常用）
for (int i = 1; i <= n; ++i) {
            pre[i] = pre[i - 1] * base + text[i - 1];
            mul[i] = mul[i - 1] * base;
        }
hash = pre[r + 1] - (LL)pre[l] * mul[r - l + 1];
  • 此类问题通常也可以使用 kmp 算法解决

应用

  • 解决回文串问题
    • 枚举回文串的中心点（分奇偶）
    • 用二分枚举回文串长度，使用字符串哈希判断长度进而确定最长回文串
    • 时间复杂度 \(O(n\log n)\)

  • P3501 [POI2010] ANT-Antisymmetry 

    #include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
const int N = 5e5+10;
char s[N],t[N];
int n,PP =131;
long long ans; 
ull P[N],f[N],g[N];         //P：计算PP的i次方，f：s的前缀哈希值，g：t的前缀哈希值
void bin_search(int x){     //用二分法寻找以s[x]为中心的回文串
    int L=0,R=min(x,n-x);    
    while(L<R){
        int mid = (L+R+1)>>1;
        if((ull)(f[x]-f[x-mid]*P[mid])==(ull)(g[x+1]-g[x+1+mid]*P[mid]))  L = mid;
        else R = mid-1;
    }
    ans += L;              //最长回文串的长度是L，它内部有L个回文串
}
int main(){
    scanf("%d",&n);   scanf("%s",s+1);
    P[0] = 1;
    for(int i=1;i<=n;i++)  s[i]=='1'? t[i]='0':t[i]='1'; //t是反串
    for(int i=1;i<=n;i++)  P[i] = P[i-1]*PP;             //P[i]=PP的i次方
    for(int i=1;i<=n;i++)  f[i] = f[i-1]*PP + s[i];      //求s所有前缀的哈希值
    for(int i=n;i>=1;i--)  g[i] = g[i+1]*PP + t[i);      //求t所有前缀的哈希值(反着计算，用于回文串匹配)
    for(int i=1;i<n;i++)   bin_search(i); 
    printf("%lld\n",ans);
    return 0;
    }

  • 1392. 最长快乐前缀 

    class Solution {
public:
    string longestPrefix(string s) {
        int n = s.size();
        int prefix = 0, suffix = 0;
        int base = 31, mod = 1000000007, mul = 1;
        int happy = 0;
        for (int i = 1; i < n; ++i) {
            //长度为i的前缀
            prefix = ((long long)prefix * base + (s[i - 1] - 97)) % mod;
            //长度为i的后缀
            suffix = (suffix + (long long)(s[n - i] - 97) * mul) % mod;
            if (prefix == suffix) {
                happy = i;
            }
            mul = (long long)mul * base % mod;
        }
        return s.substr(0, happy);
    }
};

  • 1316. 不同的循环子字符串
    • 为了避免冲突，对不同长度字符串单独开辟 unordered_set
  • 1044. 最长重复子串
    • 二分优化长度选择
  • 187. 重复的DNA序列
  • 214. 最短回文串

例题