存图¶
邻接矩阵¶
- 查找边十分方便
- 适用于稠密图,占用空间大
邻接表¶
- 判断两点间是否存在边较慢,节约空间
链式前向星¶
-
使用静态数组进行模拟,效率最高,节约空间,速度快
//存储有向图模板 #include<bits/stdc++.h> using namespace std; const int N = 1e6+5, M = 2e6+5; //1百万个点,2百万条边 int head[N],cnt; //cnt记录当前存储位置 struct { int to, next; //to=边的终点v;next = u的下一个邻居 int w; //边权,根据题目设定有int,double等类型 }edge[M]; //存边 void init(){ //链式前向星初始化 for(int i=0; i<N; ++i) head[i] = -1; //点初始化 for(int i=0; i<M; ++i) edge[i].next = -1; //边初始化 cnt = 0; } void addedge(int u, int v, int w){ //前向星存边(u,v),边的权值为w edge[cnt].to = v; edge[cnt].w = w; edge[cnt].next = head[u]; head[u] = cnt++; } -
遍历方式
for(int i=head[u]; ~i; i=edge[i].next) -
将next初始化为0的简洁版本
using namespace std;
const int N = 1e6+5, M = 2e6+5; //1百万个点,2百万个边
int cnt=0,head[N]; //cnt等于其他值也行,根据题目要求赋值
struct {int to, next, w;} edge[M];
void addedge(int u,int v,int w) {
cnt++;
edge[cnt].to = v;
edge[cnt].w = w;
edge[cnt].next = head[u];
head[u] = cnt;
}
int main() {
int n, m; cin>>n>>m;
for(int i=0;i<m;i++){int u,v,w; cin>>u>>v>>w; addedge(u,v,w);}
for(int i=head[2]; i>0; i=edge[i].next) //遍历结点2的所有邻居
printf("%d ",edge[i].to); //输出:5 4 3 1
return 0;
}
二分图¶
匈牙利算法(匹配)¶
- 求解二分图的最大匹配问题
- 思想:使用增广路径进行匹配

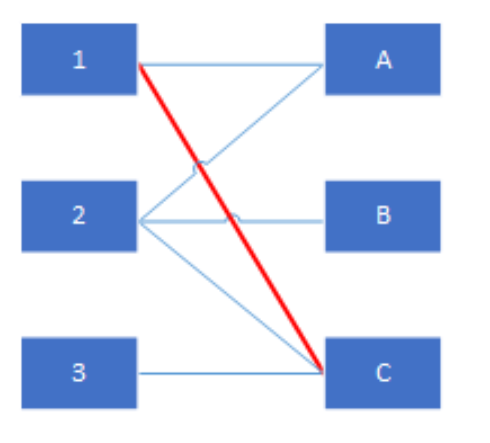
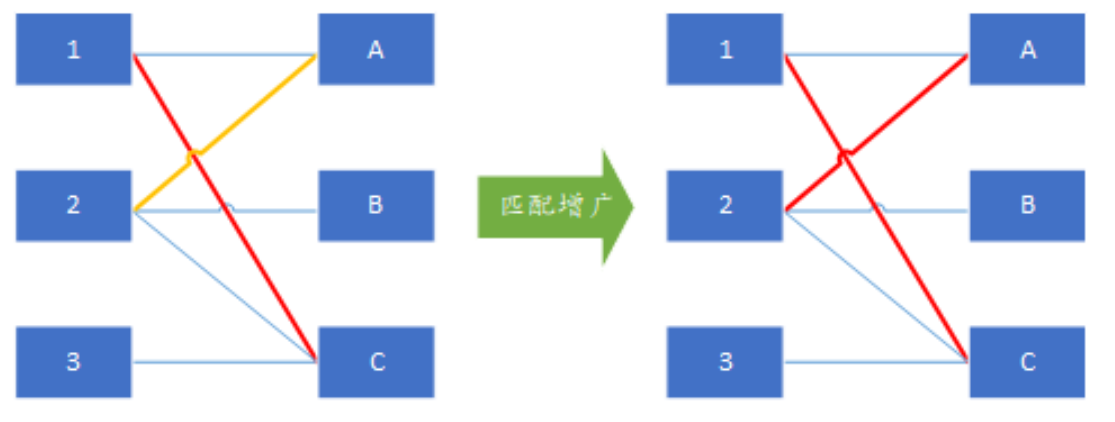
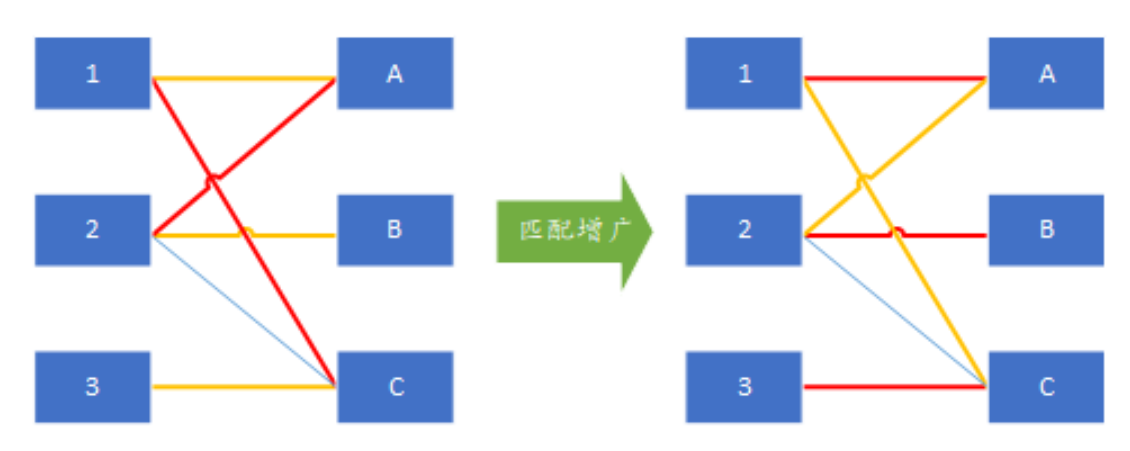
- 时间复杂都\(O(nm)\)
模板¶
const int maxn=105;
int n,m;
int match[maxn];
int vis[maxn];
int e[maxn][maxn];
int dfs(int u){
for(int i=1;i<=n;i++){
if(!vis[i]&&e[u][i]==1){
vis[i]=1;//标记顶点i已访问过
if(!match[i]||dfs(match[i])){//如果点i未被配对或者找到了新的配对、
match[i]=u;//更新配对关系
match[u]=i;
return 1;
}
}
}
return 0;
}
int main()
{
int u,v;
int sum=0;
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d %d",&u,&v);
e[u][v]=e[v][u]=1;
}
for(int i=1;i<=n;i++)
match[i]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
vis[j]=0;//清空上次搜索时的标记
if(dfs(i)) sum++;//寻找增广路,如果找到,配对数加1
}
printf("%d\n",sum);
return 0;
}
最短路算法¶

Dijkstra 算法¶
原理¶
- 用于求解带权图的单源最短路径问题
- 即一点到图中任意一点的最短路径
- 过程:L(v)表示从原点s到v的最短路径,w(e)表示边的权
- 初始化i=0,S={s}(已经遍历到的点),L(s)=0,其他点L(v)=无穷大
- 对于所有不在S中的点(未找到最短路径)vϵVG-S,L(v)=min{L(v),min uϵs{L(u)+W(u,v)}}更新
- 找到新的具有最小L(v)的v,将其加入S
- 直至做有点都加入S终止
- 如果需要记录最短路径,通常记录上一节点即链式存储
- 还可以用来统计最短路径数目
- 因为优先队列取出最近的点,因此在由一个点向外继续延伸时到这个点的路径数目已经确定下来了
-
模板
#include<bits/stdc++.h>
using namespace std;
const long long INF = 0x3f3f3f3f3f3f3f3fLL; //这样定义的好处是: INF <= INF+x
const int N = 3e5+2;
struct edge{
int from, to; //边:起点,终点,权值。起点from并没有用到,e[i]的i就是from
long long w; //边:权值
edge(int a, int b,long long c){from=a; to=b; w=c;}
};
vector<edge>e[N]; //存储图
struct node{
int id; long long n_dis; //id:结点;n_dis:这个结点到起点的距离
node(int b,long long c){id=b; n_dis=c;}
bool operator < (const node & a) const
{ return n_dis > a.n_dis;}
};
int n,m;
int pre[N]; //记录前驱结点
void print_path(int s, int t) { //打印从s到t的最短路
if(s==t){ printf("%d ", s); return; } //打印起点
print_path(s, pre[t]); //先打印前一个点
printf("%d ", t); //后打印当前点。最后打印的是终点t
}
long long dis[N]; //记录所有结点到起点的距离
bool done[N]; //done[i]=true表示到结点i的最短路径已经找到
void dijkstra(){
int s = 1; //起点s = 1
for (int i=1;i<=n;i++) {dis[i]=INF; done[i]=false; } //初始化
dis[s]=0; //起点到自己的距离是0
priority_queue <node> Q; //优先队列,存结点信息
Q.push(node(s, dis[s])); //起点进队列
while (!Q.empty()) {
node u = Q.top(); //pop出距起点s距离最小的结点u
Q.pop();
if(done[u.id]) continue; //丢弃已经找到最短路径的结点。即集合A中的结点
done[u.id]= true;
for (int i=0; i<e[u.id].size(); i++) { //检查结点u的所有邻居
edge y = e[u.id][i]; //u.id的第i个邻居是y.to
if(done[y.to]) continue; //丢弃已经找到最短路径的邻居结点
if (dis[y.to] > y.w + u.n_dis) {
dis[y.to] = y.w + u.n_dis;
Q.push(node(y.to, dis[y.to])); //扩展新邻居,放到优先队列中
pre[y.to]=u.id; //如果有需要,记录路径
}
}
}
// print_path(s,n); //如果有需要,打印路径: 起点1,终点n
}
int main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) e[i].clear();
while (m--) {
int u,v,w; scanf("%d%d%lld",&u,&v,&w);
e[u].push_back(edge(u,v,w));
// e[v].push_back(edge(v,u,w)); //本题是单向边
}
dijkstra();
for(int i=1;i<=n;i++){
if(dis[i]>=INF) cout<<"-1 ";
else printf("%lld ", dis[i]);
}
}
- Dijkstra 求所有点相互的最短距离事件复杂度为 \(O(nm\log m)\) 相对较优,但是无法处理负边
- floyd 时间复杂度为 \(O(n^3)\)
- spfa 最差为 \(O(n^2m)\)
Johnson 算法¶
- 对 Dijkstra 修改,求所有点对之间的最短距离,效率较高并且可以处理负边的情况
- 新建一个虚拟节点,从这个点向其它所有点连一条边权为 0 的边
- 接下来用 Bellman-Ford 算法求出从 0 号点到其他所有点的最短路,记为 \(h_i\)
- 对于从 \(u\) 到 \(v\) 边权为 \(w\) 的边将边权设置为 \(w+h_{u}-h_{v}\)
- 之后再以每个点为起点做一次 Dijkstra
- 时间复杂度为 \(O(nm\log m)\)
#include <cstring> #include <iostream> #include <queue> #define INF 1e9 using namespace std; struct edge { int v, w, next; } e[10005]; struct node { int dis, id; bool operator<(const node& a) const { return dis > a.dis; } node(int d, int x) { dis = d, id = x; } }; int head[5005], vis[5005], t[5005]; int cnt, n, m; long long h[5005], dis[5005]; void addedge(int u, int v, int w) { e[++cnt].v = v; e[cnt].w = w; e[cnt].next = head[u]; head[u] = cnt; } bool spfa(int s) { queue<int> q; memset(h, 63, sizeof(h)); h[s] = 0, vis[s] = 1; q.push(s); while (!q.empty()) { int u = q.front(); q.pop(); vis[u] = 0; for (int i = head[u]; i; i = e[i].next) { int v = e[i].v; if (h[v] > h[u] + e[i].w) { h[v] = h[u] + e[i].w; if (!vis[v]) { vis[v] = 1; q.push(v); t[v]++; if (t[v] == n + 1) return false; } } } } return true; } void dijkstra(int s) { priority_queue<node> q; for (int i = 1; i <= n; i++) dis[i] = INF; memset(vis, 0, sizeof(vis)); dis[s] = 0; q.push(node(0, s)); while (!q.empty()) { int u = q.top().id; q.pop(); if (vis[u]) continue; vis[u] = 1; for (int i = head[u]; i; i = e[i].next) { int v = e[i].v; if (dis[v] > dis[u] + e[i].w) { dis[v] = dis[u] + e[i].w; if (!vis[v]) q.push(node(dis[v], v)); } } } return; } int main() { ios::sync_with_stdio(false); cin >> n >> m; for (int i = 1; i <= m; i++) { int u, v, w; cin >> u >> v >> w; addedge(u, v, w); } for (int i = 1; i <= n; i++) addedge(0, i, 0); if (!spfa(0)) { cout << -1 << endl; return 0; } for (int u = 1; u <= n; u++) for (int i = head[u]; i; i = e[i].next) e[i].w += h[u] - h[e[i].v]; for (int i = 1; i <= n; i++) { dijkstra(i); long long ans = 0; for (int j = 1; j <= n; j++) { if (dis[j] == INF) ans += j * INF; else ans += j * (dis[j] + h[j] - h[i]); } cout << ans << endl; } return 0; } - P5905 【模板】全源最短路(Johnson) - 洛谷 | 计算机科学教育新生态
例题¶
- 882. 细分图中的可到达节点
- 自定义权值
- 1631. 最小体力消耗路径
- 778. 水位上升的泳池中游泳
- 1976. 到达目的地的方案数
- 小心溢出,全要用long long,以及LONG_MAX
- 2203. 得到要求路径的最小带权子图
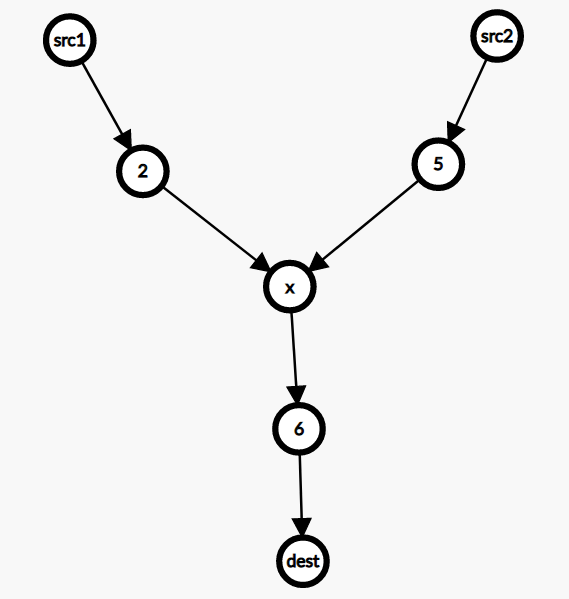
- 两个点到一个点的路径生成的子图权值和的最小值
- 我们可以枚举三岔口的交点 xx,然后求 src1和 src2 到 x的最短路,以及 x 到 dest 的最短路,这可以通过在反图(即所有边反向后的图)上求从 dest出发的最短路得出。累加这三条最短路的和,即为三岔口在 x 处的子图的边权和。枚举所有 x,最小的子图的边权和即为答案。
long long minimumWeight(int n, vector<vector<int>> &edges, int src1, int src2, int dest) {
vector<vector<pair<int, int>>> g(n), rg(n);
for (auto &e: edges) {
int x = e[0], y = e[1], wt = e[2];
g[x].emplace_back(y, wt);
rg[y].emplace_back(x, wt);
}
auto d1 = dijkstra(g, src1);
、、、、auto d2 = dijkstra(g, src2);
auto d3 = dijkstra(rg, dest);
long ans = LONG_MAX / 3;//dijkstra中用LONG_MAX/3初始化,意味着找不到路径
for (int x = 0; x < n; ++x)//枚举x
ans = min(ans, d1[x] + d2[x] + d3[x]);
return ans < LONG_MAX / 3 ? ans : -1;
}
class Solution {
public:
vector<vector<int>>move{{},{0,1},{0,-1},{1,0},{-1,0}};
int minCost(vector<vector<int>>& grid) {
vector<vector<int>>ans=dijkstra(grid,make_pair(0,0));
return ans.back().back();
}
vector<vector<int>>dijkstra(vector<vector<int>>&grid,pair<int,int>start)
{
vector<vector<int>>dist(grid.size(),vector<int>(grid[0].size(),INT_MAX));//初始化权重
dist[start.first][start.second]=0;
priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,greater<>>pq;
pq.emplace(0,start);//权重加坐标的组合
while(!pq.empty())
{
auto[d,x]=pq.top();
pq.pop();
if(d>dist[x.first][x.second])
continue;
for(int i=1;i<=4;i++)
{
pair<int,int>nx=make_pair(x.first+move[i][0],x.second+move[i][1]);
if(nx.first<0||nx.first>=grid.size()||nx.second<0||nx.second>=grid[0].size())
continue;
int weight=dist[x.first][x.second];
if(i!=grid[x.first][x.second])//需要更改箭头的路径
weight++;
if(weight<dist[nx.first][nx.second])
{
dist[nx.first][nx.second]=weight;
pq.emplace(weight,nx);
}
}
}
return dist;
}
};
bellman-ford&SPFA¶
思路¶
- 定理
- 负权环没有最短路径
- 一个有N个顶点的非负权环中两点间最短路径最多经过N-1条边
- 动态规划思想:记录最短路径长度最长为k时的最短值
- dp[k][u]=min(dp[k][u],dp[k-1][v]+w(u,v))
- 优化:使用滚动数组只需要存k和k-1就行
-
bellman算法
- 只用一维数组存储(初始化为正无穷)
- 每次选择入边最小值 dp[u]=min(dp[v]+w(u,v))
- 最多循环 N-1次或 dp[i]不在发生变化(已经到达最优)
- 每次循环遍历一次所有边即可
-
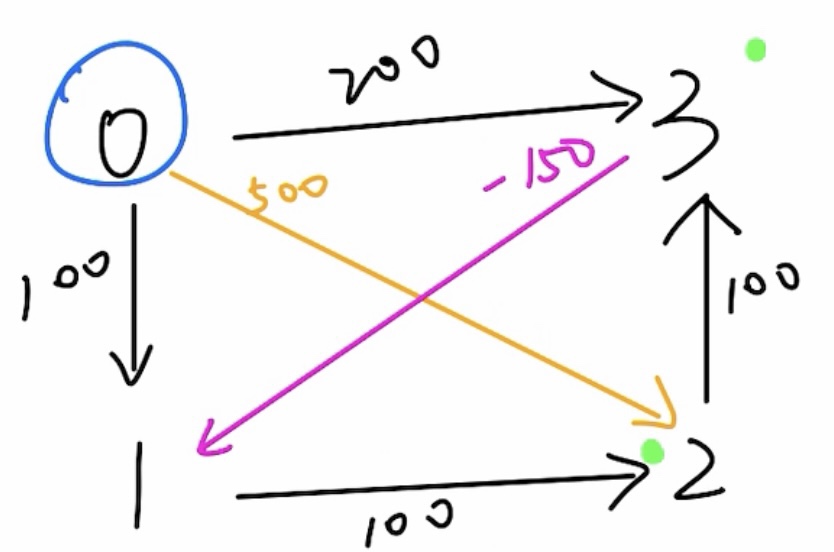
spfa 算法(基于队列优化的 bellman)
- 思想:每轮计算只需要更新上一轮有变化的那些点的邻居
- 主要是通过「队列」来维护我们接下来要遍历边的起点,而不是「Bellman Ford」算法中的任意还没有遍历过的边。每次只有当某个顶点的最短距离更新之后,并且该顶点不在「队列」中,我们就将该顶点加入到「队列」中。一直循环以上步骤,直到「队列」为空,我们就可以终止算法。此时,我们就可以得到「图」中其他顶点到给定顶点的最短距离了。
- 从出发开始便历所有出边,更新到一个点的最短距离,如果更新了则加入队列(并标记为已经加入),之后从队列中依次取出元素进行操作,直至队列为空。
- 如果一个点入队超过 n 次则说明存在负权环
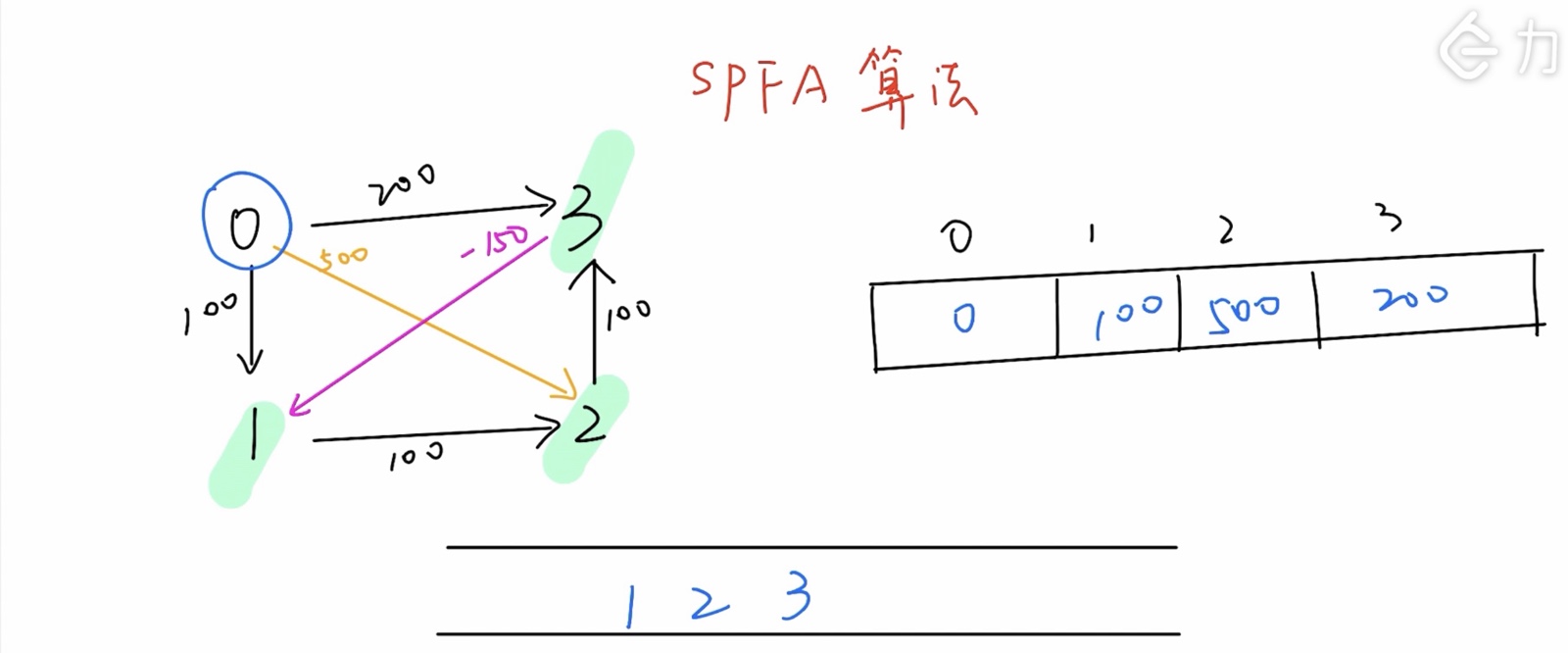
- 接近 Dijkstra 的效率,但是不稳定:最差时间复杂度 O (\(V*E\))
模板¶
-
bellmen
vector<int>dp_l(n,1e7),dp(n,1e7); dp_l[src]=0; dp[src]=0; for(int i=0;i<=k;i++) { for(auto &a:flights) { dp[a[1]]=min(dp[a[1]],dp_l[a[0]]+a[2]); } dp_l=dp; } -
spfa
struct edge { int v, w; }; vector<edge> e[maxn]; int dis[maxn], cnt[maxn], vis[maxn]; queue<int> q; bool spfa(int n, int s) { memset(dis, 63, sizeof(dis)); dis[s] = 0, vis[s] = 1; q.push(s); while (!q.empty()) { int u = q.front(); q.pop(), vis[u] = 0; for (auto ed : e[u]) { int v = ed.v, w = ed.w; if (dis[v] > dis[u] + w) { dis[v] = dis[u] + w; cnt[v] = cnt[u] + 1; // 记录最短路经过的边数 if (cnt[v] >= n) return false; // 在不经过负环的情况下,最短路至多经过 n - 1 条边 // 因此如果经过了多于 n 条边,一定说明经过了负环 if (!vis[v]) q.push(v), vis[v] = 1; } } } return true; } - 入队优化 SLF
- 使用双端队列
- 队头出队后需要把有变化的邻居入队,把入队的点 u 与新队头进行比较如果 dis[u]<dis[v] 则将 u 插入到对头,否则插入到队尾。
- 使得弹出的队头都是路径较短的点加快计算
- 出队优化 LLL
- 计算队列中所有点的距离的平均值每次选一个小于 x 的点出队,即如果队头 u 的 dis[u]>x 就弹出后放入到队尾,直到检查到合法的队头
应用-差分约束¶
- P5960 【模板】差分约束 - 洛谷 | 计算机科学教育新生态
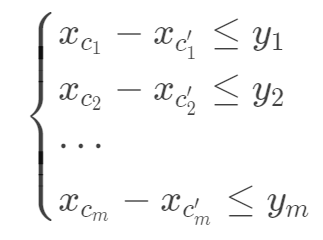
- 差分约束系统要么无解要么有无限解(每个 \(x\) 加上相同值)
- 每个 \(x_{i}\) 为一个节点,进行建图,\(x_{i}-x_{j}\leq c_{k}\) 转化为节点 j 指向节点 i 的长度为 \(c_{k}\) 的有向边
- \(x_{i}-x_{j}\geq c_{k}\) 转化为 \(x_{j}-x_{i}\leq -c_{k}\) 即 i 指向节点 j 的长度为 \(-c_{k}\) 的有向边
- \(x_{i}-x_{j}=c_k\) 转化为两个反向不等式
- 增加一个 0 号点,从 0 号点向其它所有点连一条权值为 0 的边,相当于增加 \(x_{i}\leq x_{0}\)
- 已 0 为起点做 SPFA 如果存在负环则约束无解,因为负环上的两点不再满足原先的约束条件,否则 \(x_i=dis[i]\) 构成差分约束系统的一组解
int main(){ cin>>n>>m; for(int i=1;i<=n;i++)addedge(0,i,0); for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;addedge(u,v,w);} if(spfa(0))cout<<"NO"<<endl; else for(int i=1;i<=n;i++)cout<<dis[i]<<' '; return 0; } //完整处理三种情况: switch (opt) { case 1: { int a, b, c; scanf("%d %d %d", &a, &b, &c); add(a, b, -c); break; } case 2: { int a, b, c; scanf("%d %d %d", &a, &b, &c); add(b, a, c); break; } case 3: { int a, b; scanf("%d %d", &a, &b); add(a, b, 0); add(b, a, 0); break; } }
- P1993 小 K 的农场 - 洛谷 | 计算机科学教育新生态
例题¶
- 边长有限制的最短路径
floyd算法¶
思想¶
- floyd算法
- O(\(n^3\))(适用于 n<300)
- 判断负环:存在 \(dp[i][i]<0\)
模板¶
// 遍历每个节点k,看将该节点作为跳板后是否可以更新节点(距离变短则更新)
for(int k = 0; k < n; ++k){
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j){
if(d[i][k] + d[k][j] < d[i][j])
d[i][j] = min(d[i][k] + d[k][j],d[i][j]);
}
}
}
-
还获取最短路径的版本:
- path[i][j]表示从 i 到 j 下一步的移动方向
- 如 path[i][j]=u ,下一步通过 path[u][j] 继续获取路径上的下一个移动点
#include<bits/stdc++.h> const int INF = 0x3fffffff; const int N = 505; int n, map[N][N], tax[N], path[N][N]; void input(){ for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) { scanf("%d", &map[i][j]); if(map[i][j] == -1) map[i][j] = INF; path[i][j] = j; //path[i][j]: 此时i、j相邻,或者断开 } for(int i = 1; i <= n; i++) scanf("%d", &tax[i]); //交税 } void floyd(){ for(int k = 1; k <= n; k++) for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) { int len = map[i][k] + map[k][j] + tax[k]; //计算最短路 if(map[i][j] > len) { map[i][j] = len; path[i][j] = path[i][k]; //标记到该点的前一个点 } else if(len == map[i][j] && path[i][j] > path[i][k]) path[i][j] = path[i][k]; //若距离相同,按字典序 } } void output(){ int s, t; while(scanf("%d %d", &s, &t)) { if(s == -1 && t == -1) break; printf("From %d to %d :\n", s, t); printf("Path: %d", s); int k = s; while(k != t) { //输出路径从起点直至终点 printf("-->%d", path[k][t]); k = path[k][t]; //一步一步往终点走 } printf("\n"); printf("Total cost : %d\n\n", map[s][t]); } } int main(){ while(scanf("%d", &n), n){ input(); floyd(); output(); } return 0; }
-
- 按照时间顺序逐步使用 k 进行更新
- P1613 跑路 - 洛谷 | 计算机科学教育新生态
- 对长度 \(2^k\) 的 \(k\) 进行倍增,将所有可以满足此条件的表设为 \(1\) ,并在新图上再进行一次 Floyd
应用 - 传递闭包¶
- 用于描述一个图中节点间可达性的关系传递闭包:如果在原图中,从节点A可以通过一系列的边到达节点B,那么在传递闭包中,A和B之间将直接存在一条边。传递闭包可以用于快速回答图中任意两个节点是否可达的问题。
- floyd 求解传递闭包
//朴素方法
for(int k=1; k<=n; k++) //floyd的3重循环
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
if(dp[i][k] && dp[k][j];)
dp[i][j] = 1; //5-6行可以合并为:dp[i][j] |= dp[i][k] & dp[k][j];
- 使用 bitset 优化
- 可以近似达到 \(O(n^2)\) 的时间复杂度,处理 \(n=1000\) 规模大小的数据(使用位运算代替了一层循环)
bitset<N> d[N]; //第三种优化:用bitset加速,能解决N = 1000的问题
void Floyd(){
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
if(d[i][k])
d[i] |= d[k]; //与11-13行等价
}
int main(){
int T; scanf("%d", &T);
while(T--){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) //初始化
for(int j = 1; j <= n; j++) d[i][j] = (i==j);
int u, v;
for(int i = 0; i < m; i++){scanf("%d%d", &u, &v); d[u][v] = 1;}
Floyd();
int tot = 0;
for(int i = 1; i <= n; i++)
for(int j = i+1; j <= n; j++)
if(d[i][j] == 0 && d[j][i] == 0) ++tot;
printf("%d\n", tot);
}
return 0;
}
- Walk - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
- \(f_k[i][j]\)表示长度为\(k\)的\(i\)到\(j\)的路径数目,有\(f_t[i][j]=\sum^n_{k=1}f_{t-1}[i][k]\times f_1[k][j]\)这本质上就是一个矩阵乘法,因此可以使用矩阵快速幂进行优化
搜索#优化¶
最小生成树¶
Prime¶
- 维护两个数组:
- lowcost 数组,表示V中的节点,保存V中每个节点离集合Vnew中所有节点的最短距离。如果节点已经加入到了集合Vnew中,则置为-1
- v 数组,表示V中节点的访问情况,最开始全部为0,表示未加入到Vnew中,若某节点加入到了集合Vnew中, 则将其置为-1
- 过程
- 随机选择一个起点,将其加入到Vnew中。同时,更新此时的数组lowcost和数组v
- 遍历lowcost,寻找lowcost中的最小值min(假设索引为 j ,j为Vnew中离V最近的点),将与索引 j 相对应的节点加入到Vnew中,并更新数组lowcost[j]和数组v[j]。
- 找到lowcost中的最小值 j 后,此时数组lowcost中的所有节点都要更新,因为此时集合Vnew中的节点增加了,集合V中的节点离Vnew的最近距离可能会缩短。
- 根据新加入集合Vnew中的节点j,更新所有的lowcost。
- 重复步骤2,直到访问了所有的节点。
- 使用数组存储复杂度为O(\(V^2\)+E)
- 使用普通堆O(\(E*log(E)\))
- 当E->\(V^2\)时效率低与数组
- 模板
int minCostConnectPoints(vector<vector<int>>& points) { vector<int>v(points.size(),1),dis(points.size(),INT_MAX); int ans=0; v[0]=0; dis[0]=0; for(int i=1;i<points.size();i++) { dis[i]=abs(points[i][0]-points[0][0])+abs(points[i][1]-points[0][1]);//以第一个点出发初始化 } for(int i=1;i<points.size();i++)//依次加点 { pair<int,int>t{-1,INT_MAX}; for(int j=0;j<points.size();j++)//找到最近的点 { if(v[j]) { if(dis[j]<t.second) { t.second=dis[j]; t.first=j; } } } v[t.first]=0; ans+=t.second; for(int j=1;j<points.size();j++)//更新最近值 { if(v[j]) { dis[j]=min(dis[j],abs(points[j][0]-points[t.first][0])+abs(points[j][1]-points[t.first][1])); } } } return ans; }
kruskal¶
- 过程
- 将边从小到大排序
- 依次加入最小生成树中(用并查集检查保证不能成环)
- 直到加入n-1条边为止
- 复杂度O(\(E*log(E)\))
- 模板
int minCostConnectPoints(vector<vector<int>>& points) { initiate(points.size()); int ans=0; auto cmp=[](tuple<int,int,int>&a,tuple<int,int,int>&b){return get<2>(a)>get<2>(b);}; priority_queue<tuple<int,int,int>,vector<tuple<int,int,int>>,decltype(cmp)>edges(cmp);//用优先队列存储边 for(int i=0;i<points.size();i++) { for(int j=i+1;j<points.size();j++) { edges.emplace(i,j,abs(points[i][0]-points[j][0])+abs(points[i][1]-points[j][1]));//构图 } } int n=points.size()-1; while(n--)//选n-1边 { auto[x,y,dis]=edges.top(); while(find(x)==find(y)) { edges.pop();//成环 x=get<0>(edges.top()); y=get<1>(edges.top()); dis=get<2>(edges.top()); } ans+=dis; merge(x,y); edges.pop(); } return ans; }
扩展问题¶
- 最大生成树:只需要改为从大到小选边即可
待看¶
- 严格次小生成树:
- P4180 [BJWC2010] 严格次小生成树 - 洛谷 | 计算机科学教育新生态
- 如果图中所有的边权各不相同则 MST 是唯一的,只有存在等长边时才可能出现相同的 MST。
- 求出 MST 之后尝试把每条不在 MST 上的边放入到 MST 对比环路上的最大边长是否与新加入的边相同
例题¶
Tarjan算法¶
寻找割点¶
思路¶
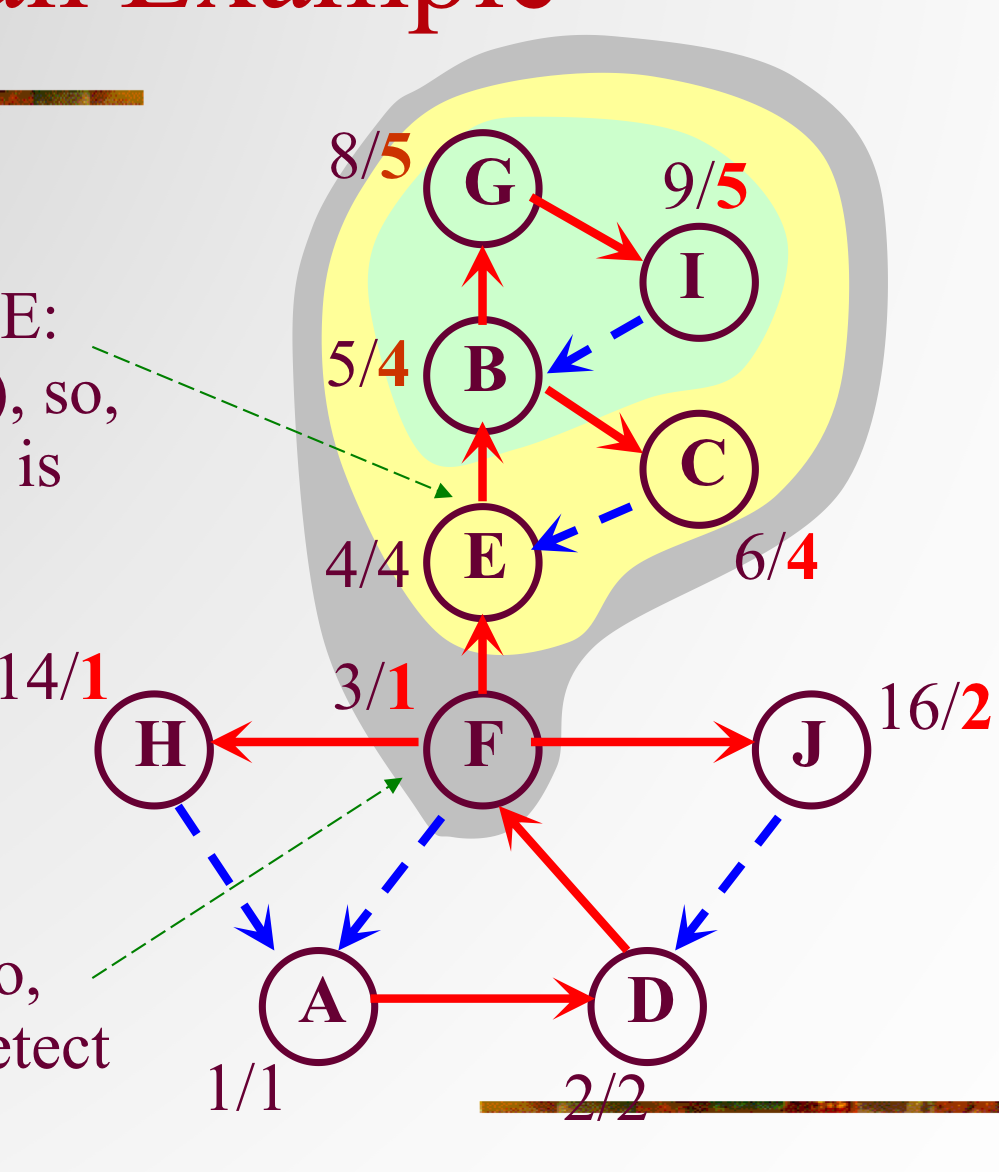
- 判断一个点是否是割点可以通过看其子节点能否不通过该节点向上越(到达一个发现时间更早的点)
- 一个点向上越(最小发现时间)有三种情况
- back=discovertime[v]:自己的发现时间
- back=min(back,discovertime[v]):自己向上越(一个灰色节点)
- back=min(back,wback):通过子节点向上越
- wback为返回值
- 如果一个点的子节点 wback 值大于等于父节点,那么该父节点就是一个割点
模板¶
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int times = 0;
int main(){
int n,m;
cin>>n>>m;
vector<int> G[n+1];
for(int i=0;i<m;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
vector<int>color(n+1), discovertime(n+1), child(n+1);
vector<bool>ans(n+1,false);
function<int(int,int)>dfs;
dfs = [&](int n, int parent)->int{
color[n] = 1;
discovertime[n] = times++;
int back = discovertime[n];
for(auto&a:G[n]){
if(color[a] == 1&&a!=parent){
back = min(back, discovertime[a]);
}
else if(color[a] == 0){
child[n]++;
int wback = dfs(a,n);
if(wback>=discovertime[n]){
ans[n] = true;
}
back = min(back, wback);
}
}
color[n] = 2;
return back;
};
for(int i=1;i<=n;i++){
if(color[i]==0){
dfs(i,-1);
//对于chu'fa节点必须还要满足有大于1个子节点(树)才能是
if(child[i]<2){
ans[i] = false;
}
}
}
return 0;
}
例题¶
寻找割边¶
思路¶
- 与割点类似,修改条件为
wback >discovertime[n] ans.push_back(vector<int>{a,n});- 不需要额外pop
例题¶
双连通分量¶
- 双连通分量是指双连通极大子图
- 点双连通分量:不存在割点
- 不同的点双连通分量最多只有一个公共点,且这个点为割点,割点一定是至少两个点双连通分量的割点
-
边双连通分量:不存在割边
-
如果在使用 tarjan 算法计算割点还想记录下双连通分量,用一个栈保存遍历的边,遇到割点时取出来得到双连通分量。
-
边双连通分量:加多少边可以消除全部割边?
- 先将所有边双连通分量缩为一点,目的就是将得到的树转化为双连通图,至少增加的边数=(总度数为 1 的节点数+ 1 )/2
- tarjan 计算过程中 low 值相同的点位于同一个边双连通分量
强联通分量¶
- 强连通分量的性质:如果一个有向图中,存在一条回路,所有的结点至少被经过一次,这样的图为强连通图。
- low 值相同的点处于相同的强连通分量
#include<bits/stdc++.h>
using namespace std;
const int N = 10005;
int cnt; // 强连通分量的个数
int low[N], num[N], dfn; // low[u]记录u或u的子树能追溯到的最早的祖先的时间戳,num[u]为节点u的时间戳
int sccno[N], stack[N], top; // sccno[u]记录节点u所在的强连通分量编号,stack用于实现DFS的系统栈,top为栈顶指针
vector<int> G[N];
void dfs(int u){
stack[top++] = u; //u进栈
low[u]= num[u]= ++dfn;
for(int i=0; i<G[u].size(); ++i){
int v = G[u][i];
if(!num[v]){ //未访问过的点,继续dfs
dfs(v); //dfs的最底层,是最后一个SCC
low[u]= min( low[v], low[u] );
}
else if(!sccno[v]) //处理回退边
low[u]= min( low[u], num[v] );
}
if(low[u] == num[u]){ //栈底的点是SCC的祖先,它的low = num
cnt++;
while(1){
int v = stack[--top]; //v弹出栈
sccno[v]= cnt;
if(u==v) break; //栈底的点是SCC的祖先
}
}
}
void Tarjan(int n){
cnt = top = dfn = 0;
memset(sccno,0,sizeof(sccno));
memset(num,0,sizeof(num));
memset(low,0,sizeof(low));
for(int i=1; i<=n; i++)
if(!num[i])
dfs(i);
}
Tarjan(n);
for(int i=1;i<=n;++i)
{
Sccnum[sccno[i]]++;
for(int j=0;j<G[i].size();++j)
{
int v = G[i][j];
if(sccno[i]!=sccno[v])
Gscc[sccno[i]].push_back(sccno[v]);
}
}
基环树¶
- 基环树是只有一个环的连通图,有 n 个点和 n 个边
- 无向图上的基环树,在一棵基于无向图的无根树上加一条边形成基环数,删除环上任何一边可以从基环数得到一个普通树
-
有向图上的基环树,一个 DAG 如果在图中加一条边能形成一个自联通的环。如果环外的点只能进入称为内向树,如果无法进入则为外向树(这两个性质可帮助找环)
-
关于基环数的题目应该先找到唯一的环再把环作为虚点
- 对于无向图可以进行类似拓扑排序的操作,最后剩下的就是环(仅适用于有一个环的基环树)
-
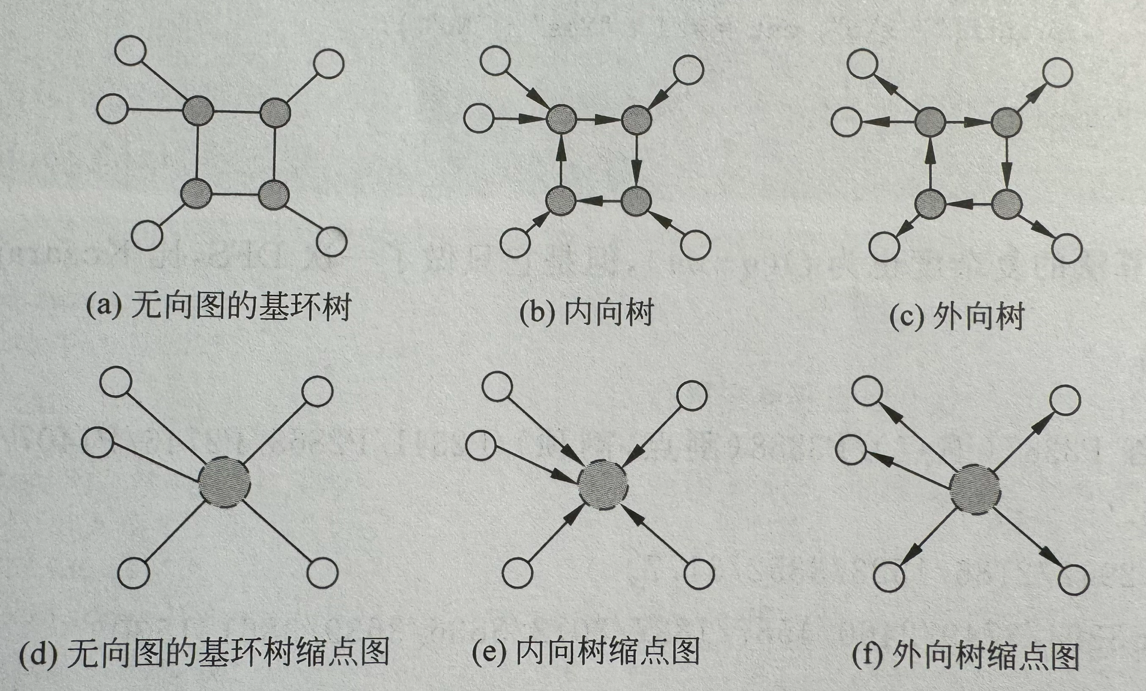
-
通常处理方式:删除一条边拆环转化为普通树上的问题
例题¶
-
P2607 [ZJOI2008] 骑士 - 洛谷 | 计算机科学教育新生态
- 特殊点在于是有 n 点 n 边的基环数而不是普通的树
- 假设如果 a 憎恨 b 则存在一条从 b 指向 a 的边
- 这样的树一定是一棵外向树,只需要逆着有向边就一定能到达环上
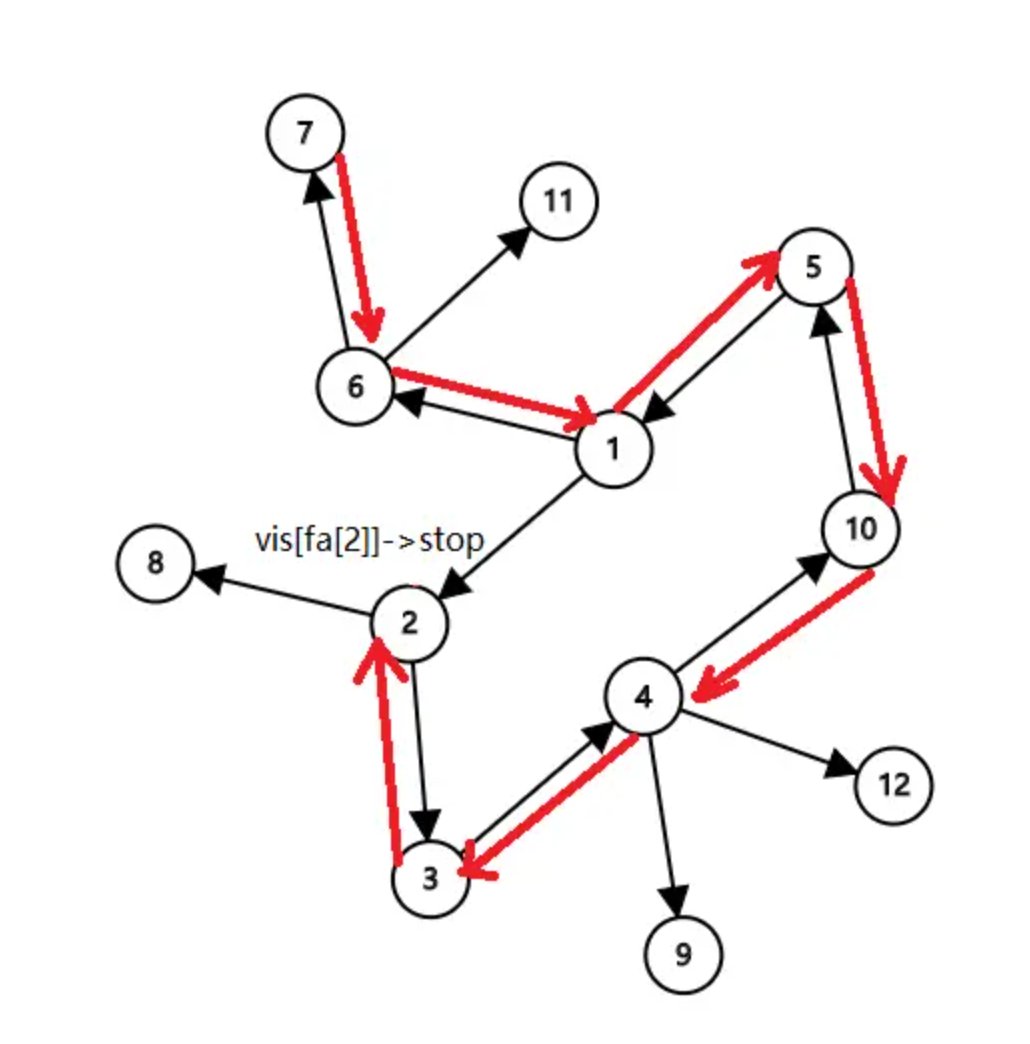
- (发现父亲也被遍历则找到环,两个点都在环上)
- 把这个边断开,就得到了一棵普通树,将这两个点分别作为根节点计算结果
- 对每个连通分量重复操作统计最终的最大值作为结果
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1000005; int head[N],to[N],nxt[N],fa[N],tot,root; ll ans,w[N],f[N][2]; bool vis[N]; void add(int u,int v) { nxt[++tot]=head[u]; head[u]=tot; to[tot]=v; } void dfs(int u){ vis[u]=1; f[u][1]=w[u]; f[u][0]=0; for(int i=head[u];i;i=nxt[i]){ int v=to[i]; if(v==root){ f[v][1]=INT_MIN;//防止选择拆边的两端(也可以考虑之选两端的f[v][0],zhe'e) } else{ dfs(v); f[u][1]+=f[v][0]; f[u][0]+=max(f[v][0],f[v][1]); } } } void FindCircle(int u){//外向环特有的方式 vis[u]=1; while(!vis[fa[u]]){ u=fa[u]; vis[u]=1; } root=u; dfs(u); ll tans=max(f[u][0],f[u][1]); u=fa[u];//以两端为根分别进行计算 root=u; dfs(u); ans+=max(tans,max(f[u][0],f[u][1])); } int main() { int n; scanf("%d",&n); for(int i=1;i<=n;++i){ int v; scanf("%d%d",&w[i],&v); add(v,i); fa[i]=v; } for(int i=1;i<=n;++i){ if(!vis[i]) FindCircle(i); } printf("%lld\n",ans); return 0; }
Hierholzer 算法¶
欧拉回路(通路)¶
- 概念
- 通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路,
- 通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路,
- 具有欧拉回路的无向图称为欧拉图,具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。
- 判定
- 对于无向图 G,G 是欧拉图当且仅当 G 是连通的且没有奇度顶点。
- 对于无向图 G,G 是半欧拉图当且仅当 G 是连通的且 G 中恰有 0 个或 2 个奇度顶点。
- 对于有向图 G,G 是欧拉图当且仅当 G 的所有顶点属于同一个强连通分量且每个顶点的入度和出度相同。
- 对于有向图 G,G 是半欧拉图当且仅当
- 如果将 G 中的所有有向边退化为无向边时,那么 G 的所有顶点属于同一个连通分量;
- 最多只有一个顶点的出度与入度差为 1;
- 最多只有一个顶点的入度与出度差为 1;
- 所有其他顶点的入度和出度相同。
思路¶
- Hierholzer 算法用于在连通图中寻找欧拉路径
- 过程
- 从起点出发,进行深度优先搜索。
- 每次沿着某条边从某个顶点移动到另外一个顶点的时候,都需要删除这条边。
- 如果没有可移动的路径,则将所在节点加入到栈中,并返回。
-
这样就能保证我们可以「一笔画」地走完所有边,最终的栈中逆序地保存了「一笔画」的结果。我们只要将栈中的内容反转,即可得到答案。
-
当我们顺序地考虑该问题时,我们也许很难解决该问题,因为我们无法判断当前节点的哪一个分支是「死胡同」分支。不妨倒过来思考。我们注意到只有那个入度与出度差为 1 的节点会导致死胡同。而该节点必然是最后一个遍历到的节点。我们可以改变入栈的规则,当我们遍历完一个节点所连的所有节点后,我们才将该节点入栈(即逆序入栈)。对于当前节点而言,从它的每一个非「死胡同」分支出发进行深度优先搜索,都将会搜回到当前节点。而从它的「死胡同」分支出发进行深度优先搜索将不会搜回到当前节点。也就是说当前节点的死胡同分支将会优先于其他非「死胡同」分支入栈。
-
在求解欧拉回路前要先检验是否存在欧拉回路,比如对于无向图就要先检查图是否连通,以及度数为奇的点数目是否小于等于 2
模板¶
- 使用邻接矩阵可以更方便的进行删除边的操作以及按照字典序进行访问
- P1341 无序字母对 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int turn(char a){
if(a>='A'&&a<'a') return a-'A';
return a-'a'+26;
}
inline char turn(int a){
if(a>=26) return a-26+'a';
return a+'A';
}
int main(){
int n;
cin >> n;
int a[52][52];
memset(a,0,sizeof(a));
int nums[52];
memset(nums,0,sizeof(nums));
//邻接矩阵建图
for(int i=0;i<n;i++){
string s;
cin >> s;
a[turn(s[0])][turn(s[1])]++;
a[turn(s[1])][turn(s[0])]++;
nums[turn(s[0])]++;
nums[turn(s[1])]++;
}
vector<int>odds;
for(int i=0;i<52;i++){
if(nums[i]%2) odds.push_back(i);
}
if(odds.size()>2){
cout << "No Solution" << endl;
return 0;
}
sort(odds.begin(),odds.end());
int begin = 0;
if(odds.size()){
begin = odds[0];
}
else{
for(int i=0;i<52;i++){
if(nums[i]){
begin = i;
break;
}
}
}
//dfs计算欧拉回路
vector<int>res;
function<void(int)>find;
find = [&](int x){
for(int i=0;i<52;i++){
if(a[x][i]){
a[x][i]--;
a[i][x]--;
find(i);
}
}
res.push_back(x);
};
find(begin);
if(res.size()!=n+1){//较为简洁的对连通性的检验方法
cout << "No Solution" << endl;
return 0;
}
reverse(res.begin(),res.end());
for(int i=0;i<res.size();i++){
cout << turn(res[i]);
}
cout << endl;
return 0;
}
- 对离散图(字符串图)的处理:使用 trie 或哈希将字符串转化为数字再作为普通的图进行处理
- P1333 瑞瑞的木棍 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
- 使用栈模拟
#include <stdio.h> const int N = 1e5; int num[N]; //num[v]:点v后加的数字,num[v]=0~9 int st_edge[10*N], top_s; //栈,用于存边。top_s指示栈顶 char st_ans [10*N]; int top_a; //栈,存序列结果。top_a指示栈顶 int m; void no_dfs(int v){ //模拟递归,递归搜点v的10条边,放进st_edge中 int edge; //边的值 while(num[v]<10){ //在点v(是一个n-1位序列)后加0~9构成10条边 edge=10*v + num[v]; //数字edge代表一个边 num[v]++; //点v添的下一个数字。按字典序递增 st_edge[top_s++] = edge; //把边存入到栈st_edge中,它是字典序的 //printf("%02d -> ",v); //打印边的起点 v = edge%m; //更新起点为原来的终点,往下走。点值等于edge的后几位 //printf("%02d: edge=%03d\n",v,edge); //打印边的终点、边的权值 } } int main(){ int n, edge; while(scanf("%d",&n)&&n!=0){ top_s = top_a = edge = 0; m = 1; for(int i=0;i<n-1;++i) m*=10; //m是点的数量,共10^(n-1)个点 for(int i=0;i<m; i++) num[i]=0; no_dfs(0); //从起点0开始,递归点0的10条边 while(top_s){ //继续走 edge = st_edge[--top_s]; st_ans[top_a++] = edge%10+'0'; //只需要存边值的最后一位 no_dfs(edge/10); //边值的前n-1位,即上一个点,作用类似DFS的回溯 } for(int i=1;i<n;++i) printf("0"); //打印第一组数,就是n个0 while(top_a) printf("%c",st_ans[--top_a]); //打印其他组数,每组打印1位 printf("\n"); } return 0; }
例题¶
- 332. 重新安排行程
- 753. 破解保险箱
- 难建图
class Solution { public: int highest,k; string temp; unordered_map<int,vector<int>>check;//记录边的访问情况 void dfs(int node) { for(int i=0;i<k;i++) { if(check.find(node)==check.end()) check[node]=vector<int>(k,1); if(check[node][i]==0) continue; check[node][i]--; dfs((node*10+i)%highest);//取模可以实现自动转化如:101+1->011 } temp.push_back(node%10+'0');//逆序装入 } string crackSafe(int n, int k) { if(n==1)//特解 { for(int i=0;i<k;i++) temp+=i+'0'; return temp; } highest=pow(10,n-1); this->k=k; dfs(0); temp.pop_back(); reverse(temp.begin(),temp.end());//反转 return string(n-1,'0')+temp;//补零 } };
拓扑排序¶
概念¶
- 针对有向无环图,可以检测是否遇到灰点来判断是否有环,有环则不存在拓扑排序
- 如果用边ab表示a是b的先验条件,则以节点变黑顺序作为top序,得到的是反top序,可以通过
n+1-top(n)来转化
模板¶
dfs实现¶
void dfs(int u) {
visited[u] = 1;
for (int v: edges[u]) {
if (visited[v] == 0) {
dfs(v);
if (!valid) {
return;
}
}
else if (visited[v] == 1) {
valid = false;//存在环,没有top序列
return;
}
}
toponum++;
topo[u]=toponum;//利用生命周期结束来标记topo序列
visited[u] = 2;
}
bfs实现¶
- 先将所有入度为1的节点入队
- 依次取出队列中的节点,对其相邻节点做入度减一的操作,并将入度变为0的节点入队
- 元素入队的顺序就是一个topo序
- 如果bfs结束后topo序中元素的数目小于元素的总数,说明铀元素的入度仍然不为0,说明有环不存在topo序
edgeout = [[] for _ in range(numCourses)]
edgein = [0 for _ in range(numCourses)]
ans = []
for a in prerequisites:
edgeout[a[1]].append(a[0])
edgein[a[0]] += 1
q = collections.deque()
for i, n in enumerate(edgein):
if n == 0:
q.append(i)
while len(q):
n = q.popleft()
ans.append(n)
for a in edgeout[n]:
edgein[a] -= 1
if edgein[a] == 0:
q.append(a)
return len(ans) == numCourses
单任务¶
- 线性执行任务
例题¶
多任务并发¶
- est:最早开始时间,等于依赖性的最早结束时间的
-
eft:最早结束时间,等于est+duration
-
关键路径:
- v0没有依赖项
- vi依赖于vi-1且vi的est等于vi-1的eft
- vk的eft是所有节点中最大的
模板dfs¶
bool dfs(int i,vector<vector<int>>&path,vector<int>&color,vector<int>&eft)
{
int bft=0;
color[i]=1;
for(auto a:path[i])
{
if(color[a]==0)
{
if(!dfs(a,path,color,eft))
return 0;
}
else if(color[a]==1)
return 0;
bft=max(bft,eft[a]);
}
color[i]=2;
eft[i]=bft+1;
sum=max(sum,eft[i]);
return 1;
}
模板bfs(更加简单)¶
for(int i=1;i<=n;i++)//添加入度为零的点
{
if(in[i]==0)
{
q.push(i);
}
}
while(!q.empty())
{
int num=q.size();
while(num-->0)//对学期数计数
{
n=q.pop();
for(auto a:path[n])
{
in[a]--;
if(in[a]==0)
{
q.push(a);
}
}
ans++;
}
}
例题¶
关键路径AOE¶
- 用点表示事件,边表示活动,整个活动有一个开始点一个完成点,完成整个工程所需的时间取决于从原点到汇点的最长路径的长度,就是关键路径
- \(Ve(i)\) 表示事件的最早开始时间(就是最长路径的长度)
- \(Vl(i)\) 保证最终任务按时完成的前提下事件的最迟开始时间
- \(Ae(k)\) 表示活动最早可能开始的时间
- \(<V_i,V_j>\) 边有 \(Ae[k]=Ve[i]\)
- \(Al(k)\) 活动最迟开始时间
- \(Al[k]=Vl[j]-dur<i,j>\)
- 对于 \(Al[k]=Ae[k]\) 的就是关键活动
- 先在正图和反图分别求解 \(Ve \ Vl\)
- \(Ve[j]=max(Ve[i]+dur<V_i,V_j>)\)
- \(Vl[j]=min(Vl[k]-dur<V_i,V_j>)\)
- 由此得到 \(Ae \ Al\) 进一步得到关键路径
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
vector<pair<int,int>>res;
int n,m;
cin >> n >> m;
vector<pair<int,int>>G[n],Gt[n];
vector<vector<int>>edges(m);
int ae[m],al[m],ve[n],vl[n];
memset(ae,0,sizeof(ae));
memset(al,0x3f,sizeof(al));
memset(ve,0,sizeof(ve));
memset(vl,0x3f,sizeof(vl));
ve[0]=0;
for(int i=0;i<m;++i){
int a,b,w;
cin >> a >> b >>w;
G[a].emplace_back(b,w);
Gt[b].emplace_back(a,w);
edges[i]={a,b,w};
}
function<void(int)>dfs1,dfs2;
dfs1=[&](int u)->void{
for(auto v:G[u]){
if(ve[u]+v.second>ve[v.first]){
ve[v.first]=ve[u]+v.second;
dfs1(v.first);
}
}
};
dfs2=[&](int u)->void{
for(auto v:Gt[u]){
if(vl[u]-v.second<vl[v.first]){
vl[v.first]=vl[u]-v.second;
dfs2(v.first);
}
}
};
dfs1(0);
vl[n-1]=ve[n-1];
dfs2(n-1);
for(int i=0;i<m;++i){
auto e=edges[i];
int a=e[0],b=e[1],w=e[2];
ae[i]=ve[a];
al[i]=vl[b]-w;
}
for(int i=0;i<m;++i){
if(ae[i]==al[i])
res.push_back({edges[i][0],edges[i][1]});
}
sort(res.begin(),res.end());
for(auto &e:res){
cout << e.first << " " << e.second << endl;
}
return 0;
}
2-SAT¶
- \(O(n+m)\)
- 步骤
xVy变成~x->y和~y->x建图- 对于要求 \(A\overline{A}\)、\(B\overline{B}\) 至少出现一个,如果 \(A\overline{B}\) 不能同时出现,则建边 \(AB\) 、\(\overline{B}\overline{A}\)
- 边表示父节点被选中时必须也选中子节点
- SCC 缩图,如果
~x x处于同一强连通分量则输出不可能,否则如果强连通分量内不存在矛盾则说明存在合法组合 - 在缩点之后的 DAG 张进行反图的拓扑排序,选点同时排除矛盾的点,就能找到合法的组合
- 当 x 所在的强连通分量的拓扑序在 ¬x 所在的强连通分量的拓扑序之后取 x 为真就可以了。在使用 Tarjan 算法缩点找强连通分量的过程中,已经为每组强连通分量标记好顺序了——不过是反着的拓扑序。所以一定要写成
color[x] < color[-x]。
- 当 x 所在的强连通分量的拓扑序在 ¬x 所在的强连通分量的拓扑序之后取 x 为真就可以了。在使用 Tarjan 算法缩点找强连通分量的过程中,已经为每组强连通分量标记好顺序了——不过是反着的拓扑序。所以一定要写成
模板¶
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int cur, head[N<<1];
struct {int to,next;}edge[N<<2];
void addedge(int u,int v){
edge[++cur].to = v;
edge[cur].next = head[u];
head[u] = cur;
}
int low[N<<1],num[N<<1],st[N<<1],sccno[N<<1],dfn,top,cnt;
int n,m;
void tarjan(int u){
st[top++] = u;
low[u] = num[u] = ++dfn;
for(int i=head[u]; i; i=edge[i].next) {
int v=edge[i].to;
if(!num[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}else if(!sccno[v])
low[u]=min(low[u],num[v]);
}
if(low[u]==num[u]) {
cnt++;
while(1){
int v=st[--top];
sccno[v]=cnt;
if(u==v) break;
}
}
}
bool two_SAT(){
for(int i=1; i<=2*n; i++)
if(!num[i])
tarjan(i); //tarjan找强连通分量
for(int i=1; i<=n; i++)
if(sccno[i]==sccno[i+n]) //a和非a在同一个强连通分量,无解
return false;
return true;
}
int main(){
scanf("%d%d",&n,&m);
while(m--){
int a,b,va,vb; scanf("%d%d%d%d",&a,&va,&b,&vb);
int nota = va^1, notb = vb^1; //非a,非b
addedge(a+nota*n, b+vb*n); //连边(非a,b)
addedge(b+notb*n, a+va*n); //连边(非b,a)
}
if(two_SAT()){
printf("POSSIBLE\n");
for(int i=1; i<=n; i++) printf("%d ",sccno[i]>sccno[i+n]);
}
else printf("IMPOSSIBLE");
return 0;
}