排序&选择
nlogn排序¶
快速排序¶
int shift3(vector<int>& arr, int num, int first, int last)//ppt思路
{
int low = first, high = last;
while (low < high)
{
for (; high > low; high--)
{
if (arr[high] < num)
{
arr[low] = arr[high];
low++;
break;
}
}
for (; low < high; low++)
{
if (arr[low] > num)
{
arr[high] = arr[low];
high--;
break;
}
}
}
return low;
}
void quicksort(vector<int>& arr, int first, int last)
{
if (first < last)
{
int num = arr[first];
int mid = shift3(arr, num, first, last);
arr[mid] = num;
quicksort(arr, first, mid - 1);
quicksort(arr, mid + 1, last);
}
}
归并排序¶
void merge(vector<int>& arr, int first, int mid, int last)
{
vector<int>temp(arr.begin() + mid + 1, arr.begin() + last + 1);
int j = mid;
int k = temp.size() - 1;
for (int i = last; i >= first; i--)//i和j的上下界不是0和arr.end(),是first和last!
{
if (j < first)
{
for (int i = 0; i <= k; i++)
arr[i + first] = temp[i];
}
else if (k < 0)
{
return;
}
else
{
if (arr[j] > temp[k])
{
arr[i] = arr[j];
j--;
}
else
{
arr[i] = temp[k];
k--;
}
}
}
}
void mergesort(vector<int>& arr, int first, int last)
{
if (first < last)
{
int mid = (first + last) / 2;
mergesort(arr, first, mid);
mergesort(arr, mid + 1, last);
merge(arr, first, mid, last);
}
}
- 链表实现
- 排序链表1
class Solution {
public:
ListNode* sortList(ListNode* head) {
return sortList(head, nullptr);
}
ListNode* sortList(ListNode* head, ListNode* tail) {
if (head == nullptr) {
return head;
}
if (head->next == tail) {
head->next = nullptr;
return head;
}
ListNode* slow = head, *fast = head;
while (fast != tail) {
slow = slow->next;
fast = fast->next;
if (fast != tail) {
fast = fast->next;
}
}
ListNode* mid
= slow;
return merge(sortList(head, mid), sortList(mid, tail));
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
归并排序的扩展应用¶
堆排序¶
void fixHeap(vector<int>& arr, int heapSize, int root)
{
int left = 2 * root, right = 2 * root + 1;
if (left <= heapSize)
{
int largeSubHeap;
if (left == heapSize)
largeSubHeap = left;
else if (arr[left] > arr[right])
largeSubHeap = left;
else
largeSubHeap = right;
if (arr[root] < arr[largeSubHeap])
{
swap(arr[root], arr[largeSubHeap]);
fixHeap(arr, heapSize, largeSubHeap);
}
}
}
void constructHeap(vector<int>& arr, int root)
{
int left = 2 * root, right = 2 * root + 1;
if (left < arr.size())
{
constructHeap(arr, left);
}
if (right < arr.size())
{
constructHeap(arr, right);
}
fixHeap(arr, arr.size() - 1, root);
}
void heapsort(vector<int>& arr)//arr下标从1开始
{
constructHeap(arr, 1);
for (int i = arr.size() - 1; i >= 2; i--)
{
swap(arr[i], arr[1]);
fixHeap(arr, i - 1, 1);
}
}
锦标赛排序¶
-
锦标赛排序的最优时间复杂度、平均时间复杂度和最坏时间复杂度均为 \(O(nlogn)\)。它用\(O(n)\)的时间初始化「锦标赛」,然后用
\(O(logn)\)的时间从\(n\)个元素中选取一个元素,空间复杂度\(O(2n-1)\)
-
是非稳定排序
-
初始化
-
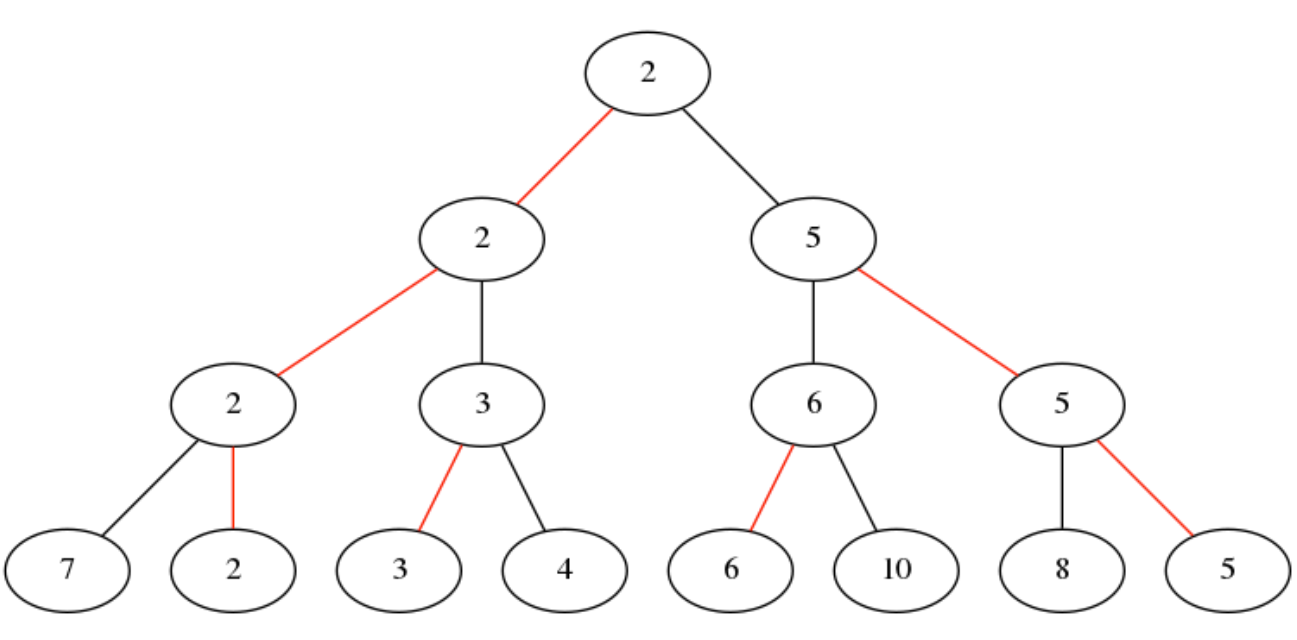
-
红色边显示的是每一轮比较中较小的元素的胜出路径。显然,完成一次"锦标赛"可以选出一组元素中最小的那一个。
-
选取元素
-
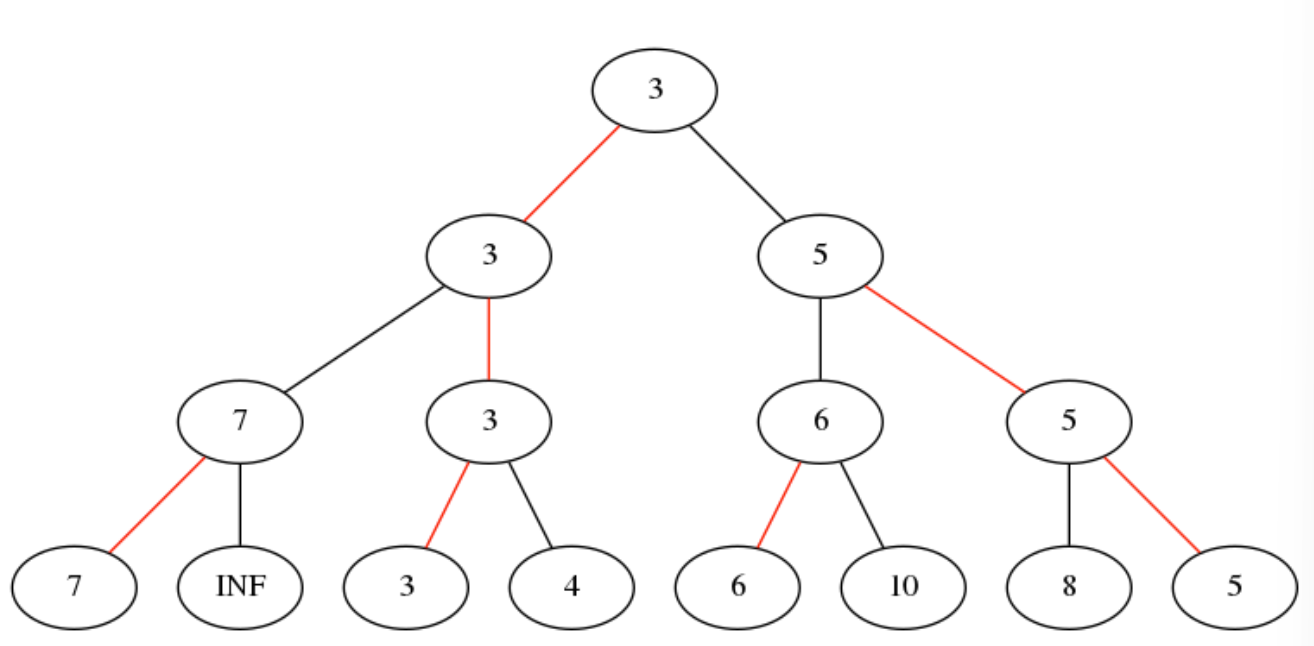
-
完成一次「锦标赛」后需要将被选出的元素去除。直接将其设置为\(+\infty\)(这个操作类似 堆排序,然后再次举行「锦标赛」选出次小的元素。
-
代码:
-
```c++ const int INF = 0x3f3f3f3f; const int maxn = 100005; int n, a[maxn], tmp[maxn << 1]; //对于tmp中的后一半(叶子节点)复制了a中的元素,而前半部风则是存储的后半部分中想要表示的指定元素在tmp数组中的下标 // 比较pos1和pos2位置上的元素大小,返回较小元素所在的位置 int winner(int pos1, int pos2) { int u = pos1 >= n ? pos1 : tmp[pos1]; int v = pos2 >= n ? pos2 : tmp[pos2]; if (tmp[u] <= tmp[v]) return u; return v; }
// 构建完全二叉树,其中value为排序后的最小值 void creat_tree(int &value) { for (int i = 0; i < n; i++) tmp[n + i] = a[i]; // 将待排序的元素存储到tmp数组的后半部分(叶) for (int i = 2 * n - 1; i > 1; i -= 2) { // 从最后一层叶子节点开始,逐层向上构建完全二叉树 int k = i / 2;//用数组模拟二叉树,与堆类似 int j = i - 1; tmp[k] = winner(i, j); // 比较i和j节点上的元素大小,将较小值存储到k节点上 } value = tmp[tmp[1]]; // 找到排序后的最小值 tmp[tmp[1]] = INF; // 将已排序的最小值标记为INF,方便后续排除。 }
// 根据已排序的最小值value,重新构建完全二叉树 void recreat(int &value) { int i = tmp[1]; // 找到标记为INF的位置,从该位置开始向上重构二叉树 while (i > 1) { int j, k = i / 2; if (i % 2 == 0 && i < 2 * n - 1) j = i + 1; else j = i - 1; tmp[k] = winner(i, j); // 比较i和j节点上的元素大小,将较小值存储到k节点上 i = k; } value = tmp[tmp[1]]; // 找到排序后的最小值 tmp[tmp[1]] = INF; // 将已排序的最小值标记为INF,方便后续排除。 }
// 进行锦标赛排序 void tournament_sort() { int value; creat_tree(value); // 构建完全二叉树,找到排序后的最小值 for (int i = 0; i < n; i++) { a[i] = value; // 将排序后的最小值存储到数组a中 recreat(value); // 根据已排序的最小值value,重新构建完全二叉树。 } }
```
线性时间排序¶
计数排序¶
- 类似于所有桶范围都是1的桶排序
概念¶
- 计数排序并不是把计数数组的下标直接作为结果输出,而是通过计数的结果,计算出每个元素在排序完成后的位置(得到有多少个更小/更大元素,可以用前缀和的方法快速计算),然后将元素赋值到对应位置。
- 思路
- 找到最大最小值确定范围
- 遍历数组计数
- 用前缀和记录比自己更小的元素的数目
- 将元素放入对应的下标中(一个大小有多个时,遇到一个就对预处理的位置(前缀和)加一即可)
- O(n+k)k为数据范围大小
模板¶
public static void countingSort(int[] arr) {
// 防止数组越界
if (arr == null || arr.length <= 1) return;
// 找到最大值,最小值
int max = arr[0];
int min = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) max = arr[i];
else if (arr[i] < min) min = arr[i];
}
// 确定计数范围
int range = max - min + 1;
// 建立长度为 range 的数组,下标 0~range-1 对应数字 min~max
int[] counting = new int[range];
// 遍历 arr 中的每个元素
for (int element : arr) {
// 将每个整数出现的次数统计到计数数组中对应下标的位置,这里需要将每个元素减去 min,才能映射到 0~range-1 范围内
counting[element - min]++;
}
// 每个元素在结果数组中的最后一个下标位置 = 前面比自己小的数字的总数 + 自己的数量 - 1。我们将 counting[0] 先减去 1,后续 counting 直接累加即可
counting[0]--;
for (int i = 1; i < range; i++) {
// 将 counting 计算成当前数字在结果中的最后一个下标位置。位置 = 前面比自己小的数字的总数 + 自己的数量 - 1
// 由于 counting[0] 已经减了 1,所以后续的减 1 可以省略。
counting[i] += counting[i - 1];
}
int[] result = new int[arr.length];
// 从后往前遍历数组,通过 counting 中记录的下标位置,将 arr 中的元素放到 result 数组中
for (int i = arr.length - 1; i >= 0; i--) {
// counting[arr[i] - min] 表示此元素在结果数组中的下标
result[counting[arr[i] - min]] = arr[i];
// 更新 counting[arr[i] - min],指向此元素的前一个下标
counting[arr[i] - min]--;
}
// 将结果赋值回 arr
for (int i = 0; i < arr.length; i++) {
arr[i] = result[i];
}
}
基数排序¶
概念¶
- 思想:
- 将数字按位拆分,进行比较
- 最高位优先法:简称 MSD 思路是从最高位开始,依次对基数进行 (计数)排序;最低位优先法:简称 LSD。思路是从最低位开始,依次对基数进行排序。使用 LSD 必须保证对基数进行排序的过程是稳定的。
- 在采用 LSD 进行基数排序时,每一轮遍历都可以将所有数字一视同仁,统一处理。所以 LSD 的基数排序更符合计算机的操作习惯。
- 以 LSD 为例,先从左到右遍历元素,将第 i 为 k 的 push 到第 k 组(一共 0-9 即 10 组),之后从左到右取出元素得到新排列;再根据第二位(十位)重做,直至所有位完成
1618984043-EyABAp-基数算法 (1).gif (608×608) (leetcode-cn.com) - 过程 - 找到数组中最大的数,获取其位数 - 获取每一位的基数并进行排序(可以使用计数排序先,因为基数范围在0~9) - 负数排序:就是在对基数进行计数排序时,申请长度为19的计数数组,用来存储[-9,9]的整数,把每一位基数计算出来后加上9对应下标[0,18] - O(d(n+k))k为基数范围,d为位数
模板¶
vector<int> sortArray(vector<int>& nums) {
int max_num=10*max(abs(*max_element(nums.begin(),nums.end())),abs(*min_element(nums.begin(),nums.end())));//找到绝对值(位数)最大的元素
vector<int>ans(nums.size());
int dev=1;
while(max_num/=10)//循环位数次
{
vector<int>counting(19,0);
for(int a:nums)//对每一位的基数使用计数排序
{
counting[a/dev%10+9]++;//由于有负数,把[-9,9]映射到[0,18]
}
for(int j=1;j<19;j++)
{
counting[j]+=counting[j-1];
}
for(int j=nums.size()-1;j>=0;j--)
{
ans[--counting[nums[j]/dev%10+9]]=nums[j];
}
nums=ans;
dev*=10;
}
return nums;
}
桶排序¶
概念¶
- 思想:
- 将区间划分为 n 个相同大小的子区间,每个子区间称为一个桶(先遍历数组确定数据范围,然后确定桶的数目进行分桶)
- 遍历数组,将每个数字装入桶中
- 对每个桶内的数字单独排序,这里需要采用其他排序算法,如插入、归并、快排等
- 最后按照顺序将所有桶内的数字合并起来
- 因素
- 桶的数量:桶的数量过少,会导致单个桶内的数字过多,桶排序的时间复杂度就会在很大程度上受桶内排序算法的影响。桶的数量过多,占用的内存就会较大,并且会出现较多的空桶,影响遍历桶的效率。具体设置多少个桶需要根据实际情况决定。
- 桶的数据结构:如果将桶的数据结构设置为数组,那么每个桶的长度必须设置为待排序数组的长度,因为我们需要做好最坏的打算,即所有的数字都被装入了同一个桶中,所以这种方案的空间复杂度会很高。那么是不是将桶的数据结构设置为链表就更好呢?使用链表有一个好处,即所有桶的总长度刚好等于待排序数组的长度,不会造成内存浪费。但链表进行排序操作时很慢。
- 理想情况下为O(n)空间复杂度很高,空间换时间
- 折中的方案:装桶时用链表,桶内排序用数组
模板¶
vector<int> bucketsort(vector<int>& nums) {
vector<int>ans;
// 找到最大值,最小值
int max=*max_element(nums.begin(),nums.end());
int min=*min_element(nums.begin(),nums.end());
int range=max-min;
// 设置桶的数量,这里我们设置为 10 个,可以任意修改。
int bucketnum=10;
// 桶和桶之间的间距
int gap=range/bucketnum;
vector<vector<int>>buckets(bucketnum+1,vector<int>());
for(int a:nums)
{
buckets[(a-min)/gap].push_back(a);
}
for(auto &a:buckets)//桶内排序
{
sort(a.begin(),a.end());//使用了快排
}
for(auto &a:buckets)//取出
{
for(auto b:a)
ans.push_back(b);
}
return ans;
}
例题¶
- 164. 最大间距
- 桶排序分桶思想(维护桶内最大最小值)/基数排序
排列问题¶
stl排列¶
next_permutation(first,end[,cmp])直接将下一个排列复制到原先的位置- 返回值为bool表示是否还有下一个
- 会自动去重
prev_permutation()
手动排列¶
- 使用dfs回溯
选择问题¶
-
线性期望时间的算法(可以结合随机取数避免出现最坏情况)
-
取随机数
c++ srand(unsigned(time(0))); //获取系统时间 number = rand()%100; //生成随机数
-
c++