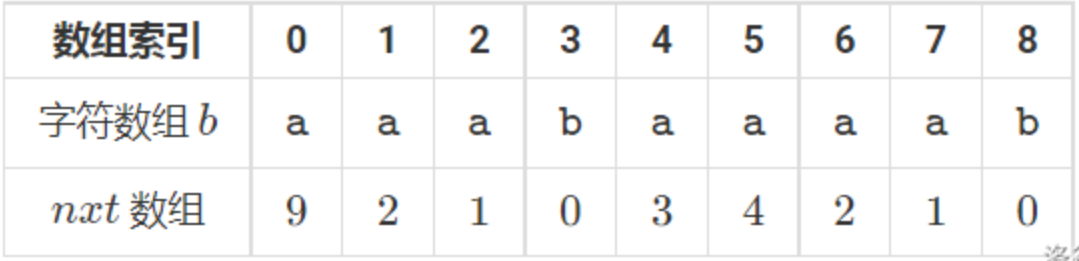
数组¶
双指针滑动窗口¶
例题¶
特殊¶
- 剑指 Offer 66. 构建乘积数组
- 前缀积*后缀积,避免除法
- 三角遍历可以避免用额外空间存储前后缀
字符串¶
特殊¶
字符串匹配¶
字符串哈希¶
KMP¶
- 单模匹配算法,在文本串中查找一个模式串
思想¶
- KMP算法讲解
- next数组:next[i]表示在[0,i]最大相同前缀与后缀的长度
- 如:asdsdas为2;asdsasd为3;
模板¶
vector<int> build_next(string&s)//构建next数组
{
vector<int>next{0};//第一位一定为零(因为规定前后缀不能为自身)
int i=1,len=0;//len记录当前位置最大重合长度
while(i<s.size())
{
if(s[len]==s[i])
{
len++;
next.push_back(len);
i++;
}
else
{
if(len==0)
{
next.push_back(0);
i++;
}
else
len=next[len-1];//找到对应的前缀的末尾位置(一种递归思想,长的匹配不上则逐渐缩短去找)
}
}
return next;
}
int kmp(string fs,string ss)//ss为待匹配的子串
{
vector<int>next=build_next(ss);
int i=0,j=0;
while(i<fs.size())
{
if(fs[i]==ss[j])
{
i++;
j++;
}
else if(j>0)
j=next[j-1];//前next[j-1]位仍相同,在这之后继续匹配
else
i++;
if(j==ss.size())
return i-j;
}
return -1;
}
- 记录所有出现位置的版本
vector<int> kmp(string &text, string &pattern) { vector<int> next = build_next(pattern); vector<int> positions; // 存放匹配位置的列表 int j = 0; for(int i = 0; i < text.size(); i++) { while(j > 0 && text[i] != pattern[j]) { j = next[j - 1]; } if(text[i] == pattern[j]) { j++; } if(j == pattern.size()) { positions.push_back(i - j + 1); // 记录匹配位置 j = next[j - 1]; // 为下一次匹配做准备 } } return positions; }
扩展 kmp¶
- 求模式串 P 和字符串 S 的每个后缀的最长公共前缀,即求解数组 extend[] ,extend[i] 表示 P 与 S[i~n] 的最长公共前缀u
-
扩展 kmp 中 nxt 数组表示 P 与 P 自身的每一个后缀的 LCP (最长公共前缀)的长度
-
[[P5410 【模板】扩展 KMP_exKMP(Z 函数) - 洛谷 _ 计算机科学教育新生态|原题解]]
- nxt 和 ext 的计算过程类似,nxt 全在 P 上操作,ext 利用 P 作为前缀 S 作为后缀
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 2e7 + 10;
ll nxt[N], ext[N];
void qnxt(char *c)
{
int len = strlen(c);
int p = 0, k = 1, l; //我们会在后面先逐位比较出 nxt[1] 的值,这里先设 k 为 1
//如果 k = 0,p 就会锁定在 |c| 不会被更改,无法达成算法优化的效果啦
nxt[0] = len; //以 c[0] 开始的后缀就是 c 本身,最长公共前缀自然为 |c|
while(p + 1 < len && c[p] == c[p + 1]) p++;
nxt[1] = p; //先逐位比较出 nxt[1] 的值
for(int i = 2; i < len; i++)
{
p = k + nxt[k] - 1; //定义
l = nxt[i - k]; //定义
if(i + l <= p) nxt[i] = l; //如果灰方框小于初始的绿方框,直接确定 nxt[i] 的值
else
{
int j = max(0, p - i + 1);
while(i + j < len && c[i + j] == c[j]) j++; //否则进行逐位比较
nxt[i] = j;
k = i; //此时的 x + nxt[x] - 1 一定刷新了最大值,于是我们要重新赋值 k
}
}
}
void exkmp(char *a, char *b)
{
int la = strlen(a), lb = strlen(b);
int p = 0, k = 0, l;
while(p < la && p < lb && a[p] == b[p]) p++; //先算出初值用于递推
ext[0] = p;
for(int i = 1; i < la; i++) //下面都是一样的逻辑啦
{
p = k + ext[k] - 1;
l = nxt[i - k];
if(i + l <= p) ext[i] = l;
else
{
int j = max(0, p - i + 1);
while(i + j < la && j < lb && a[i + j] == b[j]) j++;
ext[i] = j;
k = i;
}
}
}
int la, lb;
char a[N], b[N];
ll ans;
int main()
{
cin.tie(0); cout.tie(0);
ios::sync_with_stdio(0);
cin >> a >> b;
qnxt(b);
exkmp(a, b);
la = strlen(a), lb = strlen(b), ans = 0;
for(int i = 0; i < lb; i++) //要注意下标从 0 开始
{
ans ^= (i + 1) * (nxt[i] + 1);
}
cout << ans << "\n";
ans = 0;
for(int i = 0; i < la; i++)
{
ans ^= (i + 1) * (ext[i] + 1);
}
cout << ans;
return 0;
}
例题¶
- 1392. 最长快乐前缀
- 应用 next 数组构建的思想
- P4824 [USACO15FEB] Censoring S
- P2375 [NOI2014] 动物园
Manacher¶
- 用于寻找长度为 \(n\) 的字符串中的最长回文子串,时间复杂度为 \(O(n)\)
-
Manacher 本质上是一种动态规划算法
-
中心扩展法(暴力)
- 把每个/两个字符看作中心然后左右扩展检查判断是否为回文
- 进行了太多重复计算,时间复杂度 \(O(n)\)
-
问题简化
- 为了避免对奇偶分别进行讨论,添加额外的字符
abcde->@#a#b#c#d#e#&- 添加 # 分隔之后所有字串的长度均变为奇数
- 添加 @& 避免发生越界
-
使用 \(P[i]\) 表示以 \(i\) 为中心的回文串半径

- 最大的 \(p[i]-1\) 就是结果
- 在原字符串中起始位置为 \(\frac{i-p[i]}{2}\)
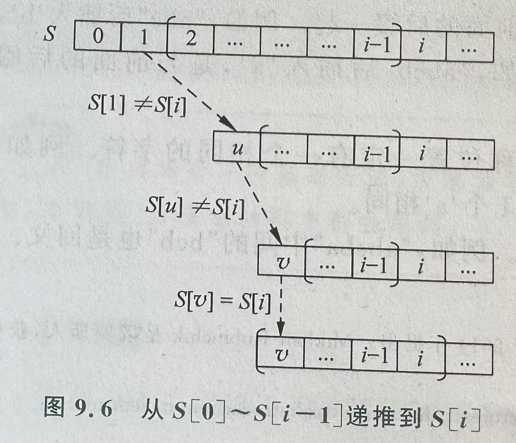
回文的镜像也是回文 - 高效的计算 \(P[i]\) : - 已经得到了 \(P[0]~P[i-1]\) 假设 \(R\) 是求得的回文串的右端点的最大值,其中心点为 \(C\) - \(i\) 关于 \(C\) 的对称点 \(j=2C-i\) - 如果遍历的位置在一致的回文半径内(i<=R)并且对称点的回文区域也在这个范围,结果已知 -
- 对称点的回文区域压线:要继续扩散试探 -
- 对称点的回文区域超出,不需要扩散,结果已知 -
- 遍历的位置在已知的半径之外,需要扩散,初始化 \(P[i]=1\) 开始计算 -
- 本质上是对 \(R\) 的移动,由于每个位置 \(R\) 只会被计算一次,因此时间复杂度为 \(O(n)\)
#include<bits/stdc++.h>
using namespace std;
const int N=11000002;
int n,P[N<<1]; //P[i]: 以s[i]为中心的回文半径
char a[N],s[N<<1];
void change(){ //变换
n = strlen(a);
int k = 0; s[k++]='$'; s[k++]='#';
for(int i=0;i<n;i++){s[k++]=a[i]; s[k++]='#';} //在每个字符后面插一个#
s[k++]='&'; //首尾不一样,保证第18行的while循环不越界
n = k;
}
void manacher(){
int R = 0, C;
for(int i=1;i<n;i++){
if(i < R) P[i] = min(P[(C<<1)-i],P[C]+C-i); //合并处理两种情况
else P[i] = 1;
while(s[i+P[i]] == s[i-P[i]]) P[i]++; //暴力:中心扩展法
if(P[i]+i > R){
R = P[i]+i; //更新最大R
C = i;
}
}
}
int main(){
scanf("%s",a); change();
manacher();
int ans=1;
for(int i=0;i<n;i++) ans=max(ans,P[i]);
printf("%d",ans-1);
return 0;
}
例题¶
- P4555 [国家集训队] 最长双回文串
- 关键:左起点最长、右起点最长及转移递推
- P1659 [国家集训队] 拉拉队排练
字典树(前缀树)¶
思想¶
- 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
- 可以实现快速查找元素是否存在,是否存在以元素为前缀的元素
- 数据结构:
- 多叉树(如只有小写字母则为26叉)
-
每个节点包含子节点指针以及一个 bool 值表示是否存在以该节点结尾的单词
-
应用:
- 字符串检索
- 词频统计
- 字典序排序(先序遍历)
- 前缀匹配
class Trie {
public:
Trie() {
root=new TreeNode;
}
void insert(string word) {
TreeNode*p=root;
for(auto a:word)
{
if(p->child[a-'a']==nullptr)
p->child[a-'a']=new TreeNode;
p=p->child[a-'a'];
}
p->check=true;//标记结尾
}
bool search(string word) {
TreeNode*p=root;
for(auto a:word)
{
if(p->child[a-'a']==nullptr)
return false;
p=p->child[a-'a'];
}
return p->check;//查找单词要求必须是结尾
}
bool startsWith(string prefix) {
TreeNode*p=root;
for(auto a:prefix)
{
if(p->child[a-'a']==nullptr)
return false;
p=p->child[a-'a'];
}
return true;//查找前缀不要求结束节点一定可以作为结尾
}
private:
struct TreeNode{
TreeNode(){
for(auto &a:child)
a=nullptr;
check=false;
}
TreeNode*child[26];//也可以使用hash存储
bool check;
};
TreeNode* root;
};
- 静态存储的字典树
#include <bits/stdc++.h>
using namespace std;
const int N = 800000;
struct node{
bool repeat; //这个前缀是否重复
int son[26]; //26个字母
int num; //这个前缀出现的次数
}t[N]; //trie
int cnt = 1; //当前新分配的存储位置。把cnt=0留给根结点
void Insert(char *s){
int now = 0;
for(int i=0;s[i];i++){
int ch=s[i]-'a';
if(t[now].son[ch]==0) //如果这个字符还没有存过
t[now].son[ch] = cnt++; //把cnt位置分配给这个字符
now = t[now].son[ch]; //沿着字典树往下走
t[now].num++; //统计这个前缀出现过多少次
}
}
int Find(char *s){
int now = 0;
for(int i=0;s[i];i++){
int ch = s[i]-'a';
if(t[now].son[ch]==0) return 3; //第一个字符就找不到
now = t[now].son[ch];
}
if(t[now].num == 0) return 3; //这个前缀没有出现过
if(t[now].repeat == false){ //第一次被点名
t[now].repeat = true;
return 1;
}
return 2;
// return t[p].num; //若有需要,返回以s为前缀的单词的数量
}
int main(){
char s[51];
int n;cin>>n;
while(n--){ scanf("%s",s); Insert(s); }
int m; scanf("%d",&m);
while(m--) {
scanf("%s",s);
int r = Find(s);
if(r == 1) puts("OK");
if(r == 2) puts("REPEAT");
if(r == 3) puts("WRONG");
}
return 0;
}
例题¶
- c++字典树题解
- P4551 最长异或路径 - 洛谷
- 将(i,j)i到j上的异或和转化为(1,i)^(1,j)
- 212. 单词搜索 II
回文树PAM¶
- 通用高效的处理回文串问题
- 效率高,时间复杂度为 \(O(n)\),空间复杂度相对较差
- 支持在线查询和更新
-
回文树本质上是一种字典树
-
后缀链跳跃
- 向字符串末尾添加的新字符只能与原字符串的后缀构成新的回文
- 新增字符与前面对称位置字符以及之间的回文串构成新的回文串(abcb+a)
- 从 s[i] 之前的回文后缀不断向后进行尝试,直到找到 s[v]=s[i] 得到以 i 为结尾的新的后缀回文,这个过程就称为后缀链跳跃
-
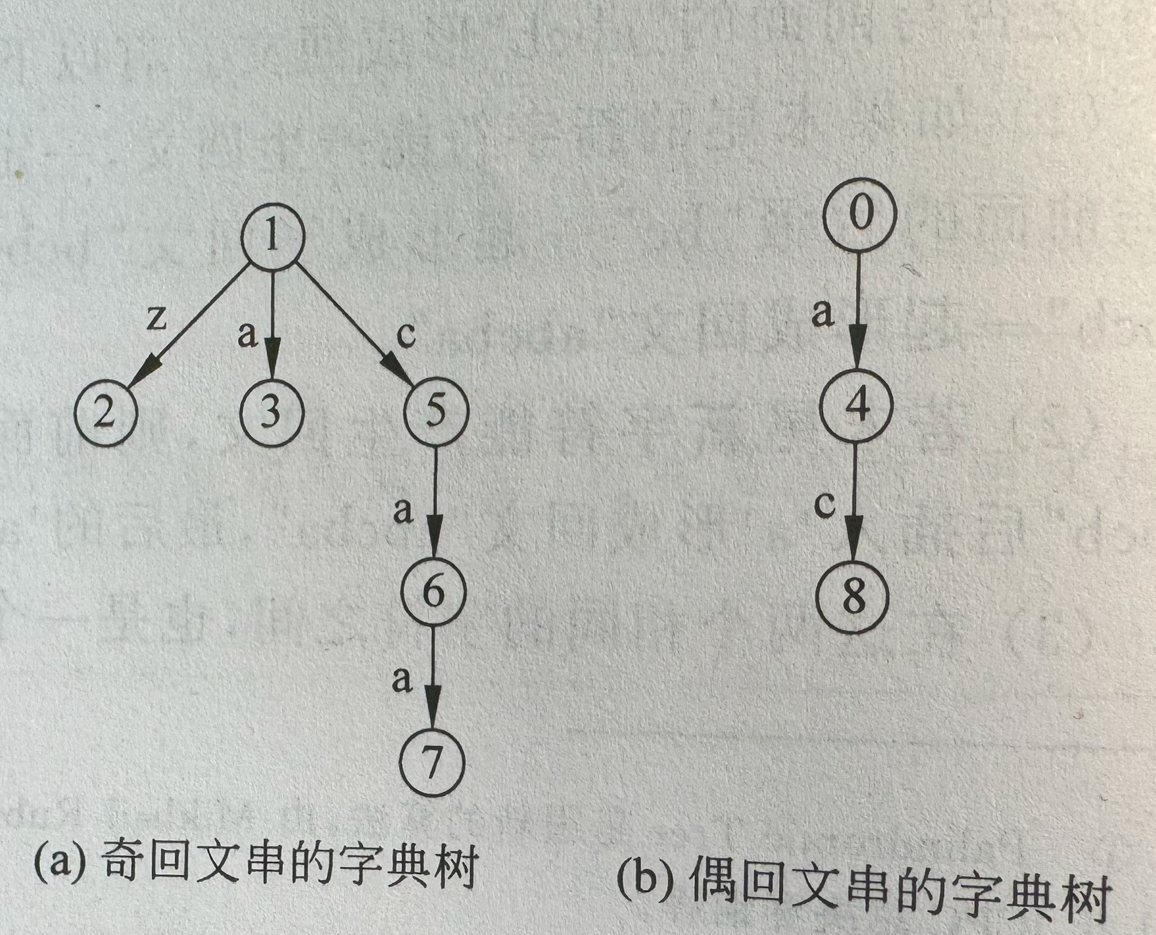
奇偶字典树
- 使用字典树存储回文串(后缀)
- 使用两棵字典树分别表示长度为奇、偶的回文串
- 0、1 节点分别为偶回文串和奇回文串的字典树的根,对于原字符串从下标为 2 开始编号
- 叶节点表示一个回文串,0 树靠近根的节点读两次,1 树读一次,对于 zaacaac 有
-
回文树的构建
- 建树的过程就是按顺序逐个处理 S 的字符的过程由于每处理一个字符就添加一个节点到树上,因此长度为 n 的字符串 s 最多有 n 个不同的回文串
- 由于所有新产生的回文子串都是新最长回文子串的回文后缀,且长度应比最长的小,我们可以把他们“翻转”一下,就可以发现他们一定在 s[0 to i−1] 的回文树里!(即同时也是前缀)
- 实线箭头表示回文字典树,令 1 节点 len 为 -1,0 节点为 0 这样所有相邻节点之间 len 的差值为 2
- 虚线箭头表示 Fail 指针,记录后缀链跳跃的过程(这个节点所代表的回文串的最长回文后缀所对应的节点)
- 若 S[i]=S[i-len-1] 则得到了新的回文串,直接将 S[i] 节点挂到 S[i-1] 节点下
- 如果不同,则需要缩小、查找新的后缀,即通过后缀链向上查找
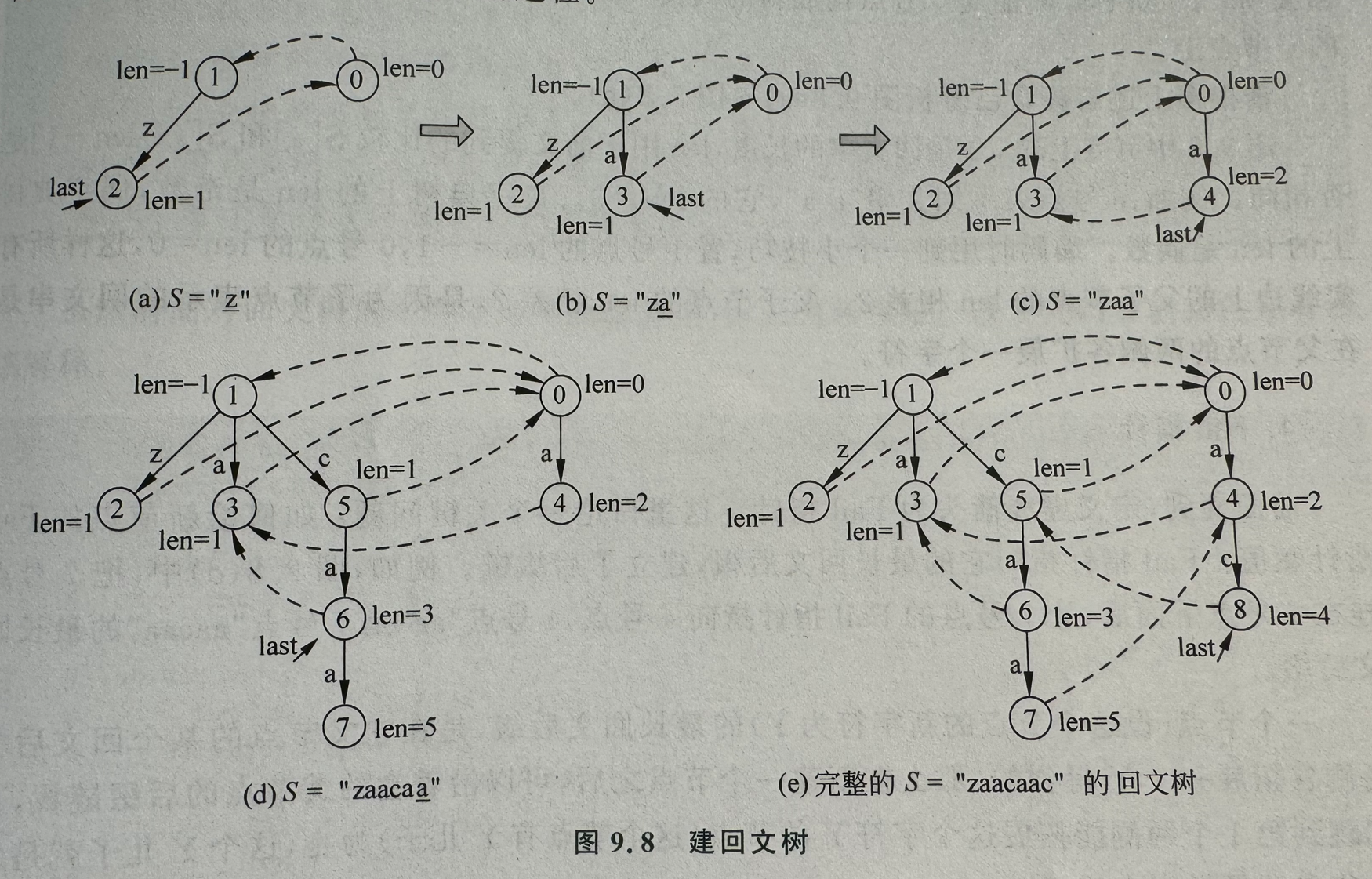
- 建树的过程就是按顺序逐个处理 S 的字符的过程由于每处理一个字符就添加一个节点到树上,因此长度为 n 的字符串 s 最多有 n 个不同的回文串
-
fail 指针(后缀链虚线)
- 一个节点的回文后缀都是由父节点两侧加上同样字符扩展得到的,因此子节点的 fail 指针可以通过沿着父节点的后缀链(尝试)得到
- cur, fail[cur], fail[fail[cur]]...... 一定包含了所有新产生的回文子串。(其中合法的是满足 s[i−len[x]−1]==s[i]s[i-len[x]-1]==s[i]s[i−len[x]−1]==s[i]的)
- 对于 01 特殊节点的 fail 设定:01 的 fail 互相指向,求新点的 fail :getfail (fail[pos], i)
-
基本模板,计算以每个字符结尾的回文串数目
#include<iostream> #include<cstdio> #include<cstring> using namespace std; char s[2000001]; int len[2000001],n,num[2000001],fail[2000001],last,cur,pos,trie[2000001][26],tot=1; int getfail(int x,int i) { while(i-len[x]-1<0||s[i-len[x]-1]!=s[i])x=fail[x]; return x; } int main() { scanf("%s",s); n=strlen(s); fail[0]=1;len[1]=-1; for(int i=0;i<=n-1;i++){ pos=getfail(cur,i); //找到cur的fail链中能匹配i位的最长回文后缀 if(!trie[pos][s[i]-'a']){ fail[++tot]=trie[getfail(fail[pos],i)][s[i]-'a']; trie[pos][s[i]-'a']=tot; len[tot]=len[pos]+2; num[tot]=num[fail[tot]]+1;//这个可以理解为后缀链上每一个点对应一个回文串,现在有了一个额外的回文串 }//不存在建立点,存在直接走过去 cur=trie[pos][s[i]-'a']; last=num[cur]; printf("%d ",last); } return 0; } - 支持双向插入和更复杂的查询的模板
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 3e5+8; int s[N]; struct node{ int len,fail,son[26],siz; void init(int _len){ memset(son,0,sizeof(son)); fail = siz = 0; len = _len; } }tree[N]; ll num,last[2],ans,L,R; //L:在S的头部加字符;R:在S的尾部加字符 void init() { //初始化一个结点 last[0]=last[1]=0; //从0号点开始 ans=0; num=1; L=1e5+8, R=1e5+7; tree[0].init(0); //小技巧,置0号点len = 0 memset(s,-1,sizeof(s)); tree[1].init(-1); //小技巧,置1号点len = -1 tree[0].fail=1; //0指向1,1不必指向0 } int getfail(int p,int d){ //后缀链跳跃。复杂度可以看成O(1) if(d) //新字符在尾部 while(s[R-tree[p].len-1] != s[R]) p = tree[p].fail; else //新字符在头部 while(s[L+tree[p].len+1] != s[L]) p = tree[p].fail; return p; //返回结点p } void Insert(int x,int d){ //往回文树上插入新结点,这个结点表示一个新回文串 if(d) s[++R] = x; //新字符x插到S的尾部 else s[--L] = x; //新字符x插到S的头部 int father = getfail(last[d],d); //插到一个后缀的子结点上 int now = tree[father].son[x]; if(!now){ //字典树上还没有这个字符,新建一个 now = ++num; tree[now].init(tree[father].len+2); tree[now].fail = tree[getfail(tree[father].fail,d)].son[x]; tree[now].siz = tree[tree[now].fail].siz+1; tree[father].son[x] = now; } last[d] = now; if(R-L+1 == tree[now].len) last[d^1]=now; ans += tree[now].siz; //char ch = x +'a'; //在这里打印回文树,帮助理解 //cout<<" fa="<<father<<",me="<<now<<",char="<<ch; //cout<<",fail="<<tree[now].fail<<",len="<<tree[now].len<<endl; } int main(){ int op,n; while(scanf("%d",&n)!=EOF){ init(); while(n--) { char c; scanf("%d",&op); if(op==1) scanf(" %c",&c), Insert(c-'a',0); if(op==2) scanf(" %c",&c), Insert(c-'a',1); if(op==3) printf("%lld\n",num-1); if(op==4) printf("%lld\n",ans); } } return 0; }
例题¶
AC 自动机¶
- 多模匹配算法,可以在文本串中同时查找不同的模式串
- 核心思想:字典树组织模式串+KMP 避免回溯
-
给定一个长度为 \(n\) 的文本 \(S\) ,以及 \(k\) 个平均长度为 \(m\) 的模式串,搜索这些模式串出现的位置
- 使用 KMP 的时间复杂度为 \(O((n+m)k)\)
-
fail 指针:(类似 KMP 中的 next 数组,用于避免回溯)
- fail 指针指向上层的满足后缀包含关系的同字符节点

-
fail 指针指向的是父节点的 fail 指针指向的节点的同字符的子节点,即 \(trie[fail[p],c]\) 存在则让 fail 指针指向
-
如果不存在则向上找 \(trie[fail[fail[p]],c]\) 重复 1 的判断,不符合则一直向上跳直到根节点,实在没有就指向根节点
- 通过
tr[u][i] = tr[fail[u]][i];对空节点赋值可以避免这种麻烦(类似并查集的路径压缩思想)
- 通过
-
建立字典树的事件复杂度为 \(O(km)\) ,求解 Fail 指针时同理
- 模式匹配的事件复杂度(取决于 fail 跳的次数)最差为 \(O(nm)\) ,但是大多情况下总复杂度近似 \(O(n)\)
应用¶
- 统计出现类型数目
#include <bits/stdc++.h> using namespace std; const int N=1000005; struct node{ int son[26]; //26个字母 int end; //字符串结尾标记 int fail; //失配指针 }t[N]; //trie[],字典树 int cnt; //当前新分配的存储位置 void Insert(char *s){ //在字典树上插入单词s int now = 0; //字典树上当前匹配到的结点,从root=0开始 for(int i=0;s[i];i++){ //逐一在字典树上查找s[]的每个字符 int ch=s[i]-'a'; if(t[now].son[ch]==0) //如果这个字符还没有存过 t[now].son[ch]=cnt++; //把cnt位置分配给这个字符 now = t[now].son[ch]; //沿着字典树往下走 } t[now].end++; //end>0,它是字符串的结尾。end=0不是结尾 } void getFail(){ //用BFS构建每个结点的fail指针 queue<int>q; for(int i=0;i<26;i++) //把第一层入队,即root的子结点 if(t[0].son[i]) //这个位置有字符 q.push(t[0].son[i]); while(!q.empty()){ int now = q.front(); //队首的fail指针已求得,下面求它孩子的fail指针 q.pop(); for(int i=0;i<26;i++){ //遍历now的所有孩子 if(t[now].son[i]){ //若这个位置有字符 t[t[now].son[i]].fail=t[t[now].fail].son[i]; //这个孩子的Fail=“父结点的Fail指针所指向的结点的与x同字符的子结点” q.push(t[now].son[i]); //这个孩子入队,后面再处理它的孩子 } else //若这个位置无字符 t[now].son[i]=t[t[now].fail].son[i];//虚拟结点,用于底层的Fail计算 } } } int query(char *s){ //在文本串s中找有多少个模式串P int ans=0; int now=0; //从root=0开始找 for(int i=0;s[i];i++){ //对文本串进行遍历 int ch = s[i]-'a'; now = t[now].son[ch]; int tmp = now; while(tmp && t[tmp].end!=-1){ //利用fail指针找出所有匹配的模式串 ans+=t[tmp].end; //累加到答案中。若这不是模式串的结尾,end=0 t[tmp].end = -1; //以这个字符为结尾的模式串已经统计,后面不再统计 tmp = t[tmp].fail; //fail指针跳转 cout << "tmp="<<tmp<<" "<<t[tmp].son; } } return ans; } char str[N]; int main(){ int k; scanf("%d",&k); while(k--){ memset(t,0,sizeof(t)); //清空,准备一个测试 cnt = 1; //把cnt=0留给root int n; scanf("%d",&n); while(n--){scanf("%s",str);Insert(str);} //输入模式串, 插入字典树中 getFail(); //计算字典树上每个结点的失配指针 scanf("%s",str); //输入文本串 printf("%d\n",query(str)); } return 0; } -
统计出现次数最多的
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N=20000; struct node{ int son[26]; string s; int fail; }t[N]; int cnt; unordered_map<string,int>mp; void Insert(char *s){ int now = 0; for(int i=0;s[i];i++){ int ch=s[i]-'a'; if(t[now].son[ch]==0) t[now].son[ch]=cnt++; now = t[now].son[ch]; } t[now].s = s; } void getFail(){ queue<int>q; for(int i=0;i<26;i++){ if(t[0].son[i]) q.push(t[0].son[i]); } while(!q.empty()){ int now = q.front(); q.pop(); for(int i=0;i<26;i++){ if(t[now].son[i]){ t[t[now].son[i]].fail=t[t[now].fail].son[i]; q.push(t[now].son[i]); } else t[now].son[i]=t[t[now].fail].son[i]; } } } void query(char *s){ int now=0; for(int i=0;s[i];i++){ int ch = s[i]-'a'; now = t[now].son[ch]; int tmp = now; while(tmp){ if(t[tmp].s.size()) mp[t[tmp].s]++; tmp = t[tmp].fail; } } } int main(){ int n; while(1){ mp.clear(); memset(t,0,sizeof(t)); scanf("%d",&n); if(n==0) break; for(int i=0;i<n;i++){ char s[100]; memset(s,0,sizeof(s)); scanf("%s",s); Insert(s); } getFail(); char s[1000005]; memset(s,0,sizeof(s)); scanf("%s",s); query(s); //选出出现次数最多的 int maxn=0; vector<string>ans; for(int i=0;i<N;i++){ if(mp[t[i].s]>maxn){ maxn=mp[t[i].s]; ans.clear(); ans.push_back(t[i].s); } else if(mp[t[i].s]==maxn){ ans.push_back(t[i].s); } } printf("%d\n",maxn); for(int i=0;i<ans.size();i++){ printf("%s\n",ans[i].c_str()); } } return 0; } - P3796 AC 自动机(简单版 II) - 洛谷 | 计算机科学教育新生态
拓扑排序优化的 AC 自动机¶
-
一直进行 fail 边跳跃效率较低,最差事件复杂度可能达到 \(O(nm)\)
- 预先记录需要在哪些位置跳 fail 计算结果,最后一并求和(fail 边一定构成有向树,可以按照拓扑排序获得的顺序进行计算)
-
在 getfail 中记录入度(方便后面进行拓扑排序)
- 查询时只为找到的节点的 ans 打上标记
- 最后进行一次额外的拓扑排序得到结果
#include <bits/stdc++.h>
#define maxn 8000001
using namespace std;
char s[maxn];
int n, cnt, vis[maxn], rev[maxn], indeg[maxn], ans;
struct trie_node {
int son[27];
int fail;
int flag;
int ans;
void init() {
memset(son, 0, sizeof(son));
fail = flag = 0;
}
} trie[maxn];
queue<int> q;
void init() {
for (int i = 0; i <= cnt; i++) trie[i].init();
for (int i = 1; i <= n; i++) vis[i] = 0;
cnt = 1;
ans = 0;
}
void insert(char *s, int num) {
int u = 1, len = strlen(s);
for (int i = 0; i < len; i++) {
int v = s[i] - 'a';
if (!trie[u].son[v]) trie[u].son[v] = ++cnt;
u = trie[u].son[v];
}
if (!trie[u].flag) trie[u].flag = num;
rev[num] = trie[u].flag;
return;
}
void getfail(void) {
for (int i = 0; i < 26; i++) trie[0].son[i] = 1;
q.push(1);
trie[1].fail = 0;
while (!q.empty()) {
int u = q.front();
q.pop();
int Fail = trie[u].fail;
for (int i = 0; i < 26; i++) {
int v = trie[u].son[i];
if (!v) {
trie[u].son[i] = trie[Fail].son[i];
continue;
}
trie[v].fail = trie[Fail].son[i];
indeg[trie[Fail].son[i]]++;
q.push(v);
}
}
}
void topu() {
for (int i = 1; i <= cnt; i++)
if (!indeg[i]) q.push(i);
while (!q.empty()) {
int fr = q.front();
q.pop();
vis[trie[fr].flag] = trie[fr].ans;
int u = trie[fr].fail;
trie[u].ans += trie[fr].ans;
if (!(--indeg[u])) q.push(u);
}
}
void query(char *s) {
int u = 1, len = strlen(s);
for (int i = 0; i < len; i++) u = trie[u].son[s[i] - 'a'], trie[u].ans++;
}
int main() {
scanf("%d", &n);
init();
for (int i = 1; i <= n; i++) scanf("%s", s), insert(s, i);
getfail();
scanf("%s", s);
query(s);
topu();
for (int i = 1; i <= n; i++) cout << vis[rev[i]] << std::endl;
return 0;
}