深度学习
- 线性回归恰好是一个在整个域中只有一个最小值的学习问题。 但是对像深度神经网络这样复杂的模型来说,损失平面上通常包含多个最小值。 深度学习实践者很少会去花费大力气寻找这样一组参数,使得在训练集上的损失达到最小。
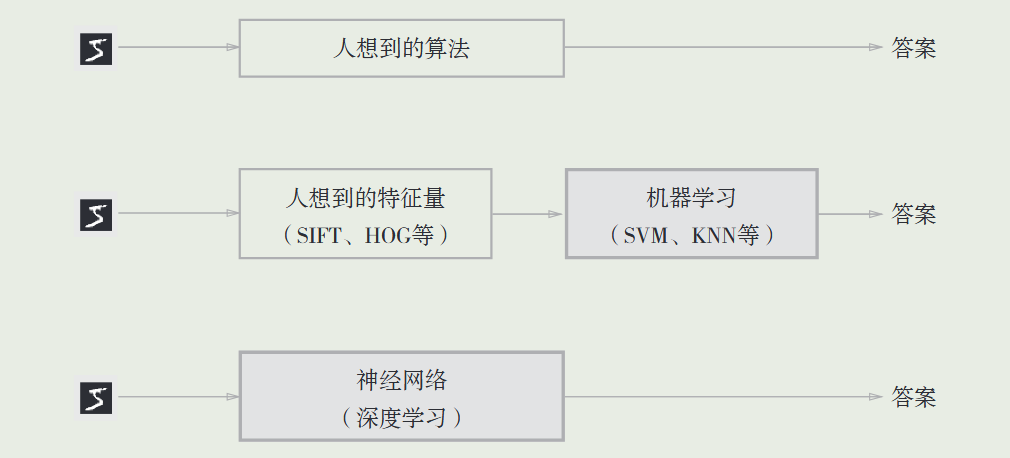
- 深度学习也被称为端到端机器学习,即直接从原始数据中获得目标结果输出,对于不同的问题可以使用相同的流程解决,饿不需要像机器学习那样使用不同的特征向量。
多层感知机¶
- 单层的神经网络只能处理线性关系(线性回归模型),通过添加隐藏层可以处理更加普遍的函数关系类型
- 这种架构就成为多层感知机 MLP
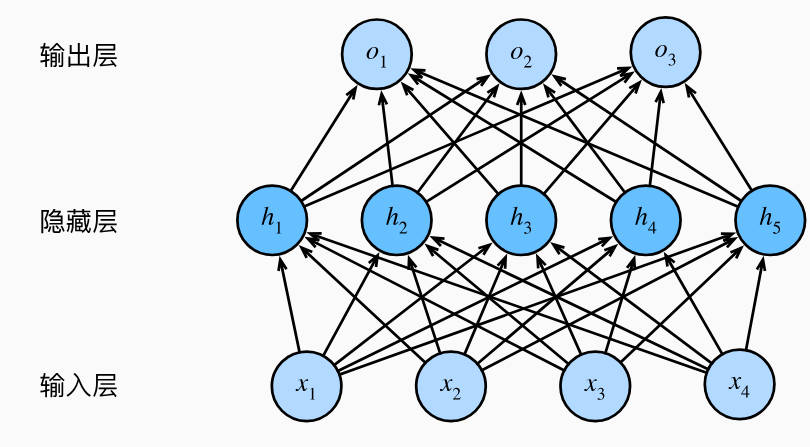
- 为了让多层结构真正提升模型的表示能力(而不是只能表示线性的仿射关系),对每个隐藏单元应用非线性的激活函数(如ReLU、Sigmoid),从而阻止多层感知机退化成线性模型 \(\mathbf{H}=\sigma(\mathbf{X}\mathbf{W}^{(1)}+\mathbf{b}^{(1)})\)
- ReLU: 修正线性单元 \(\mathrm{ReLU}(x)=\max(x,0)\)。它求导表现得特别好:要么让参数消失,要么让参数通过。这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题。
- sigmoid:机爱你个 R 上的输入映射到 \((0,1)\),\(\mathrm{sigmoid}(x)=\frac1{1+\exp(-x)}.\)在隐藏层中已经较少使用, 它在大部分时候被更简单、更容易训练的ReLU所取代。
- tanh:将输入压缩到 \((-1,1)\),\(\tanh(x)=\frac{1-\exp(-2x)}{1+\exp(-2x)}\)
- 过使用更深的网络,可以更容易地逼近许多函数。
实现¶
# 创建多层网络
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
暂退法¶
- 希望模型深度挖掘特征,将权重分散到许多特征中,而不是过于依赖少数潜在的虚假关联
- 线性模型没有考虑到特征之间的交互作用,对于每个特征,线性模型必须指定正的或负的权重,而忽略其他特征。
- 泛化性和灵活性之间的这种基本权衡被描述为偏差-方差权衡
- 线性模型
- 很高的偏差:它们只能表示一小类函数
- 方差很低:它们在不同的随机数据样本上可以得出相似的结果。
-
深度神经网络:不局限于单独查看每个特征,而是学习特征之间的交互
-
在标准暂退法正则化中,通过按保留(未丢弃)的节点的分数进行规范化来消除每一层的偏差
- 每个中间活性值 \(h\) 以暂退概率 \(p\) 由随机变量 \(h`\) 替代
- \(h^{\prime}=\begin{cases}0&\text{概率为 }p\\\frac h{1-p}&\text{其他情况}&\end{cases}\)
def dropout_layer(X, dropout): assert 0 <= dropout <= 1 # 在本情况中,所有元素都被丢弃 if dropout == 1: return torch.zeros_like(X) # 在本情况中,所有元素都被保留 if dropout == 0: return X mask = (torch.rand(X.shape) > dropout).float() return mask * X / (1.0 - dropout)
- 只需在每个全连接层之后添加一个
Dropout层,将暂退概率作为唯一的参数传递给它的构造函数。在训练时,Dropout层将根据指定的暂退概率随机丢弃上一层的输出。在测试时,Dropout层仅传递数据(测试时通常不进行丢弃)。net = nn.Sequential(nn.Flatten(), nn.Linear(784, 256), nn.ReLU(), # 在第一个全连接层之后添加一个dropout层 nn.Dropout(dropout1), nn.Linear(256, 256), nn.ReLU(), # 在第二个全连接层之后添加一个dropout层 nn.Dropout(dropout2), nn.Linear(256, 10))
计算图与传播¶
前向传播¶
- 从输入层到输出层按顺序来计算和存储神经网络中每层的结果
反向传播¶
- 计算神经网络采纳数梯度的方法,根据微积分中的链式规则,按早相反的顺序从输出层到输入层遍历网络,存储了计算某些参数梯度时所需的任何中间变量
数值稳定性和模型初始化¶
- 神经网络的结构如下:每一层都是上一层输出和本层参数为变量的函数 \(\mathbb{H}^{(l)}=f(\mathbb{H}^{(l-1)};\mathbb{W}^{(l)})\)
- 那么网络的输出就可以表示为 \(\mathbb{H}^{(L)}=f(f(\cdots f(\mathbb{X};\mathbb{W}^{(1)})\cdots;\mathbb{W}^{(L-1)});\mathbb{W}^{(L)})\)
- 对 \(l\) 参数的更新就依赖梯度 \(\frac{\partial\mathcal{L}}{\partial\mathbb{W}^{(l)}}=\frac{\partial\mathcal{L}}{\partial\mathbb{H}^{(L)}}\cdot\prod_{i=l}^{L-1}\frac{\partial\mathbb{H}^{(i+1)}}{\partial\mathbb{H}^{(i)}}\)
- 梯度是一个累积乘积,每一层的梯度都依赖于前面所有层的梯度,通过反向传播算法计算梯度时,梯度会随着层数增加而出现指数性衰减或增长
- 如果每一层的梯度的值非常小或非常大,那么它们的乘积会导致梯度整体上指数性地减小或增大。
- 梯度消失
- 当每一层的梯度都小于 1,就可能导致梯度消失
- 当sigmoid函数的输入很大或是很小时,它的梯度都会消失,因此更稳定的ReLU系列函数已经成为从业者的默认选择
- 靠近输入层的参数更新非常缓慢:因为梯度接近 0,导致这些层的权重几乎不会变化,模型无法有效学习深层特征。
- 训练时间变长或停止:模型可能无法收敛。
- 梯度爆炸
- 如果权重初始化得过大,或者激活函数(如 ReLU)在大范围值上表现不稳定,那么每一层的梯度值会变大。
- 如果网络的权重在初始化时值很大,正向传播中的激活值会不断增大,反向传播的梯度也会随之增大,导致梯度爆炸。
- 参数更新过大:导致模型的损失函数值变得不稳定,甚至出现 NaN。
- 优化难以收敛:爆炸的梯度会破坏优化算法的稳定性。
参数初始化¶
- 假设我们有一个简单的多层感知机,它有一个隐藏层和两个隐藏单元,如果我们在隐藏层的所有单元的参数初始化时,给定相同的值,这就会导致一种对称性
- 由于隐藏单元的输出完全相同,网络的行为就好像隐藏层只有一个单元,失去了隐藏单元的多样性。
- 可以通过随机初始化和暂退法正则化来解决
- 更好的初始化方案:Xavier 初始化
- 通过控制权重的方差,确保前向传播和反向传播中方差的稳定性,从而减轻梯度消失或梯度爆炸问题。
环境和分布偏移¶
- 协变量偏移:输入分布 \(P(X)\) 发生变化,但分布条件 \(P(Y|X)\) 和标签分布 \(P(Y)\) 不变
-
为训练集中的每个样本赋予权重,来调整训练分布使其更加接近测试分布 \(w(X)=\frac{P_{\mathrm{target}}(X)}{P_{\mathrm{source}}(X)}\)
- 这个系数可以通过混合输入输出用对数几率回归进行计算
-
标签偏移:标签分布发生变化,但分布条件和输入分布不变
- 在训练数据上构造混淆矩阵(行表示预测结果类型,列表示实际标签,用于表示模型预测结果)
- 在测试数据集上做预测
- 结合混淆矩阵反推测试数据的真实标签分布
- 利用估计的真实标签分布结合训练数据集调整训练数据集的权重
-
概念偏移:条件分布本身发生变化,其他条件不变
- 使用新数据更新现有的网络权重,而不是从头开始训练。
深度学习计算¶
层和块¶
- 块:可以描述单个层、由多个层组成的组件或整个模型本身
- 自定义块 (下面实现一个顺序块)
class MySequential(nn.Module): def __init__(self, *args): super().__init__() for idx, module in enumerate(args): # 这里,module是Module子类的一个实例。我们把它保存在'Module'类的成员 # 变量_modules中。_module的类型是OrderedDict self._modules[str(idx)] = module def forward(self, X): # OrderedDict保证了按照成员添加的顺序遍历它们 for block in self._modules.values(): X = block(X) return X # 使用创建的网络 net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10)) net(X) - 自定义层
# 无参数的层 class CenteredLayer(nn.Block): def __init__(self, **kwargs): super().__init__(**kwargs) def forward(self, X): return X - X.mean() # 有参数的层 class MyDense(nn.Block): def __init__(self, units, in_units, **kwargs): super().__init__(**kwargs) self.weight = self.params.get('weight', shape=(in_units, units)) self.bias = self.params.get('bias', shape=(units,)) def forward(self, x): linear = np.dot(x, self.weight.data(ctx=x.ctx)) + self.bias.data( ctx=x.ctx) return npx.relu(linear)
参数管理¶
- 获取模型一层的参数
net[2].state_dict()OrderedDict([('weight', tensor([[-0.0427, -0.2939, -0.1894, 0.0220, -0.1709, -0.1522, -0.0334, -0.2263]])), ('bias', tensor([0.0887]))])
- 一次性访问所有采纳数
print(*[(name, param.shape) for name, param in net[0].named_parameters()]) print(*[(name, param.shape) for name, param in net.named_parameters()]) - 通过下标访问
net.state_dict()['2.bias'].data - 对具有复杂层级的块也可以嵌套访问
rgnet[0][1][0].bias.data
参数初始化¶
- 正态分布初始化
nn.init.normal_(m.weight, mean=0, std=0.01) - 初始化为 0
nn.init.normal_(m.weight, mean=0, std=0.01) - 自定义初始化
def my_init(m): if type(m) == nn.Linear: print("Init", *[(name, param.shape) for name, param in m.named_parameters()][0]) nn.init.uniform_(m.weight, -10, 10) m.weight.data *= m.weight.data.abs() >= 5 net.apply(my_init) net[0].weight[:2]
延后初始化¶
- 使得在没有指定输入维度等信息时就可以先建立网络
- 直到数据第一次通过模型传递时,框架才会动态地推断出每个层的大小
- 延后初始化使框架能够自动推断参数形状,使修改模型架构变得容易
读写文件¶
- 实现将模型保存到文件中
- 加载和保存张量
x = torch.arange(4) torch.save(x, 'x-file') x2 = torch.load('x-file') # 存储一个列表(同理也可以存储字典等) torch.save([x, y],'x-files') x2, y2 = torch.load('x-files') - 加载和保存模型参数
torch.save(net.state_dict(), 'mlp.params') clone.load_state_dict(torch.load('mlp.params'))
GPU¶
- 获取 GPU 的数目
torch.cuda.device_count() - 查看张量所在的位置
x.device - 将张量存储在 GPU 上
X = torch.ones(2, 3, device=try_gpu())- 指定存储的 GPU
torch.rand(2, 3, device=try_gpu(1))
- 指定存储的 GPU
- 进行张量运算之前,要决定在哪里执行这个操作(将其他数据移动过去, 否则找不到数据会发生异常)
- 将数据复制到 GPU 1 上
Z = X.cuda(1) - 之后就可以进行计算
- 将数据复制到 GPU 1 上
- 指定神经网络模型运行到 GPU 上
net = net.to(device=try_gpu())
优化¶
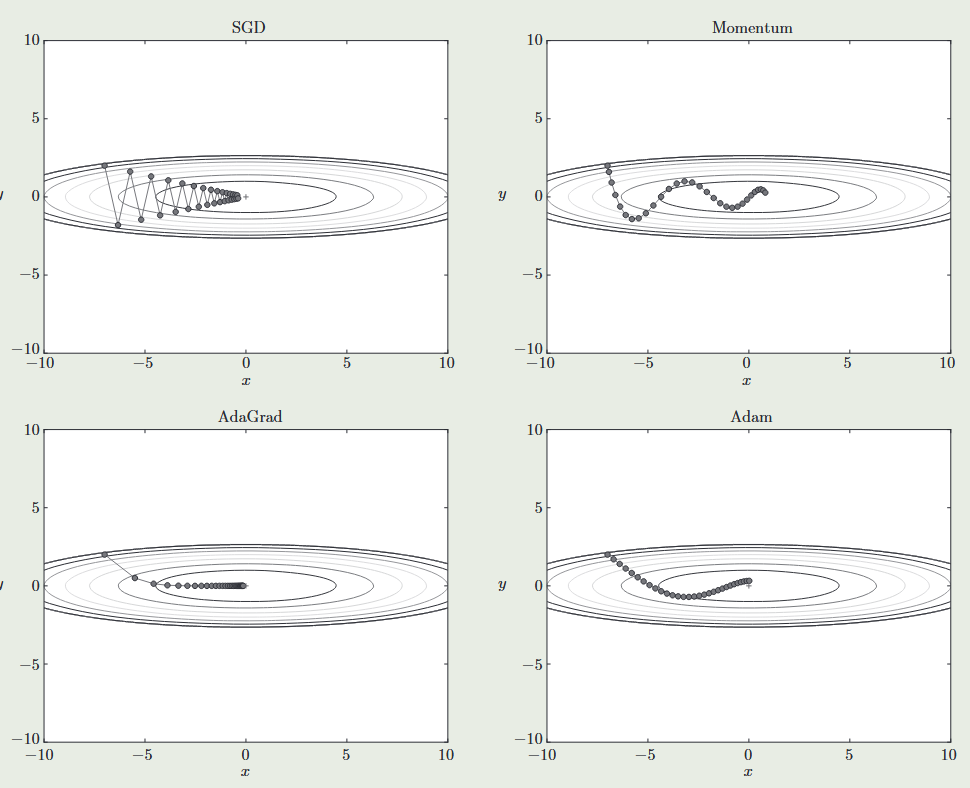
- 使用其他参数更新算法,如
- 更恰当的对权重的初始值初始化
- 让激活值的分布更加均匀
- Xavier 初始值:使用标准差为 \(\frac{1}{\sqrt{ n }}\) 的高斯分布
- 批量归一化:
- 使学习快速进行、不那么依赖初始值、并抑制过拟合
- 将 batchnorm 层添加到神经网络中来调整各层的激活值分布使其拥有适当的广度
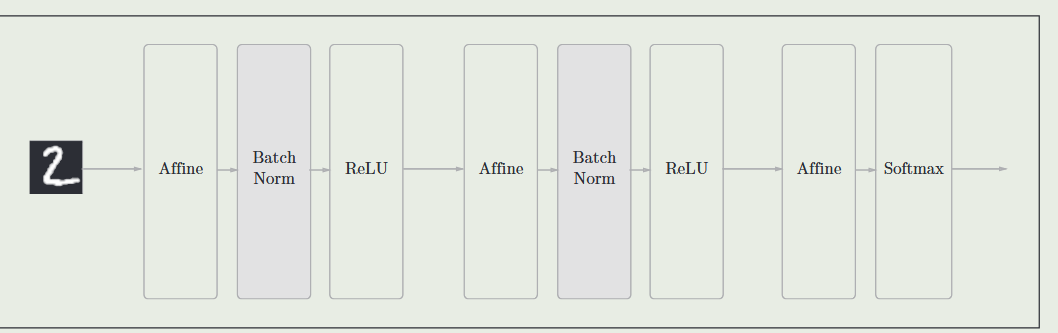
卷积神经网络 CNN¶
- 强大的、为处理图像数据而设计的神经网络
- 图片中有太多的像素点,传统的机器学习算法无法处理如此海量的参数
- 卷积神经网络正是将空间不变性的这一概念系统化,从而基于这个模型使用较少的参数来学习有用的表示。
- 平移不变性:不管检测对象出现在图像中的哪个位置,神经网络的前面几层应该对相同的图像区域具有相似的反应,即为“平移不变性”。(即如果输入图像中的某个对象从左侧移动到了右侧,模型应该能够识别到这是同一个对象,而不因为其位置的改变对输出产生完全不同的影响)
- 局部性:神经网络的前面几层应该只探索输入图像中的局部区域,而不过度在意图像中相隔较远区域的关系,这就是“局部性”原则。最终可以聚合这些局部特征,以在整个图像级别进行预测。
- 这个原则与现实中图像的性质相符:一个像素的特征通常与其周围的像素紧密相关,而与距离较远的像素关系较弱。
-
输入的图像表示为矩阵 \(X\),形状为 \((H, W)\)
- 隐藏层中的表示也都为相同形状的二维矩阵
- 因此对于全连接层每层的参数可以使用一个四阶张量来表示
- \(W(h
,w,h,w)\) 表示连接输入图像中位置 \((h,w)\) 的像素与隐藏表示中位置 \((h,w)\) 的像素权重 \(\mathbf{H}(h^{\prime},w^{\prime})=\sum_{h=1}^H\sum_{w=1}^W\mathbf{X}(h,w)\cdot\mathbf{W}(h^{\prime},w^{\prime},h,w)+\mathbf{b}(h^{\prime},w^{\prime}),\) - 传统的多层感知机全连接具有太多的参数,而且并不具有平移不变形,难以处理平移
-
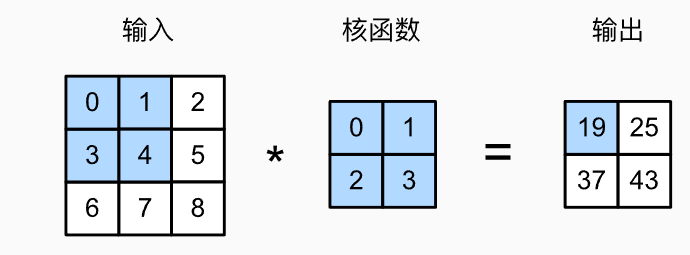
卷积操作通过一个小的权重窗口(卷积核)对图像的局部区域进行加权求和。
- 每一个输出像素值只依赖于输入图像的局部像素区域,而不是整个图像 \(\mathbf{H}(i,j)=\sum_{m,n}\mathbf{X}(i+m,j+n)\cdot\mathbf{K}(m,n)\) 其中 \(K\) 表示卷积核的权重

- 卷积操作中的权重在整个输入图像中共享。无论输入图像的某个特征出现在左上角还是右下角,卷积核都能对该特征进行相同的加权计算。
- 当输入图像中的对象发生平移时,卷积操作产生的隐藏表示也会随之平移,而不会改变表示的内容。
- 有点:参数数量少,平移不变形,捕获局部特征
- 添加上表示 RGB 通道的 \(c\) 参数 \([\mathsf{H}]_{i,j,d}=\sum_{a=-\Delta}^\Delta\sum_{b=-\Delta}^\Delta\sum_c[\mathsf{V}]_{a,b,c,d}[\mathsf{X}]_{i+a,j+b,c},\)
卷积层的创建与训练¶
- 创建卷积层
- 卷积层同样是对输入和卷积核权重进行相关运算,添加标量偏置之后产生输出
- 也就是要训练卷积核权重和标量偏置
class Conv2D(nn.Module): def __init__(self, kernel_size): super().__init__() self.weight = nn.Parameter(torch.rand(kernel_size)) self.bias = nn.Parameter(torch.zeros(1)) def forward(self, x): return corr2d(x, self.weight) + self.bias
- 先构造一个卷积层,并将其卷积核初始化为随机张量。接下来,在每次迭代中,我们比较
Y与卷积层输出的平方误差,然后计算梯度来更新卷积核。# 构造一个二维卷积层,它具有1个输出通道和形状为(1,2)的卷积核 conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False) # 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度), # 其中批量大小和通道数都为1 X = X.reshape((1, 1, 6, 8)) Y = Y.reshape((1, 1, 6, 7)) lr = 3e-2 # 学习率 # 通过 10 次迭代训练卷积核,使得卷积层对输入 X 进行卷积后输出 Y_hat 能够更接近目标 Y for i in range(10): Y_hat = conv2d(X) l = (Y_hat - Y) ** 2 conv2d.zero_grad() l.sum().backward() # 迭代卷积核 conv2d.weight.data[:] -= lr * conv2d.weight.grad if (i + 1) % 2 == 0: print(f'epoch {i+1}, loss {l.sum():.3f}')
填充和步幅¶
- 假设输入形状为 \(n_{h}\times n_{w}\) 卷积核形状为 \(k_{h}\times k_{w}\) 那么输出的形状为 \((n_h-k_h+1)\times(n_w-k_w+1)\)
- 使用较大的卷积核以及较深的层次后图像尺寸会显著减小,丢失很多有用的边界信息
填充¶
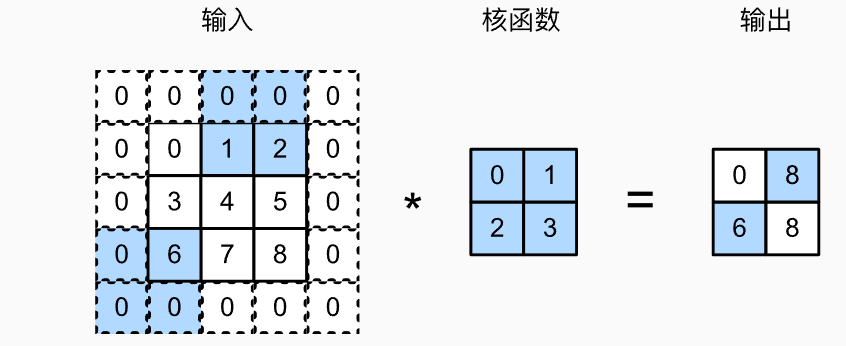
- 通过填充可以解决边缘像素丢失的问题
- 通过填充 \(p_h=k_h-1\) 以及 \(p_w=k_w-1\) 就可以实现使输入和输出具有相同的高度和宽度
- 通常在左右/上下均匀的填充在两侧
import torch from torch import nn # 为了方便起见,我们定义了一个计算卷积层的函数。 # 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数 def comp_conv2d(conv2d, X): # 这里的(1,1)表示批量大小和通道数都是1 X = X.reshape((1, 1) + X.shape) Y = conv2d(X)# 进行卷积操作 # 省略前两个维度:批量大小和通道 return Y.reshape(Y.shape[2:]) # 请注意,这里每边都填充了1行或1列,因此总共添加了2行或2列 # 由于卷积层边长为3,因此计算后为8+2*1-(3-1)=8维持不变 conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1) X = torch.rand(size=(8, 8)) comp_conv2d(conv2d, X).shape
- 通常在左右/上下均匀的填充在两侧
步幅¶
- 卷积计算时从左上角开始向下向右滑动,默认下每次只滑动一个元素,为了高效计算或缩减采样次数,有时可以跳过中间位置,即一次滑动多个元素。
- 一次滑动元素的数量就成为步幅
- 一个垂直步幅为 3 水平步幅为 2 的例子
- 此时输出的规模就为\(\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor\times\lfloor (n_w-k_w+p_w+s_w)/s_w\rfloor\)
- 设置步幅为 2:\(conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)\)
- 分别设置宽度和高度\(conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))\)
多输入输出通道¶
- 比如为了处理彩色图像使用 RGB 三维张量,每个输入图像具有 \(3\times h\times w\) 的形状
多输入通道¶
- 需要构造一个与输入数据具有相同输入通道数的卷积核,从而与输入数据进行互相关运算
- 多输入时,得到形状为的 \(c_i\times k_h\times k_u\) 卷积核,可以对每个通道输入的二维张量和卷积核的二维张量进行互相关运算,再对通道求和(将 \(c_i\) 的结果相加)得到二维张量。
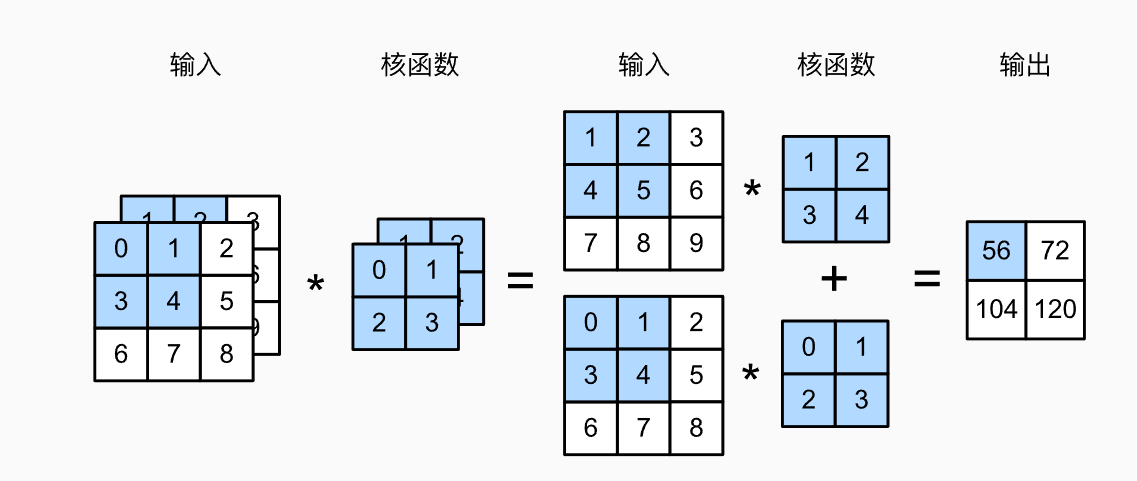
def corr2d_multi_in(X, K): # 先遍历“X”和“K”的第0个维度(通道维度),再把它们加在一起 return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
多输出通道¶
- 通过创建一个 \(c_o\times c_i\times k_h\times k_w\) 的卷积核从而实现具有 \(c_{i}\) 个输入通道 \(c_{0}\) 个输出通道的互相光计算
import torch # 实现多输入通道的二维互相关 def corr2d_multi_in(X, K): return sum(torch.nn.functional.conv2d(x.unsqueeze(0).unsqueeze(0), k.unsqueeze(0).unsqueeze(1)) for x, k in zip(X, K)) # 实现多输入多输出通道的二维互相关 def corr2d_multi_in_out(X, K): # 遍历卷积核的第 0 个维度(输出通道),对每个输出通道计算结果(分别计算每一个输出通道) return torch.stack([corr2d_multi_in(X, k) for k in K], 0) # 构造输入张量 X (2 输入通道, 3x3 尺寸) X = torch.tensor([[[0, 1, 2], [3, 4, 5], [6, 7, 8]], [[1, 2, 3], [4, 5, 6], [7, 8, 9]]], dtype=torch.float32) # 构造卷积核 K (3 输出通道, 2 输入通道, 2x2 尺寸) K = torch.stack((torch.tensor([[[0, 1], [2, 3]], [[1, 2], [3, 4]]], dtype=torch.float32), torch.tensor([[[1, 2], [3, 4]], [[2, 3], [4, 5]]], dtype=torch.float32), torch.tensor([[[2, 3], [4, 5]], [[3, 4], [5, 6]]], dtype=torch.float32)), 0) # 执行多输入多输出通道的互相关运算 output = corr2d_multi_in_out(X, K) print(output) - 在多输入输出通道下 \(1\times1\) 卷积变的更有意义,不再是单纯复制一个点的值,而是可以对不同层进行运算生成输出(即可以实现一个“纵向”的卷积)
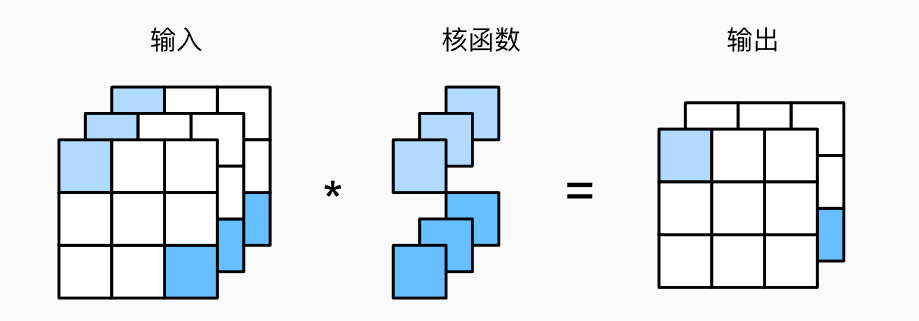
def corr2d_multi_in_out_1x1(X, K): c_i, h, w = X.shape c_o = K.shape[0] X = X.reshape((c_i, h * w)) K = K.reshape((c_o, c_i)) # 全连接层中的矩阵乘法 Y = torch.matmul(K, X) return Y.reshape((c_o, h, w))
汇聚层¶
- 当我们处理图像时,我们希望逐渐降低隐藏表示的空间分辨率、聚集信息,这样随着我们在神经网络中层叠的上升,每个神经元对其敏感的感受野(输入)就越大。
- 即越靠后的神经元越具有更好的全局感受能力,最后一层的神经元应该对整个输入的全局敏感。
- 而低层有希望具有平移不变性
- 汇聚层的功能
- 降低卷积层对位置的敏感性:汇聚层通过在局部区域内提取统计特征,增强了模型对小尺度位置变化的鲁棒性。即使输入图像中的物体位置发生小幅度的移动,汇聚层也可以提取相似的特征,从而提升模型的泛化能力。
- 降低对空间降采样表示的敏感性:汇聚层通过减少特征图的分辨率,减少了数据量和计算复杂度。这种降采样过程不仅加速了计算,还帮助模型聚焦于更重要的全局特征,而不是受局部细节的干扰。
- 汇聚层运算符由一个固定形状的窗口组成,该窗口根据其步幅大小在输入的所有区域上滑动,为固定形状窗口遍历的每个位置计算一个输出。
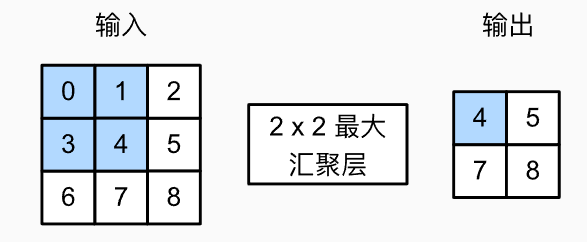
- 最大汇聚层呢个
- 保留窗口内的最大值
- 平均汇聚层
- 结果为窗口内的平均值
def pool2d(X, pool_size, mode='max'): p_h, p_w = pool_size Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1)) for i in range(Y.shape[0]): for j in range(Y.shape[1]): if mode == 'max': Y[i, j] = X[i: i + p_h, j: j + p_w].max() elif mode == 'avg': Y[i, j] = X[i: i + p_h, j: j + p_w].mean() return Y
- 结果为窗口内的平均值
- 汇聚层也可以改变输出形状, 并且可以通过填充和步幅以获得所需的输出形状。
- 在处理多通道输入数据时,汇聚层在每个输入通道上单独运算,而不是像卷积层一样在通道上对输入进行汇总。
- 即汇聚层的输出通道数与输入通道数相同
- 对所有通道使用一个相同的汇聚层
卷积神经网络的实例与分析¶
LeNet¶
- 最古老的神经网络,用于从 \(28\times28\) 的图像中识别手写数字
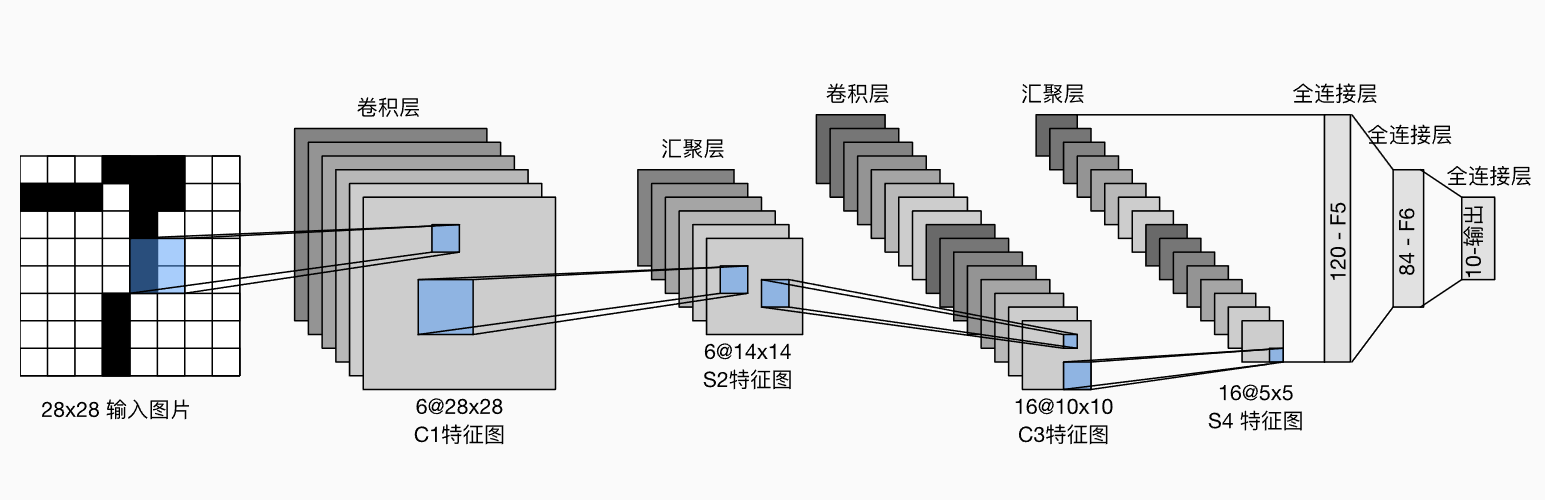 输入层
输入层- 输入是一个大小为 28×28 的灰度图像。
- 无通道数,因为这是单通道灰度图像。
- 图像像素值范围通常归一化到 [0, 1],便于网络学习。 C1:第一个卷积层
- 输入:28×28 的图像。
- 卷积核:6 个 5×5 的卷积核(权重共享)。
- 输出:6 个特征图,每个特征图大小为 28−5+1=24×24。
-
作用:通过卷积操作提取低级特征(如边缘、角点等)。 S2:第一个汇聚层
-
输入:6 个 24×24 的特征图。
- 操作:**平均汇聚,每 2×2 的区域取平均值,步幅为 2。
- 输出:6 个特征图,每个特征图大小为 24/2 = 12×12。
- 作用:
- 降低特征图的分辨率(降采样),减少计算复杂度。
- 增强模型对位置变化的鲁棒性。 C3:第二个卷积层
- 输入:6 个 12×12 的特征图。
- 卷积核:16 个 5×5 的卷积核。
- 输出:16 个特征图,每个特征图大小为 12−5+1=8×8。
- 作用:提取更高层次的特征(如纹理、形状等)。 S4:第二个汇聚层
- 输入:16 个 8×8 的特征图。
- 操作:平均汇聚,每 2×2 的区域取平均值,步幅为 2。
- 输出:16 个特征图,每个特征图大小为 8/2 = 4×4。
- 作用:
- 进一步降采样,减少特征图的尺寸。
- 提供更紧凑的特征表示,降低计算需求。 C5:全连接卷积层
- 输入:16 个 4×4 的特征图(共 16×4×4=256 个特征)。
- 卷积核:120 个大小为 5×5 的卷积核,将输入特征图映射到更高维的空间。
- 输出:1×1×120 的特征向量。
- 作用:
- 将前面提取到的特征压缩成更高的特征表示。
- 这一层实际上类似于全连接层,因为输入的尺寸与卷积核匹配。 F6:全连接层
- 输入:120 个特征值。
- 输出:84 个特征值(隐藏神经元)。
- 作用:进一步学习非线性组合,缩小到更小的特征空间,准备分类。 输出层
- 输入:84 个特征值。
- 输出:10 个类别(数字 0 到 9)。
- 作用:输出最终的分类结果,表示输入图像属于哪个类别。
net = nn.Sequential( nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2), nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(), nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(), nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(), nn.Linear(120, 84), nn.Sigmoid(), nn.Linear(84, 10)) - 与上一层相比,每一层特征的高度和宽度都减小了,随着层叠的上升,通道的数量从输入时的1个,增加到第一个卷积层之后的6个,再到第二个卷积层之后的16个。 同时,每个汇聚层的高度和宽度都减半。最后,每个全连接层减少维数,最终输出一个维数与结果分类数相匹配的输出。
- 训练模型
def train(net, train_iter, test_iter, num_epochs, lr, device): """用GPU训练模型""" def init_weights(m): if type(m) == nn.Linear or type(m) == nn.Conv2d:# 如果网络层是 `nn.Linear`(全连接层)或 `nn.Conv2d`(卷积层),就使用 Xavier 均匀分布初始化其权重 nn.init.xavier_uniform_(m.weight) net.apply(init_weights)# 将 `init_weights` 函数应用到 `net` 中的每一层 print('training on', device) net.to(device) optimizer = torch.optim.SGD(net.parameters(), lr=lr) loss = nn.CrossEntropyLoss() animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], legend=['train loss', 'train acc', 'test acc']) timer, num_batches = d2l.Timer(), len(train_iter) for epoch in range(num_epochs): # 训练损失之和,训练准确率之和,样本数 metric = d2l.Accumulator(3) net.train() for i, (X, y) in enumerate(train_iter): timer.start() optimizer.zero_grad() X, y = X.to(device), y.to(device) y_hat = net(X) l = loss(y_hat, y) l.backward() optimizer.step() with torch.no_grad(): metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0]) timer.stop() train_l = metric[0] / metric[2] train_acc = metric[1] / metric[2] if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1: animator.add(epoch + (i + 1) / num_batches, (train_l, train_acc, None)) # 测试集评估 test_acc = evaluate_accuracy_gpu(net, test_iter) animator.add(epoch + 1, (None, None, test_acc)) print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, ' f'test acc {test_acc:.3f}') print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec ' f'on {str(device)}')
深度学习¶
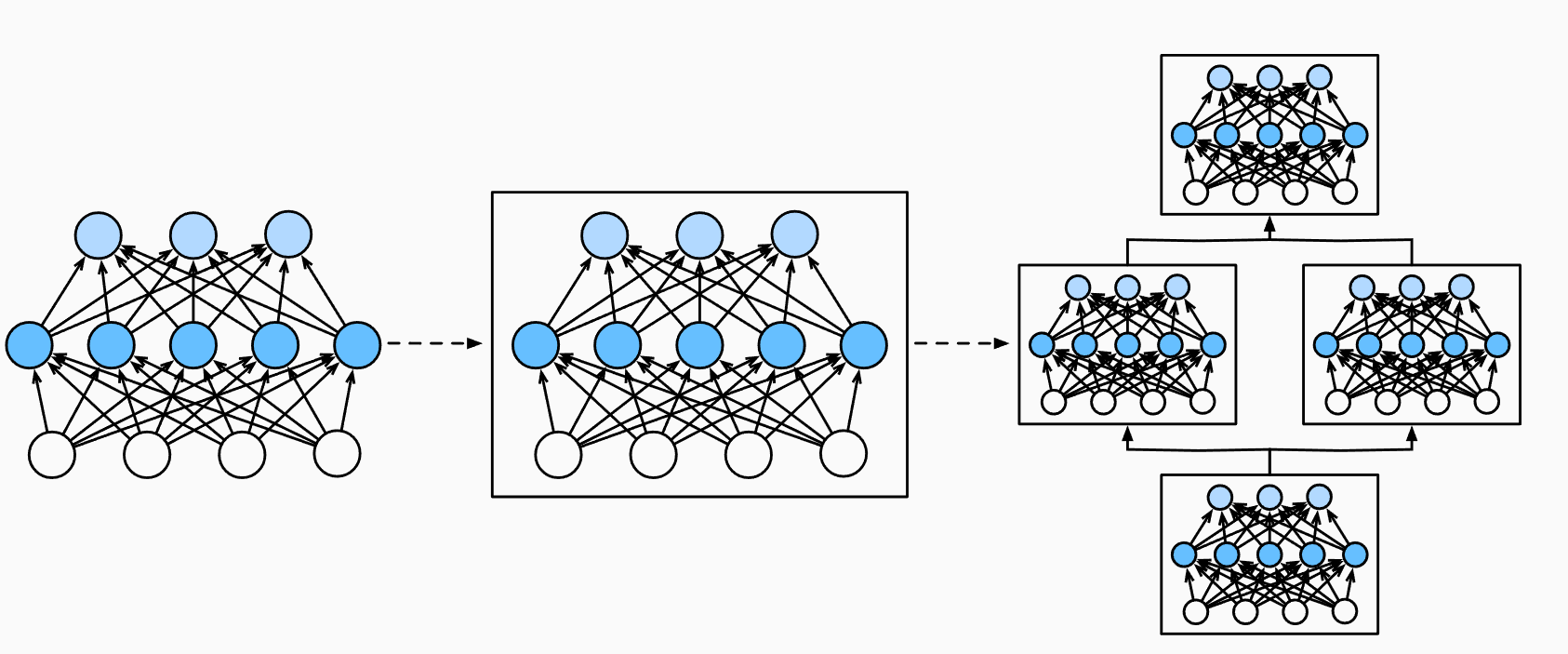
- 通常来说可以通过加深网络来提高识别的准确率
- 加深层次可以减少模型的总参数量
- 如一个 5*5 卷积层的参数(35)就多于具有同样缩小效果的两个 3*3 卷积层的参数数目(18)
- 此外还能提升模型的表现力