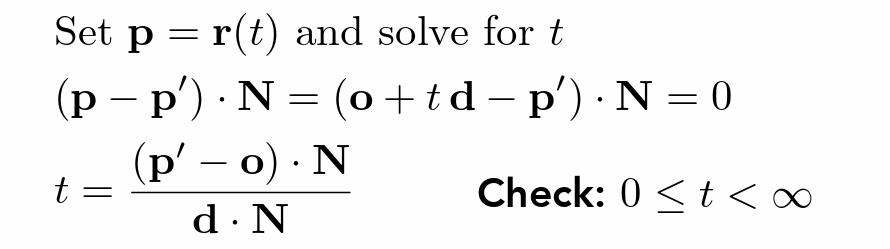光线追踪
- Shadow Mapping 阴影映射(只能处理点光源、硬阴影)光栅化的阴影处理
- 阴影:人能看到的位置,但光源看不到的位置
- 记录光源到不同物体的最短距离,将摄像机看到的位置与光源的深度距离比较来判断是否被遮挡形成阴影
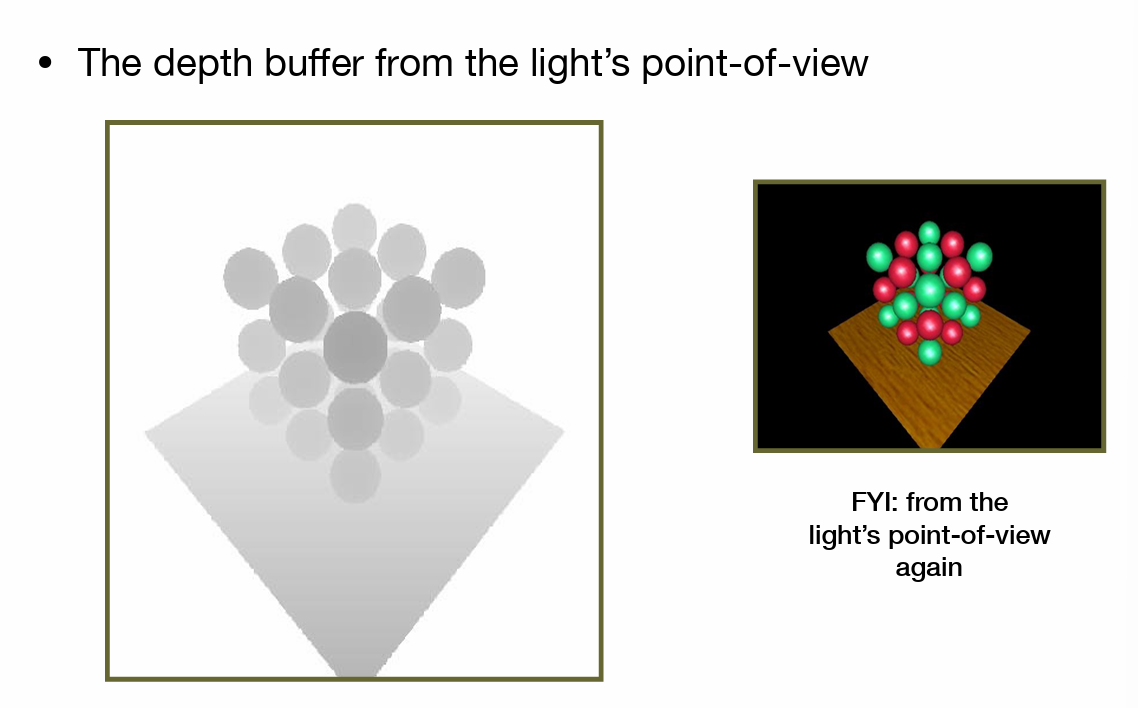

- 存在数值精度问题
- 存在深度信息图(shadowmap)分辨率与实际渲染分辨率不匹配的问题

- 硬阴影与软阴影

- 点光源只会产生硬阴影
- 当光源被部分遮挡时会产生软阴影
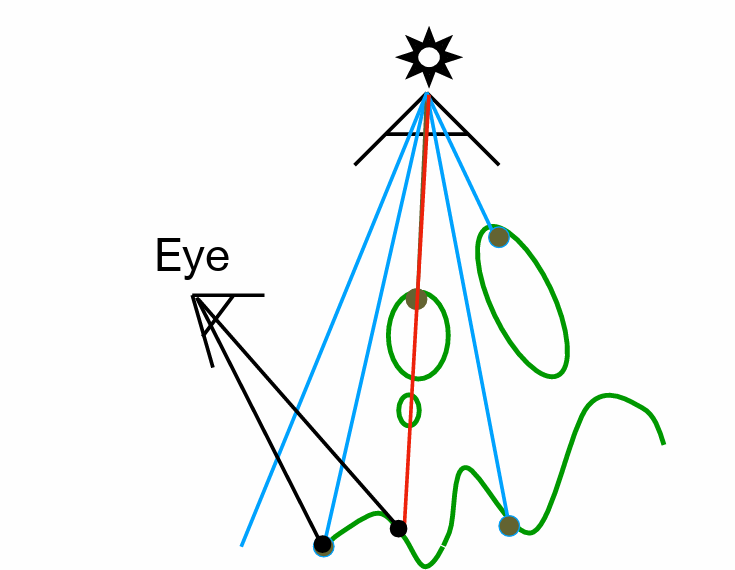
- 光线追踪应用了光路可逆性,从眼睛出发直至光源进行追踪
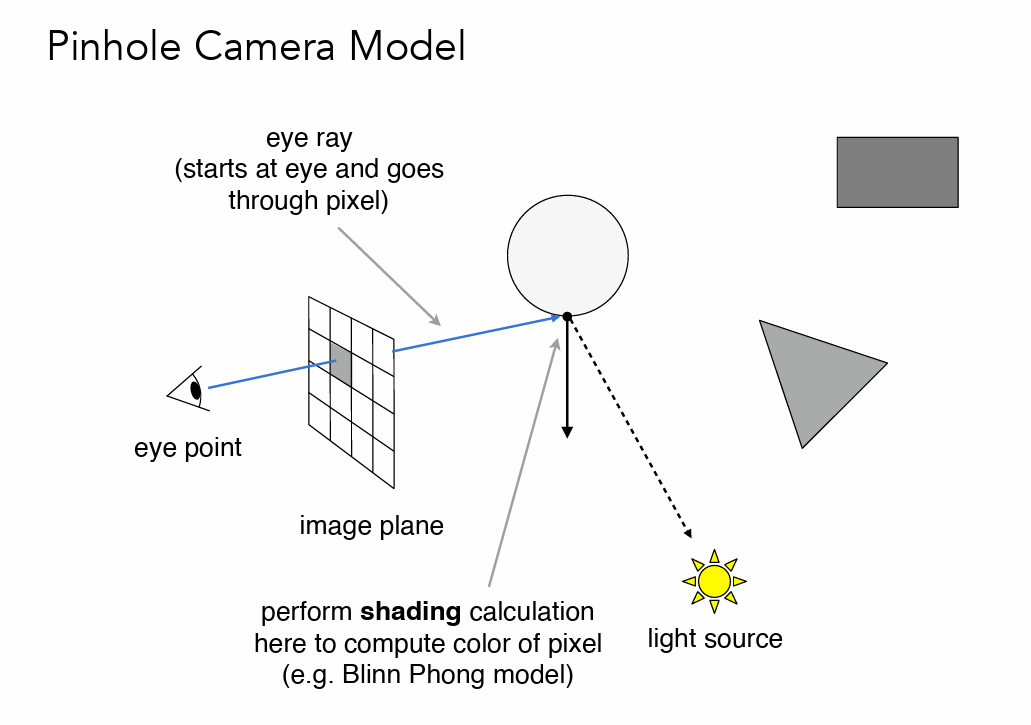
- 从眼睛向外寻找,到达最近的(可观察物体)然后与光源连线计算着色结果(可见性)
光源的分类¶
点光源¶
- 对于距离较近且足够小的点光源,会以不同的方式照亮不同位置(方向会发生变化)
- 对于足够远的小点光源(如太阳),可以认为在不同方式具有相同的方向,即以相同的方式照亮
- 大部分的点光源是各向同性的,即向四周均匀的发光,辐照度可以表示为:\(Irradiance \quad E = I \frac{\cos{\theta}}{r^2}\) 其中 \(I=\frac{P}{4\pi}\)
定向光源¶
- 是一种明亮而遥远的特殊点光源,通常认为衰减较小,即不随距离显著变化,通常表示为 \(Irradiance \quad E = H\cos{\theta}\) 其中的 \(H\) 为一个常数
环境照明¶
- 环境光照包含了二次、多次反射等一系列的光,是十分复杂的。大多数时可以先假设为一种均匀的背景光,即在所有方向和位置中都完全相同。
- 可以表示为环境反射系数与环境强度的乘积\(L_r=k_a*I_a\)
光线追踪中的坐标变换¶
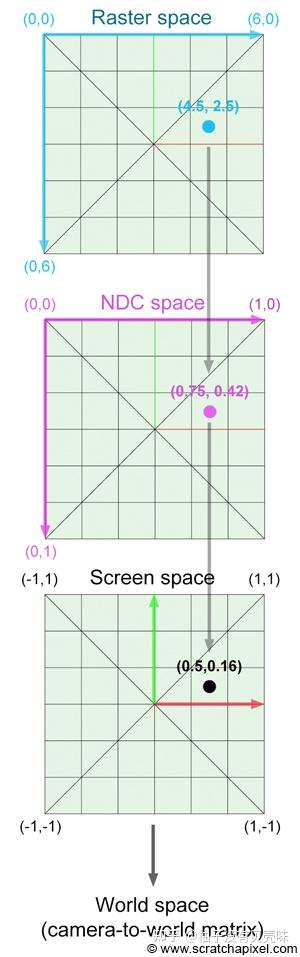
- 先将像素坐标-> NDC 坐标->屏幕坐标->世界坐标
- 像素坐标:\((x_{0},y_{0})(i+0.5,j+0.5)\)
- NDC 坐标:\((x_{1},y_{1})=\left( \frac{x_{0}}{width},\frac{y_{0}}{height} \right)\)
- 屏幕坐标: \((x_{2},y_{2})=(2x_{1}-1,1-2y_{1})\)
- 世界坐标:\((x_{3},y_{3})=\left( x_{2}*\frac{width}{height}*\tan\left( \frac{\alpha}{2} \right),y_{2}*\tan{\frac{\alpha}{2}} \right)\)
Whitted-Style Ray Tracing¶
- 一种递归算法,可以处理多次反射(折射)的情况(打到光滑表面就继续反射,打到漫反射就停止)
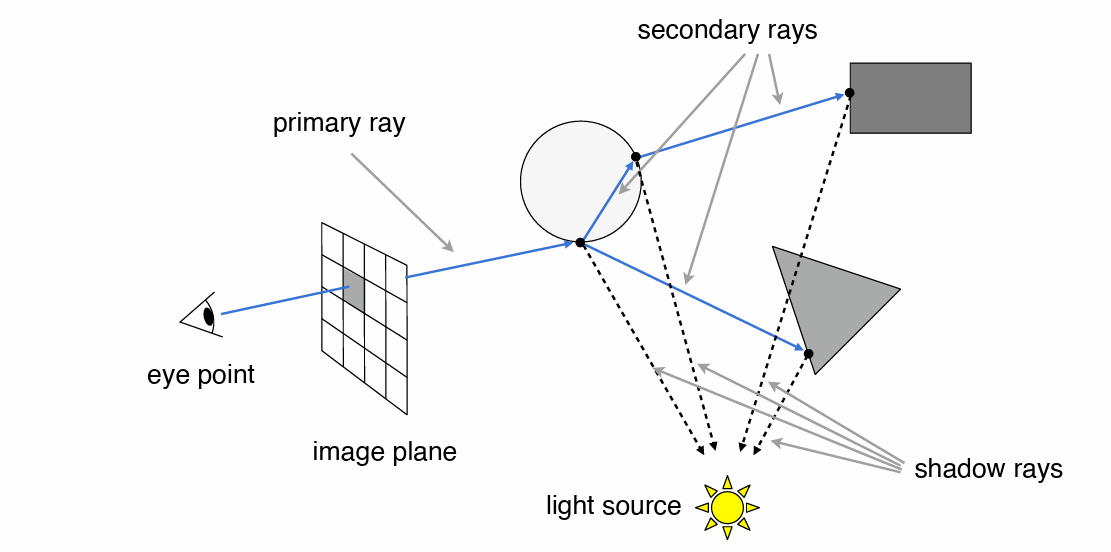
- 着色叠加
- 光线与图形的交点(几何隐式表示)

- 点加方向表示光线 \(r(t)=o+td\)
- 解任意曲面与光线的交点
- 光线与三角形面求交(几何显式表示)
- 使用一条法向量加上一个点来表示一个平面,并且通过向量乘法判断一个点是否在平面上

- 法一:先求和平面的交点,再判断是否属于某个三角形
- 法二:利用重心坐标直接判断(三个参数都非负)Moller Trumbore Algorithm 算法

- 用于快速进行射线和三角形求交 (不需要先求解射线与平面的交点)
- Möller–Trumbore
优化¶
- 包围盒
- 用简单的几何图形框住物体

- 只有光线和包围盒会发生碰撞才去考虑光线和物体三角形面的相交情况
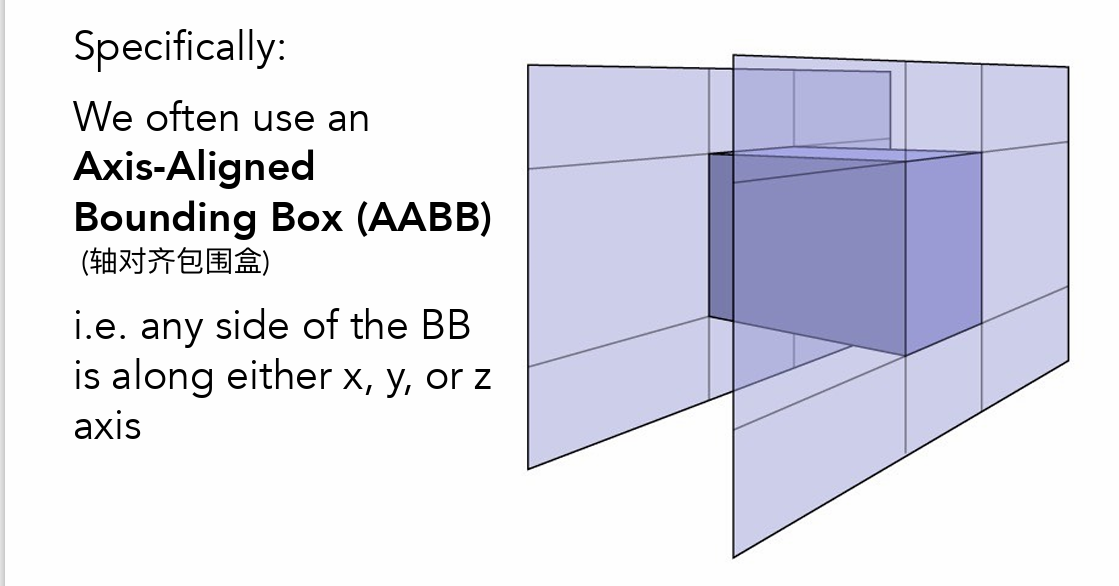
- AABB 轴对齐(xyz)包围盒
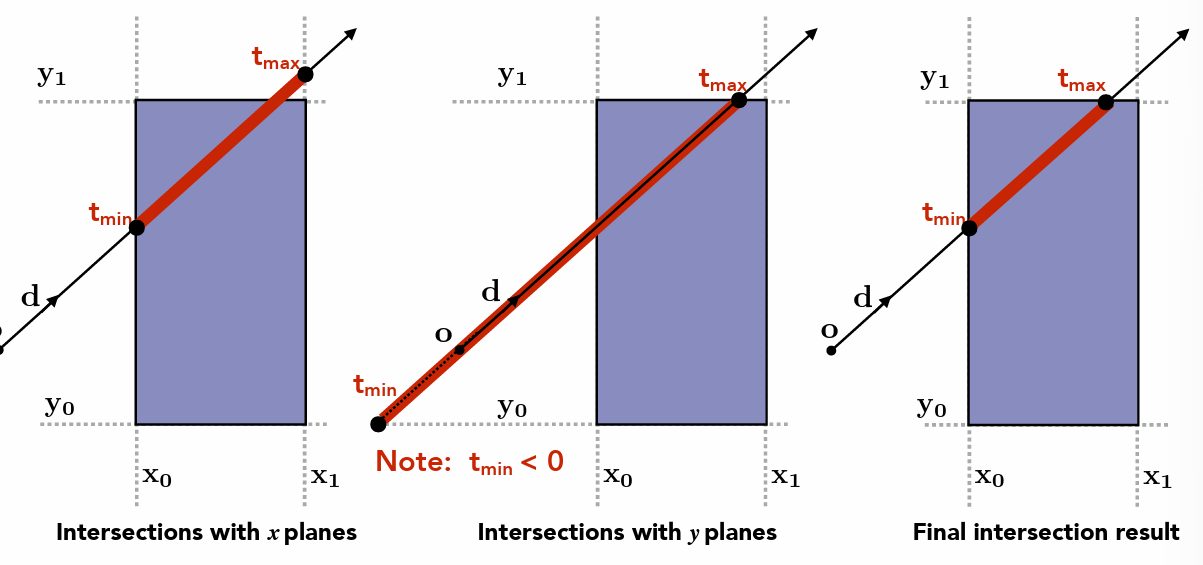
- 记录与平面的交点,求交后得到与包围盒的交点
-
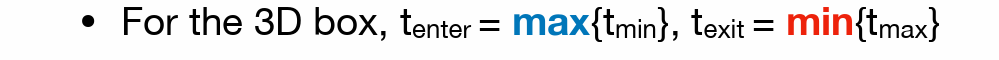
- 光线进入所有对面才真正进入了盒子,光线离开任何一个对面就离开了盒子

-
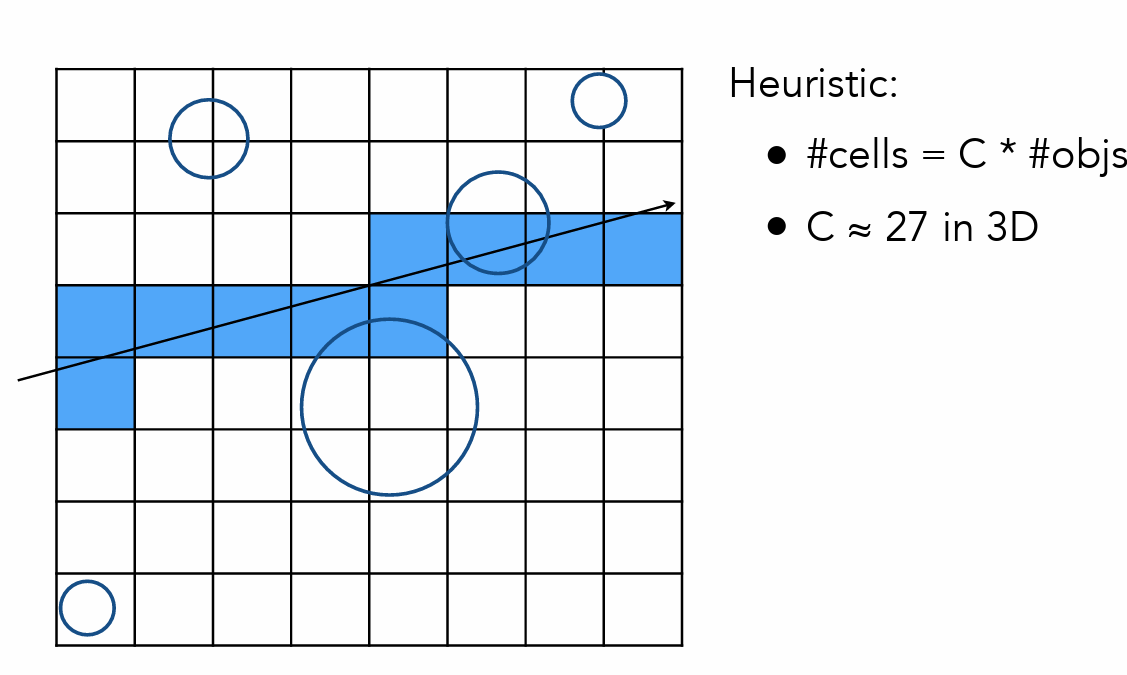
Uniform Spatial Partitions(AABB 加速光线追踪)
- 先和盒子求交,再决定是否要和物体求交
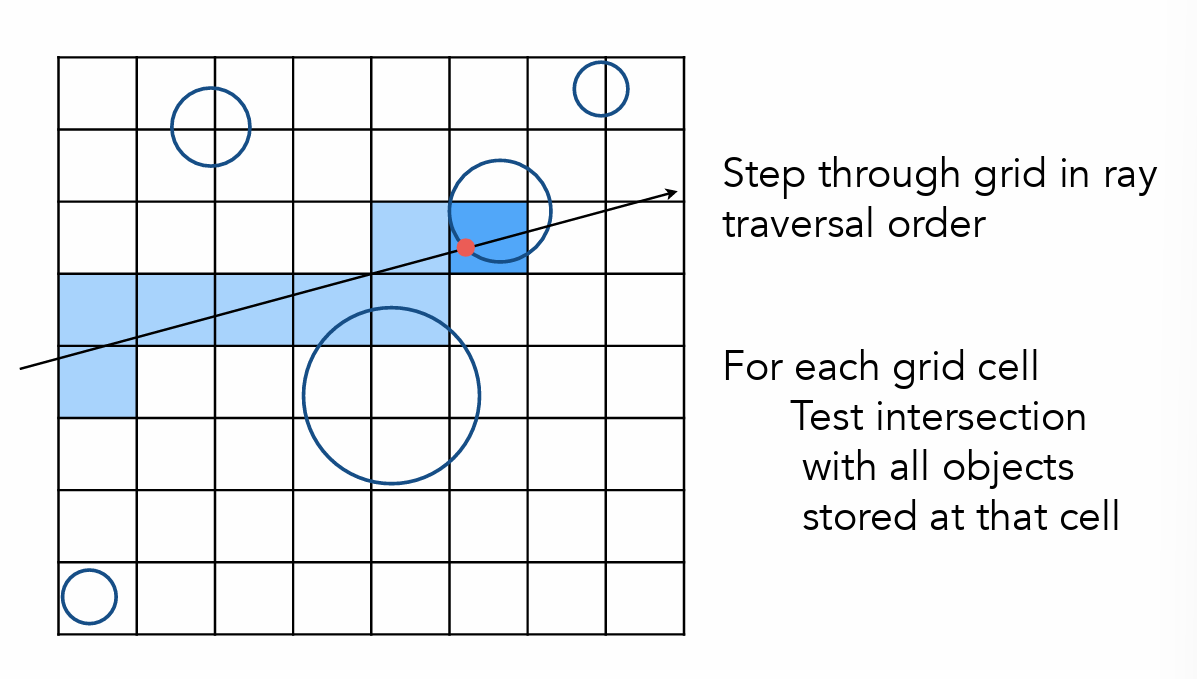
-
划分的各自数目要恰当(但是均匀划分存在一系列问题,因为物体的分布不是均匀的)
-
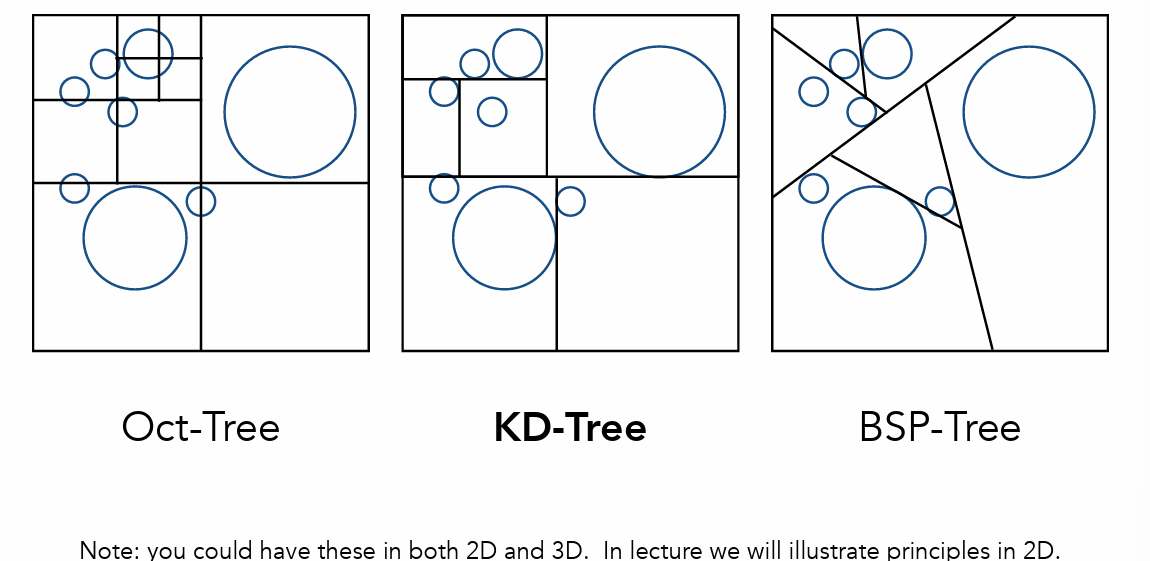
空间划分方法
-
-
Oct-Tree(八叉树):问题:随着维度增加,划分数目指数增加
-
KD-Tree

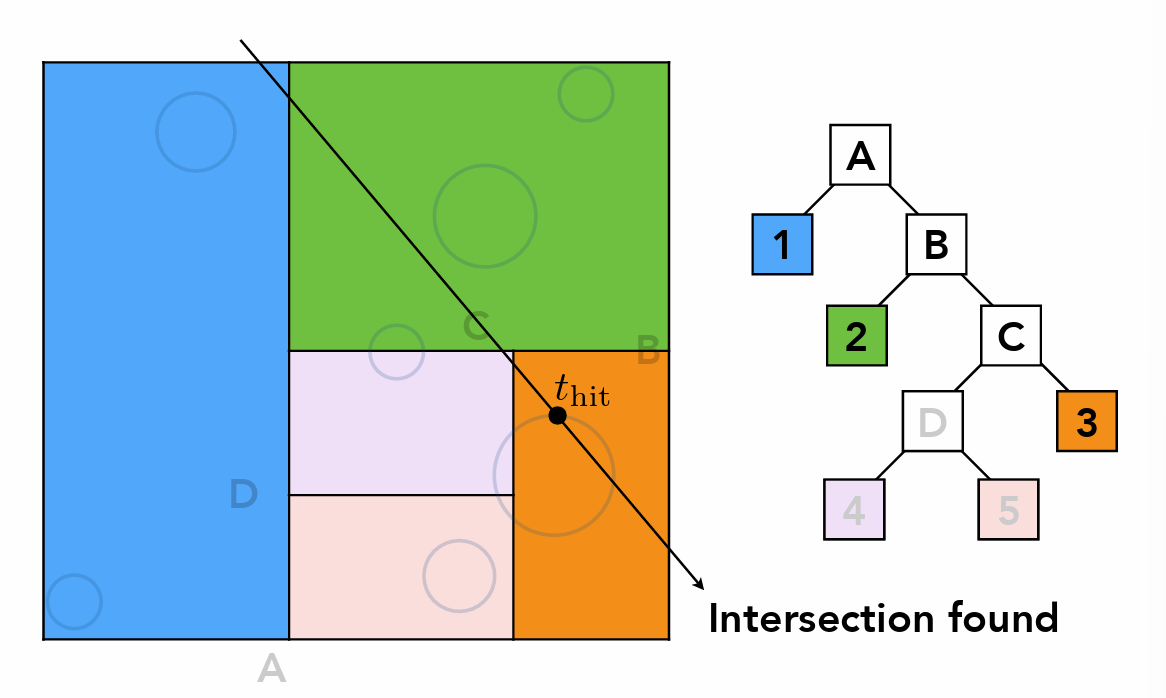
-
难点:判断三角形与盒子是否交很难,并且三角形可能跨盒子
-
(BVH)物体划分
-
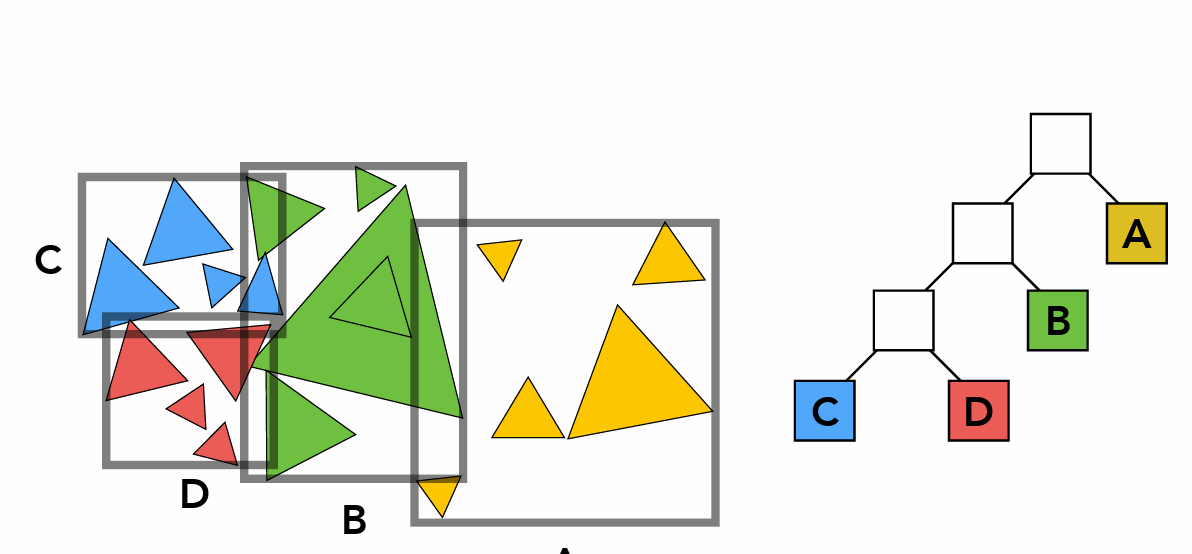
- 确定包围盒;对包围盒内的物体进行划分;分别重新计算包围盒;继续计算。
- 先找到最长的轴;然后在那个轴上把三角形均等划分到左右两个包围盒,保持左右两边数量相等或差一,即平行二叉树;重复这两个步骤直到只剩一个或两个三角形。
-
一个物体只会出现在一个盒子中(盒子中也一定有物体)
- 可以每次都选择位于中间的三角形用于划分
-
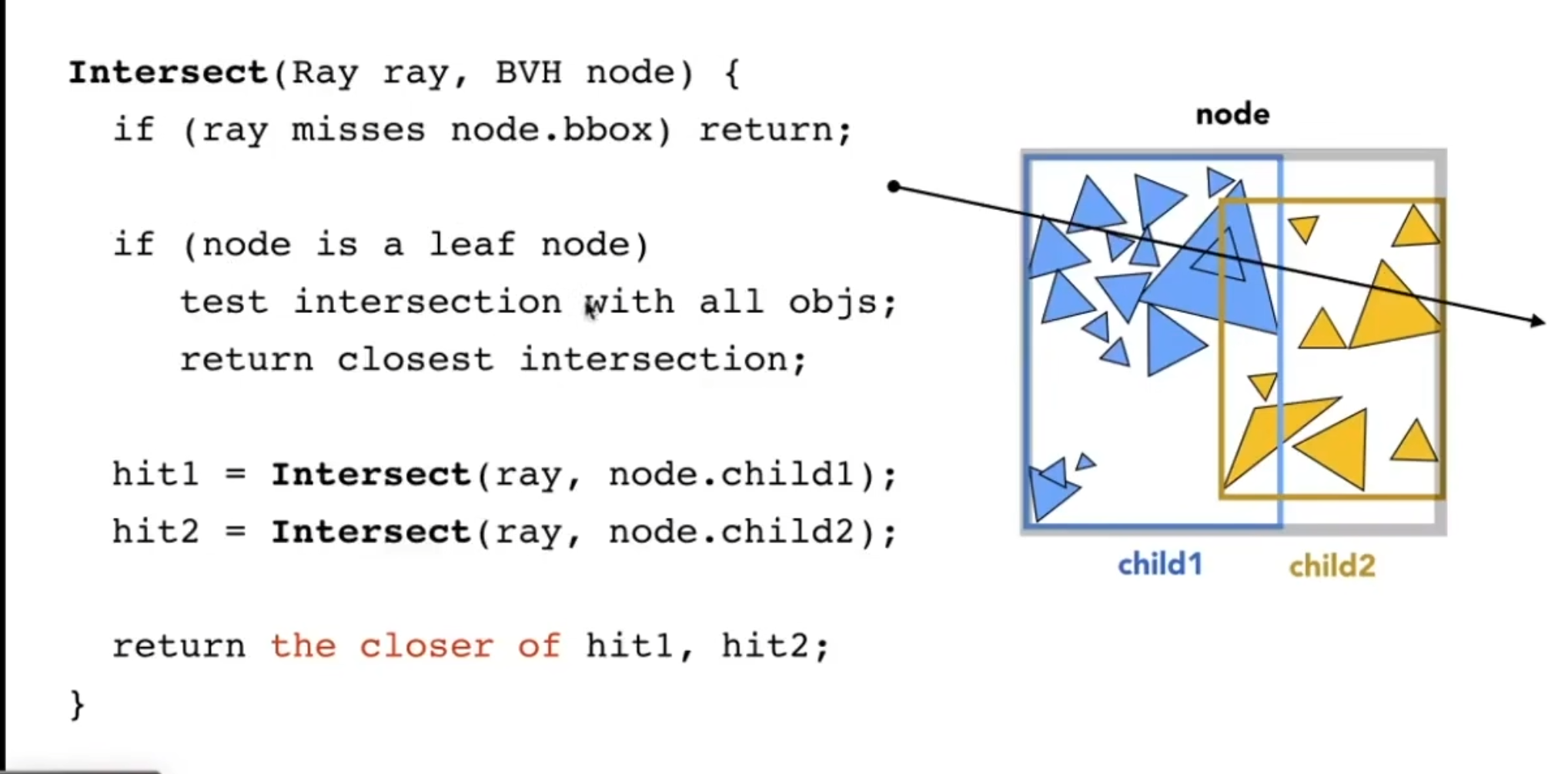
求交过程(与节点相交了,再继续去看子节点)
-
SAH 划分
- BVH 存在不平衡划分的问题:
- SAH 通过计算优化这个划分方式,使得包围盒划分更有效率
辐射度量学¶
- 准确定义物理光照
- Radiant flux:单位时间的能量
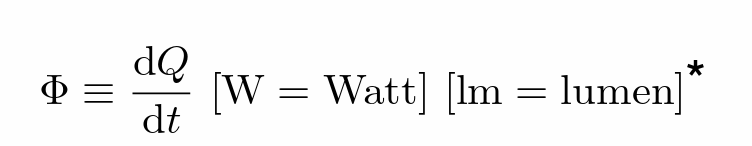
- Radiant Intensity:辐射强度(辐射能量)
- Radiant Intensity 是指光源在特定方向上单位立体角内的辐射功率(Radiant Flux,单位是 Watts)。它描述了光源在某个方向上的“亮度”有多强。
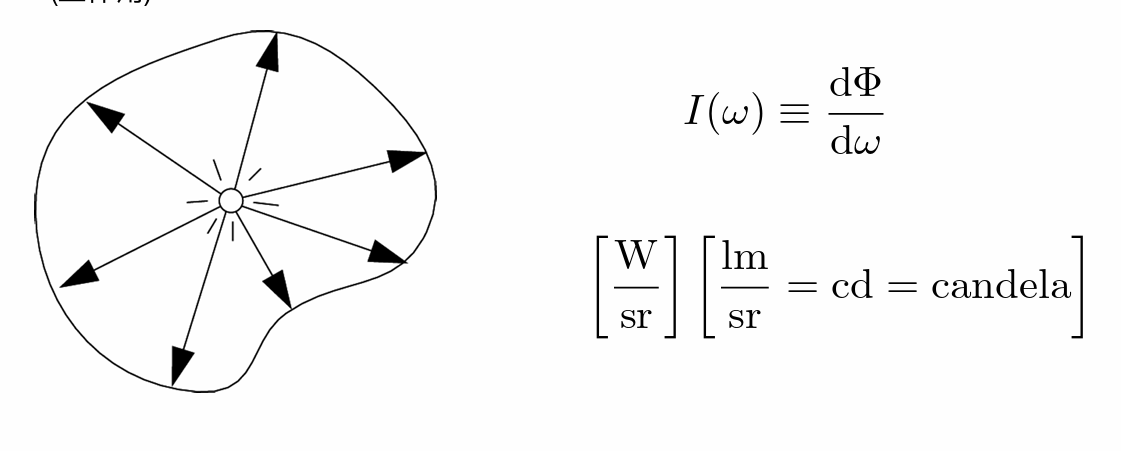
- 立体角:

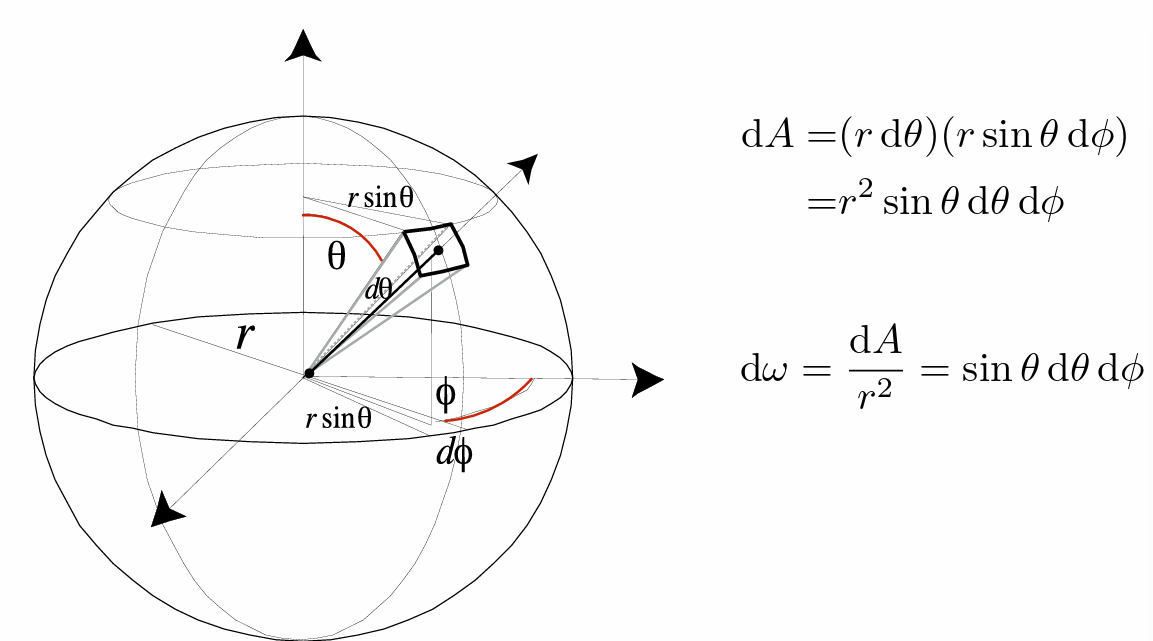
- 注意强度只与立体角相关,与距离无关
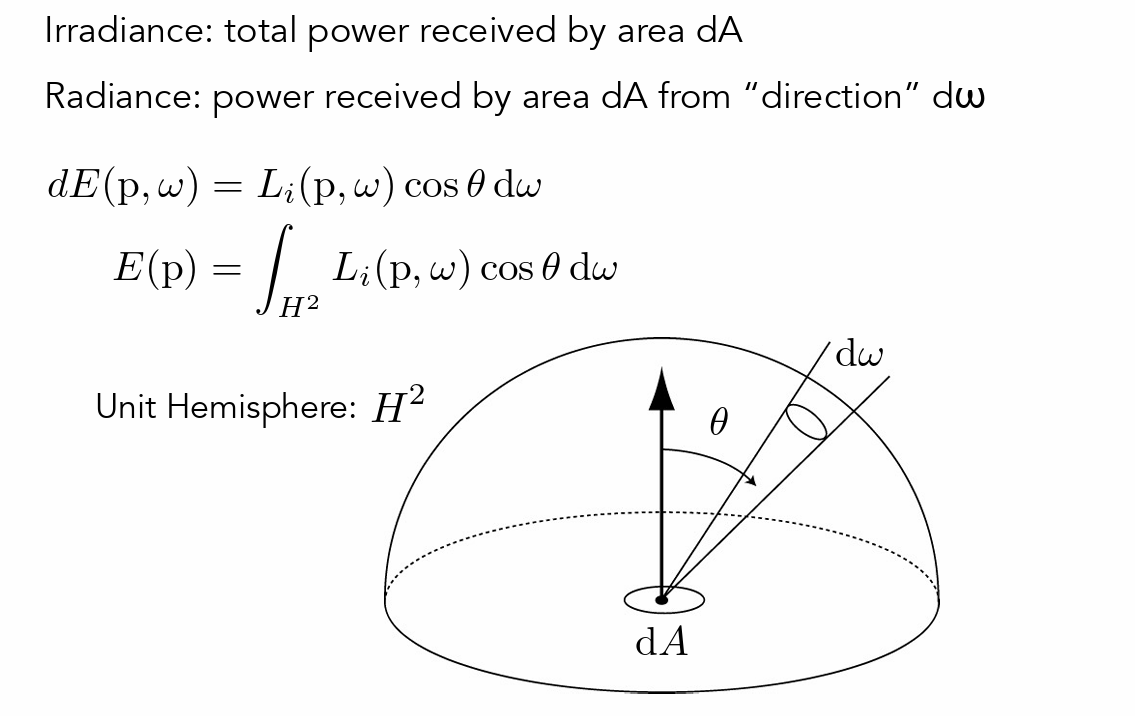
- Irradiance:辐照度(单位面能量)
- Irradiance 是指达到某个表面单位面积上的辐射功率。它衡量的是光源对物体表面的照射能力,反映了物体表面接收到的光能量有多少。
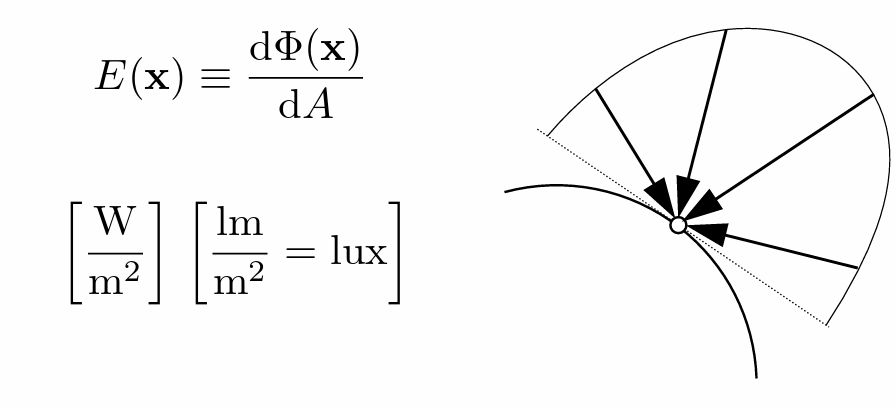
-
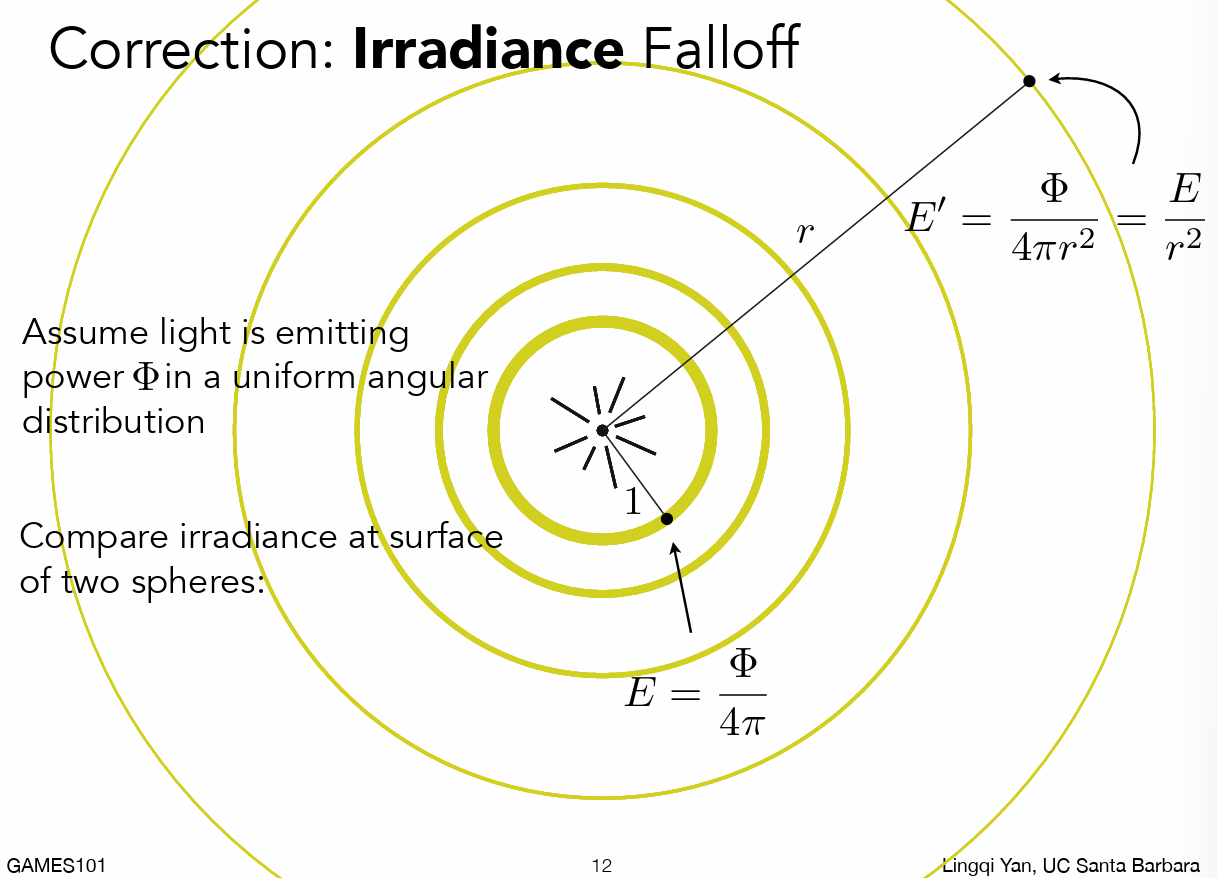
- 随着半径增大,Irradiance 减小;Radiant Intensity 恒定
-
Radiance:辐射亮度(传播过程的能量)
- 单位面积上单位立体角内的辐射功率。它是描述光在空间中传播的基本物理量,综合考虑了方向性和空间分布
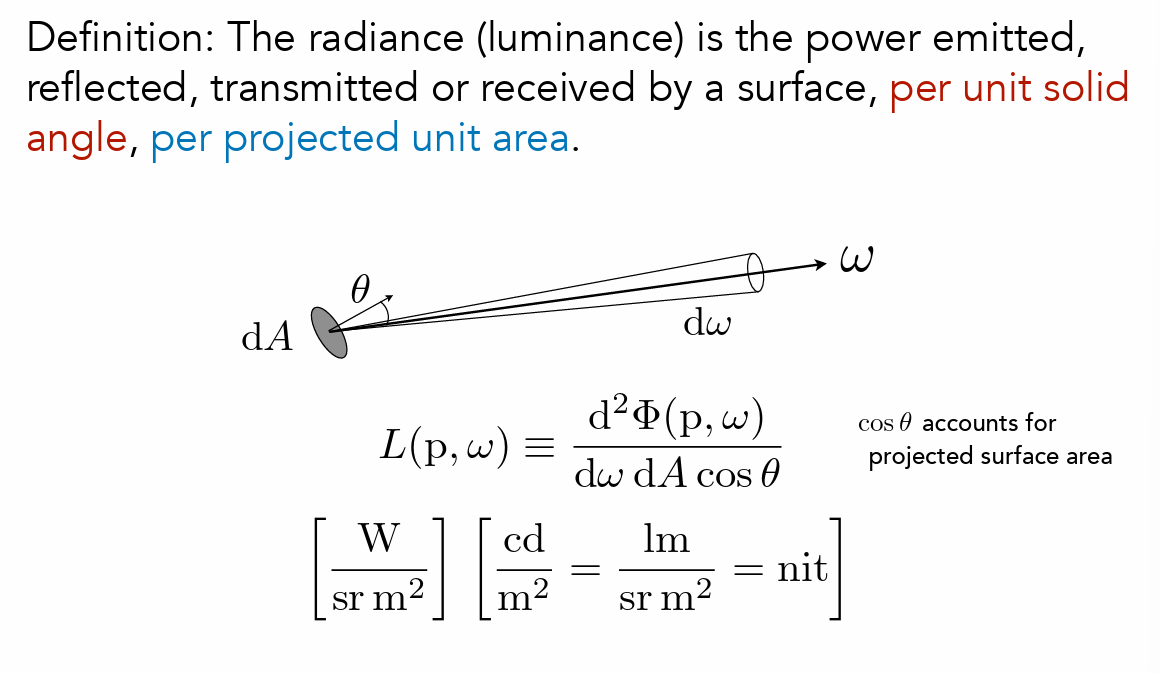
- 单位面积向特定方向的单位角内的能量辐射
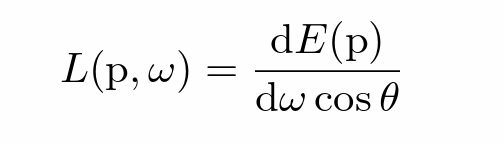
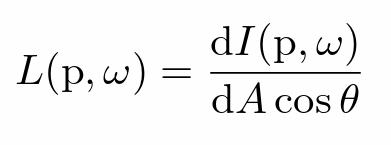
- Radiance 是考虑特定入射方向的 Irradiance
BRDF¶
- 描述一个方向反射到另外一个方向的过程
- 接受能量=输出能量
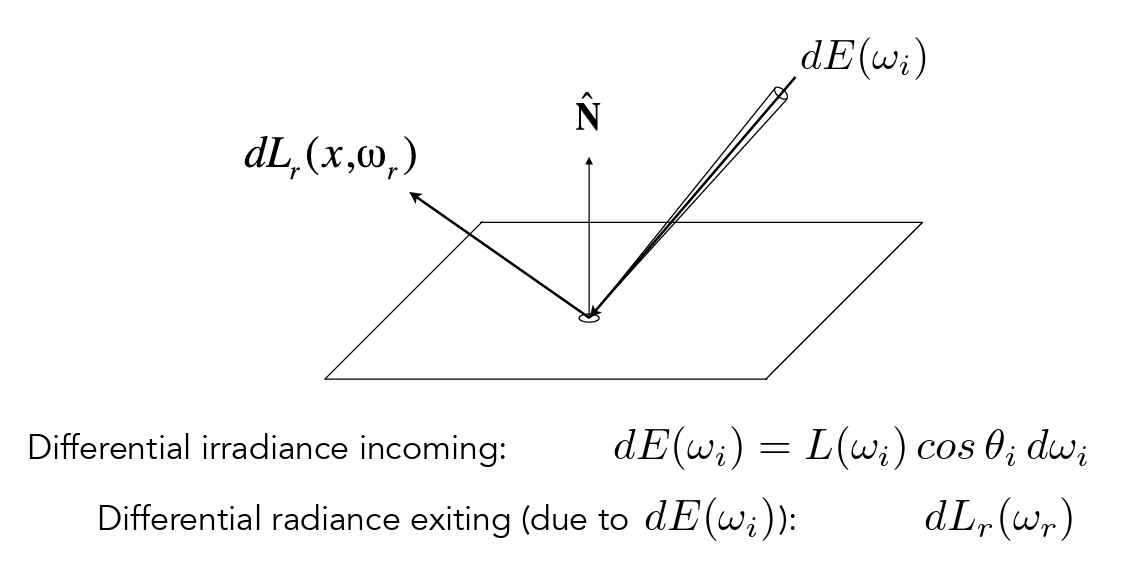
- BRDF 就是能量被如何分配到不同方向
- 所有光源的辐射->反射总光线
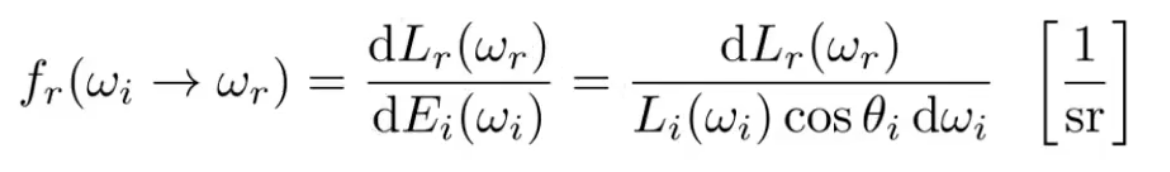
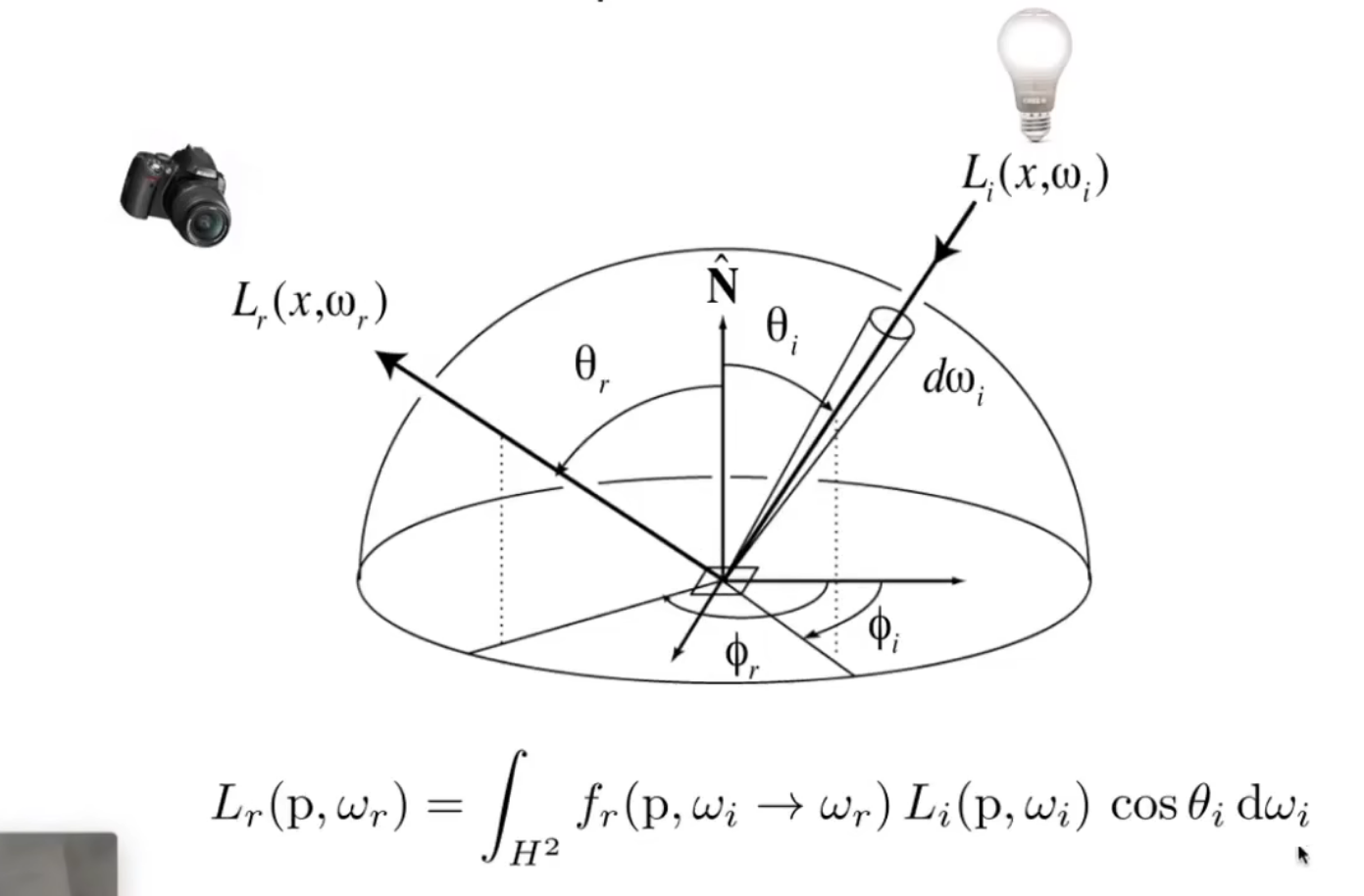
- 这是一个递归计算过程
- 渲染方程:自发光+反射光加和(包含多次反射递归)
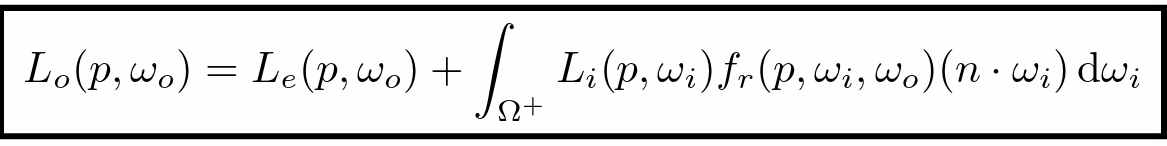

- 简化表示

- 递归弹射(包含多次反射即全局光照(直接光照+间接光照))
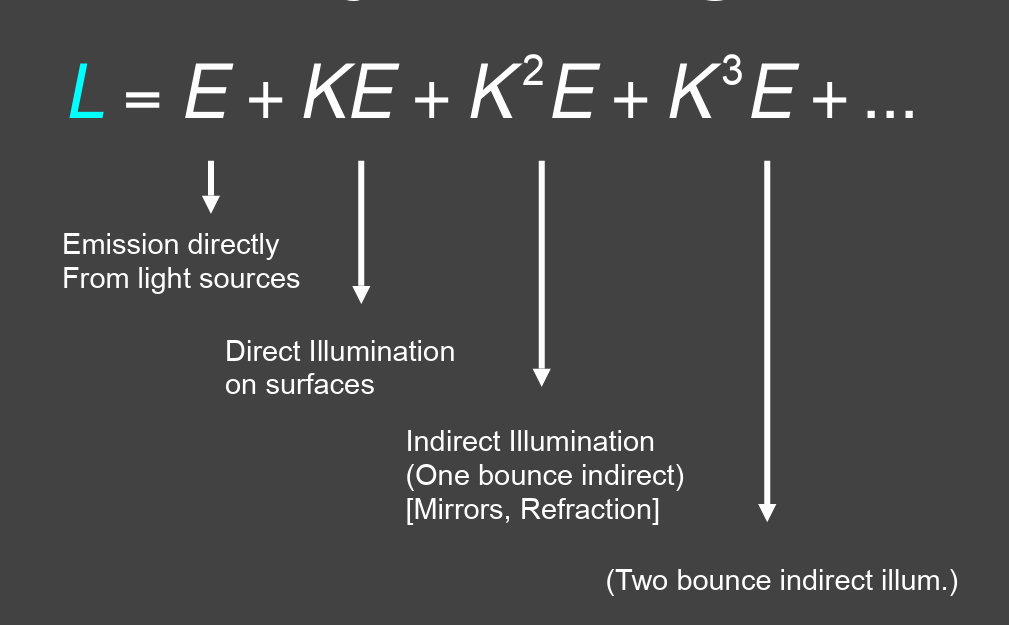

蒙特卡罗路径追踪¶
- 蒙特克罗积分

- 使用随机采样获取积分区域内的值,用于进一步的积分计算
- (均匀采样)
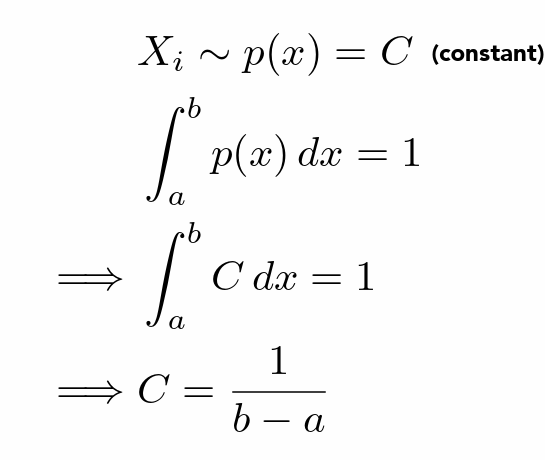
-

-
解决 Whitted-Style Ray 不正确的地方,Whitted 不能处理好漫反射
-

-
用蒙特卡洛积分表示反射方程
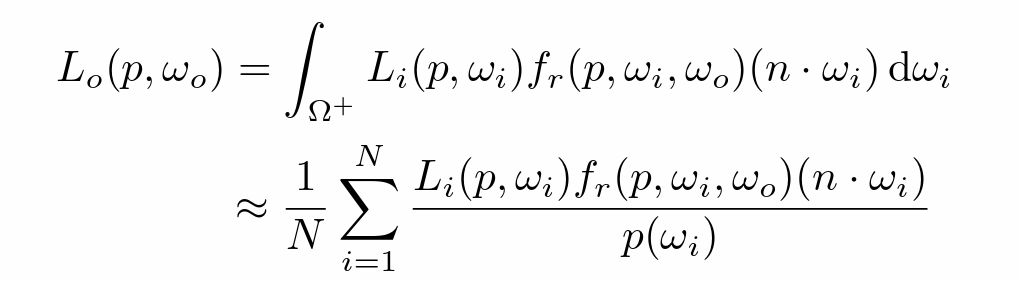

- N(一根光线反射后探测数目)!=1 时 N 会指数级增长
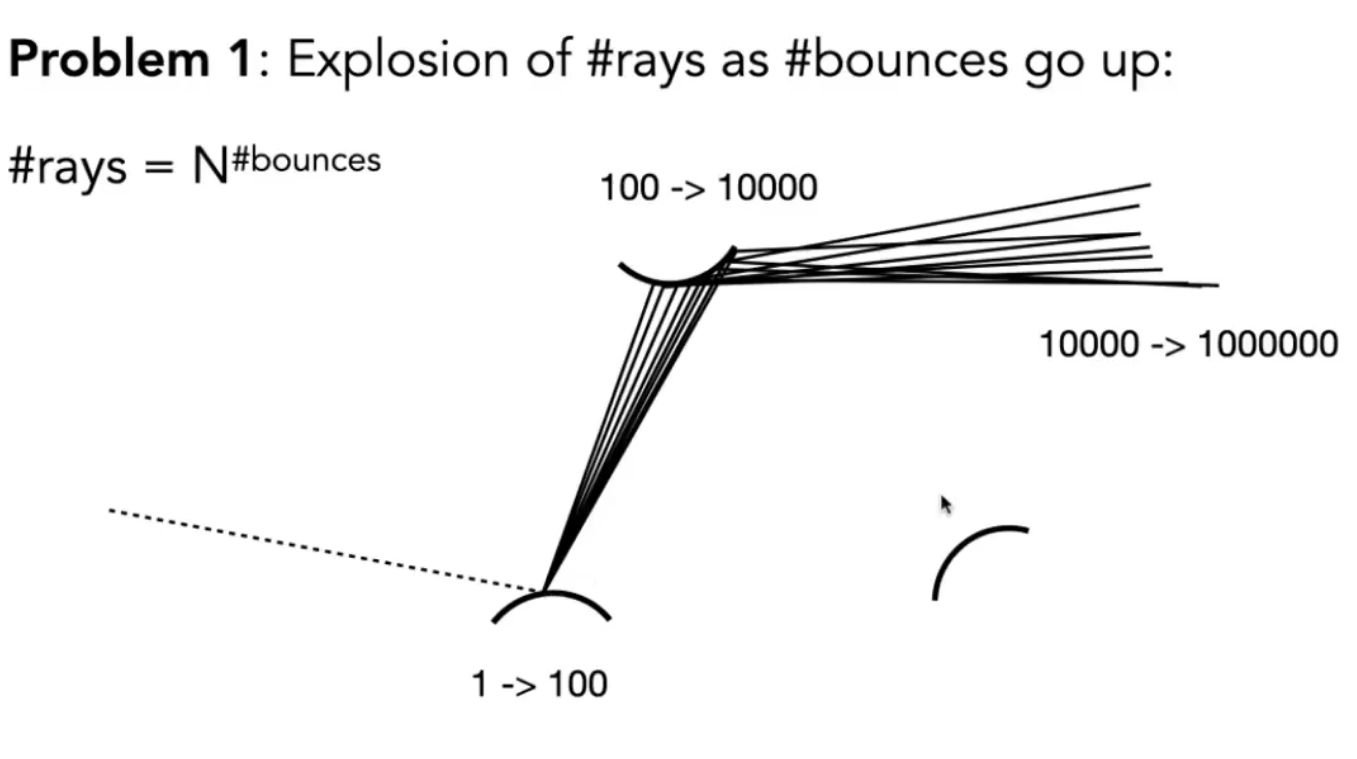

- 为了避免指数增长,只考虑一个方向(这就是路径追踪)
- 采样足够多的经过同一个像素的光线来减少误差
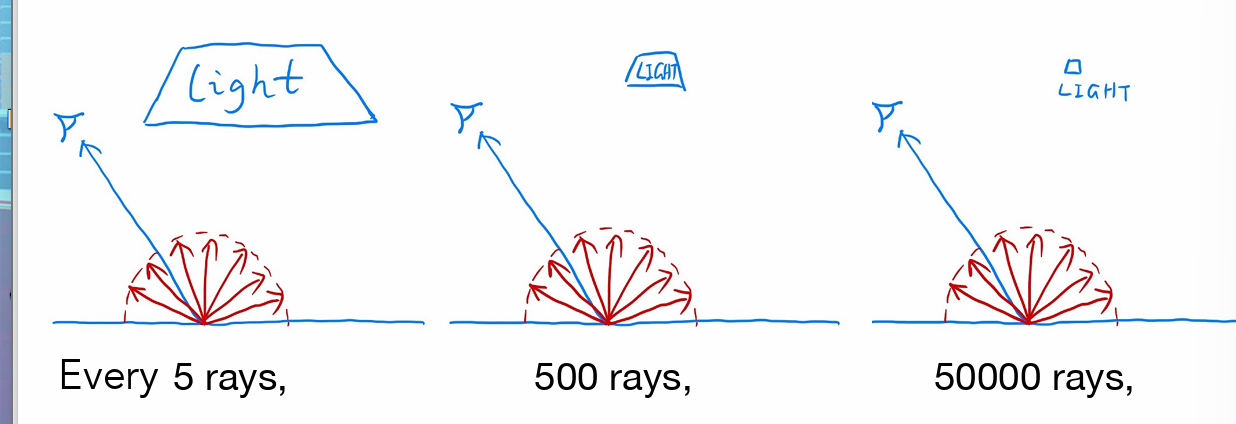
- 向不同方向随机发光

- 为了避免无限递归,(RR) 随机决定发反射次数(何时开始停止反射)
- 概率 p 继续反射,(1-p)不再继续发射

- 渲染结果要 \(L_0/p\),这样保证期望不变,即:\(E=P*(L_0/P)+(1-P)*0=L_0\)

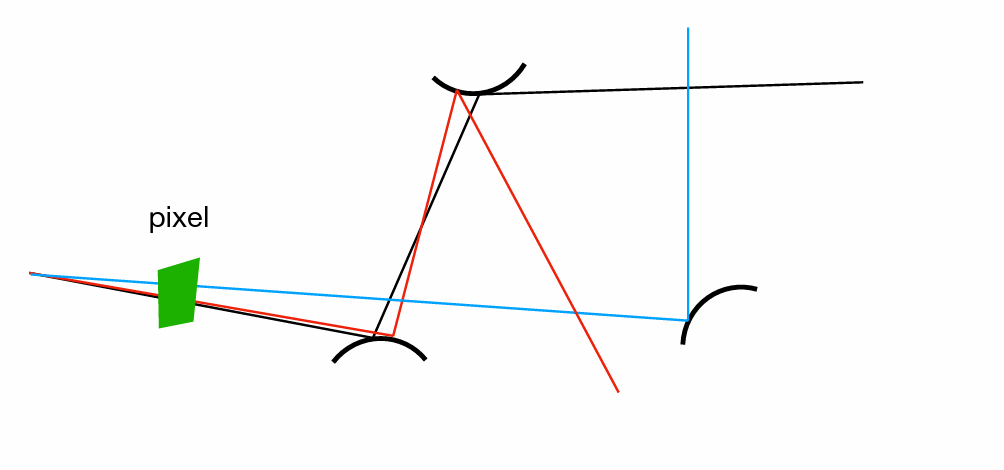
- 采样效率低:光源太小,大部分发出的路径都不会到达光源
- 改用向光源来进行采样、积分
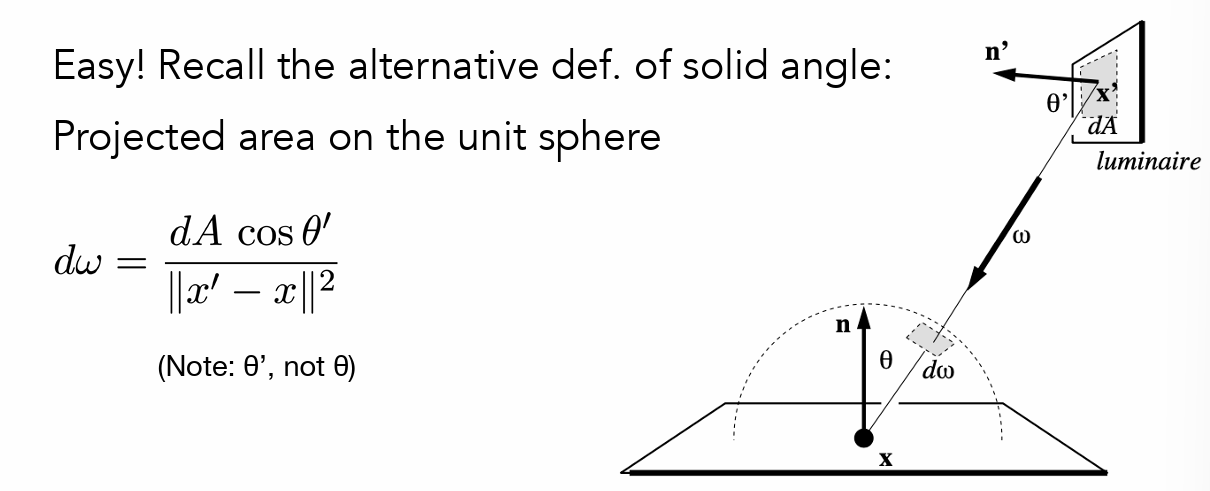
- dA 是立体角 dw 对应光源上的区域(先将 dA 映射到平行方向,然后两个平行表面是成比例的)


- 对于直接光照采用 dA 计算,对于间接光照仍然采用随机方式