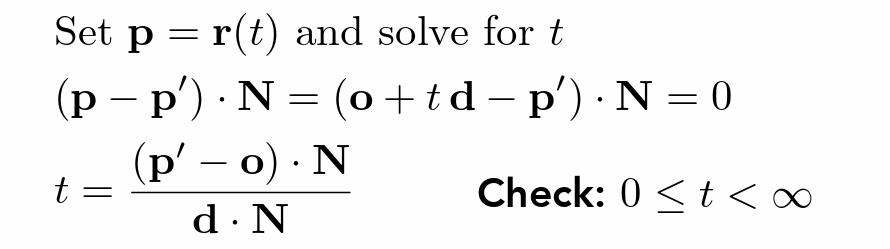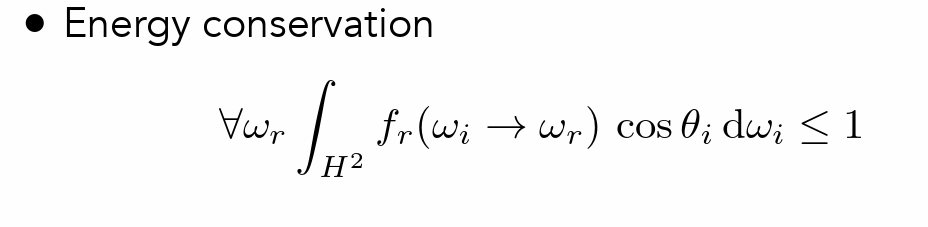现代图形学基础
线性代数基础¶
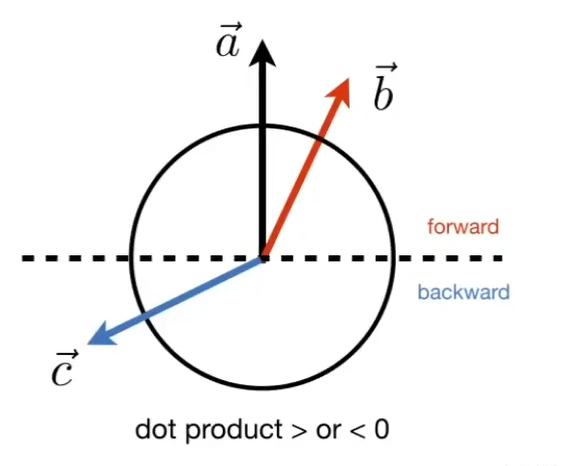
- 点乘主要用来求两个单位向量的夹角
- 可以用于判断两个方向的接近程度(夹角),判断前后
-
-
叉乘
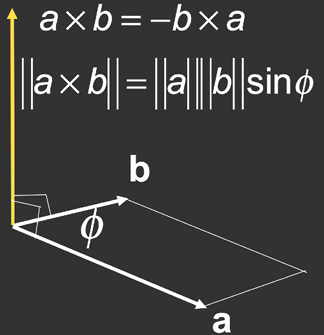
- 可以用于求出三维直角坐标系(右手坐标系),指导两个方向就能推导出第三个方向\(\overrightarrow{x}\times \overrightarrow{y}=\overrightarrow{z}\)
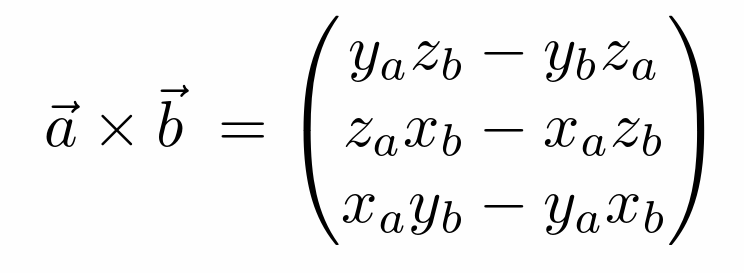
- 判断左右、内外(p在三角形三条边的同一边(左边))
- 矩阵
- 乘法符合结合律、分配律,没有交换律
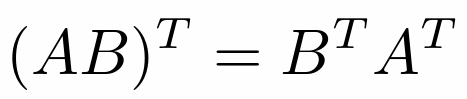
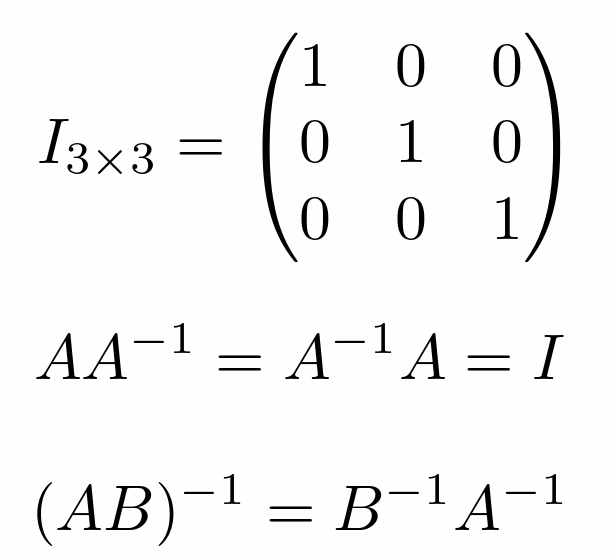
- 表示向量运算
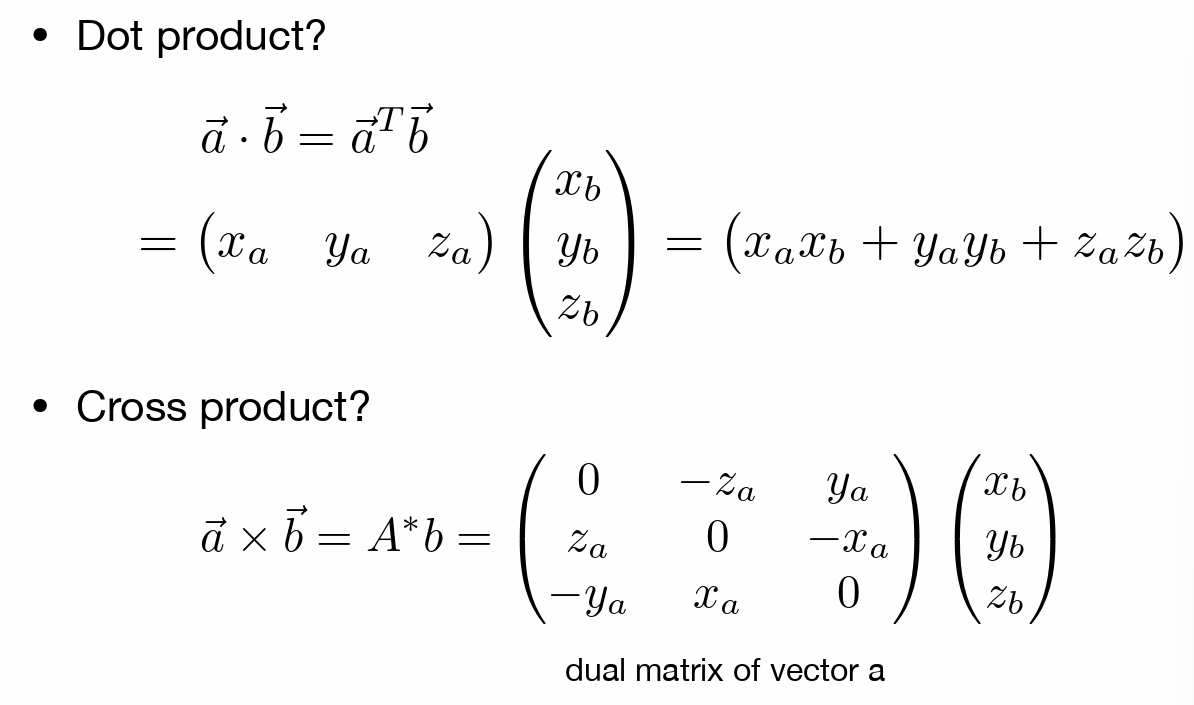
变换¶
变换基础¶
- 缩放
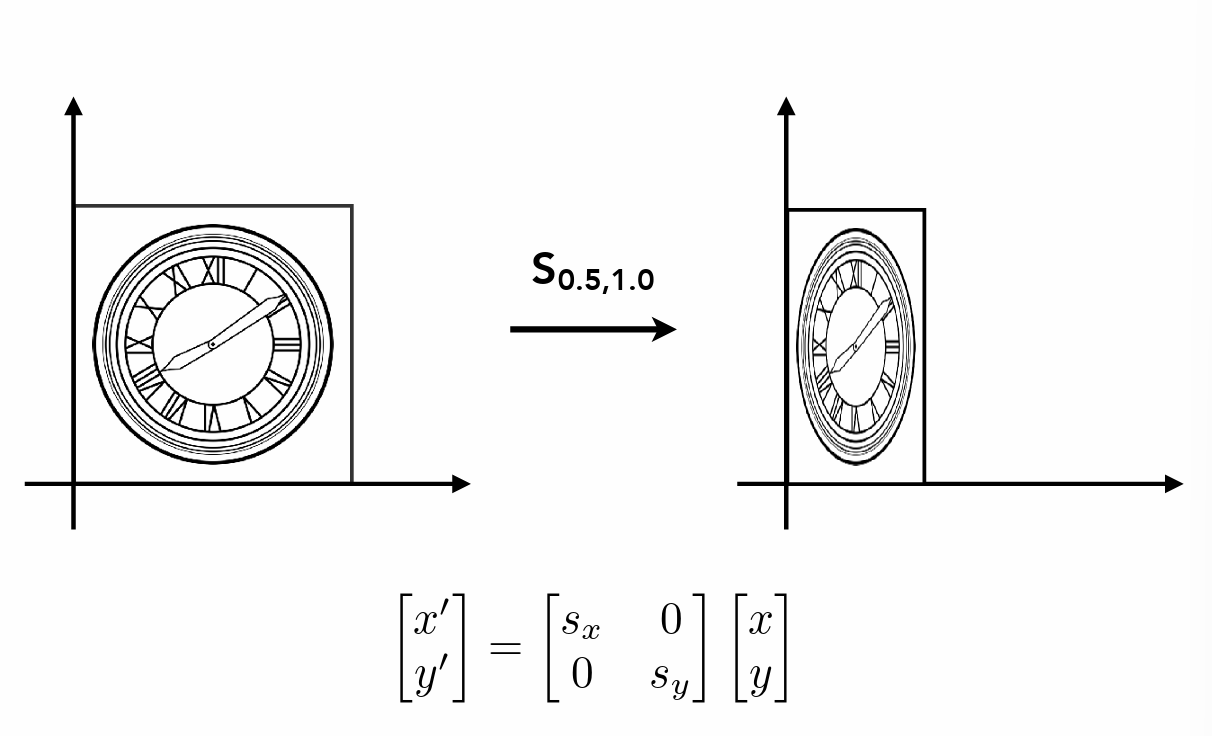
- s为负数时也可以用于图像的翻转
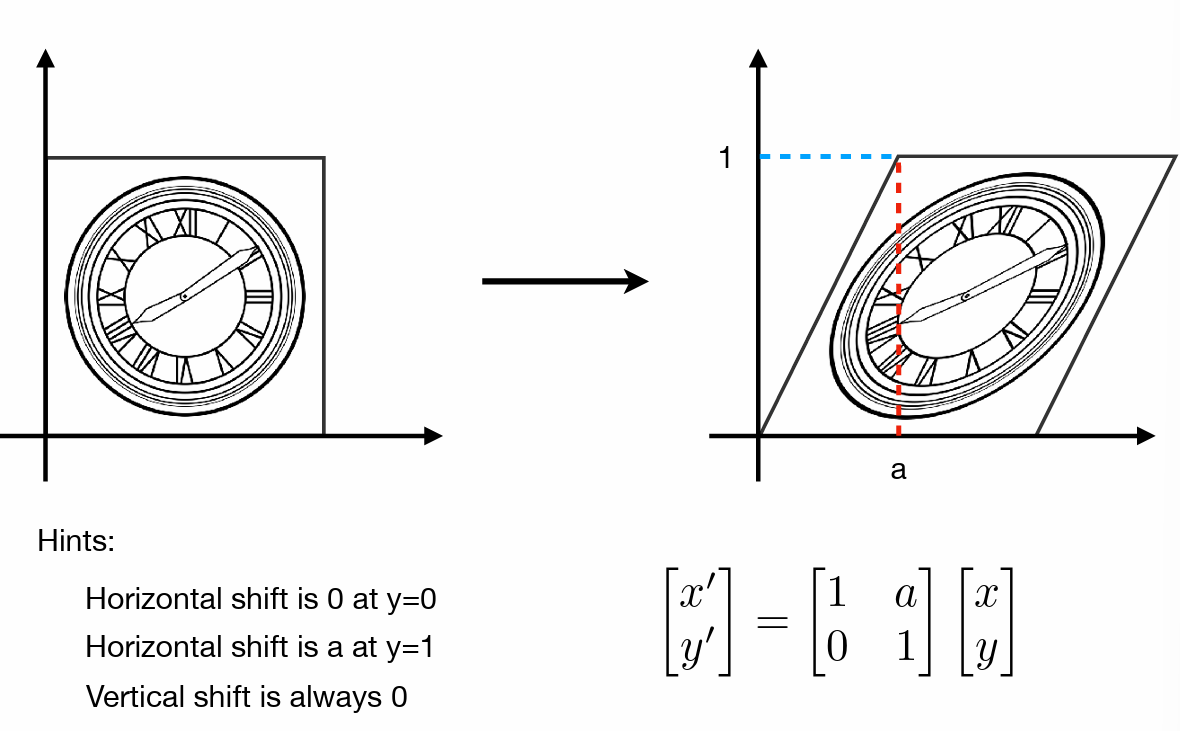
- 变形(切变)
- 旋转(以原点为中心点)

- 旋转矩阵的转置等于逆(正交矩阵)
齐次坐标¶
- 目的:用矩阵乘法(线性变化)无法表示平移
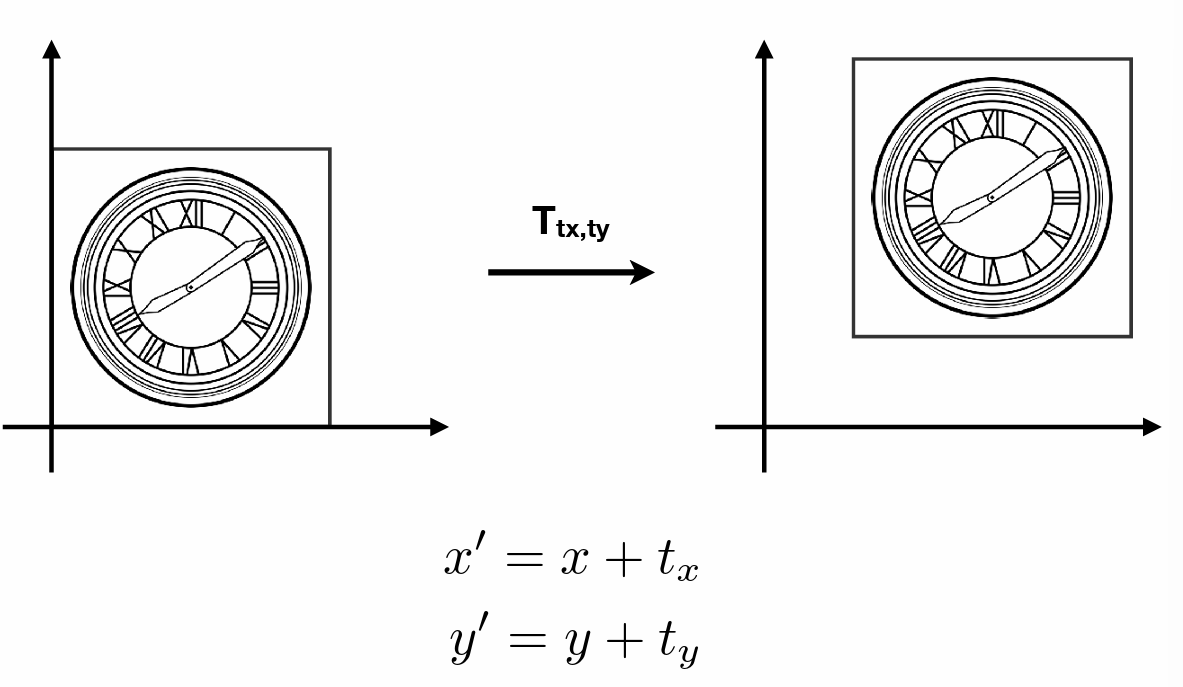
- 用三维向量表示二维坐标

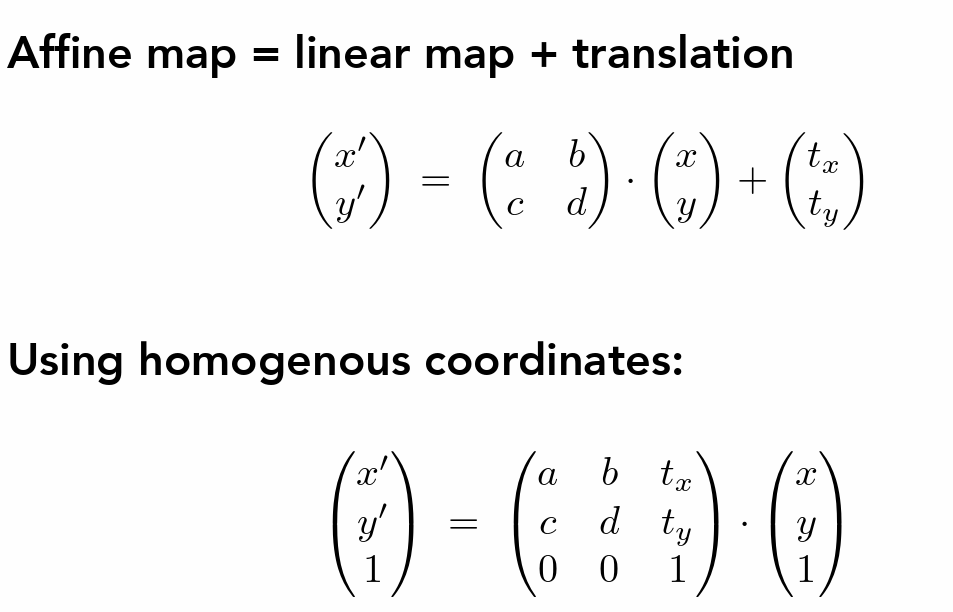
- 先线性变化再平移
- 通过第三维度是1/0来判断是点还是向量,向量的第三维为0,因而向量不会因为平移而发生改变
-

- 点加点表示两个点的中点(规格化,保证第三维为1)
-

- 逆矩阵可以表示逆变换
- 连乘(注意先进行的在右侧)
- 组合变换通常先旋转后平移
-
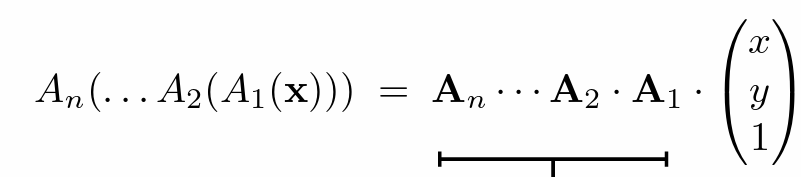
-
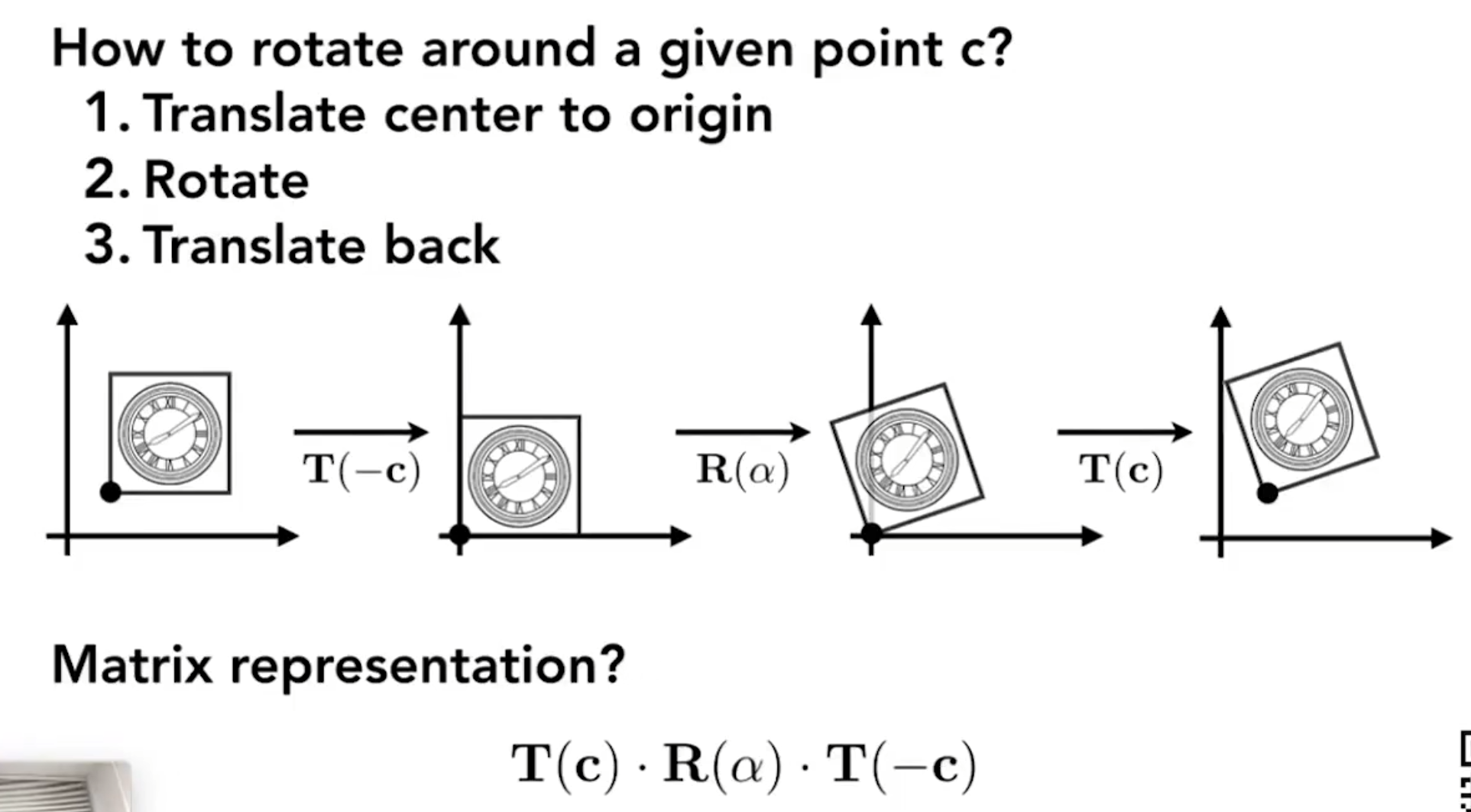
以任一点为原点旋转
三维变换¶
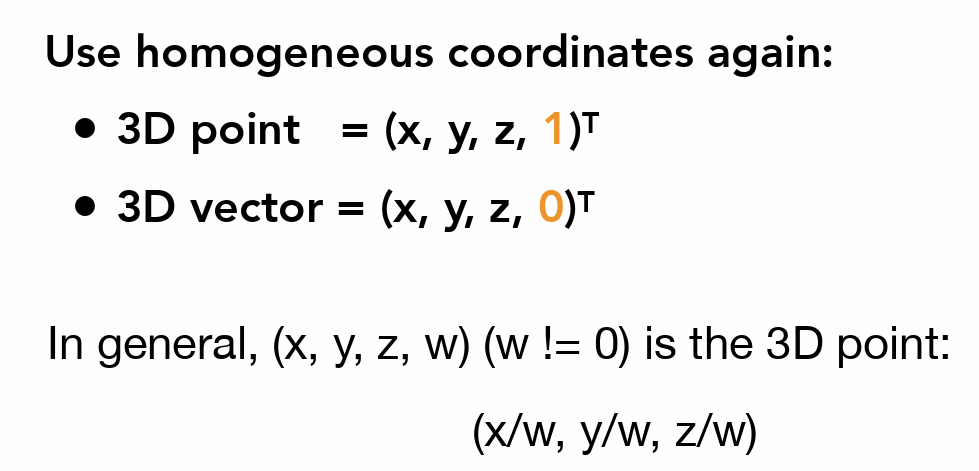
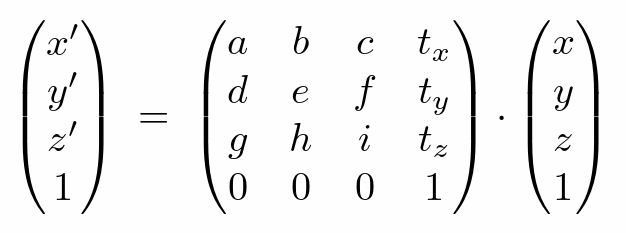
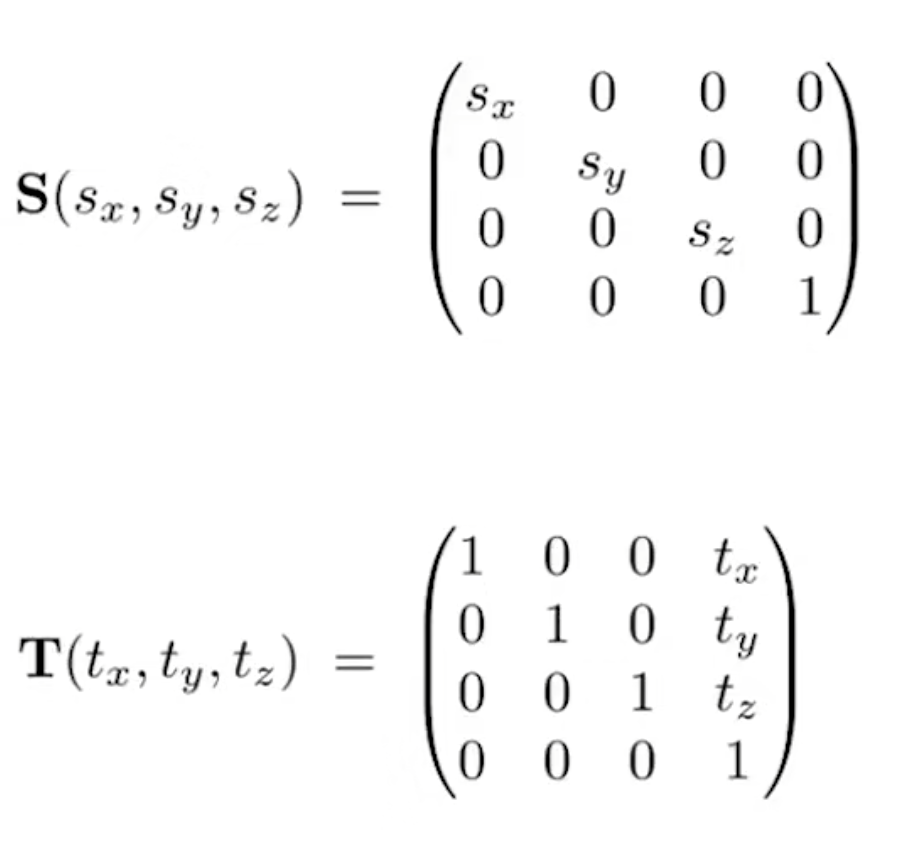
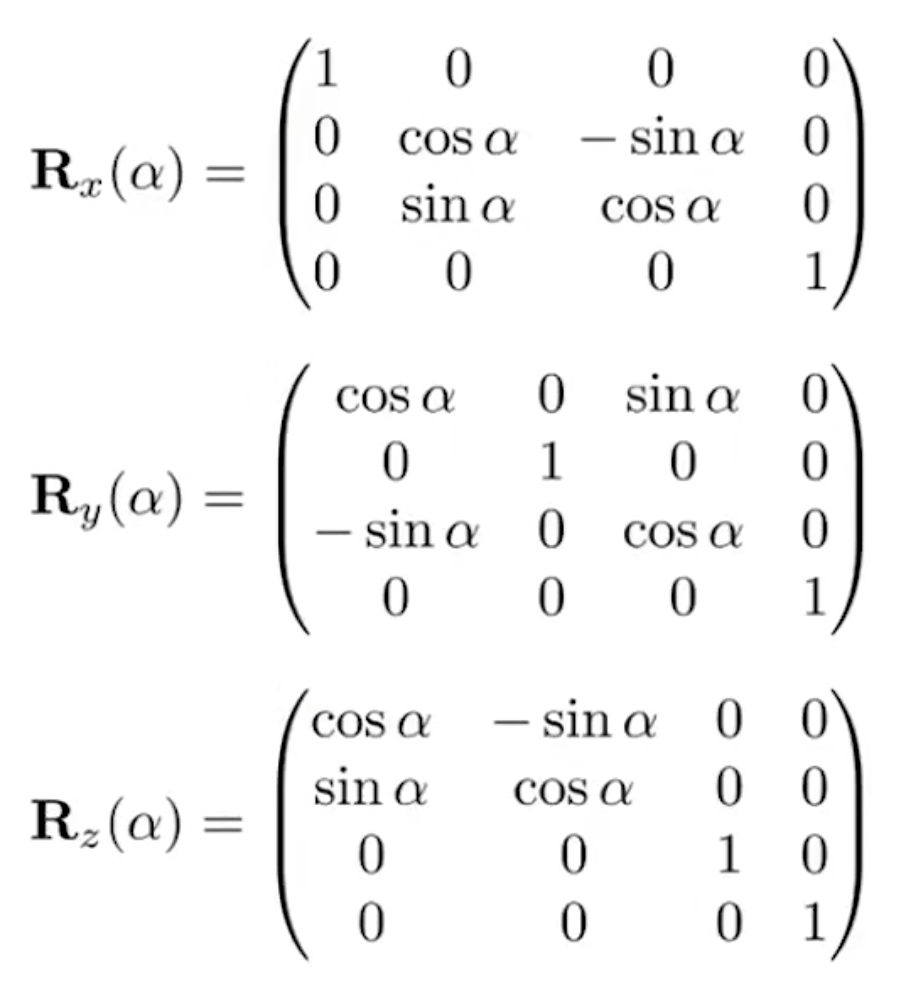
- 罗德里格旋转公式(绕任一过原点的向量n旋转)
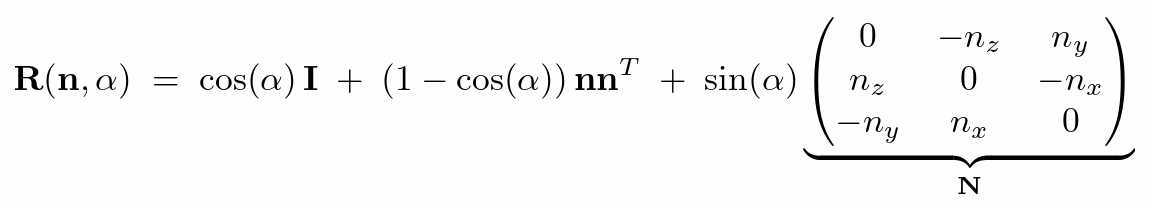
- 以上矩阵变换的方式不适用于线性插值(并不是线性连续变化的),如果需要动画、插值需要使用四元数
视图变化¶
- mvp 矩阵变化
- 代表了模型(Model)、视图(View)、投影(Projection)三个变换矩阵的乘积
- 模型矩阵:将对象的局部坐标系(模型空间)转换到世界坐标系(世界空间)。这个变换涉及到物体的位移、旋转和缩放。
- 视图矩阵:将世界坐标系转换到观察者(或摄像机)的坐标系(视图空间)。这个变换通常涉及到将摄像机(视点)移动到原点,并进行必要的旋转,使得观察者面向场景的特定部分。
-
投影矩阵:将视图空间中的坐标转换到裁剪空间,进而通过透视除法转换为归一化设备坐标(NDC)。这个变换定义了一个可视范围,通常是一个锥形体(透视投影)或者一个长方体(正交投影)。
-
相机参数(视图 矩阵)
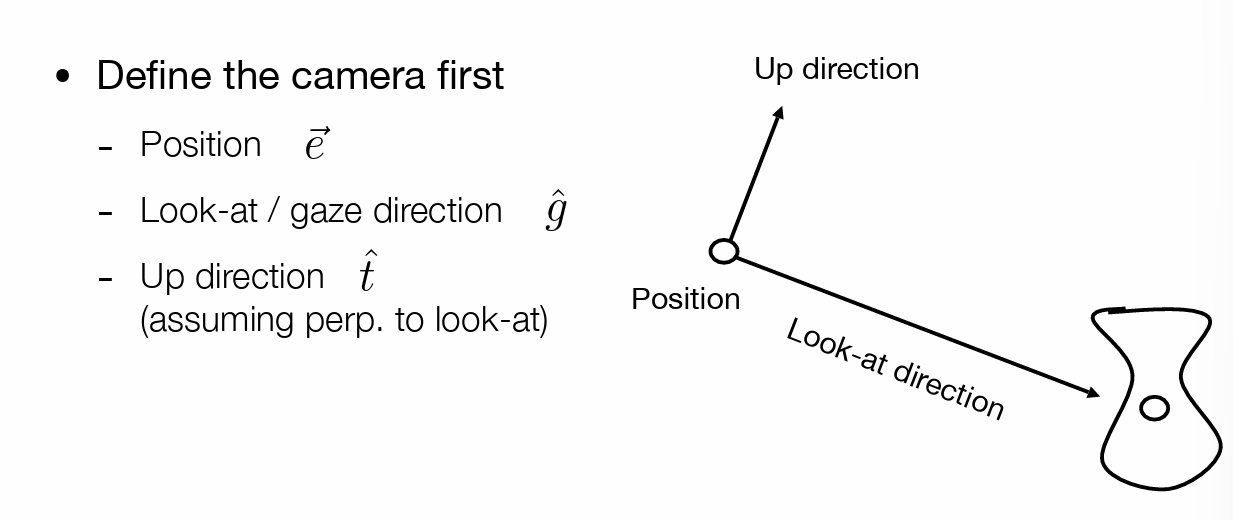
- position:原点位置
- look-at:相机指向
- up direction:相机头方向(即绕指向的旋转,就是相机上方的指向)
- 固定相机的位置,移动物体,标准位置:
- 回正过程(同时移动相机和物体,相对关系不变)
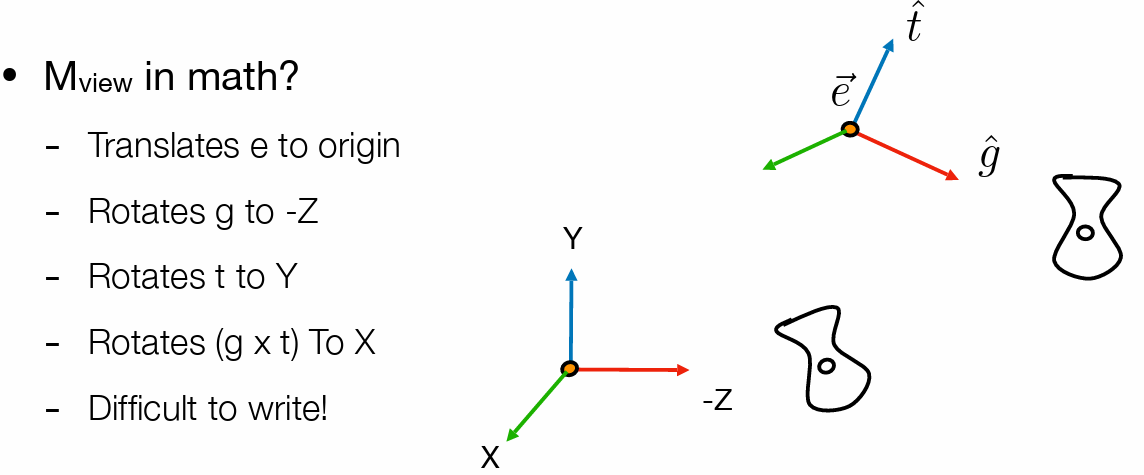
- 先平移再旋转(逆矩阵便于确定旋转方式)

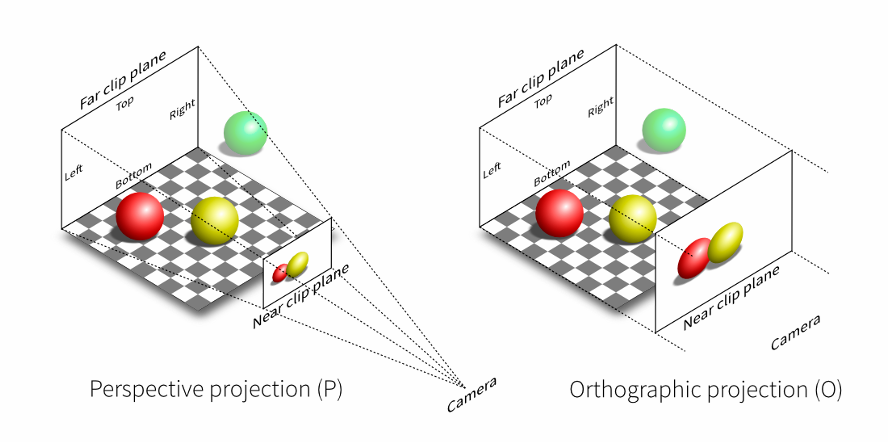
投影变化¶
正交投影¶
- 平行线仍然平行
- 看作摄像机无限远,平行投射
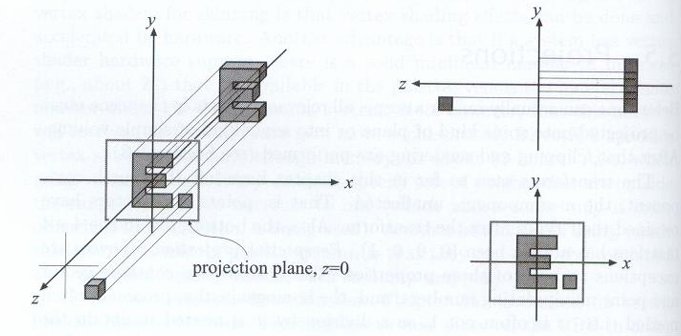
- 相当于扔掉z坐标
- 长方形投影到标准正方体(观测矩阵)
- 先平移到原点,再进行缩放
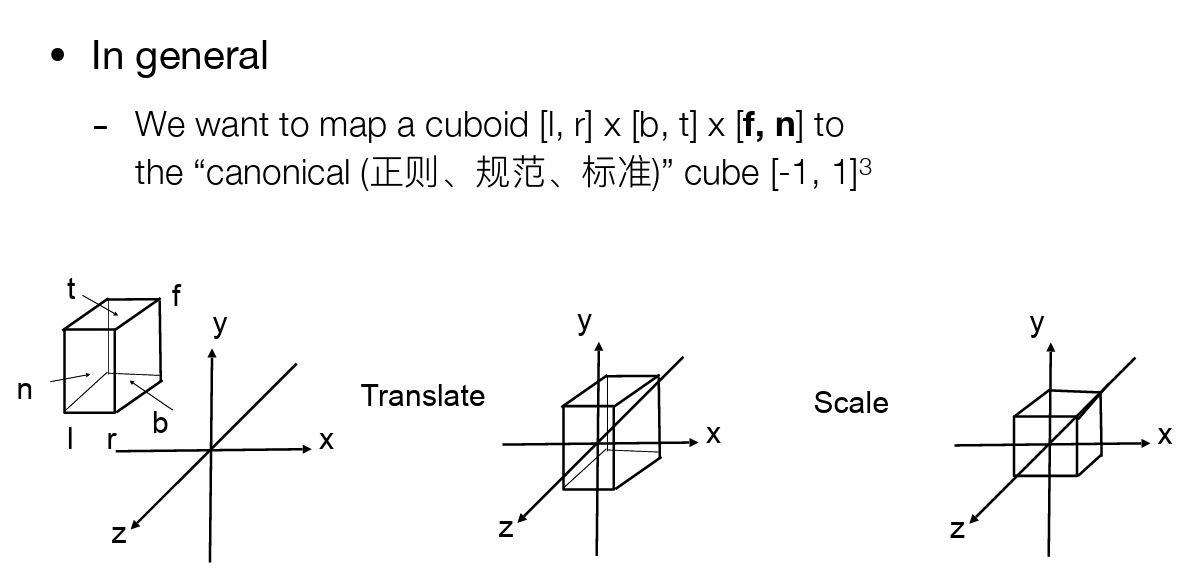
- 归一化到长度为1(-1,1 的立方体),具体的长宽由 fov 和比率计算得到
- 通常由fov得到y,再乘以比率得到x;
透视投影¶
- 近大远小
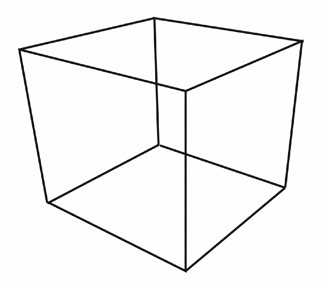
- 四棱锥投射
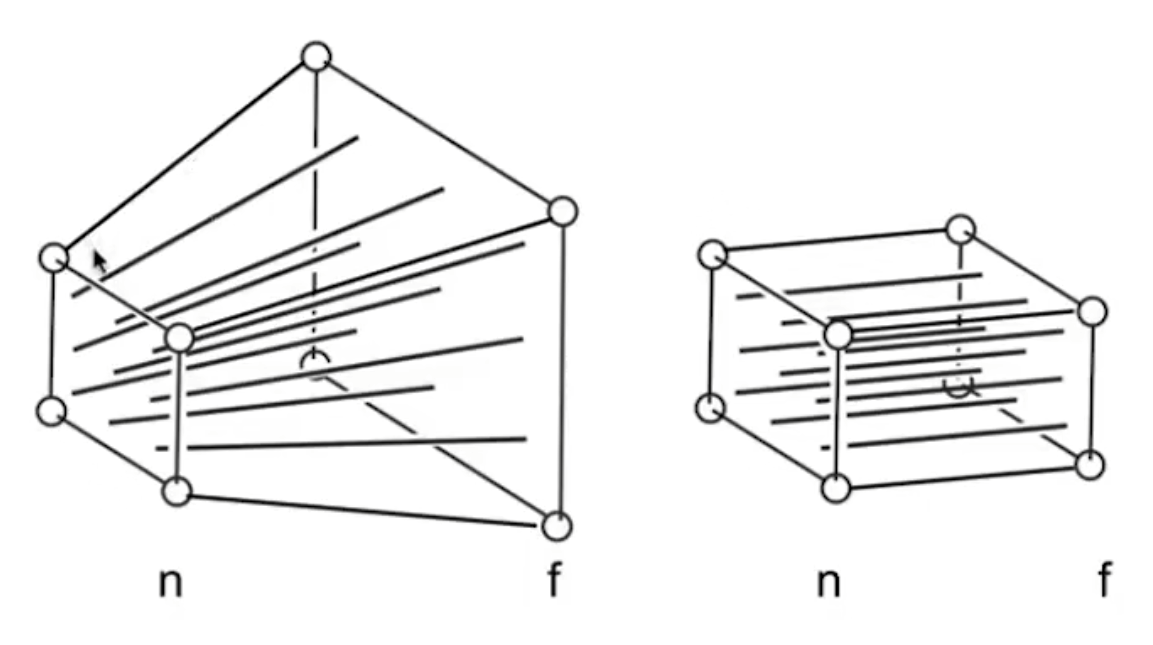
- 先将锥形“挤压”为长方体,再做正交投影
- 坐标变换
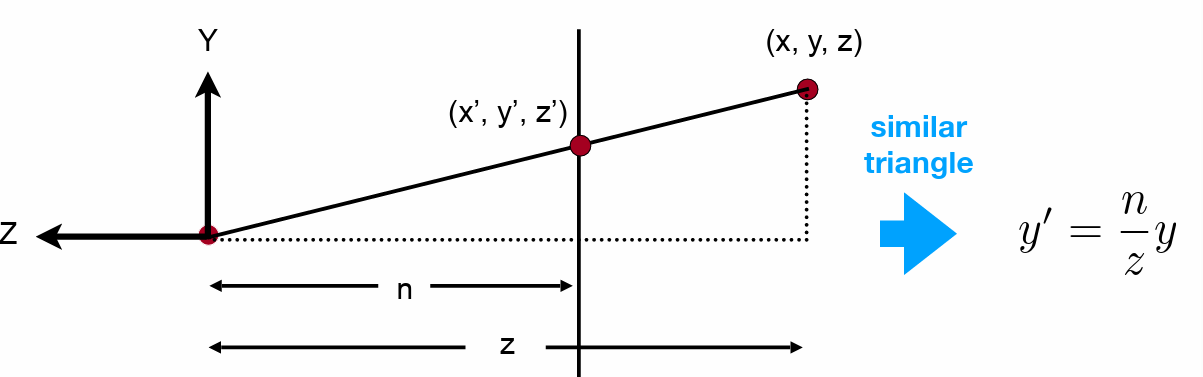
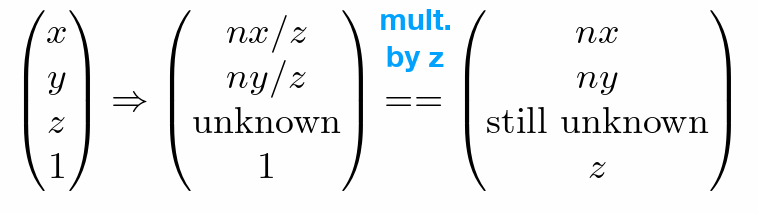
- 变换矩阵
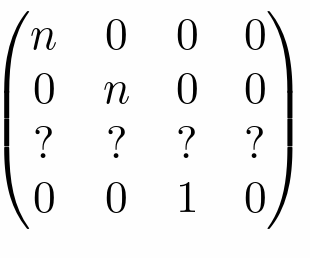
- 还无法确定z如何变化
- 明确的是在近/远平面的 \(z\) 均不发生变化
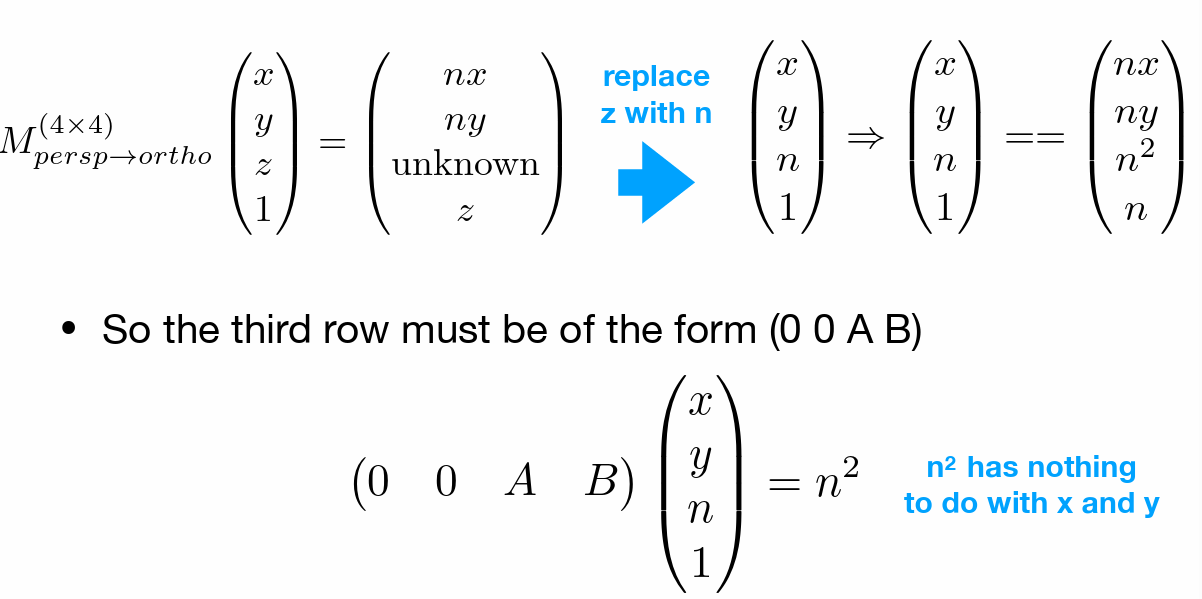
- 可知与xy无关,前两项为0(利用近平面上变化前后的\(z\)不发生变化来进行计算)
- 远平面的xy发生压缩,但是z不发生变化(中心点的xyz均不变)
- 即
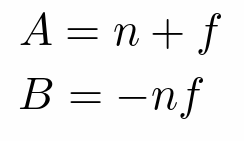
- 更确切的说n=zNear;f=zFar即最近/远可见距离
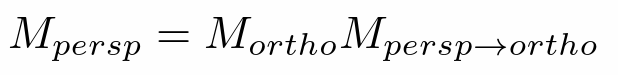
- 压缩+正交
Eigen::Matrix4f projection; Eigen:: Matrix4f persp_to_ortho; persp_to_ortho << zNear, 0, 0, 0, 0, zNear, 0, 0, 0, 0, zNear + zFar, -zNear * zFar, 0, 0, 1, 0; Eigen::Matrix4f ortho; float top = zNear * tan(eye_fov / 2 / 180 * MY_PI); float right = top * aspect_ratio; ortho << 1 / right, 0, 0, 0, 0, 1 / top, 0, 0, 0, 0, 2 / (zNear - zFar), 0, 0, 0, 0, 1; projection = ortho * persp_to_ortho;
透视除法¶
- 经过投影变化将点投射到了标准正方体,现在还需要将三维空间中的点映射到二维屏幕,得到归一化设备坐标(NDC)
- 如果有一个齐次坐标点 P(x, y, z, w),透视除法后的坐标为 (x/w, y/w, z/w)。这个新的点现在位于归一化设备坐标系内,其值通常限制在-1到1之间。
- 透视除法是透视投影不可分割的一部分,它确保了远处的物体在屏幕上呈现得更小,近处的物体呈现得更大,从而创造了深度感。
光线追踪¶
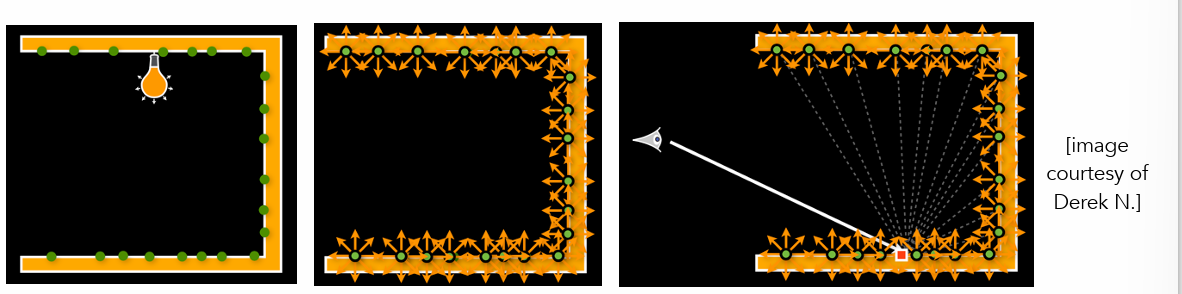
- Shadow Mapping阴影映射(只能处理点光源、硬阴影)光栅化的阴影处理
- 阴影:人能看到的位置,但光源看不到的位置
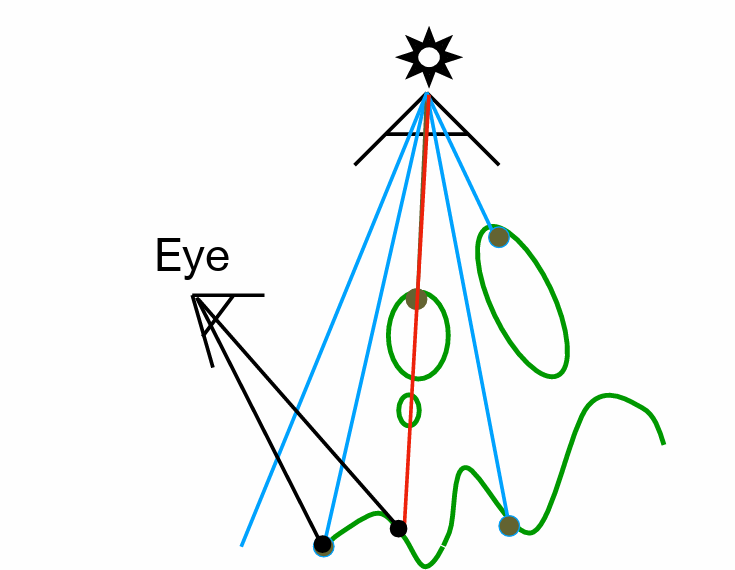
- 记录光源到不同物体的最短距离,将摄像机看到的位置与光源的深度距离比较来判断是否被遮挡形成阴影
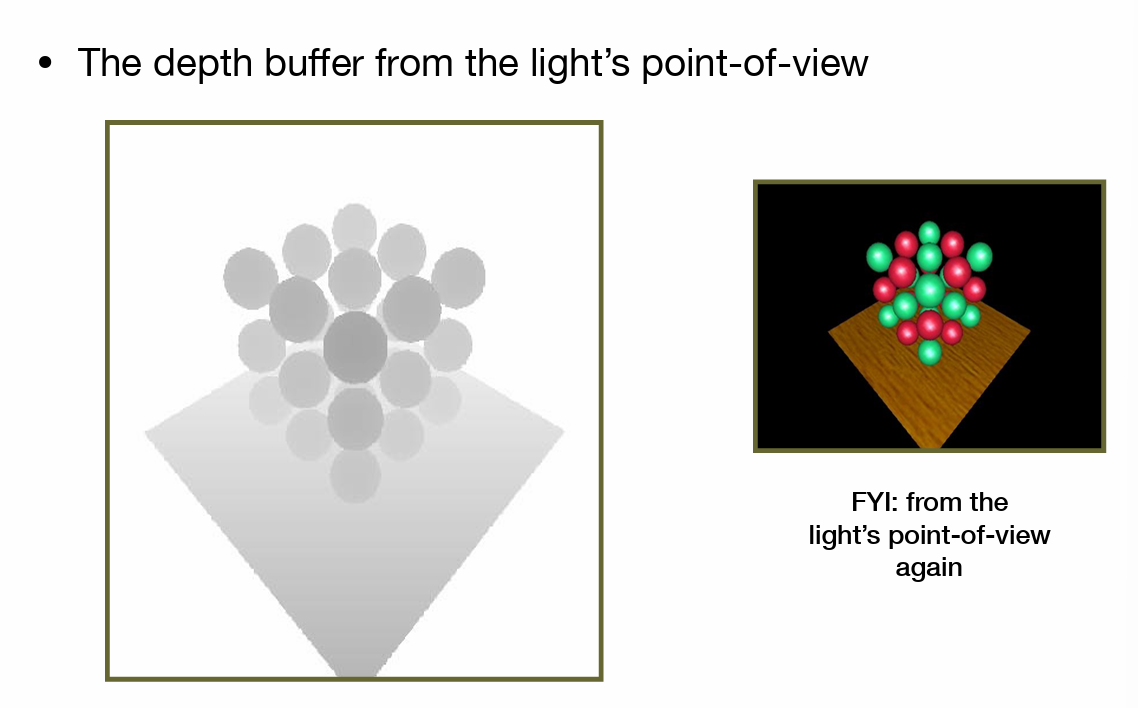

- 存在数值精度问题
- 存在深度信息图(shadowmap)分辨率与实际渲染分辨率不匹配的问题

- 硬阴影与软阴影

- 点光源只会产生硬阴影
- 当光源被部分遮挡时会产生软阴影
- 光线追踪应用了光路可逆性,从眼睛出发直至光源进行追踪
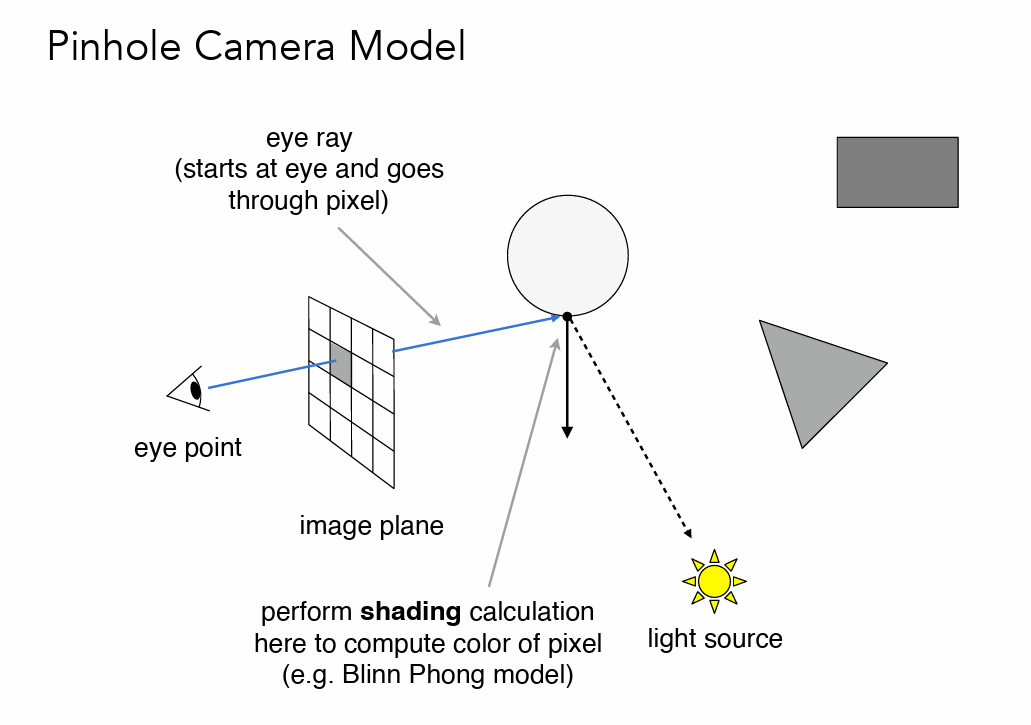
- 从眼睛向外寻找,到达最近的(可观察物体)然后与光源连线计算着色结果(可见性)
光线追踪中的坐标变换¶
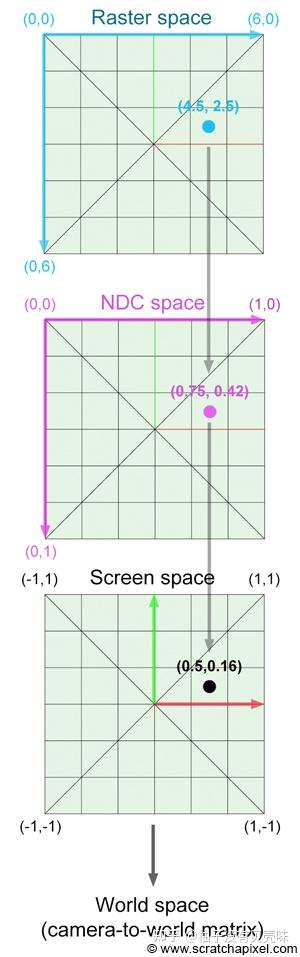
- 先将像素坐标-> NDC 坐标->屏幕坐标->世界坐标
- 像素坐标:\((x_{0},y_{0})(i+0.5,j+0.5)\)
- NDC 坐标:\((x_{1},y_{1})=\left( \frac{x_{0}}{width},\frac{y_{0}}{height} \right)\)
- 屏幕坐标: \((x_{2},y_{2})=(2x_{1}-1,1-2y_{1})\)
- 世界坐标:\((x_{3},y_{3})=\left( x_{2}*\frac{width}{height}*\tan\left( \frac{\alpha}{2} \right),y_{2}*\tan{\frac{\alpha}{2}} \right)\)
Whitted-Style Ray Tracing¶
- 一种递归算法,可以处理多次反射(折射)的情况(打到光滑表面就继续反射,打到漫反射就停止)
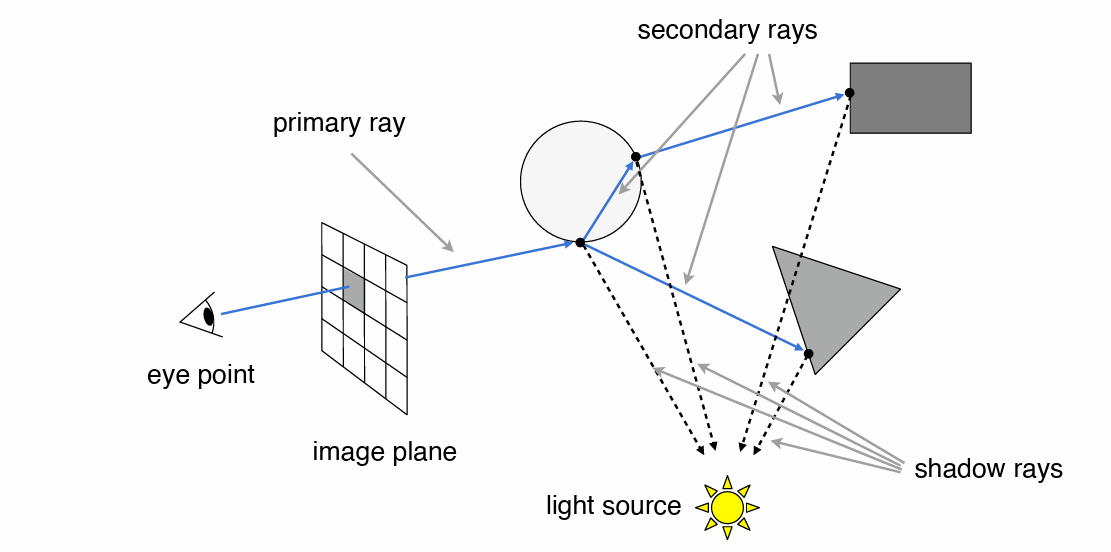
- 着色叠加
- 光线与图形的交点(几何隐式表示)

- 点加方向表示光线 \(r(t)=o+td\)
- 解任意曲面与光线的交点
- 光线与三角形面求交(几何显式表示)
- 使用一条法向量加上一个点来表示一个平面,并且通过向量乘法判断一个点是否在平面上

- 法一:先求和平面的交点,再判断是否属于某个三角形
- 法二:利用重心坐标直接判断(三个参数都非负)Moller Trumbore Algorithm 算法

- 用于快速进行射线和三角形求交 (不需要先求解射线与平面的交点)
- Möller–Trumbore
优化¶
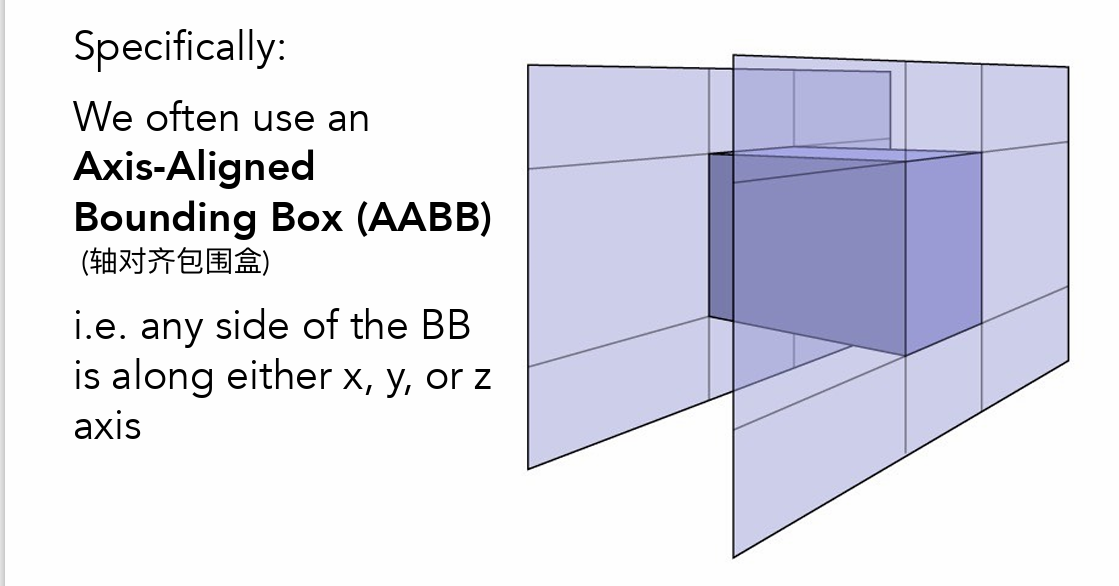
- 包围盒
- 用简单的几何图形框住物体

- 只有光线和包围盒会发生碰撞才去考虑光线和物体三角形面的相交情况
- AABB轴对齐(xyz)包围盒
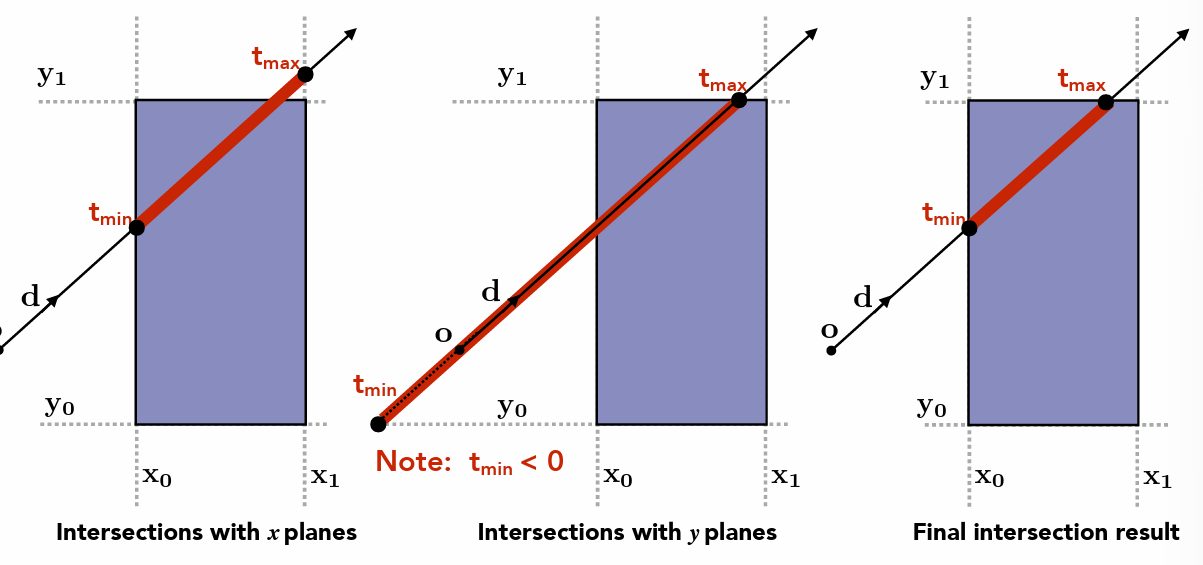
- 记录与平面的交点,求交后得到与包围盒的交点
-
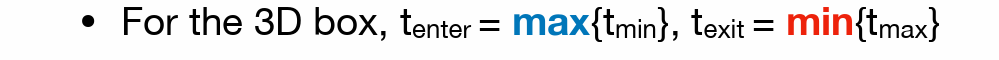
- 光线进入所有对面才真正进入了盒子,光线离开任何一个对面就离开了盒子

-
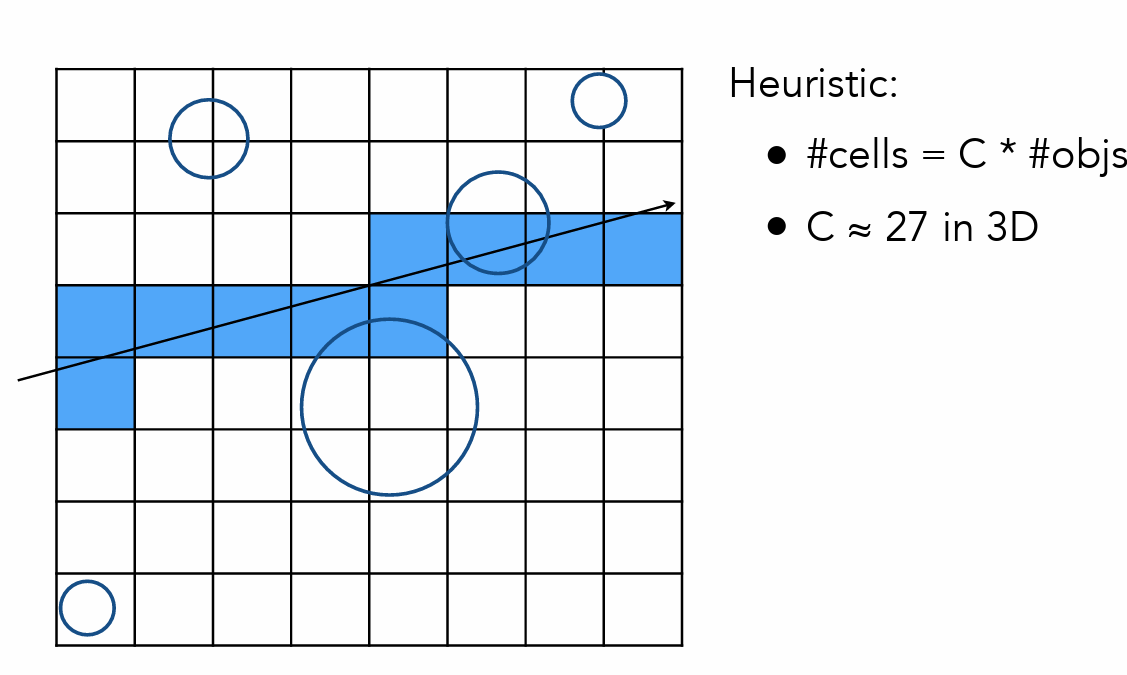
Uniform Spatial Partitions(AABB加速光线追踪)
- 先和盒子求交,再决定是否要和物体求交
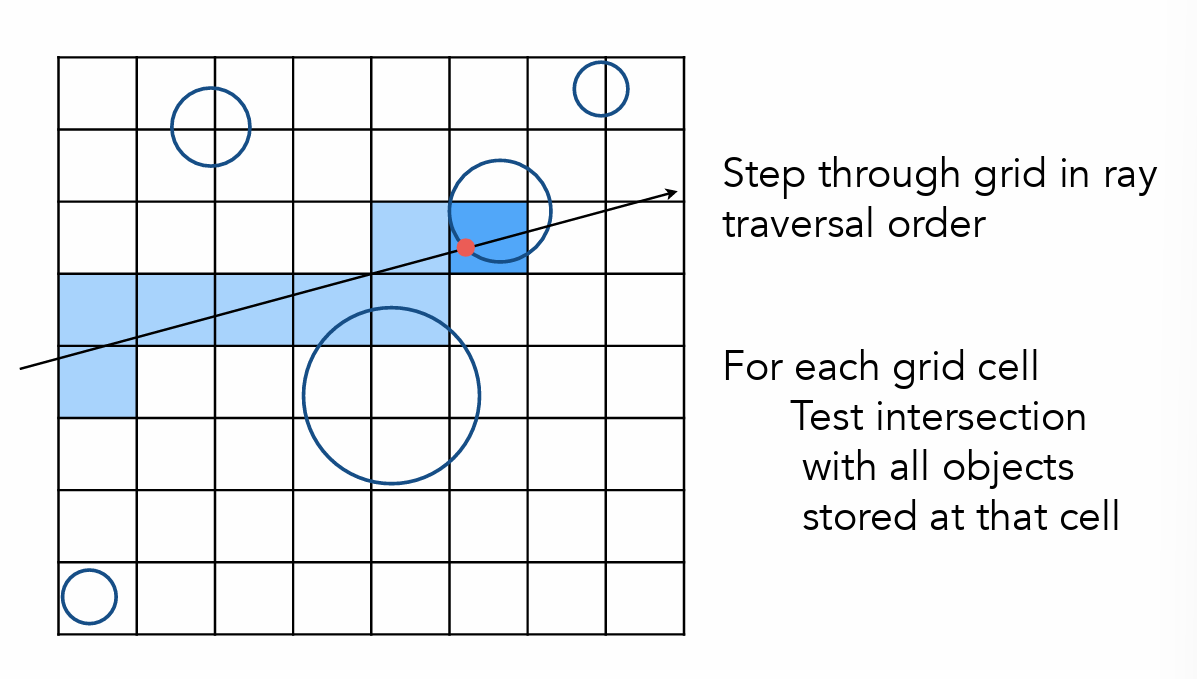
-
划分的各自数目要恰当(但是均匀划分存在一系列问题,因为物体的分布不是均匀的)
-
空间划分方法
-
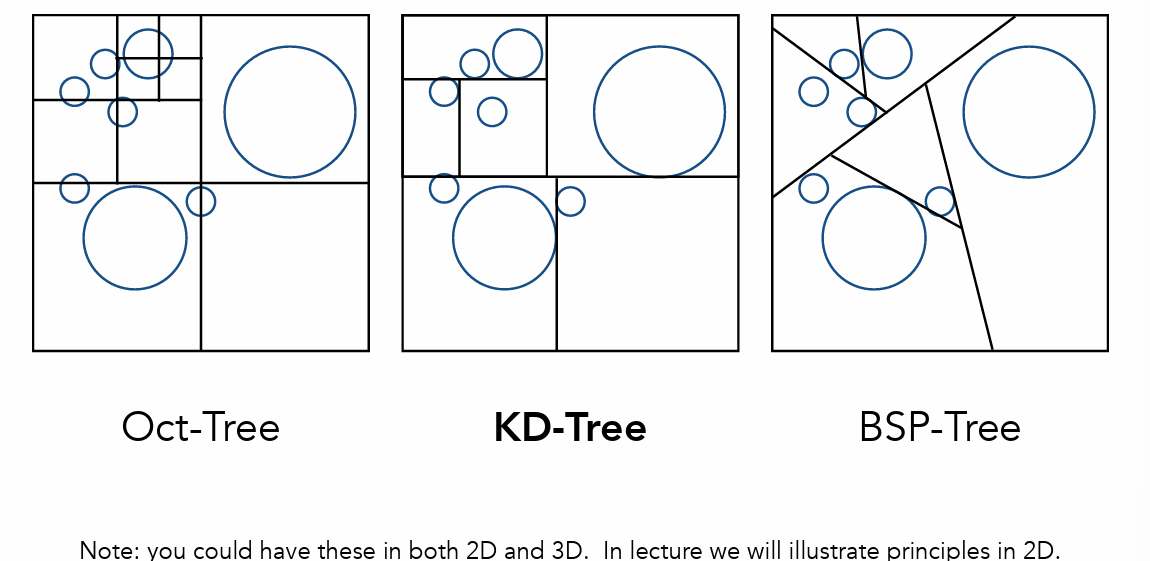
-
Oct-Tree(八叉树):问题:随着维度增加,划分数目指数增加
-
KD-Tree

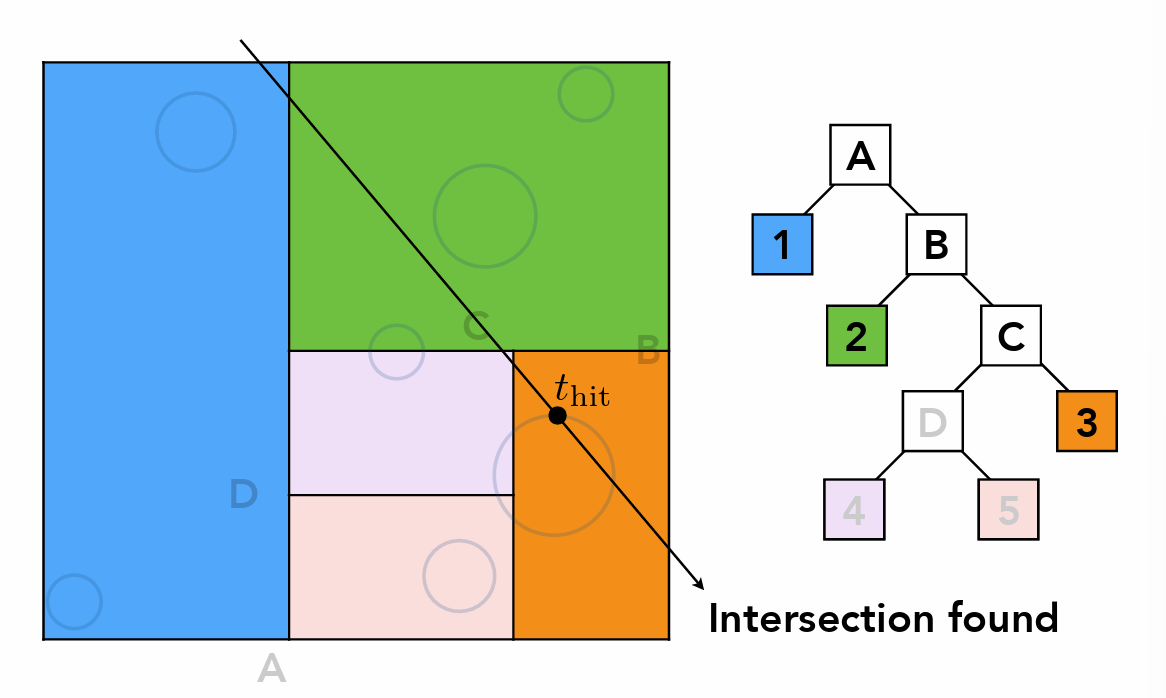
-
难点:判断三角形与盒子是否交很难,并且三角形可能跨盒子
-
(BVH)物体划分
-
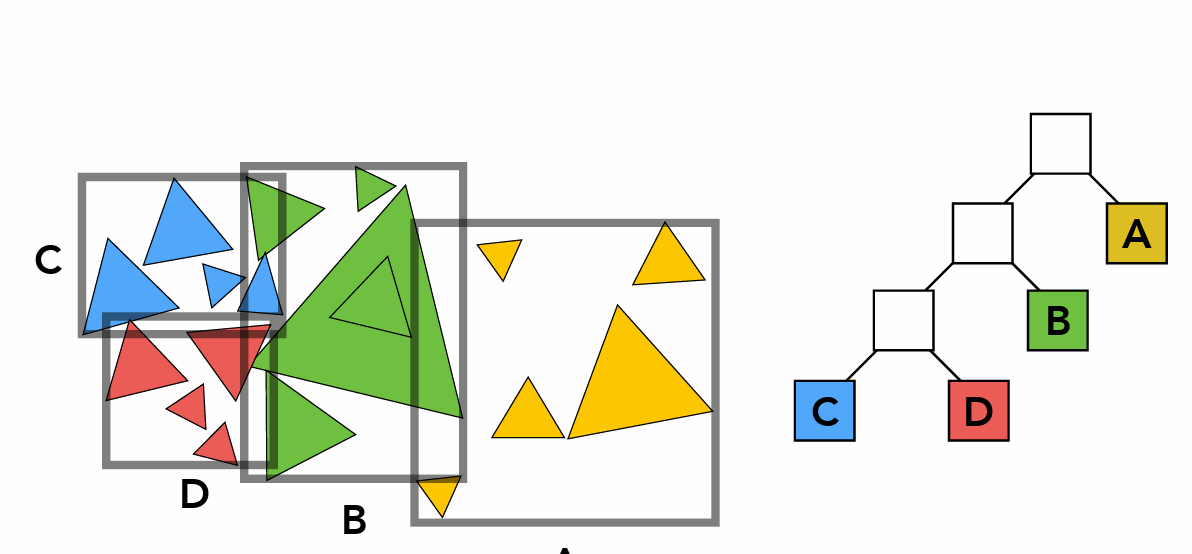
- 确定包围盒;对包围盒内的物体进行划分;分别重新计算包围盒;继续计算。
- 先找到最长的轴;然后在那个轴上把三角形均等划分到左右两个包围盒,保持左右两边数量相等或差一,即平行二叉树;重复这两个步骤直到只剩一个或两个三角形。
-
一个物体只会出现在一个盒子中(盒子中也一定有物体)
- 可以每次都选择位于中间的三角形用于划分
-
求交过程(与节点相交了,再继续去看子节点)
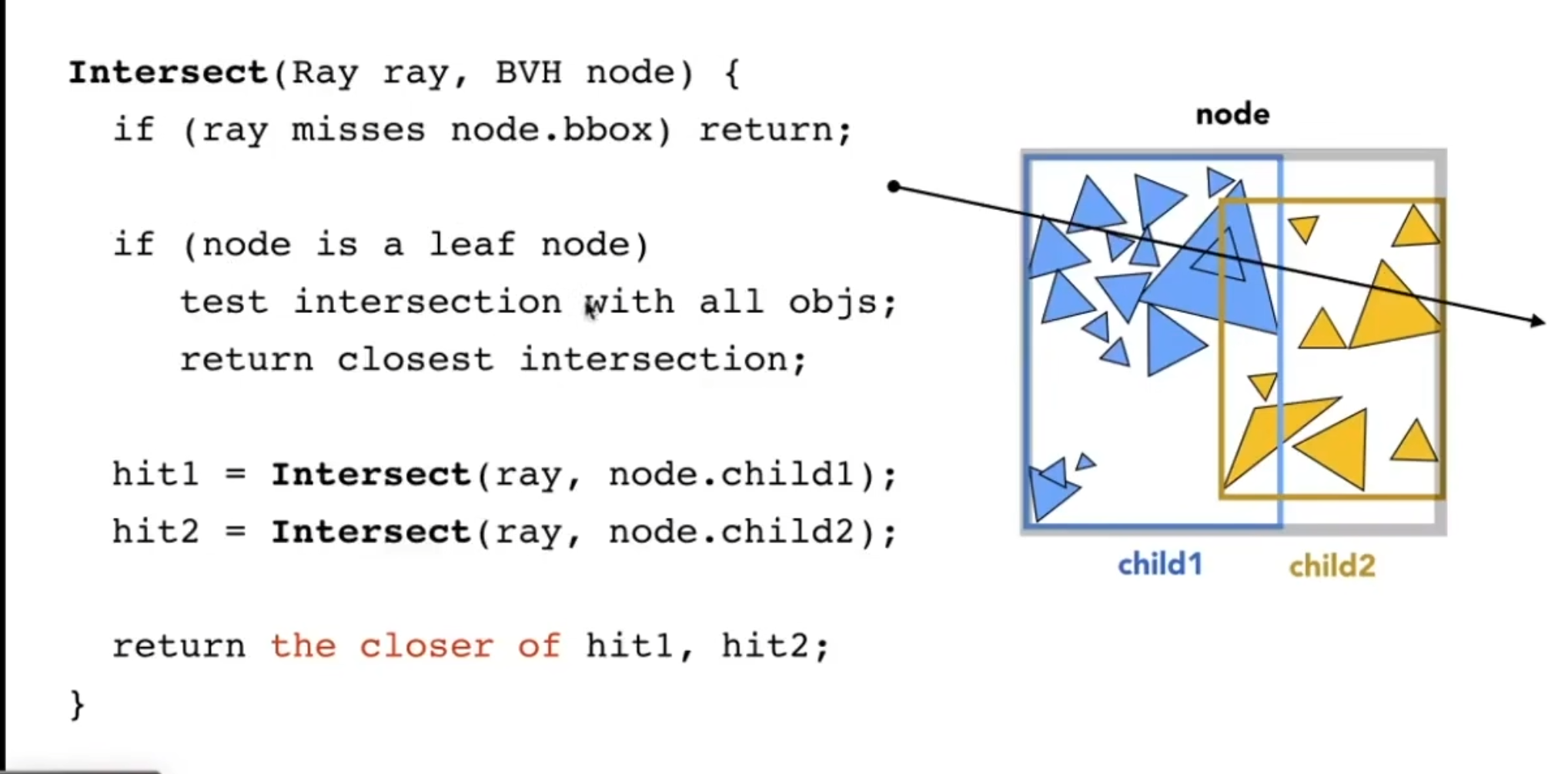
-
SAH 划分
- BVH 存在不平衡划分的问题:
- SAH 通过计算优化这个划分方式,使得包围盒划分更有效率
辐射度量学¶
- 准确定义物理光照
- Radiant flux:单位时间的能量
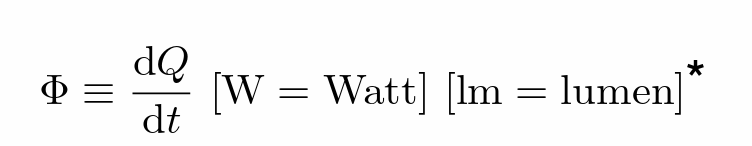
- Radiant Intensity:辐射强度(辐射能量)
- Radiant Intensity是指光源在特定方向上单位立体角内的辐射功率(Radiant Flux,单位是Watts)。它描述了光源在某个方向上的“亮度”有多强。
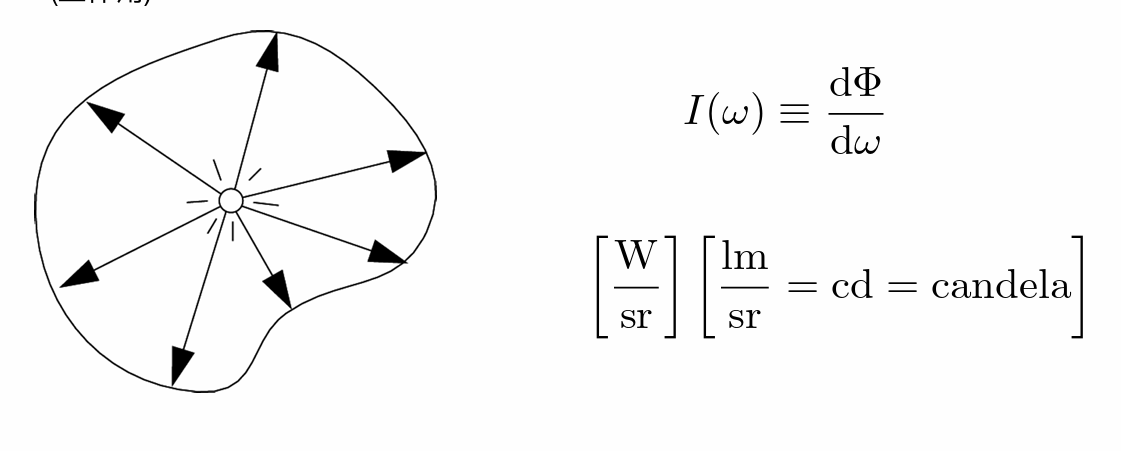
- 立体角:

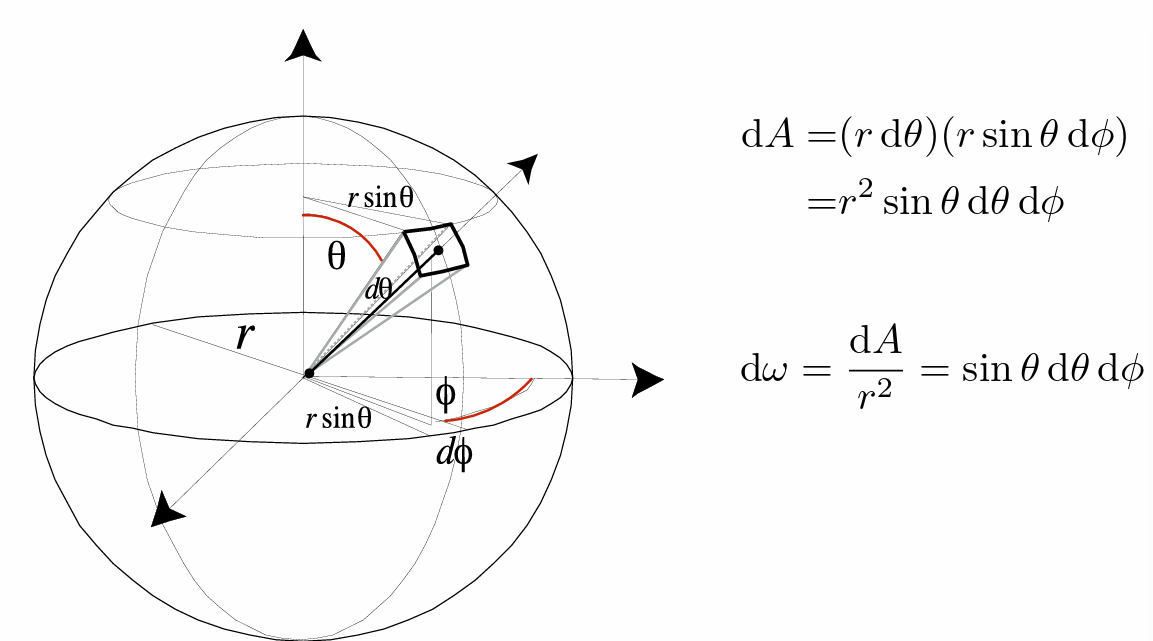
- 注意强度只与立体角相关,与距离无关
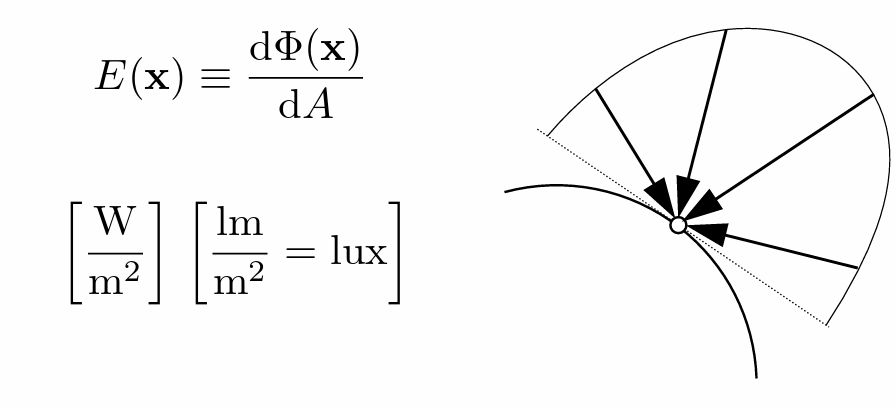
- Irradiance:辐照度(单位面能量)
- Irradiance 是指达到某个表面单位面积上的辐射功率。它衡量的是光源对物体表面的照射能力,反映了物体表面接收到的光能量有多少。
-
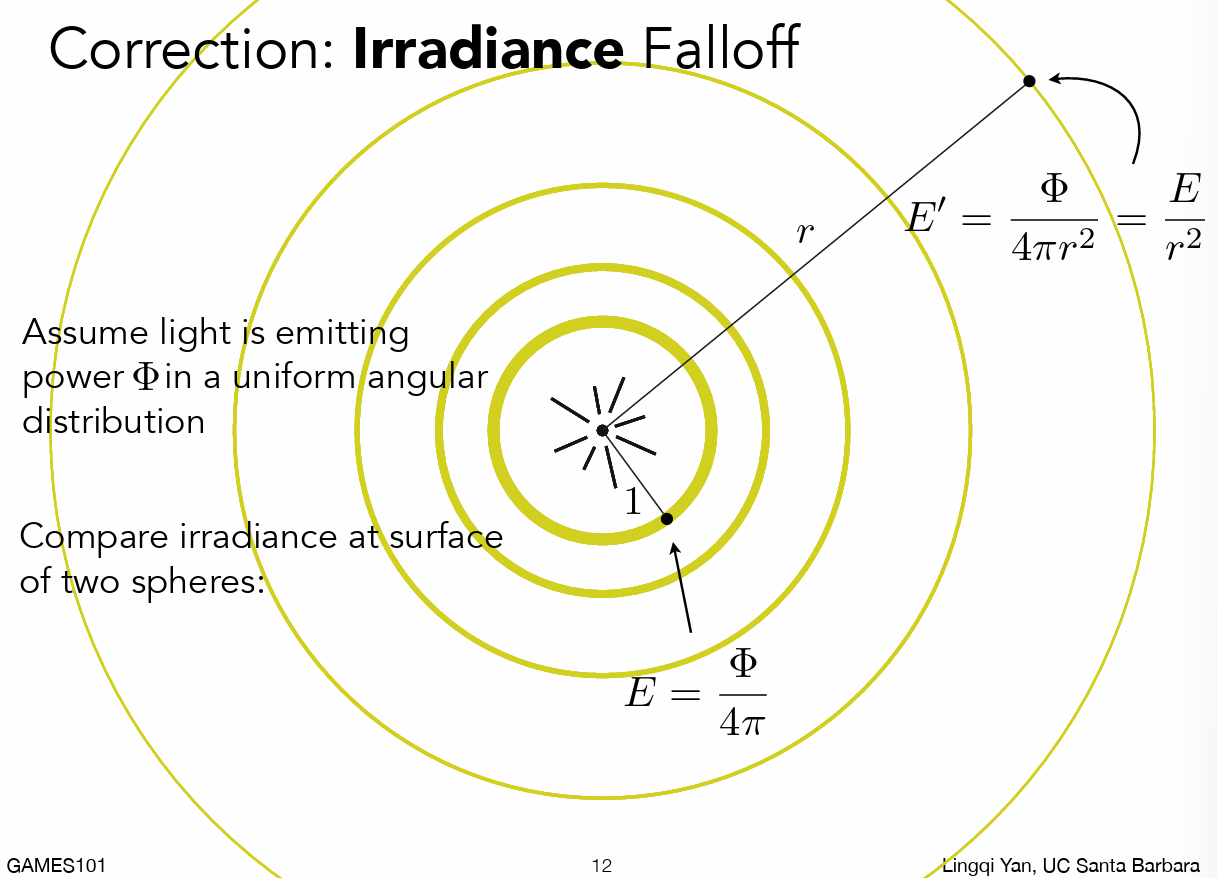
- 随着半径增大,Irradiance减小;Radiant Intensity恒定
-
Radiance:辐射亮度(传播过程的能量)
- 单位面积上单位立体角内的辐射功率。它是描述光在空间中传播的基本物理量,综合考虑了方向性和空间分布
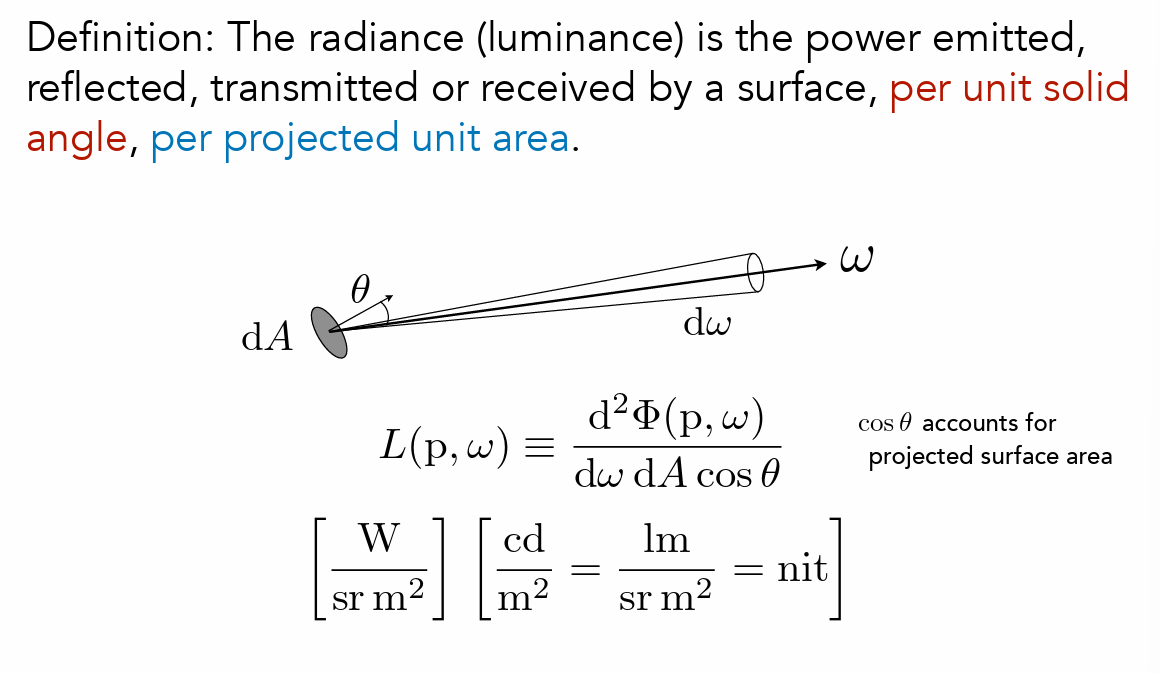
- 单位面积向特定方向的单位角内的能量辐射
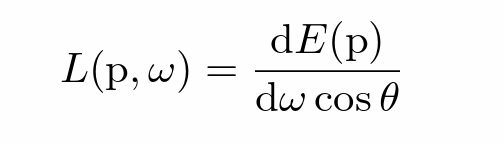
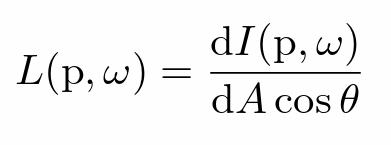
- Radiance是考虑特定入射方向的Irradiance
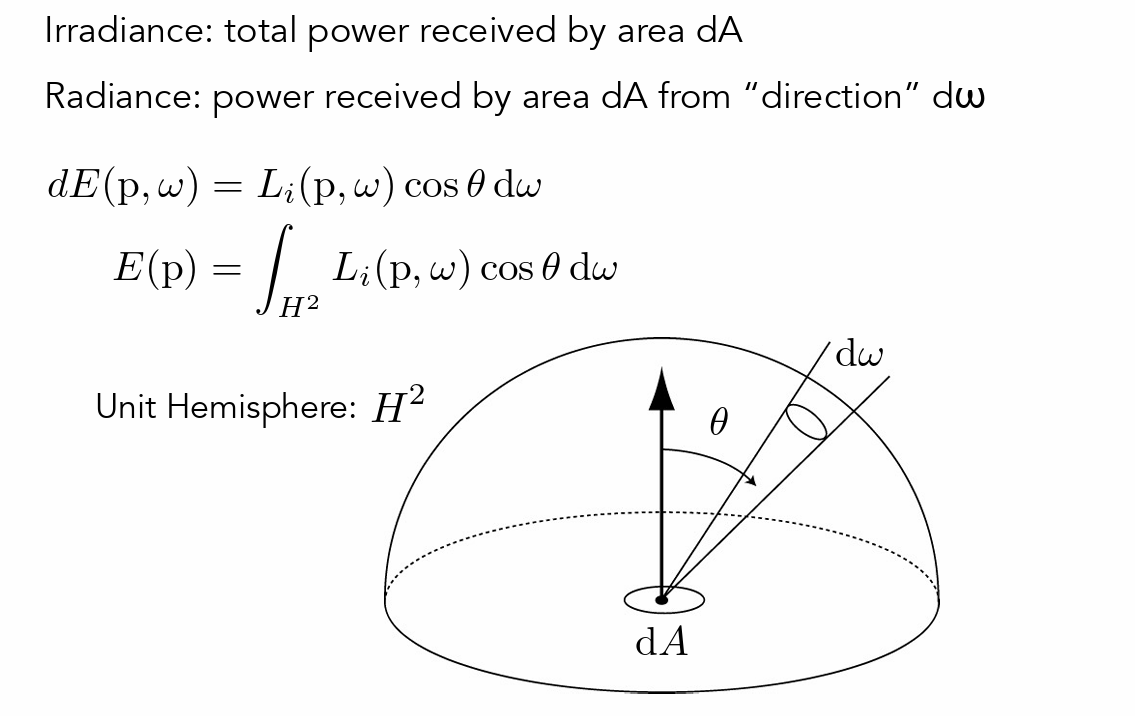
BRDF¶
- 描述一个方向反射到另外一个方向的过程
- 接受能量=输出能量
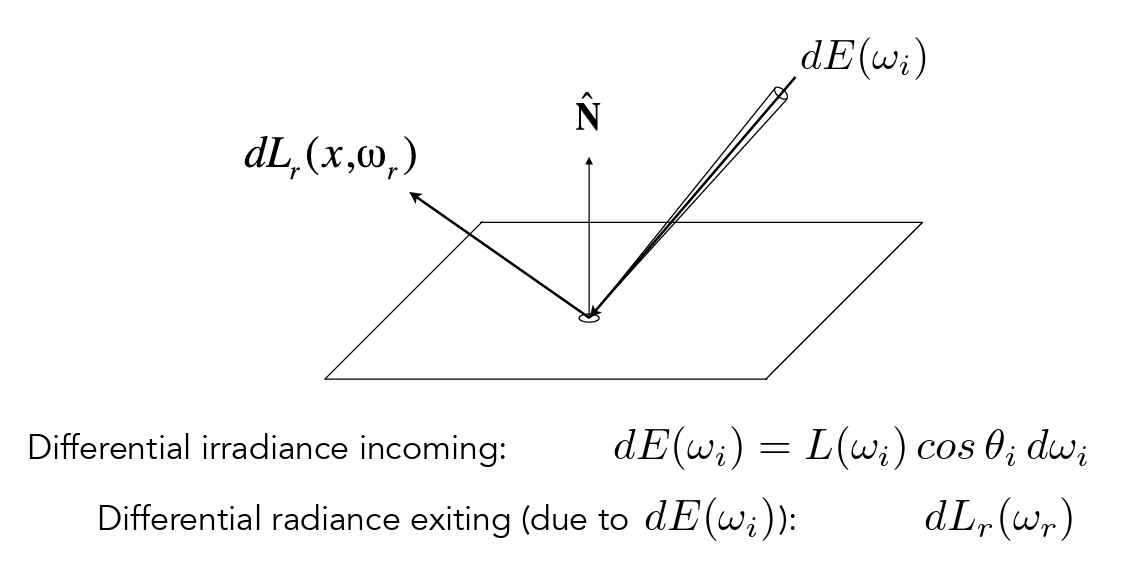
- BRDF就是能量被如何分配到不同方向
- 所有光源的辐射->反射总光线
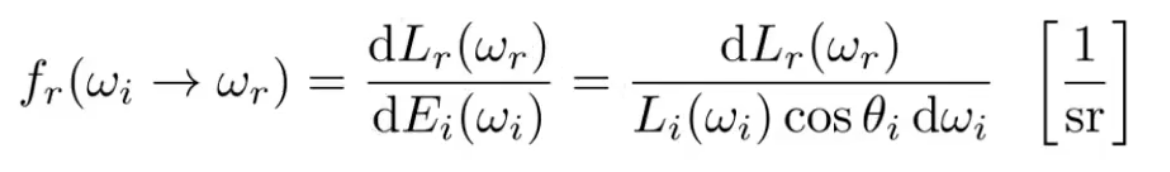
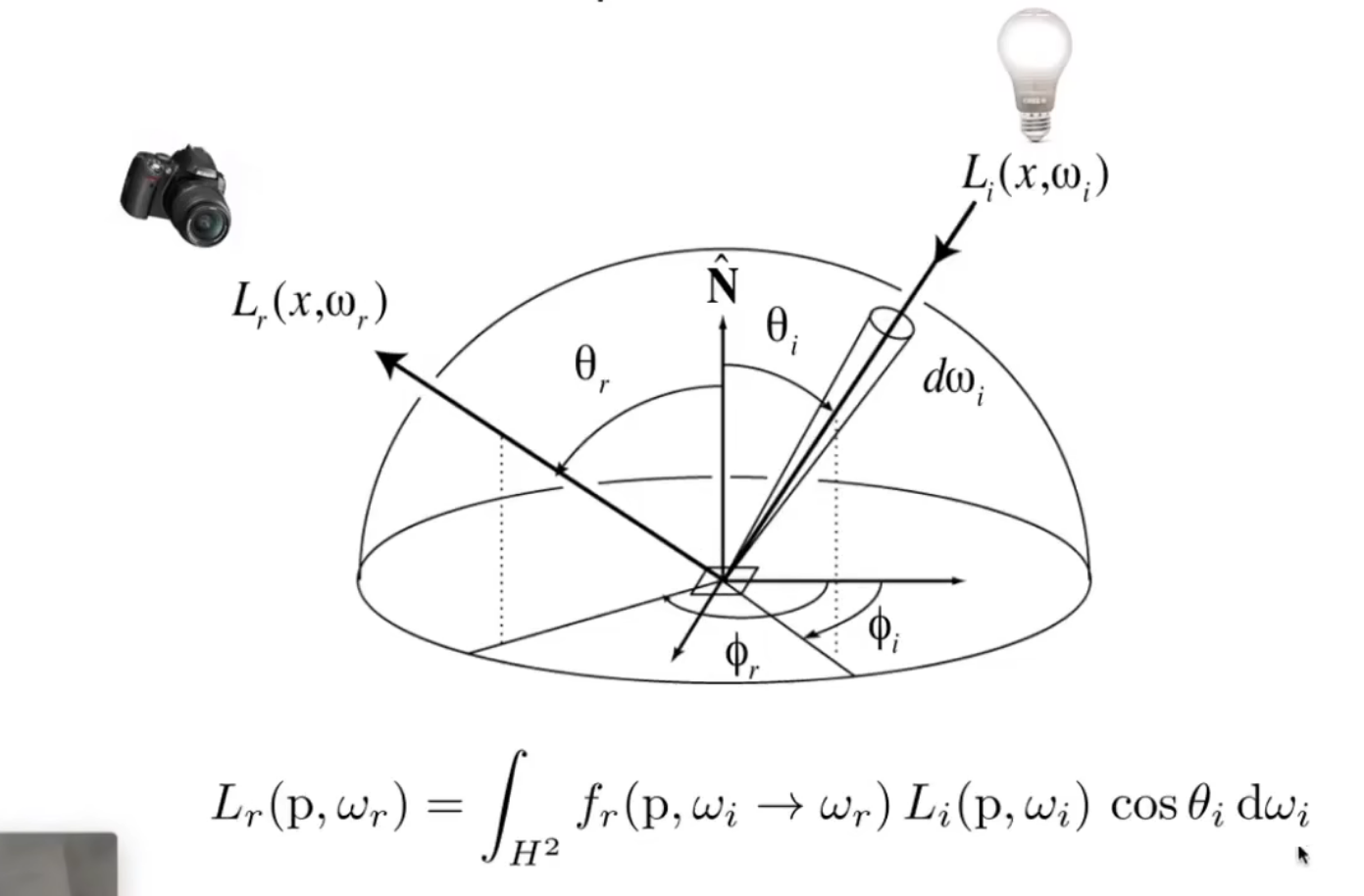
- 这是一个递归计算过程
- 渲染方程:自发光+反射光加和(包含多次反射递归)
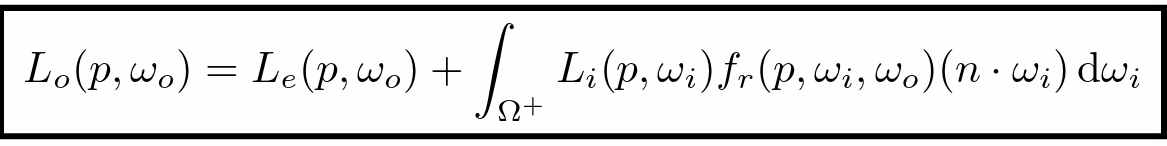

- 简化表示

- 递归弹射(包含多次反射即全局光照(直接光照+间接光照))
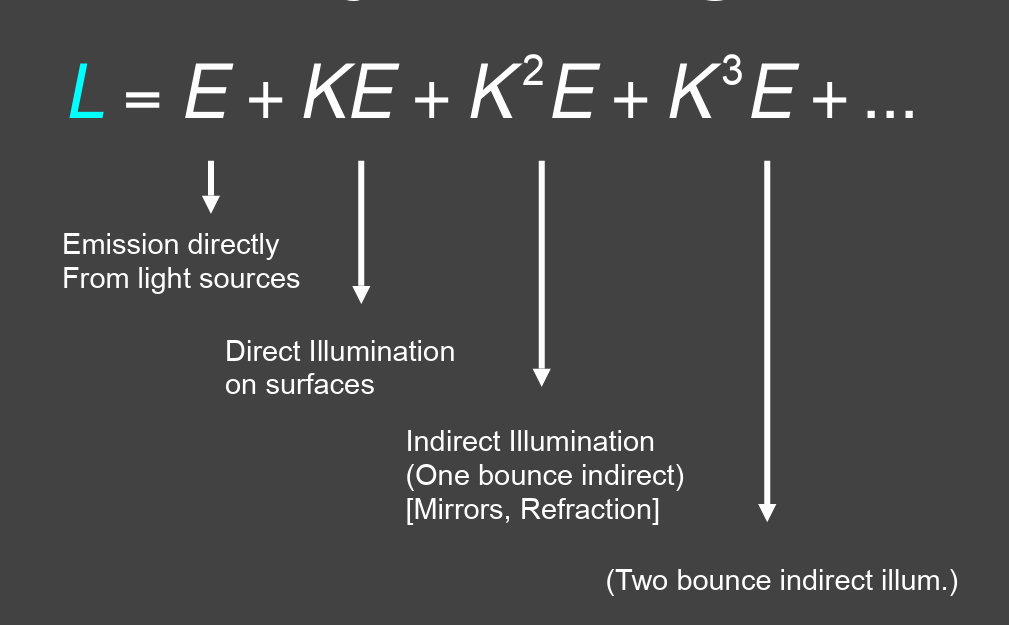

蒙特卡罗路径追踪¶
- 蒙特克罗积分

- 使用随机采样获取积分区域内的值,用于进一步的积分计算
- (均匀采样)
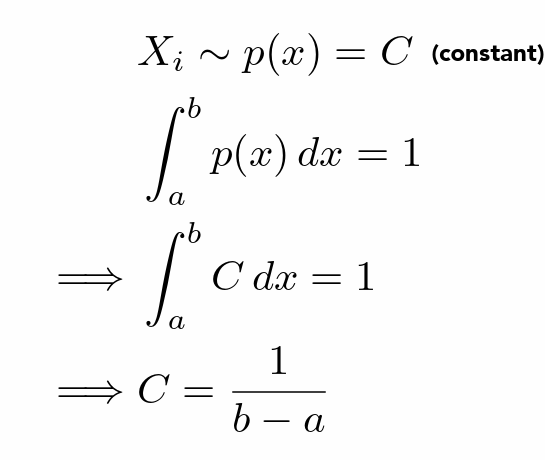
-

-
解决Whitted-Style Ray不正确的地方,Whitted不能处理好漫反射
-

-
用蒙特卡洛积分表示反射方程
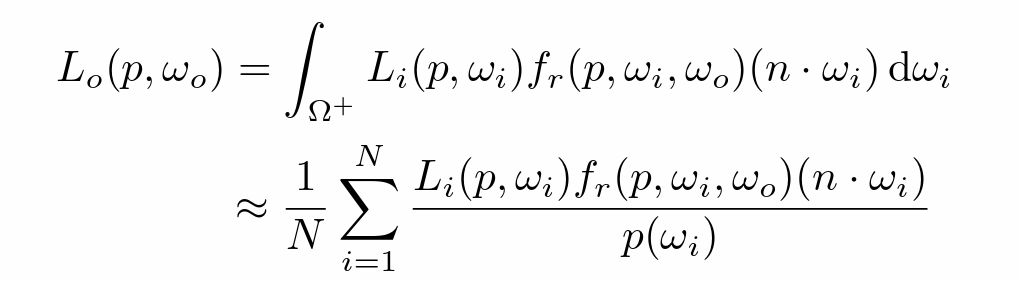

- N(一根光线反射后探测数目)!=1时N会指数级增长
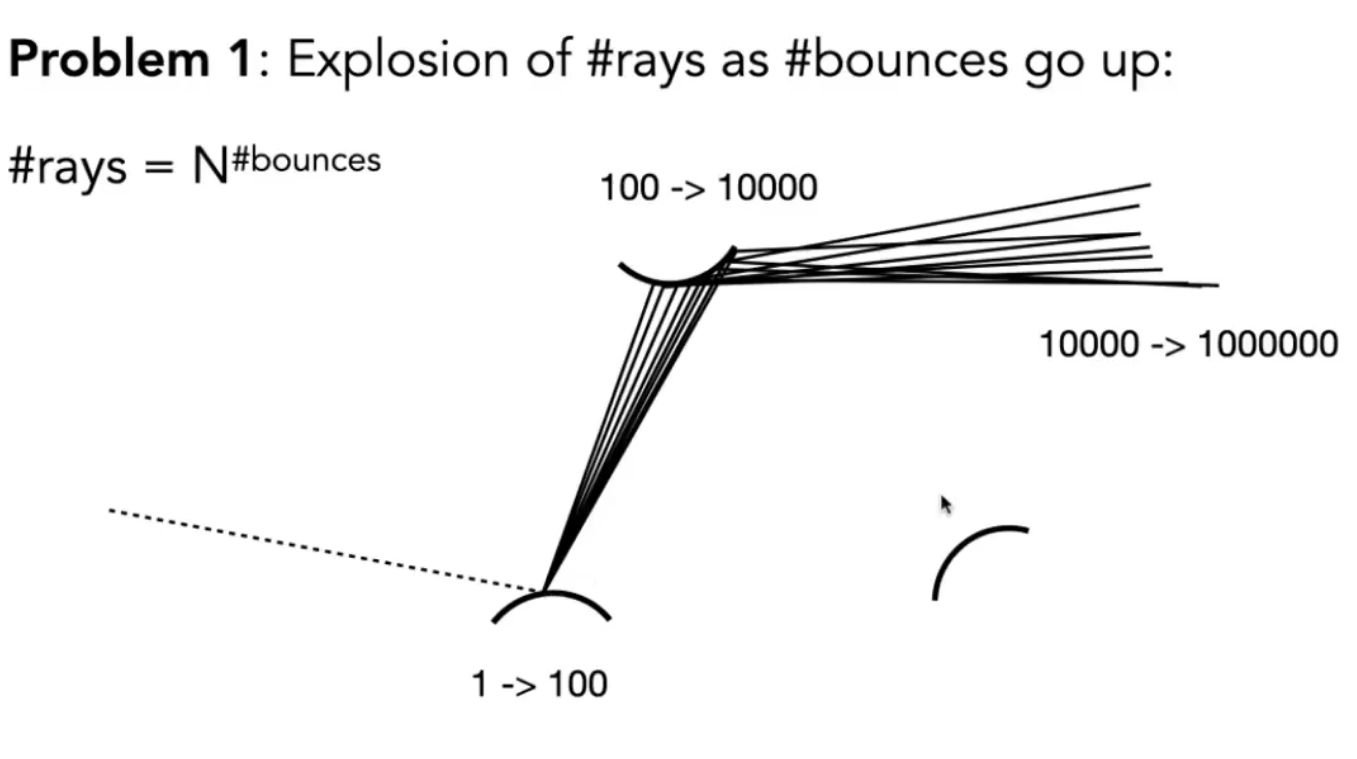

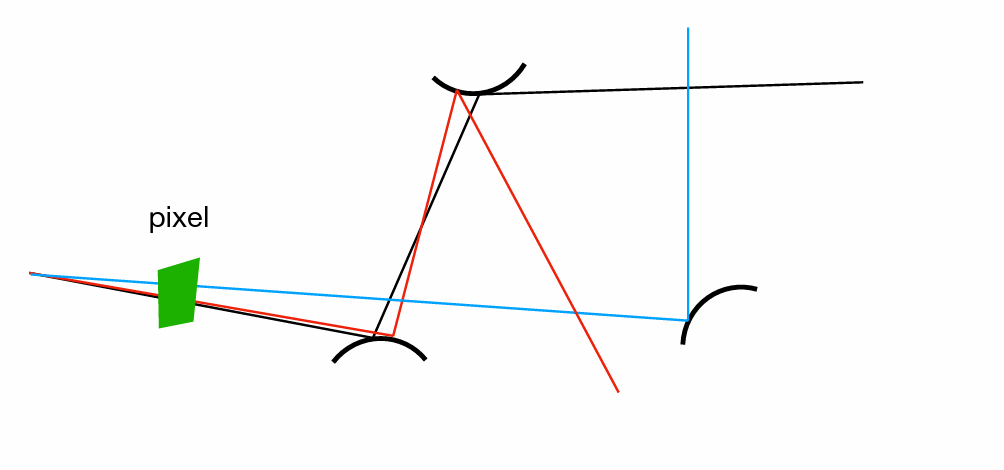
- 为了避免指数增长,只考虑一个方向(这就是路径追踪)
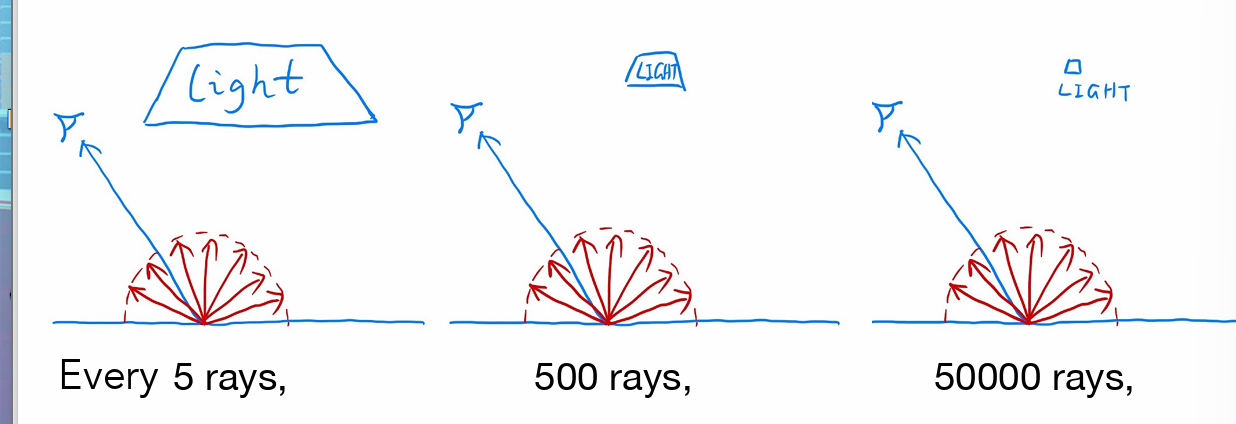
- 采样足够多的经过同一个像素的光线来减少误差
- 向不同方向随机发光

- 为了避免无限递归,(RR)随机决定发反射次数(何时开始停止反射)
- 概率p继续反射,(1-p)不再继续发射

- 渲染结果要\(L_0/p\),这样保证期望不变,即:\(E=P*(L_0/P)+(1-P)*0=L_0\)

- 采样效率低:光源太小,大部分发出的路径都不会到达光源
- 改用向光源来进行采样、积分
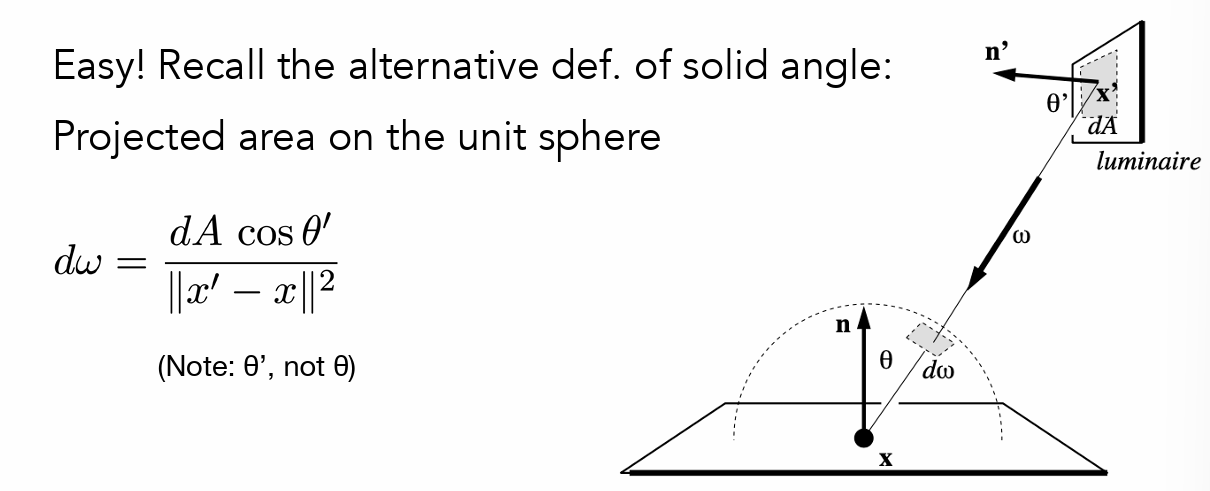
- dA是立体角dw对应光源上的区域(先将dA映射到平行方向,然后两个平行表面是成比例的)


- 对于直接光照采用dA计算,对于间接光照仍然采用随机方式
材质与外观¶
- 材质=BRDF决定如何进行反射
反射与折射¶
- 类镜面反射材质(如铜镜)、
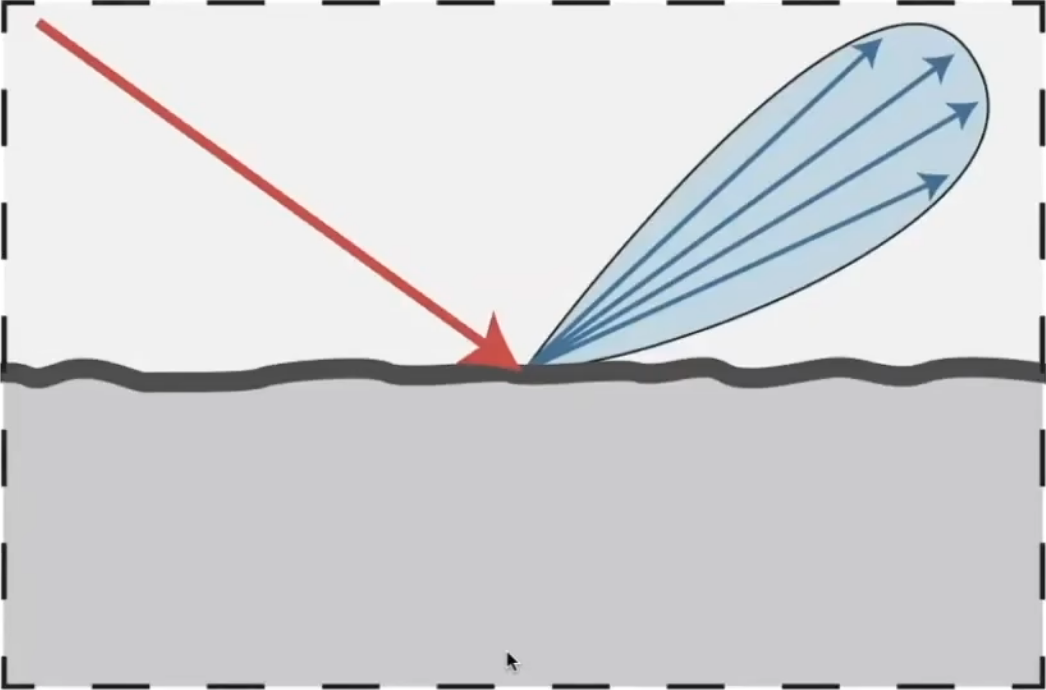
- 透明物体(如水,可以折射进去)
-
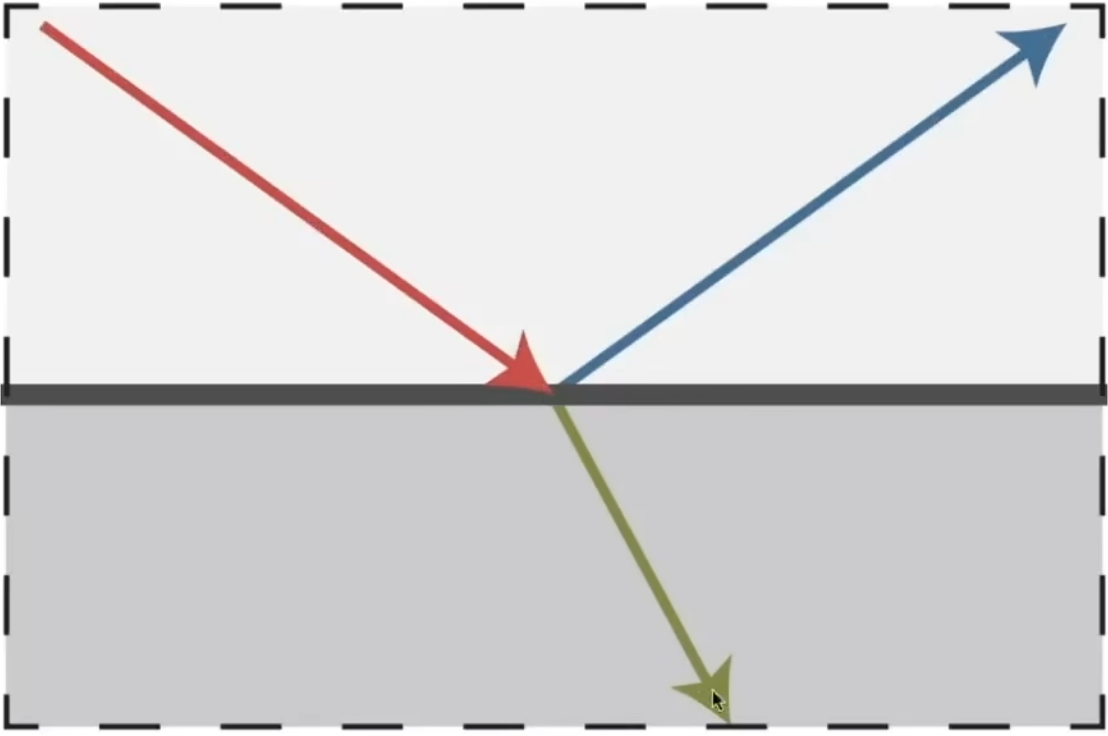
-
反射角计算
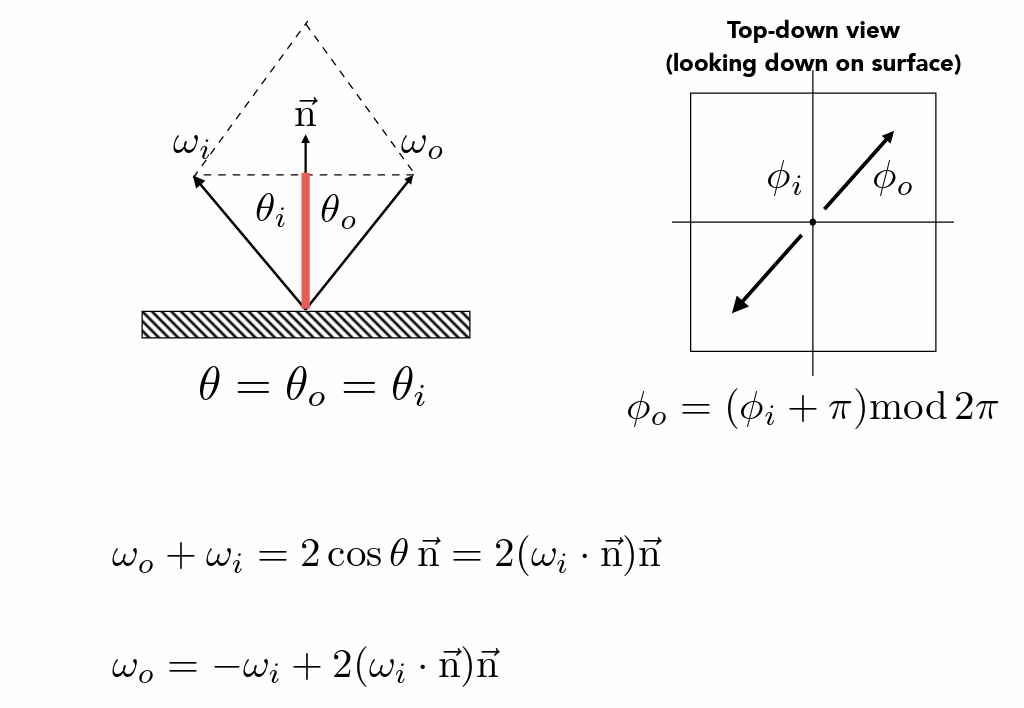
- 菲涅⽿项,反射的程度与夹角(入射角)有关
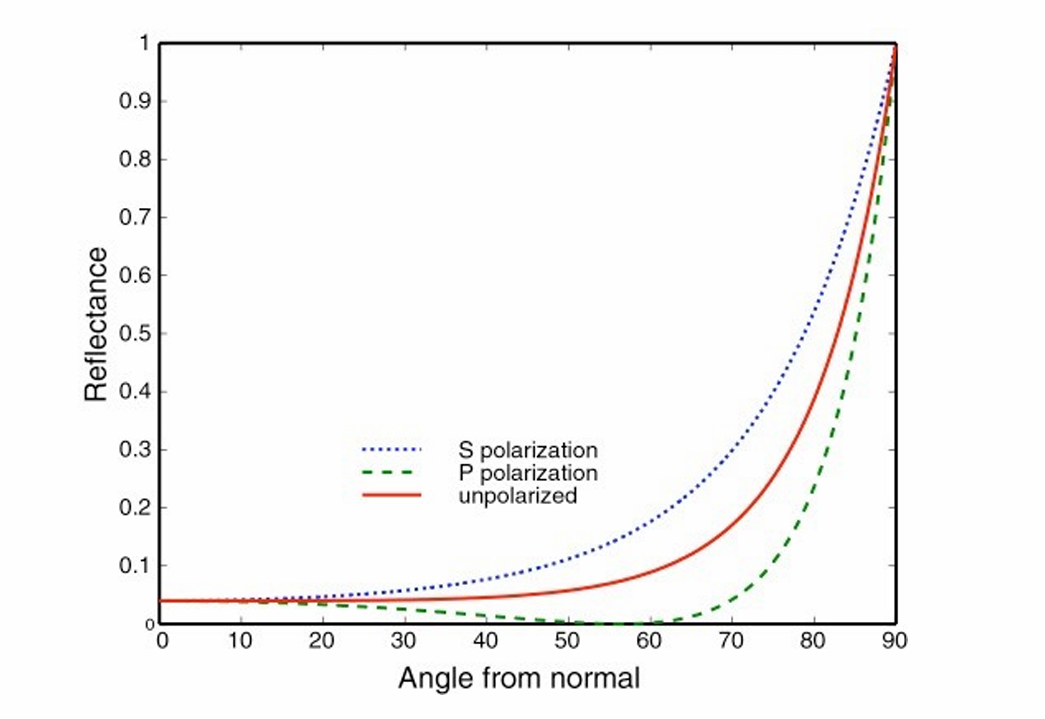
- 入射角越大,反射越强 (绝缘体,如玻璃)
- 金属

- 折射
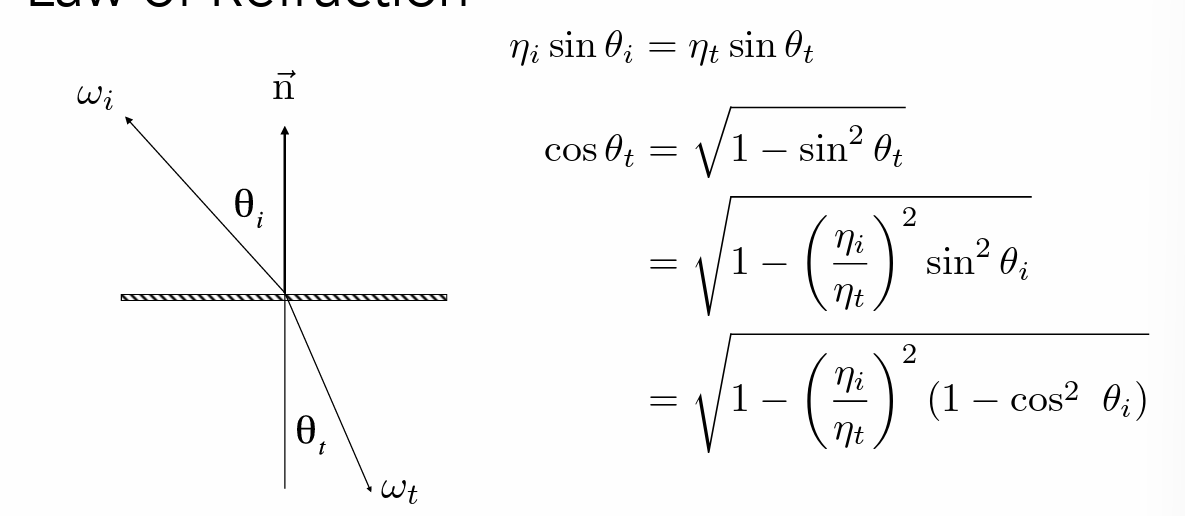
微表面模型¶
- 远处看材质,近处看几何(表面凹凸不平 )

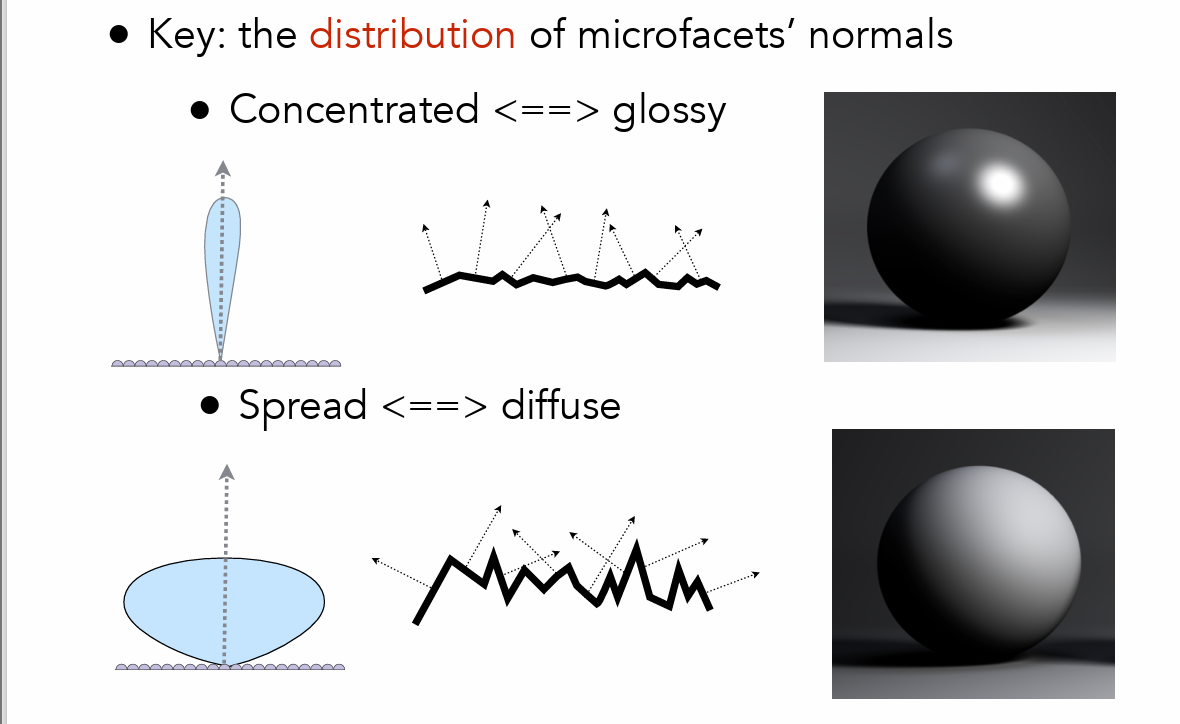
- 法线分布是否集中决定是漫反射还是镜面反射
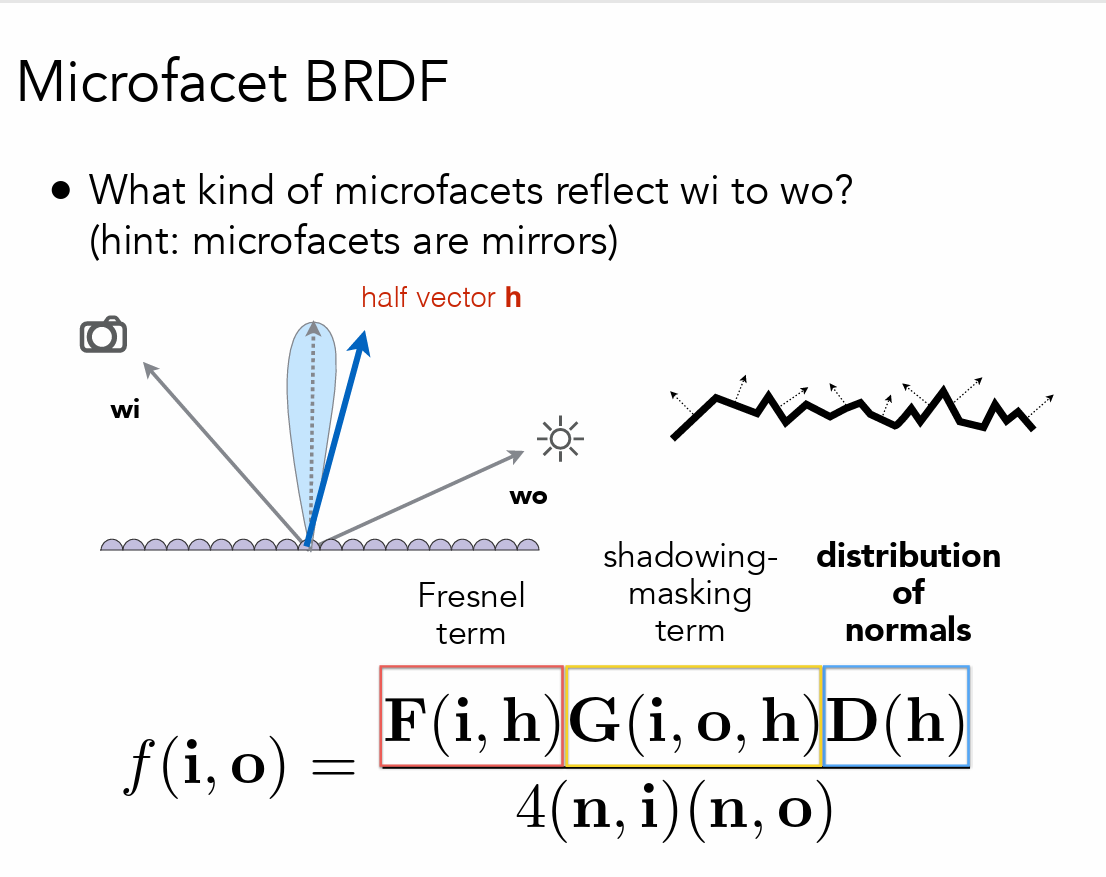
- 菲涅尔项:总共有多少能量被反射
- shadowing-masking:修正光线遮挡(入射角很大时反射光发现很可能会被表面上的凹凸遮挡)
- distribution of normals:法线分布情况
- 微表面的方向性:各向同性/各向异性

-
各向同性:反射结果只与 入射光与反射光的夹角相关
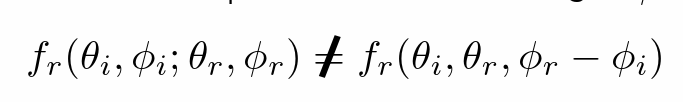
- 各向异性下(四维):入射光线和反射光线的坐标
- 对于各向同性可以化简为三维(两个坐标->差)
-
BRDF性质
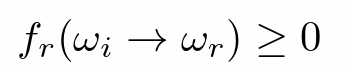
- BRDF是非负的
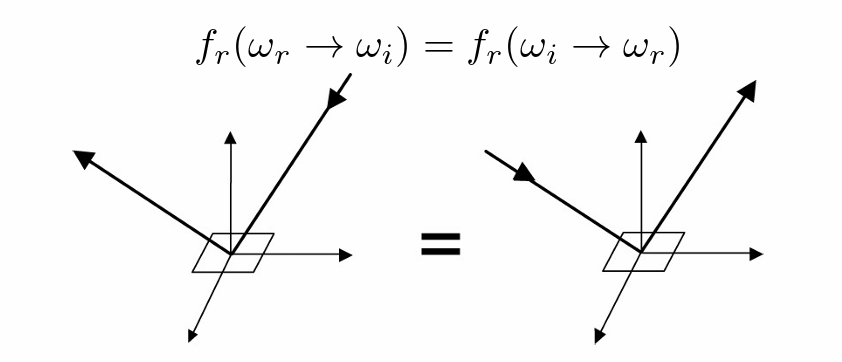
- 具有可逆性(交换入射、出射)
- 能量收敛
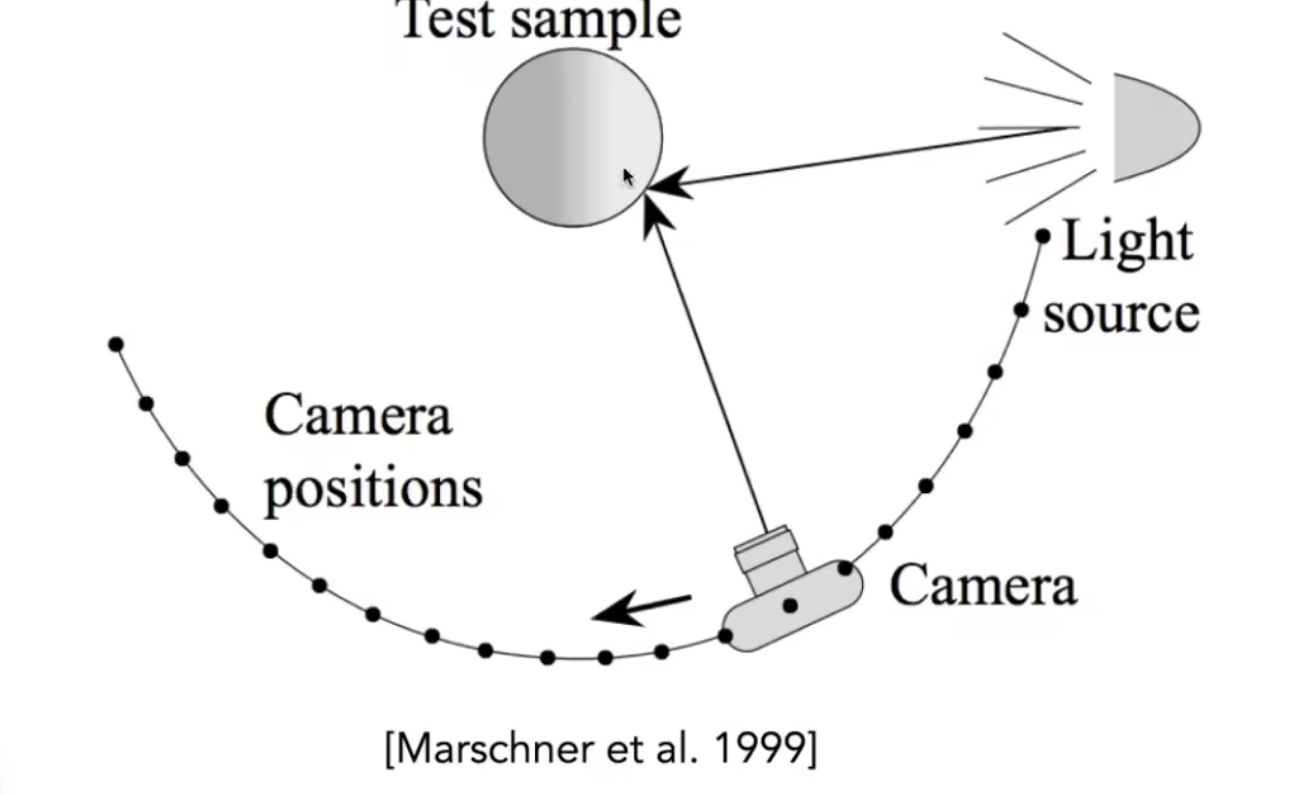
- BRDF的测量
高级光线传播¶
- 无偏:蒙特卡洛估计的期望是正确的
无偏光线传输¶
- BDPT双向路径追踪
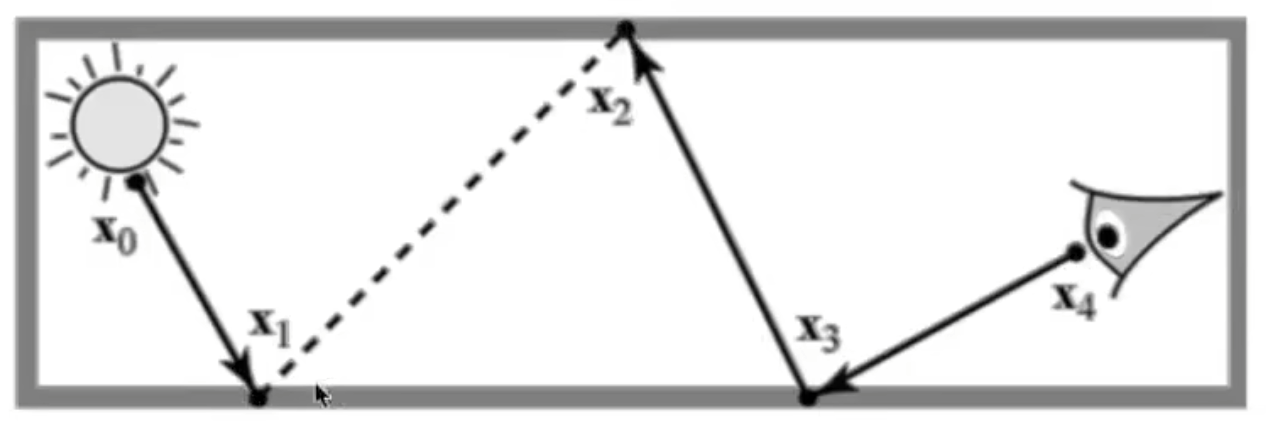

- MLT
- 适用于较为困难的场景
- 使用马尔科夫链,找到一条有效路径后可以更好地找到有用的相关路径
- 问题:难以确定覆盖率(局部自动推导),可能存在覆盖率不均匀,何时收敛(因此不适用与连续动画)
有偏光线传输¶
- Photon Mapping 光子映射
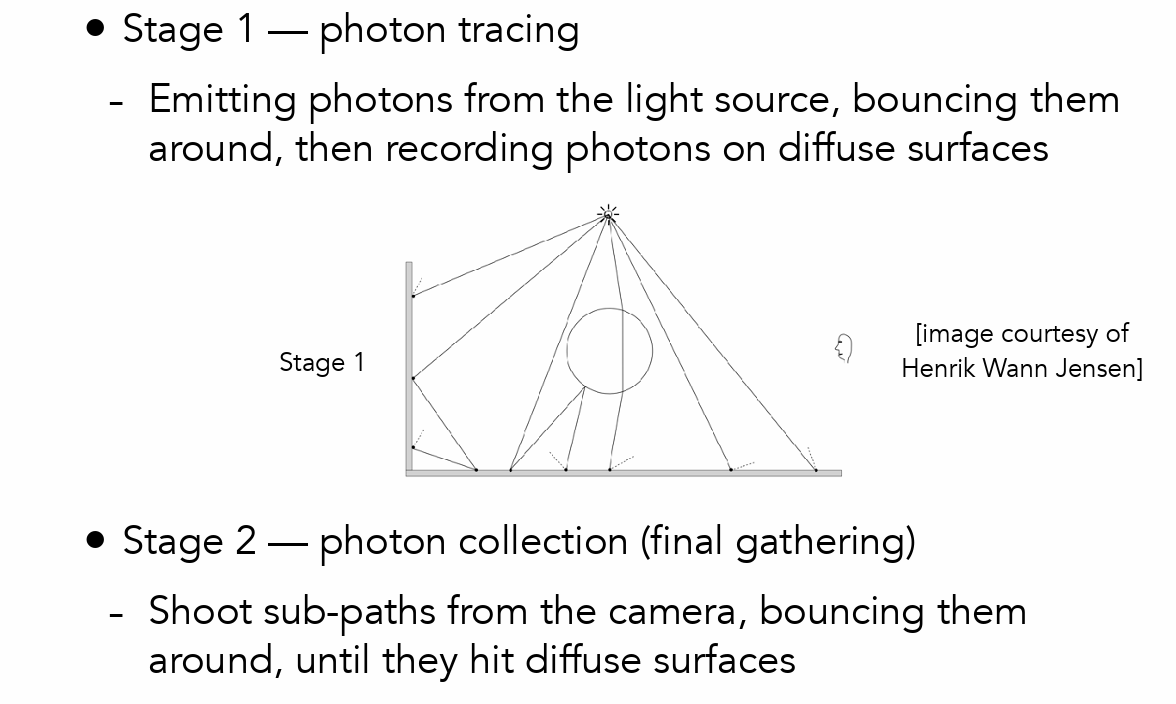
- 首先由光源发射光子,然后由摄像机发送进行观察
- 擅长渲染光斑
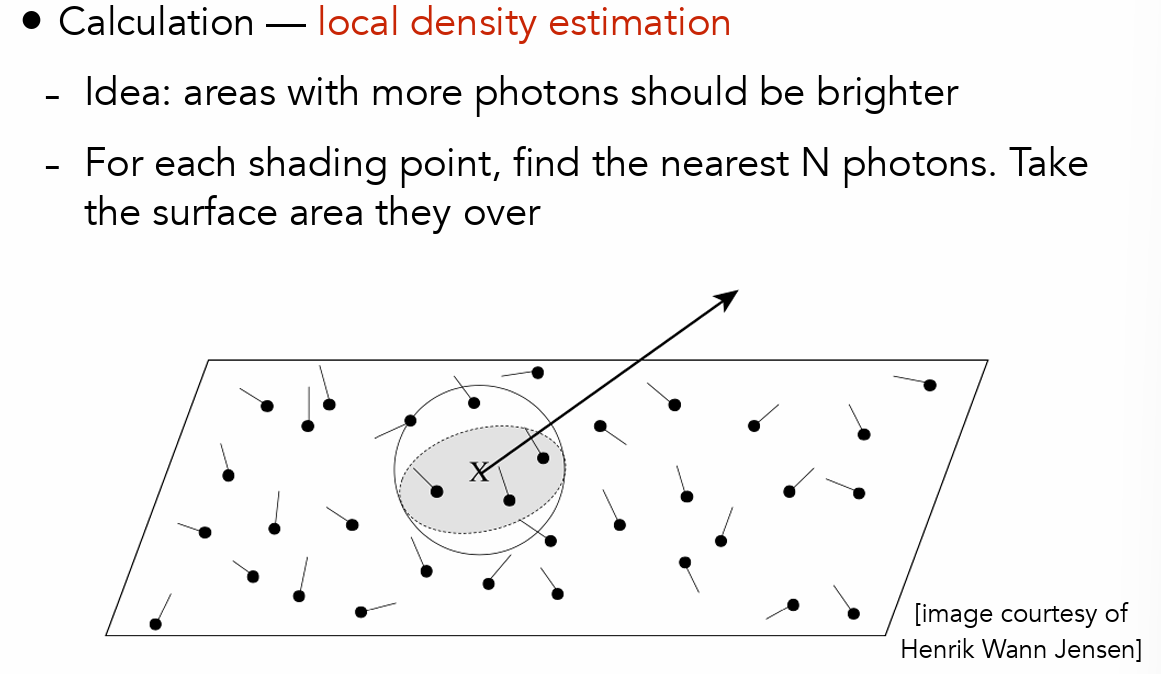
- 找周围最近n个光子占据的面积大小,从而得到光子密度
- 根据局部光子密度进行渲染
- 不过由于光子数目有限,因此存在偏差
- 有偏:存在偏差,会造成模糊(用一个范围的数目估计一个点),但样本足够多时会收敛
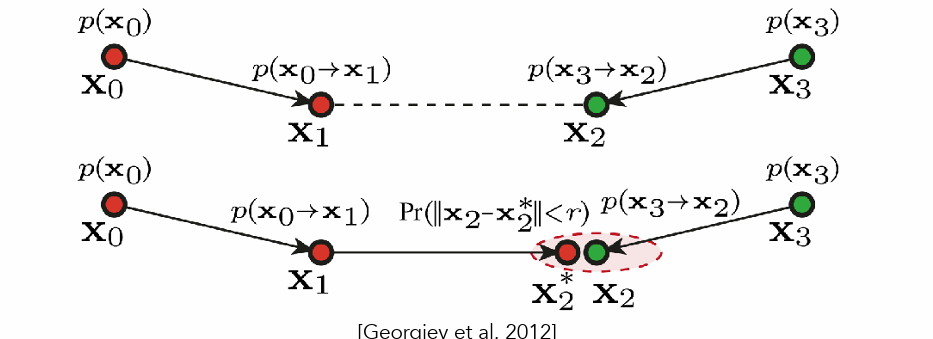
- VCM:双向路径+光子追踪
- IR实时辐射度
- 将已经被照亮的面认为光源,用他们再去照亮别的
外观建模¶
非表面模型¶
- 光线会进入到物体内部
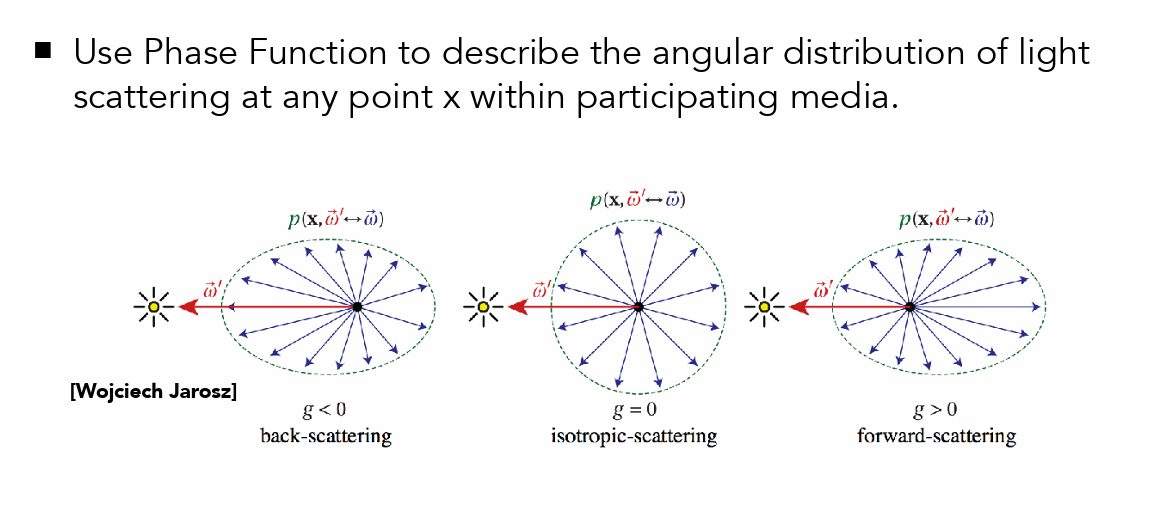
- 如在云雾中的散射
毛发¶
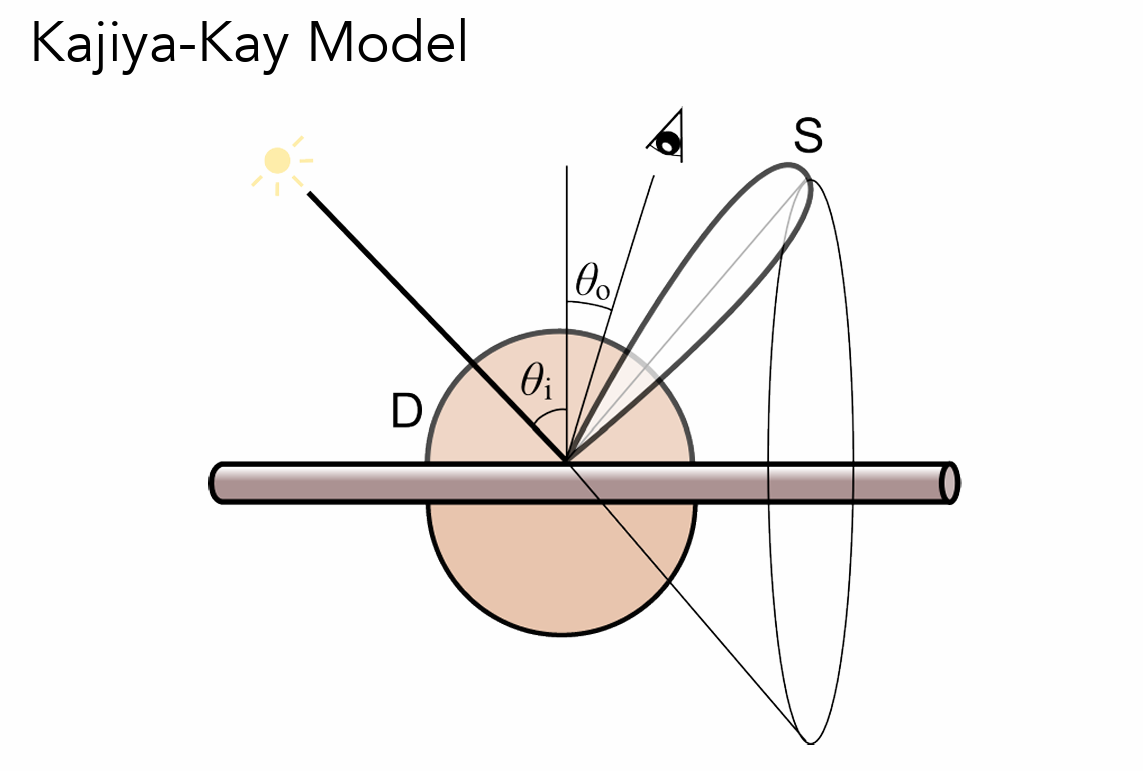
- 光线穿入
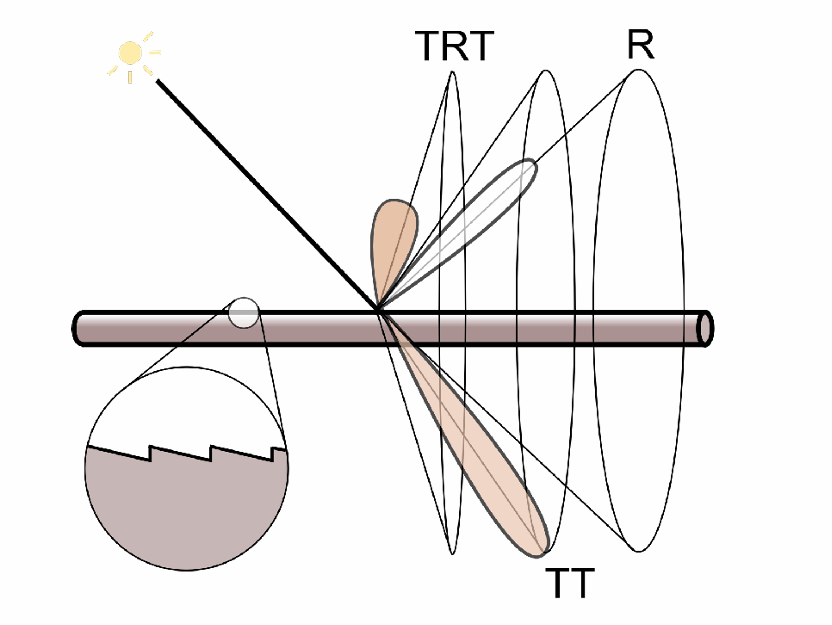
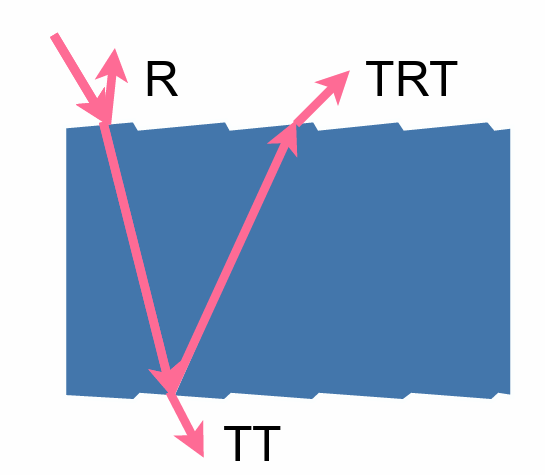
- (动物毛发)双重圆柱模型
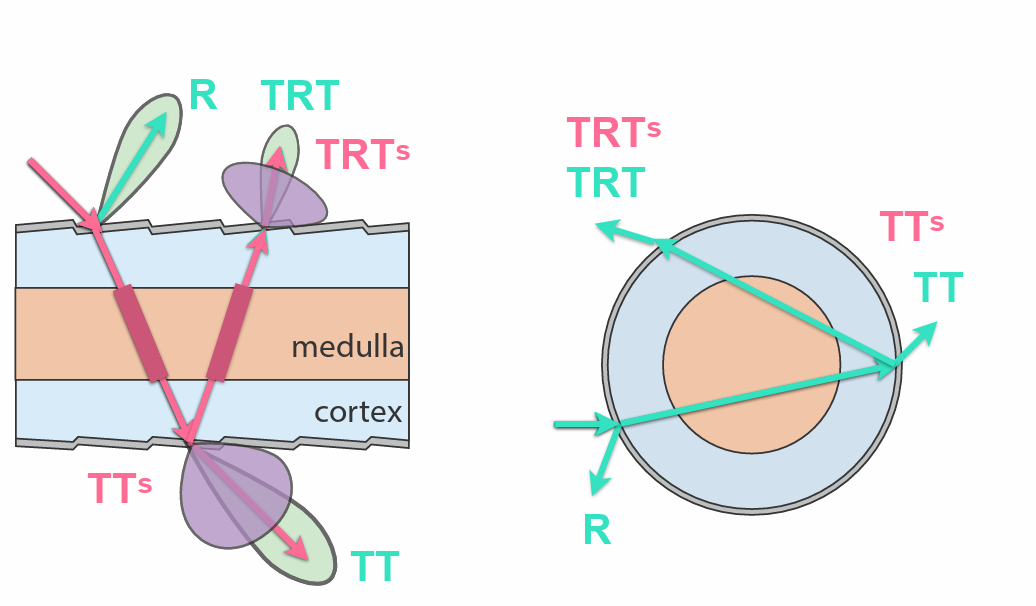

表面模型¶
- Translucent Material:(指光线射入后从不确定的位置出来)
- 次表面反射
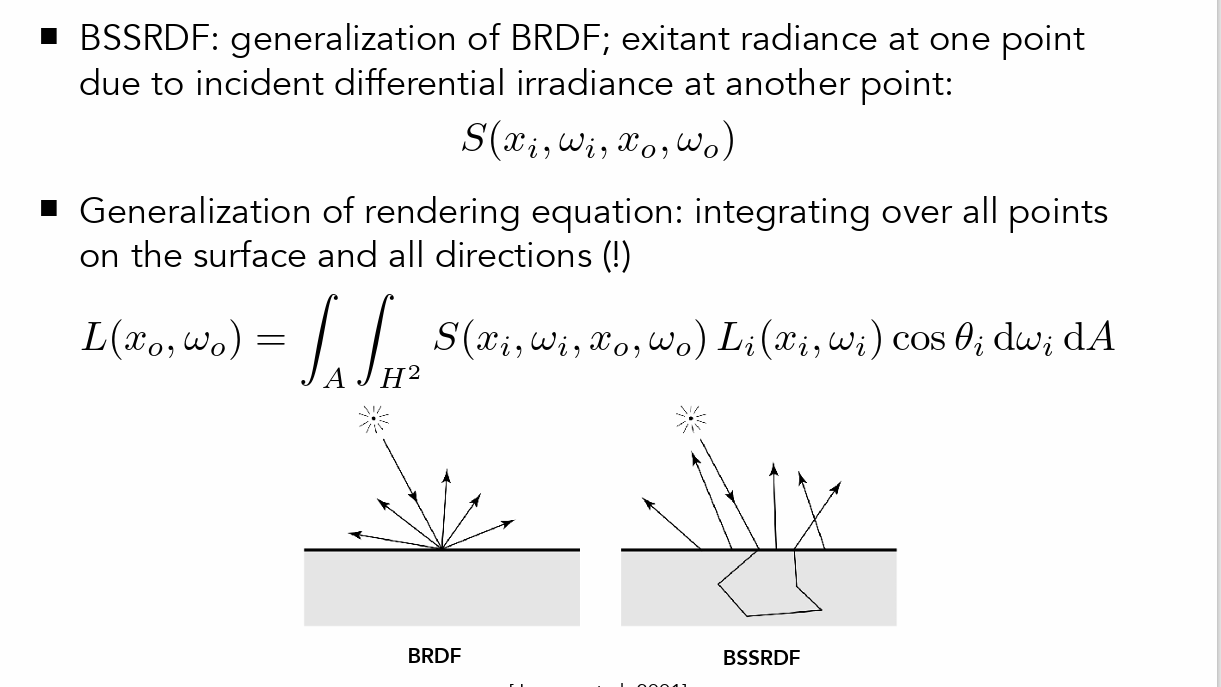
-
BSSRDF就好像内部也有一个光源(双光源模拟)
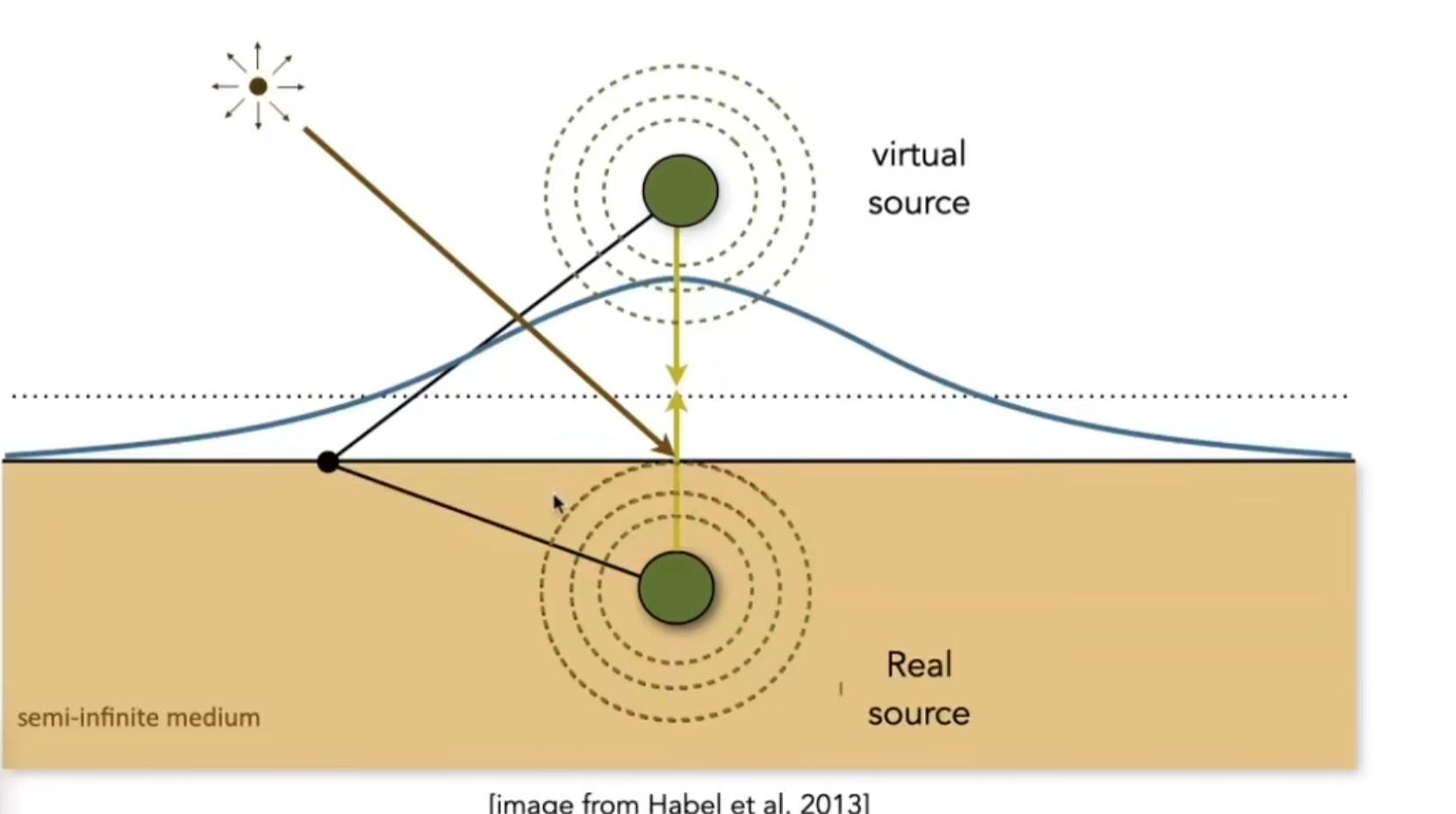
-
布料材质
-

相机¶
- 不能直接使用传感器捕获图像,因为来自所有方向的光线会映射到同一点,无法区分
- 视场FOV
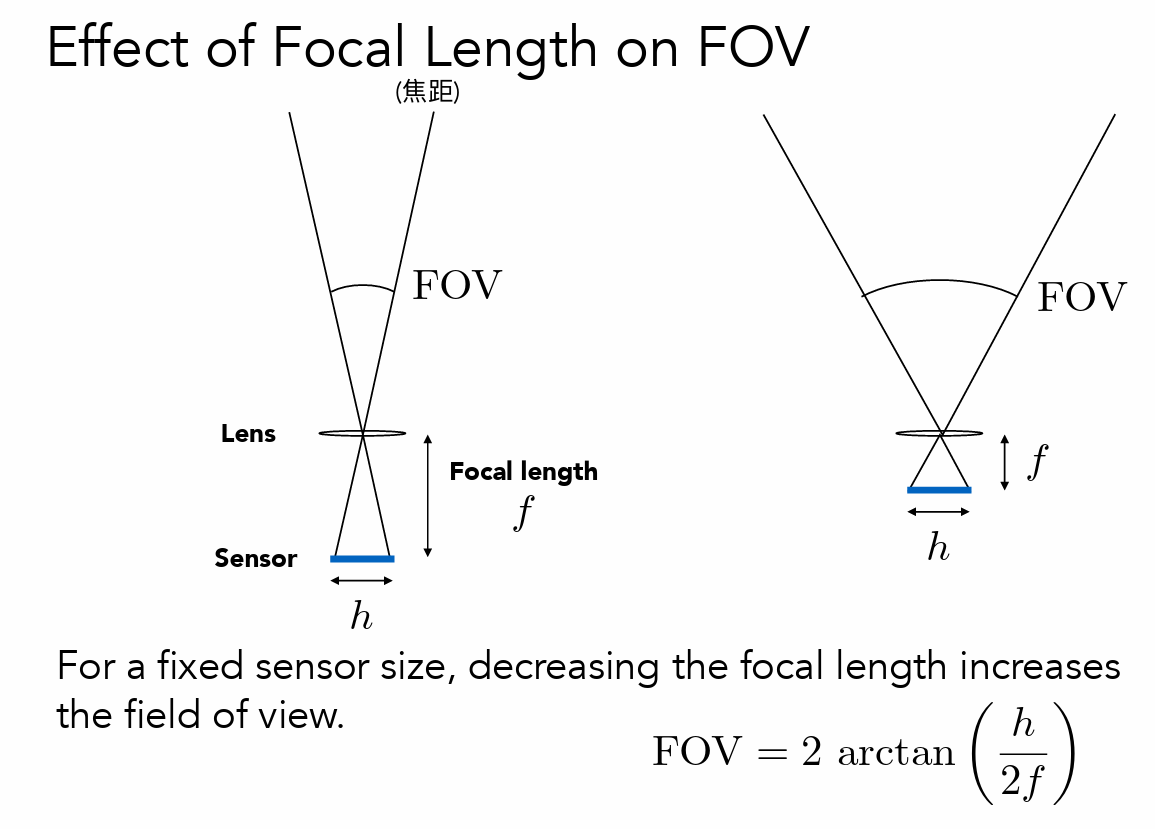
- 以35mm胶片为基准(传感器大小)来定义fov
- 画面裁切

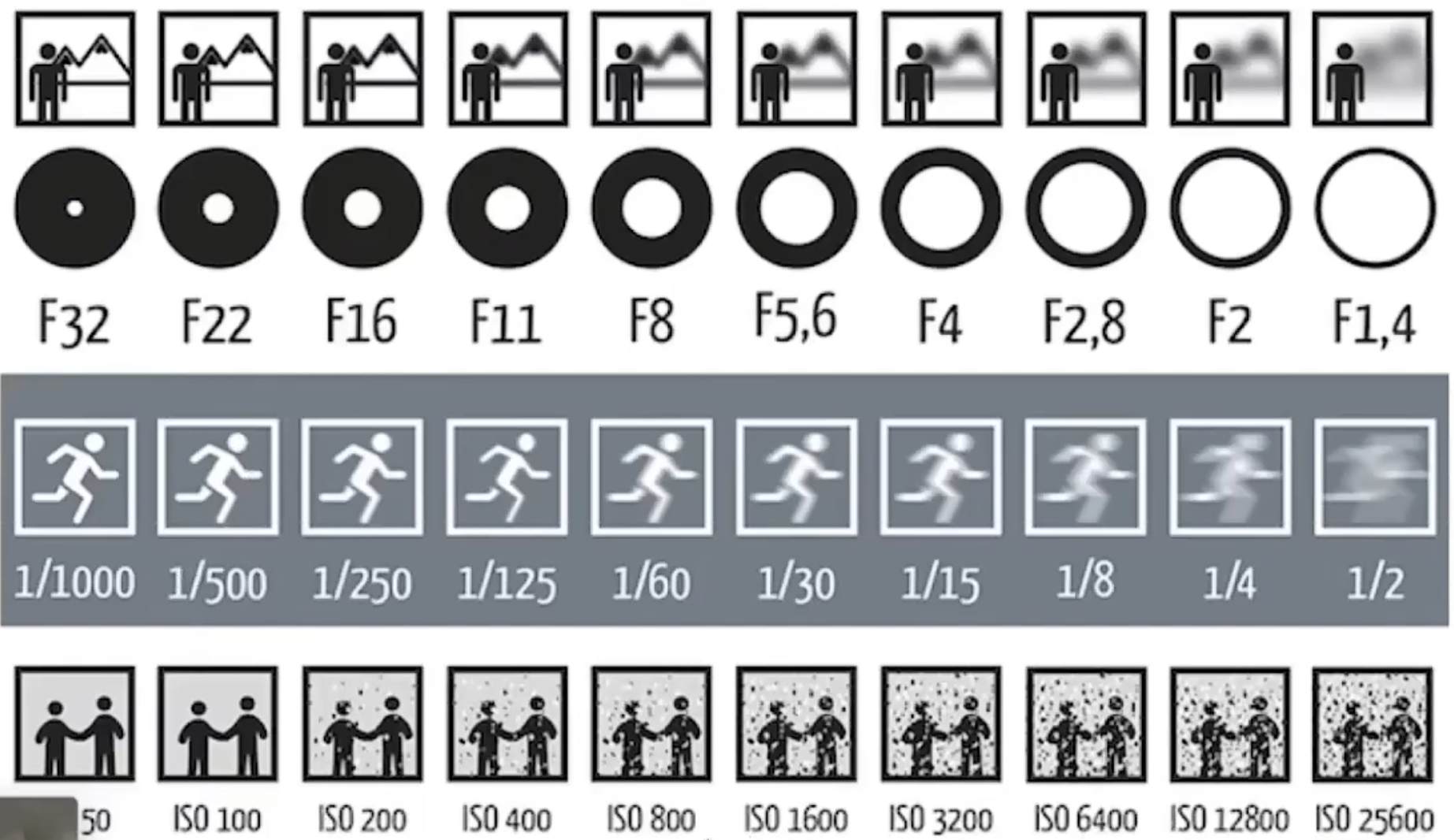
- 曝光
- 进光量*时间

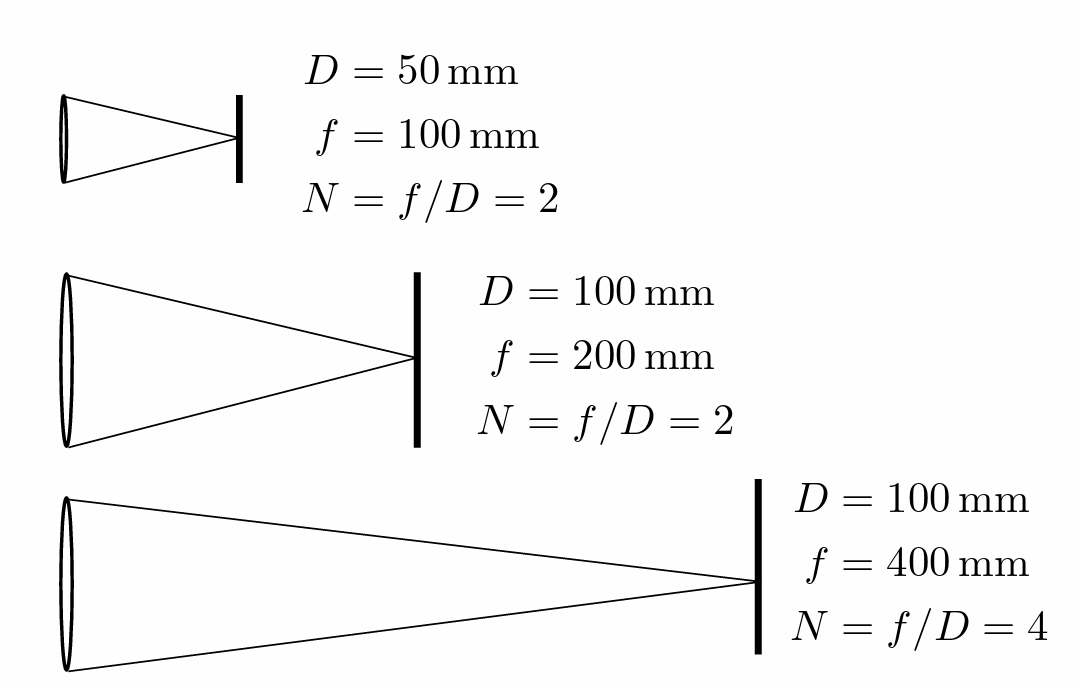
- 光圈
- FN中的N是1/光圈直径
- 快门速度(曝光时长)
- 由于快门让然是逐渐打开的,不同位置的曝光时间存在误差,因此存在果冻效应
- 光圈大小减小一倍,曝光面积会减少为1/4即快门要延长为原来的4倍
- iso
- 简单增益,增大信号强度
- 会放大噪声
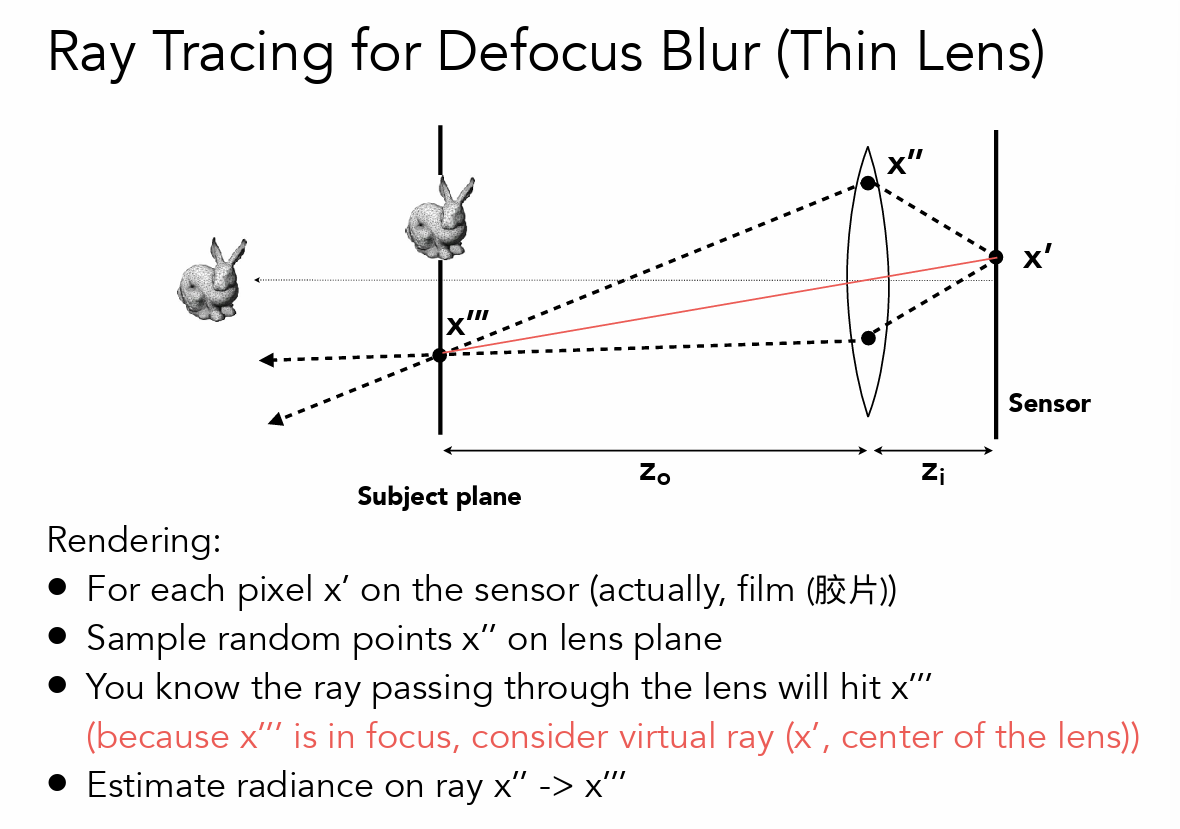
镜头¶
- 物距、像距
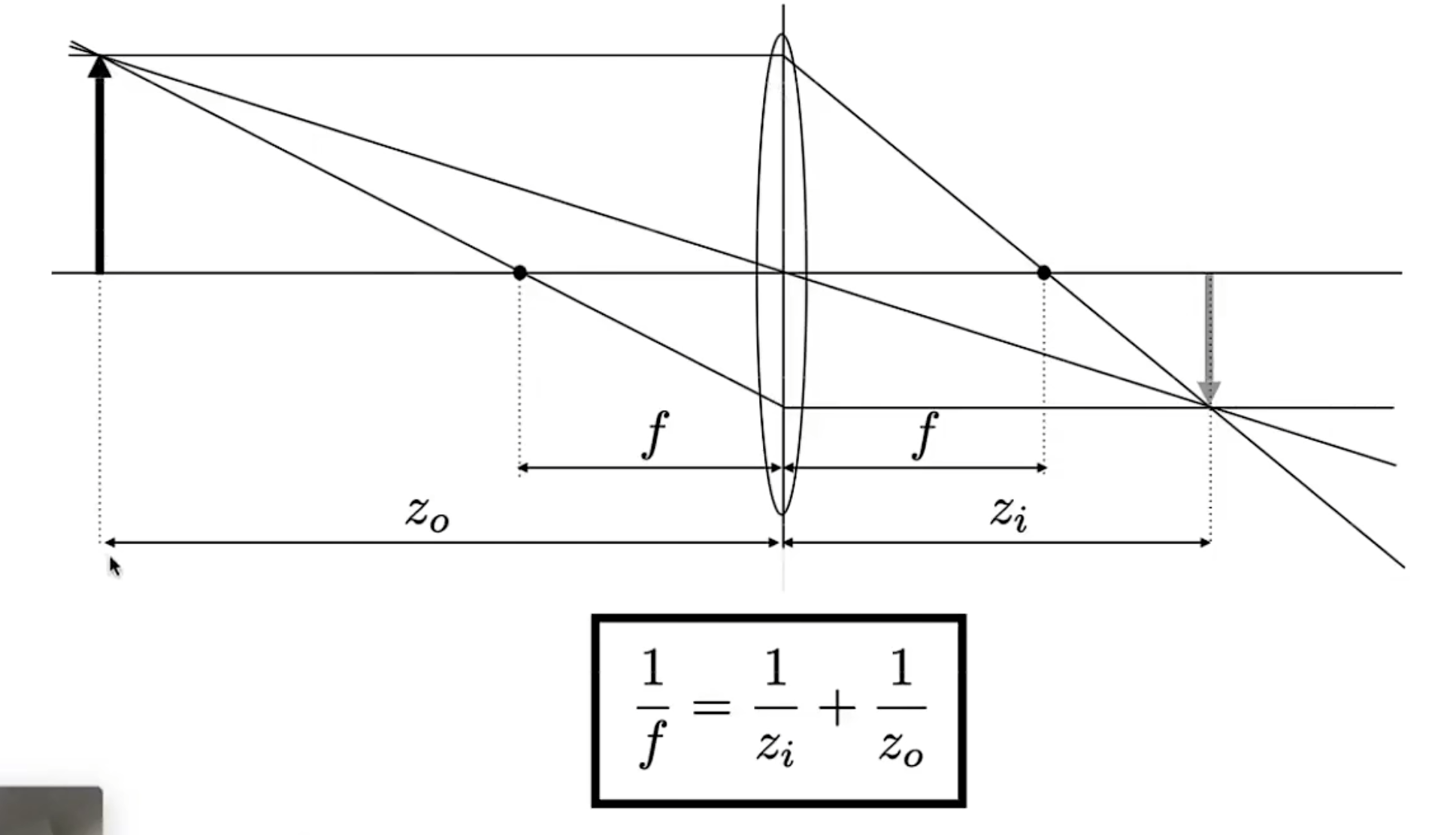
- 景深
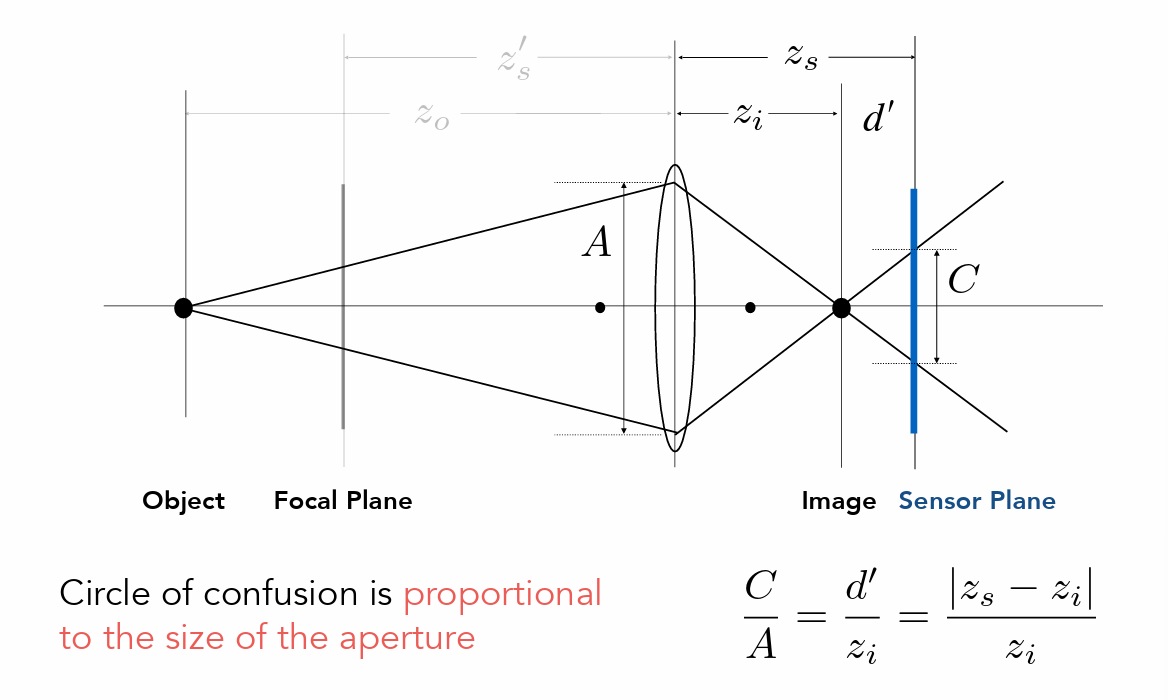
- 像投射在了传感器前面,在传感器上呈圆形(称为CoC)
- 其他条件一定时光圈越小(改变C的长度)CoC也越小,景深越弱
- 认为当CoC足够小时图象是清晰的
- 光圈f数=焦距/光圈直径

- 焦距越大、光圈越小CoC越大
模拟渲染¶
- 清晰范围(可接受CoC大小的成像范围)
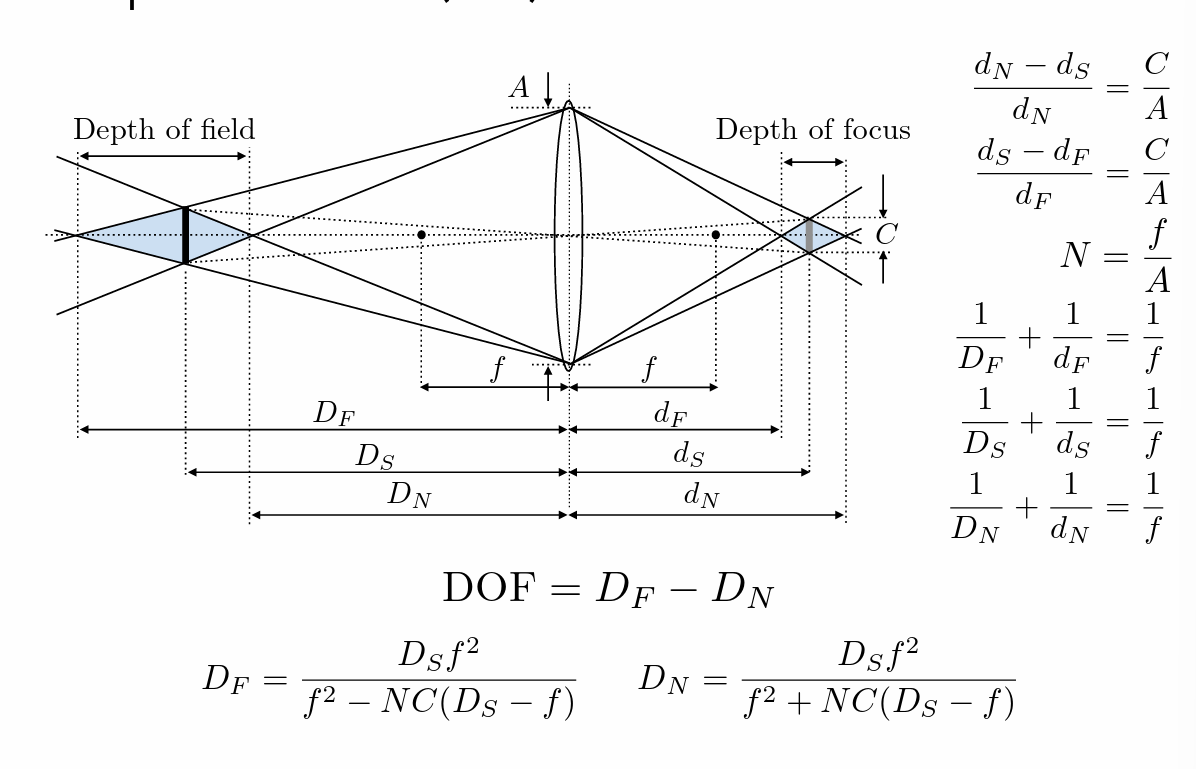
- Depth of field表示在焦内的区域,越小表示景深越严重
光场¶
全光函数¶

-
任何时间从任意位置以不同角度来看世界
-
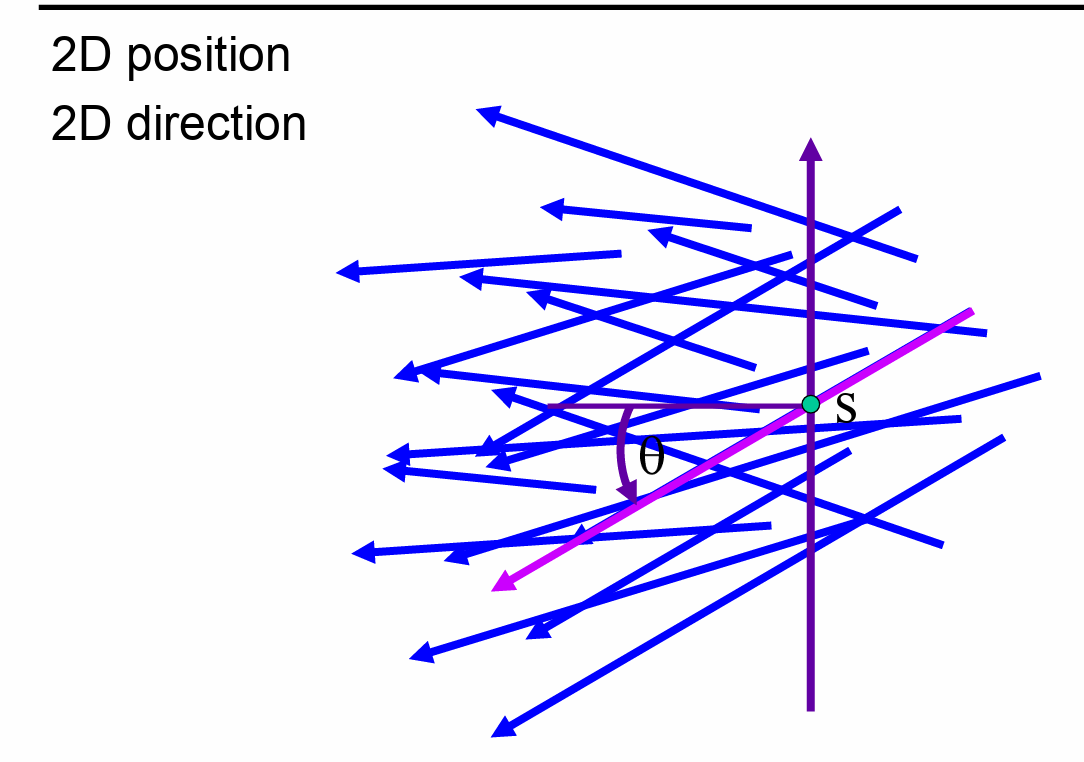
光线
- 起点+方向
-
两点
-
光场
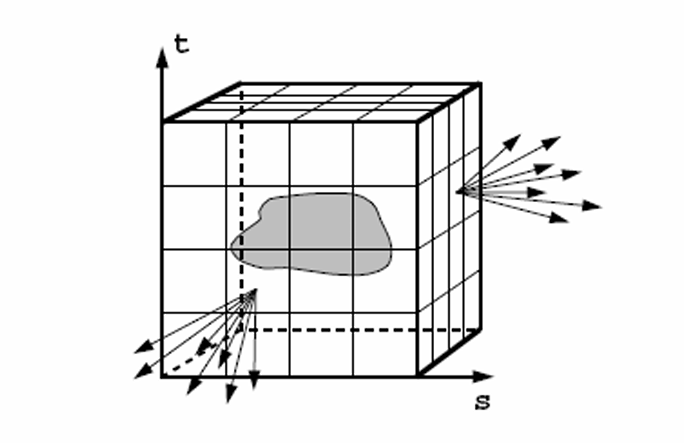
- 看物体就是从物体向外看的状况
- 全光函数就记录了物体向不同方向发光的情况
-
可以得到任意方向物体观测情况
-

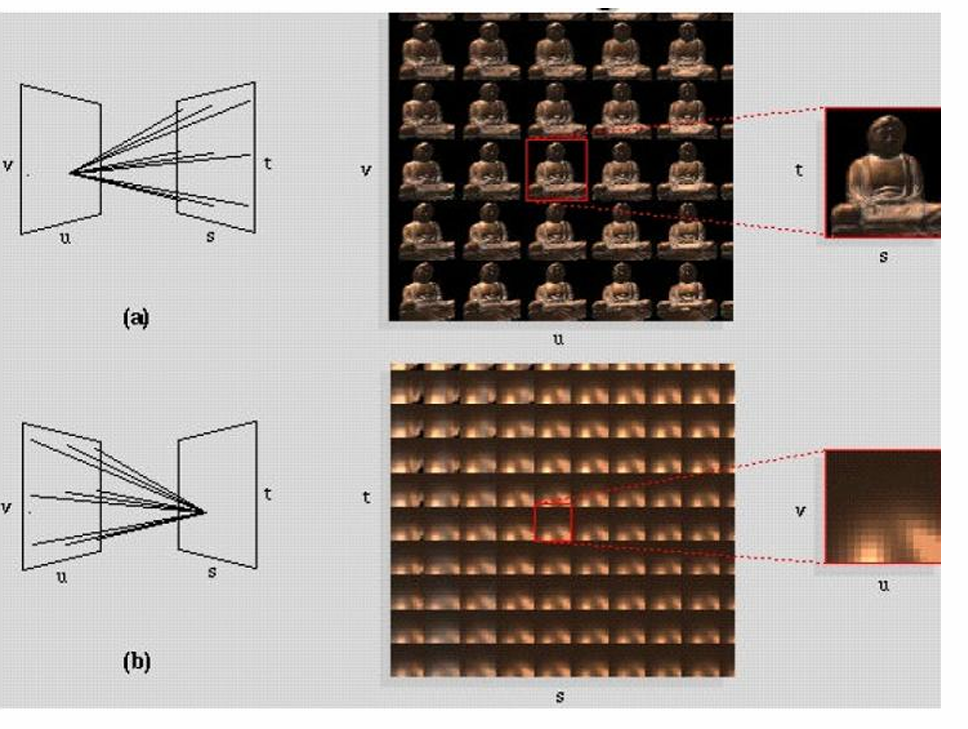
- 两种观察模式(uv为物体盒内st为外侧)
- 一点看向世界
- 不同角度去看向同一点
光场照相机¶
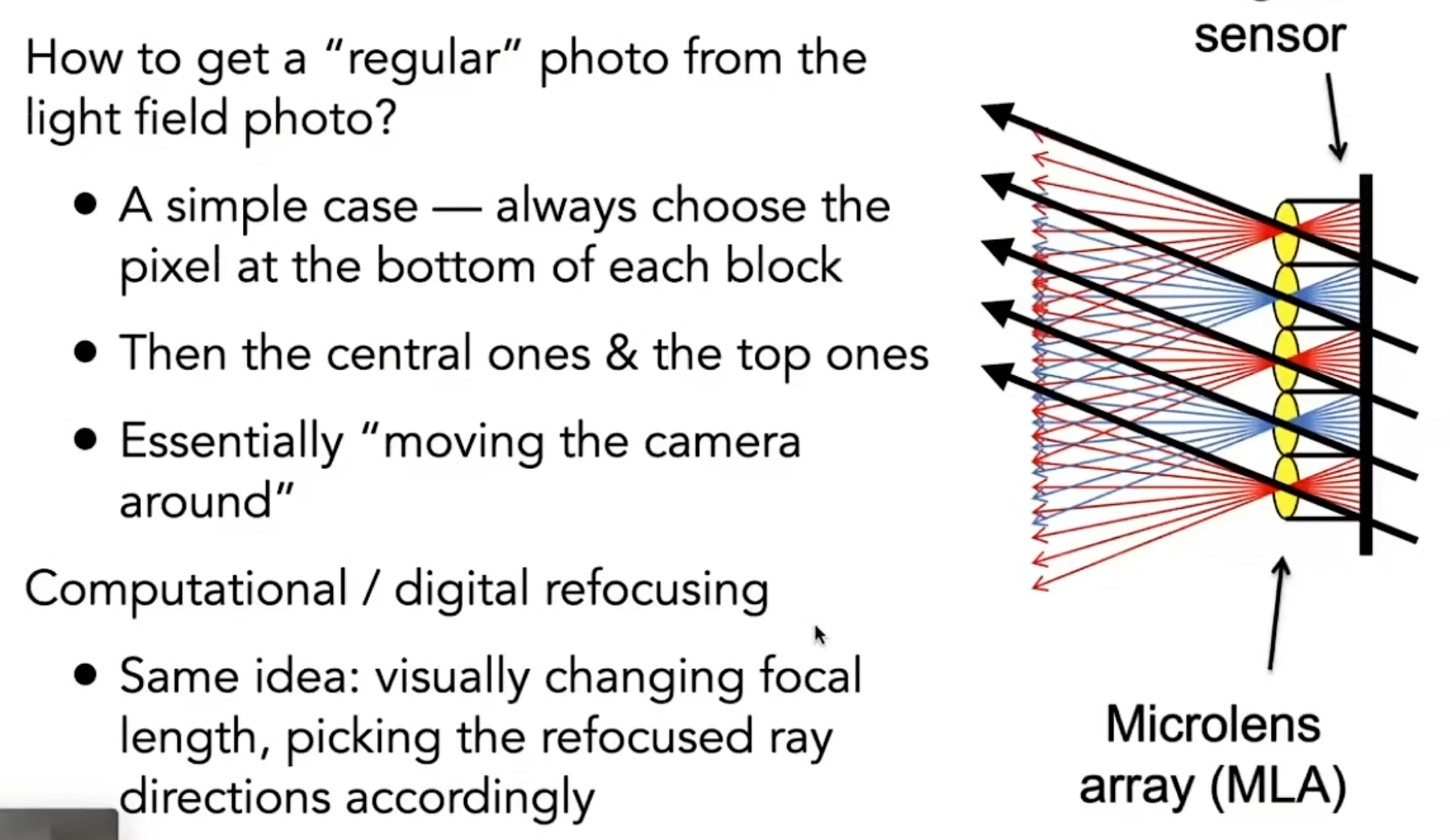
- 将原本的单个像素进一步拆分,将单个像素细分为不同的方向
- 选择来自不同方向的信息,对画面做出调整
色彩¶
- SPD谱功率密度:描述光在不同波长上的分布
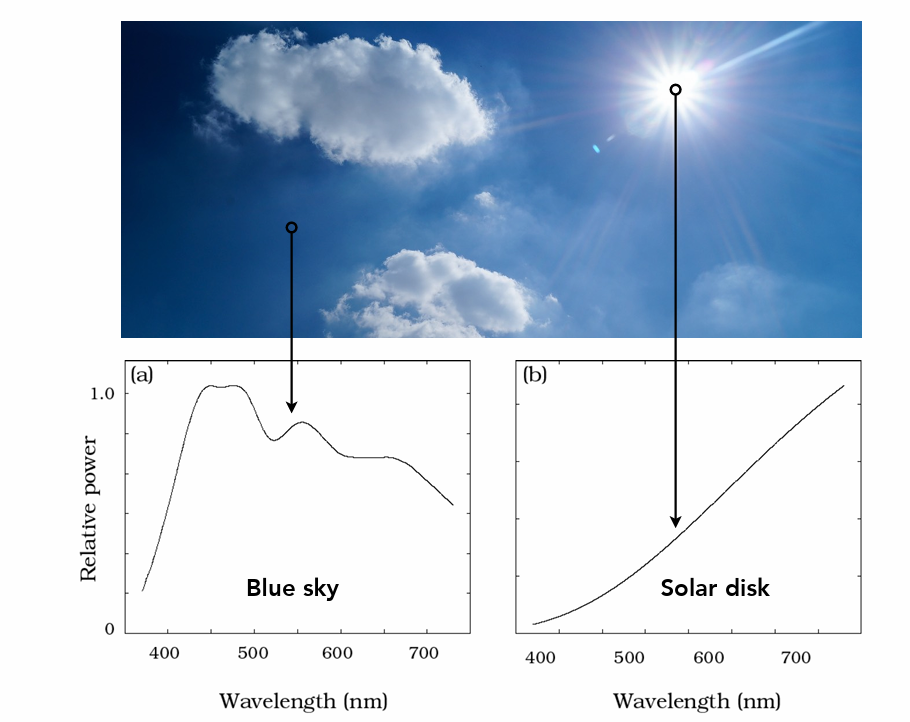
- 人眼
- 三种细胞对颜色的到三个不同的值SML(不同颜色对不同细胞的刺激值)
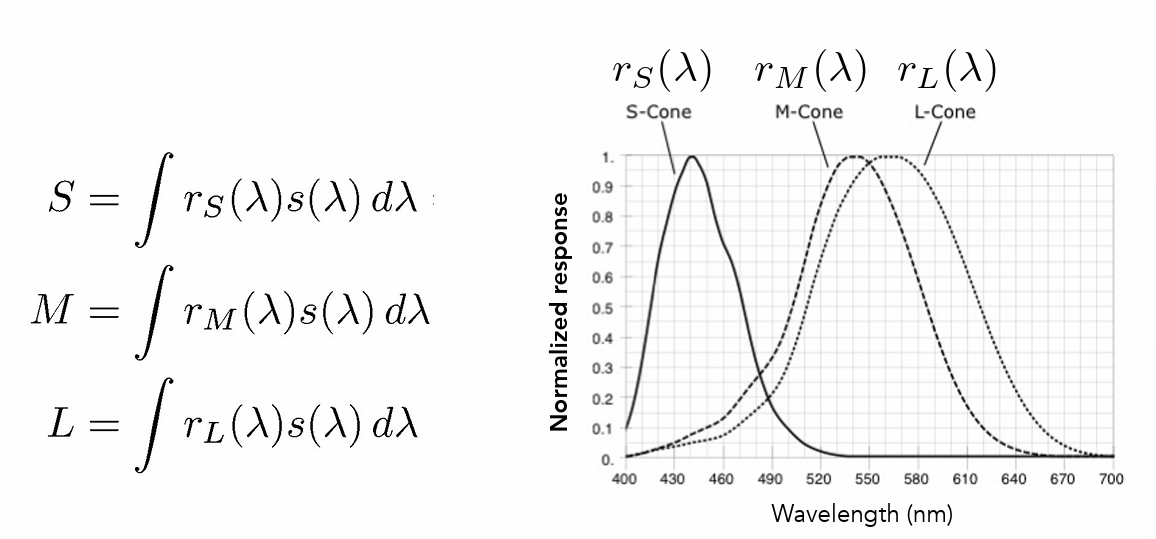

- 同色异谱:不同颜色,但是SML值相同
- 色彩混合
- 加色系统

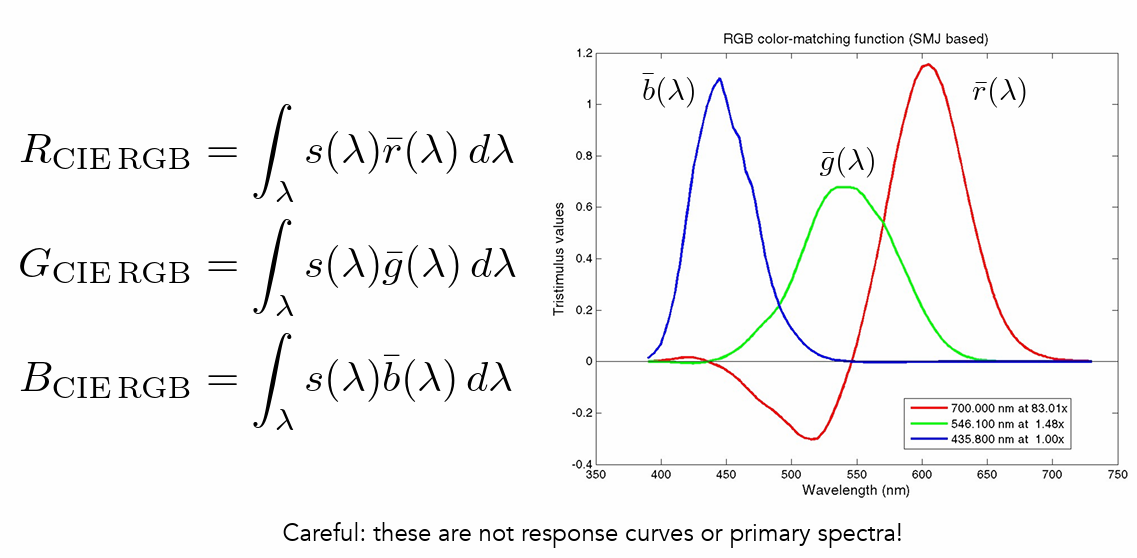
- CIE RGB
颜色空间¶
- sRGB:Standardized RGB
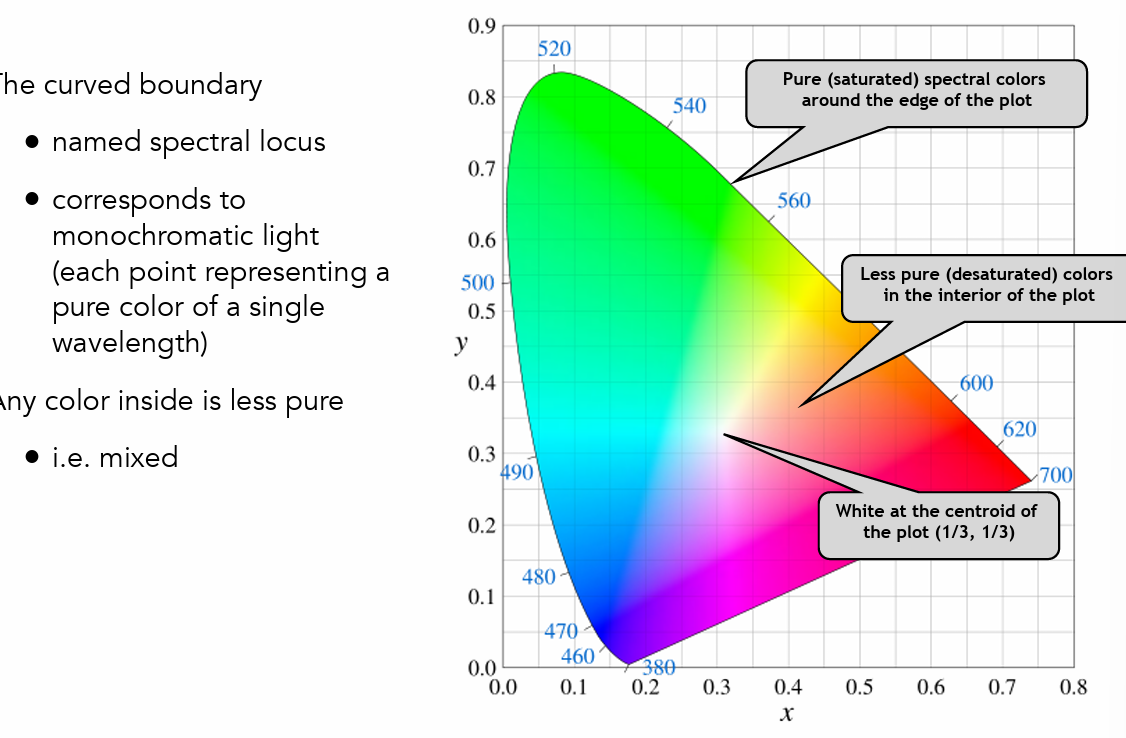
- CIE XYZ
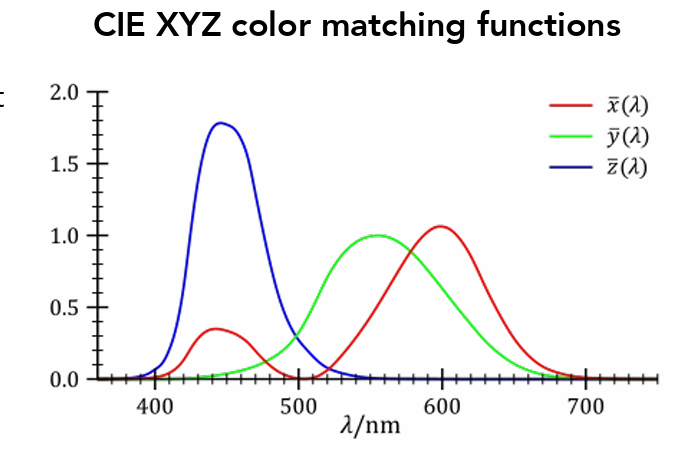
- 人造匹配系统(这些)
- XZ表示颜色,Y表示明度,归一化后可以得到
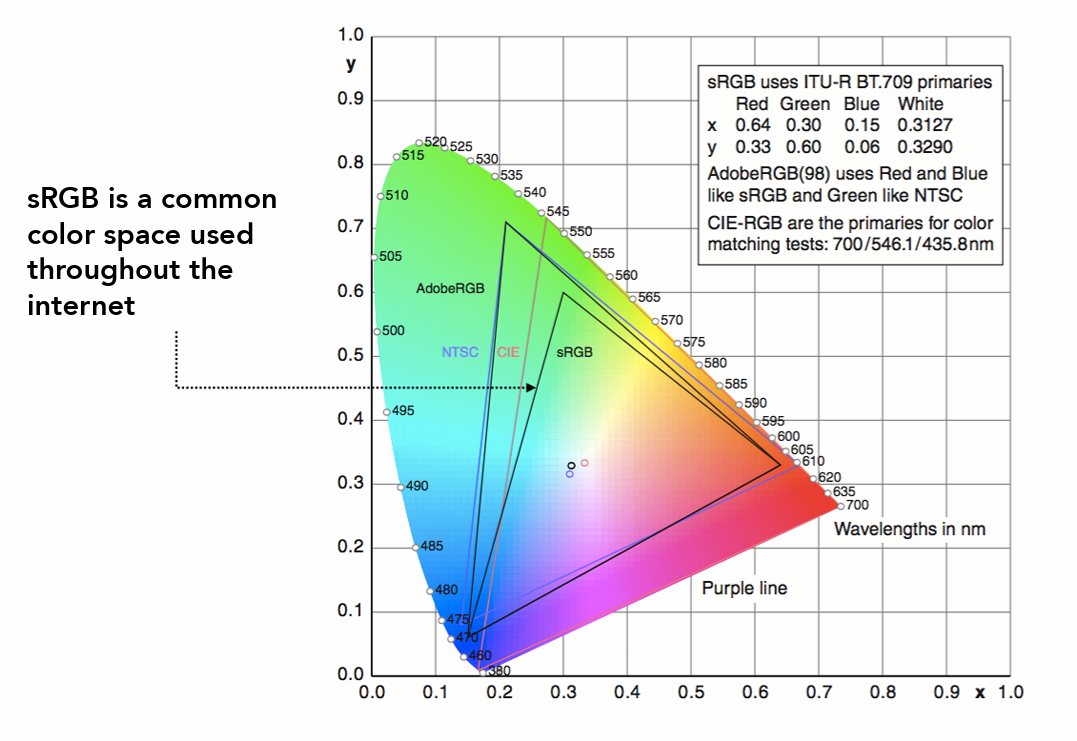
- HSL

- 减色系统(打印)

动画¶
- 关键帧动画
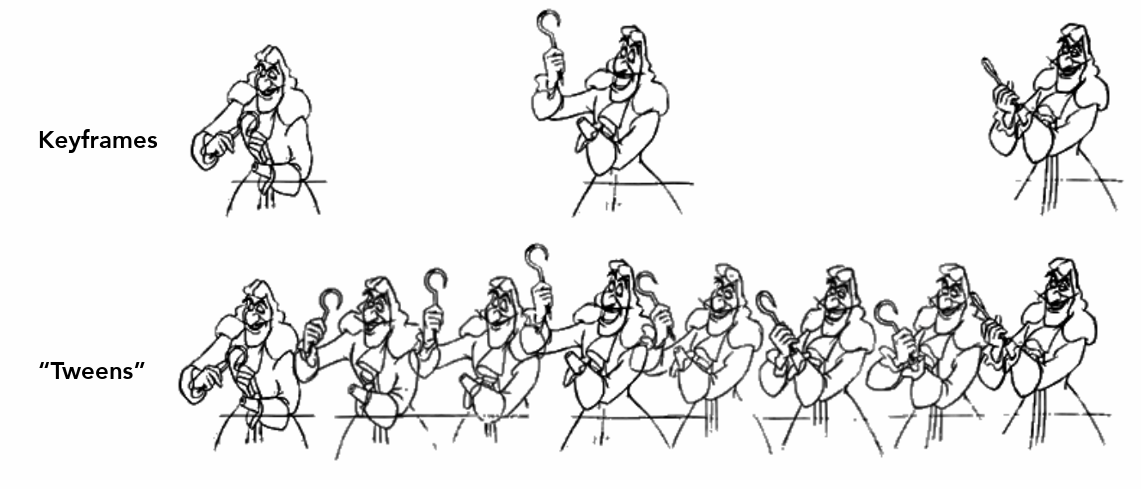
质点弹簧系统¶
- 弹簧连接质点
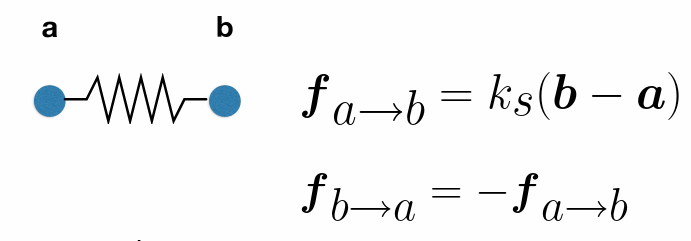
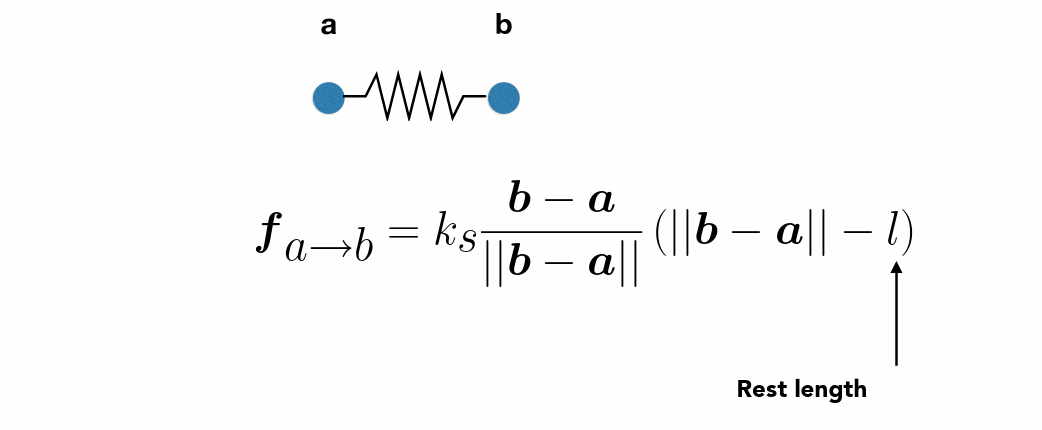
- 单位向量表示方向
- 为了让物体最终停下来,添加反方向摩擦力(弹簧内部的摩擦力)

- 添加抵抗各方向弯折的弹簧
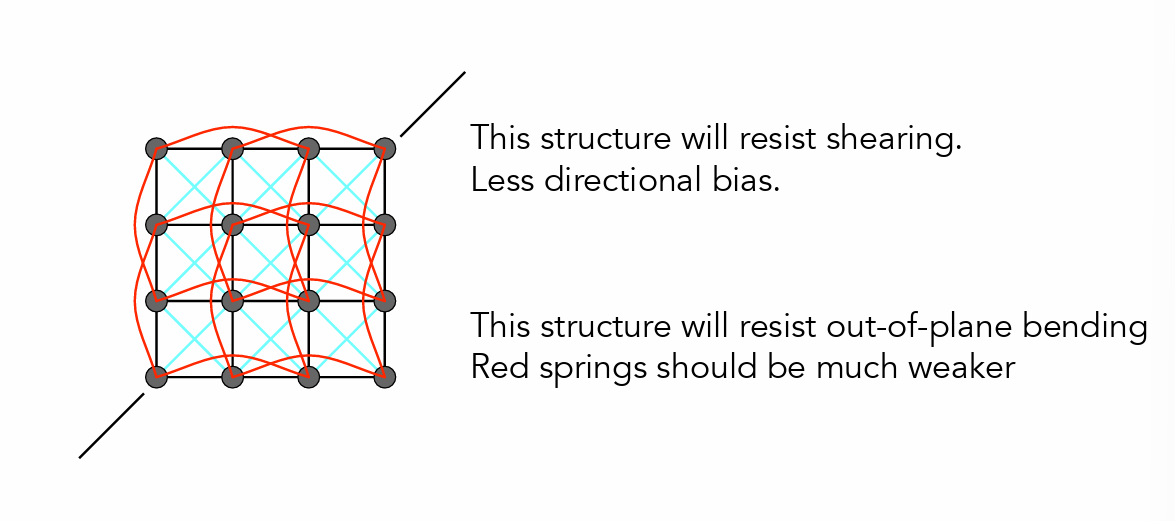
粒子系统¶
-

-
粒子在速度场中的运动(知道粒子在任意位置的速度),结合起点,计算例子的运动方程
-
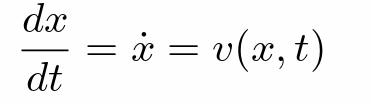
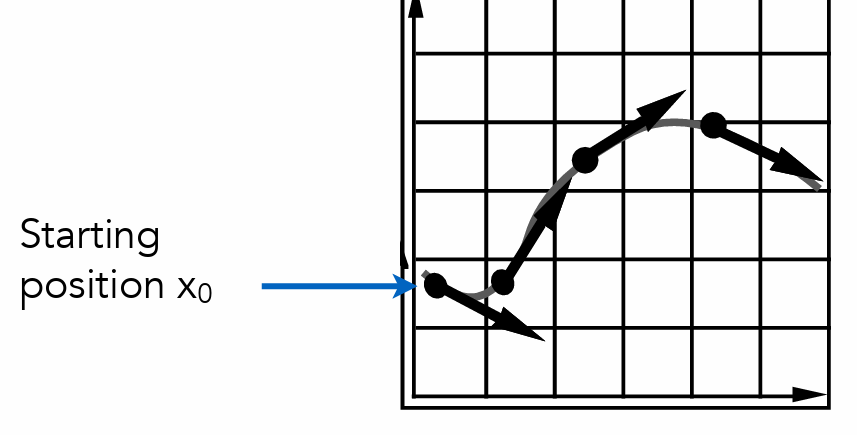
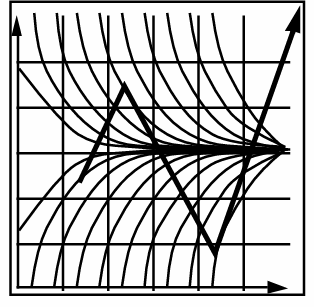
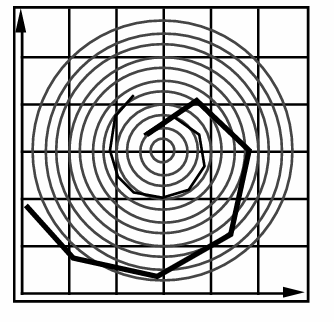
- 欧拉法方法(上一帧估计下一帧)
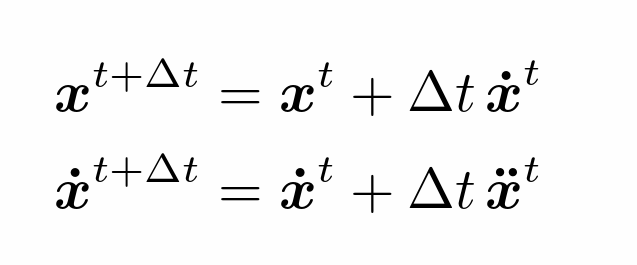
-
要求t很小才能足够精细并且不稳定
-
改进
-
中点法

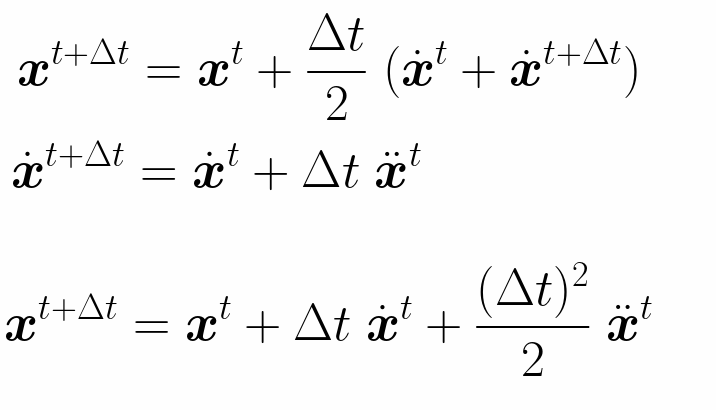
- 先用欧拉方法计算,得到中点,用中点的方向再移动
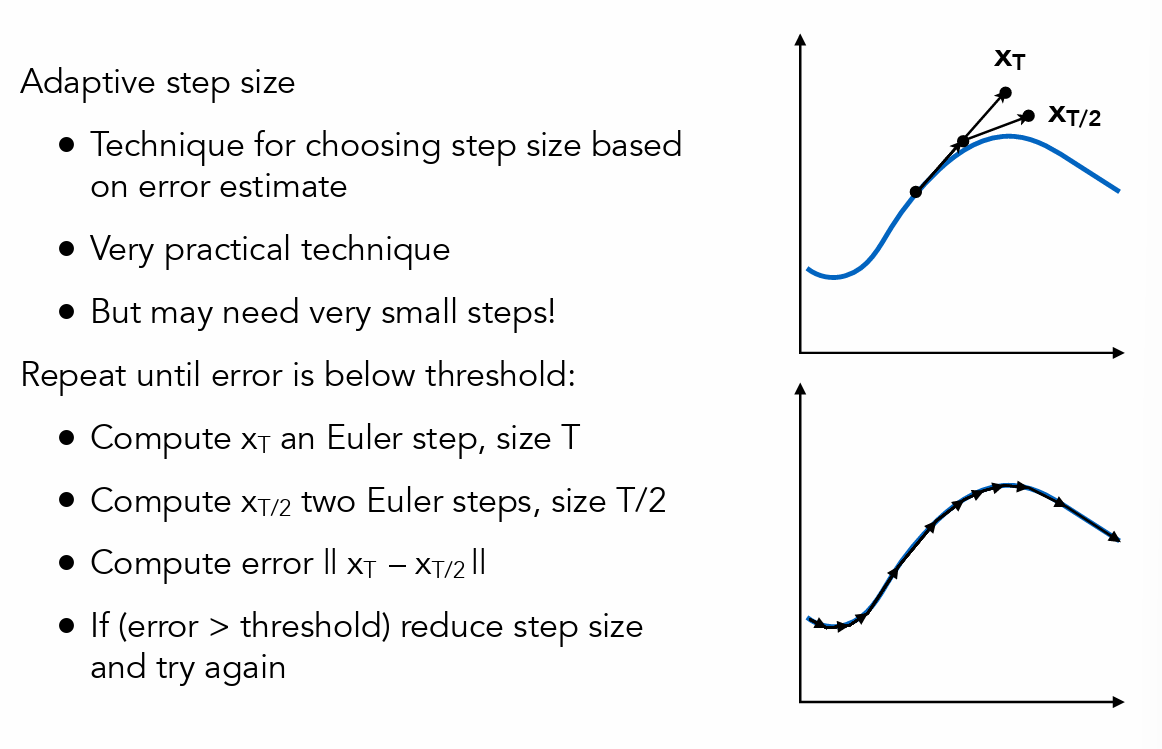
- 自适应法,根据误差判断是否还需要继续划分
-
隐式欧拉方法
-
Runge-Kutta Families
- Position-Based
- 根据位置利用数学、机器学习的方法而不是物理模拟,如利用水的不可压缩性,通过水的密度,对流体运动进行约束和模拟
- 刚体模拟
运动学¶
-
正向运动学:告知如何进行运动
-
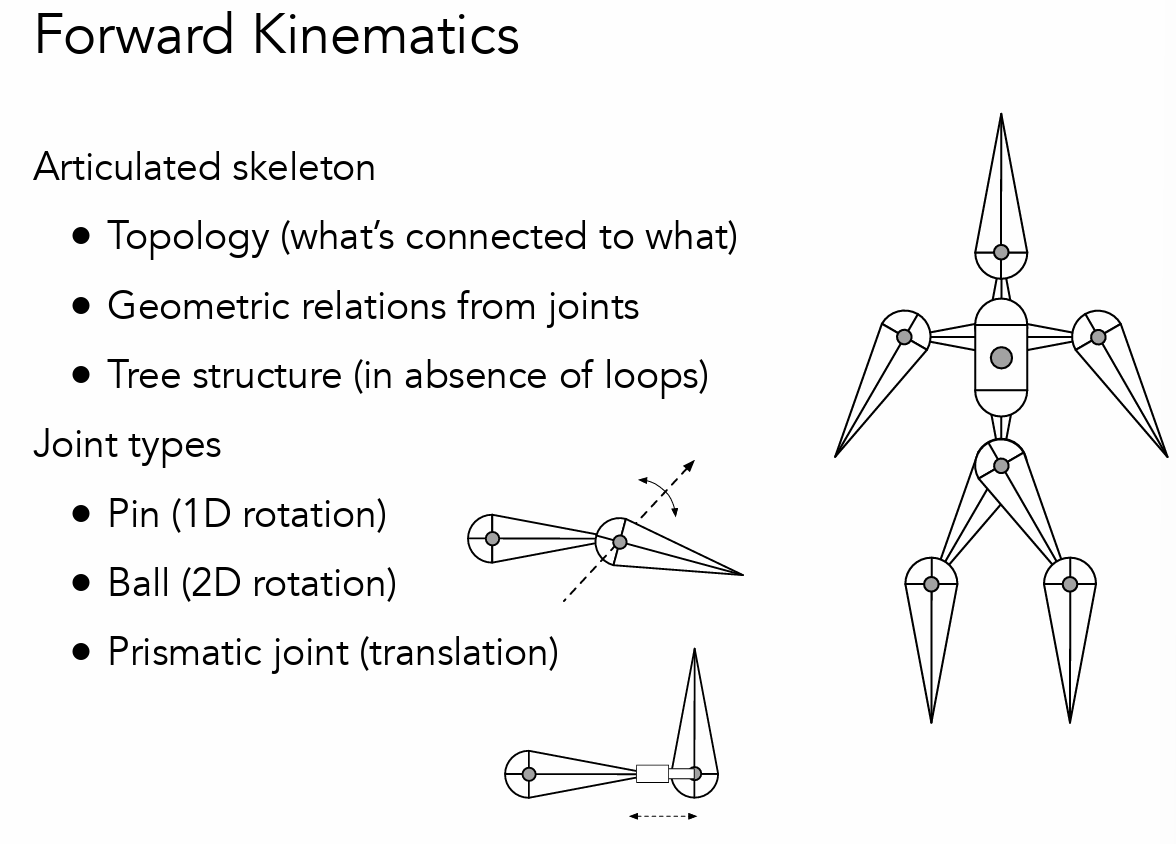
-
逆运动学:告知运动轨迹,自动计算运动方向
-
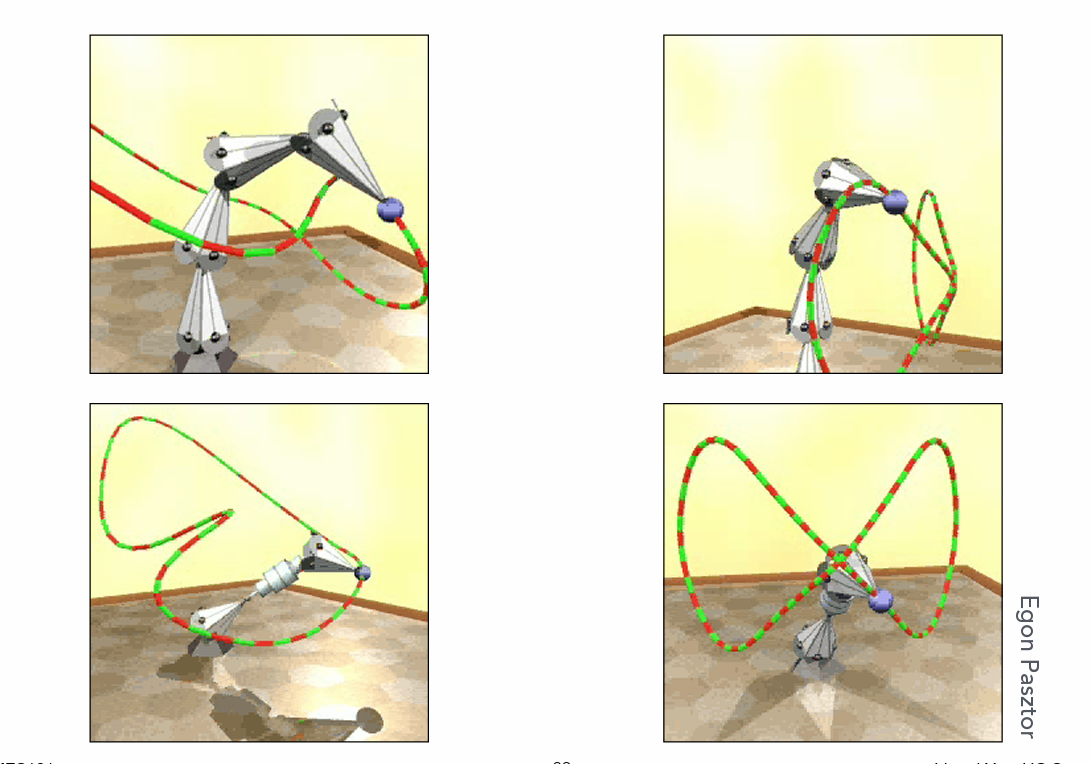
- 手动操控
- 动作捕捉