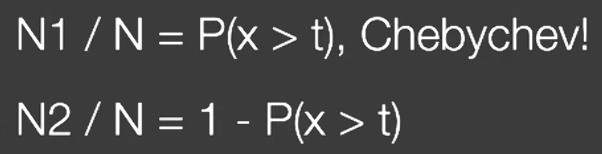Skip to content

Games202高质量实时渲染

数学

  • 两个重要的微积分不等式
    • Schwarz 不等式：\(\left[\int_{a}^{b}f(\:x\:)\:g(\:x\:)\:\mathrm{d}x\:\right]^{2}\leqslant\int_{a}^{b}f^{2}\left(\:x\:\right)\mathrm{d}x\cdot\int_{a}^{b}g^{2}\left(\:x\:\right)\mathrm{d}x\)
    • Minkowski 不等式：\(\left\{\int_{a}^{b}\left[f(x)+g(x)\right]^{2}\mathrm{d}x\right\}^{\frac{1}{2}}\leqslant\left\{\int_{a}^{b}f^{2}(x)\mathrm{d}x\right\}^{\frac{1}{2}}\:+\:\left\{\int_{a}^{b}g^{2}(x)\mathrm{d}x\right\}^{\frac{1}{2}}\)
    • \(\int_\Omega f(x)g(x)\:\mathrm{d}x\approx\frac{\int_\Omega f(x)\:\mathrm{d}x}{\int_\Omega\:\mathrm{d}x}\cdot\int_\Omega g(x)\:\mathrm{d}x\) 约等条件：\(\Omega\) 积分范围很小或 g 函数足够光滑，积分域内变化较小
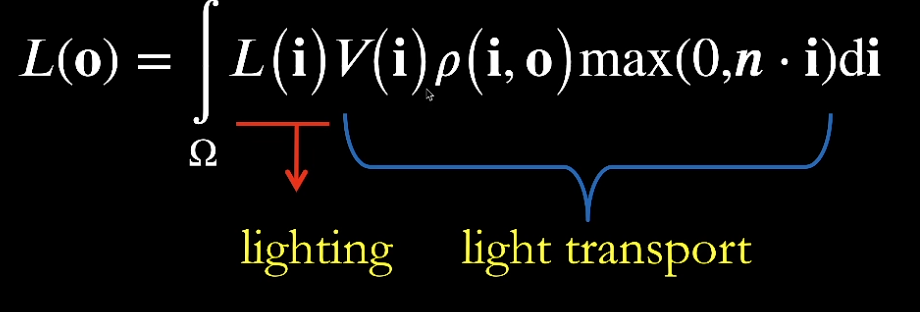
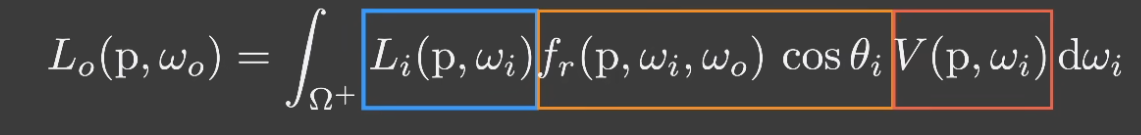
  • 应用：渲染方程 image.png|450
    • 蓝色为入射光相关；黄色为反射性质；红色为集合修正因子
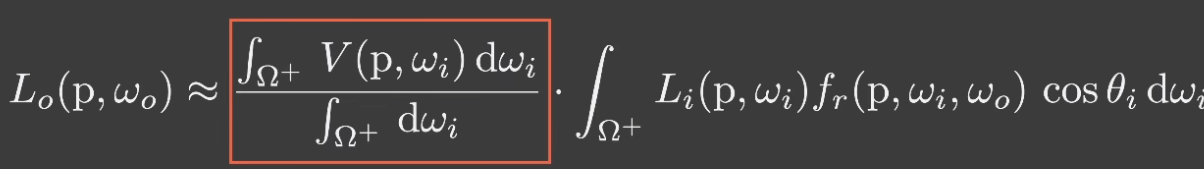
    • 可以近似为 image.png|550
  • 其条件就是：积分域小（入射光范围小，如一个点光源）或积分内的函数比较光滑（如比较漫反射的 BRDF）

实时阴影

percentage closer soft shadows（PCSS）

percentage closer filtering（PCF）

  • 硬阴影相当于只有 01 两种状态，通过 pcf 可以生成含中间状态的软阴影
    • 是在阴影生成阴影过程中使用，而不只是后处理
  • 从 shadowmap 取样时取一个较大范围的值，并取平均值作为阴影的强度
    • 采样范围就决定了阴影的硬度
  • image.png|600

软阴影的渲染

  • 通常阴影的硬度并不是恒定的，与遮挡物与投射平面的距离相关，距离越近阴影的硬度越大

    • 具体的规则 \(w_{Penumbra}=(d_{Receiver}-d_{Blocker})\cdot w_{Light}/d_{Blocker}\)
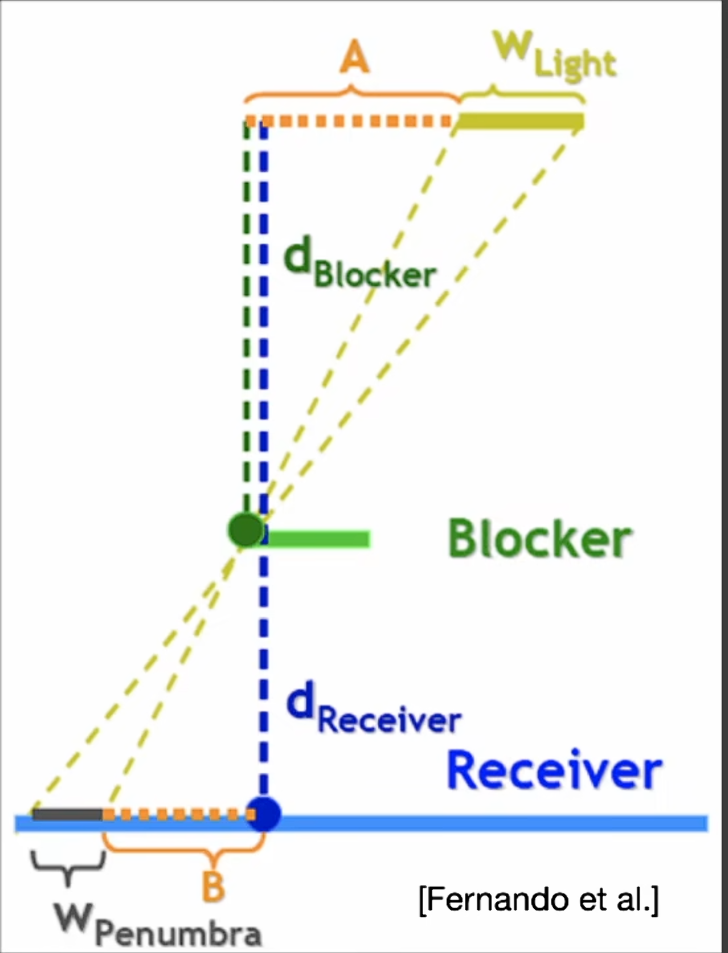
    • image.png|350
    • 通过估计不同位置的 penumbra 大小来决定 pc 采样防范未的大小，即阴影的硬度
      • image.png|550

  • 更简单的估计：只根据灯光范围大小，scene 和灯光的距离来估计

    • image.png|600

Variance Soft Shadow Mapping (VSSM)

  • 解决 PCSS 第一步和第三步范围操作速度慢的问题
  • 优化 step 3：shadowmap 在一定范围内小于一个距离的点的数目
    • 假设正态分布，只需要平均值和方差来确定分布就能估计数目
    • 平均可以使用 mipmap 存储（mipmap 存储误差较大）使用前缀和存储更加请准
    • 方差使用均值计算 \(\mathrm{Var}(X)=\mathrm{E}(X^2)-\mathrm{E}^2(X)\)
    • 再使用切比雪夫不等式进行估计 \(P(x>t)\leq\frac{\sigma^2}{\sigma^2+(t-\mu)^2}\) 当做"等式"
  • 优化 step 1：blocker depth 阴影硬度的求解
    • 注意求的是遮挡物（比目标点距离近的点）的距离平均值（如图中蓝色部分平均值），而不是 mipmap 一定范围内所有点的平均值
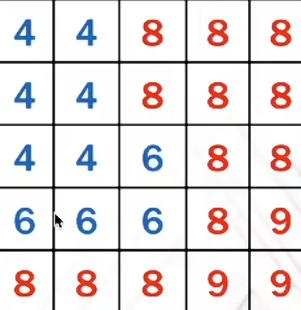
    • image.png|151
    • 比如目标点为 7，那么只对红色部分求平均值
    • \(\frac{N_{1}}{N}Z_{unocc}+\frac{N_{2}}{N}Z_{occ}=Z_{Avg}\) 遮挡物的百分比乘以遮挡物平均深度+非遮挡物部分分就是总共的平均深度
    • 设采样点深度为 \(t\) 则可以假定 \(Z_{unocc} = t\)
    • 同样可以用切比雪夫不等式求解
      • image.png|300

SDF 软阴影

  • 使用 SDF 距离场估计软阴影
    • 速度快
    • 质量高
  • 从投影面上一点看向面光源
    • image.png|238
    • 一个角度上一点的 SDF 越小表示不收遮挡的安全角越小，阴影就越硬
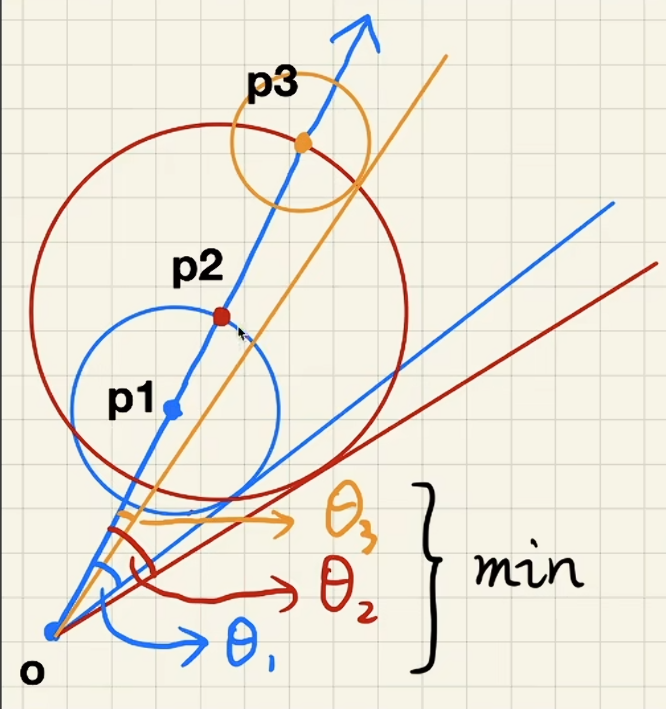
    • image.png|450
    • 取角度方向上距离场最小值作为安全距离
    • 计算近似角度 \(\min\left\{\frac{k\cdot\mathrm{SDF}(p)}{p-o},1.0\right\}\) 通过使用 \(k\) 而不是反三角函数精确计算来减少计算的开销
      • image.png|246
      • k 决定了阴影的硬度

环境光照

splitsum 方法预处理的 IBL

  • IBL 基于图片的光照
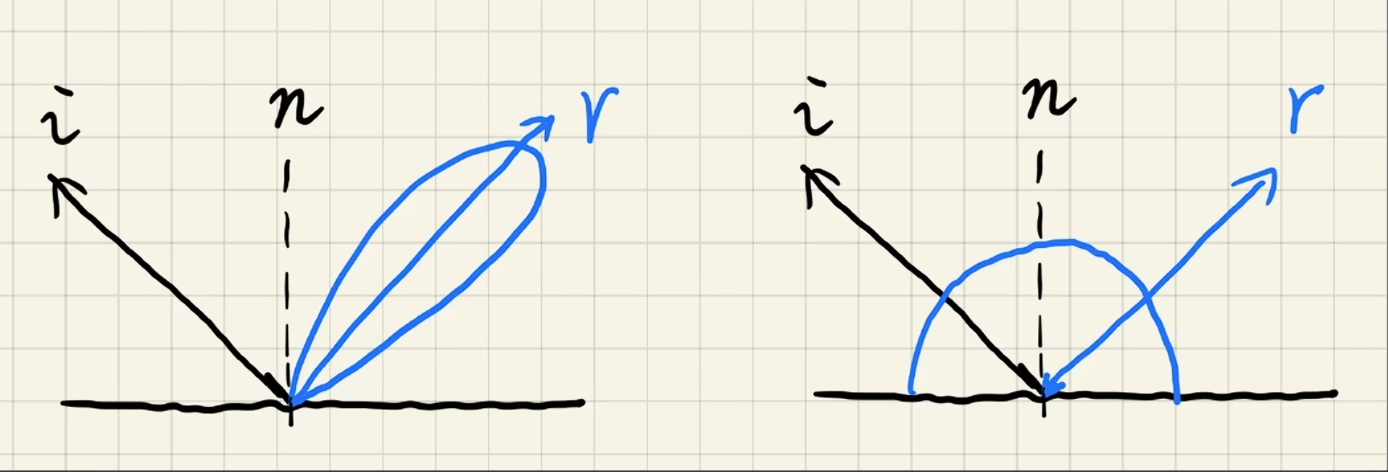
  • image.png|500
    • 通常 BRDF 有以下性质中的一个：镜面反射（范围小）；漫反射（变化小, 更光滑）
    • 这就可以使用近似 \(\int_\Omega f(x)g(x)\mathrm{~d}x\approx\frac{\int_{\Omega_G}f(x)\mathrm{~d}x}{\int_{\Omega_G}\mathrm{~d}x}\cdot\int_\Omega g(x)\mathrm{~d}x\)（为了避免通过采样计算，这很慢）
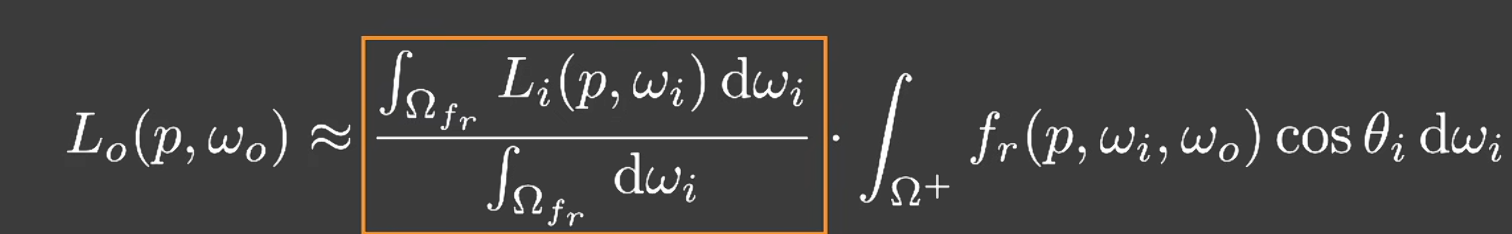
    • image.png|600
    • image.png|600
    • 因此可以对环境光贴图进行预 prefiltering（如生成一系列 mipmap）针对不同 BRDF 预生成
    • image.png|550
    • 前半部分的计算就是相当于对一定区域的环境光贴图做 filtering
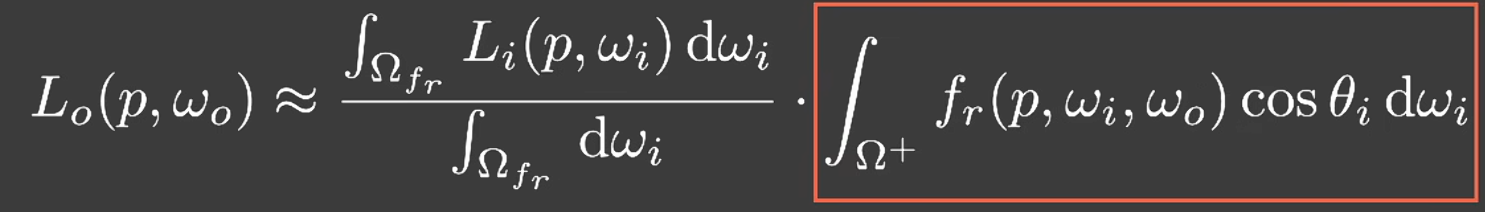
  • image.png|600
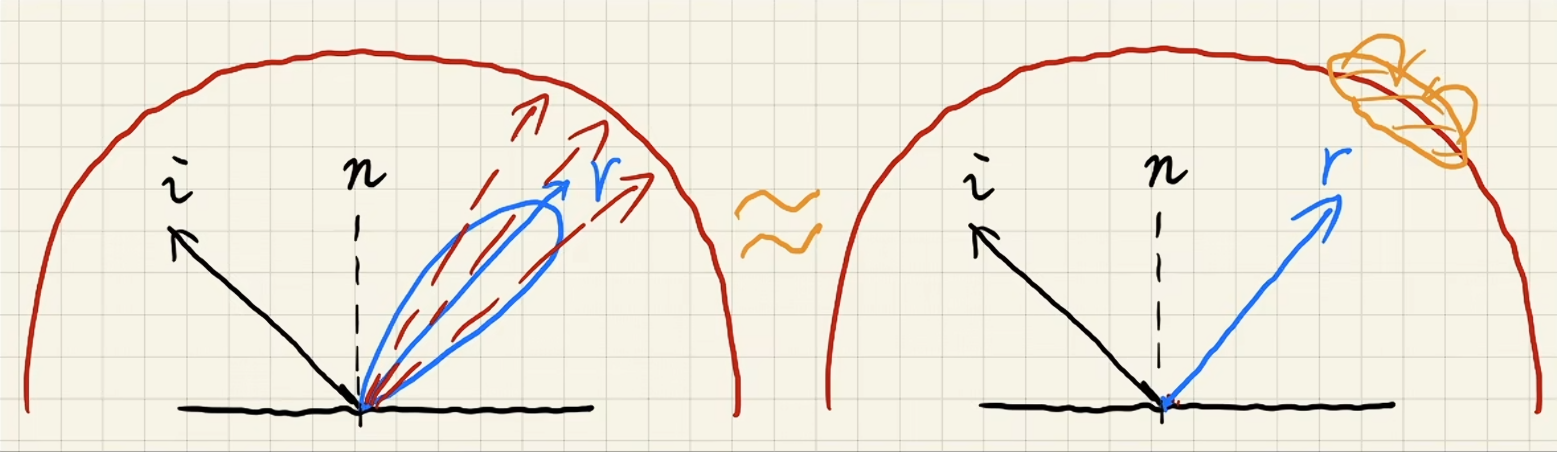
    • 计算后半部分
    • image.png|450
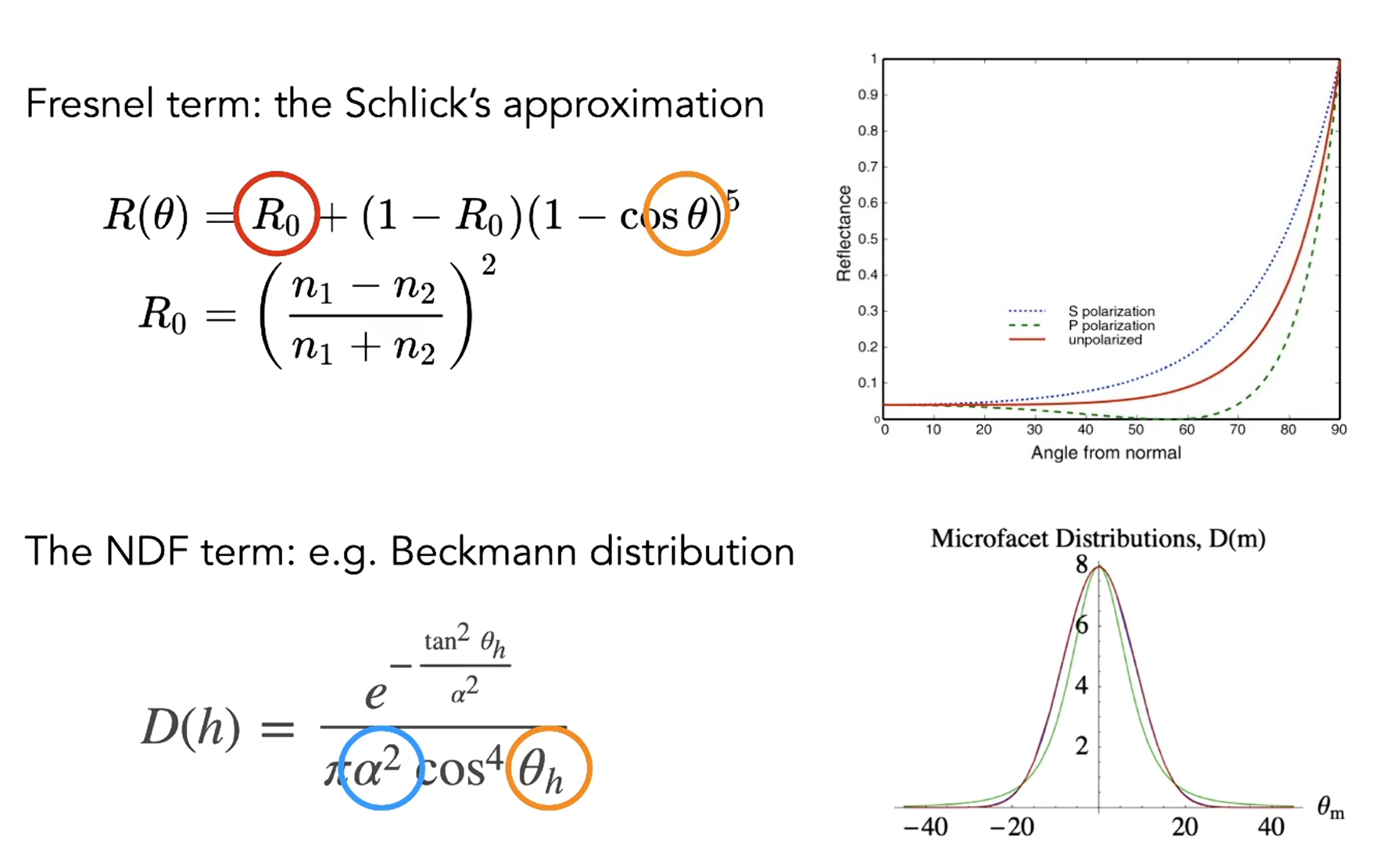
    • 两个近似描述 image.png|600
    • 由此利用菲涅尔项的近似
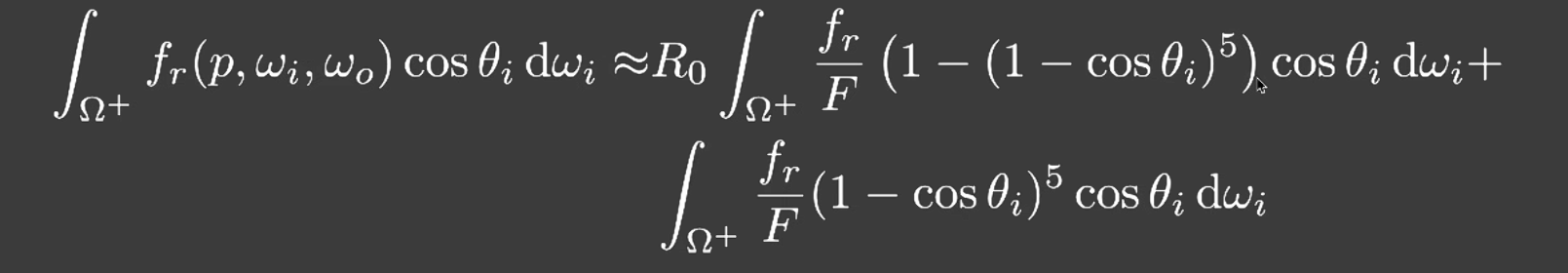
    • image.png|600
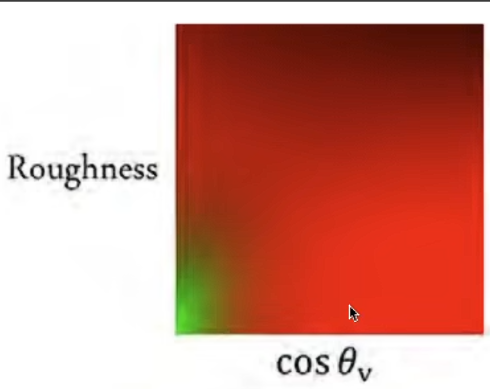
    • 可以近似认为只和 roughness 和 \(\theta\) 有关，可以用一个纹理存储二维预计算结果 image.png|290
    • 这里的角度是出射方向，入射方向是在积分预计算时对所有方向进行了计算

环境光照的阴影

  • 只从最亮的（几）个光源生成阴影（来减少计算量）

实时环境光照

  • 使用渲染方程，真正的计算阴影和光照

球面谐波函数

  • 球函数就是一系列二维基函数
    • 球面谐波函数十一组定义在球面上的拯救函数，作用类似于在一维场合中用傅里叶级数分解函数
    • 通过球面谐波函数，可以高效逼近环境光，并简化积分运算
    • image.png|500

  • 可以通过积分求出任何函数 \(f\) 在基函数 \(B_{i}\) 上的投影（即 \(B_i\) 的系数）\(c_i=\int_\Omega f (\omega) B_i (\omega)\:\mathrm{d}\omega\)

  • 漫反射的 BRDF 表现就像一个低通滤波

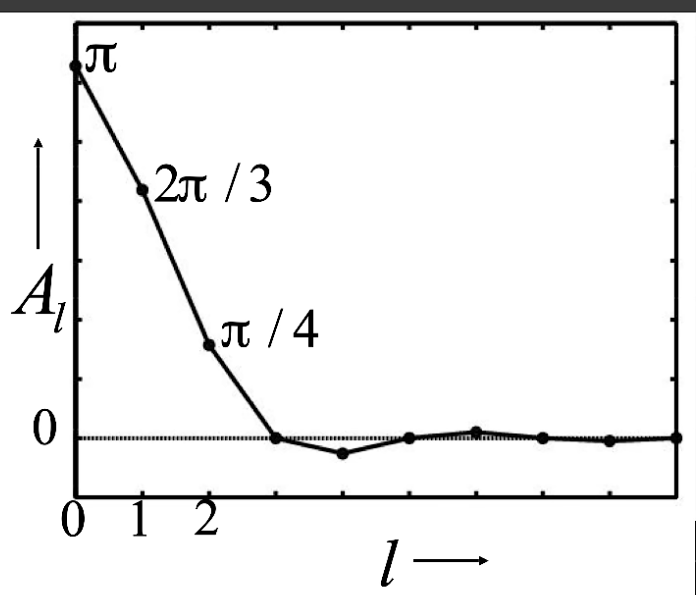
    • image.png|200
    • 只有前三阶的系数较大，后面系数都趋近 0，也就是只需要使用少量的球面谐波函数就可以描述 \(E_{Im}=A_1L_{Im}\) 就有很好的效果

  • 优点：

    • 低频高效逼近：许多自然现象（例如环境光照或漫反射光）通常属于低频函数。只要使用较低阶数的球面函数就能有效地捕捉其主要特征，从而大幅降低计算和储存的负担。
    • 旋转不变性与变换简便：球面函数在坐标变换（如旋转）时有着良好的数学特性，这使得在渲染和辐射传输计算中，对物体或光源的旋转操作可以通过变换球面函数系数高效地实现，而无需重新计算整个函数分解。

  • 通常用其表示的

    • 环境光照分布：描述来自各个方向的光强，常在预计算辐射传输（PRT）中进行投影表示，从而实现快速实时光照计算。
    • 散射和反射特性：将物体表面的散射函数投影到球面函数基底上，便于分析和模拟光与表面交互时的角度依赖表现。
    • 其他在球面上定义的物理量：任何涉及全方位角度分布的信号（如某些大气现象的模拟）都可以利用球面函数进行有效表示。

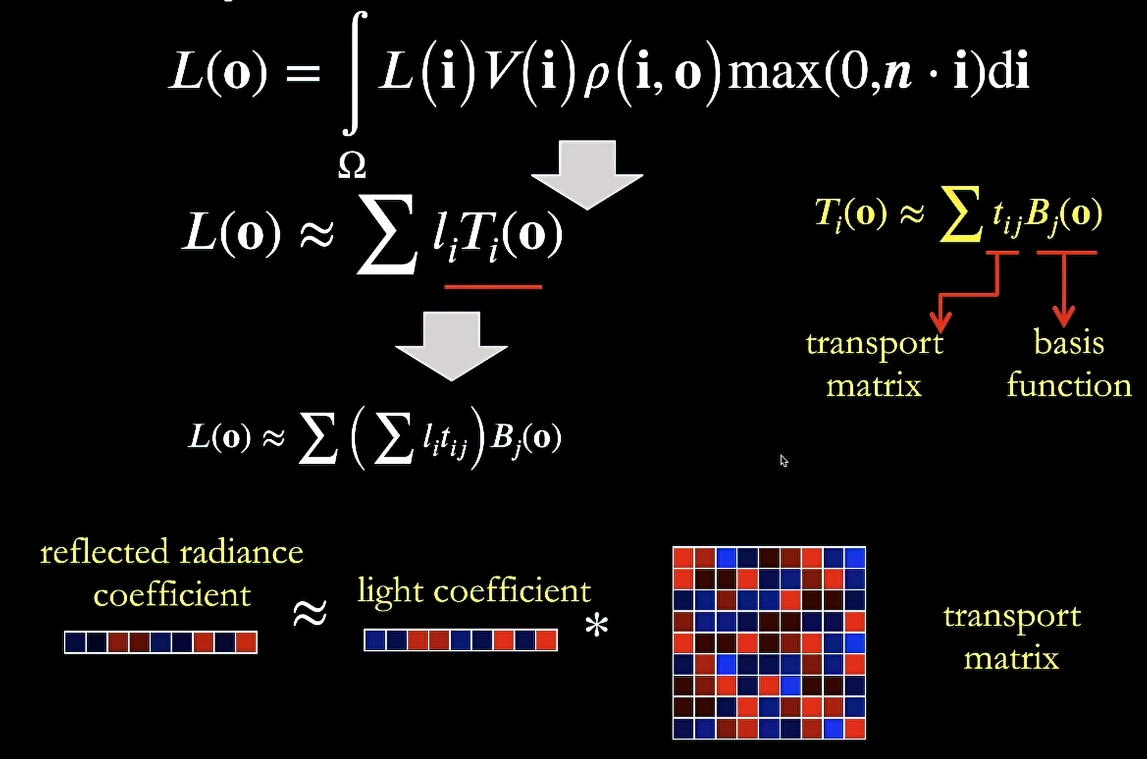
  • 用球面函数表示时，就是用一个一维向量（指示每个基向量的系数）来进行表示，还原出原始函数 \(L(\mathbf{i})\approx\sum l_iB_i(\mathbf{i})\)

  • 球面函数具有正交性 \(B_{p}(w_{i})B_q{(w_{i})}\neq 0 \iff p=q\)

Precomputed Radiance Transfe（PRT）预计算辐射传输

  • 环境光照通常可以近似为低频信号，通过将入射光照投影到一组球面谐波基底上，只需要少量系数就能高效表达出主要的光照信息。

  • 除了投影环境光照外，PRT 还会预先计算物体各点与入射光照交互产生的传递函数，将这种复杂的光传输过程同样表示为球面基底上的系数。在实际的渲染过程中，无论是光源还是物体旋转，只需对这些系数进行快速变换，从而实现实时计算。

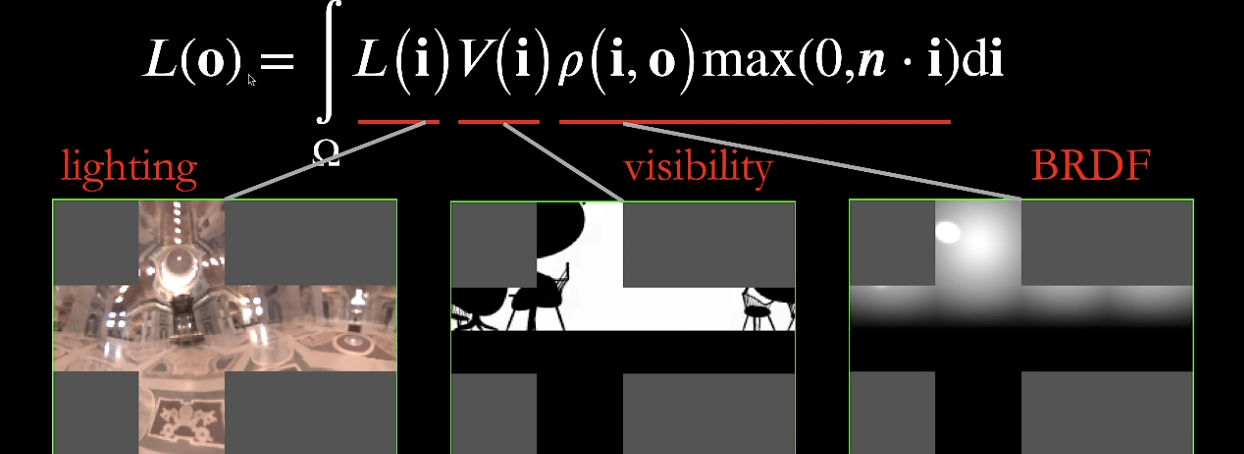
  • 渲染方程：image.png|600

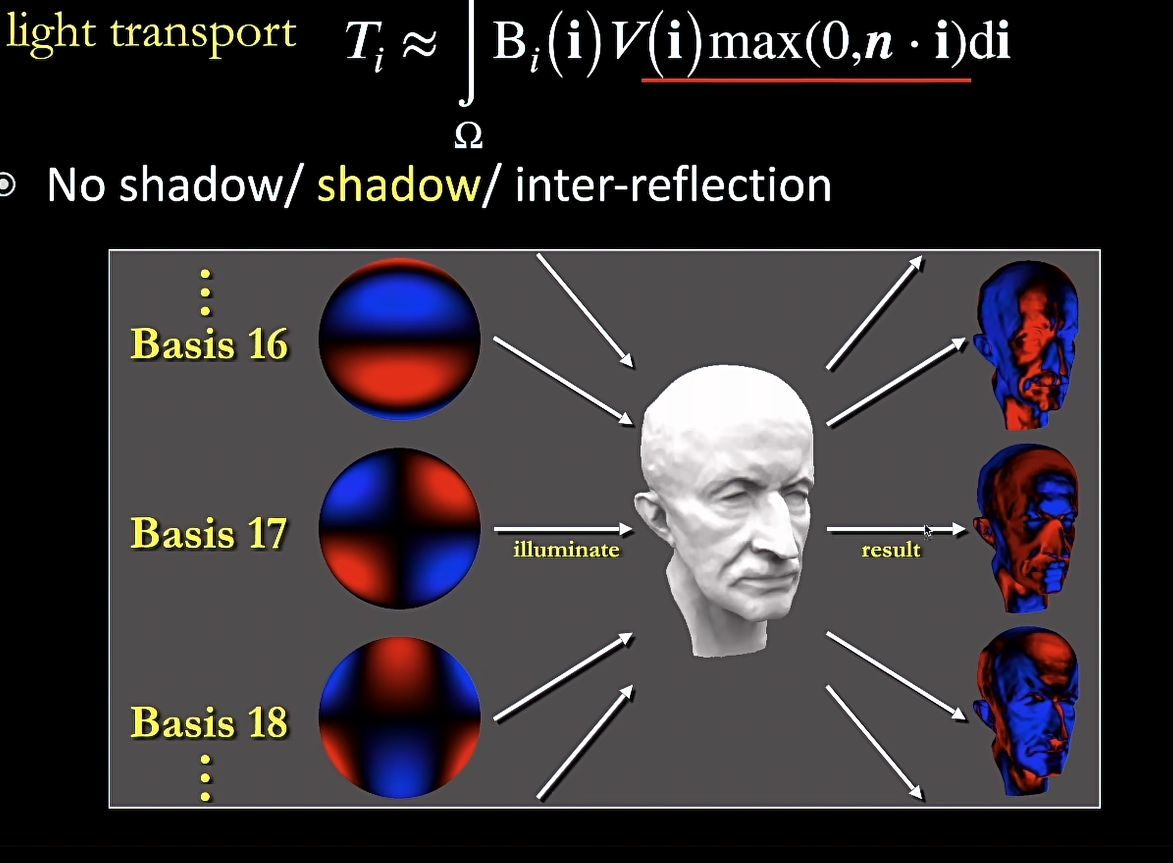
    • 三项均可以用球面函数来描述

  • 进行拆分：认为只有光照在渲染过程中变化，因此 transport 部分可以预计算（球面函数）用基函数表示

    • image.png|450
漫反射

  • 对于漫反射 BRDF 可以看做常数，并用基函数表示环境光照入射光

    • image.png|500
    • 仅剩的积分部分可以通过预计算得到
    • 实时渲染过程中只需要计算最后的点乘，速度很快
    • 问题：场景不能动，因为 \(V(i)\) visibality 固定；

  • 用球面函数表示环境光照本质上就是对光源进行了分解，变成系列标准形态的光照的组合

    • image.png|400
非漫反射 Glossy
  • image.png|500
  • 光线的分类
    • LE：直接入射到观察点的光线
    • LGE：经过一次Glossy 反射后入射到观察点的光线
    • L(D|G)*E：经过多次 Glossy 或 Deffuse 反射到观察点的光线
    • LS*(D|G)*E：先打到 specular（镜面反射物体）上 image.png|500

全局光照

所说的“全局光照”实际上就是想实现一次间接光照

3 D 空间

Reflective Shadow Maps (RSM) 反射阴影贴图

  • 采集更多信息：与传统阴影贴图只记录场景中各点到光源的深度信息不同，RSM在从光源视角渲染时，还同时捕获了表面反射相关的信息，如光通量、表面法线以及位置等。这些额外的信息能反映出当直接光照射到物体表面时的反射特性。（有多少个光源就要有多少个贴图）

  • 间接照明的快速估计：利用从光源采集到的这些数据，RSM能够近似计算场景中的间接照明。通过对捕获的反射光进行散射和积分，可以在渲染过程中快速估计光在场景中多次反射后的能量传递，从而产生更自然的全局光照效果。

  • 需要解决的问题

    • 哪些部分会被直接光照照射，成为次级光源：通过 shadowmap
      • 假设所有次级光源都是 diffuse 的
    • 如何计算所有次级光源的贡献并汇总
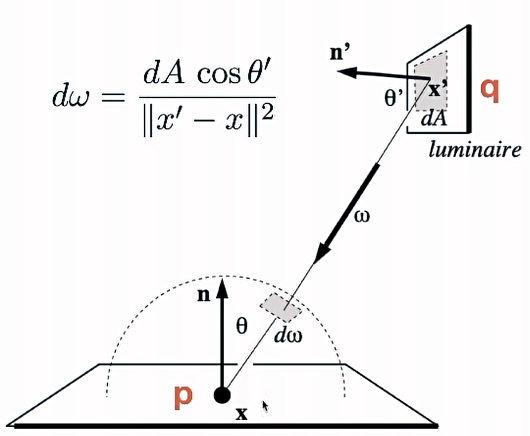
      • image.png|230
      • 图中 \(q\) 点为次级光源，将光照反射到 \(p\)

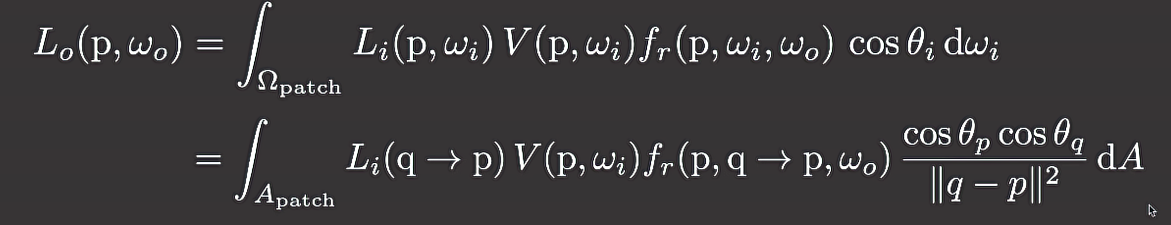
  • image.png|500

    • 将对立体角的积分转化为对光源 area 的积分

  • 对于 diffuse 的反射 \(f_{r}=\frac{\rho}{\pi}\) (对应图中的 \(q\) 点)

    • q 点出射光线的强度 \(L_{i}=f_{r}\cdot\frac{\Phi}{dA}\) (因为是漫反射，所以不同方向均匀亮度)
    • \(V\) 难以计算，因此就不算了

  • 一般来说只需要考虑距离比较近的次级光源（因为平方衰减）

    • 可以在 shadowmap 上找较近的点
  • 预存储的内容：深度、世界坐标、法线、flux
    • image.png|450
  • 应用：手电筒光的二次反射效果

Light Propagation Volumes（LPV）光体积传播

  • 关键思想
    • 将场景用 3 D 网格划分：通过将连续的3D空间离散化成网格体素，每个体素内都可以存储一定的光照能量信息，这样便于对光照在整个场景中的传播进行分区处理，而无需在每个光线与表面相交时都做复杂的连续模拟。
  • 过程
    • 确定哪些点接收到了直接光照可以作为次级光源 (可以使用 RSM 来做)
    • 将虚拟光源信息注入到体素（网格格子）
      • image.png|123
      • 可以使用球面谐波函数表示一个格子内 radiance 的方向和强度分布（用前两阶即可表示大概分布）
    • 传播 radiance
      • 会通过格子向四面八方传播（扩散到周围的 6 个网格）
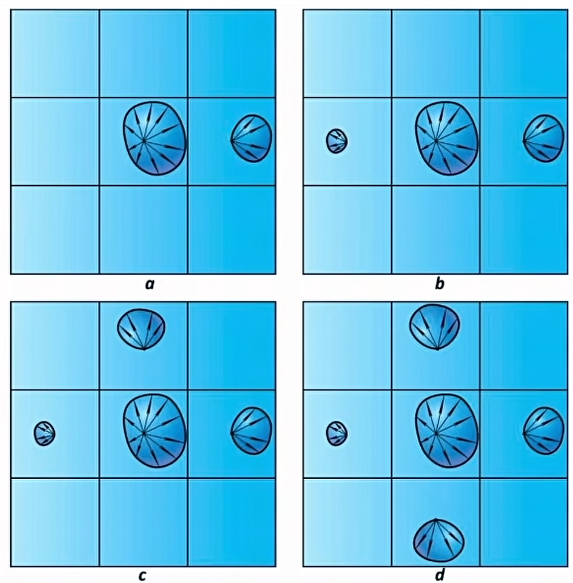
      • image.png|423
      • 多次迭代后获得稳定的结果
    • 渲染：
      • 拿到每个格子的强度，即可进行渲染
  • 问题
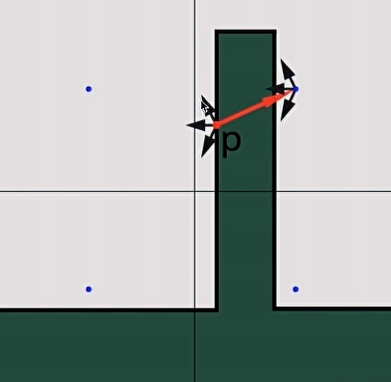
    • image.png|241
      • 格子分辨率不够时可能产生错误的光照效果，比如左侧的漫反射错误的作用于了右侧（因为在同一个方格中）
      • image.png|400

Voxel Global ILLumination(VXGI)

  • 两趟的算法
    • 将场景离散化为格子, 格子作为次级光源，使用八叉树等层次结构来存储池不同精度的体素数据，体素中存储用于之后计算光线散射方向得的发现数据等
    • 利用体素进行光线追踪：从摄像机发射光线，找到第一个交点，再从交点发射锥形光线到场景中（通过体素）来采样间接光照
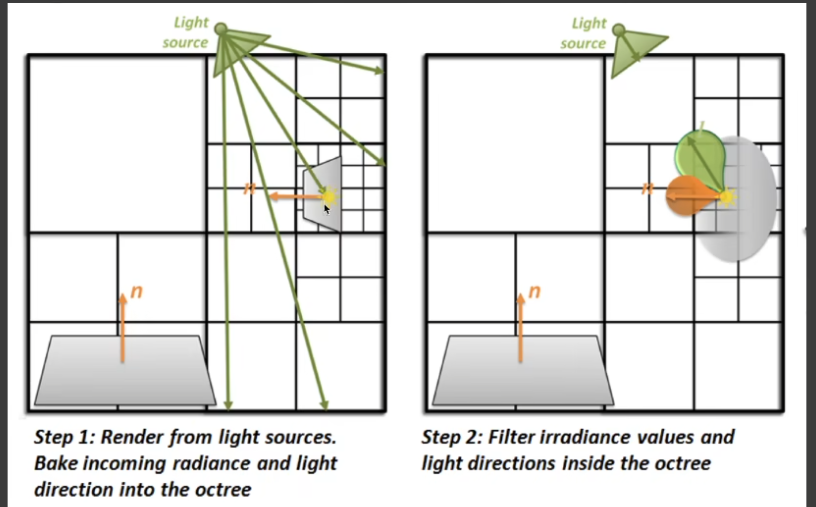
  • image.png|550
  • 问题：体素化工作量的，速度慢

屏幕空间上的处理方法

  • 利用直接光照结果信息进行后处理，添加全局光照的效果

屏幕空间环境光遮蔽Screen Space Ambient Occlusion(SSAO)

  • 环境光遮蔽：在物体接触位置添加阴影（左），以增添立体感
    • image.png|500
    • 是全局光照的一种近似

  • idea

    • 不知道间接光照的具体值，难就假设为一个常数
    • 考虑不同方向上的光线 visibility 不同image.png|400
    • 假设均为漫反射材质

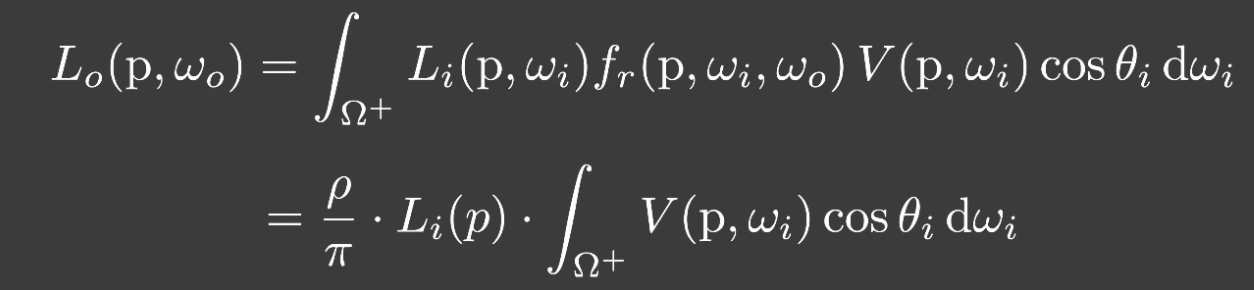
  • image.png|500

    • L 和 f 均为常数，乘以 v 的加权平均
    • 重点就变成了如何在屏幕空间计算 v 的加权平均

  • 限制一定的查找范围，检查光线是否会在这个范围内被挡住

    • image.png|350
  • 为了减少计算量，只在范围内采样一些点，利用这些点是否在物体内部来估计这道那个情况image.png|450
    • 可以通过将这些点投射到摄像机的距离与 shadowmap 中存储的最近物体数据进行对比，来判断是不是在物体内部（但这可能存在误判，如图中的红线处点被误判为红色）
    • 如果有法相信息就只需要考虑半圆而不是整个圆了

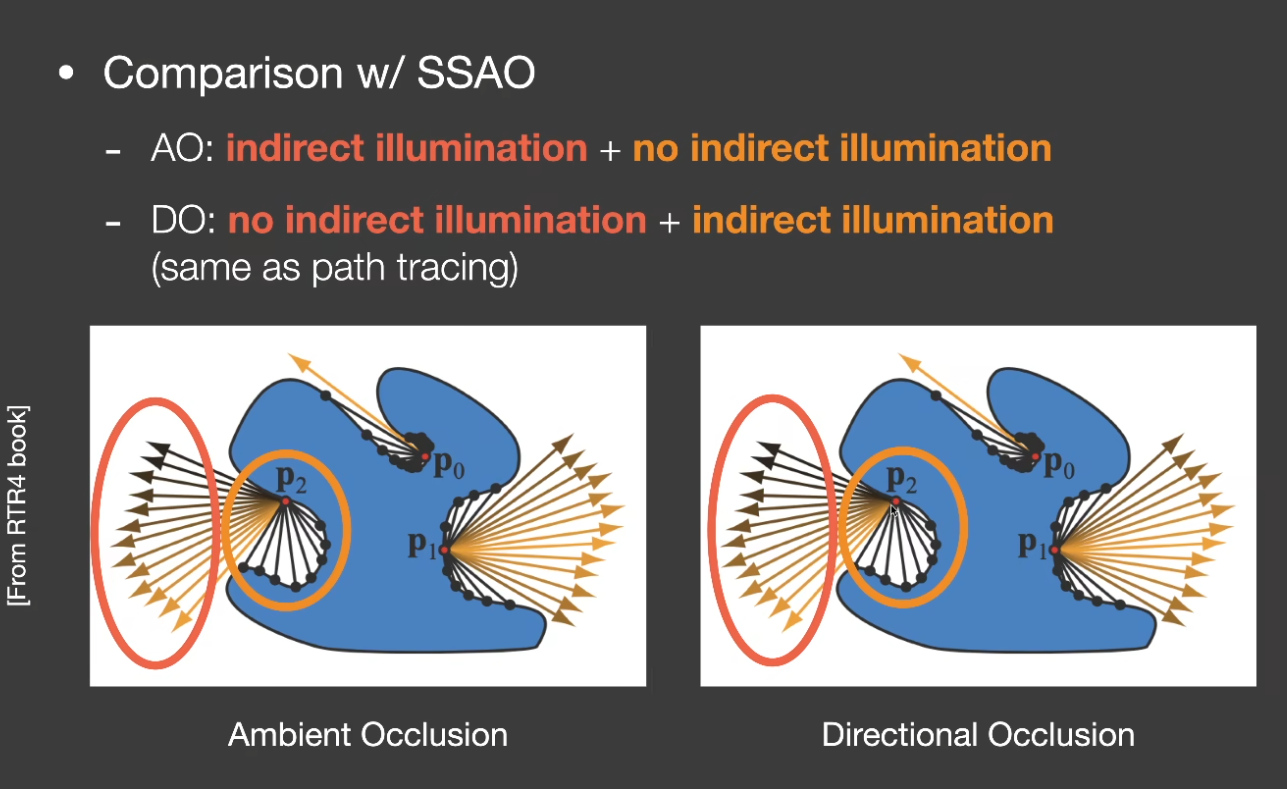
Screen Space Directional Occlusion(SSDO)

  • 对 SSAO 的提高，不再假设所有点有相同的次级光照
  • 从点向外发射射线，如果没有打到障碍物，那么就是直接光照；否则是间接光照（这与 SSAO 完全相反）
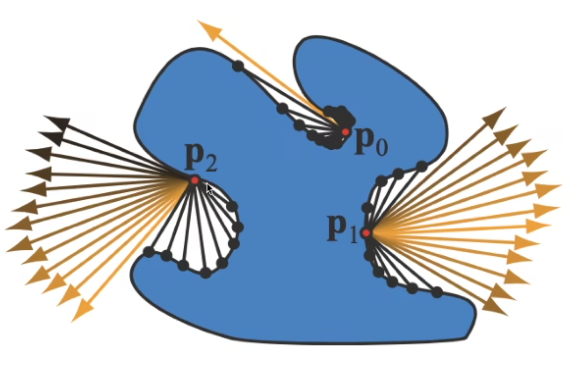    • image.png|232、
    • image.png|500
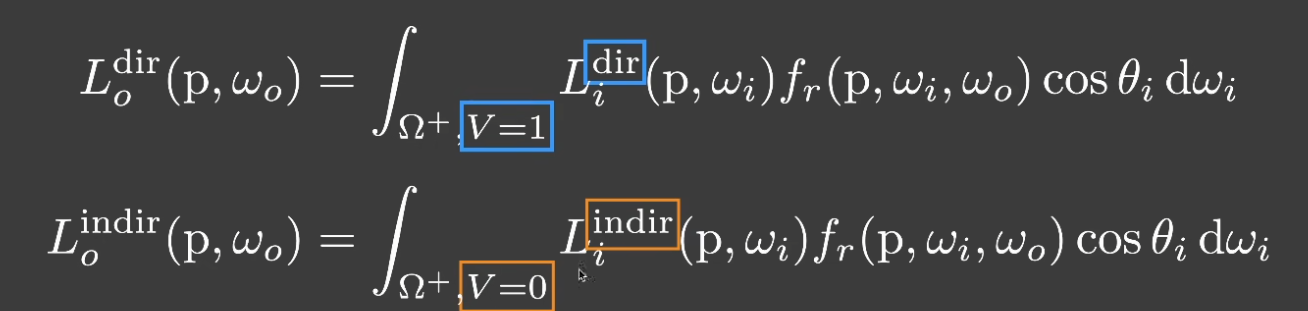
  • image.png|550
    • 判断是否有遮挡的方式与 SSAO 相同
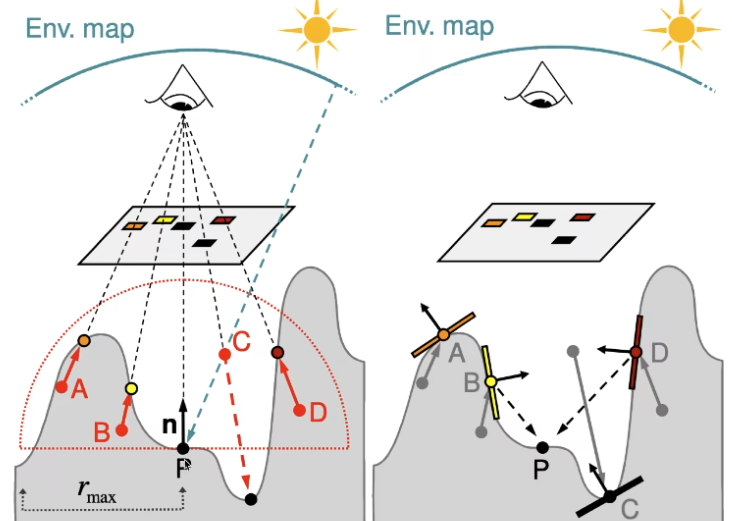
    • image.png|400
  • 问题：
    • 被遮挡住（摄像机看不到的部分）就完全不会对这次光照产生影响
    • 只能处理小范围的（每个点搜查二次光照影响的范围有限，像下图就不回去找到最右侧的绿墙）
    • image.png|400

Screen Space Reflection(SSR)

  • 在屏幕空间上做光线追踪（只能使用摄像机可以看到的信息）
    • 一种 2 D 的光线追踪
  • 通过线性探测，找方向上与壳相交的点
    • image.png|350
  • 希望通过调整步长，减少探测的开销
    • 对深度图做 mipmap，但是上层的值为下层四个像素的深度最小值image.png|238
    • 探测时使用上层值先判断（如果不和上层相交那么也不会和下层相交），从而快速跳过格子
    • 根据是否相交动态调整步长
  • 仍然存在的问题：摄像机看不到的信息就不知道
    • image.png|450

基于物理的材质

  • 基于表面：微表面模型、迪士尼 BRDF
  • 基于体积：快速近似进行散射, 模拟运动、皮肤、毛发等

微表面 BRDF

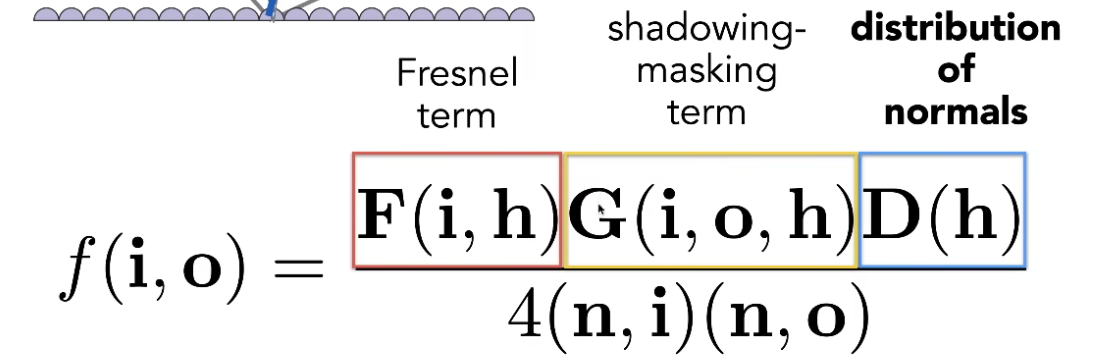
  • image.png|550
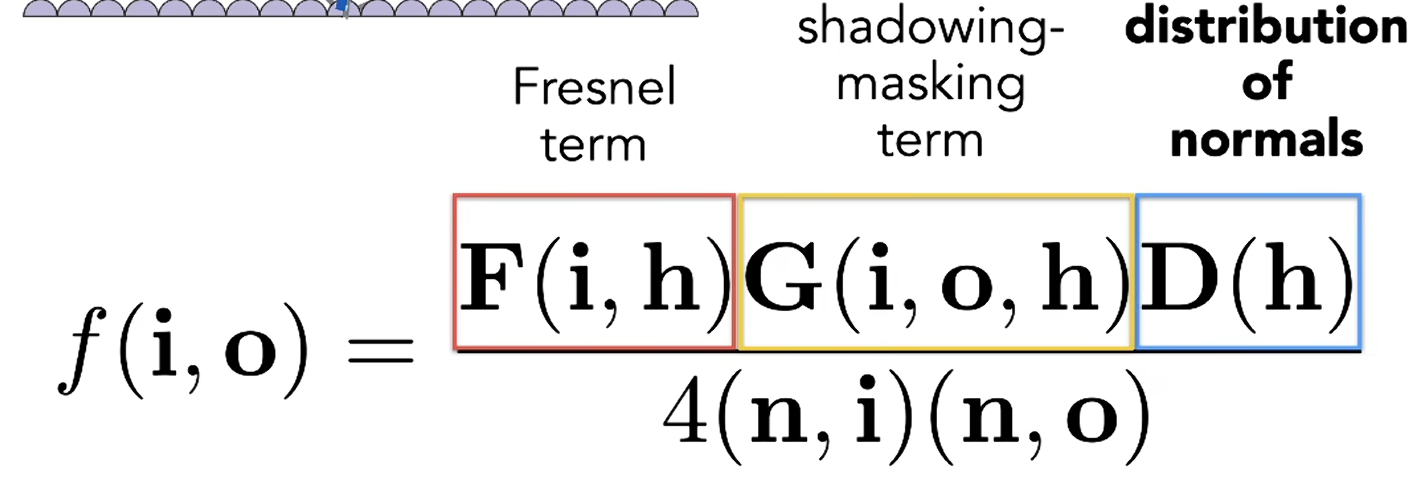
  • F 菲涅尔项：反射强度与入射光与法线夹角相关
  • D 描述表面法线分布（粗糙程度）

描述法线分布 NDF

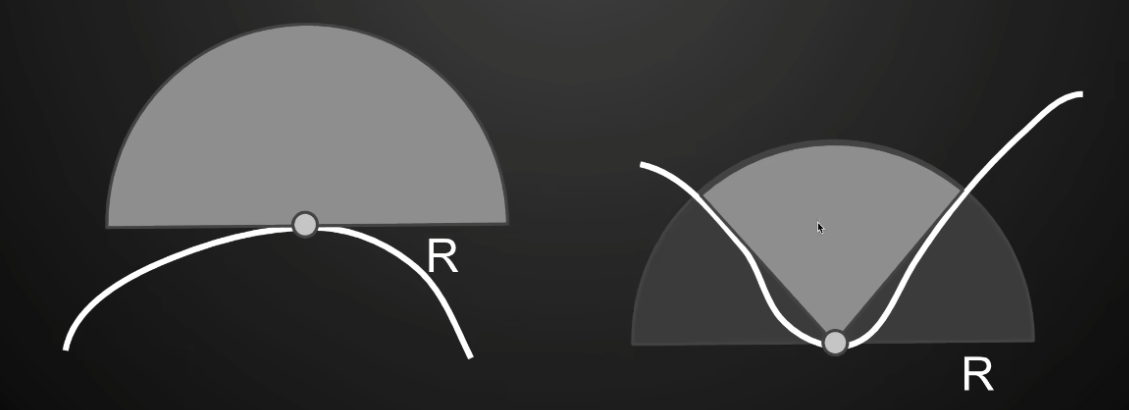
  • 使用半球来描述法线分布：
    • 微面的法线方向是一个单位向量，它的方向可以用半球上的一个点表示。
    • 半球是一个自然的几何空间，可以用来约束和表达微面的法线方向分布。法线分布函数只能在半球范围内定义，因为微面的法线必须朝向表面的正半球，而不能指向表面内部（负半球）。
    • 有 \(\int_\text{半球}D(h)\cos\theta_h\:d\omega_h=1\)

  • \(D(h)\) 输入法线方向 \(h\) 输出一个标量表示微平面法线方向 \(h\) 上的分布密度

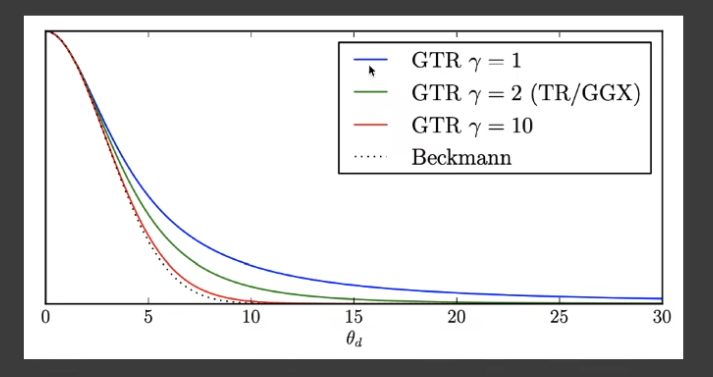
  • Beckmann NDF

    • \(D(h)=\frac{e^{-\frac{\tan^2\theta_h}{\alpha^2}}}{\pi\alpha^2\cos^4\theta_h}\) 其中 \(\alpha\) 表示表面的粗糙程度；
    • 类似于高斯分布（离法线越远 \(\theta_{h}\) 越大，分布越少）
  • GGX（TR）模型
    • image.png|550
    • 相比之下衰减较慢，相比之下会更加柔和
    • image.png|350
  • 进一步扩展的 GGX（GTR），进一步延长尾部长度
    • image.png|400

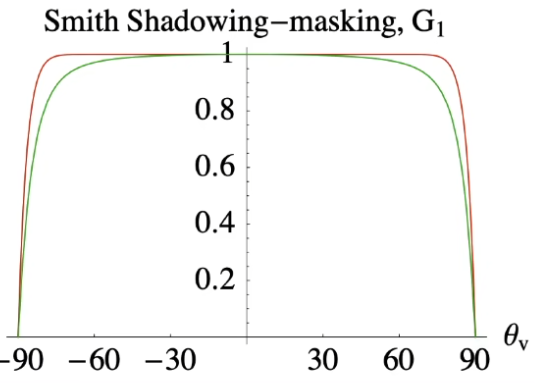
shadowing-masking

  • 解决微表面之间自遮挡的问题（将图像变暗）image.png|400
  • shadowing 遮挡：当光线照射到一个粗糙表面时，微表面中的某些区域会被其他微面遮挡，导致这些区域无法直接接收到光线。
  • masking 掩蔽：当光线从一个粗糙表面反射到观察者时，微表面中的一些区域会被其他微面挡住，从而无法被观察者看到。
  • \(G(i,o,h)\) 就是综合表现 shadowing 和 masking 对渲染造成的影响
    • 最终通常分开表示为 \(G(\mathbf{i},\mathbf{o},\mathbf{m})\approx G_1(\mathbf{i},\mathbf{m})G_1(\mathbf{o},\mathbf{m})\)
    • image.png|239

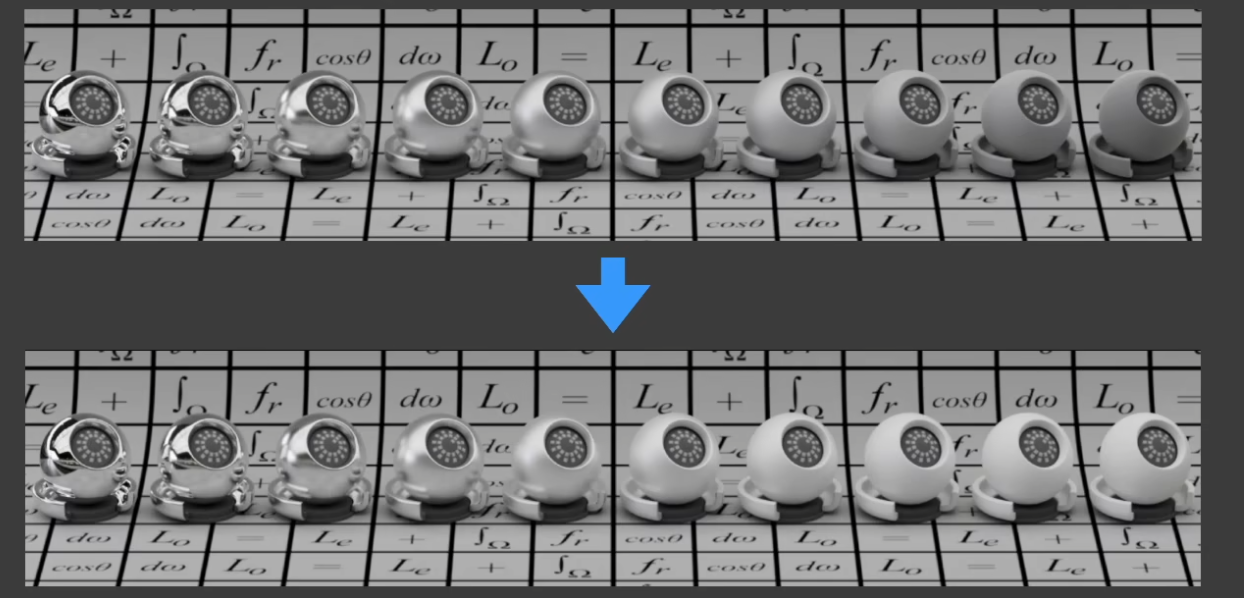
能量损失 Kulla-Conty

  • 前面的几个部分都削弱了光的反射，导致物体显示偏暗（如严重自遮挡，因为忽略了多次反射，会导致损失）
  • 增加一个能量 bonus 进行修饰：Kulla-Conty
    • \(E (\mu_o)=\int_0^{2\pi}\int_0^1 f (\mu_o,\mu_i,\phi)\mu_i\mathrm{d}\mu_i\mathrm{d}\phi\)
    • 损失的能量就是 \(1-E(\mu_o)\)，因此就把这些能量补上
  • image.png|600

Linearly Transformed Cosines(LTC)着色

  • 实时、高效地计算面积光源的微表面BRDF积分。提供一种通用、简单、实时且高质量的BRDF光照积分近似方案。
  • 用于解决微表面模型上的着色问题，主要用于 GGX 分布，无阴影
    • 在传统方法中，微表面模型中需要对光源的形状（如矩形光源）和表面反射进行积分，这涉及到复杂的采样和计算，难以在实时渲染中高效实现。
    • LTC 方法 提供了一种非常高效的近似方案，通过将复杂的光照分布转换为一个 **线性变换的余弦分布，从而简化积分计算，同时保留视觉上的高真实性。

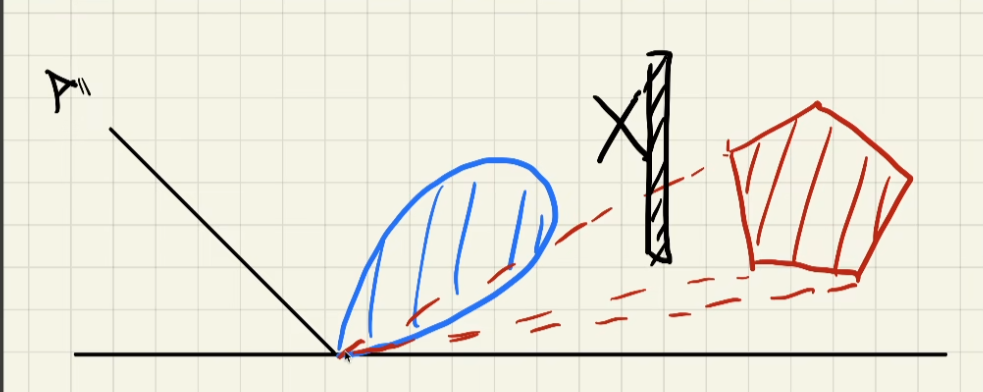
  • image.png|450

  • 核心思想：将复杂不贵则的 2 DBRDF 分布变换为规则易于计算的标准余弦分布image.png|550

    • image.png|550

迪士尼原子模型

  • 微表面模型并不能表示所有材质，并且对艺术家不友好，不便于调整
    • 迪士尼原子模型不保证物理正确性

  • 原则：

    • 使用艺术家友好的参数
    • 使用尽可能少的参数
    • 参数要便于调整（如拖动条）

  • image.png|500

非真实感渲染 Non-Photorealistic Rendering (NPR)

  • 常用方式
    • Bold Contours粗线条轮廓（描边）
    • Blocks of Colors色块（使用大面积均匀色块来填充物体表面）
    • Strokes on Surfaces表面笔触（模仿真实绘画的手绘感）

描边

  • outline rendering：描边包含：外边缘；折痕；材质边界；
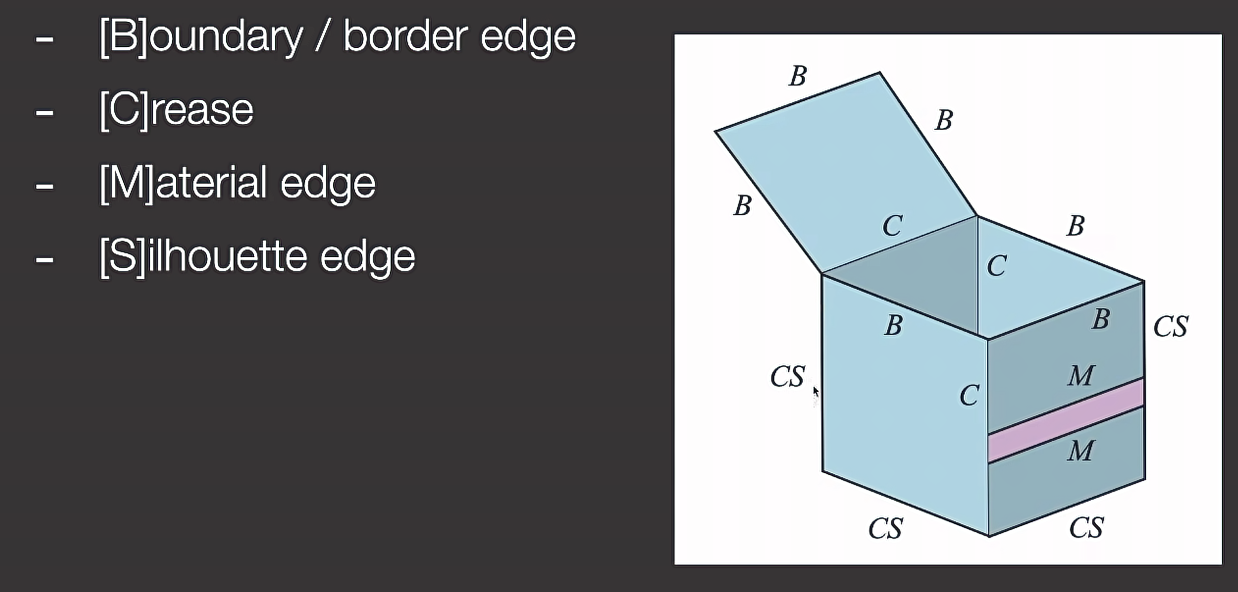
    • image.png|550
    • S 外边界要求至少两个面共享（B 不要求）C 表示折痕 M 表示材质边界
  • 通过 shading 实现：可以认为法线与摄像机视线垂直的部分就是边界，需要描边
    • image.png|450
    • 问题，法线是渐变的，描边宽度也可能很大
  • 通过几何实现
    • 把一个大一圈的模型放在后面，渲染成黑色
  • 图像后期处理
    • 卷积做边缘检测并添加描边
    • （锐化的实现类似）
    • image.png|500

色块

  • image.png|400
    • 先渲染，然后用阈值化处理
    • 减少渐变，量子化（颜色不再连续）
  • image.png|500

表面笔触

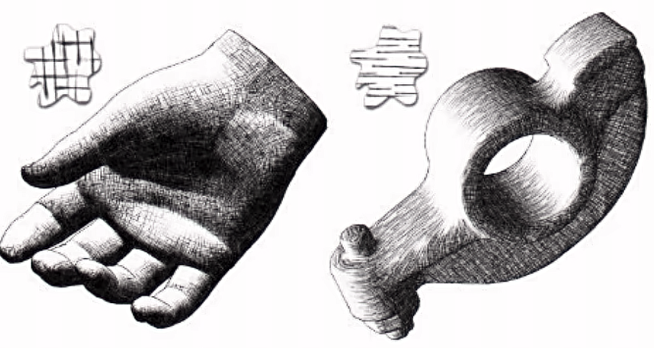
  • 手绘风 image.png|550
  • 使用手绘风格的纹理
    • 为了让不同距离的看起来一样的纹理，mipmap 上的纹理并不进行缩放，只裁剪image.png|500

光线追踪 Real-Time Ray Tracing (RTRT)

  • RTX 提供针对光线追踪定值的硬件，提供 1 SPP（sample per pixel）的光线追踪
    • 1 rasterization (primary)： 首先通过光栅化（Rasterization）方法生成初级可见性信息（Primary Visibility），即确定每个像素对应的场景中最初可见的物体表面。
    • 1 ray (primary visibility)：投射一条初级光线（Primary Ray），进一步确定初始的交点、材质信息。
    • 1 ray (secondary bounce)：从初级光线与物体表面的交点发出一条次级反射光线（Secondary Bounce Ray），用于计算间接光照（Indirect Illumination），也就是场景中其他物体对当前交点的光照贡献。
    • 1 ray (secondary vis.)：投射额外的次级可见性光线（Secondary Visibility Ray），检查次级反射光线的可见性，确定该交点处是否有其他物体遮挡、或进一步反射折射效果。
    • image.png|209
    • 光栅化初始化+三条光线
  • 1 SPP 由于采样率不足，会造成大量的噪点，还需要降噪处理

降噪

  • 问题：通常的降噪不是针对实时渲染&光线追踪设置的，速度太慢难以满足实时性
  • idea：
    • 假设前一帧已经处理过了，并复用其信息（帧之间的连续性）
    • 使用运动向量来找到上一帧的位置
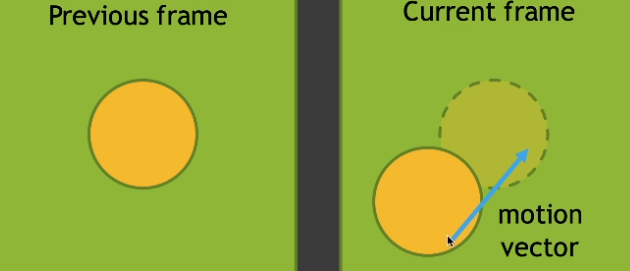
    • image.png|450
    • 能起到提高 SPP 的效果

Motion vector 运动向量

  • Gbuffer 缓冲区 image.png|600

    • 缓存从摄像机看到的不同信息：直接光照、法线、深度等等（屏幕空间的信息）
    • 生成的速度很快，代价极低

  • 运动向量的目标：找到上一帧哪一个像素对应这一帧一个像素对应的物体上的点（后向投影）

    • image.png|450
  • 过程
    • 首先拿到当前点的世界坐标（通过 GBuffer 中存储的世界坐标）或者做逆变换来还原出世界坐标 \(s=M^{-1}V^{-1}P^{-1}E^{-1}x\)，
    • 世界坐标的变换（运动）可以描述成 \(s^{\prime}\xrightarrow{T}s\) 即 \(s^{\prime}=T^{-1}s\)
    • 再找到上一帧的屏幕坐标 \(x^{\prime}=E^{\prime}P^{\prime}V^{\prime}M^{\prime}s^{\prime}\)
    • 这接得到了当前屏幕空间内一点与上一帧屏幕空间内一点的关系
  • 具体降噪过程：~ 表示没有滤波（处理）; — 表示处理之后的
    • 自己滤波（由于采样数目有限，效果一般）：\(\bar{C}^{(i)}=Filter[\tilde{C}^{(i)}]\)
    • 时间滤波（利用上一帧的信息）：\(\bar{C}^{(i)}=\alpha\bar{C}^{(i)}+(1-\alpha)C^{(i-1)}\) 其中 \(\alpha=0.1-0.2\) 主要依赖上一帧的信息
    • 问题：需要时间“预热”，积累足够的历史数据才能很好的实现预测降噪
  • 不可复用的情况：
    • 场景、镜头切换&变换较大，不再能信息复用
    • 难以处理倒退行走的情况（与正向行走不同，越来越多的之前没有出现的内容从后向前推进，这部分是没有可以利用的历史信息的）
    • 被遮挡的东西露出来，上一帧的信息不能复用 image.png|350
    • 无法处理非实体移动（如光源移动而不是物体移动），难以处理阴影、反射等，静止平面上的反射，都会存在变化滞后的问题
  • 判断上一帧的信息能否复用
    • clamping：先把上一帧的值拉到与当前帧类似
    • Detection：标记每个物体的信息，如果发现上一帧的信息完全不符，则考虑降低上一帧的权重（即不可靠）
    • 但是缺少上一帧还是会引入噪声

滤波

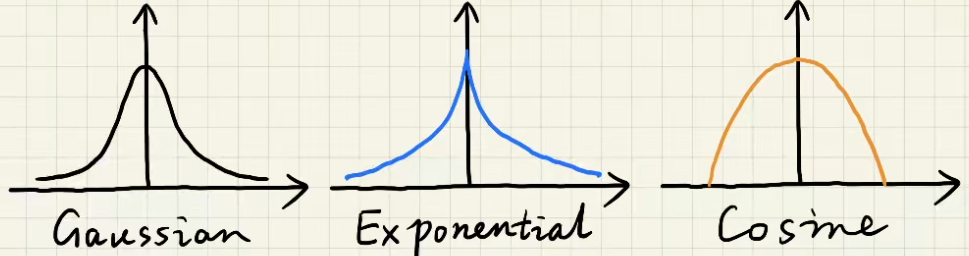
  • 高斯滤波
    • 但是高斯滤波会对整个图像模糊，而不仅仅是噪声
    • image.png|450
  • 双边滤波
    • 希望保留明锐的图像边界（边界就是颜色剧烈变化的位置）
    • 减少边界之外（不同颜色）的像素对目标渲染位置的错误共享
    • \(w(i,j,k,l)=\exp\left(-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2}-\frac{\|I(i,j)-I(k,l)\|^2}{2\sigma_r^2}\right)\) 减去了额外的一项，表示颜色差距越大权重越小
    • image.png|450
    • 问题：无法区分边界之外的点和噪声（噪声的颜色差距也很大）
联合双边滤波
  • 综合考虑更多的特性（法线、深度等 Gbuffer 中易于获得的信息）来决定权值的大小，很适合用于路径追踪的降噪
    • image.png|350
    • AB 之间深度差距大，要降低权值
    • BC 法线差距大，要降低权值
    • DE 颜色差距大，要降低权值

  • 可以使用任何的函数模型，不一定是高斯分布，也先不考虑是否满足守恒，最后再进行归一化即可

    • image.png|450

  • 大的过滤盒（如 64*64）会产生很大的开销，需要进行过优化

    • 将一次 N*N 的过滤替换为一次水平 1*N 和一次垂直 N*1 的过滤，即 \(N^{2}\to N+N\)
    • 用逐渐增大的滤波盒（间隙）进行多趟滤波：如进行 5 趟 5*5 的过滤
      • image.png|400
Outlier removal
  • 移除超级亮点，难以通过滤波直接解决image.png|350
    • 因此要在滤波之前处理掉
  • 检测
    • 以一个小盒子来扫描（7*7）并计算每个区域的平均值和方差
    • 可以认为超出范围 \([\mu-k\sigma,\mu+k\sigma]\) 的点就是Outlier
  • 消除
    • 直接讲点回归到范围 \([\mu-k\sigma,\mu+k\sigma]\) 内

特殊滤波方式

Spatiotemporal Variance-Guided Filtering (SVGF)

  • 结合时间信息与空间信息来进行滤波，对噪点平滑处理

  • 判断因素

  • 深度：
    • \(w_z=\exp\left(-\frac{|z(p)-z(q)|}{\sigma_z|\nabla z(p)\cdot(p-q)|+\epsilon}\right)\)
    • 问题：对摄像机倾斜角度较大的面上的两点深度差别很大
    • 可以通过两点研法线方向上的深度差异取代直接从摄像机视角出发的深度差距
  • 法线：
    • \(w_n=\max(0,n(p)\cdot n(q))^{\sigma_n}\)
    • 只需要考虑物体表面（几何）大致的法线方向，而不需要使用法线贴图的具体法线方向

  • 颜色差异：

    • \(w_l=\exp\left(-\frac{|\:l_i(p)-l_i(q)|}{\sigma_l\sqrt{g_{3\times3}(\mathrm{Var}(l_i(p)))}+\epsilon}\right)\)

  • 改进

    • SVGF 结合 空间滤波（当前帧的像素间滤波）和 时间滤波（结合前几帧的信息），通过重投影和方差引导技术，显著减少噪点。
    • 动态场景一致性：在处理动态场景时，SVGF 能够有效减少帧与帧之间的噪点波动，避免闪烁问题。
Recurrent AutoEncoder (RAE)
  • 使用神经网络，结合 Gbuffer 的信息来实现对 RTRT 的降噪

工业界的解决思路

Temporal Anti-Aliasing(TAA)

  • 时域上复用，复用上一帧的信息
  • 每一个像素点对应改点在最近几帧的渲染结果的平均值（即，每一帧的渲染结果通过综合连续的几帧来确定）

Temporal Super Resolution

  • 时域超分辨率技术
  • 结合历史帧信息来超分
    • 关键：确保能高效的从历史帧中获取信息（而不是与当前渲染重复的信息）从而真正的增加分辨率，减少猜测的走样

延迟渲染

  • 减少 shading 耗时，减少通不过深度测试的部分着色造成的浪费
  • 进行两趟渲染
    • 第一趟不做 shading，只更新深度缓冲
    • 第二趟再进行 shading（frag 数目降低为可见的 frag 数目）

tailed shading

  • 将屏幕分成许多小块（如 32*32）对每个小块分别做 shading
  • 减少每个点需要考虑的光源数目
    • 由于光源的衰减，可以筛选掉几乎没有影响的远处光源
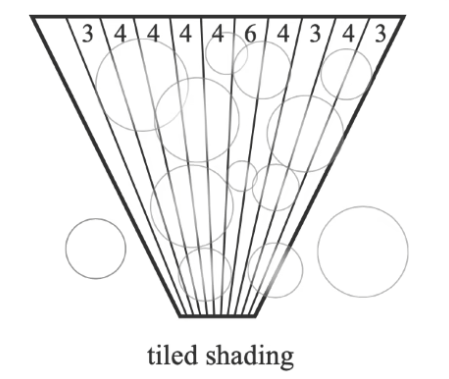
  • image.png|299

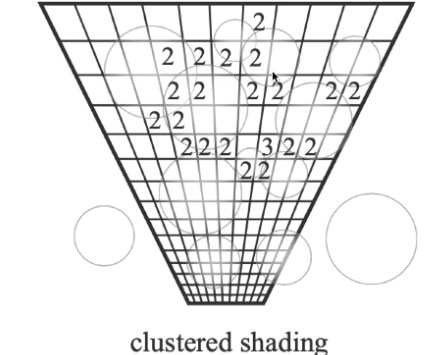
clustered shading

  • 增添距离方向上的更细的小块
    • image.png|243

Level of Detail Solutions (LOD)

  • mipmap 就是一种 lod
  • 控制显示的细节等级
    • 如根据距离来决定要渲染的精细程度
  • 问题：切换时的平滑过渡问题
  • UE 5 Nanite

Global Illumination Solutions（GI）

  • 全局光照
  • 结合多种方案，同时使用