TAASR

https://atyuwen.github.io/posts/optimizing-fsr/
https://github.com/ndepoel/FSR3Unity
https://zhuanlan.zhihu.com/p/401030221 https://blog.csdn.net/JMXIN422/article/details/129412650 https://zhuanlan.zhihu.com/p/637639295 FSR包括两个部分（两个Pass）：上采样（EASU）+ 锐化（RCAS)）

EASU 上采样

上采样与下采样

• 上采样：就是把原来的纹理放大，然后空的部分通过比如线性插值之类的进行填充。
• 下采样：就是把原来的纹理缩小，缩小的方式很多比如mipmap就是把四个像素取平均值算做一个。

边缘与非边缘的上采样

• 上采样将纹理放大之后，空出来的像素点需要填充，此时就有两种情况：

• 非边缘：对于采样的像素点 P 周围像素的灰度值应该与像素点P非常接近，那么像素点 P 只需要进行加权平均即可：\(f(P)=\frac{\sum_if(Q_i)w_i}{\sum_iw_i}\)

• 边缘：直接的简单插值会造成模糊

  • 因此可以在简单的插值（权重计算）基础上加一点高频成分f(P) = f(Q) + λ·F(Q)
  • Q：用来参考的“最近那个”原图像素位置；F(Q)：对 Q 做一个高频滤波；λ：缩放高频成分的系数，决定锐化强度。
  • 这个权重可以使用拉普拉斯算子计算（一个点和周围四个点的插值越大，说明这个点点变化就越大，就有更大的权值）
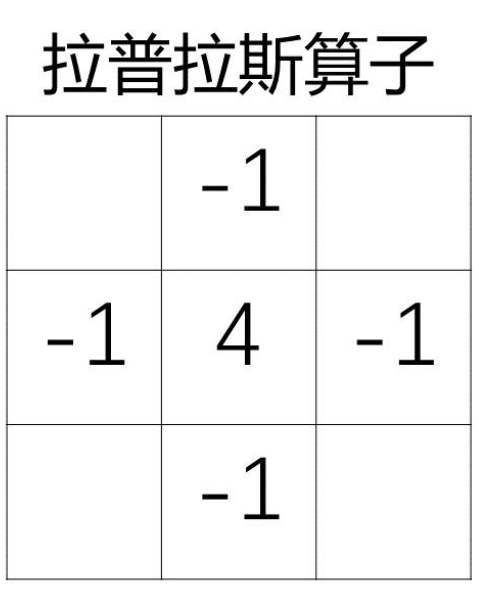
  • 更为统一的表达方式 \(f(P)=\frac{\sum_if(Q_i)H(Q_i)}{\sum_iH(Q_i)}\) 为了表达边缘，其权值可以为负数
    • “正权重”＝ 保持邻近像素的平均值 → 低通 / 平滑
    • “负权重”＝ 从平均里减掉跨边缘的部分 → 高通 / 锐化
• lanczos 函数 \(L(x)=\frac{asin(\pi x)sin(\pi x/a)}{\pi^2x^2},x\in[-a,a)\) 就非常适合做这个高通滤波器
  • 
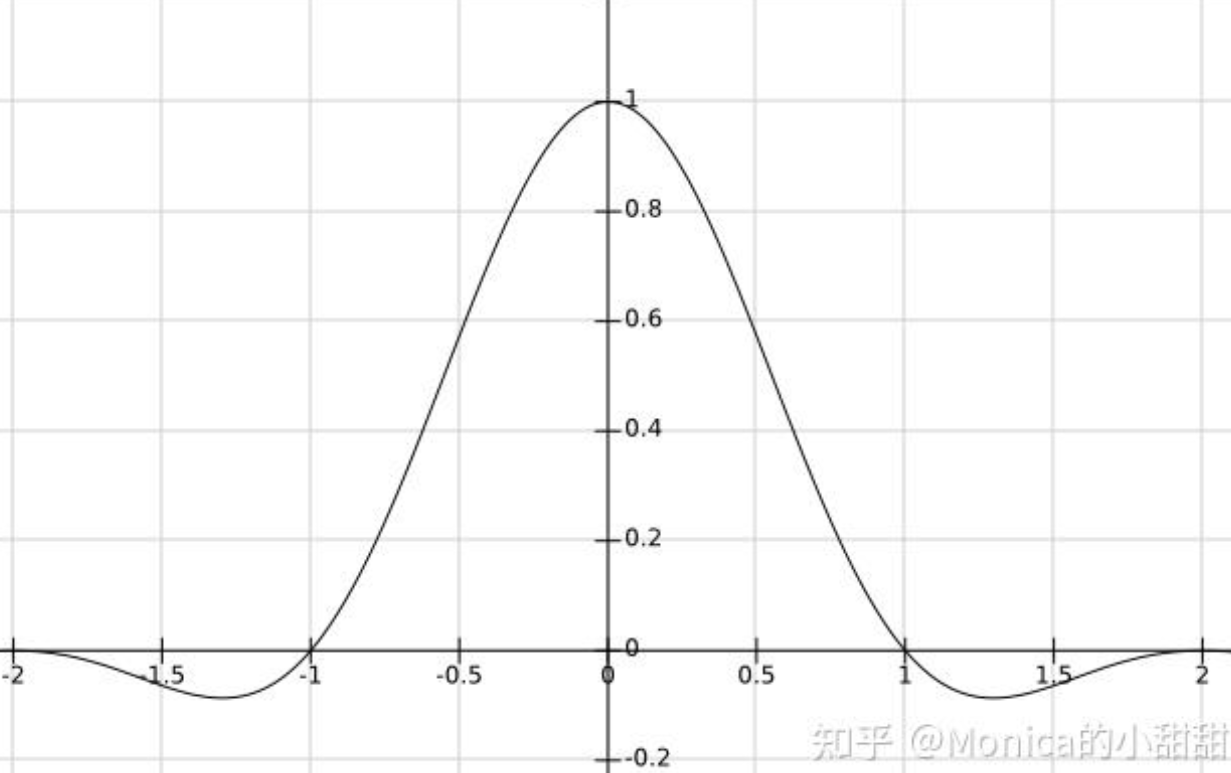
  • 中心为正，周围为负
• 为了减少三角函数开销，一种快速近似 \(L(x)=[\frac{25}{16}(\frac25x^2-1)^2-(\frac{25}{16}-1)](wx^2-1)^2\)
  • \(w\) 用来控制函数在 \([-2,-1][1,2]\) 上的具体形状
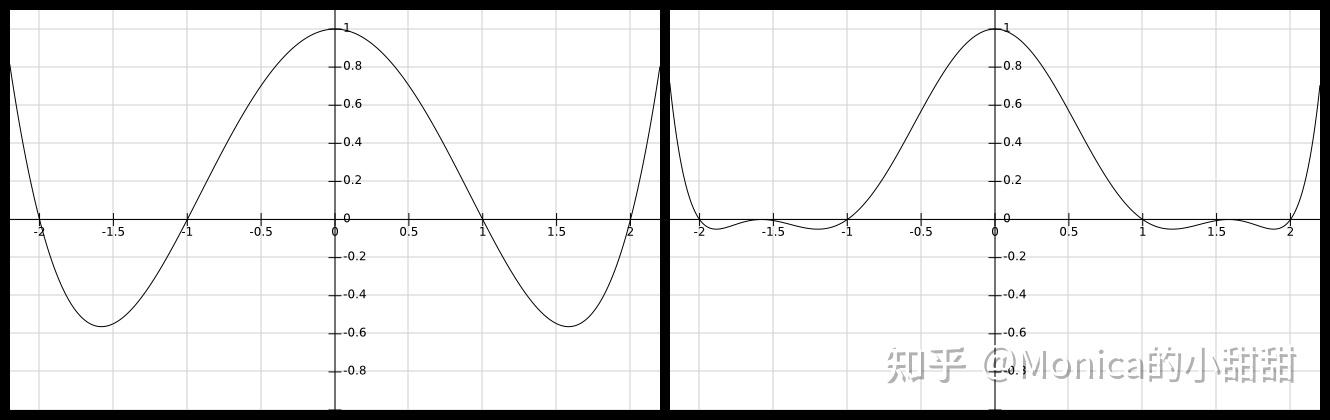
  • 可见：w 越大，Window 在 x=±1/√w 处归零→负瓣范围越窄、强度越弱；w 越小，Window 趋近恒 1 →保留更多负瓣→越强的锐化。

边缘特征

• 有了处理边缘和非边缘的采样方法，还需要能判断一个像素是否为边缘
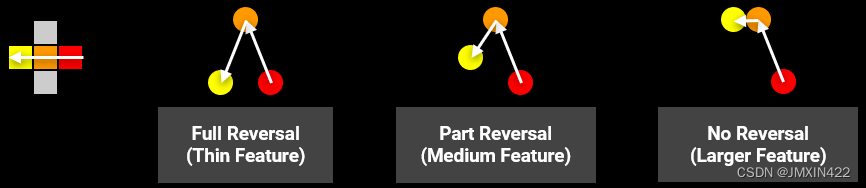
• EASU 主要处理下面两种边缘(灰度值下)

• 边缘检测特征值的计算

  • 
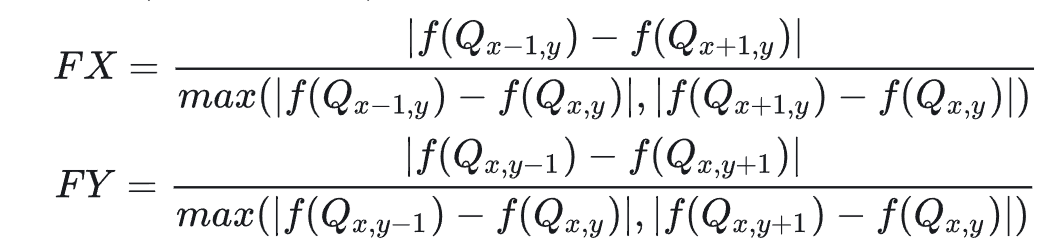
  • 最终 \(F=(FX^2+FY^2)\) 范围为 \([0,2]\)，归一化映射得到 \(Feature=(F/2)^2\)

    • 对边缘强度的解读
    • 1. 平坦区域
    • 如果 lB ≈ lC ≈ lD (几乎相同)
    • 则分子和分母都接近0
    • 但分子(总变化)比分母(局部最大变化)更接近0
    • 比值较小，接近0
    • 1. 噪声区域
    • 像素值变化不规律，如 lB=100, lC=200, lD=150
    • |lD-lB|=50，max(|lD-lC|, |lC-lB|)=100
    • 比值=0.5，表示总变化小于局部最大变化
    • 1. 边缘区域
    • 在lC处有明显边缘，如 lB=100, lC=200, lD=210
    • |lD-lB|=110，max(|lD-lC|, |lC-lB|)=100
    • 比值=1.1，经saturate后为1
    • 表示总变化与局部最大变化相当
    • 1. 线性梯度区域
    • 像素值均匀变化，如 lB=100, lC=150, lD=200
    • |lD-lB|=100，max(|lD-lC|, |lC-lB|)=50
    • 比值=2，经saturate后为1
    • 表示总变化大于局部最大变化
    • 

• 

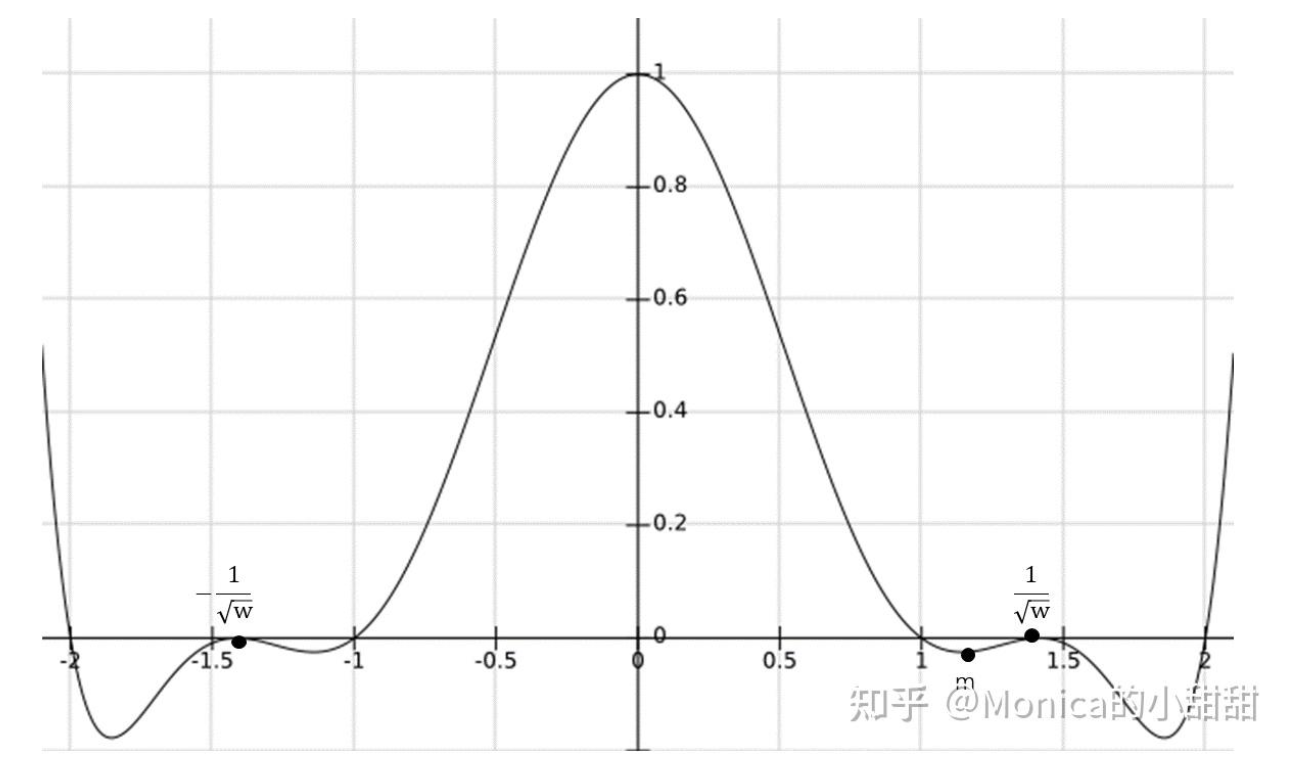
  • \(\frac{1}{\sqrt{ w }}\) 刚好为零点
• 这个 feature 值就可以用于设置上面lanczos 函数的 w 参数
  • 平坦区域（Feature≈0）我们不想锐化，w 要打到最大（1），使负瓣几乎消失；
  • 强边缘（Feature≈1）我们要最猛烈的锐化，w 要打到最小（1/4），留下最大负瓣。
  • 因此 \(w=\frac12-\frac14Feature\)

    

• 还要对 x 进行裁剪 \(x=min(x,\frac1{\sqrt{w}})\)

双线性插值与上下半行

• 单单只计算上下左右四个像素可能会导致毕竟大的偏差, 因此改为采样周围的 12 个像素，分成四组分别进行，后进行双线性插值
  • 
• 
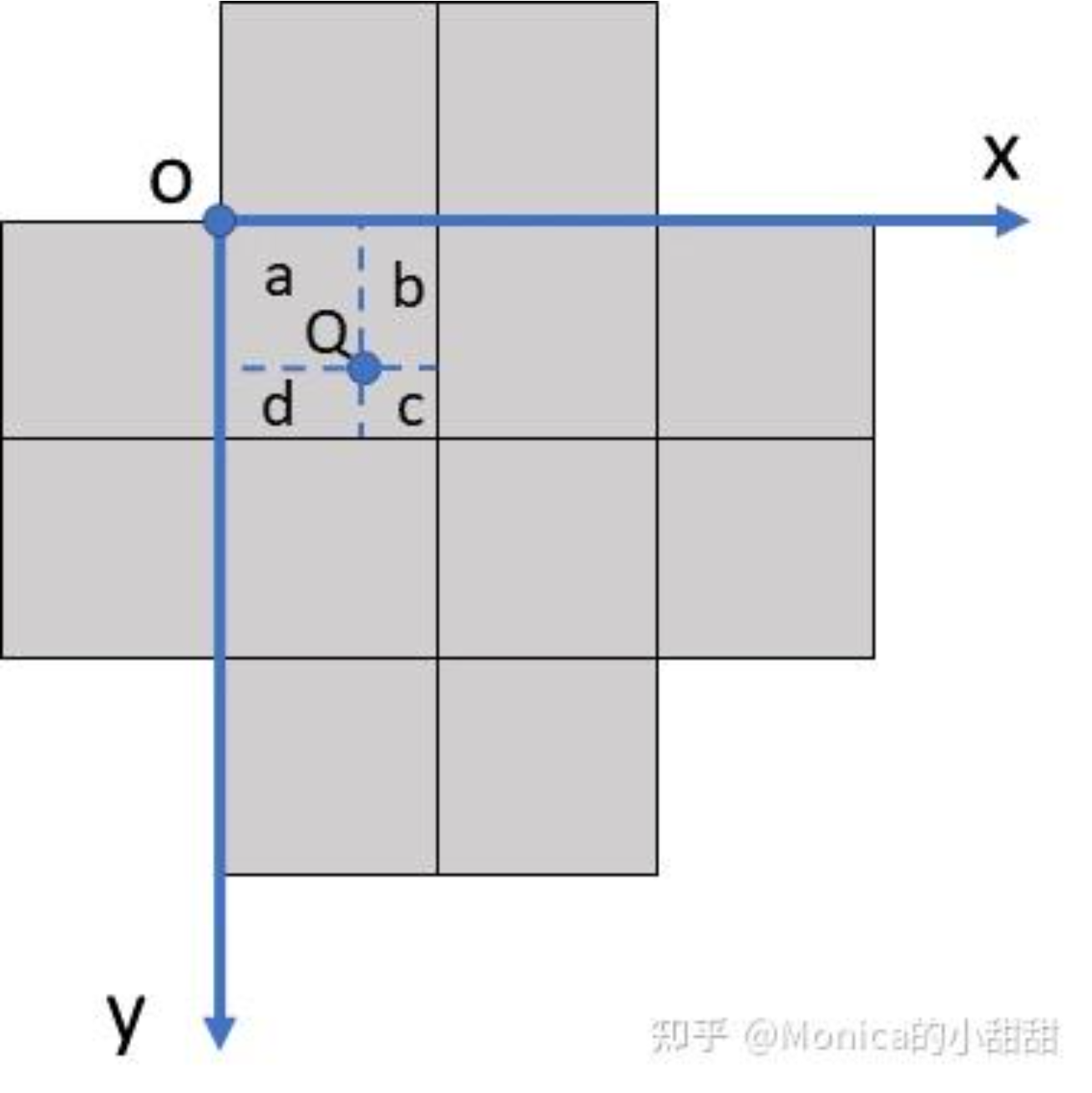
  • 设 \(Q\) 的坐标为 \((x,y)\) 则双线性插值之后的结果就是 \(\begin{aligned}w=w_{red}*(1-x)*(1-y) \\ +w_{orange}*x*(1-y) \\ +w_{yellow}*(1-x)*y \\ +w_{green}*x*y\end{aligned}\)

    void func_EASUSetF(inout float2 dirPX, inout float2 dirPY, inout float2 lenP, float2 pp, bool biSTUV, float2 lA, float2 lB, float2 lC, float2 lD, float2 lE)
    {
        float2 w = biSTUV ? (float2(1.0f, 0.0f) + float2(-pp.x, pp.x)) * (1.0f - pp.y) : (float2(1.0f, 0.0f) + float2(-pp.x, pp.x)) * pp.y;
        //dirX/dirY: the X/Y direction grads（水平垂直方向上的梯度（值的变化））
        //dirPX/dirPY: the X/Y direction grads with bilinear weight accumulate (f,g,j,k)//累加后的梯度
        //lenX=saturate(|lD-lB|/max(|lD-lC|,|lC-lB|)) ^2 ： the edges feature of X-axis//边缘强度
        //lenY=saturate(|lA-lE|/max(|lA-lC|,|lC-lE|)) ^2 ： the edges feature of Y-axis
        //lenP: the edges feature of X-axis and Y-axis with bilinear weight accumulate (f,g,j,k)//累加后的边缘强度
        //lenP=1 large feature, represents edge
        //lenP=0 small feature, represents flat
    
        //      +---+---+
        //      |   |   |
        //      +--(0)--+
        //      | b | c |
        //  +---F---+---+---+
        //  | e | f | g | h |
        //  +--(1)--+--(2)--+
        //  | i | j | k | l |
        //  +---+---+---+---+
        //      | n | o |
        //      +--(3)--+
        //      |   |   |
        //      +---+---+
    
        //  A
        //B C D
        //  E
        float2 dc = lD - lC;
        float2 cb = lC - lB;
        float2 lenX = 1.0f / max(abs(dc), abs(cb));
        float2 dirX = lD - lB;
        dirPX += dirX * w;
        lenX = saturate(abs(dirX) * lenX);
        lenX *= lenX;
        lenP += lenX * w;
        float2 ec = lE - lC;
        float2 ca = lC - lA;
        float2 lenY = 1.0f / max(abs(ec), abs(ca));
        float2 dirY = lE - lA;
        dirPY += dirY * w;
        lenY = saturate(abs(dirY) * lenY);
        lenY *= lenY;
        lenP += lenY * w;
    }
    

• 聚合一行中左右两种情况，分别放到 float 2 的 xy 中一次就做完，总共只需要分为上半行和下半行进行两次
  • 第一趟 bejg+cfkh
  • 第二趟 fink+gjol

旋转

• 为了更加适宜各种角度的边缘，还可以通过旋转来进一步的优化
• 两个方向上的梯度 \(\begin{aligned}Dx&=f(Q_{x-1,y})-f(Q_{x+1,y})\\Dy&=f(Q_{x,y-1})-f(Q_{x,y+1})\end{aligned}\)
  • 得到梯度向量 \(Dir=(Dx,Dy)\) 这是垂直于边缘的，归一化后得到方向向量 \(Dir=(cos\theta,sin\theta)\)
  • 对采样偏移进行旋转，按照旋转之后的方向上进行采样，从而取得更好的效果 \(\begin{aligned}x=x*cos\theta+y*sin\theta\\y=-x*sin\theta+y*cos\theta\end{aligned}\)
• 各向异性缩放，不使用统一的半径来做Lanczos2 插值
  • 一是对各种斜角边缘的采样密度不均
  • 二是沿边缘和跨边缘该给不同强度的锐化/平滑
  • 策略：
    • 沿边缘，对于强边缘时采样更远（核长轴更长）→保持足够平滑
    • 跨边缘，对于强边缘时采样更近（核短轴更短）→锐化更集中
  • \(\begin{aligned} S_x=1+(Stretch-1)*Feature\\S_y=1.0-0.5*Feature\\Stretch=\frac1{max(sin\theta,cos\theta)}\end{aligned}\)

RCAS 锐化

• 通过自使用算子进一步强化边缘信息
• RCAS 就是一个拉普拉斯算子的变种
  • 
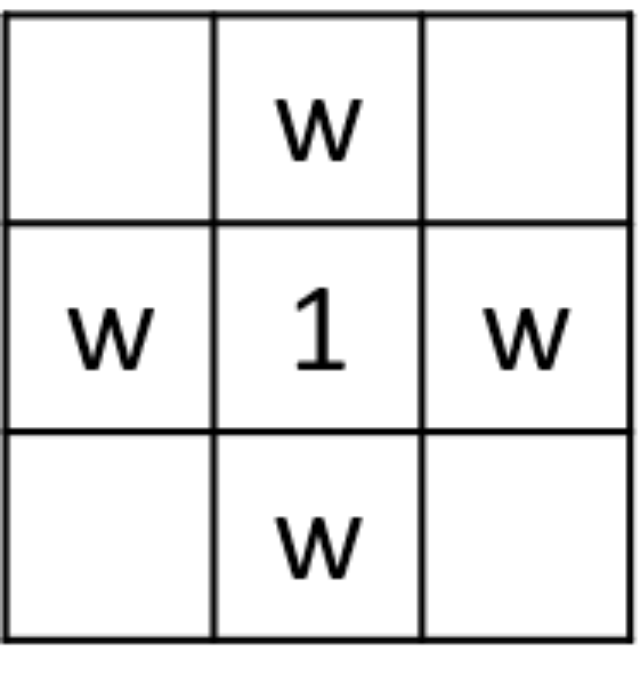
  • 即 \(F(Q)=\frac{w*(f(Q_{x-1,y})+f(Q_{x+1,y})+f(Q_{x,y-1})+f(Q_{x,y+1}))+f(Q)}{4*w+1}\)
• 据像素周围的对比度来计算 w
  • min、max 分别为图中的最大最小值
  • Scale 为上采样之后的分辨率与原分辨率的比值
  • \(w=max(-\frac{Min}{4Max},\frac{1-Max}{4Min-4})*Scale\)