几何
模型表示¶
隐式表述¶
- 数学表达式
- 不告诉点都在哪,只告诉点的位置是否满足的约束(判断是否在几何上),如
f(x,y,z)=0 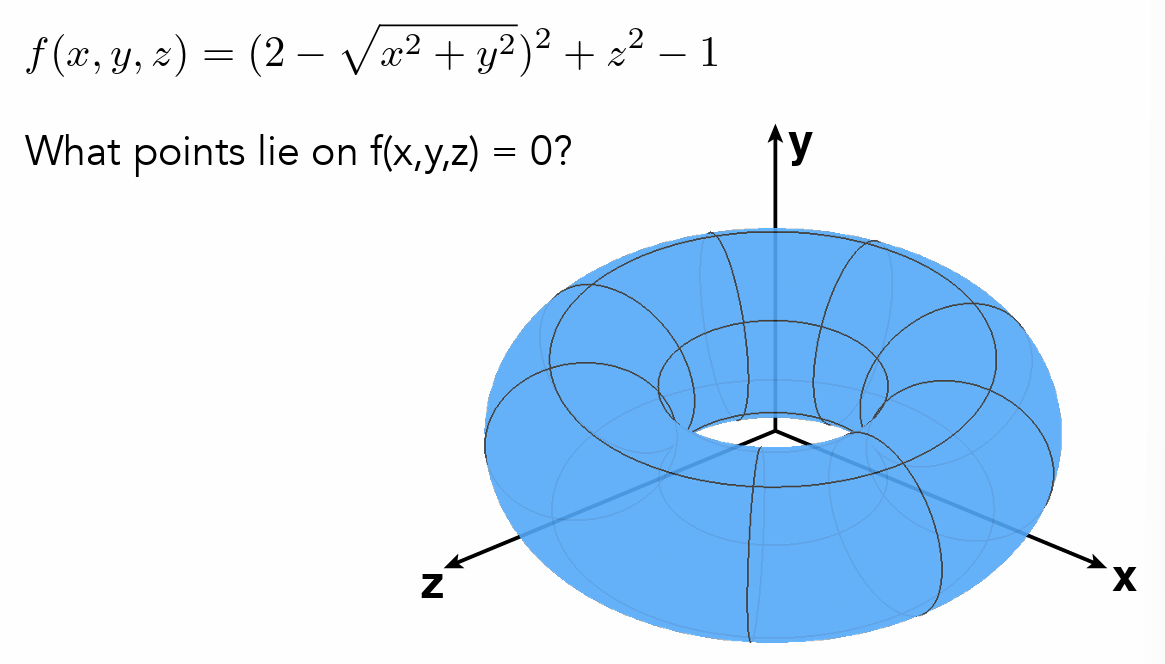
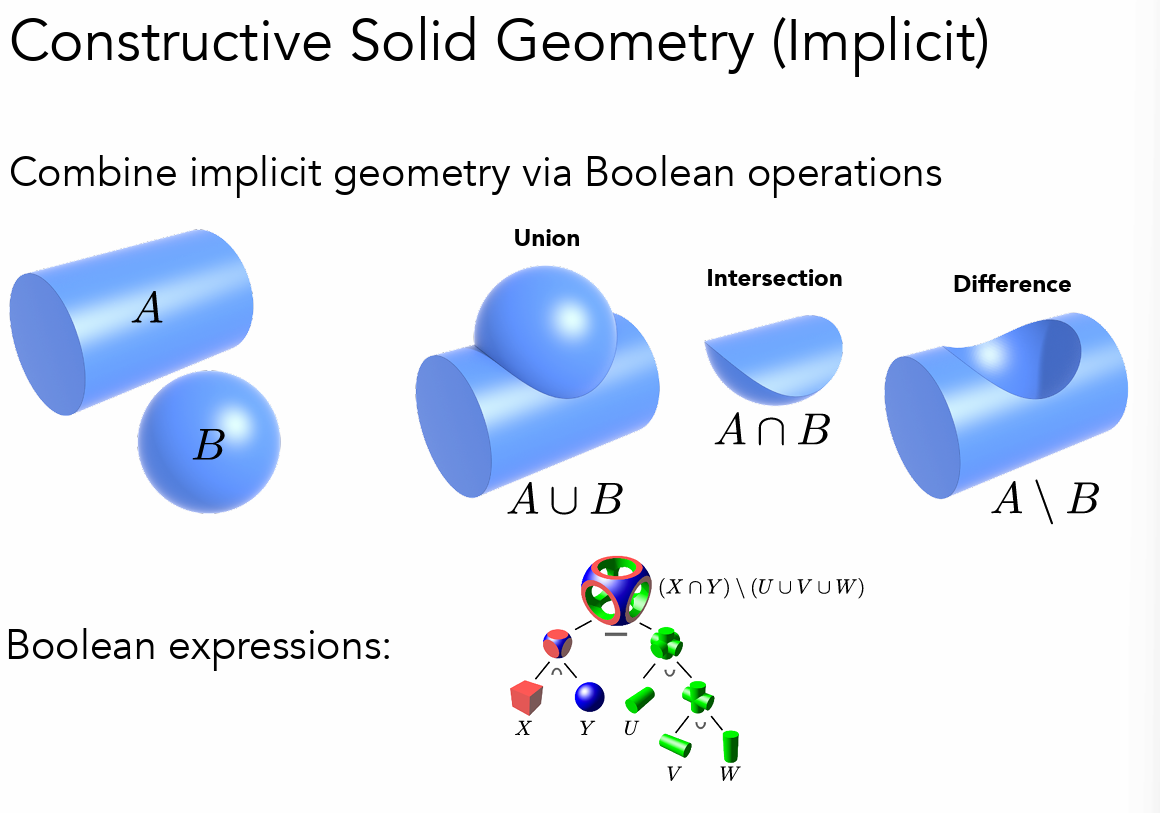
- csg 法
- 距离函数
- 空间中任何一个点到物体表面的最短距离
- 通过距离函数来得到几何形体混合的效果
- 插值(应用)
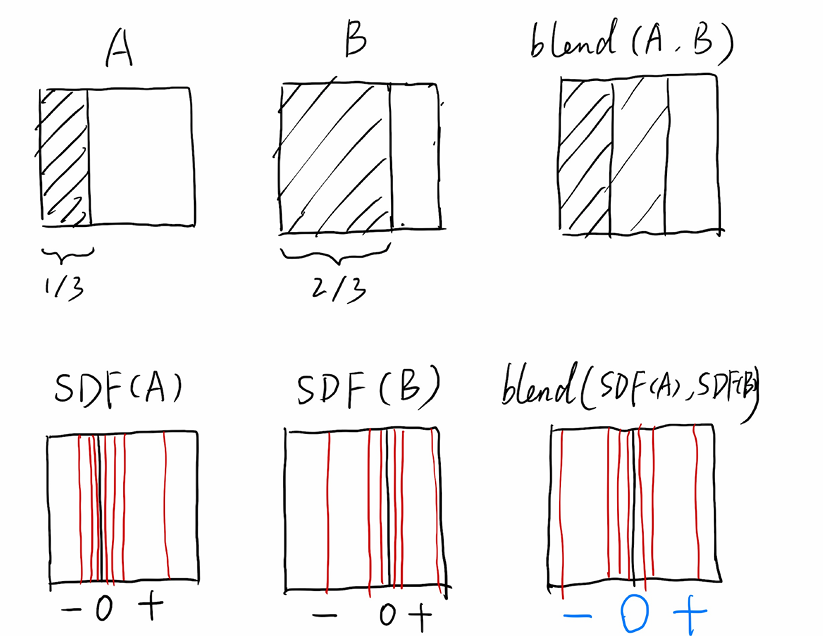
- 通过正负划分边界
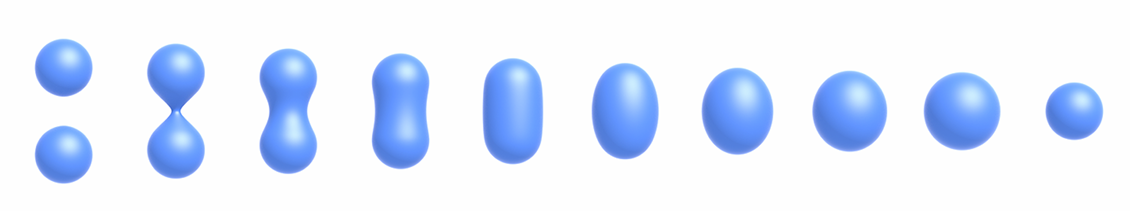
- 分型描述(自相似)

SDF 距离场¶
- 场就是一个点/向量到向量/值的映射(如磁场就是从点到磁感应矢量)
- SDF 表示一个点到一个曲面的最小距离,同时用正负来区分点在曲面内外。点在曲面内部则规定距离为负值,点在曲面外部则规定距离为正值,点在曲面上则距离为 0.
- 二维 SDF:圆
- 对于 \(f(x,y,z)=\sqrt{x^2+y^2+z^2}-1\) 这样一个球体,其 SDF 函数就是
float sphereSDF(vec3 p) { return length(p) - 1.0; } - 绘制 sdf 的片元着色器
#version 330 core out vec4 FragColor; // 输出颜色 // 圆形 SDF float sdf_circle(vec2 p, float radius) { return length(p) - radius; // 点到圆心距离减去半径 } void main() { // 获取当前片元的坐标,并映射到屏幕中心,归一化到[-1,1] vec2 iResolution = vec2(800.0, 600.0); // 固定屏幕分辨率 vec2 uv = (gl_FragCoord.xy - 0.5 * iResolution) / iResolution.y; // 定义圆的半径 float radius = 0.3; // 计算 SDF float d = sdf_circle(uv, radius); // 直接写死的颜色 vec3 circleColor = vec3(1.0, 0.0, 0.0); // 圆的颜色:红色 vec3 backgroundColor = vec3(0.0, 0.0, 0.0); // 背景颜色:黑色 // 根据 SDF 绘制颜色 vec3 color = mix(circleColor, backgroundColor, step(0.0, d)); FragColor = vec4(color, 1.0); } - 常见几何体的 SDF 表述:Inigo Quilez :: computer graphics, mathematics, shaders, fractals, demoscene and more
RayMatching¶
- 一种基于符号距离场 SDF 的技术,通过迭代地沿着光线前进直到碰到对象表面(或超出最大距离)来检测交点
- 比 raytracing 效率更高
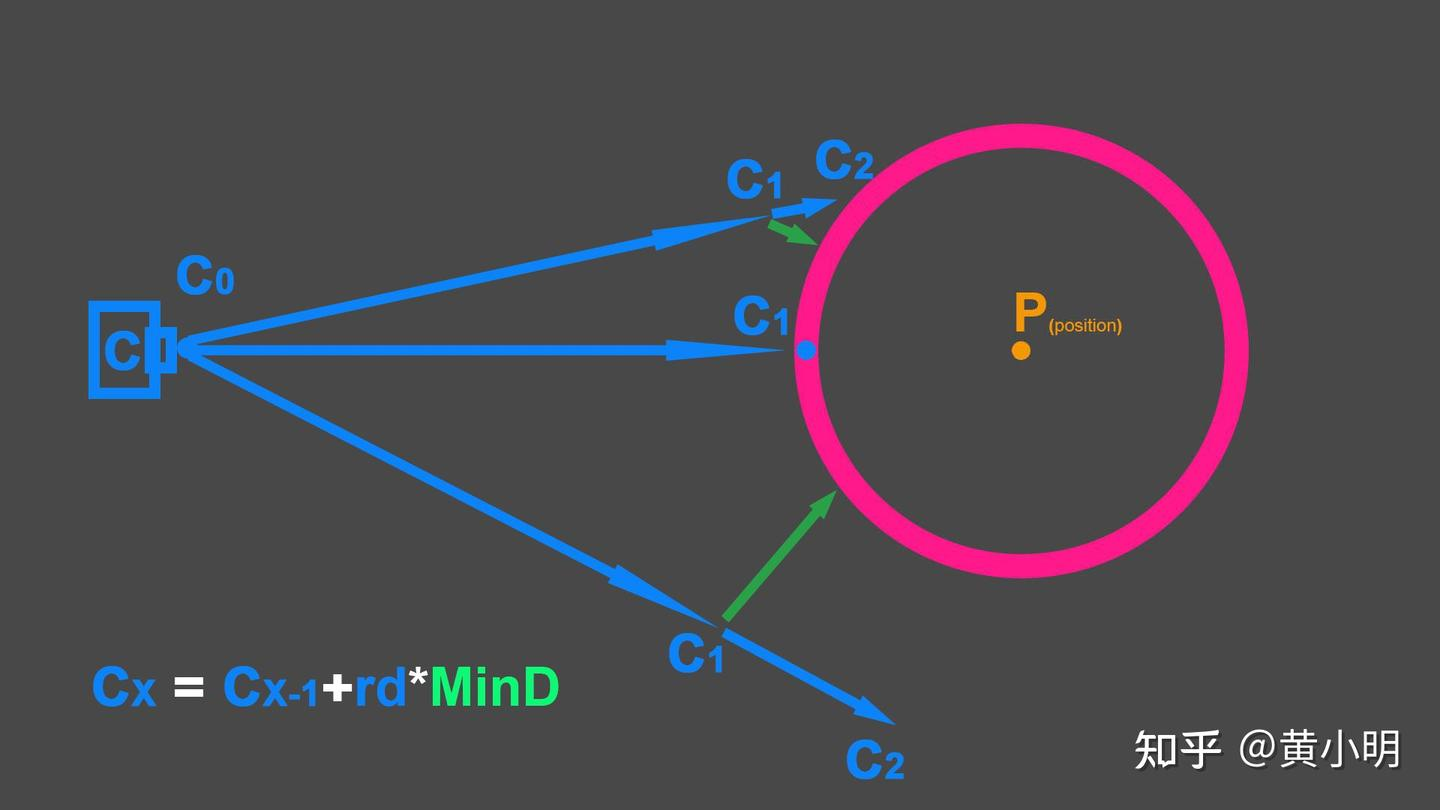
- 按照摄像机方向 (Ray)逐步前进(March)进行采样,是以迭代方式一步一步向前步进的
- 这个步长就可以通过 SDF 来确定
- 如果在步进一次并没有达到表面时,可以以此时距离物体的距离场再次按照原方向进行步进。
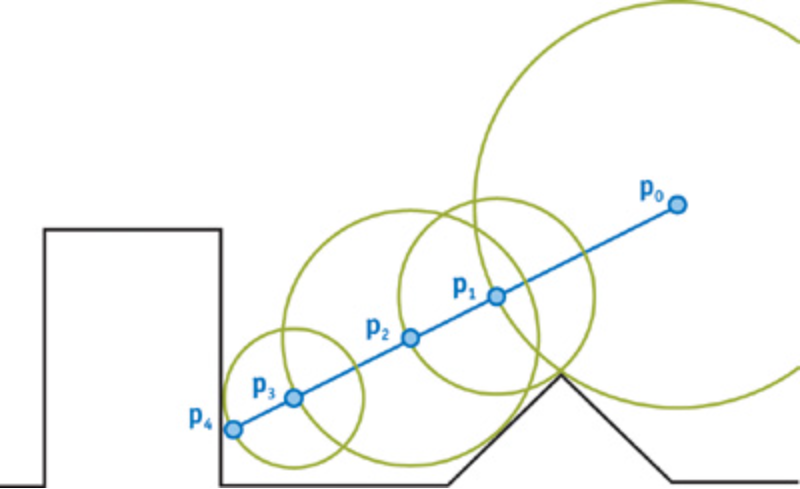
- 如果某条线在步进多次后一直逐渐远离,也就是说明这根射线永远无法与物体相交
- 如果一根射线在步进多次后距离场的值越来越小,如果设值为 0.01,那么就可以确定这个点的位置就是物体表面。
float depth = start; for (int i = 0; i < MAX_MARCHING_STEPS; i++) { float dist = sceneSDF(eye + depth * viewRayDirection); if (dist < EPSILON) { // We're inside the scene surface! return depth; } // Move along the view ray depth += dist; if (depth >= end) { // Gone too far; give up return end; } } return end;
- 完整代码
const int MAX_MARCHING_STEPS = 255; const float MIN_DIST = 0.0; const float MAX_DIST = 100.0; const float EPSILON = 0.0001; //球的SDF函数 float sphereSDF(vec3 samplePoint) { return length(samplePoint) - 1.0; } //场景的SDF函数 float sceneSDF(vec3 samplePoint) { return sphereSDF(samplePoint); } //raymatching float shortestDistanceToSurface(vec3 eye, vec3 marchingDirection, float start, float end) { float depth = start; for (int i = 0; i < MAX_MARCHING_STEPS; i++) { float dist = sceneSDF(eye + depth * marchingDirection); if (dist < EPSILON) { return depth; } depth += dist; if (depth >= end) { return end; } } return end; } //光线方向计算函数 vec3 rayDirection(float fieldOfView, vec2 size, vec2 fragCoord) { vec2 xy = fragCoord - size / 2.0; float z = size.y / tan(radians(fieldOfView) / 2.0); return normalize(vec3(xy, -z)); } //片元着色器主函数 void mainImage( out vec4 fragColor, in vec2 fragCoord ) { vec3 dir = rayDirection(45.0, iResolution.xy, fragCoord); vec3 eye = vec3(0.0, 0.0, 5.0); float dist = shortestDistanceToSurface(eye, dir, MIN_DIST, MAX_DIST); if (dist > MAX_DIST - EPSILON) { // Didn't hit anything fragColor = vec4(0.0, 0.0, 0.0, 0.0); return; } fragColor = vec4(1.0, 0.0, 0.0, 1.0); } rayDirection计算从相机(观察者)发出的光线方向向量(每个像素对应的光线方向)vec2 xy = fragCoord - size / 2.0;将像素坐标转为相对屏幕中心的坐标z是光线在屏幕前方方向上的分量。
SDF 的法线¶
- SDF 的法线计算:根据距离场梯度来计算
- 梯度是一个矢量场,表示函数值变化最快的方向。
- 梯度方向就是指向 SDF 值变化最快的方向,这个方向恰好是法线的方向。
- \(\nabla f(x,y,z)\) 表示点 \((x,y,z)\) 的梯度向量 \(\nabla f=\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\right)\)
- 表面法线的计算公式:有限差分法
- 通过采样点附近的值变化来估算梯度
- 近似计算公式 \(\nabla f(x,y,z)\approx\left(\frac{f(x+\epsilon,y,z)-f(x-\epsilon,y,z)}{2\epsilon},\frac{f(x,y+\epsilon,z)-f(x,y-\epsilon,z)}{2\epsilon},\frac{f(x,y,z+\epsilon)-f(x,y,z-\epsilon)}{2\epsilon}\right)\)
vec3 estimateNormal(vec3 p) { return normalize(vec3( sceneSDF(vec3(p.x + EPSILON, p.y, p.z)) - sceneSDF(vec3(p.x - EPSILON, p.y, p.z)), sceneSDF(vec3(p.x, p.y + EPSILON, p.z)) - sceneSDF(vec3(p.x, p.y - EPSILON, p.z)), sceneSDF(vec3(p.x, p.y, p.z + EPSILON)) - sceneSDF(vec3(p.x, p.y, p.z - EPSILON)) )); }
- 完整代码Shader - Shadertoy BETA
几何体布尔运算¶
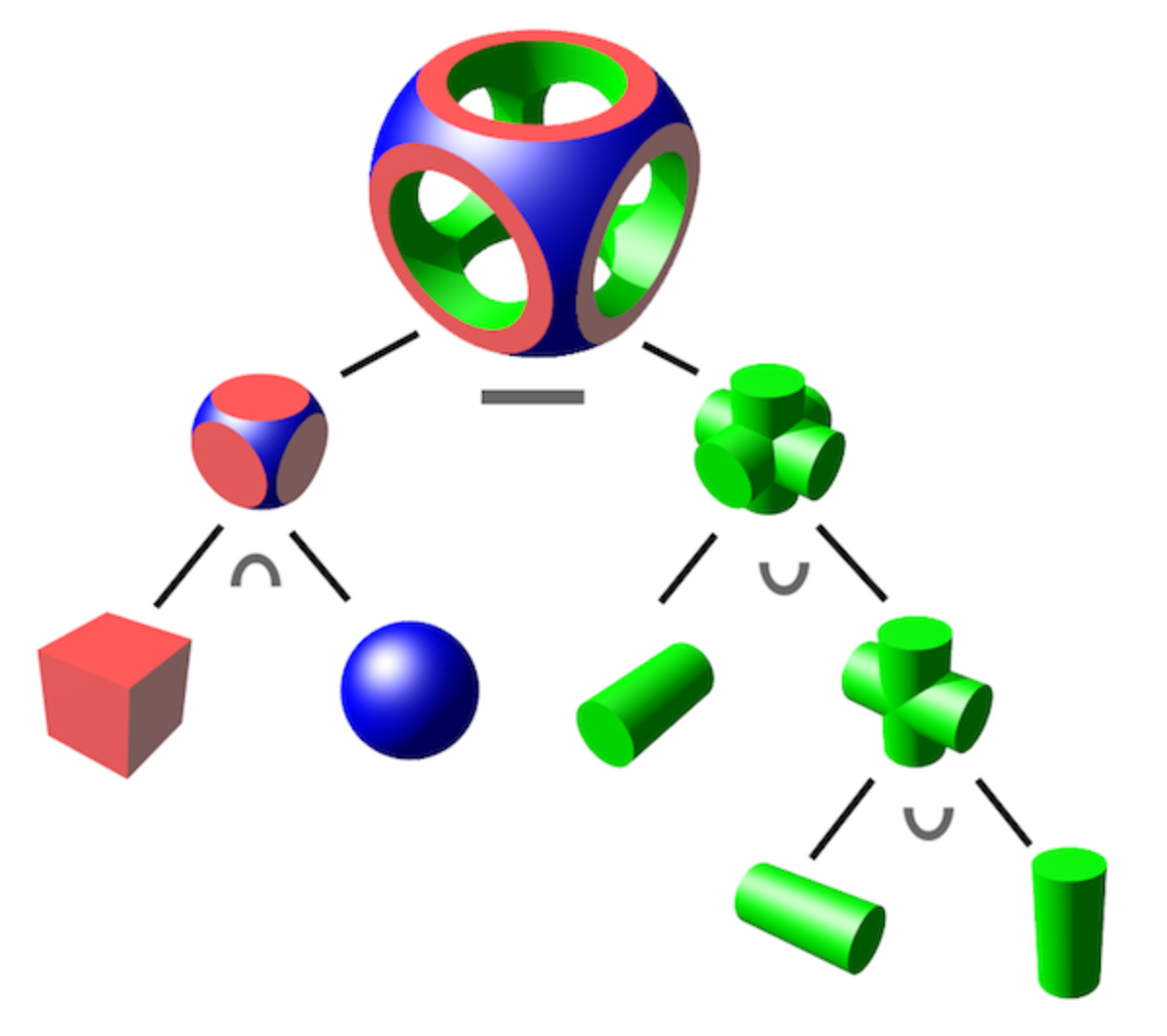 - 三种基本运算:并、与、减
- 三种基本运算:并、与、减
float intersectSDF(float distA, float distB) {
return max(distA, distB);
}
float unionSDF(float distA, float distB) {
return min(distA, distB);
}
float differenceSDF(float distA, float distB) {
return max(distA, -distB);
}
模型变换¶
- 平移很简单,直接改变生成 SDF 的坐标参数即可
float sdSphere( vec3 p, float s ) { return length(p)-s; } - 也可以对采样点施加反方向的偏移来实现
mat4 rotateY(float theta) { float c = cos(theta); float s = sin(theta); return mat4( vec4(c, 0, s, 0), vec4(0, 1, 0, 0), vec4(-s, 0, c, 0), vec4(0, 0, 0, 1) ); } float sceneSDF(vec3 samplePoint) { float sphereDist = sphereSDF(samplePoint / 1.2) * 1.2; vec3 cubePoint = (invert(rotateY(iGlobalTime)) * vec4(samplePoint, 1.0)).xyz; float cubeDist = cubeSDF(cubePoint); return intersectSDF(cubeDist, sphereDist); } -
这里就单独对正方体的采样点进行偏移,来实现正方体旋转的效果
-
缩放(以世界坐标系的原点为中心点)、
- 想要实现其他中心点可以通过平移缩放平移来实现
-
对一个 SDF 进行缩放 n 倍率
float sphereDist = sphereSDF(samplePoint / n) * n;- 通过
/n来实现模拟放大 - 通过
*n来修正距离
- 通过
-
非均匀缩放(比如对 x 缩放,不对 yz 修改)
- 非均匀缩放修正距离失真更为复杂
- 修正的目的是避免高估(这可能导致跳过表面,渲染出错),又尽可能保持安全的最大步长(提高效率)
- 由于精确计算复杂度较高,因此使用保守估计方式,采用最小缩放因子进行修正 \(\mathrm{dist}=\mathrm{SDF}(p^{\prime})\times\mathrm{min}(s_x,s_y,s_z)\) 即不均匀缩放不同维度中最小的缩放因子
显示表述¶
- 直接表示
- 规定平面图形和二维到三维的映射

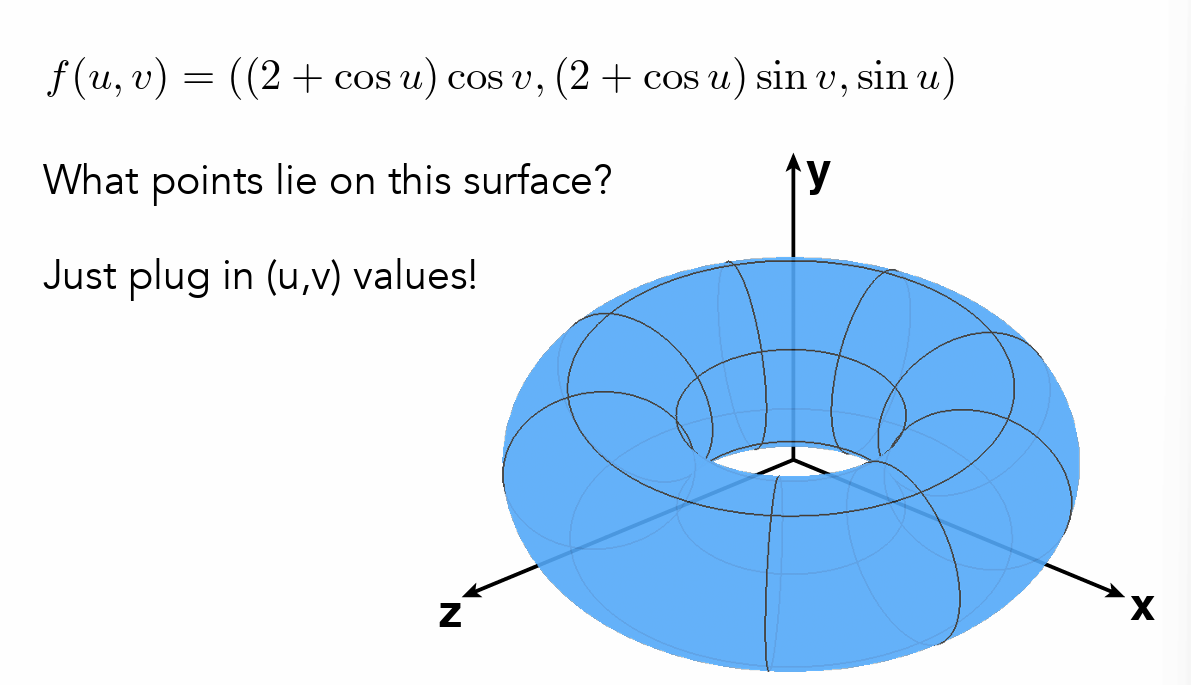
- 区别隐式曲面与显示曲面的关键就在于是否可以直接表示出所有的点
- 显示的问题在于不容易判断一个点在不在几何体上
- 点云表示

- 多边形面

贝塞尔曲线¶
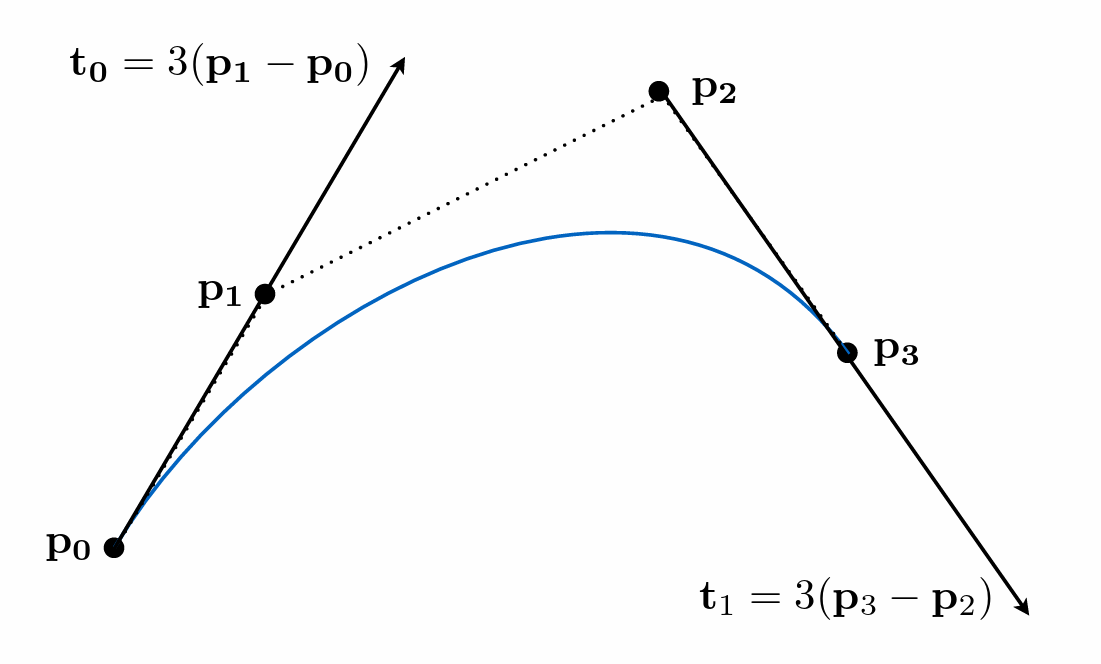
- 两个端点、方向(切线)确定一条曲线
- 时间 t 贝塞尔曲线上的点
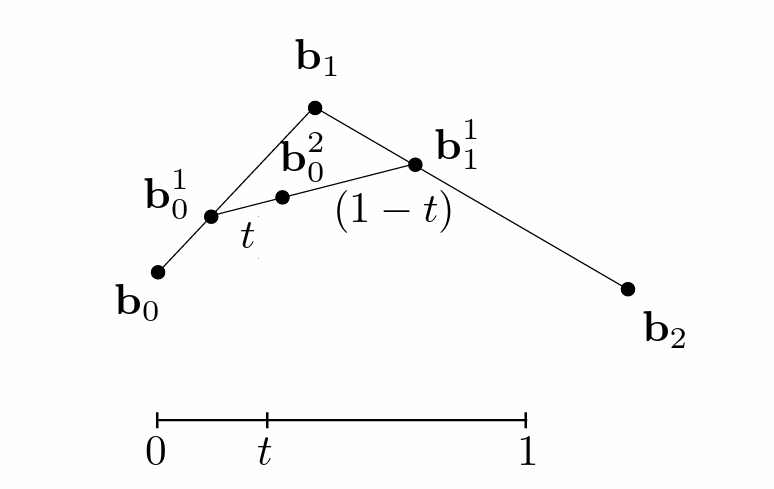
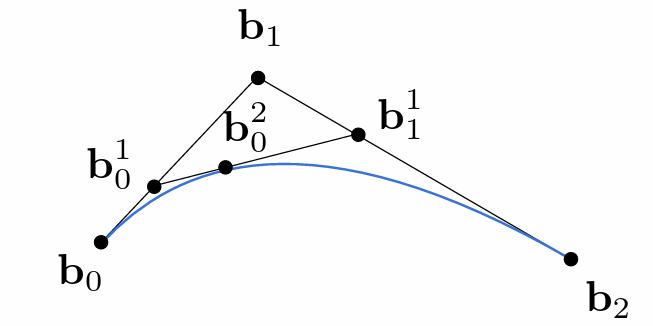
- 将每个时间 t 的点连起来就得到了贝塞尔曲线
- 四点
- 多次 t 划分直至剩下一个点
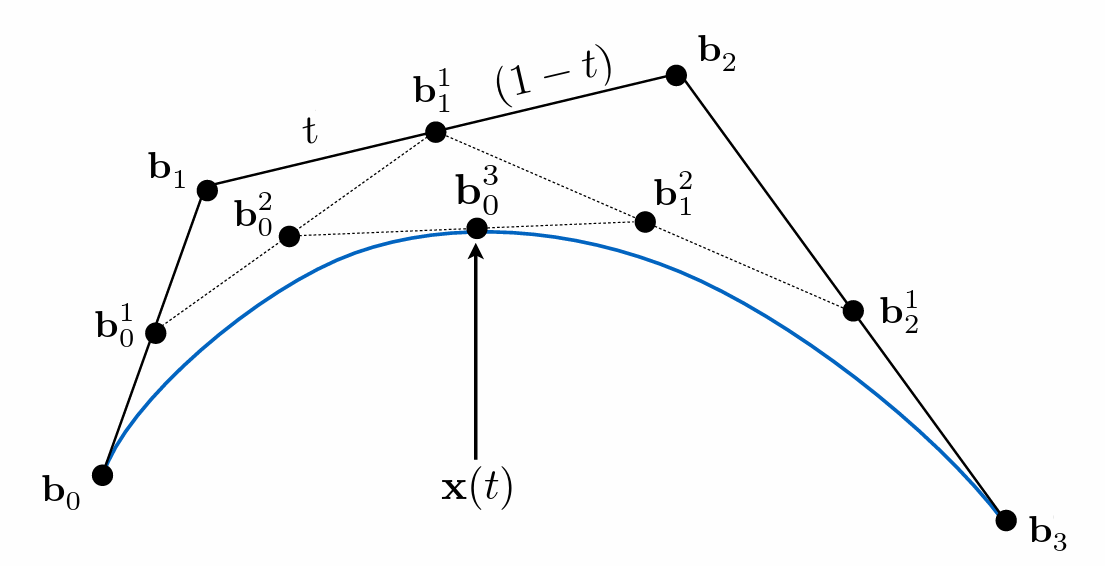
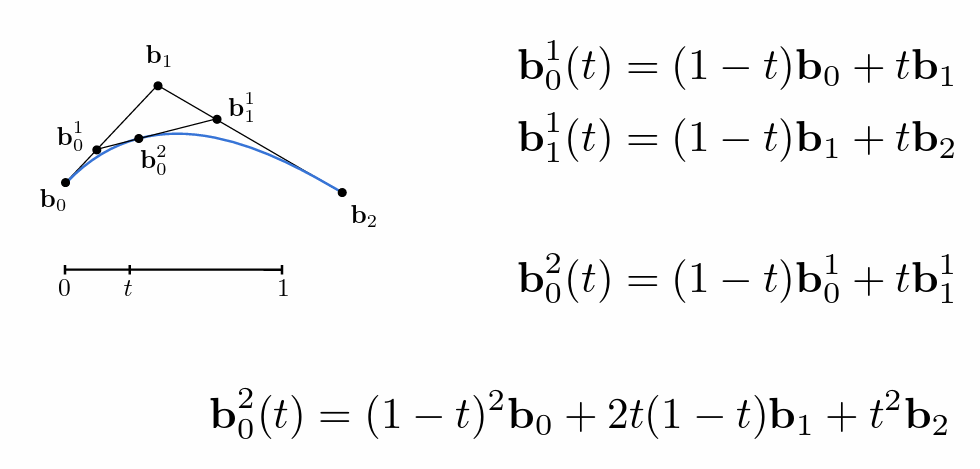
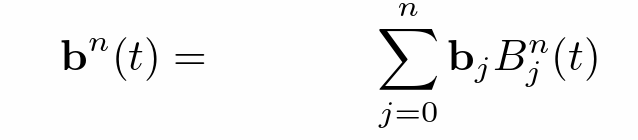
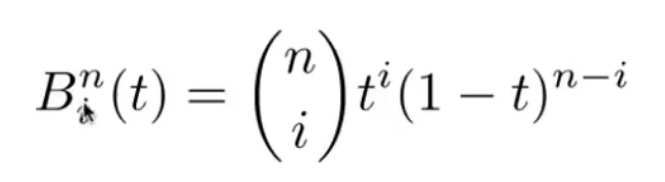
- 分段:点过多时不易于控制;贝塞尔曲线还具有凸包性质,在几个控制点限定的范围之内
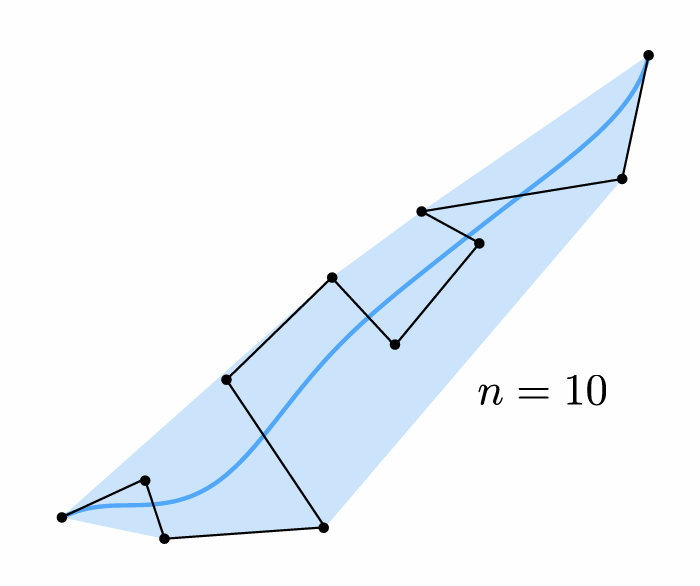
- 直接分段不够平滑(4 个点一段)

- c0连续:曲线首尾相接
-
c1连续:切线连续
-
不同的绘制方式
void naive_bezier(const std::vector<cv::Point2f> &points, cv::Mat &window) { auto &p_0 = points[0]; auto &p_1 = points[1]; auto &p_2 = points[2]; auto &p_3 = points[3]; for (double t = 0.0; t <= 1.0; t += 0.001) { auto point = std::pow(1 - t, 3) * p_0 + 3 * t * std::pow(1 - t, 2) * p_1 + 3 * std::pow(t, 2) * (1 - t) * p_2 + std::pow(t, 3) * p_3; window.at<cv::Vec3b>(point.y, point.x)[2] = 255; } } cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) { std::vector<cv::Point2f> _control_points = control_points; for(int i=0;i<_control_points.size()-1;i++) { for(int j=0;j<_control_points.size()-i-1;j++) { _control_points[j] = (1-t)*_control_points[j] + t*_control_points[j+1]; } } return _control_points[0]; }
曲面¶
- 贝塞尔曲面
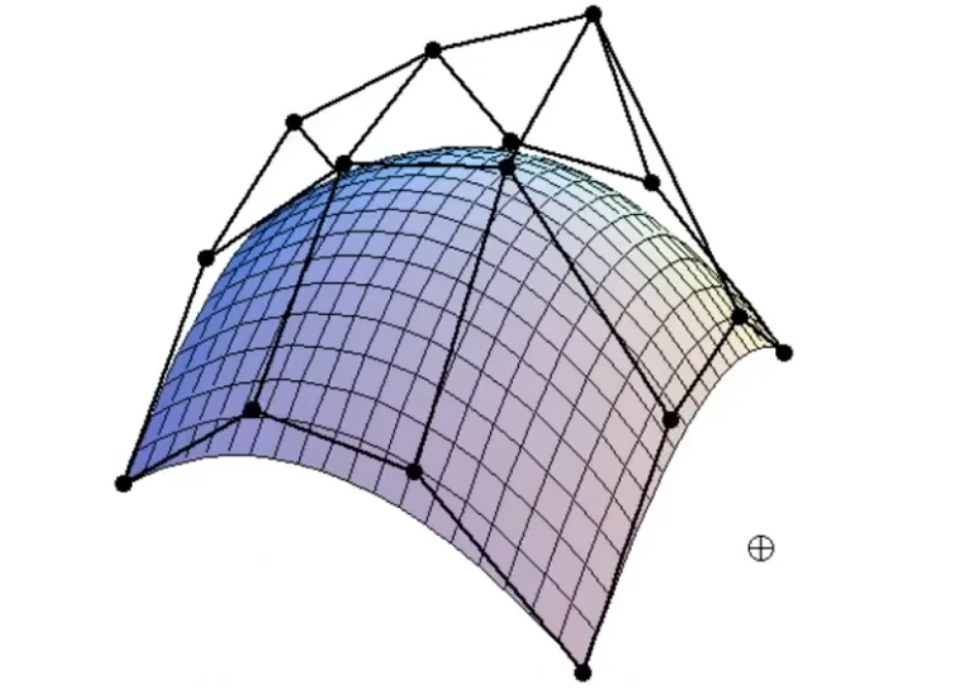
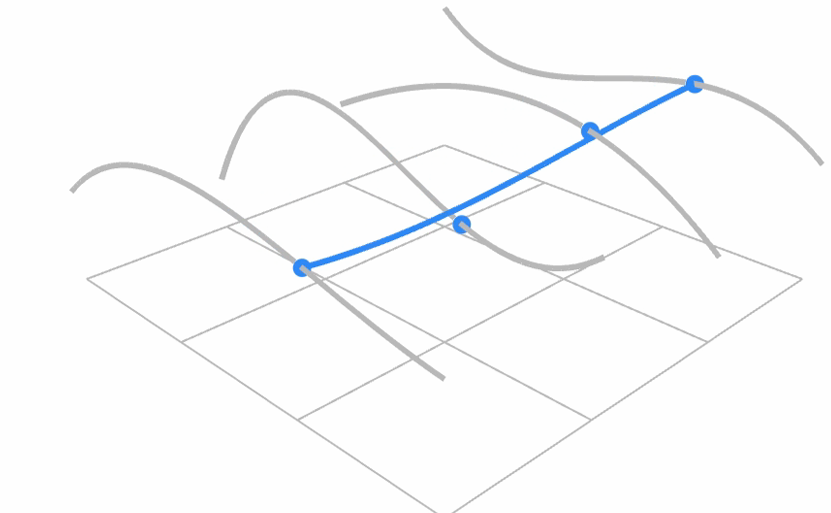
- 双重贝塞尔曲线
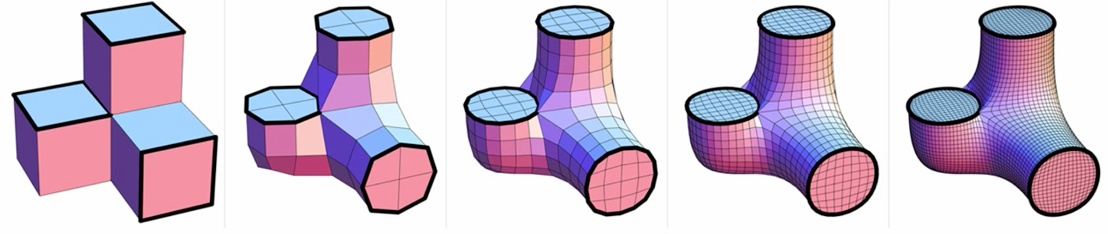
曲面细分¶
- 曲面细分的基本思路
- 划分为更多三角形并调整位置使得更加贴近原先的图像
-
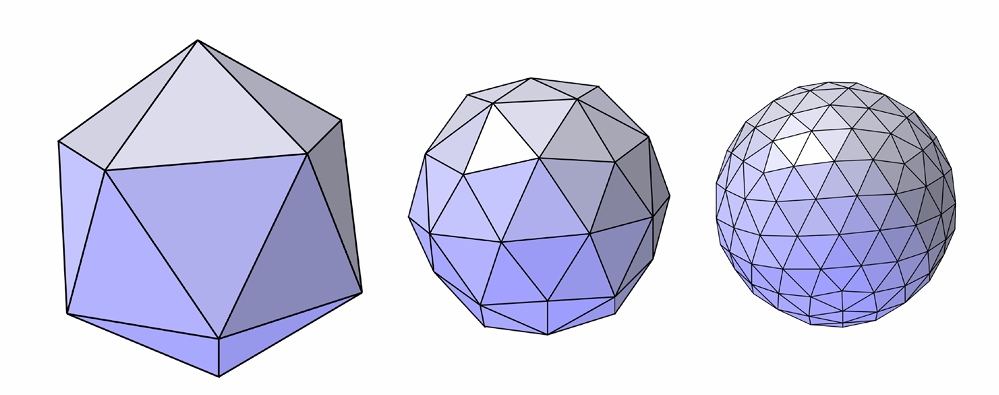
-
曲面loop 细分
- 新顶点(如每条边的中点)的位置由周围旧顶点的位置计算得到
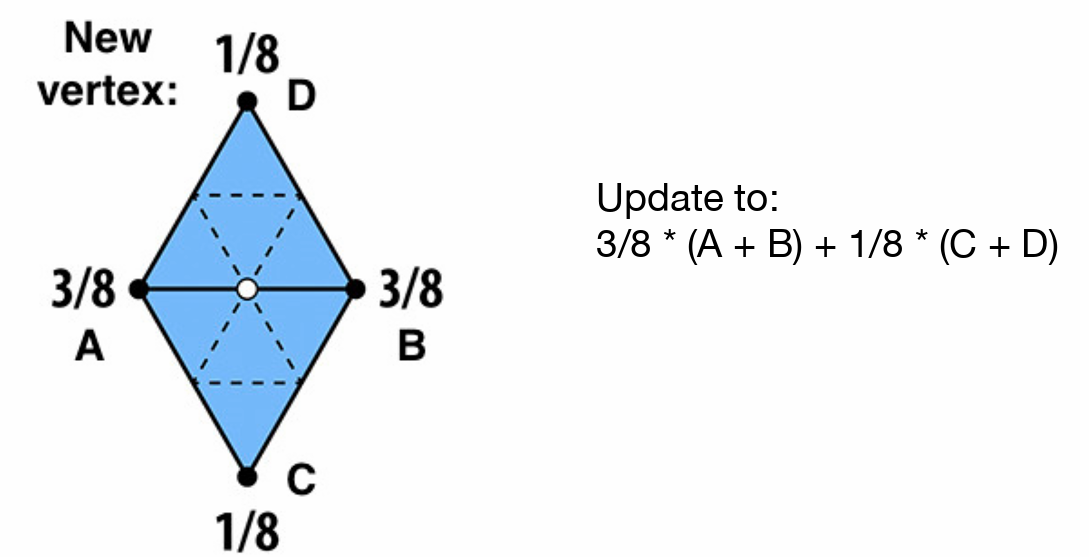
- 由周围旧点的加权平均得到
- 旧顶点的位置由原先的位置和周围点的位置决定
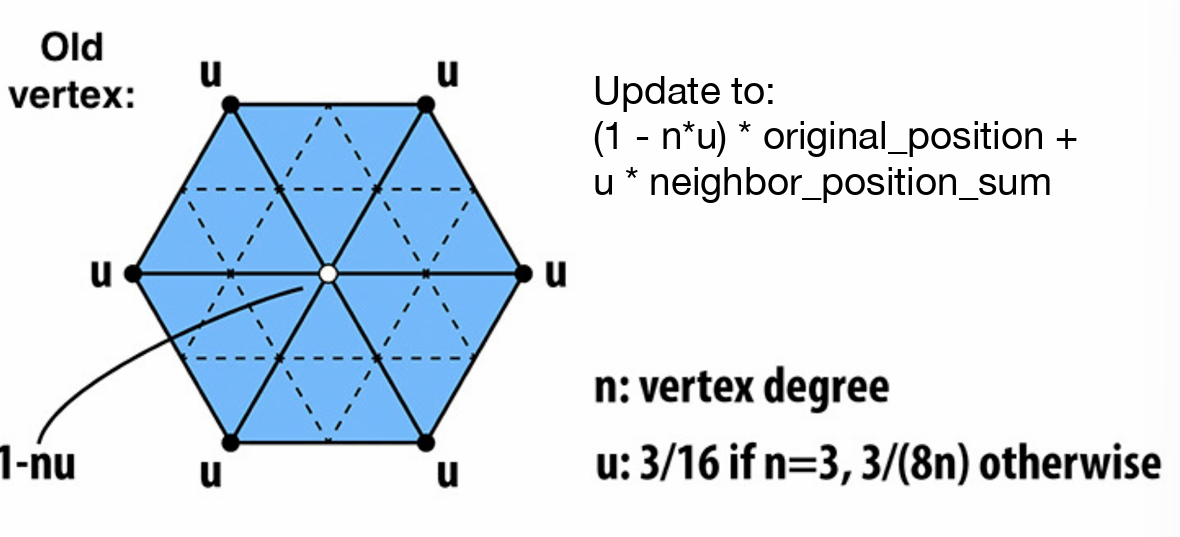
- 相信自己也相信周围旧点,计算加权平均
- Catmull-Clark 细分(处理四边形面)
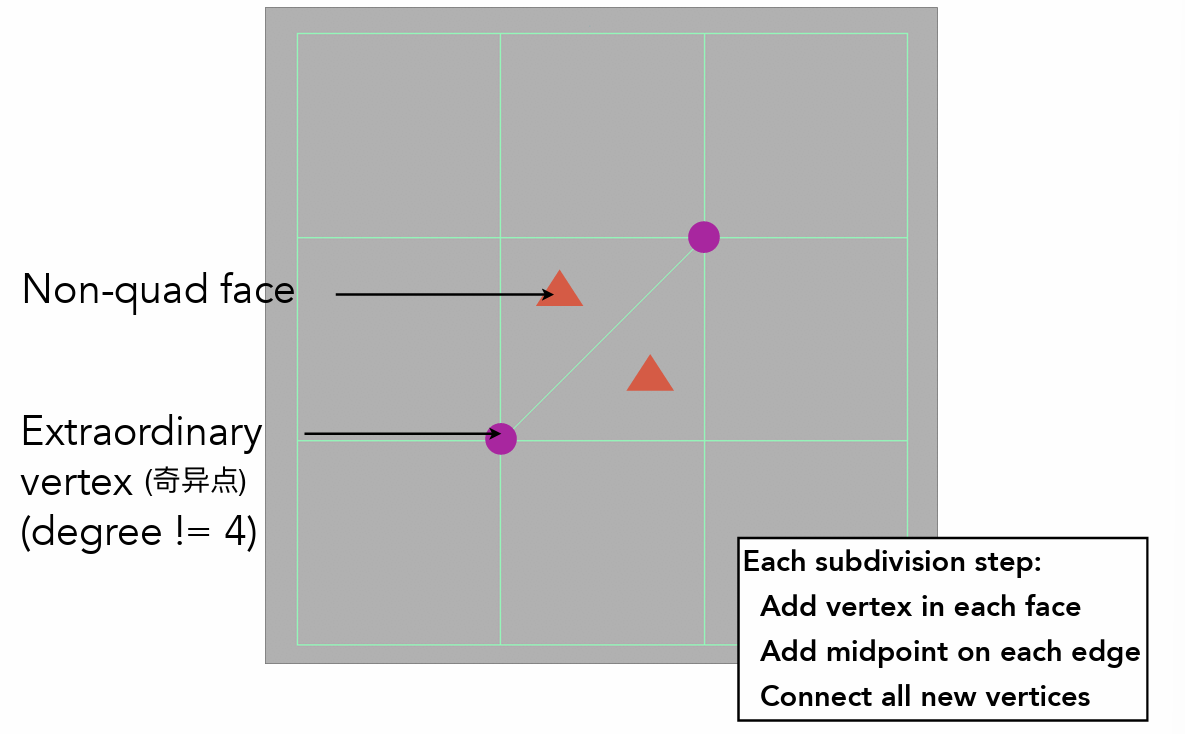
- 称度不为 4 的点为奇异点
- 连接边、面的中点
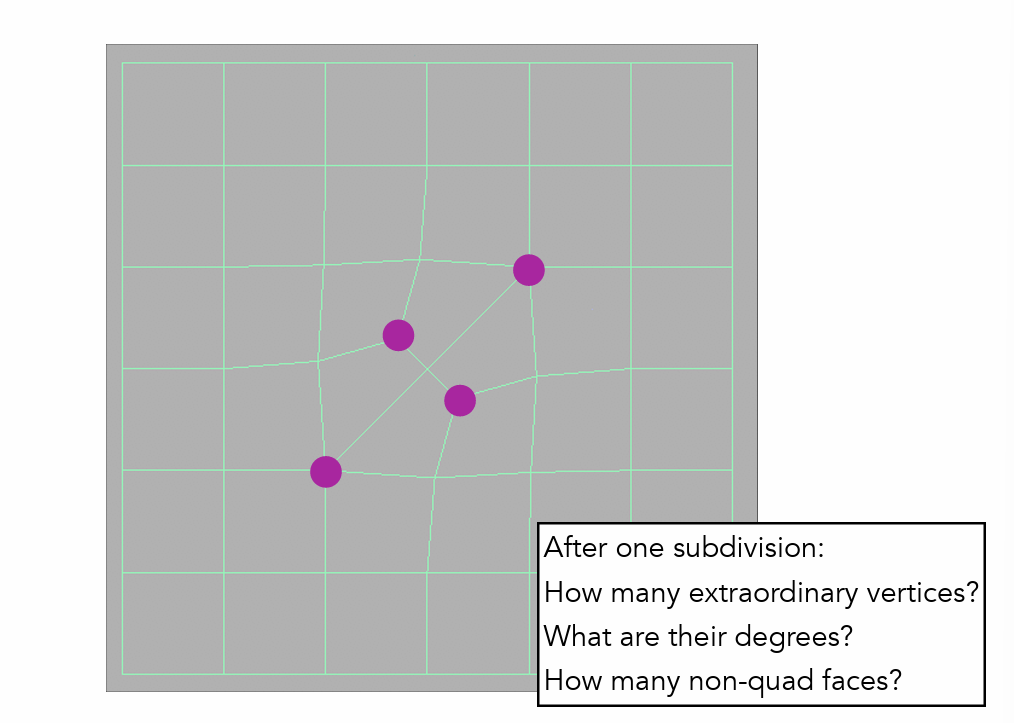
- 非四边形会产生奇异点,非四边形面会在细分之后消失(做一次细分之后只有四边形面了,因此之后奇异点数目不会再发生变化,即只有第一次细分时变化)
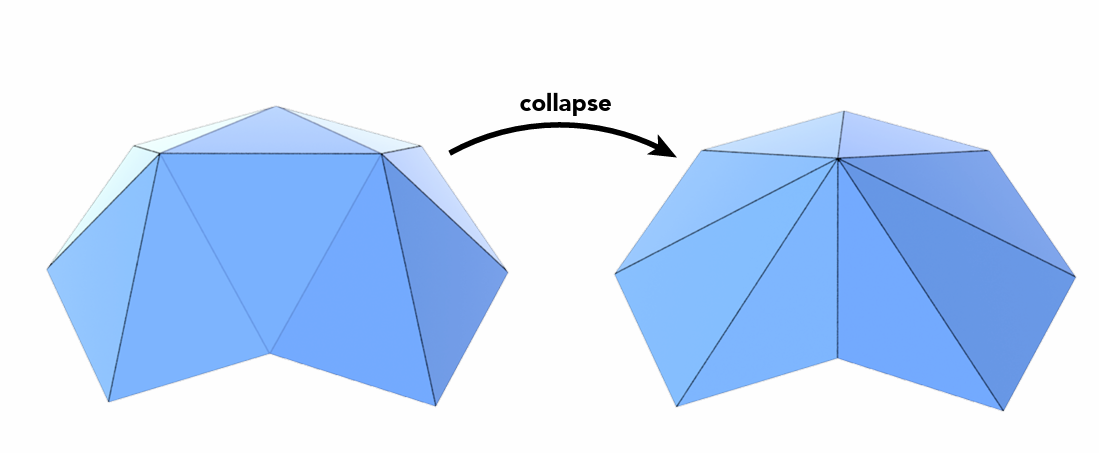
曲面简化¶
- 边坍缩
- 删去边,捏成一个点
- 用偏差(二次误差)计算新位置(到原先各面的平方和最小)
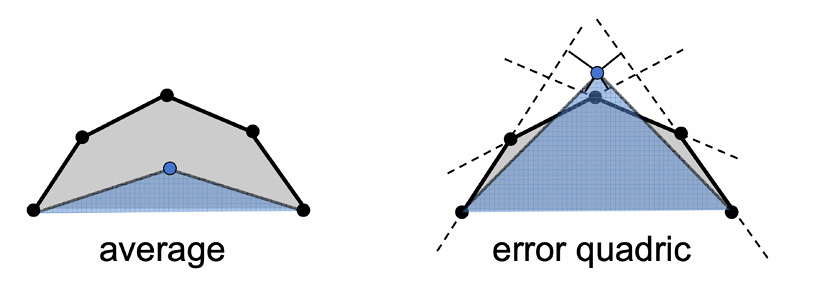
- 优先坍缩造成二次误差最小的边(使用优先队列)
曲面正则化¶
- 曲面正则化(直到曲面简化,减少细节丢失)