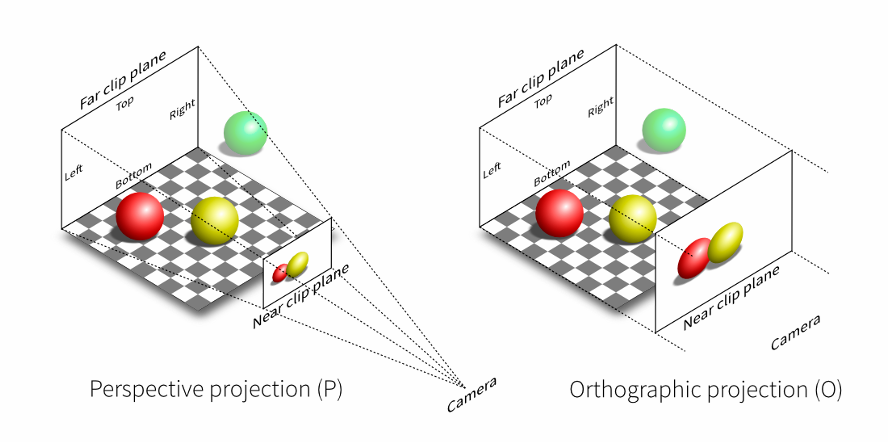
线性代数与变换

线性代数基础¶

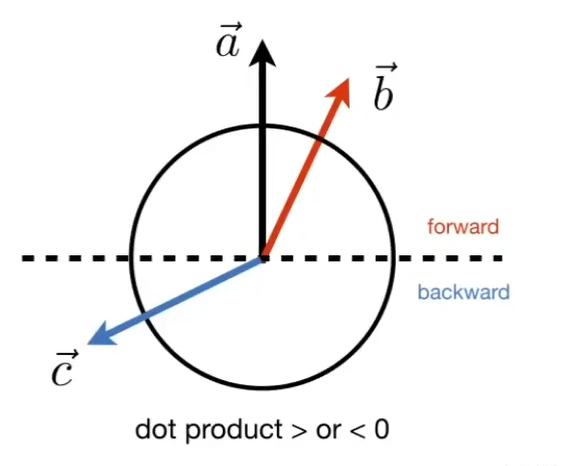
点乘主要用来求两个单位向量的夹角
可以用于判断两个方向的接近程度（夹角），判断前后
射线与球面求交：给定射线 \(P(t)=e+td\) 和一个隐式曲面 \(f(p)=0\)，当射线上的点满足方程时，交点便产生了 \(f(p(t))=0\quad or \quad f(e+td) = 0\)
射线与三角形求交：通常直接用三点式三角面和射线联立，判断是否与该平面有交点，但具体是否在三角形内还要额外进行判断
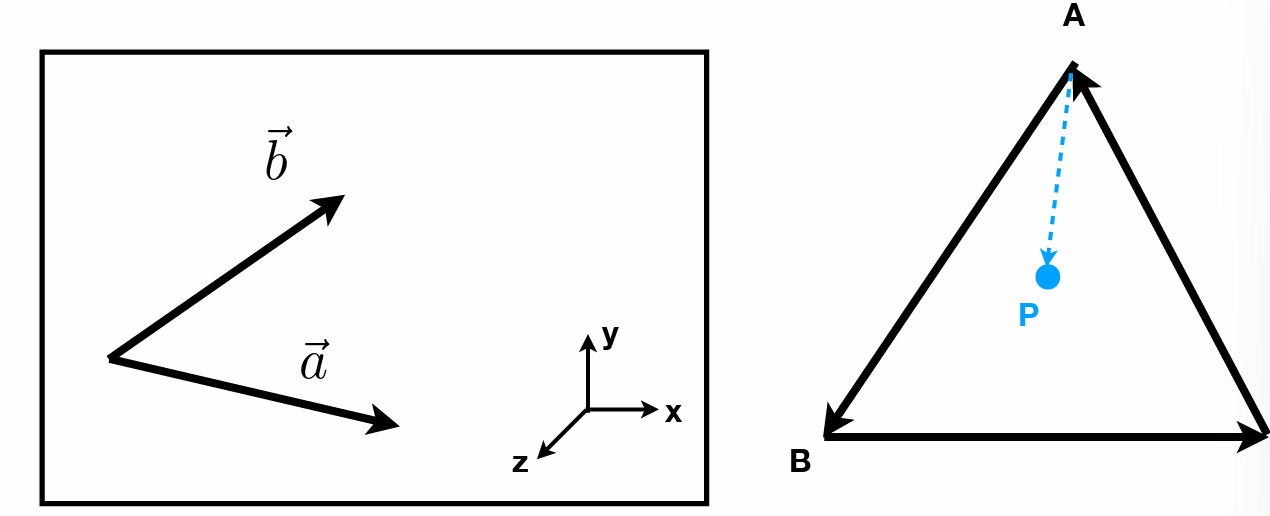
叉乘
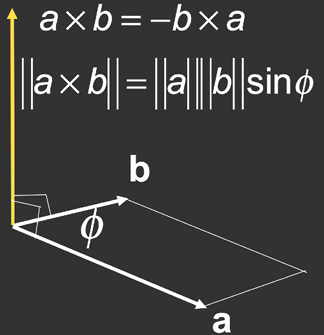
可以用于求出三维直角坐标系 (右手坐标系)，指导两个方向就能推导出第三个方向 \(\overrightarrow{x}\times \overrightarrow{y}=\overrightarrow{z}\)
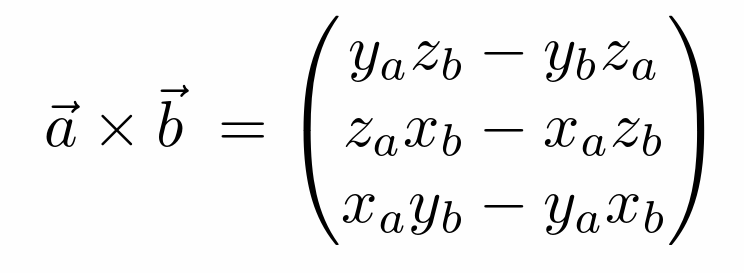
三角形面积：\(A = \frac{1}{2} \begin{vmatrix} x_b-x_a & x_c-x_a \\ y_b-y_a & y_c-y_a \end{vmatrix}\)，abc 三点逆时针排列时 A 为正，反之为负。
判断左右、内外（p 在三角形三条边的同一边（左边））
- 三角形内的点可以表示：\(P = \alpha a+\beta b+ \gamma c\quad where \quad \alpha+\beta+\gamma = 1 \quad \alpha, \beta, \gamma \lt 1\)
矩阵
乘法符合结合律、分配律，没有交换律
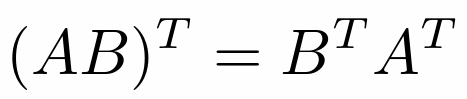
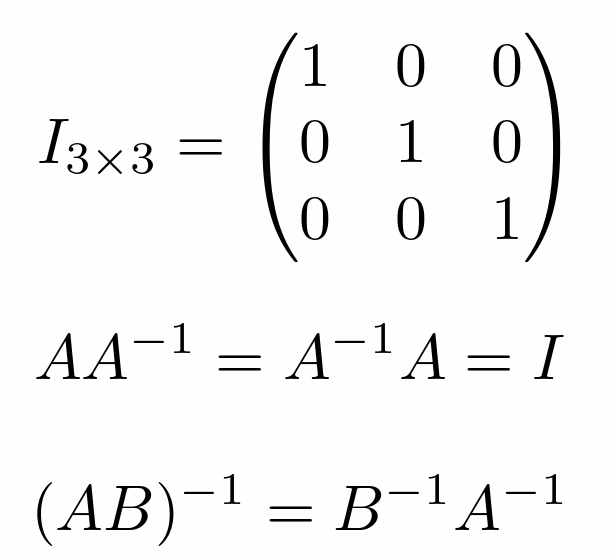
表示向量运算

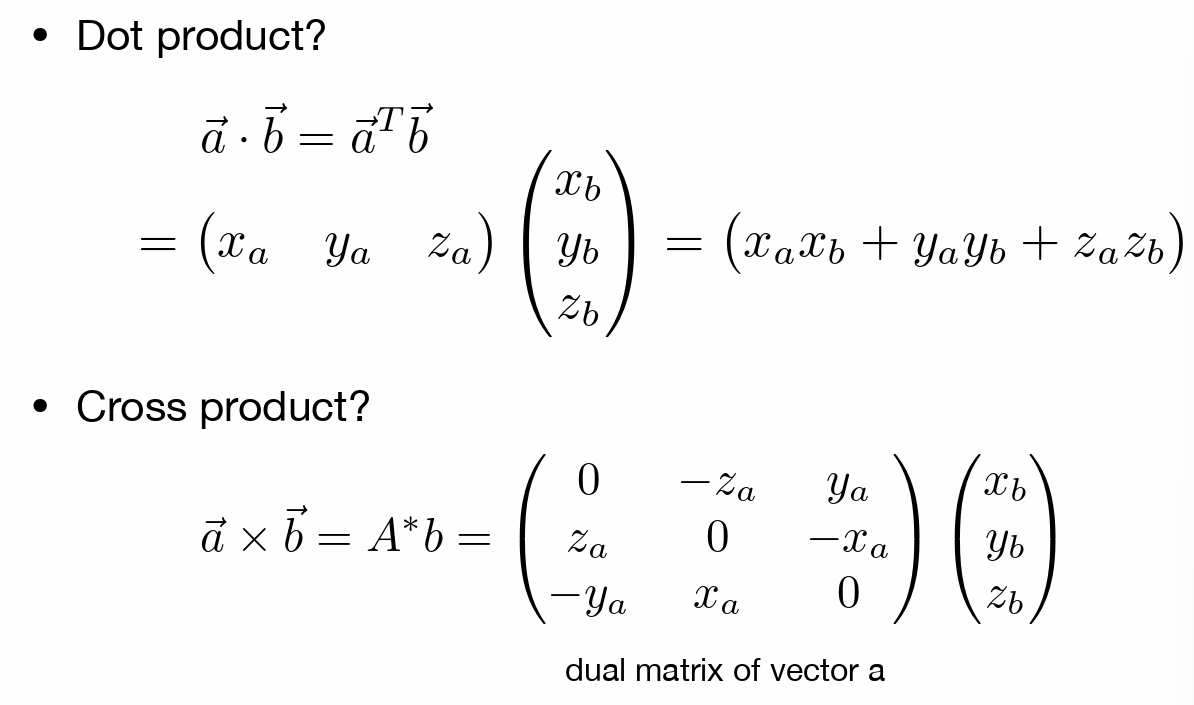
变换¶

变换基础¶

缩放
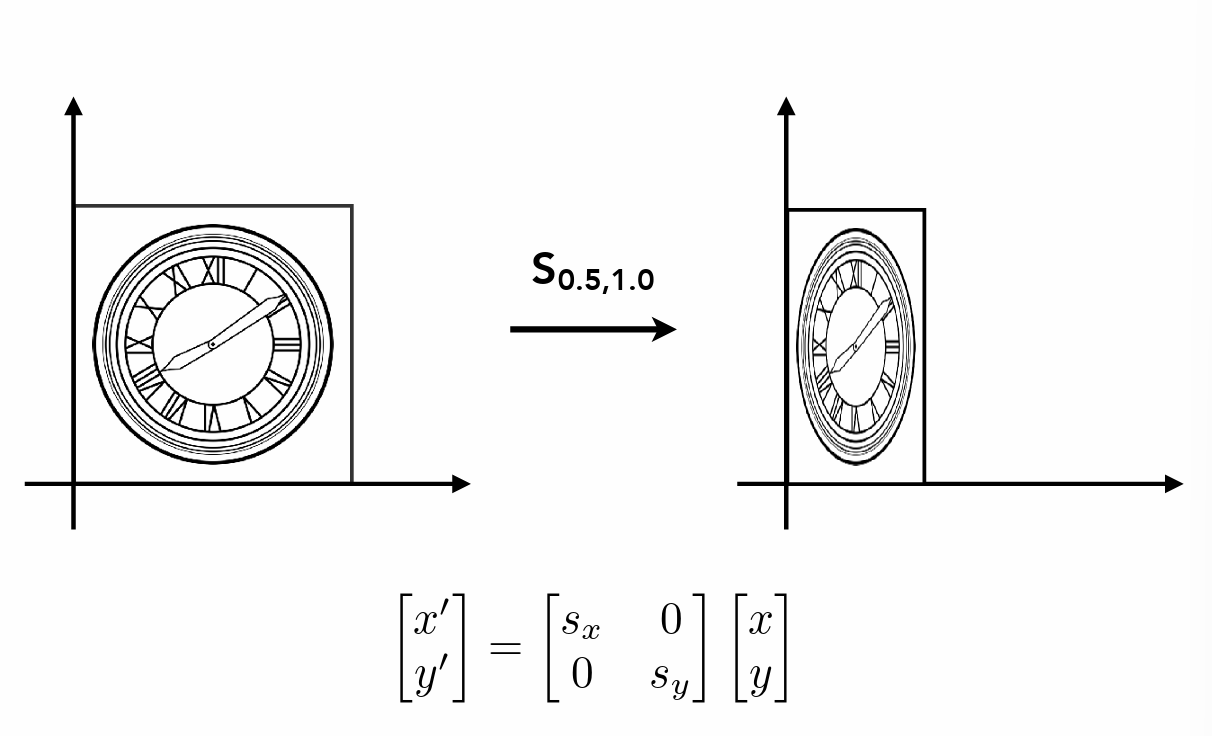
s 为负数时也可以用于图像的翻转
变形（切变）
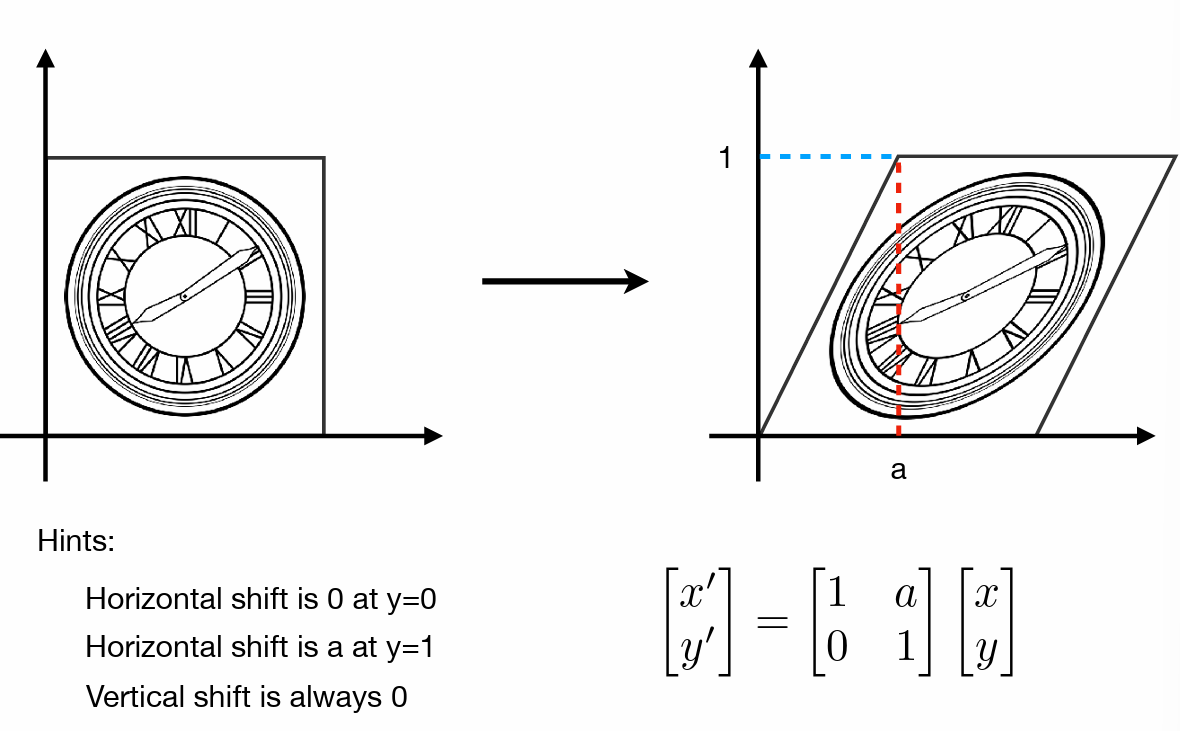
旋转（以原点为中心点）
旋转矩阵的转置等于逆（正交矩阵）

齐次坐标¶

目的：用矩阵乘法（线性变化）无法表示平移
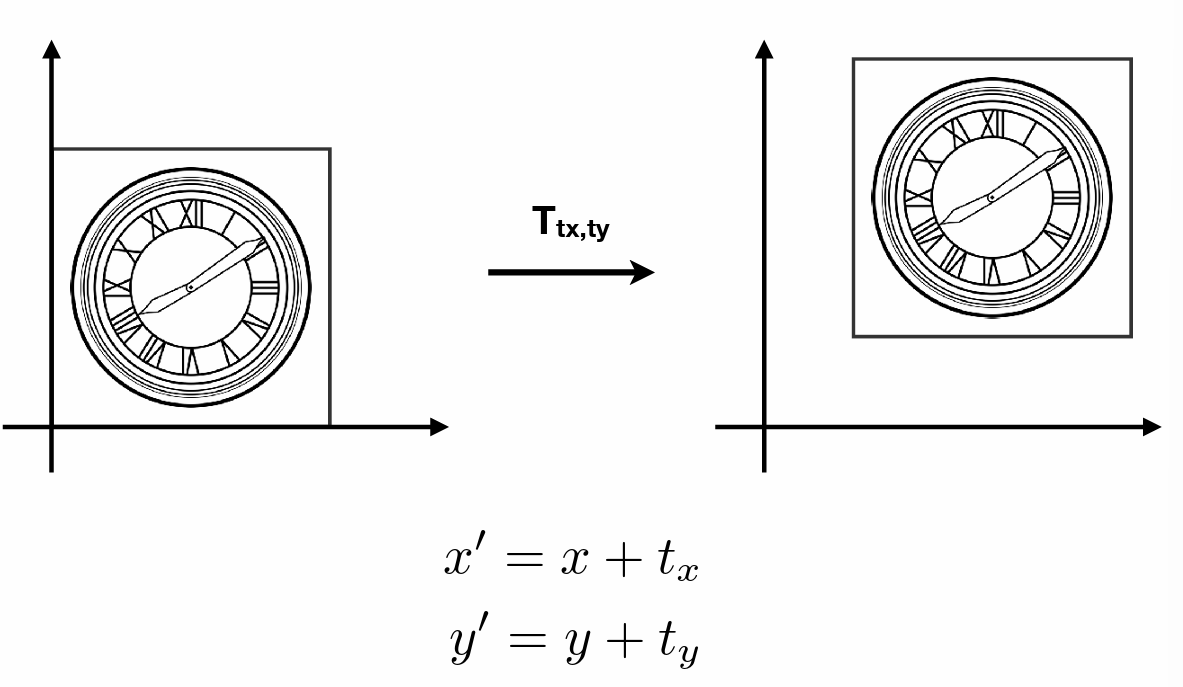
用三维向量表示二维坐标
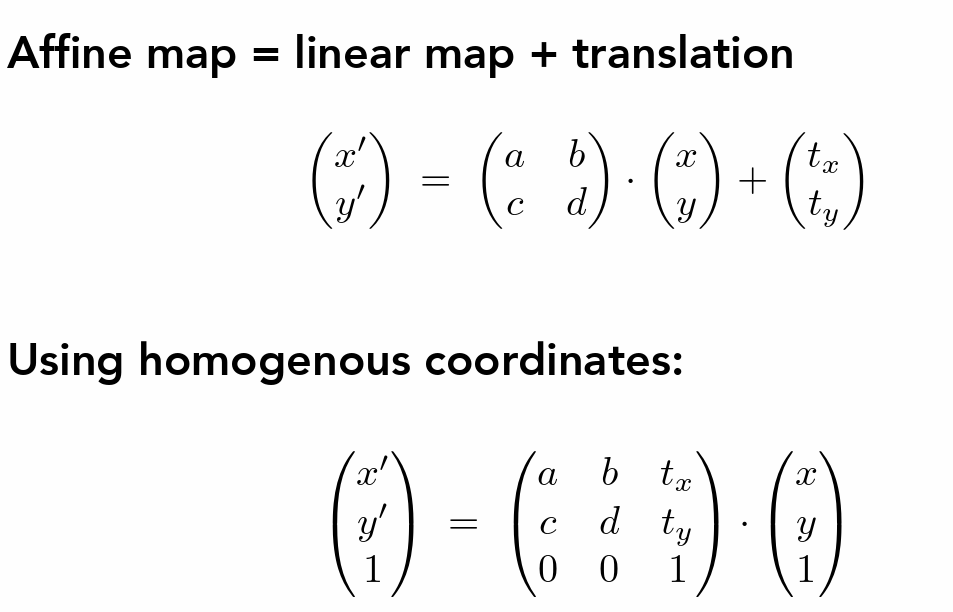
- 先线性变化再平移
通过第三维度是 1/0 来判断是点还是向量，向量的第三维为 0，因而向量不会因为平移而发生改变
- 点加点表示两个点的中点（规格化，保证第三维为 1）
逆矩阵可以表示逆变换
连乘（注意先进行的在右侧）
组合变换通常先旋转后平移
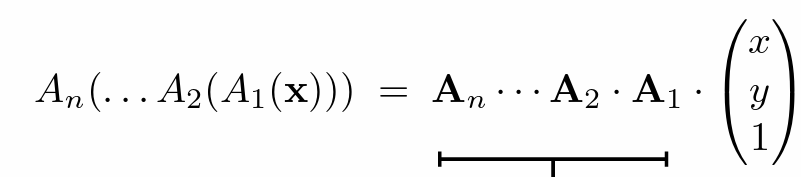
以任一点为原点旋转

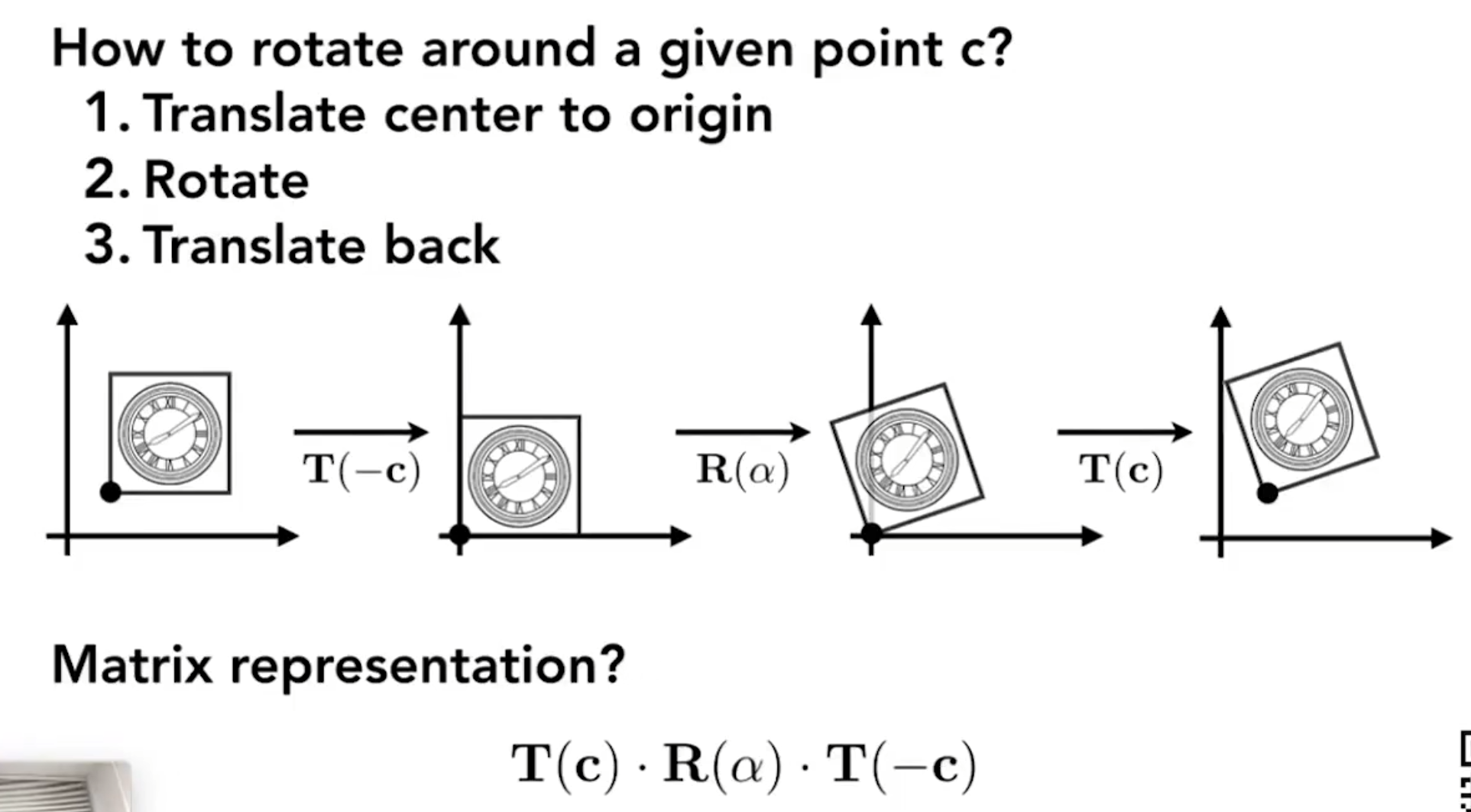
三维变换¶

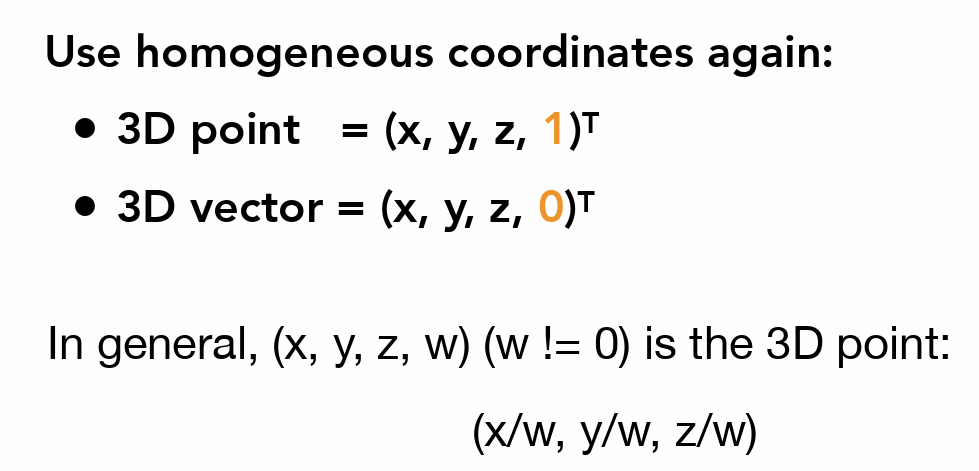
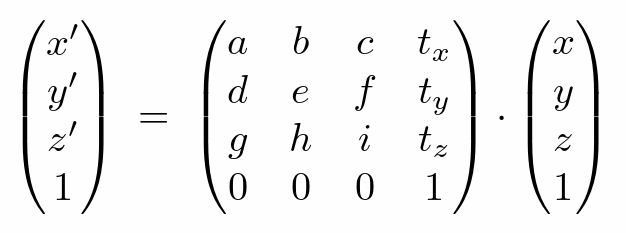
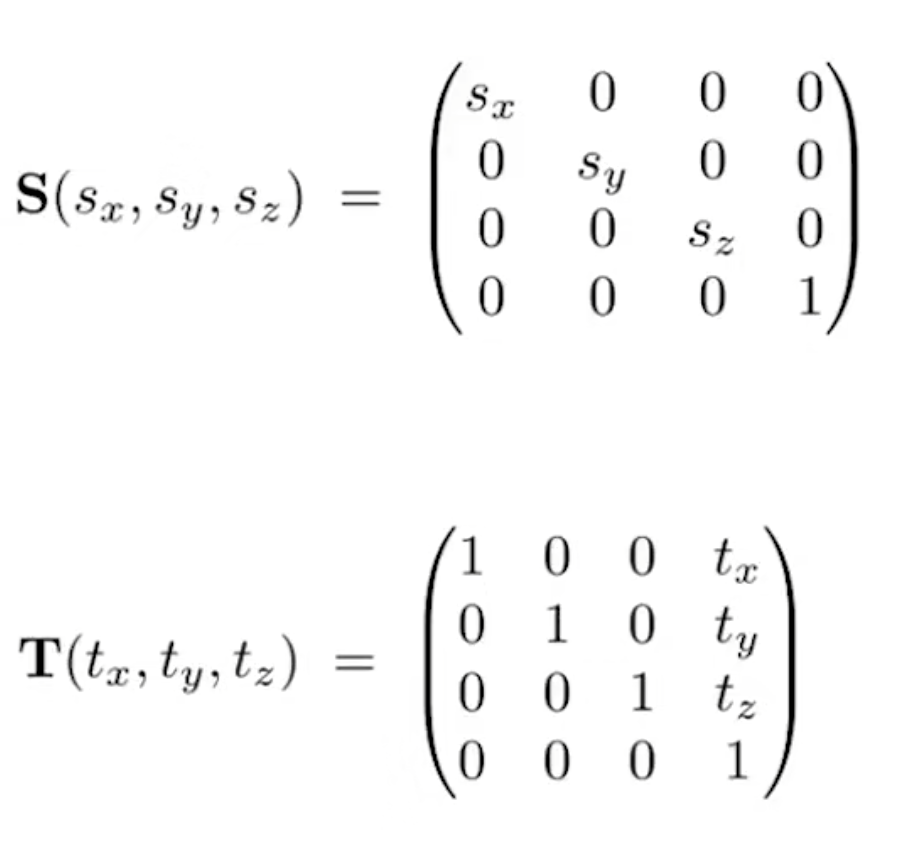
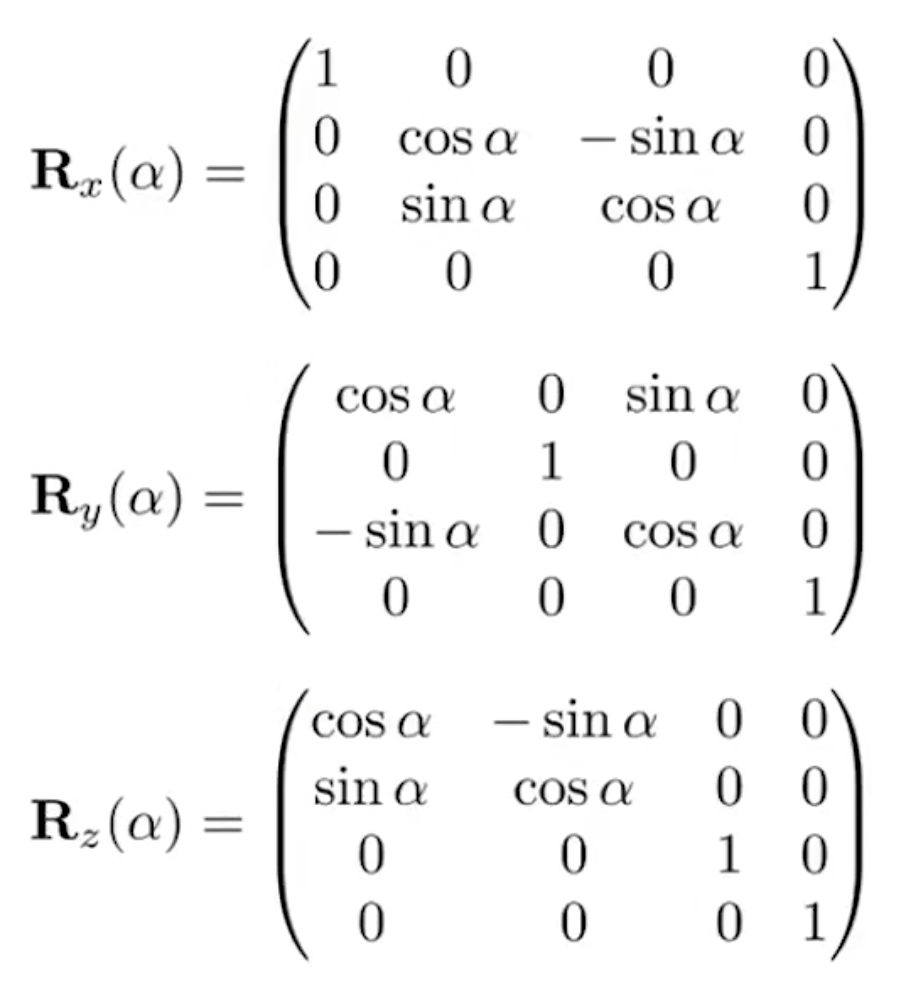
罗德里格旋转公式（绕任一过原点的向量 n 旋转）
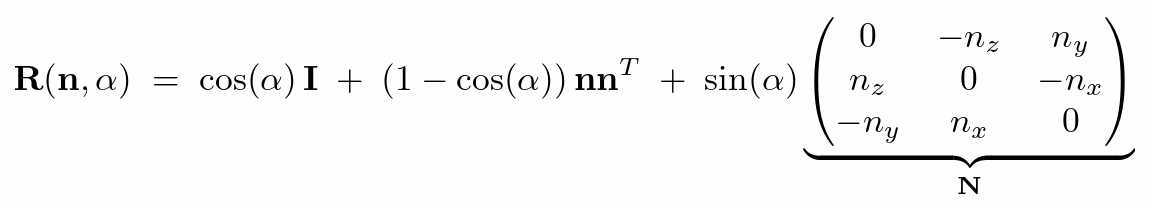
以上矩阵变换的方式不适用于线性插值（并不是线性连续变化的），如果需要动画、插值需要使用四元数

视图变化¶

mvp 矩阵变化
代表了模型（Model）、视图（View）、投影（Projection）三个变换矩阵的乘积
模型矩阵：将对象的局部坐标系（模型空间）转换到世界坐标系（世界空间）。这个变换涉及到物体的位移、旋转和缩放。
视图矩阵：将世界坐标系转换到观察者（或摄像机）的坐标系（视图空间）。这个变换通常涉及到将摄像机（视点）移动到原点，并进行必要的旋转，使得观察者面向场景的特定部分。
投影矩阵：将视图空间中的坐标转换到裁剪空间，进而通过透视除法转换为归一化设备坐标（NDC）。这个变换定义了一个可视范围，通常是一个锥形体（透视投影）或者一个长方体（正交投影）。
相机参数（视图矩阵）
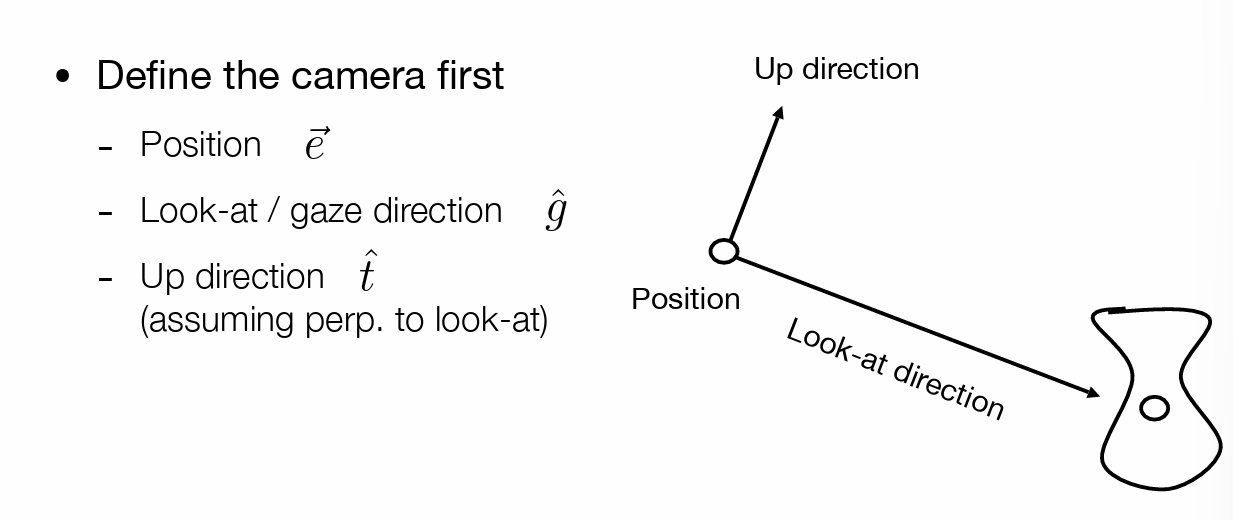
- position：原点位置
- look-at：相机指向
- up direction：相机头方向（即绕指向的旋转，就是相机上方的指向）
固定相机的位置，移动物体，标准位置：
回正过程（同时移动相机和物体，相对关系不变）
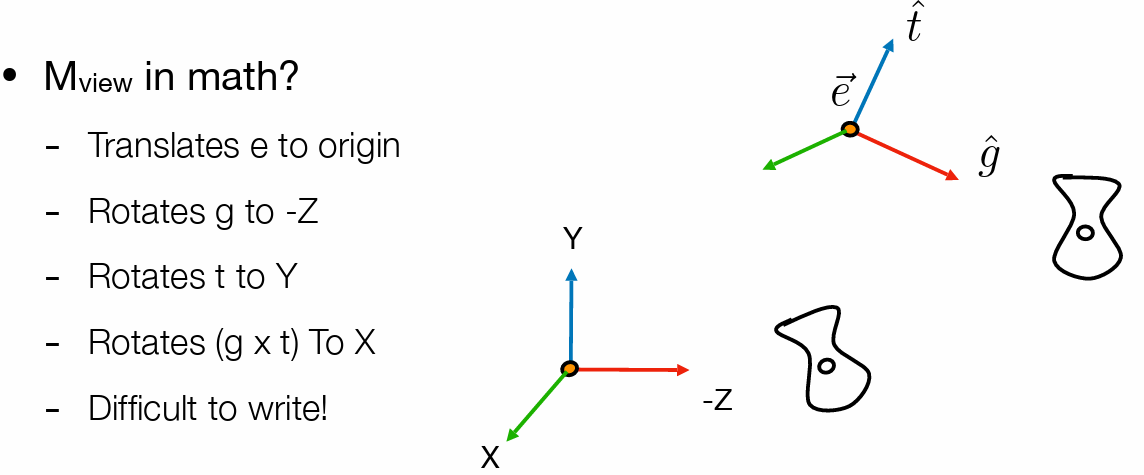
- 先平移再旋转（逆矩阵便于确定旋转方式）

投影变化¶

正交投影¶

平行线仍然平行
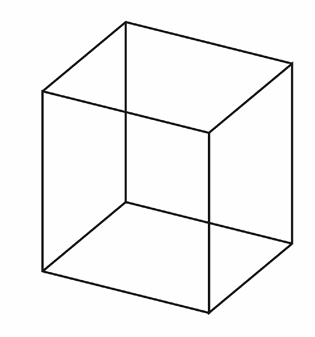
看作摄像机无限远，平行投射
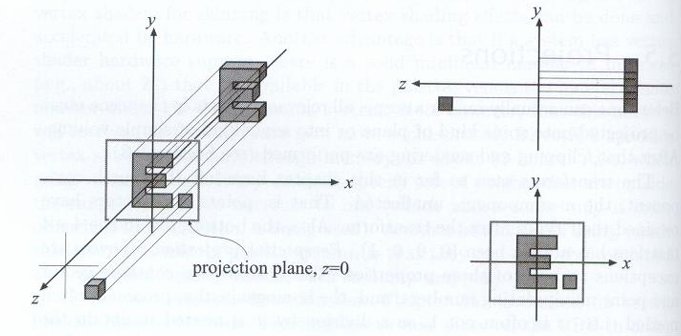
相当于扔掉 z 坐标
长方形投影到标准正方体（观测矩阵）
先平移到原点，再进行缩放
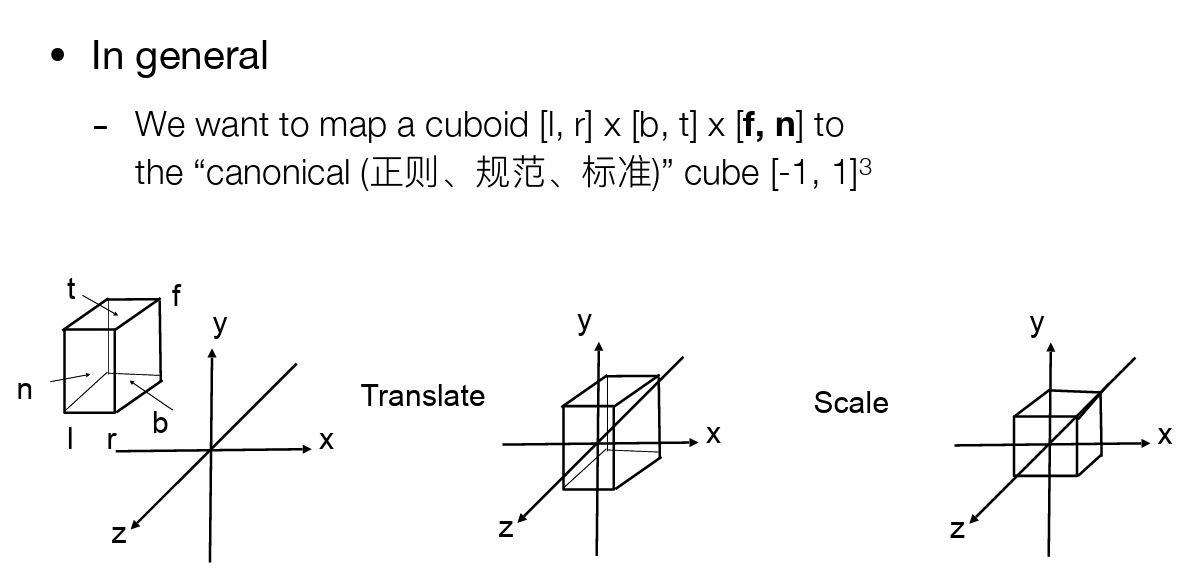
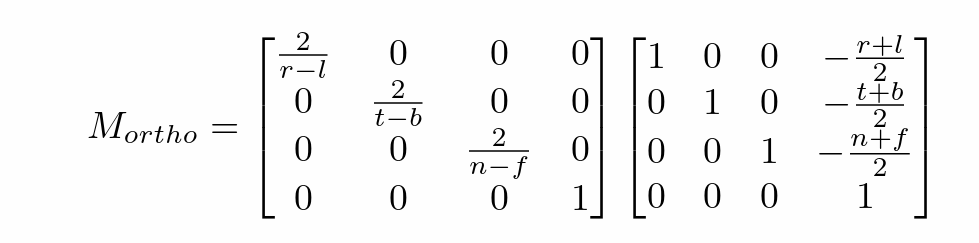
归一化到长度为 1（-1,1 的立方体），具体的长宽由 fov 和比率计算得到
- 通常由 fov 得到 y，再乘以比率得到 x；

透视投影¶

近大远小
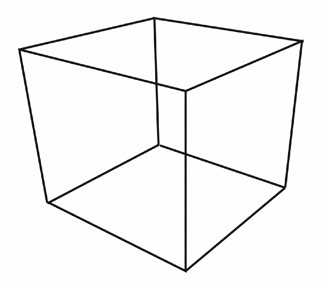
四棱锥投射
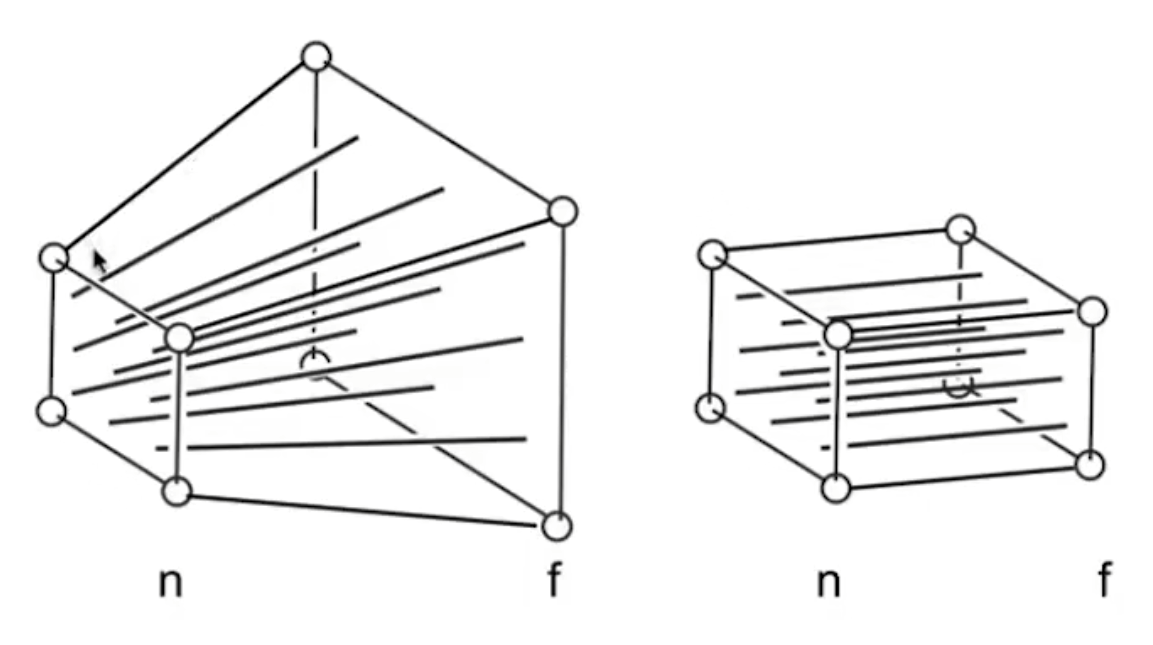
先将锥形“挤压”为长方体，再做正交投影
坐标变换
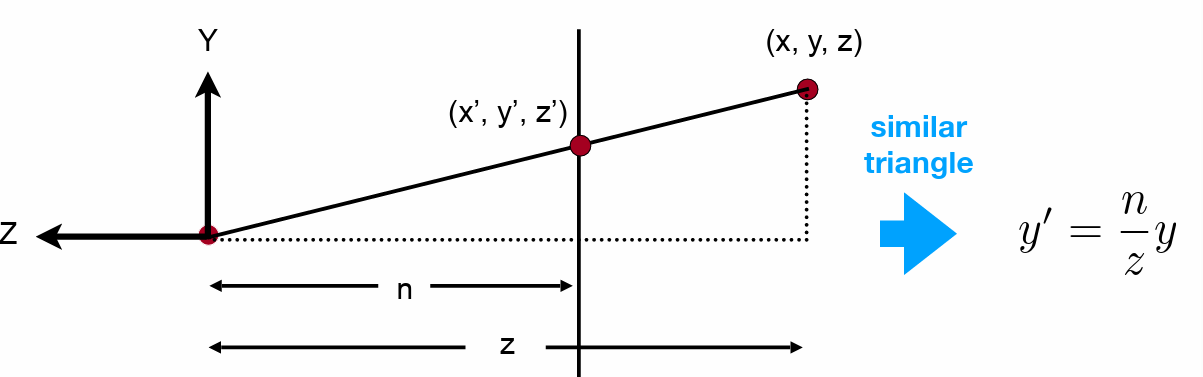
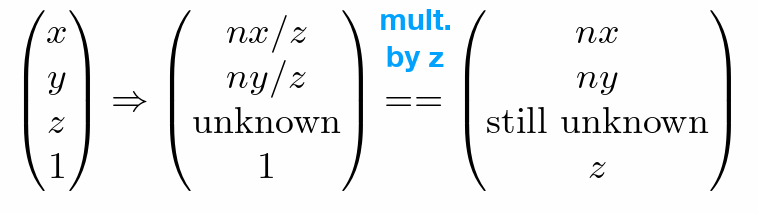
变换矩阵
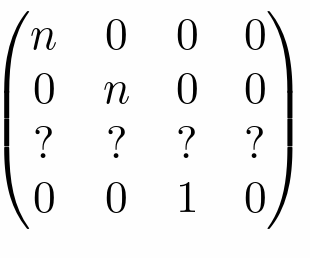
- 还无法确定 z 如何变化
明确的是在近/远平面的 \(z\) 均不发生变化
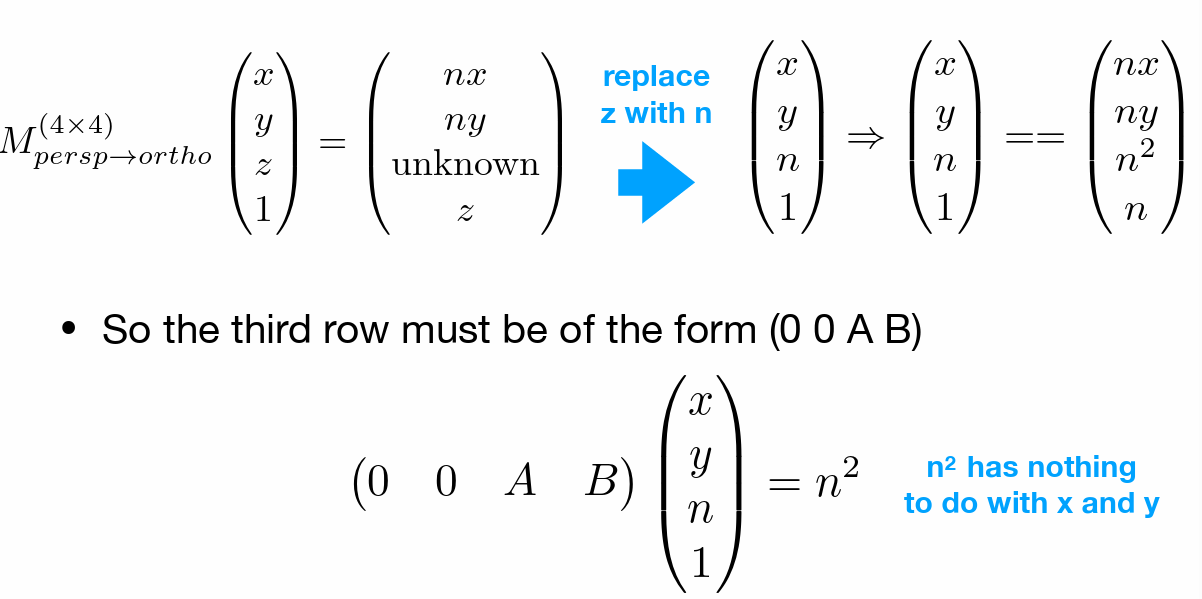
- 可知与 xy 无关，前两项为 0（利用近平面上变化前后的\(z\) 不发生变化来进行计算）
远平面的 xy 发生压缩，但是 z 不发生变化（中心点的 xyz 均不变）
即
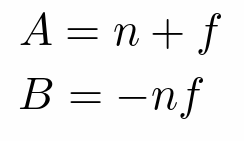
更确切的说 n=zNear; f=zFar 即最近/远可见距离

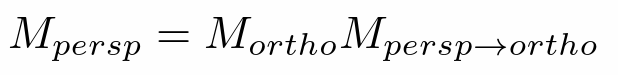
压缩+正交

Eigen::Matrix4f projection;

    Eigen:: Matrix4f persp_to_ortho;
    persp_to_ortho << zNear, 0, 0, 0,
                      0, zNear, 0, 0,
                      0, 0, zNear + zFar, -zNear * zFar,
                      0, 0, 1, 0;
    Eigen::Matrix4f ortho;
    float top = zNear * tan(eye_fov / 2 / 180 * MY_PI);
    float right = top * aspect_ratio;
    ortho << 1 / right, 0, 0, 0,
             0, 1 / top, 0, 0,
             0, 0, 2 / (zNear - zFar), 0,
             0, 0, 0, 1;
    projection = ortho * persp_to_ortho;

透视除法¶

经过投影变化将点投射到了标准正方体，现在还需要将三维空间中的点映射到二维屏幕，得到归一化设备坐标（NDC）
如果有一个齐次坐标点 P (x, y, z, w)，透视除法后的坐标为 (x/w, y/w, z/w)。这个新的点现在位于归一化设备坐标系内，其值通常限制在-1 到 1 之间。
透视除法是透视投影不可分割的一部分，它确保了远处的物体在屏幕上呈现得更小，近处的物体呈现得更大，从而创造了深度感。

透视矫正插值¶

通常直接在三角形顶点之间对像素属性（如 uv、颜色、法线等）直接做线性插值
但是在透视投影的 3D 场景下这种直接线性插值是错误的。
- 之前的透视投影算法中计算质心坐标时，用到的点已经是屏幕坐标系下的表示了，插值运算在这个时候不会考虑近大远小。首先绘制ABC，通过插值得到屏幕上AB的中点N，和屏幕上AC的中点P，同理在绘制ACD时得到M。此时，算法得到的中点是屏幕上线段AC的中点P，如图中紫色线所示。
- 产生问题的主要原因是：通过屏幕坐标来计算质心坐标
  
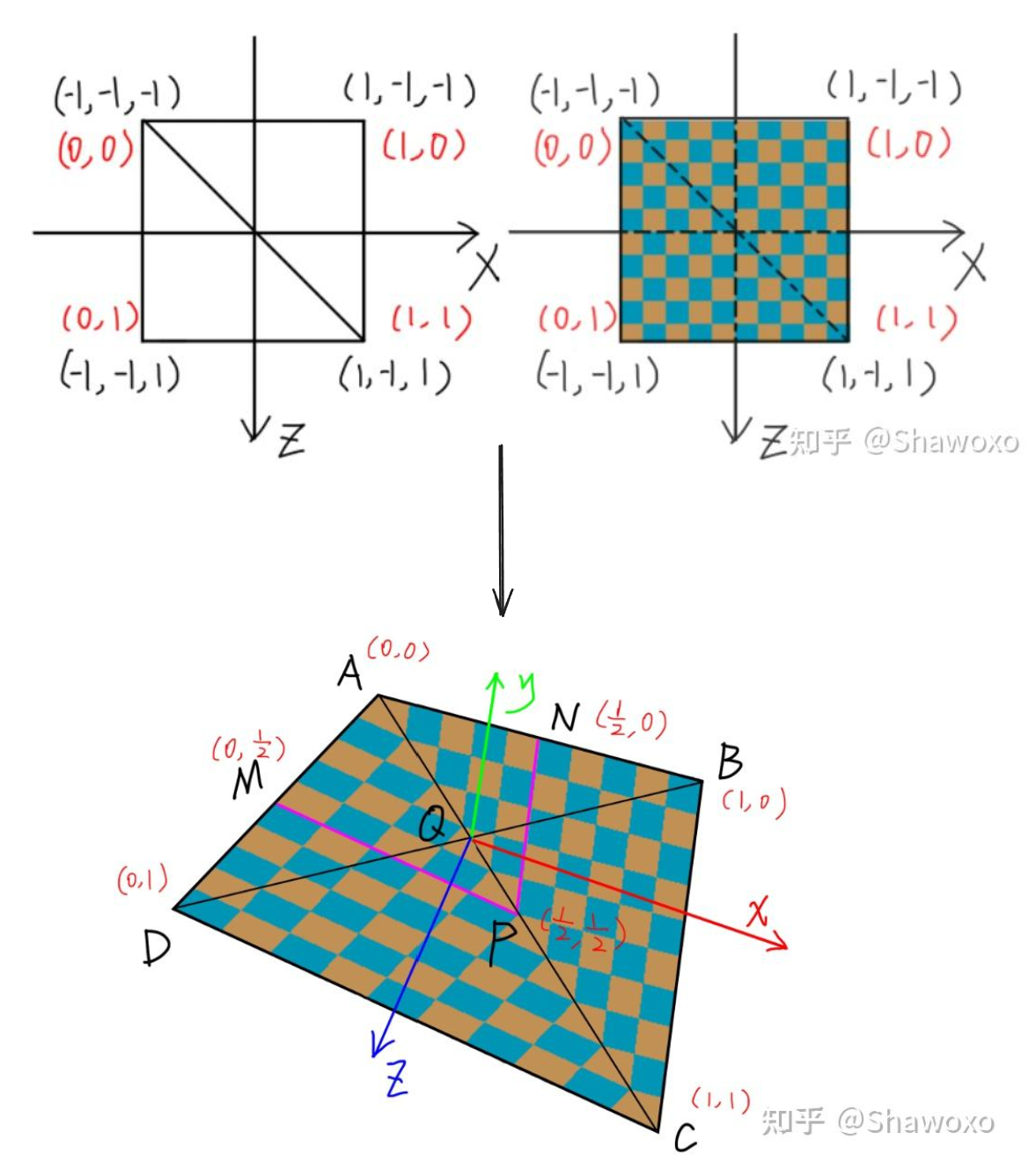
  图中纹理的映射就出现了明显的错误，纹理的中心点 P 应该出现在对角线加点 Q 处
透视矫正插值就是为了对属性插值过程进行矫正，保证插值结果符合实际空间中透视投影的规律
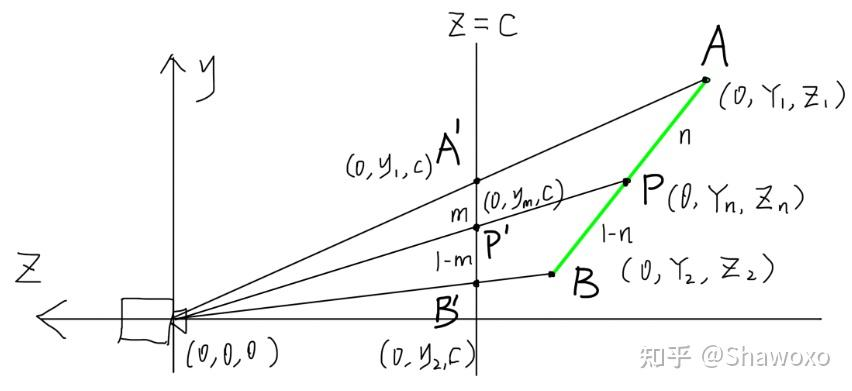
如图所示一个简单的 2 D 上的透视投影，上面 uv 计算出现问题就是因为使用 \(A'B'P'\) 直接计算比例对 UV 进行映射，而真正要使用的则是 \(ABP\)
- 要解决的问题：已知 \(P^{\prime}=(1-m)A^{\prime}+mB^{\prime}\) 要得到 \(P=(1-n)A+nB\)
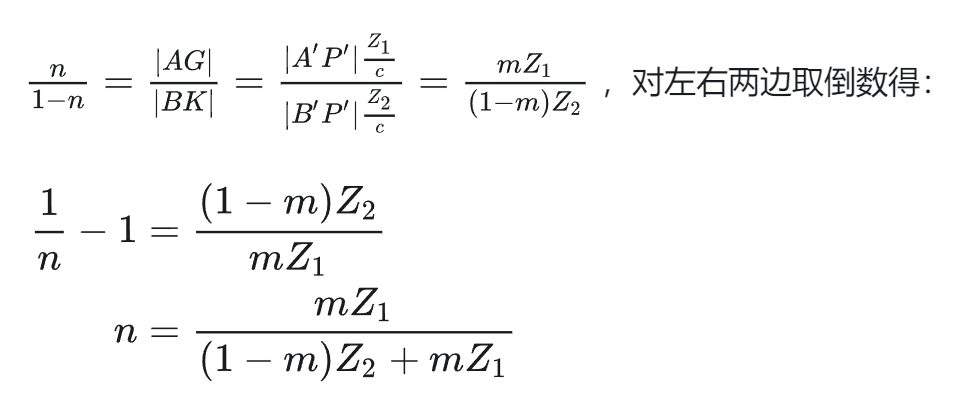
- 接下来吧 \(AB\) 替换为要插值的参数，就可以计算得到插值结果了
进一步扩展到三维 \(Z_n=\frac1{\frac{1-u-v}{Z_1}+\frac u{Z_2}+\frac v{Z_3}}\)