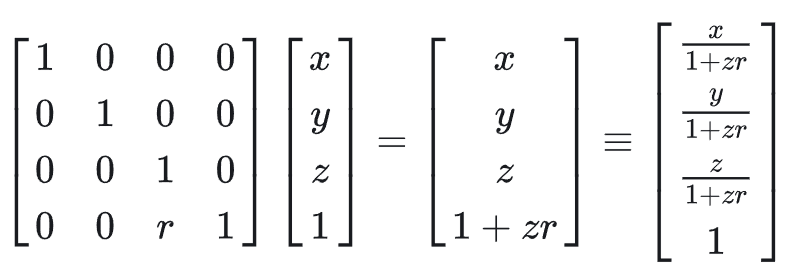Tinyrender
1-线条绘制(DDA)¶
void line(int x0, int y0, int x1, int y1, TGAImage &image, TGAColor color) {
int dx = abs(x1-x0),dy=abs(y1-y0);
if(dx>dy){
if(x0>x1) {
std::swap(x0, x1);
std::swap(y0, y1);
}
for (int x=x0; x<=x1; x++) {
float t = (x-x0)/(float)(x1-x0);
int y = y0*(1.-t) + y1*t;
image.set(x, y, color);
}
}
else{
if(y0>y1) {
std::swap(x0, x1);
std::swap(y0, y1);
}
for (int y=y0; y<=y1; y++) {
float t = (y-y0)/(float)(y1-y0);
int x = x0*(1.-t) + x1*t;
image.set(x, y, color);
}
}
}
 - obj 格式
-
- obj 格式
- v 0.608654 -0.568839 -0.416318 表示点的坐标
- f 1193/1240/1193 1180/1227/1180 1179/1226/1179 表示三角形(1193,1180, 1179 三个点组成)
2-三角形光栅化¶
- 扫描线方法:逐行扫描
- 缺点:单线程老方法
void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { std::vector<Vec2i> points={t0,t1,t2}; sort(points.begin(),points.end(),[](Vec2i a,Vec2i b){return a.y<b.y;}); for(int i=points[0].y;i<=points[1].y;i++) { int left=points[0].x+(points[1].x-points[0].x)*(i-points[0].y)/(points[1].y-points[0].y); int right=points[0].x+(points[2].x-points[0].x)*(i-points[0].y)/(points[2].y-points[0].y); if(left>right)std::swap(left,right); for(int j=left;j<=right;j++) { image.set(j,i,color); } } for(int i=points[1].y+1;i<=points[2].y;i++) { int left=points[1].x+(points[2].x-points[1].x)*(i-points[1].y)/(points[2].y-points[1].y); int right=points[0].x+(points[2].x-points[0].x)*(i-points[0].y)/(points[2].y-points[0].y); if(left>right)std::swap(left,right); for(int j=left;j<=right;j++) { image.set(j,i,color); } } }
- 缺点:单线程老方法
- 包围盒算法,判断点是否在三角形内部
- 这里使用质心坐标法(而不是通过叉积进行判断)
- \(P=(1-u-v)A+uB+vC\) (对于三角形内的点 u, v, 1-u-v 均大于 0)
- \(P=A+uAB+vAC\to uAB+vAC+PA=0\)
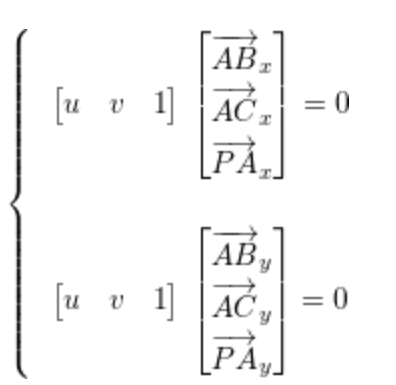
- 本质上就是求解这个方程组(之后得到 uv 判断是否大于零,进而判断是否在三角形内部)对于三维点也是一样的,因为两个方程就能解出两个量了
- 求解方程就是找一条直线与(ABx,ACx,PAx) and (ABy,ACy,PAy)垂直,这可以通过一次叉积解决
//求三角形的重心坐标 Vec3f barycentric(Vec2i *pts, Vec2i P) { Vec3f u = Vec3f(pts[2][0]-pts[0][0], pts[1][0]-pts[0][0], pts[0][0]-P[0]) ^ Vec3f(pts[2][1]-pts[0][1], pts[1][1]-pts[0][1], pts[0][1]-P[1]); if (std::abs(u.z)<1) return Vec3f(-1,1,1); return Vec3f(1.f-(u.x+u.y)/u.z, u.y/u.z, u.x/u.z); } //包围盒绘制三角形 void triangle(Vec2i t0, Vec2i t1, Vec2i t2, TGAImage &image, TGAColor color) { int minx = std::max(0,std::min(t0.x, std::min(t1.x, t2.x))); int maxx = std::min(image.get_width()-1,std::max(t0.x, std::max(t1.x, t2.x))); int miny = std::max(0,std::min(t0.y, std::min(t1.y, t2.y))); int maxy = std::min(image.get_height()-1,std::max(t0.y, std::max(t1.y, t2.y))); for(int i=minx;i<=maxx;i++){ for(int j=miny;j<=maxy;j++){ Vec3f bc_screen = barycentric(&t0, Vec2i(i,j)); if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue; image.set(i, j, color); } } }
- 稍作修改可以得到 3 f 版本
3-深度缓冲¶
//zBuffer单例类
class zBuffer {
private:
zBuffer(int width, int height) {
this->width = width;
this->height = height;
buffer = new float[width*height];
for(int i=0;i<width*height;i++){
buffer[i] = -std::numeric_limits<float>::max();
}
}
~zBuffer() {
delete [] buffer;
}
public:
int width, height;
float *buffer;
static zBuffer* getInstance(int width, int height) {
static zBuffer instance(width, height);
return &instance;
}
bool test(int x, int y, float z) {
if(x<0||x>=width||y<0||y>=height) return false;
if(z>buffer[y*width+x]) {
buffer[y*width+x] = z;
return true;
}
return false;
}
};
4-投影与 mvp 矩阵¶
- 正交投影就是从-1~1 的立方体映射到二维平面上
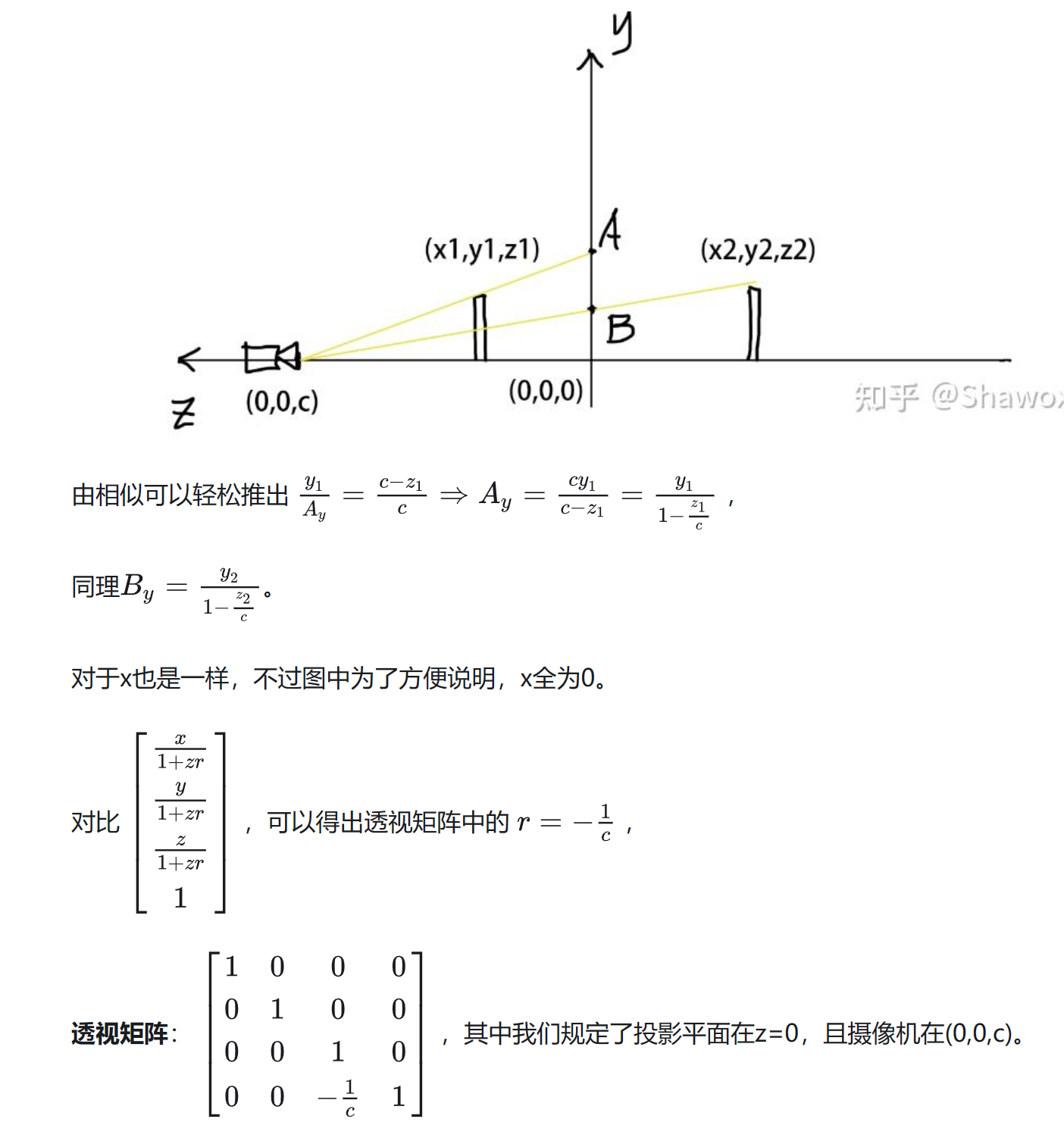
Vec3f world2screen(Vec3f v) { return Vec3f(int((v.x+1.)*width/2.+.5), int((v.y+1.)*height/2.+.5), v.z); } - 透视投影(另一种透视思路,不是压缩透视为正交)
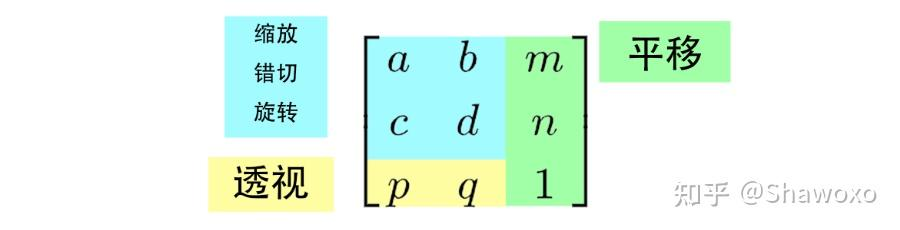
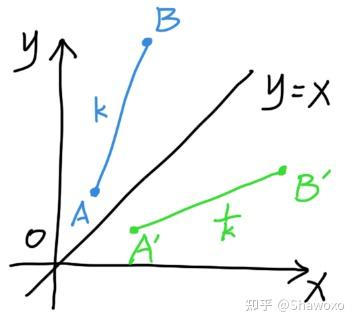
- 左下角区域可以进行一种
透视操作 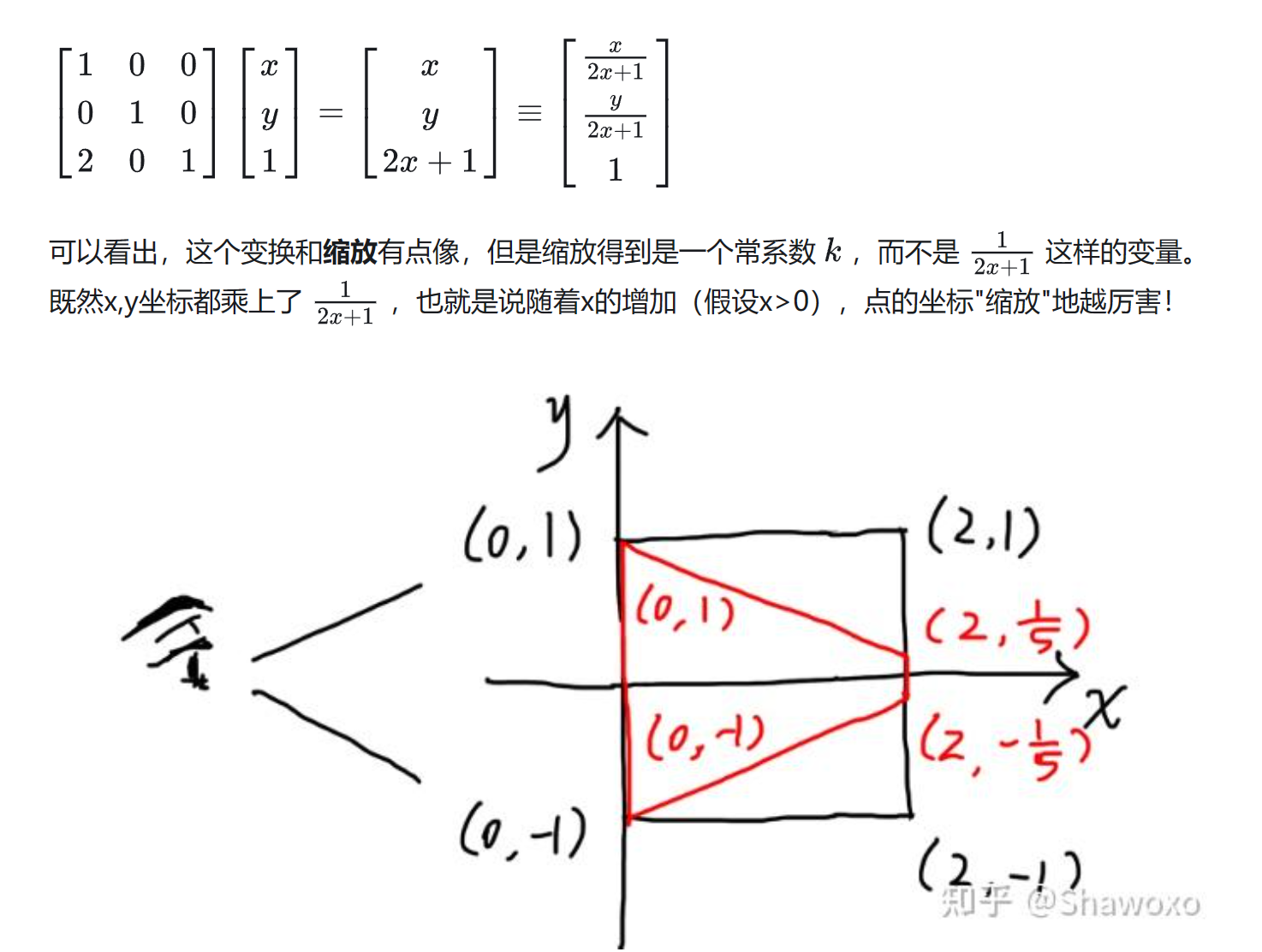
- 因此,可以定义一种新的操作:透视
5-摄像机旋转¶
- 将摄像机旋转转化为物体的旋转
- 对于平移以及旋转操作,只需要将摄像机的运动转化为物体的反方向运动
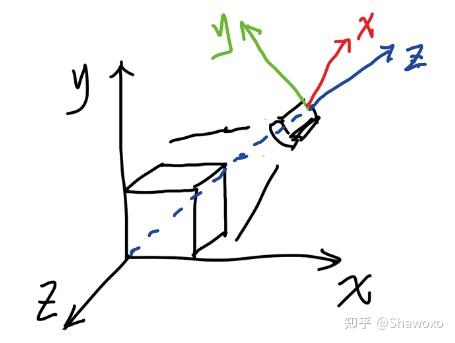
- 摄像机旋转之后的 z 轴实际上就是摄像机和物体之间的连线方向
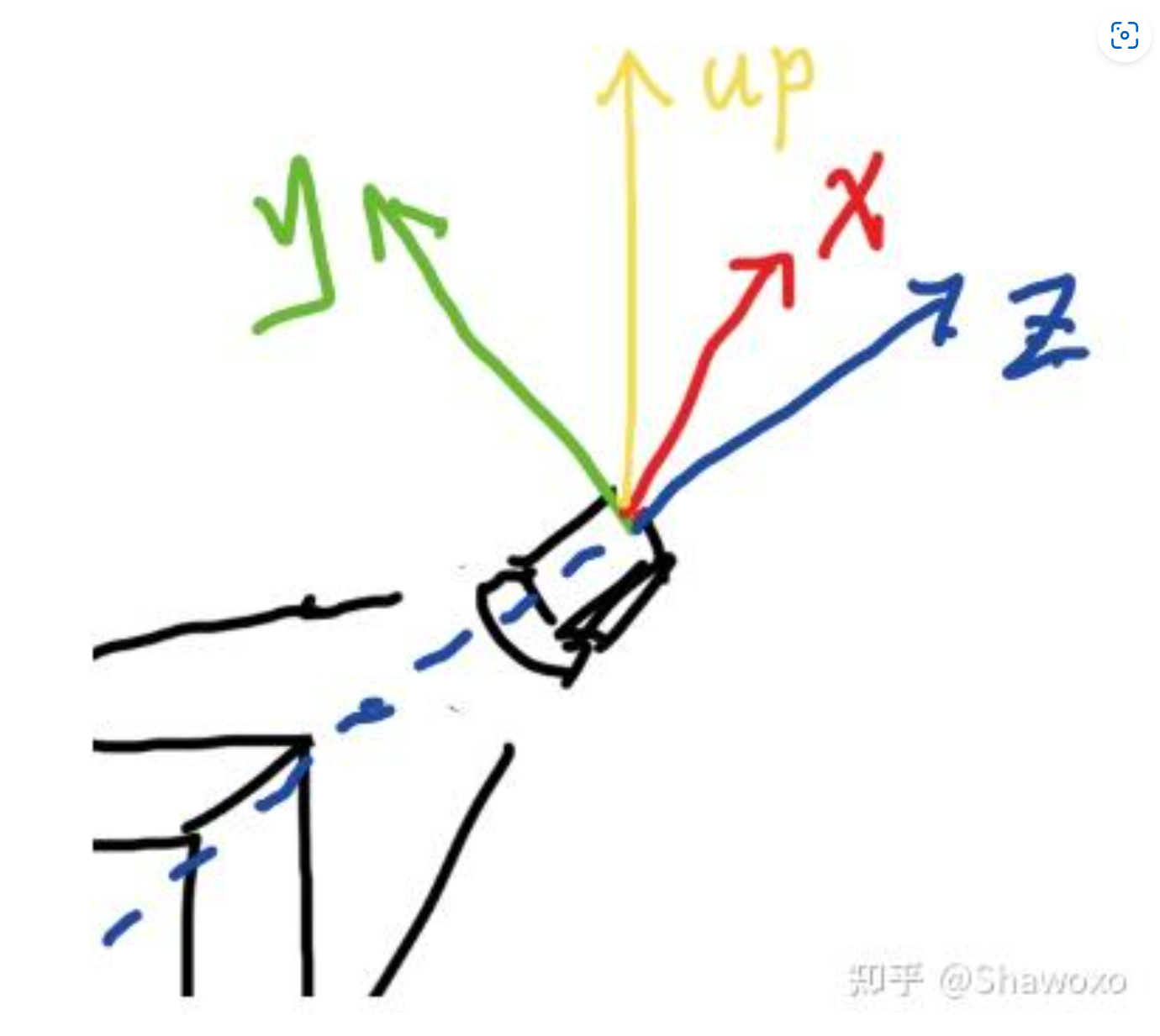
- 此外还定义一个 up 方向,这样就可以完全确定新坐标系
- \(up\times z=x\),\(z\times x=y\)

void lookat(Vec3f eye, Vec3f center, Vec3f up) { Vec3f z = (eye-center).normalize(); Vec3f x = cross(up,z).normalize(); Vec3f y = cross(z,x).normalize(); Matrix Minv = Matrix::identity(); Matrix Tr = Matrix::identity(); for (int i=0; i<3; i++) { Minv[0][i] = x[i]; Minv[1][i] = y[i]; Minv[2][i] = z[i]; Tr[i][3] = -eye[i]; } ModelView = Minv*Tr; }- 视口变换:从-1~1 立方体转化到屏幕空间 (x~x+w; y~y+h)
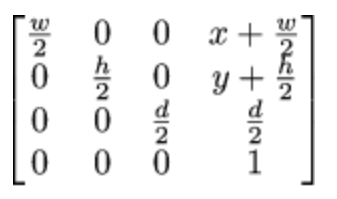
Matrix Viewport(int x, int y, int w, int h, int depth) { Matrix m = Matrix::identity(4); m[0][3] = x+w/2.f; m[1][3] = y+h/2.f; m[2][3] = depth/2.f; m[0][0] = w/2.f; m[1][1] = h/2.f; m[2][2] = depth/2.f; return m; }
法线变换¶
- 常用于处理光照
- 直接对法线向量应用相同的仿射变换并不会保留它们与表面的垂直关系。这是因为仿射变换可能包括拉伸(缩放)和扭曲(倾斜),这些变换会改变原始形状的角度和比例,从而破坏了法线与表面的垂直关系。
- 正确方法:使用原始仿射变换矩阵的逆矩阵的转置来变换法线向量。
- 用 ABC 表示法向量,xyz 平面上任意一点,因此有
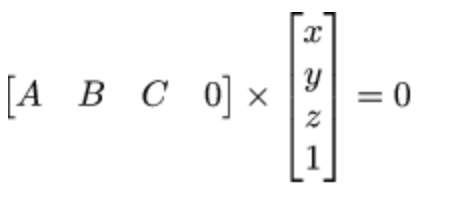
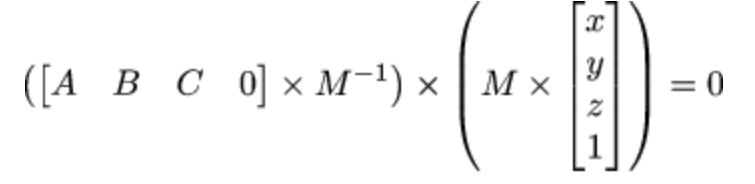
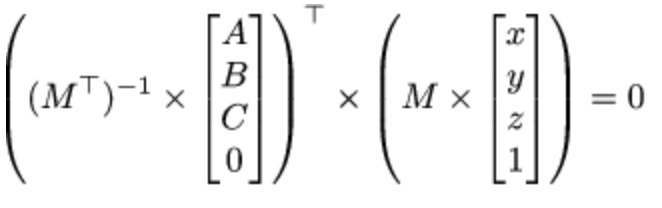
- 由此得知应该进行一次逆仿射变换
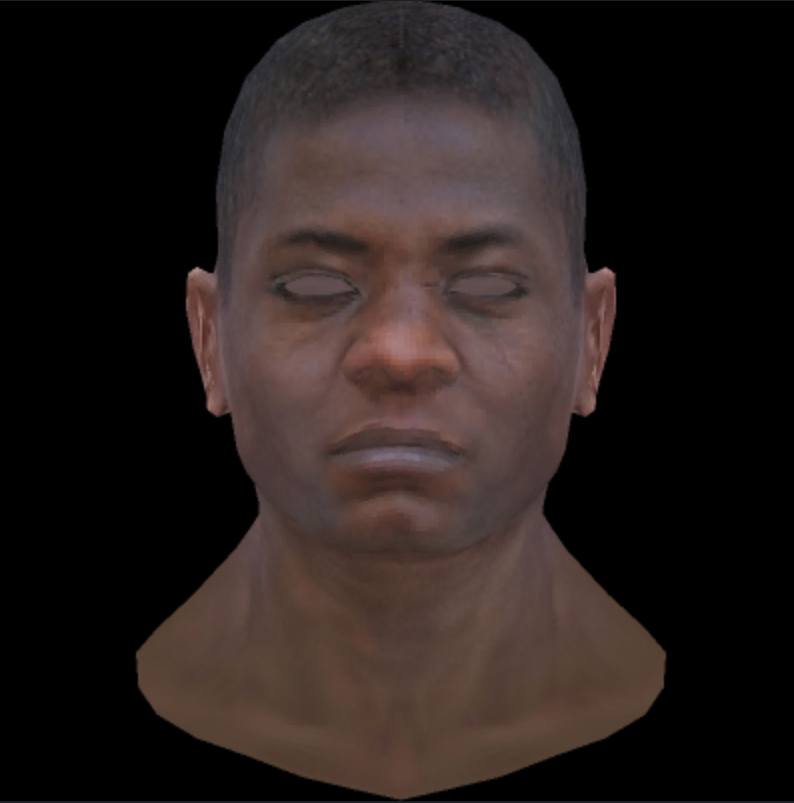
6-着色 Shader¶
- 着色器接口
struct IShader { virtual ~IShader(); virtual Vec3i vertex(int iface, int nthvert) = 0; virtual bool fragment(Vec3f bar, TGAColor &color) = 0; }; - 顶点着色器:转换顶点坐标(mvp),并为片段着色器准备数据。(如法线,用于处理光照)
- 面着色器:对三角形内的像素进行具体着色
struct GouraudShader : public IShader { //存储三个点的法向量 Vec3f varying_intensity; Vec3f vertex(int iface, int nthvert) override { varying_intensity[nthvert] = std::max(0.f, model->normal(iface, nthvert)*light_dir); Vec3f gl_Vertex = model->vert(iface, nthvert); return m2v(ModelView*v2m(gl_Vertex)); } bool fragment(Vec3f bar, TGAColor &color) override { float intensity = varying_intensity*bar; color = Vec3f(255,255,255)*intensity; return false; } }; - 由于遍历顺序是,枚举每一个面,然后对面上的点进行处理,最后对面进行渲染,因此在点着色时一方面进行了坐标变化,另一方面收集了法向量,用于之后的插值
- 在面渲染阶段使用法向量结合重心坐标进行插值计算。
- 面渲染器的返回值可以用于在光栅化渲染时跳过一些绘图
TGAColor color; bool discard = shader.fragment(c, color); if (!discard) { zbuffer.set(P.x, P.y, TGAColor(P.z)); image.set(P.x, P.y, color); } - phongshader 版本,使用法线贴图对每个点的反射进行具体计算
bool fragment(Vec3f bar, TGAColor &color, Vec3f p) override { Vec2f uv = varying_uv[0]*bar.x + varying_uv[1]*bar.y + varying_uv[2]*bar.z; Vec3f normal = m2v((ModelView).transpose()*v2m(model->normal(uv))).normalize(); Vec3f light = m2v(ModelView*v2m(light_dir)).normalize(); Vec3f see = (m2v(ModelView*v2m(camera))-m2v(ModelView*v2m(p))).normalize(); Vec3f mid = (light+see).normalize(); float dis = (m2v(ModelView*v2m(p))-m2v(ModelView*v2m(camera))).norm()/100; float attenuation = 100.0 / (0.5 * dis + 0.1 * dis * dis); Vec3f ambient = Vec3f(1.2, 1.2, 1.2); Vec3f diffuse = Vec3f(1, 1, 1)*std::max(0.f, normal*mid)*attenuation; Vec3f specular = Vec3f(0.2, 0.2, 0.2)*pow(std::max(0.f, normal*mid), 50)*attenuation; Vec3f result = ambient+diffuse+specular; TGAColor c = model->diffuse(uv); color = TGAColor(std::min(255.f,c[2]*result[2]), std::min(255.f,c[1]*result[1]), std::min(255.f,c[0]*result[0])); return false; }
6-2 切线贴图映射 Darboux¶
- 全局坐标系 (Global Frame):
- 在全局坐标系中,纹理的坐标是直接映射到3D世界空间中的坐标系上的。例如,一个法线贴图中的法线向量直接对应到全局空间中的方向。这意味着纹理是独立于模型表面的方向和位置的。
- 全局坐标系下的法线贴图不依赖于模型表面的局部属性,因此,它可能在模型的不同部位重复使用时出现不连贯的情况,尤其是在模型拥有复杂的几何形状和多个面时。
-
达布桑坐标系 (Darboux Frame):
- 达布桑坐标系,也被称为切线空间(Tangent Space),是一种依赖于模型表面的局部坐标系。在这个坐标系中,纹理坐标是相对于模型表面上某一点的局部坐标系定义的。法线贴图通常存储在这个坐标系中,因此它们表示的法线是相对于表面局部区域的。
- 使用达布桑坐标系的好处是,即使模型在空间中旋转或者变形,纹理(尤其是法线贴图)仍然可以正确地表现模型表面的局部细节。这使得法线贴图可以更加灵活地应用于复杂的几何体,并在视觉上保持一致性。
- 此外,还能在运动时保持正确切线方向(如张嘴)
- 并且也可以减少一部分贴图,如只给出一只手臂,另一只对称计算
- 法线贴图中存储的是切线空间下的一个向量,使用 RGB 三个通道来存储
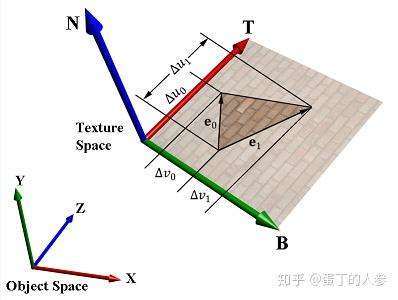
-
切线空间:TBN 变换
- 切线 T:纹理坐标 U 方向的单位向量
- 副切线 B:副切线与切线和模型表面的法线向量都正交,定义为沿着模型表面纹理坐标的 V 方向的单位向量
- 切线空间是一个以模型表面上某点的法线为 Z 轴,切线为 X 轴,副切线为 Y 轴的局部坐标系。在这个空间中,表面的局部细节(如法线贴图中的凹凸)可以被独立于模型整体位置和方向的方式描述。
- 思想:把 uv 看做等高线

- 计算过程
7-(硬)阴影 shadowmap¶
- 先从光源位置看,看哪些部分可以被点亮,哪些部分会被隐藏起来
- 使用类似 zbuffer 的系统
- 对 pongshader 的修改
struct PhongShader : public IShader { Vec2f varying_uv[3]; Vec3f sb_p[3]; Vec3f vertex(int iface, int nthvert) override { varying_uv[nthvert] = model->uv(iface, nthvert); Vec3f gl_Vertex = model->vert(iface, nthvert); sb_p[nthvert] = gl_Vertex; return m2v(ModelView*v2m(gl_Vertex)); } bool fragment(Vec3f bar, TGAColor &color, Vec3f p) override { Vec3f shadowp = m2v(ShadowView*v2m(sb_p[0]*bar.x + sb_p[1]*bar.y + sb_p[2]*bar.z)); float shadowdeep = shadowBuffer.getdeep(shadowp.x, shadowp.y); float shadow_deffuse = 0.7+.3*(shadowdeep<shadowp.z+43.34); float shadow_reflect = .3+.7*(shadowdeep<shadowp.z+43.34); Vec2f uv = varying_uv[0]*bar.x + varying_uv[1]*bar.y + varying_uv[2]*bar.z; Vec3f normal = m2v((ModelView).transpose()*v2m(model->normal(uv))).normalize(); Vec3f light = m2v(ModelView*v2m(light_p)).normalize(); Vec3f see = (m2v(ModelView*v2m(camera))-m2v(ModelView*v2m(p))).normalize(); Vec3f mid = (light+see).normalize(); float dis = (m2v(ModelView*v2m(p))-m2v(ModelView*v2m(camera))).norm()/100; float attenuation = 300.0 / (0.5 * dis + 0.1 * dis * dis); Vec3f ambient = Vec3f(0.8, 0.8, 0.8); Vec3f diffuse = Vec3f(1, 1, 1)*std::max(0.f, normal*mid)*attenuation; Vec3f specular = Vec3f(0.3, 0.3, 0.3)*pow(std::max(0.f, normal*mid), model->specular(uv))*attenuation; Vec3f result = ambient*shadow_deffuse+(diffuse+specular)*shadow_reflect; TGAColor c = model->diffuse(uv); color = TGAColor(std::min(255.f,c[2]*result[2]), std::min(255.f,c[1]*result[1]), std::min(255.f,c[0]*result[0])); return false; } }; - 效果展示

扩展¶
抗锯齿¶
- 使用 ssaa 4
class zBuffer { private: int width, height; Vec3f *frameBuffer; float *deepBuffer; zBuffer(int width, int height) { this->width = width; this->height = height; frameBuffer = new Vec3f[width*height*4]; deepBuffer = new float[width*height*4]; for(int i=0;i<width*height*4;i++) { frameBuffer[i] = Vec3f(0,0,0); deepBuffer[i] = -std::numeric_limits<float>::max(); } } ~zBuffer() { delete [] frameBuffer; delete [] deepBuffer; } public: static zBuffer* getInstance(int width=0, int height=0) { static zBuffer instance(width, height); return &instance; } bool test(int x, int y, int i, float z, Vec3f color) { if(x<0||x>=width||y<0||y>=height) return false; if(z>deepBuffer[y*width*4+x*4+i]) { deepBuffer[y*width*4+x*4+i] = z; frameBuffer[y*width*4+x*4+i] = color; return true; } return false; } float getdeep(int x, int y) { float res=-std::numeric_limits<float>::max(); for(int i=0;i<4;i++) { res = std::max(res, deepBuffer[y*width*4+x*4+i]); } return res; } Vec3f getcolor(int x, int y) { Vec3f res(0,0,0); for(int i=0;i<4;i++) { res = res + frameBuffer[y*width*4+x*4+i]; } return res; } }; class SSAA4 { std::vector<Vec3f> spts; public: SSAA4(float x, float y, float z) { spts.emplace_back(x+0.25f, y+0.25f, z); spts.emplace_back(x+0.75f, y+0.25f, z); spts.emplace_back(x+0.25f, y+0.75f, z); spts.emplace_back(x+0.75f, y+0.75f, z); //spts.emplace_back(x,y,z); } void cal(Vec3f *pts, Vec2i *uvs, Model*model,TGAImage&image) { Vec3f colorAccumulator; int num=0; for(int i=0;i<spts.size();i++) { Vec3f a = spts[i]; Vec3f bc_screen = barycentric(pts, a); if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue; a.z = 0; Vec2i uv; for (int j=0; j<3; j++) { a.z += pts[j][2]*bc_screen[j]; uv = uv + uvs[j]*bc_screen[j]; } TGAColor color = model->diffuse(uv); zBuffer::getInstance()->test(a.x,a.y,i,a.z,Vec3f(color.r/4.f, color.g/4.f, color.b/4.f)); } } }; - 分为对 buffer 的修改和 ssaa 实现
- 将像素一分四处理,最终渲染时取颜色平均值
- 与 mxaa 区别:mxaa 是对一个点的颜色深浅进行调整,而 ssaa 则则真正拆分为四个像素,取平均值
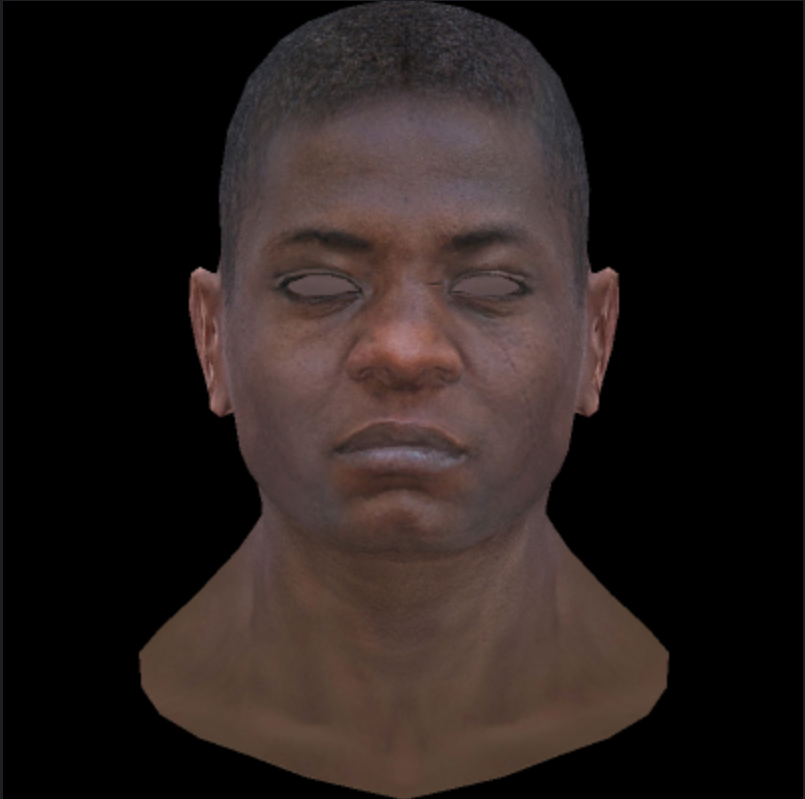
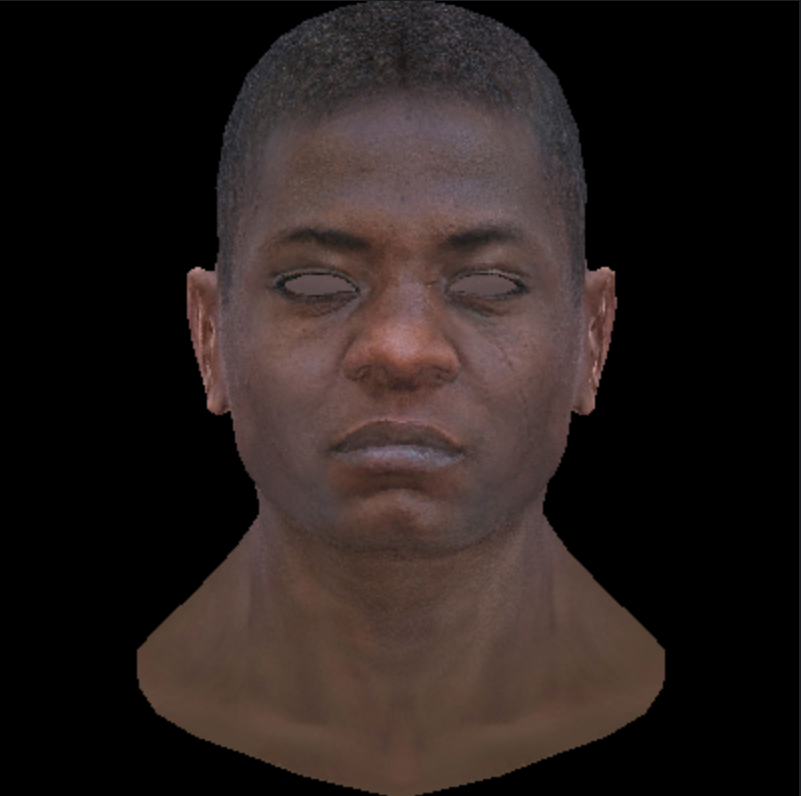
贴图¶
- 双线性插值
//双线性插值 TGAColor bilerp(Vec2f uv, Model*model) { float x0=floor(uv.x), y0=floor(uv.y), x1=x0+1, y1=y0+1; float u=uv.x-x0, v=uv.y-y0; TGAColor c00 = model->diffuse(Vec2i(x0, y0)); TGAColor c01 = model->diffuse(Vec2i(x0, y1)); TGAColor c10 = model->diffuse(Vec2i(x1, y0)); TGAColor c11 = model->diffuse(Vec2i(x1, y1)); Vec3f color = Vec3f(c00.r*(1-u)*(1-v) + c01.r*(1-u)*v + c10.r*u*(1-v) + c11.r*u*v, c00.g*(1-u)*(1-v) + c01.g*(1-u)*v + c10.g*u*(1-v) + c11.g*u*v, c00.b*(1-u)*(1-v) + c01.b*(1-u)*v + c10.b*u*(1-v) + c11.b*u*v); return color; }